第五章 图
建筑图学课件 第五章 立体的阴影(建筑细部的阴影)
门洞的阴影
a’0
1.分别求雨蓬阴 线ED、DC、AB、 BC的落影 2.求门洞上阴线 的落影 3.为落影上色
门洞的阴影
1.分别求雨蓬阴线AB、 BC、ED、DC的落影
2.分别求左、右门柱 阴线的落影 3.为阴面和落影上色
门洞的阴影
1.分别求雨蓬阴线CD、DE、AB、BC的落影 2.分别求左、右门柱阴线的落影 3.为落影上色
c’
平行
返回光线
门洞的阴影
平行
廊柱
1.分别求雨蓬阴线ED、 DC、AB、BC的落影 2.分别求门洞和左、 右门柱阴线的落影 3.为落影上色
带有不同挡墙的台阶阴影的比较
(b)
(a)
矩形挡墙台阶的阴影
斜挡墙台阶的阴影
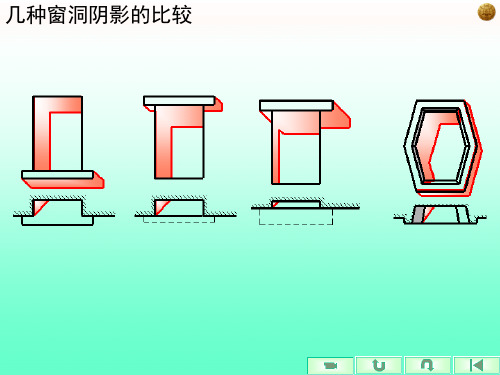
几种窗洞阴影的比较
带窗台的窗洞的落影
B
C
A
求窗台的影线 求窗洞的影线 给落影上色
带遮阳板的窗洞的落影
C
A
D
求遮阳板的影线 求窗洞的影线 给落影上色
B
带遮阳板的窗洞的落影
A
B
求遮阳板的影线 求窗洞的影线 给落影上色
六棱窗洞的落影
1.求六棱形窗套在墙 面上的影线
求点B的落影 根据平面平行线的落影 规律求其他点的落影
2.求六棱形窗套在窗洞 内的影线
3.给阴面和落影上色
c’
圆形的 落影 2.求圆形窗洞阴影的 H投影
阴线
带有窗套的圆形窗洞的阴影
1. 几种门洞阴影的比较
(a)
(b)
(c)
(e) (d)
门洞的阴影
1.分别求雨蓬阴线AB、 BC、CD、DE的落影 2.为落影上色
第五章 轴测图

轴测图
四、轴测图分类
正轴测图 轴测图 正等轴测图 S垂直于P 正二轴测图 正三轴测图 p=q=r p=rq pqr
斜轴测图
斜等轴测图 p = q = r 斜二轴测图 S倾斜于P p = r q 斜三轴测图 p q r
正等轴测图
正二轴测图
斜二轴测图
轴测图有两种表示方法:线条图和具有真 实感的图形(图像)。
(d)将中心后移H/2,并以D2为 直径画圆,得后端面的斜二测图
穿孔圆锥台的斜二轴测图
H/2
(d)将中心后移H/2,并以D2为 直径画圆,得后端面的斜二测图
穿孔圆锥台的斜二轴测图
(e)作前、后端面圆的公切线,即 得圆锥台斜二测图
穿孔圆锥台的斜二轴测图
(f)擦去多余图线
穿孔圆锥台的斜二轴测图
(f)擦去多余图线
X
Y
步骤1
25
步骤2
Z
18
Z 10
Z
25
8
16 Y 36 O O X 20 X O
X
16 Y
O
Y
完成
18 10
25
8
36
20
16
切割法
z
例7-3求作三面投影 图 所示的正等测 图
x x
c`
z1
o o
o1
y
y1 x1
切割法
z
例7-3求作三面投影 图 所示的正等测 图
x x
c`
z1
o o
o1
y
y1 x1
Y1
轴向伸缩系数:p= r=0.94 q=0.47
例4-8 穿孔圆锥台的 斜二轴测图
(a) 已知
穿孔圆锥台的斜二轴测图
数电第5章

第五章 触 发 器
图 5 – 7 由与非门构成的基本RS触发器
第五章 触 发 器
1. 功能描述 (1) 当Rd=1, Sd=0时,不管触发器原来处于什么状态, 其次态一定为“1”,即Qn+1=1,故触发器处于置位状态。 (2) 当Rd=0, Sd=1时,Qn+1=0,触发器处于复位状态。 (3) 当Rd=Sd=1 时,触发器状态不变,处于维持状态, 即Qn+1=Qn。 (4) 当Rd=Sd=0 时,Qn+1=Q n+1=1,破坏了触发器的正常 工作,使触发器失效。而且当输入条件同时消失时,触发 器是“0”态还是“1”态是不定的,这种情况在触发器工作 时是不允许出现的。因此使用这种触发器时, 禁止 Rd=Sd=0出现。
发生的。这种电路中没有统一的时钟脉冲。任何输入信
号的变化都可能立刻引起异步时序电路状态的变依从关系来分,又可分为米里 (Mealy)型和莫尔(Moore)型两类。米里型电路的输出是输 入变量及现态的函数,即
F (t ) f [ x(t ),Qn (t )]
器和JK触发器。在基本RS触发器的基础上, 加两个与非
门即可构成钟控RS触发器, 如图 5-10 所示。
第五章 触 发 器
图 5 – 10 钟控RS触发器
第五章 触 发 器
1. 功能描述 当CP=0时,触发器不工作,此时C、D门输出均为 1, 基本RS触发器处于保持态。此时无论R、S如何变化,均 不会改变C、D门的输出,故对状态无影响。 当CP=1 时,触发器工作,其逻辑功能如下: R=0, S=1, Qn+1=1,触发器置“1”; R=1, S=0, Q n+1=0,触发器置“0”; R=S=0, Qn+1=Qn,触发器状态不变; R=S=1, 触发器失效,工作时不允许。
地图与测量第五章地形图及其应

地图比例尺 1:1万 1:2.5万 1:5万 1:10万
方里网间隔 10厘米 4厘米 2厘米 2厘米 .
相应实地长 1公里 1公里 1公里 2公里
坐标系与方里网
在1:1万---1:10万地形图上,只在内外 图廓间绘有间隔为1分的经、纬度刻划线, 称为分度带,不在图幅内绘制经纬网格。
1:25及1:50万地形图只绘经纬网,其间 隔见下表
118 o 120
122
20带
21带
120o 30
117
123
每幅1: 100万 图幅范 围内各 种比例 尺地形 图需绘 邻带方 里网的 图幅
经 差 7.5分 内 的 1: 1万 图 绘西边邻带方里网
经 差 7.5分 内 的 1: 2.5万 图 绘东边邻带方里网
经 差 3 0 分 内 的 1 : 1 0.万 、 1 : 5 万 、 1: 2.5万 图 绘 东 边 邻 带 方 里 网
.
第五章 地形图和普通地图
第二节 地形图的数学基础
一、高斯----克吕格投影 由于地球是一个接近于椭球的不规则形体,无法用数学 公式表示,这给地面点的精确定位造成困难,人们构造 了一个非常接近地球的形体——旋转椭球体来表示地球, 可以用数学公式表示,但它与地球一样不可无变形地展 在平面上。地图学中,通过选择可展的过渡面(圆柱面、 圆锥面、平面),使它们与旋转椭球体相切或相割,再 设定投影的变形条件(等积、等距、等角、任意),从 而建立了从椭球面到平面的数学关系——地图投影。
我国规定:每个投影带西边缘 30分以内及东边缘7.5分(1: 2.5万)、15分(1:5万)以 内的图幅,加绘邻带方里网。 即西带方里网延伸到东带30 分内,中央经线以东应该投 影到经差3度30分。
银行从业资格证——第五章 存款业务思维导图

第五章 存款业务个人存款业务个人存款的概念居民个人将闲置不用的货币资金存入银行,并可以随时或按照约定时间支取存款的一种信用行为,是银行对存款人的负债。
活期存款概念一元起存不规定存款期限随时存取计息金额计息起点元,元以下角分不计利息利息金额算至分位,分以下尾数四舍五入。
分段计息算至厘位合计利息后分以下四舍五入活期存款每季度复利,其他种类不复利计息时间按季度计息,每季度月末的的20日为结息日(按结息日挂牌利率计息),次日付息一年按365天算,闰年按366天算计息方式(一般年利率为0.3%)积数计息法(银行多数使用其计算活期存款利息)利息=累计计息基数*日利率(累计计息基数=每日余额合计数)逐笔计息法(计算整存整取定期利息)整年月利息=本金*年数(月数)*年利率(月利息)有整年月又有零头天数利息=本金*年(月)利率*年数(月数)+本金*零头天数*日利率定期存款存款种类整存整取适合长期闲置资金整笔存入到期一次付清期存金额50元三个月(1.35%);六个月(1.55%);一年(1.75%);两年(2.10%);三年(2.75%);五年零存整取利率低整存整取的定期存款,高于活期存款每月存入固定金额到期一次支付本息起存金额5元一年(1.1%,与整存零取和存本取息利率相同);三年(1.3%,与整存零取和存本取息利率相同);五年整存零取本金可全部提前支取,不可部分支取;利息于期满结清时支付;利率高于活期存款整笔存入固定期限分期支取起存金额1000元存款日期分为一三五年;取款日期分为一三六个月一次存本取息本金可提前全部支取,不可部分;不可提前支取利息,可提后,但不复利整笔存入取息期到期一次性支付本金,分期支取利息起存金额5000元存期分为一三五年;可以一个月或几个月取息一次存款利率如变动,按照存单开户日的定期存款利率计息计息到期逾期除约定自动转存外,按支取日的活期存款利率计算利息提前支取部分按支取日挂牌公告的活期存款利率计息,支取部分的利息与本金一并支取其他种类的储蓄存款定活两便存款存期灵活开户时不约定存期一次存入本金随时可以支取银行根据客户存款的实际存钱规定计息利率优惠高于活期存款个人通知存款只提供一天七天通知储蓄存款两个品种5万起存开户时不约定存期预先确定品种支取时只要提前一定时间通知银行教育储蓄存款特点存期灵活属于零存整取存;分一年、三年和六年;提前支取必须全额支取利率优惠一年期三年期按照整存整取定期存款利率计息六年期按开户日五年期整存整取定期存款利率计息储户特定在校小学四年级和四年级以上学生总额控制本金合计最高2万元分次存入,到期一次支取本金和利息起存金额50元保证金存款解决自费出国、留学的费用个人存款业务的管理要求业务的内部控制制度业务管理办法业务操作规程财务核算办法储蓄存款业务授权制度岗位责任制度主要风险操作风险单位存款业务概念机关、团体、部队、企业、事业单位、其他组织、个体工商户分类(支取方式)单位活期存款基本存款账户主办账户办理日常转账结算和现金收付一家商业银行一个一般存款账户借款或其他结算需求基本户所在银行的其他银行开立的银行结算账户办理现金缴存、但不办理现金支取专用存款账户存款人对其特定用处的资金进行专项管理和使用而开立的银行结算账户(社保金)临时存款账户因临时需要并在规定期限内使用而开立(注册验资,设立临时机构,异地临时经营活动)不超过两年单位定期存款单位通知存款单位协定存款概念单位协定存款是一种单位类客户通过与商业银行签订合同的形式约定合同期限、确定结算账户需要保留的基本存款额度,对超过基本存款额度的存款按中国人民银行规定的上浮利率计付利息、对基本存款额度按活期存款利率付息的存款类型。
工程制图第5章组合体(付画图及作业参考)

3. 圆的直径
(1) 直径尺寸应在尺寸数字前加注符号“”。
(2) 尺寸线应通过圆心,其终端画成箭头。 (3) 整圆或大于半圆应注直径。
4. 圆弧半径
(1) 半径尺寸数字前加注符号“R ”。 (2) 半径尺寸必须注在投影为圆弧的图形上,
且尺寸线或其延长线应通过圆心。 (3) 小于或等于半圆的圆弧应注半径尺寸。
(二) 尺寸的组成
1. 尺寸的组成 2. 尺寸线终端的放大图 3. 尺寸界线 4. 尺寸线 5. 同一张图上,数字及箭头的大小应保持一致
1. 尺寸的组成
尺寸数字
数字高度约3.5毫米
箭头
尺寸界线 尺寸线
尺寸线间距大于7毫米 尺寸界线超出箭头约25毫米
尺寸的组成: (1) 尺寸界线(细实线) (2) 尺寸线(细实线) (3) 尺寸数字 (4) 尺寸终端
正垂线的投影
铅垂线的投影
侧垂线的投影
投影面平行面的投影具有实形性和积聚性
题目
正平面的投影
水平面的投影
侧平面的投影
垂直面和一般面的投影具有类似性
正垂面
侧垂面
铅垂面
一般面
三、组合体读图举 例
1.切割式组合体 2.切割、叠加式组合体
1.切割式组合体读图举例
由主、左视图,画侧视图。
分 析
尺寸线成为中心线的延长线 尺寸线与中心线重合 尺寸线与轮廓线重合
(1) 尺寸线不能用其它图线代替,一般也不得与其它图线重合或画在其延长线上。 (2) 标注线性尺寸时,尺寸线必须与所标注的线段平行。
5. 同一张图上,数字及箭头的大小应保持一致
数字与箭头太小
数字与箭头太大
数字要采用标准字体,且书写工整,不得潦草。在同一张 图上,数字及箭头的大小应保持一致。
第五章 第五节 函数y=A sin (ωx+φ)的图象 课件(共55张PPT)
)
C [因为|tan x|≥0, 所以当 x∈0,π2 时,cos x≥0,y≥0, 当 x∈π2 ,π 时,cos x≤0,y≤0.]
4.(必修
4P56
练习
T3
改编)已知函数
f(x)=2sin
π (3
x+φ)φ<π2
的图象
经过点(0,1),则该函数的振幅为________,周期 T 为________,频率为
A.向右平移π6 个单位长度 B.向右平移π3 个单位长度 C.向左平移π6 个单位长度 D.向左平移π3 个单位长度
A [因为 y=2sin 2x=2sin 2x+π6 -π3 ,所以将 y=2sin 2x 的图象向
π
π
右平移 6 个单位长度可得 y=2sin (2x- 3 )的图象.]
3.函数 y=cos x|tan x|0≤x≤π且x≠π2 的图象大致为(
坐上摩天轮,则第 7 分钟时他距地面大约为( )
A.75 米
B.85 米
C.100 米
D.110 米
B [设该人距地面高度与时间 t 的关系 f(t)=A sin (ωt+φ)+B(A>0,ω
>0,φ∈[0,2π)),由题意可知:A=50,B=110-50=60,T=2ωπ =21, 所以 ω=22π1 ,
________,初相 φ 为________. 解析: 振幅 A=2,T=2ππ =6,f=16 , 3
因为图象过点(0,1),所以 1=2sin φ,
所以 sin φ=12 ,又 φ <π2 ,所以 φ=π6 . 答案: 2;6;16 ;π6
5.函数 f(x)=2sin (ωx+φ)ω>0,-π2<φ<π2 的部分图象如图所示,则 ω=________,φ=________.
变电站电气主接线图
精心整理学习帮手精心整理学习帮手精心整理学习帮手精心整理学习帮手精心整理学习帮手精心整理学习帮手精心整理学习帮手精心整理学习帮手2×8MW(a)2×10MVA1G G1TG2G2T110KV 35KV2×8MW(b)20MVAG1G 2GG110KV2T2G(c)2×8MW2×10MVAG1G 1T G35KV精心整理 学习帮手TMY-100X8ZN21-10/1250配CD10ⅢLZZBJ-101000/5 0.5/10P 2×(ZR-YJV 22-6/3×240)RN2-6/0.5ASFWG8000-6/4950Ue=6.3kV Ie=916.45A COSφ=0.8LZX-10Q800/5 0.5/10PJ Y N 2-10-03(改)1G励磁变(厂家配套)励磁互感器(厂家配套)JDJ-6 36 0.1√3√J Y N 2-10-17J Y N 2-10-18RN2-6/0.5A 36 0.1 0.1JDZJ-63√√3J Y N 2-10-20√ 6 0.1 0.1√333JDZJ-6RN2-6/0.5AHY5WZ-10/302G同左ZN21-10/2500配CD10ⅢLFZJ-102000/5 0.5/0.5/10/10PJ Y N 2-10-03SF9-20000/110Y,d11121±3×2.5%/6.3kV U k %=10.5%LGJ-120GW4-110DW/630左接地LW25-1261250A,40kA GW4-110DW/630双接地LCWB 6-110100/50.2/0.5/10P/10PTYD-110/ -0.07H 3√LRD-60-B 50/5GW4-110DW/630双接地JDCF-110Y5W1-100/260√110 0.1 0.13√√33GW 13-60G/400Y1W-73/15ZN21-10/630配CD10ⅢLZZBJ-10100/5 0.5/10PJ Y N 2-10-03ZR-YJV 22-6/3×50SC9-800/6.3D,yn116.3±5%/0.4kV Ud%=7LMZ1-0.5 1200/5LMZ1-0.5 1200/5SC9-800/10D,yn1110±5%/0.4kV Ud%=7ZR-YJV 22-10/3×50LZZBJ-10100/5 0.5/10PZN21-10/630配CD10ⅢJ Y N 2-10-06(改)ZR-YJV 22-10/3×5010kV外来电源J Y N 2-10-19JDZJ-10HY5WZ-17/51RN2-10/0.5A10/0.1kV0.4kVLMY100×8-40×8DW15-1200DW15-1200DW15-12000.1LMY100×8-40×8G~G~TMY-100X8GW4-110DW/630左接地图5-19 某水电站电气主接线全图精心整理学习帮手精心整理 学习帮手图5-20 地区变电所接线8回35kV220kV4 回2×120MVA至无功补偿装置6 回2×60MVA4回2×10MVA1T图5-21 终端变电所接线4回10kV2T110kV 35kV第六章图形精心整理学习帮手精心整理学习帮手精心整理学习帮手精心整理 学习帮手VV22-13×50+1×251#厂变进线V 42L6-A,0~150A DT864-2,380/220V,3(6A)42L6-V,0~450V说明:BT95O9为事故照明切换板,其直流电源用VV22-1-2×4电缆引至直流屏。
第五章,轴测投影图
例2-2
画轴测轴 画 沿轴测量画动平面 各顶点沿Y方向画20 画动平面(终止位置) 画 检查、描深
*
例3 画出给定形体的正等轴测图
画空间轴 画轴测轴 画长方体 画五棱柱 检查、描深
例4 画出圆锥的正等轴测图
确定坐标轴 画轴测轴 画圆锥底面(侧平圆) 画锥顶 画转向线 判别可见性、描深
例5 根据已知的两面投影,画出正等轴测图
三、斜二轴测图画法
例13:已知两视图,画斜二轴测图。
第五章 轴测投影图
[例14] 作出如图所示带孔圆锥台的斜二轴测图。
z′
z〞
x′
o′
o〞
a″ y〞
L
Z1
X1
O1
L2
A
O1 A
Y1
圆弧公切线
[例15] 作出如图所示物体的斜二轴测图。
z′
z〞
x′
o′
L1
L
o〞 y〞圆弧公切线
Z1
X1 L1/2 L/2
2 平行于H面的圆为椭圆,长 轴对O1X1轴偏转7°, 长轴≈1.06d, 短轴≈0.33d。
3 平行于W面的圆与平行于H 面的圆的椭圆形状相同,长 轴对O1Z1轴偏转7°。
由于两个椭圆的作图相当繁,所以当物体这 两个方向上有圆时,一般不用斜二轴测图,而采 用正等轴测图。 斜二轴测图的最大优点:
物体上凡平行于V面的平面都反映实形。
x′
x1
2
z′
Z1
圆弧公切线
A
o′ o4
A1 41
o
31
11
3
X1
21
Y1
圆
弧
y
公 切
线
[例12] 作出如图所示支架的正等轴测。
云南地理-第五章水文环境_图文
第五章水文环境云南地域广,地势起伏大;地貌类型复杂,山地为主;气候湿润,降水丰富。
这样的条件下发育了众多的江河湖泊及地下水系(图5-1)。
又地处第一、二级阶梯的过渡区,蕴藏着丰富的水能资源。
图5-1云南省河流水系分布图第一节水系与河流云南省大小河流共600多条,其中较大的有180条,多为入海河流的上游。
一、云南水系云南省地跨六大水系(图5-1),具体说明如下:1、太平洋水系①长江水系:金沙江、龙川江、螳螂川(普渡河)、小江、以礼河、牛栏江横江、程海、泸沽湖、滇池等,注入东海。
②珠江水系:南盘江、曲江、可渡河、黄泥河、驮娘江、抚仙湖、星云湖、杞麓湖、阳宗海、异龙湖等,注入南海。
③元江(红河)水系:礼社江、绿汁江、把边江、阿墨江、李仙江、南溪河、盘龙江等,注入北部湾。
④澜沧江(湄公河)水系:漾濞江、威远江、曼老江、南腊河、南览河、流沙河、洱海等,注入南海。
2、印度洋水系⑤怒江(萨尔温江)水系:老窝河、枯柯河、南汀河、南滚河、南卡江等,注入安达曼海。
⑥伊洛瓦底江水系:独龙江、槟榔江、大盈江、瑞丽江等,注入安达曼海。
二、主要河流介绍1、怒江属于印度洋水系的怒江(萨尔温江)水系。
1.1河流概况又称潞江,怒江因江水深黑,我国最早的地理著作《禹贡》把它称为“黑水河”,云南省的怒族把怒江称为“阿怒日美”、“阿怒”是怒族人的自称,“日美”汉译为江,含义为怒族人居住区域的江。
发源于青藏高原的唐古拉山南麓的吉热拍格。
怒江在西藏嘉玉桥流入他念他翁山和伯舒拉岭之间的峡谷中时才正式叫怒江,嘉玉桥以上为怒江上游,称为那曲河;西藏嘉玉桥至云南省的泸水县为怒江的中游,进入云南境内以后,经怒江傈僳族自治州、保山市和德宏傣族景颇族自治州,怒江奔流在碧罗雪山与高黎贡山之间,西岸高黎贡山的峡谷高差达5000米,东岸碧罗雪山的峡谷高差达4000多米,平均高差3000多米,山谷幽深,危崖耸立,水流在谷底咆哮怒吼,故称“怒江”,江面海拔在2000-800米之间;怒江州境内,4000米以上高峰有20余座,群山南北逶迤、绵亘起伏,雪峰环抱,雄奇壮观。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7
5.1 基本概念和运算
1 2 3 4 连通图示例 5
若无向图中任意两点间都存在路径 无向图中任意两点间都存在路径 连通图。 —— 则称为连通图。 则称为连通图 否则,称为不连通图 非连通图) 不连通图( 否则,称为不连通图(非连通图)。 非连通图包含若干连通分量 连通分量。 非连通图包含若干连通分量。
1 2 4 5 3
5阶无向完全图 1 2
3
4
4阶有向图示例 阶有向图示例
吉林财经大学管理科学与信息工程学院
9
5.1 基本概念和运算
1 2 3 4 5 7 树的示例 1 3 4 6 7 有向树示例 5 2
若无向图满足: 若无向图满足:连通并且无回路 ——则称为树。 则称为树 则称为 树的定义有如下几个等价的描述: 树的定义有如下几个等价的描述: 等价的描述 有最少边数的连通图。 有最少边数的连通图。 条边的连通图。 有n-1条边的连通图。 条边的连通图 连通的无环图。 连通的无环图。 如果在有向图中, 有向树 —— 如果在有向图中, 有一个顶点的入度为0,其余顶点的入度为1, 有一个顶点的入度为 ,其余顶点的入度为 , 则称此图为有向树。 则称此图为有向树。 并称其中入度为0的顶点为有向根。 的顶点为有向根 并称其中入度为 的顶点为有向根。 右下图就是一个有向树,其中顶点1就是有向根 就是有向根。 右下图就是一个有向树,其中顶点 就是有向根。
6 dfs(6)
吉林财经大学管理科学与信息工程学院
17
5.3.1 深度优先搜索遍历
将dfs(1)执行过程中所搜索的边连接起来(有标注 ( )执行过程中所搜索的边连接起来( 的边), 的边), 得到一棵生成树----dfs生成树。 生成树。 得到一棵生成树 生成树
1 1
2 4 7
8 3
2 4 7
8
3
1 2
2 1 1 1
3 4 4 2 ^ ^
4
^
3
4
3 4
3
^
吉林财经大学管理科学与信息工程学院
13
5.2 图的存储
1 2 data firstadj
对应关系
1 2
4
2 4 4 1 ^ ^ ^
3
^
3
3 4
逆邻接链表
代表弧<4,1>
-----将“邻接自”的顶点连成链表data firstadj 将 邻接自” 1 2 3 4
吉林财经大学管理科学与信息工程学院
19
5.3.1 深度优先搜索遍历
1
2 3
有向图中的任意两点间可以 中的任意两点间可以互相到达 若有向图中的任意两点间可以互相到达 ——则称为强连通图。 则称为强连通图 则称为强连通图。
1 3 4 6 7 5 2 4 6
5 7
非连通图示例 ----三个连通分量
8
强连通图示例 吉林财经大学管理科学与信息工程学院
5.1 基本概念和运算
吉林财经大学管理科学与信息工程学院
16
5.3.1 深度优先搜索遍历
下面以下图为例来讨论dfs算法的执行过程:调用 下面以下图为例来讨论 算法的执行过程:调用dfs(1) 算法的执行过程
此箭头表示是从遍历运 算dfs(1)中调用dfs(2), 即从顶点1直接转到2
此虚箭头表示是在dfs(3) 执行完毕后返回到遍历 运算dfs(2)中,即从顶点 3返回到2
5.1 基本概念和运算
由顶点集V和连接顶点的弧集 或边集) 所组成的结构 和连接顶点的弧集( 所组成的结构, 图 —— 由顶点集 和连接顶点的弧集(或边集)E所组成的结构, 记作 G = ( V, E )。 。 其中弧的形式为<Vi,Vj>, 其中弧的形式为 , 表示从顶点Vi到 之间有一条弧 图形表示为: 之间有一条弧, 表示从顶点 到Vj之间有一条弧,图形表示为: Vi —> Vj ----有向图 有向图 如右图中的G1就是一个有向图 就是一个有向图: 例:如右图中的 就是一个有向图:
若无向图中任意两点间都有一条边 无向图中任意两点间都有一条边 ——则称为无向完全图。 则称为无向完全图 则称为无向完全图。 共有n 条边) (共有 (n-1) / 2条边) 条边 若有向图中每个顶点到其余各点均有一条弧 有向图中每个顶点到其余各点均有一条弧 ——则称为有向完全图。 则称为有向完全图 则称为有向完全图。 共有n 条弧) (共有 (n-1) 条弧)
深度优先搜索遍历 图的两种遍历算法 广度优先搜索遍历
5.3.1 深度优先搜索遍历(Depth First Search) 深度优先搜索遍历(
这一问题求解包括几个部分。 这一问题求解包括几个部分。 1. 基本算法 从顶点v0出发深度优先搜索遍历图 出发深度优先搜索遍历图G的 描述如下: 从顶点 出发深度优先搜索遍历图 的dfs (v0)描述如下: 描述如下 (1) 访问 ; 访问v0; (2) 依次从 的未被访问过的邻接点出发深度遍历。 依次从v0的未被访问过的邻接点出发深度遍历 的未被访问过的邻接点出发深度遍历。
1 2
3
4
图G1 有向图示例
中间经过的顶点不重复的路径。 简单路径 —— 中间经过的顶点不重复的路径。 都是简单路径。 例:图G1中,( 1,2,4 ) ( 1,3,4 ) ( 1,3,4,1 ) 都是简单路径。 图 中 首尾顶点相同的路径。 回路 —— 首尾顶点相同的路径。 例如, 例如, ( 1,3,4,1 ) 简单回路 —— 回路中顶点不重复
6
吉林财经大学管理科学与信息工程学院
10
5.2 图的存储
图的存储----图结构在计算机中的存储形式 图的存储 图结构在计算机中的存储形式 1. 邻接矩阵
(1)不带权值 假设图中有n个顶点。则采用n×n的矩阵A来表示, 1 <i,j>∈E 其中 Aij= 0 否则 例:
1 2 0 0 0 1 1 0 0 0 1 0 0 0 0 1 1 0
1
2
3
4
其中: 其中: 顶点集合 V={1,2,3,4} , , , 边集 E={ (1,2),(1,3),(1,4) )( )( ) (2,4),(3,4) )( ) }
图G2 无向图示例
吉林财经大学管理科学与信息工程学院
4
⊆
5.1 基本概念和运算
中每条边( 若G中每条边(弧)对应一个数值 中每条边 ——表示关系的程度,则称图 为 表示关系的程度, 表示关系的程度 则称图G为 网络。 网络。 例: 图G3 就是一个网络 对图G 对图 = ( V, E ),若存在 ,若存在G1=(V1, , E1), , 满足V1 , 满足 ⊆V,E1⊆ E。则G1是 。 是 G的子图。 的子图。 1 例如:右图G4 就是 就是G2 的子图。 的子图。 例如:右图
6
1
5 7 8 3
2
3
4
图G3 网络示例
2
1
2
3
4
3
4
图G2 无向图示例 图G4 子图示例 吉林财经大学管理科学与信息工程学院
5
5.1 基本概念和运算
顶点间关系: 顶点间关系: 如果 <Vi,Vj>∈E ∈ 则称—— Vi,Vj相邻接, 则称 , 相邻接,
1 2
Vi邻接到 ,Vj邻接自 。 邻接到Vj, 邻接自 邻接自Vi。 邻接到 例如, 图中, 邻接到 邻接到V2, 邻接自 邻接自V3 例如,右 图中, V1邻接到 ,V4邻接自 则称Vi, 相邻接 若( Vi,Vj )∈E——则称 ,Vj相邻接 ∈ 则称 顶点的度 顶点的邻接点的数目。 顶点的度 —— 顶点的邻接点的数目。 有向图中:入度,出度。 有向图中:入度,出度。 入度+出度。 度=入度+出度。
行的方向:发出的弧 列的方向 :进入的弧
3
4
对应关系
吉林财经大学管理科学与信息工程学院
11
5.2 图的存储
1 2 0 1 1 1 1 0 0 1 1 0 0 1 1 1 1 0
无向图的邻接矩阵 对称
34ຫໍສະໝຸດ (2) 网络的表示方法 wij <i,j>∈E Aij= 0 或∞ 否则 4 例: 1 2
3 3 6 5 2
∞ 4 3 5 4∞∞ 2 3∞∞ 6 5 2 6∞
4 吉林财经大学管理科学与信息工程学院
12
5.2 图的存储
2. 邻接表表示法 ----将每个顶点的邻接点构成链表,并将各链表的表头指针合在一起。 将每个顶点的邻接点构成链表,并将各链表的表头指针合在一起。 将每个顶点的邻接点构成链表 对应关系 例: data firstadj 1 2
吉林财经大学管理科学与信息工程学院
4 1 1 2
^ ^ ^ 3 ^
14
5.2 图的存储
用邻接表存储网络 6 9 B 8
A 5
D 2 C
data firstadj
A B C D
B 5 C 8∧ D 2∧ B 9∧
D 6∧
吉林财经大学管理科学与信息工程学院
15
5.3 图的遍历
图的遍历——按某种次序访问图中所有顶点一次且仅 按某种次序访问图中所有顶点一次且仅 图的遍历 且一次。 且一次。
数 据 结 构
第五章 图
Data Structures
吉林财经大学管理科学与信息工程学院
1
第五章 图 (Graph)
第五章 图(Graph)
5.1 基本概念和运算 5.2 图的存储 5.3 图的遍历 5.4 最小生成树 5.5 5.6 有向无环图的应用 最短路径
吉林财经大学管理科学与信息工程学院
2
吉林财经大学管理科学与信息工程学院
3
4
图G1 有向图示例
6
5.1 基本概念和运算
路径 ——若 顶点序列 i1,Vi2,…,Vij, 若 顶点序列V , 满足< 满足 Vik,Vi(k+1)>∈E或 ∈ 或 )(k=1,2,…,j-1), 者(Vik,Vi(k+1))∈E)( ∈ )( ), 则该顶点序列V 则该顶点序列 i1,Vi2,…,Vij , 构成一条路径。 构成一条路径。 例: 图G1中,1,2,4,1,3,4是一条路径 中 是一条路径
