中考数学总复习第一轮考点系统复习第6章圆第1节圆的有关性质课件
合集下载
重庆市中考数学一轮复习 第六章 圆 第1节 圆的基本概念及性质课件.ppt

2.在同圆或等圆中,如果两条弦相等,那么
它们所对的圆心角相等,所对的优弧相等,
所对的劣弧相等
返回
定理:在同圆或等圆中,一条弧所对的圆周角等
于它所对的圆心角的③
一半.
圆周 角定
1. 在同圆或等圆中,同弧或等弧所对的圆周 角④ 相等 ;
理及
其推
论
推论
2. 在同圆或等圆中,相等的圆周角所对的圆 心角相等
第六章 圆
第1节 圆的基本概念及性质
弧、弦、圆心角之间的关系
圆的 基本
圆周角定理及其推论
概念
垂径定理及其推论
及性 质
垂径定理及其推论的延伸
圆内接四边形的性质
弧、
定理:在同圆或等圆中,相等的圆心角所对的弧 ① 相等 ,所对的弦② 相等 .
弦、
圆心
角之
间的 关系
推论
1.在同圆或等圆中,如果两条弧相等,那么 它们所对的圆心角相等,所对的弦相等
即知二推三
返回
1.圆内接四边形的对角⑯ 互补 ,如图②,
圆内
∠A+∠BCD=⑰180°,∠B+∠D=180°
接四
边形
2.圆内接四边形的任意一个角的外角等于
它的⑱内对角
,如图②,∠DCE=∠A
返回
推论
2.弦的垂直平分线经过圆心,并且⑪平分 弦 所对的两条弧
3.圆的两条平行弦所夹的弧⑫ 相等 .
未完继续
垂径定理及其推论的延伸:根据圆的对称性, 如图①,在以下五个结论中:(1)»AC = ⑬ B»C ;(2)⑭ »AD =D»B ;(3)AE= ⑮ BE;(4)AB⊥CD;(5)CD是直径.只 要满足其中两个结论,另外三个结论一定成立,
它们所对的圆心角相等,所对的优弧相等,
所对的劣弧相等
返回
定理:在同圆或等圆中,一条弧所对的圆周角等
于它所对的圆心角的③
一半.
圆周 角定
1. 在同圆或等圆中,同弧或等弧所对的圆周 角④ 相等 ;
理及
其推
论
推论
2. 在同圆或等圆中,相等的圆周角所对的圆 心角相等
第六章 圆
第1节 圆的基本概念及性质
弧、弦、圆心角之间的关系
圆的 基本
圆周角定理及其推论
概念
垂径定理及其推论
及性 质
垂径定理及其推论的延伸
圆内接四边形的性质
弧、
定理:在同圆或等圆中,相等的圆心角所对的弧 ① 相等 ,所对的弦② 相等 .
弦、
圆心
角之
间的 关系
推论
1.在同圆或等圆中,如果两条弧相等,那么 它们所对的圆心角相等,所对的弦相等
即知二推三
返回
1.圆内接四边形的对角⑯ 互补 ,如图②,
圆内
∠A+∠BCD=⑰180°,∠B+∠D=180°
接四
边形
2.圆内接四边形的任意一个角的外角等于
它的⑱内对角
,如图②,∠DCE=∠A
返回
推论
2.弦的垂直平分线经过圆心,并且⑪平分 弦 所对的两条弧
3.圆的两条平行弦所夹的弧⑫ 相等 .
未完继续
垂径定理及其推论的延伸:根据圆的对称性, 如图①,在以下五个结论中:(1)»AC = ⑬ B»C ;(2)⑭ »AD =D»B ;(3)AE= ⑮ BE;(4)AB⊥CD;(5)CD是直径.只 要满足其中两个结论,另外三个结论一定成立,
2024年中考数学一轮复习考点精讲课件—圆的相关概念及性质

3)圆周角定理成立的条件是“同一条弧所对的”两种角,在运用定理时不要忽略了这个条件,把不同弧所
对的圆周角与圆心角错当成同一条弧所对的圆周角和圆心角.
考点二 圆的性质
题型01 由垂径定理及推论判断正误
【例1】(2023·浙江·模拟预测)如图,是⊙ 是直径,是弦且不是直径, ⊥ ,则下列结论不一定正
【详解】解:如图,连接,
∵线段是⊙ 的直径, ⊥ 于点E, = 16,
1
1
∴ = = 2 = 2 × 16 = 8,
∴在Rt △ 中,可有 = 2 + 2 = 62 + 82 = 10,
∴⊙ 半径是10.
故选:D.
考点二 圆的性质
题型03 根据垂径定理与全等三角形综合求解
直径)(4)平分弦所对的优弧(5)平分弦所对的劣弧,若已知五个条件中的两个,那么可推出其中三个,简
称“知二得三”,解题过程中应灵活运用该定理.
常见辅助线做法(考点):1)过圆心,作垂线,连半径,造Rt △,用勾股,求长度;
2)有弦中点,连中点和圆心,得垂直平分.
考点二 圆的性质
3. 弧、弦、圆心角的关系
即的最小值是8.故选:C.
考点二 圆的性质
1. 圆的对称性
内容
补充
圆的轴对称 经过圆心任意画一条直线,并沿此直线圆对折,直线两旁的部分能够 ①圆的旋转不变性是其他中心对称图形所
性
完全重合,因此圆是轴对称图形,每一条直径所在的直线都是它的 没有的性质.
对称轴,圆有无数条对称轴.
圆的中心对 将圆绕圆心旋转180°能与自身重合,因此它是中心对称图形,它
①圆心,它确定圆的位置.
②半径,它确定圆的大小.
的点组成的图形.
对的圆周角与圆心角错当成同一条弧所对的圆周角和圆心角.
考点二 圆的性质
题型01 由垂径定理及推论判断正误
【例1】(2023·浙江·模拟预测)如图,是⊙ 是直径,是弦且不是直径, ⊥ ,则下列结论不一定正
【详解】解:如图,连接,
∵线段是⊙ 的直径, ⊥ 于点E, = 16,
1
1
∴ = = 2 = 2 × 16 = 8,
∴在Rt △ 中,可有 = 2 + 2 = 62 + 82 = 10,
∴⊙ 半径是10.
故选:D.
考点二 圆的性质
题型03 根据垂径定理与全等三角形综合求解
直径)(4)平分弦所对的优弧(5)平分弦所对的劣弧,若已知五个条件中的两个,那么可推出其中三个,简
称“知二得三”,解题过程中应灵活运用该定理.
常见辅助线做法(考点):1)过圆心,作垂线,连半径,造Rt △,用勾股,求长度;
2)有弦中点,连中点和圆心,得垂直平分.
考点二 圆的性质
3. 弧、弦、圆心角的关系
即的最小值是8.故选:C.
考点二 圆的性质
1. 圆的对称性
内容
补充
圆的轴对称 经过圆心任意画一条直线,并沿此直线圆对折,直线两旁的部分能够 ①圆的旋转不变性是其他中心对称图形所
性
完全重合,因此圆是轴对称图形,每一条直径所在的直线都是它的 没有的性质.
对称轴,圆有无数条对称轴.
圆的中心对 将圆绕圆心旋转180°能与自身重合,因此它是中心对称图形,它
①圆心,它确定圆的位置.
②半径,它确定圆的大小.
的点组成的图形.
2024年中考数学一轮复习课件--圆的性质

成立,则其余对应的两项也成立.如图,①∠AOB=∠COD,
②弧AB=弧CD,③AB=CD,“知一推二”.
注意点
①进一步拓展,在同圆或等圆中,弧、弦、圆心角、弦心距
这四个量中,有一个量相等,则其余三个量都相等.
②一条弦所对的圆心角只有一个,而所对的弧有两条.
圆周角的概念与性质
1.圆周角
顶点在
圆周 上,角的两边都与圆 相交
可以A为圆心,AB长为半
径作圆
图形
模型
特征
①共斜边的两个直角三角形的四
个顶点共圆,圆心为斜边中点,
四点 如图
共圆
②共边三角形且边所对角相等的
四个顶点共圆,如图
图形
模型
特征
四点 ③对角互补四边形的四个顶
共圆 点共圆,如图
图形
特征
模型
在☉O中,AB的长度为定值(即定
弦),C为动点,且∠C为定值,根
圆心
,并且平
分弦所对的两条弧;
(2)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦
所对的另一条弧;
(3)圆的两条平行弦所夹的弧 相等 .
注意点
(1)根据圆的对称性,在以下5个结论中:①过圆心;②垂直
于弦;③平分弦;④平分弦所对的优弧;⑤平分弦所对的劣弧.
如果满足其中的2个结论,那么可推出其余3个结论,注意解题
径,点P为OB上任意一点(点P不与点B重合),连接CP.若
∠BAC=70°,则∠BPC的度数可能是( D )
第8题图
A.70°
B.105°
C.125°
D.155°
9.(2023·泰安模拟)如图,AB是☉O的直径,∠ACD=∠CAB,
②弧AB=弧CD,③AB=CD,“知一推二”.
注意点
①进一步拓展,在同圆或等圆中,弧、弦、圆心角、弦心距
这四个量中,有一个量相等,则其余三个量都相等.
②一条弦所对的圆心角只有一个,而所对的弧有两条.
圆周角的概念与性质
1.圆周角
顶点在
圆周 上,角的两边都与圆 相交
可以A为圆心,AB长为半
径作圆
图形
模型
特征
①共斜边的两个直角三角形的四
个顶点共圆,圆心为斜边中点,
四点 如图
共圆
②共边三角形且边所对角相等的
四个顶点共圆,如图
图形
模型
特征
四点 ③对角互补四边形的四个顶
共圆 点共圆,如图
图形
特征
模型
在☉O中,AB的长度为定值(即定
弦),C为动点,且∠C为定值,根
圆心
,并且平
分弦所对的两条弧;
(2)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦
所对的另一条弧;
(3)圆的两条平行弦所夹的弧 相等 .
注意点
(1)根据圆的对称性,在以下5个结论中:①过圆心;②垂直
于弦;③平分弦;④平分弦所对的优弧;⑤平分弦所对的劣弧.
如果满足其中的2个结论,那么可推出其余3个结论,注意解题
径,点P为OB上任意一点(点P不与点B重合),连接CP.若
∠BAC=70°,则∠BPC的度数可能是( D )
第8题图
A.70°
B.105°
C.125°
D.155°
9.(2023·泰安模拟)如图,AB是☉O的直径,∠ACD=∠CAB,
中考数学复习第六章圆第一节圆的基本性质课件

(2)证明:∵△ABC是等边三角形,∴AC=BC, ∴∠5=∠6,∵∠3=∠2, ∴△AED∽△CEB.
8.(2024·泰安)如图,AB是⊙O的直径,C,D是⊙O上两点,BA平分∠CBD, 若∠AOD=50°,则∠A的度数为( A ) A.65° B.55° C.50° D.75°
C
D
11.如图,在Rt△ABC中,∠ACB=90°,∠ABC=40°,AB=4,斜边AB是半
(1)证明:∵四边形ABCD是⊙O的内接四边形, ∴∠ADE=∠ABC, ∵AB=AC, ∴∠ABC=∠ACB, ∵∠ACB=∠ADB,∴∠ADB=∠ADE.
13.如图,⊙O外接于△ABC,延长BO交⊙O于点D,过点C作CE⊥BD交BD于 点E. (1)求证:∠BAC=∠BCE; (2)若∠BAC=60°,BC=2 ,求⊙O的半径.
第六章 圆 第一节 圆的基本性质
B
2.(2024·吉林)如图,四边形ABCD内接于⊙O,过点B作BE∥AD,交CD于 点E.若∠BEC=50°,则∠ABC的度数是( C ) A.50° B.100° C.130° D.150°
3.(2024·临夏州)如图,AB是⊙O的直径,∠E=35°,则∠BOD的度数为( D ) A. 80° B. 100° C. 120° D. 110°
(1)证明:连接CD, ∵BD是⊙O的直径, ∴∠BCD=90°, ∴∠DCE+∠BCE=90°, ∵CE⊥BD,∴∠CED=90°, ∴∠BDC+∠DCE=90°, ∴∠BCE=∠BDC, ∵∠BAC=∠BDC, ∴∠BAC=∠BCE.
C
90°
6.(2024·龙东)如图,△ABC内接于⊙O,AD是直径,若∠B=25°,则∠CAD= 65° .
7.(2023·贵州)如图,已知⊙O是等边三角形ABC的外接圆,连接CO并延长交A B于点D,交⊙O于点E,连接EA,EB. (1)写出图中一个度数为30°的角:∠1(答案不唯一),图中与△ACD全等的三角 形是 △BCD ; (2)求证:△AED∽△CEB; (3)连接OA,OB,判断四边动点,连接CD与AB交于点E,若△BCE是等
2024年中考数学总复习第一部分考点精讲第六单元圆第1课时与圆有关的性质
返回目录
名称
公式
中心角
360 正n边形的每个中心角θ为__n___
图例
正多边 形与圆
边心距
正n边形的边心距r=
R2
a 2
2
周长 面积
正n边形的周长l=na 1
正n边形的面积S=__2___rl(l为
正n边形的周长)
R:半径 r:边心距 a:边长 θ:中心角
第1课时 与圆有关的性质
一题串讲重难点
理及其推
_的__圆__心__角__的__一__半_____,
论(图③) 即∠BAC= 12∠BOC
图③
第1课时 与圆有关的性质
返回目录
1.____同__弧__或__等__弧__所__对__的__圆__周__角__相__等_____,即
∠BAC=∠BDC
推论 2.直径(或半圆)所对的圆周角是___直__角____,
返回目录
基础知识巩固
例1
如图,△ABC内接于⊙O,BC为⊙O的
直径,点D为劣弧 AC上一点,连接OD,BD.
(1)∠BAC=__9_0___°;
(2)若∠COD=70°,
则∠CBD=___3_5__°,
∠BDO=___3_5__°;
例1题图
第1课时 与圆有关的性质
(3)如图②,点A为 BD的中点,若∠ACB=20°, 则∠ABD=__2_0___°,∠CBD=__5_0___°; (4)如图③,OD⊥AC交AC于点F,AC=8. ①AF的长为__4____; ②若∠CBD=27°,则∠ABD=__2_7___°; ③若⊙O的直径为10,则DF的长为__2____.
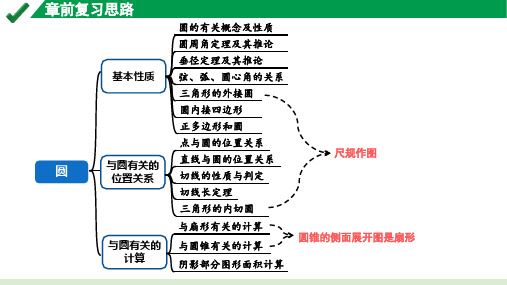
尺规作图 圆锥的侧面展开图是扇形
1 考点精讲 2 一题串讲重难点 3 广东8年真题子母题
中考数学一轮复习第六章圆第一节圆的有关概念及性质课件

等弧只存在同圆或等圆中,大小不等圆中不存在等弧.
(5)圆心角:顶点在__圆__心___的角叫做圆心角. (6)圆周角:顶点在__圆__上___,两边分别与圆还有另一个 交点.像这样的角,叫做圆周角.
知识点二 圆的有关性质 1.圆的对称性 (1)圆是轴对称图形,其对称轴是任意一条 _过__直__径__的直 线,有__无__数___条对称轴. (2)圆是中心对称图形,对称中心为__圆__心__.
3.垂径定理及其推论 (1)垂径定理:垂直于弦的直径__平__分___这条弦,并且__平__分__
弦所对的弧. (2)推论:①平分弦(不是直径)的直径__垂__直___于弦,并且 __平__分___弦所对的弧; ②弦的垂直平分线经过_圆__心__,并且平分弦所对的两条弧; ③平分弦所对的一条弧的直径垂直平分弦,并且__平__分___另 一条弧.
2
在同圆或等圆中,两个圆心角、两条弧、两条弦,其中有 一组量相等,那么它们所对应的其余两组量也分别相等.
1.如图,P是⊙O外一点,PA,PB分别交⊙O于C,D两点. 已知 AB ,CD 的度数别为88°,32°,则∠P的度数为
( B)
A.26° B.28° C.30° D.32°
2.如图,已知⊙O的半径等于1 cm,AB是直径,C,D是⊙O
7.(2017·遵义)如图,AB是⊙O的直径,AB=4,点M是OA 的中点,过点M的直线与⊙O交于C,D两点.若∠CMA=45°, 则弦CD的长为____1_4__.
根据圆的对称性可知,圆具有旋转不变性,即圆围绕 它的圆心旋转任意角度,所得的圆与原图重合.
2.圆心角、弧、弦之间的关系 (1)在同圆或等圆中,相等的圆心角所对的弧__相__等___, 所对的弦__相__等___. (2)在同圆或等圆中,如果两个圆心角、两条弧、两条弦 中有一组量相等,那么它们所对应的其余各组量都分别 __相__等___.
中考数学一轮复习课件:第6章 第1节 圆的基本性质
●
③如图3,若∠ABC=25°,则∠BDC=________.
65°
●
④如图4,若CD=2OE,则∠BCD=__________.
22.5°
图2
图3
图4
●
⑤如图5,若AC=5,∠ADC=30°,则⊙O的直径AB=______.
10
●
⑥如图6,CD⊥AB于点F,OE⊥AC于点E,若OE=3,OB=5,则CD的长度是_______.
(2)填空: ①若 AB=4,且点 E 是B︵D的中点,则 DF 的长为__4_-__2___2____; ②取A︵E的中点 H,当∠EAB 的度数为___3_0_°___时,四边形 OBEH 为菱形.
2.圆周角定理及其推论
定理 一条弧所对的圆周角等于它所对的圆心角的一半
常见 图形
结论 推论
∠AOB=2∠ACB
(1)同弧或等弧所对的圆周角相等; (2)半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直 径
●
应用圆周角定理和推论时,一定注意“在同圆或等圆中”的条件,同时要特别注意一条弦是对着
两条弧的.
●
3.垂径定理及其推论
定理 推论
垂直于弦的直径平分弦,并且平分弦所对的两条弧 (1)平分弦(非直径)的直径垂直于弦,并且平分弦所对的两条弧; (2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧; (3)平分弦所对的一条弧的直径垂直平分弦,并且平分弦所对的 另一条弧
考点 3 圆内接四边形及其性质
第一节 圆的基本性质
闪充考点
考点 1 圆的有关概念及性质
图示
弦 直径
圆弧
连接圆上任意两点的线段,如图中的 AC,BC
经过圆心的弦,直径等于半径的 2 倍
中考数学总复习第一部分基础知识复习圆圆的有关概念及性质PPT
★知识要点导航 ★知识点1 ★知识点2 ★知识点3 ★知识点4 ★知识点5 ★知识点6 ★热点分类解析 ★考点1 ★考点2 ★考点3
★知识要点导航 ★知识点1 ★知识点2 ★知识点3 ★知识点4 ★知识点5 ★知识点6 ★热点分类解析 ★考点1 ★考点2 ★考点3
★知识要点导航 ★知识点1 ★知识点2 ★知识点3 ★知识点4 ★知识点5 ★知识点6 ★热点分类解析 ★考点1 ★考点2 ★考点3
★知识要点导航 ★知识点1 ★知识点2 ★知识点3 ★知识点4 ★知识点5 ★知识点6 ★热点分类解析 ★考点1 ★考点2 ★考点3
★热点分类解析 ★热点分类解析 ★热点分类解析 ★知识要点导航 ★热点分类解析 ★热点分类解析 ★热点分类解析 ★热点分类解析 ★热点分类解析 ★热点分类解析 ★热点分类解析 ★热点分类解析 ★热点分类解析 ★热点分类解析 ★知识要点导航 ★热点分类解析
★知识要点导航 ★知识点1 ★知识点2 ★知识点3 ★知识点4 ★知识点5 ★知识点6 ★热点分类解析 ★考点1 ★考点2 ★考点3
★知识要点导航 ★知识点1 ★知识点2 ★知识点3 ★知识点4 ★知识点5 ★知识点6 ★热点分类解析 ★考点1 ★考点2 ★考点3
★知识要点导航 ★知识点1 ★知识点2 ★知识点3 ★知识点4 ★知识点5 ★知识点6 ★热点分类解析 ★考点1 ★考点2 ★考点3
★知识点5 ★知识点6
★知识点5 ★知识点6 ★知识点5 ★知识点6
★知识点5 ★知识点6 ★知识点5 ★知识点6
★知识要点导航 ★知识点1 ★知识点2 ★知识点3 ★知识点4 ★知识点5 ★知识点6 ★热点分类解析 ★考点1 ★考点2 ★考点3
★知识要点导航 ★知识点1 ★知识点2 ★知识点3 ★知识点4 ★知识点5 ★知识点6 ★热点分类解析 ★考点1 ★考点2 ★考点3
