控制工程基础第三版习题答案_清华大学出版社(1-8章)完全版
控制工程基础课后答案

控制工程基础课后答案第一题题目:什么是控制工程?它的主要任务是什么?答案:控制工程是一门工程技术学科,它以数学、物理和工程技术为基础,研究如何通过设计、分析和实现控制系统来实现对动态系统的控制。
控制工程的主要任务是利用反馈原理,通过感知系统输出信号与期望信号之间的差异并使用控制器进行调整,从而使系统达到预期的目标和性能指标。
第二题题目:什么是开环控制系统和闭环控制系统?它们有什么区别?答案:开环控制系统是一种基本控制系统结构,它将输入直接转换为输出,没有考虑实际输出与期望输出之间的差异。
闭环控制系统是在开环控制系统基础上增加了反馈回路,实时监测系统输出,并将实际输出与期望输出进行比较,以校正错误并调整控制器的输出信号。
区别在于开环控制系统没有反馈回路,因此无法纠正系统误差,而闭环控制系统利用反馈回路实现系统的自动校正。
闭环控制系统具有更好的鲁棒性和稳定性,可以使系统在存在不确定性和干扰的情况下仍能达到预期的控制目标。
第三题题目:什么是传递函数?如何将动态系统表示为传递函数?答案:传递函数是用于描述线性时不变系统的数学模型。
它是输出与输入之间关系的比值函数,衡量了系统对输入信号的响应程度。
传递函数可以用于分析和设计控制系统。
将动态系统表示为传递函数需要进行系统的数学建模。
通常,通过对系统的微分方程进行拉普拉斯变换,可以得到系统的传递函数。
拉普拉斯变换将微分方程转换为一个以变量s为复数的函数的代数表达式,其中s表示频域复平面上的复变量。
第四题题目:什么是反馈控制?它在控制系统中起到什么作用?答案:反馈控制是一种控制技术,通过测量系统输出并将其与期望输出进行比较,根据差异调整控制器的输出信号。
反馈控制可以使系统对不确定性和干扰具有鲁棒性,并实现系统的自动校正,使系统能够快速、准确地响应外部变化。
在控制系统中,反馈控制起到了校正系统误差的作用。
通过与期望输出进行比较,反馈控制可以检测到系统偏差,并通过调整控制器的输出信号来纠正这些偏差。
控制工程基础123章答案

第一章绪论内容提要一、基本概念1.控制:由人或用控制装置使受控对象按照一定目的来动作所进行的操作。
2.输入信号:人为给定的,又称给定量。
3.输出信号:就是被控制量。
它表征对象或过程的状态和性能。
4.反馈信号:从输出端或中间环节引出来并直接或经过变换以后传输到输入端比较元件中去的信号,或者是从输出端引出来并直接或经过变换以后传输到中间环节比较元件中去的信号。
5.偏差信号:比较元件的输出,等于输入信号与主反馈信号之差。
6。
误差信号:输出信号的期望值与实际值之差。
7。
扰动信号:来自系统内部或外部的、干扰和破坏系统具有预定性能和预定输出的信号。
二、控制的基本方式1.开环控制:系统的输出量对系统无控制作用,或者说系统中无反馈回路的系统,称为开环控制系统。
2.闭环控制:系统的输出量对系统有控制作用,或者说系统中存在反馈回路的系统,称为闭环控制系统.三、反馈控制系统的基本组成1.给定元件:用于给出输入信号的环节,以确定被控对象的目标值(或称给定值)。
2。
测量元件:用于检测被控量,通常出现在反馈回路中。
3.比较元件:用于把测量元件检测到的实际输出值经过变换与给定元件给出的输入值进行比较,求出它们之间的偏差。
4.放大元件:用于将比较元件给出的偏差信号进行放大,以足够的功率来推动执行元件去控制被控对象。
5.执行元件:用于直接驱动被控对象,使被控量发生变化。
6.校正元件:亦称补偿元件,它是在系统基本结构基础上附加的元部件,其参数可灵活调整,以改善系统的性能.四、控制系统的分类(一)按给定信号的特征分类1. 恒值控制系统2。
随动控制系统3。
程序控制系统(二)按系统的数学描述分类1. 线性系统2. 非线性系统(三)按系统传递信号的性质分类1. 连续系统2. 离散系统(四)按系统的输入与输出信号的数量分类1。
单输入单输出系统2。
多输入多输出系统(五)按微分方程的性质分类1。
集中参数系统2。
分布参数系统五、对控制系统的性能要求1。
《控制工程基础》练习一答案.doc
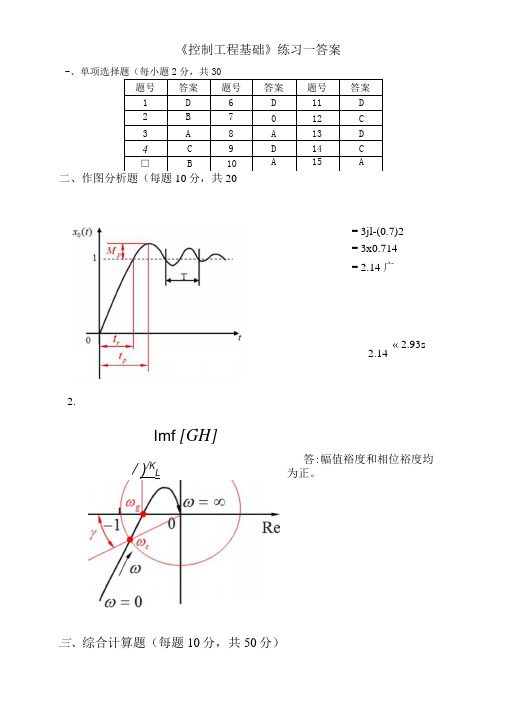
《控制工程基础》练习一答案-、单项选择题(每小题2分,共30题号答案题号1D6 2B7 3A8 4C9□B10答案题号答案D11D 012C A13D D14C A15A二、作图分析题(每题10分,共20= 3jl-(0.7)2= 3x0.714= 2.14 广2.14« 2.93s 2.Imf [GH]/)/K L答:幅值裕度和相位裕度均为正。
三、综合计算题(每题10分,共50分)10010101、解: 由题意可写出Gg(s) = -------------- = ------------------ ,s(s + 10) + k 10s+ 100 根据二阶系统的标准形式可知:气2 = ] 00,2初=10 .・. co n = 10,S = 0.5:.M = e xlOO% = 16.4%,/ = ----------------- f= 0.363s,八=-^― — 0.8s「 1口〃"2、解:由题意得系统的开环频率特性为:G"问)=, k /以,2口 + 1)(,0.5切+1) A (69) = —/ 七 ,(p(co )= -90° - tg 10.569- tg 12a )6A/1+467 71 + 0.256?当口=使时,(p^co*) = -90° -tg~l0.5绥,一鬼一'2绥=-180° => 饱=14/、 10 10zy )= ___ = 4 g « J1+4.2 J1+0.25 绥 2 V5A /L25・・・《(dB) = 201g-^- = 201g :=-UdB g *(饱) 4o3、解:由题意得G R (S ) = ---- ---- =—-—,其频率特性为2s + 15 + 5 2s + 20 A 例=/5 = -5 =,伊(口)= _侦_\ 2L,7(2^y)2+ 202VW+40010由输入信号可知,X,. = 20=2*.(口) = 45°,根据频率响应的特点,有 x o (O = x o (69)sin[6/ + ^(69)] = A (69)匚K sin[2? +(p(cd) +(p {(69)]52=/ 、x 2 sin[2, + (Tg—I 二)+ 45°] = 0.49 sin(2f + 33.69°) V4X22+4001。
控制工程基础习题答案_清华大学出版社_沈艳_孙锐主编

1 ,依题意 s
C ( s)
1 2 1 3s 2 1 s s 2 s 1 ( s 1)(s 2) s C ( s) 3s 2 R( s) ( s 1)(s 2)
G( s)
4 1 k (t ) L1 G ( s ) L1 4e 2t e t s 1 s 2
( s)
F ( s)
?
G1 ( s )
G2 ( s )
G3 ( s )
C (s)
G4 ( s )
解 首先按方框图化简规则,将图 2-34( a )化简成图 2-34( c ) ,应用图 2-34( c )
G2 ( s ) G1 ( s ) 可以方便地求出开环传递函数和四种闭环传递函数,即
第二章
2-1 试证明图 2-28 中所示的力学系统(a)和电路系统(b)是相似系统(即有相同形式的数 学模型) 。
解 (a) 取A、B两点分别进行受力分析,如图 解2-2(a)所示。对A点有
y ) f1 ( y y 1 ) k 2 ( x y) f 2 ( x
(1) 对 B 点有
2-3 某位置随动系统原理框图如图 2-31 所示,已知电位器最大工作角度 Qm =
3300,功率放大器放大系数为 k3 。 (1) (2) (3) 分别求出电位器的传递函数 k 0 ,第一级和第二级放大器的放大系数 k1 , k 2 ; 画出系统的结构图; 求系统的闭环传递函数 Qc (s)
Qr (s) 。
1-5 图 1.16 是控制导弹发射架方位的电位器式随动系统原理图。图中电位器 P 1 、 P2 并 联后跨接到同一电源 E 0 的两端,其滑臂分别与输入轴和输出轴相联结,组成方位角的给定 元件和测量反馈元件。输入轴由手轮操纵;输出轴则由直流电动机经减速后带动,电动机采 用电枢控制的方式工作。试分析系统的工作原理,指出系 统的被控对象、被控量和给定量,画出系统的方框图。
控制工程基础第三版课后答案 (3)

控制工程基础第三版课后答案第一章1.1 分析控制系统的对象控制系统的对象通常指的是待控制的物理系统或过程。
在分析控制系统对象时,首先需要了解系统的动态特性。
为了分析控制系统的特性,我们可以通过选取一个合适的数学模型来描述物理系统的动态行为。
一种常用的方法是通过微分方程来描述系统的动态特性。
例如,对于一个简单的电路系统,可以使用基尔霍夫电流定律和基尔霍夫电压定律来建立描述电路中电流和电压之间关系的微分方程。
然后,通过求解这个微分方程,我们可以得到系统的传递函数。
另外,我们还可以使用频域分析的方法来分析控制系统的对象。
通过对信号的频谱进行分析,我们可以得到系统的频率响应。
1.2 常见的控制系统对象控制系统的对象存在各种各样的形式,下面列举了一些常见的控制系统对象:•机械系统:例如机器人、汽车悬挂系统等。
•电气系统:例如电路、电机等。
•热力系统:例如锅炉、冷却系统等。
•化工系统:例如反应器、蒸馏塔等。
针对不同的控制系统对象,我们需要选择合适的数学模型来描述其动态特性,并进一步分析系统的稳定性、性能等指标。
第二章2.1 控制系统的数学模型控制系统的数学模型描述了物理系统的动态特性和输入与输出之间的关系。
常见的控制系统数学模型包括:•模型中几何图形法:通过几何图形来描述系统的动态特性。
•传递函数法:采用以系统输入和输出的转移函数来描述系统的动态特性。
•状态方程法:将系统的状态变量与输入变量和输出变量之间的关系用一组偏微分方程或代数方程来描述。
在使用这些模型时,我们可以选择合适的数学工具进行分析和求解,例如微积分、线性代数等。
2.2 传递函数的定义和性质传递函数是描述控制系统输入输出关系的数学函数,通常用G(s)表示。
传递函数的定义和性质如下:•定义:传递函数G(s)是系统输出Y(s)和输入U(s)之间的比值,即G(s) = Y(s)/U(s)。
•零点和极点:传递函数可以有零点和极点,零点是使得传递函数为零的s值,极点是使得传递函数为无穷大的s值。
《控制工程基础》第3版 课后答案 PPT课件

Y (s) 1
X (s)
k
Pk k
s2
s2 a1s a2
s2
b a1s
a2
Y (s) X (s)
s2
b a1s
a2
s2
(b)
p1
b2 s2
P2
b1 s
L1
a1 s
L2
a2 s2
1 ( a1 s
a2 s2
)
s2
a1s a2 s2
Y (s) 1
X (s)
k
Pk k
b1 s
b2 s2
s 2 a1s a2
s2
b1s b2 a1s
a2
s2
第三章
可得系统的传递函数
1 U o (s) Cs 1 1 U i (s) R 1 RCs 1 4s 1
Cs
Ui
(s)
L[ui
(t)]
1 s
1 s
e 30s
Uo (s)
Ui (s) 4s 1
1 (1 4s 1 s
1 s
T2 (t)
J1Βιβλιοθήκη &&A (t)
D1
&A (t )
T2 (t) k2[A (t) o (t)]
T1(s) k1[i (s) A (s)]
TT12((ss))
T2 (s) J1s
k2[ A (s)
2 A (s) o (s)]
D1s
A
(s)
T2 (t) J2 &&o (t) D2 &o (t)
X i2 (s) 1 G1G2 G4 G1G4G5H1H2 G1G2G4
Xo2(s)
G4G5G6 (1 G1G2 )
《控制工程基础》第三版课后答案

控制工程基础习题解答第一章1-1.控制论的中心思想是什么?简述其发展过程。
维纳(N.Wiener)在“控制论——关于在动物和机器中控制和通讯的科学”中提出了控制论所具有的信息、反馈与控制三个要素,这就是控制论的中心思想控制论的发展经历了控制论的起步、经典控制理论发展和成熟、现代控制理论的发展、大系统理论和智能控制理论的发展等阶段。
具体表现为:1.1765年瓦特(Jams Watt)发明了蒸汽机,1788年发明了蒸汽机离心式飞球调速器,2.1868年麦克斯威尔(J.C.Maxwell)发表“论调速器”文章;从理论上加以提高,并首先提出了“反馈控制”的概念;3.劳斯(E.J.Routh)等提出了有关线性系统稳定性的判据4.20世纪30年代奈奎斯特(H.Nyquist)的稳定性判据,伯德(H.W.Bode)的负反馈放大器;5.二次世界大仗期间不断改进的飞机、火炮及雷达等,工业生产自动化程度也得到提高;6.1948年维纳(N.Wiener)通过研究火炮自动控制系统,发表了著名的“控制论—关于在动物和机器中控制和通讯的科学”一文,奠定了控制论这门学科的基础,提出了控制论所具有的信息、反馈与控制三要素;7.1954年钱学森发表“工程控制论”8.50年代末开始由于技术的进步和发展需要,并随着计算机技术的快速发展,使得现代控制理论发展很快,并逐渐形成了一些体系和新的分支。
9.当前现代控制理论正向智能化方向发展,同时正向非工程领域扩展(如生物系统、医学系统、经济系统、社会系统等),1-2.试述控制系统的工作原理。
控制系统就是使系统中的某些参量能按照要求保持恒定或按一定规律变化。
它可分为人工控制系统(一般为开环控制系统)和自动控制系统(反馈控制系统)。
人工控制系统就是由人来对参量进行控制和调整的系统。
自动控制系统就是能根据要求自动控制和调整参量的系统,系统在受到干扰时还能自动保持正确的输出。
它们的基本工作原理就是测量输出、求出偏差、再用偏差去纠正偏差。
控制工程基础课后答案

第二章2.1求下列函数的拉氏变换 (1)s s s s F 232)(23++=(2)4310)(2+-=s s s F (3)1)(!)(+-=n a s n s F (4)36)2(6)(2++=s s F(5) 22222)()(a s a s s F +-= (6))14(21)(2s s s s F ++= (7)521)(+-=s s F 2.2 (1)由终值定理:10)(lim )(lim )(0===∞→∞→s t s sF t f f (2)11010)1(10)(+-=+=s s s s s F 由拉斯反变换:t e s F L t f ---==1010)]([)(1 所以 10)(lim =∞→t f t2.3(1)0)2()(lim )(lim )0(2=+===∞→→s ss sF t f f s t )0()0()()()](['2''0''f sf s F s dt e t f t f L st --==-+∞⎰)0()0()(lim )(lim'2''0f sf s F s dt e t f s st s --=+∞→-+∞+∞→⎰1)2()(lim )0(222'=+==+∞→s s s F s f s (2)2)2(1)(+=s s F , t te s F L t f 21)]([)(--==∴ ,0)0(2)(22'=-=--f te et f tt又,1)0('=∴f2.4解:dt e t f e t f L s F st s--⎰-==22)(11)]([)(⎰⎰------+-=2121021111dt e e dt e e sts sts)11(11)11(11222s s s s se s e s e e s s e -------+--=22)1(111s s e s e ---∙-=2.5求下列函数的拉氏反变换(1)t t f 2sin 21)(= (2)t e t t f -=361)((3)t t e e t f 32321)(+-=- (4)t t e e t f 235352)(+=-(5)t e t e t f t t 3sin 313cos 2)(22--+= (6)t t t e e te t f 222)(----+-=2.6(1)0)()()(22=--dtt y d m t ky t f(2)0)()()(222121=-+-dt t y d m t y k k k k t f2.7(1)14312)(23++++=s s s s s G(2)210)(22++=-s s e s G s2.8 解 水的流量Q1由调节控制阀的开度控制,流出量Q2则根据需要可通过负载阀来改变,被调量H 反映了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目录
第一章 (1)
第二章 (4)
第三章 (21)
第四章 (34)
第五章 (41)
第六章 (47)
第七章 (61)
第八章 (70)
第一章
1-1
解:(1)B (2)B (3)B (4)A
1-2
解:
优点缺点
开环简单,不存在稳定性问题精度低,不抗干扰
闭环精度高,抗干扰复杂,设计不当易振荡
1-3
解:(1)自行车打气如图1-1所示职能方块图,为闭环系统。
图1-1
(2)普通电烙铁的职能方块图如图1-2所示,为开环系统。
图1-2
(3)车玩具的职能方块图如图1-3所示,为开环系统。
图
1-3
(4)船自动舵的职能方块图如图1-4所示,为闭环系统。
图1-4
(5)灯自动开关的职能方块图如图1-5所示,为开环系统。
图1-5
1-4
解:系统输入量:被记录的电压信号U2
系统输出量:记录笔的位移L
被控对象:记录笔
1-5
解:(a):对于图(a)所示的系统,水箱中输出流量和输入流量决定了水箱的水位变化,水位的高低决定了浮球的位置,流量通过杠杆机械对应阀门的开启大小,阀门的大小决定输入流量补偿输出流量,最终水位保持一定值。
其职能方块图如下图所示:
(b):对于(b)图所示的系统,控制水位的过程与图(a)系统中浮球的位置通过杠杆机构操纵双向触点电开关,两个触点电机正、反转,电机的正、反转对应阀门的开大、开小,系统由于使用了电机,系统的反应加快,其职能方块图如下图所示:
1-6:试画出实验室用恒温箱职能方块图。
解:根据一般实验室用恒温箱的工作原理图,画出其职能方块图如下:
(注:1-5中有部分文学是根据上下文理解的,因为原版中缺失;1-6为类似书中原体,不是原体,请注意!)
第二章
2-1 解:
(1): )](12[)](1[)](5[)]()4[()(t L t t L t L t t L S F ⋅+⋅++=δδ S
S S S 215215022++=+++= (2): )
25(25
3)(2
++=
s s S F (3): 1
1)(2++=-s e S F s
π
(4): )}(1)6
(1)]6(2cos 4{[)(5t e t t L S F t ⋅+-⋅-
=-π
π
5
1
44512426
226
+++=+++=
--S s Se S s Se s
s π
π
(5): S
e S e S F s
s 226600)(--+=+++= (6): )]4
(1)90453cos(6[)(π
-
⋅--=t t L S F ο
ο
9
636)]4(1)4(3cos 6[24
224
+=+=-⋅-=--S Se
S Se t t L S S
π
πππ
(7): )](18sin 25.0)(18cos [)(66t t e t t e L S F t t ⋅+⋅=--
100
128
8)6(28)6(62
2222+++=++++++=
S S S S S S (8): 9
9)20(52022)(26
2++
++++=-s e
s s S F s π
2-2 解:
(1): )(1)2()3
2
21(
)(321t e e S S L t f t t ⋅+-=+++-=--- (2): )(12sin 2
1
)(t t t f ⋅=
(3): )(1)2sin 2
1
2(cos )(t t t e t f t ⋅+=
(4): )1(1)1
(
)(11
-⋅=-=---t e S e L t f t s
(5): )(1)22()(2t e e te t f t t t ⋅-+-=---
(6): )(1215sin 15158))
215()21(215
15158()(22
21t t e S L t f t
⋅=++⋅=-- (7): )(1)3sin 31
3(cos )(t t t t f ⋅+=
2-3 解:
(1) 对原方程取拉氏变换,得:
S
S X x S SX x Sx S X S 1)(8)]0()([6)0()0()(2
=+-+--⋅
• 将初始条件代入,得:
6
1
)()86(1)(86)(6)(22++=++=+-+-S S
S X S S S
S X S SX S S X S
4
87247
81)86(16)(22+-++=
++++=S S S S S S S S S X 取拉氏反变换,得:
t t e e t x 428
74781)(---+=
(2) 当t=0时,将初始条件50)0(=•
x 代入方程,得:
50+100x(0)=300 则x(0)=2.5
对原方程取拉氏变换,得: sx(s)-x(0)+100x(s)=300/s
将x(0)=2.5代入,得:
S
300
100X(S)2.5-SX(S)=
+ 100
5
.03100)S(S 3002.5S X(S)+-=++=
s s
取拉氏反变换,得:
-100t 0.5e -3x (t)=
2-4
解:该曲线表示的函数为:
)0002.0(16)(-⋅=t t u
则其拉氏变换为:
s
e s U s
0002.06)(-=
2-5 解:
)0()0()
(3)
(2)(2)(3
0100==+=+i i x y t x dt
t dx t y dt t dy 将上式拉氏变换,得:
2
33
2)()()()32()()23()(3)(2)(2)(30000++=
+=++=+S S S X S Y S X S S Y S S X S SX S Y S SY i i i i
23
-S 32-S Z p ==∴零点极点
又当 时)(1)(t t x i =
S
S X i 1
)(=
S S S S X S X S Y S Y i i 12332)()()()(00⋅++=⋅=
32
123
32)
()0(2
3
12332)()(lim lim lim lim 000
000=
⋅++⋅=⋅=∴=⋅++⋅=⋅=∞∴∞→∞→→→S S S S S Y S y S S S S S Y S y s s s s
2-6 解:
(a )传递函数:
1
321232333211
2
3233321232333
211111H G G G H G G H G G G G H H G G H G G G G H G G H G G G G R C
+++=
⋅++⋅+++⋅
=
(b )传递函数:
(c)传递函数:
(d)传递函数:
3
2121212211211H G G H H G G H G H G G G R C
++++= 2-7 解:
通过方块图的变换,系统可等价为下图:
2-8 解:
2-9 解:(a)
(b)
(c)
(d)
(e)
(f)
(g)
2-10 解:(a)
(b)
(c)
2-11 解:(a)
(b)
(c)
(d)
2-12 解:(a)
(b)
2-13 解:(a)
(b)
2-14 解:
2-15 解:(1)
(2)
2-16 解:
2-17
解:
2-18
解:
以题可画出方块图如下:
2-19 解:
2-20 解:
2-21
解:
(1)
(2、3、4)缺2-22 以后缺
第三章3-1解:
3-3 解:
3-4 解:
3-5
3-6 解:
3-7 解:
3-8 解:
3-9 解:
3-10
3-11
3-12 解:
3-13 解:
3-14解:
3-15
3-16
3-17 解:
3-18
3-19 解:
3-20 解:
3-21 解:
3-22 解:
3-23 解:
3-24
3-25
解:
3-26、3-27 缺3-28
解:
3-29、3-30 缺3-31
解:
3-32、3-33缺
第四章4-1
解:
4-2
解:
4-3 解:
4-4 解:
4-5 解:
4-6 解:(a)
(b)
(c)
(d)
(e)
4-7
4-8、4-9 缺4-10
解:
4-11
解:
4-12解:
4-13、4-14、4-15 缺4-16解:
4-17 缺
4-18
解:。
