分数除法-讲义
《分数除法一》》课件

03
分数除法在几何中的应用
在几何学中,分数除法可以用于计算图形的面积和周长等。例如,在计
算矩形、三角形和圆的面积时,常常需要使用分数除法来计算长度或高
度等参数。
2023
PART 02
分数除法的运算规则
REPORTING
分数除以整数
总结词
分数除以整数时,可以直接将分 子相除,分母保持不变。
详细描述
。
整数除以分数
总结词
整数除以分数时,可以将整数转化为分数,然后进行相乘 。
详细描述
为了将整数转化为分数,可以将整数写作与分母相同的分 数的形式,然后进行相乘。例如,$3 div frac{2}{3} = 3 times frac{3}{2} = 4.5$。
示例
$4 div frac{4}{5} = 4 times frac{5}{4} = 5$。
运算意义的实际应用
理解分数除法的实际意义有助于更好地理解和应用这一运算方法 。
2023
PART 05
练习与巩固
REPORTING
基础练习题
分数除法的基本概念
通过简单的除法运算,帮助学生理解分数除法学生通过实际操作掌握计算方法 。
整数除以分数
2023
《分数除法一》ppt 课件
REPORTING
2023
目录
• 分数除法的定义与性质 • 分数除法的运算规则 • 分数除法的实际应用 • 分数除法的注意事项 • 练习与巩固
2023
PART 01
分数除法的定义与性质
REPORTING
分数除法的定义
分数除法的定义
分数除法是一种数学运算,其定义为 将一个分数除以另一个分数。具体来 说,分数a除以分数b的结果定义为分 数a与分数b的倒数相乘。
第三讲分数除法讲义

第三讲分数除法讲义(1)一、倒数的概念、特征以及特殊数的倒数。
1、倒数:乘积是一的两个数互为倒数。
强调:互为倒数的意义。
2、整数的倒数小于它本身。
3、真分数的倒数大于它本身。
4、假分数的倒数小于或等于它本身。
5、1的倒数是1,0没有倒数。
6、积与乘数的关系:一个数(零除外)乘大于1的数,积比第一个因数大;乘小于1的数,积比第一个因数小;乘以1,积与第一个因数相等。
7、商的大小与除数的关系:一个数(零除外)除以小于1的数,商大于被除数;除以大于1的数,商小于被除数;除以1,商等于被除数。
二、基础题1、求一个分数的倒数,只要把( )2、 的倒数是( ),( )的倒数是7,1的倒数是( ),0( )3、261时=( )分钟 ; 12.5时=( )分钟 ;453时=( )分钟 4、24等于乙数的倒数,乙数是( )。
5、( )是40的倒数,45是( )的倒数。
二、分数除法的意义分数除法的意义和法则:意义:分数除法与整数除法的意义完全相同,都是已知两个数的积与其中一个因数,求另一个因数的运算。
法则:甲数除以乙数(不为0),等于甲数乘乙数的倒数。
甲数、乙数可以是整数、小数和分数。
一个数(0除外)除以真分数,商>被除数。
一个数(0除外)除以1,商=被除数。
一个数(0除外)除以假分数(大于1),商<被除数【例1】:1)说一说下面各除法算式所表示的意义。
769÷ 251310÷ 14157÷ 10918÷2)列式计算。
①把78平均分成4份,每份是多少? ②已知一个数的32是24,求这个数? ③已知两个因数的积是98,其中的一个因数是40,求另一个因数? 【例2】比较大小。
432743()÷ 545454()÷ 237323()÷小结:整数除以分数,可以转化为乘以这个分数的倒数计算,分数除以分数,可以用被除数乘以除数的倒数计算。
【例3】一个正方体的表面积是43平方米,那么这个正方体一个面的面积是多少平方米?【例4】一辆汽车53小时行36千米,平均每小时行多少千米?四、 课堂练习1、简便运算: 611×360÷7 1÷1001÷10001 454×1353-454×3.62、光明小学六(1)班有学生45人,约占全校人数的1.5%,全校大约有学生多少人?3、一段铁丝长20米,剪成每段4/5米,可以剪成几段?4、 58X = 40 \F(2,5) X = \F(4,9) ×\F(3,8)5、154除51的商,再除以253,商是多少?6、154除以51的商,再除以253,商是多少?五、综合训练判断正误1. 35÷5 = \F(5,3) ×5 ( ) 2、4分米的15和5分米的错误!相等。
分数除法讲义

倒数与分数除法1、了解倒数、分数除法的意义教学目的2、掌握计算方法3、会运用在实际冋题中重点:计算方法及实际问题中的运用难点:实际问题中的运用教学内【知识点一】:倒数1、倒数的意义:乘积为1的两个数互为倒数。
(1)、倒数是两个数的关系,它们互相依存,不能单独存在。
单独一个数不能称为倒数。
(必须说清谁是谁的倒数)(2)、判断两个数是否互为倒数的唯一标准是:两数相乘的积是否为“1。
例如:a>b=1则a、b互为倒数。
2、求倒数的方法:①求分数的倒数:交换分子、分母的位置②求整数的倒数:整数分之一。
③求带分数的倒数:先化成假分数,再求倒数。
④求小数的倒数:先化成分数再求倒数。
3、1的倒数是它本身,因为1>=10没有倒数,因为任何数乘0积都是0,且0不能作分母。
非零整数a的倒数为1;分数b的倒数是空。
a a b1真分数的倒数是假分数,真分数的倒数大于1,也大于它本、身。
假分数的倒数小于或等于1。
带分数的倒数小于1。
2用倒数解决问题、(1)用转化的方法解决倒数问题例题1: 一个自然数与它的倒数的和是5.2,这个自然数是多少?小结:已知一个自然数与它的倒数的和,可以把这个和分成整数和纯小数(或真分数)两部分。
整数部分就是这个自然数,纯小数(或真分数)部分就是这个自然数的倒数。
1、用假设的方法比较数的大小3 3 7例题2:如果aX _ = bX— = cX —,且a,b,c均不为0,把a, b,c这三个数按从大到小的顺4 5 3序排列。
(3):用假设的方法解决倒数问题1例题3:两个连续自然数的倒数差是12,求这两个自然数。
小结:解决此类问题,解可以假设其中一个自然数是a,另一个为a+1,再根据题意中的数量关系求【巩固练习二】31、3的倒数是(812、一X()2 ),0.25 和()互为倒数。
18)X 2 = 1X( )= 3 X( )= 17213. 一个自然数与它的倒数的差是21-22,这个数是多少?4 2 14.如果X X - = y X -=z X 1,且X, y,z均不为0,请按照从小到大的顺序排列这三个数。
分数除法讲义【精选】

课 题倒数与分数除法教 学 目 的1、了解倒数、分数除法的意义2、掌握计算方法3、会运用在实际问题中重 难 点重点:计算方法及实际问题中的运用 难点:实际问题中的运用教 学 内 容【知识点一】 :倒数1、倒数的意义:乘积为1的两个数互为倒数。
(1)、倒数是两个数的关系,它们互相依存,不能单独存在。
单独一个数不能称为倒数。
(必须说清谁是谁的倒数)(2)、判断两个数是否互为倒数的唯一标准是:两数相乘的积是否为“1”。
例如:a×b=1则a 、b 互为倒数。
2、求倒数的方法:①求分数的倒数:交换分子、分母的位置。
②求整数的倒数:整数分之一。
③求带分数的倒数:先化成假分数,再求倒数。
④求小数的倒数:先化成分数再求倒数。
3、1的倒数是它本身,因为1×1=10没有倒数,因为任何数乘0积都是0,且0不能作分母。
非零整数a 的倒数为a 1 ;分数 a b的倒数是ba 。
1、真分数的倒数是假分数,真分数的倒数大于1,也大于它本身。
假分数的倒数小于或等于1。
带分数的倒数小于1。
2、用倒数解决问题(1)用转化的方法解决倒数问题例题1:一个自然数与它的倒数的和是5.2,这个自然数是多少?小结:已知一个自然数与它的倒数的和,可以把这个和分成整数和纯小数(或真分数)两部分。
整数部分就是这个自然数,纯小数(或真分数)部分就是这个自然数的倒数。
1、用假设的方法比较数的大小 例题2:如果a ×43 = b ×53 = c ×37,且a ,b ,c 均不为0,把a ,b ,c 这三个数按从大到小的顺序排列。
(3): 用假设的方法解决倒数问题 例题3:两个连续自然数的倒数差是121,求这两个自然数。
小结:解决此类问题,可以假设其中一个自然数是a ,另一个为a+1,再根据题意中的数量关系求解【巩固练习二】1、83的倒数是( ),0.25和( )互为倒数。
2、21×( )=( )×718=1×( )=3×( )=13. 一个自然数与它的倒数的差是212221,这个数是多少?4.如果x ×74 = y ×92=z ×21,且x ,y ,z 均不为0 ,请按照从小到大的顺序排列这三个数。
分数除法(一)ppt课件

目
CONTENCT
录
• 分数除法概述 • 分数除法的基本性质 • 分数除法的计算实例 • 分数除法的应用实例 • 分数的乘除混合运算
01
分数除法概述
分数除法的定义
02
01
03
分数除法是一种数学运算,通常表示为两个分数相除 。
分数除法是将一个分数除以另一个分数的结果。
例如,将一个分数2/3除以另一个分数3/4,即表示为 (2/3) ÷ (3/4)。
分数乘除混合运算的技巧和注意事项
通分
在进行分数的乘除混合运算时, 常常需要运用通分的技巧,将不 同的分母变为相同的分母,以便
于计算。
约分
在分数的乘除混合运算中,约分 也是一个常用的技巧。通过约分 ,可以简化分数的形式,从而更
方便地进行计算。
灵活运用公式
在进行分数的乘除混合运算时, 需要灵活运用各种公式,以便于
快速准确地得到结果。
THANK YOU
感谢聆听
进行运算
将分子相除,分母相乘得到结果
。例如,$\frac{3}{4}
Hale Waihona Puke \div\frac{2}{3} = \frac{3}{4} \times
\frac{3}{2}$。
03
分数除法的计算实例
简单的分数除法计算实例
题目
计算 1/2 ÷ 3/4
答案
1/2 ÷ 3/4 = 2/3
解释
首先,将除法转换为乘法,即 (1/2) × (4/3)。分子乘以一个数,分母除以同一个数,可 以得到新的分数。所以,1/2 × 4/3 = 2/3。
乘法是加法的重复
分数乘法可以看作是加法的重复,即把相同的数加起来。例如,$\frac{3}{4} \times 3 = \frac{3}{4} + \frac{3}{4} + \frac{3}{4}$。
人教6上分数除法讲义

章节复习考点讲义(人教版)人教版数学六年级上册章节考点精讲精练第三单元《分数除法》知识点一:倒数的认识1.倒数的意义乘积是1的两个数互为倒数。
倒数具备两个条件:一是两个数;二是乘积是1。
2.互为倒数的两个数特点如果两个数都是分数,那么两个分数的分子和分母正好颠倒了位置;如果一个是整数,则另一个分数的分子是1,分母是这个整数。
3.求一个数倒数的方法知识互联网知识导航(1)通过计算,乘积是1的两个数互为倒数。
(2)交换这个数的分子和分母的位置。
4.特殊的1的倒数是1,0没有倒数。
知识点二:分数除法的计算法则一个数除以一个不等于0的数,等于乘这个数的倒数。
知识点三:分数四则混合运算规律1. 只有乘、除法,按照从左到右的顺序依次进行计算。
2. 在没有括号的算式里,既有加、减法又有乘、除法,要先算乘、除法,再算加、减法。
3. 在一个有小括号的算式里,应该先算小括号里面的,后算小括号外面的。
知识点四:分数除法的应用题1.解决“已知一个数的几分之几是多少,求这个数”的问题,一般方法:方程法:(1)找出单位“1”,设未知量为x;(2)找出题中的等量关系式;(3)列出方程并解答;(4)检验并写出答案。
2. “已知比一个数多(少)几分之几的数是多少,求这数”的问题的解法:方程法:根据题中的等量关系:“单位‘1’的量×(1±几分之几)=已知量”或“单位‘1’的量±单位‘1’的量×几分之几=已知量”,设单位“1”的量为x,列方程解答。
3. 已知两个量的和(差),其中一个量是另一个量的几分之几,求这两个量的问题的解法:有两个量都是未知的,先把谁看作单位“1”都可以,设其中一个量为未知数x,用这个量表示另一个量,然后找出等量关系,列方程解答出一个量,再解答第二个量。
4. 利用抽象的“1”解决实际问题:工程问题是分数问题的特例,工作总量与工作效率都不是具体的数,而是用抽象的分数来表示。
(完整版)分数除法讲义.doc
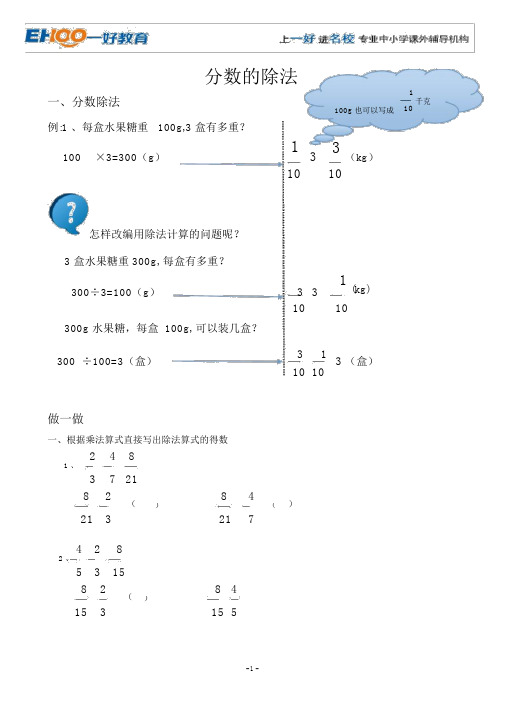
分数的除法一、分数除法例:1 、每盒水果糖重 100g,3 盒有多重? 100g 也可以写成 110千克100 ×3=300(g )133(kg )10 10怎样改编用除法计算的问题呢?3 盒水果糖重 300g, 每盒有多重?300÷3=100(g )3 3 1(kg)1010300g 水果糖,每盒 100g, 可以装几盒?300 ÷100=3(盒)3 13 (盒)10 10做一做一、根据乘法算式直接写出除法算式的得数2 4 8 1 、7 21 38 2(8 4 )21 3 )(2174 2 82 、3 15 58 2( 8 4 15 3 )5154 2、把一张纸的平均分成 2 份,每份是这张纸的几分之几?自己试着折一折,5算一算。
42 份,就是把 4 个 1把 5 平均分成5 平1 ,就是2 均分成两份, 每份就是两个5 544 25 25把4 平均分成 2 份,每份就是455的 1,也就是412524 4 15 225 如果把这张纸的4平均分成 3份,每份是这张纸的几分之几?5453根据上面的折纸实验和算式,你能发现什么规律?3、小明2小时走 2km,小红5小时走了5km。
谁走得快些?312 62小明平均每小时走: 23 怎么计算呢?画个图试试吧想:先求1小时走了多少千米,也就是求 2 的1,即21。
再求 3 个1小时走了3 2 2 3多少千米,即 2 1 3 。
22 2 1333 (km)32 22 2小红平均每小时走:5 5 5 122(km)6 12 6 512为什么写成“”答:小明走得快。
通过以上两个例子,你发现了什么?分数除法的计算法则:甲数除以乙数(0除外),等于甲数乘乙数的倒数。
做一做一、用你发现的规律计算下面各题。
9 3 2381024897 4 16 5二、直接写出得数。
1 1= 4÷12=8 3= 13=3 ÷12 7 9 ÷7 ÷4 10 14 5 5 9 35 ÷11 = 11 ÷ 21= 8 ÷6 = 10 ÷5 =三、填一填。
分数除法讲义

分数除法导学:一、解题技巧:一抓,二找,三确定,四对应。
1、一抓:抓住关键句——分率句;(含几分之几的句子)2、二找:找准单位“1”的量;(“的”前“比”后的量)3、三确定:确定单位“1”是已知还是未知(已知单位1用除法,未知单位1用乘法)4、四对应:找出相对应的数量与分率,列出算式。
单位“1”的量×分率=分率对应量(分率对应量÷分率=单位“1”的量)第一步:分数除法1、分数除法的运算意义已知两个因数的积与其中一个因数,求另一个因数的运算。
2、分数除法的计算法则除以一个数(0除外),等于乘这个数的倒数。
3、分数混合运算分数混合运算与整数混合运算的顺序相同。
【典型例题1】张师傅53小时做6个零件,1小时可以做几个零件? 【思路导航】根据分数除法的计算法则,列出算式。
【举一反三】(1)7÷61 (2)52÷54 (3)2116÷32【典型例题2】一盒果汁53升,每杯可以装101升,已经装了2杯,这盒果汁还可以装几杯? 【思路导航】用一盒果汁的总量÷每杯装的总量 = 一共装的杯数。
再用一共装的杯数-已经装的杯数 = 还可以装的杯数【举一反三】(1)2÷41+3 (2)1200÷53-500 (3)12÷54÷83第二步:解决问题简单的和稍复杂的“已知一个数的几分之几,求这个数”的问题的解题规律:1、设“单位1”的量为x ,列方程解答。
2、已知量÷已知量所对应总量的几分之几 = “单位1”的量。
【典型例题1】新安村种棉花9公顷,占全村耕地面积的53,全村耕地面积有多少公顷? 【思路导航】找出解决问题所需要的条件,得出等量关系。
全村耕地面积×53 = 棉花种植面积【举一反三】林场有柳树180棵,是杨树棵树的43,林场有杨树多少棵?【典型例题2】果园里有桃树168棵,比枣树多71,枣树有多少棵? 【思路导航】本题是把枣树看做“单位1”,桃树比枣树多出的部分,相当于枣树的71。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分数除法-讲义-CAL-FENGHAI.-(YICAI)-Company One1分数的除法一、分数除法例:1、每盒水果糖重100g,3盒有多重100×3=300(g ) 1033101=⨯(kg怎样改编用除法计算的问题呢3盒水果糖重300g,每盒有多重 300÷3=100(g ) 1013103=÷(kg)300g 水果糖,每盒100g,可以装几盒300÷100=3(盒) 3101103=÷(盒)做一做一、根据乘法算式直接写出除法算式的得数1、 2187432=⨯=÷32218 ( ) =÷74218( ) 2、1583254=⨯ =÷32158( ) =÷54158100g 也可以写成101千2、把一张纸的54平均分成2份,每份是这张纸的几分之几自己试着折一折,算一算。
=÷=÷524254=⨯=÷2154254 如果把这张纸的54平均分成3份,每份是这张纸的几分之几=÷354根据上面的折纸实验和算式,你能发现什么规律3、小明32小时走2km,小红125小时走了65km 。
谁走得快些小明平均每小时走:322÷想:先求31小时走了多少千米,也就是求2的21,即212⨯。
再求3个31小时走了多少千米,即3212⨯⨯。
32323212322=⨯=⨯⨯=÷(km ) 小红平均每小时走:)(25126512565km =⨯=÷答:小明走得快。
通过以上两个例子,你发现了什么分数除法的计算法则:甲数除以乙数(0除外),等于甲数乘乙数的倒为什么写成“512⨯” 怎么计算呢画个图试试做一做一、用你发现的规律计算下面各题。
=÷3109=÷283=÷9824 54167÷二、直接写出得数。
13 ÷112 = 47 ÷12= 89 ÷37 = 1÷34 =5÷1011 = 1411 ÷21= 58 ÷56 = 910 ÷35 = 三、填一填。
3例:4、小红用长8m 的彩带做了一些花,每朵花用2m 的彩带。
她把其中的四朵花送给了同学,小红还剩几朵花=-÷4328答:小红还剩_______朵花。
5、计算下面两题。
15)5132(51⨯+÷ ]15)5132[(51⨯+÷做一做1、陈爷爷每天绕操场跑6圈,2分钟可以跑半圈。
照这个速度,陈爷爷每天跑步要用多少时间2、324318÷÷ 76)3261(÷+ 294)]8343(4[⨯--125)8143(÷- 135717138⨯+÷ 879720÷-3、解下列方程19155=x 154218=x 281554=÷x 124132=÷x二、解决问题例:1、根据测定,成人体内的水分约占体重的32,而儿童体内的水分约占体重的54。
一个儿童体内有28kg 的水分,他的体重是他爸爸的157。
(1)小明的体重是多少千克解:设小明的体重是x 千克。
2854=xx=5428÷ x=35 答:小明的体重是35kg.(2)小明的爸爸体重是多少千克小明的体重⨯54=小明体内水分的质量爸爸的体重⨯157=小明的体重根据“儿童体内的水分占体重的54”可以列出下面的关系式解:设小明的爸爸体重是x 千克。
157x=35 x=______ x=_________ 答:小明爸爸的体重是x 千克。
做一做1、友谊超市有进口水果120千克,恰好是国产水果的45 。
这个超市有国产水果多少千克(用两种方法解答)2、某工厂有女职工1008人,占全厂职工总数的 611 ,全厂职工共有多少人(用两种方法解答)例:2、学校美术小组有25人,美术小组的人数比航模小组多41。
航模小组有多少人解:设航模小组有x 人。
x+x 41=25 (1+41)x=25 x=25÷45x=______答:航模小组有_____人。
做一做一、解方程43x —41=52 X÷51=25 32X —83X=167X - 23 X = 29 4÷ 23 X = 25二、解决问题1、(1)某电视机厂去年上半年生产电视机48万台,是下半年产量的54。
这个电视机厂去年的产量是多少万台航模小组的人数 + 美术小组比航模小组多的人数=美术小组的人数(2)某电视机厂去年上半年生产电视机48万台,上半年比下半年多51。
这个电视机厂去年的产量是多少万台三、比和比的应用比的意义例:2003年10月15日,我国第一艘载人飞船“神州”五号顺利升空。
在太空中,执行此次任务的杨利伟在飞船向人们展示了联合国和中华人民共和国国旗。
杨利伟展示的两面旗都是长15cm,宽10cm.怎样用算式表示他们长和宽的关系两个数相除又叫做两个数的 比 15比10 记作 15:10 10比15 记作 10:15 42252比90 记作 42252:90在两个数的比中,比号前面的数叫做比的 前项,比后面的数叫做比的 后项。
比的前项除以后项所得商,叫做 比值。
15 : 10 =15 ÷ 1 0 =23 前 比 后 比 项 号 项 值“:”是比号比值通常用分数表示,也可以用小数或整数表示根据分数与除法的关系,两个数的比也可以写成分数形式。
例如:15:10也可以写成1015,仍读作“15比10”做一做一、填空1、小明和小亮在文具店买同样的练习本。
小明买了6本,共花了元。
小亮买了8本,共花了元。
小明和小亮买的本数之比是( ):( ),比值是( );花的钱数之比是( ):( ),比值是( )。
2、3:( )=24 ( ):8=0.53、()()()()=÷===40:1248:6填小数 4、在○里填上﹥、﹤或﹦。
785÷855141÷41 6565 5、甲与乙的比是2:5,那么甲是乙的()(),乙是甲乙两数和的()()。
比的基本性质商不变的性质:被除数和除数同时除以相同的数,商不变。
分数的基本性质:分数的分子和分母同时乘或除以相同的数,分数值不变。
(1)15:10=(15÷5):(10÷5) =3:2180:120=(180÷__):(120÷__)=( ):( )(2)把下面各比化成最简单的整数比。
92:61 : 2 :61 想:为什么要乘18=( ):( ):2=(×100):(2×10) =75:200=( ):( )当一个比的前后项不是整数时,怎样把它化成最简单的整数比做一做一、把下面的比化成最简单的整数比。
: 25:100 1:32:16 : :85二、求比值。
13:39 61:41 6.0:21: : :21三、选择题1.化简比的依据是( )。
A.除法的运算B.分数的基本性质C.比的基本性质2.一杯盐水,盐占盐水的203,则盐和水的比是( )。
:20 :17 :233.比的前项缩小2倍,后项扩大2倍,比值( )。
A.缩小4倍 B.扩大2倍 C.不变4.一种彩电降价51后是960元,这种彩电原价是( )元。
A.51960÷ B. ()511960+÷ C. ()511960-÷5.一段路,甲车用6小时走完,乙车用3小时走完,甲乙两车的速度比是( )。
A 、1∶2 B 、2∶3 C 、6∶3比的应用8321例:某种清洁剂浓缩液的稀释瓶,瓶子上标明的比表示浓缩液和水的体积之比。
小红按1:4的比配制了一瓶500ml 稀释液,其中浓缩液和水的体积分别是多少 小亮:我把总体积平均分成5份…… 小丽:浓缩液占总体积的141+ 每份是:500÷5=100(ml ) 浓缩液有:)(100411500ml =+⨯浓缩液有:100×1=100(ml ) 水有:)()(()()500ml =⨯水有:100×4=400(ml )答:浓缩液有_____ml,水有____ml.做一做1、某妇产医院上月新生婴儿303名,男女婴儿人数之比是51:50.上月新生男女婴儿各有多少人2、一个长方形的周长是70厘米,长与宽的比是4:3,这个长方形的面积是多少3、用120厘米的铁丝做一个长方形的框架。
长、宽、高的比是3:2:1.这个长方形的长、宽、高分别是多少基础务实一、直接写得数 =÷274 =÷683 =÷5210 =÷324 =÷5432 =÷3249 =⨯274 =÷⎪⎭⎫ ⎝⎛+2814175二、解下列方程。
6532892716318376=+⨯==÷x x x X :47 =32三、下面各题,怎样简便就怎样计算。
943253375.07648496515714÷+÷⨯÷÷⎪⎭⎫ ⎝⎛-⨯÷÷+⨯+÷+216598125591679416771343768四、看图列式计算。
1、(1) (2)2、(1) (2)90棵棵 71420甲组乙组71人甲组 乙组 棵 90棵五、填空题。
1、()()()():122425.0:3=÷===2、在○里填上“>”、“<”或“=”。
7575175757523759475⨯÷÷÷÷ 3、18分=()()时 450米=()()千米 600毫升=()()升4、已知两个因数的积是3225,其中一个因数是21,另一个因数是( )。
5、修一条路,每在修这条路的72,( )天修完。
6、把3米长的绳子平均剪成8段,每段是( )米,每段是这条绳子的()()7、一辆汽车行6千米用油54升,平均行1千米用油( )升,平均用油1升行( )千米 ;这辆汽车行驶路程与用油量的最简比是( )。
(1)1615平方米是65平方米的( );15千克是( )千克的45倍。
(2)36千克的61是( );( )千克的61是36千克。
(3)60千克比( )千克多51;60千克比( )千克少51。
8、女同学人数是男同学的54。
(1)男、女同学人数之比是( );女、男同学人数之比是( )。
(2)男同学与总人数之比是( );女同学与总人数之比是( )。
男同学人数比女同学多()();女同学人数比男同学多()()。
能力提升一、列式计算:1、比40千克多51千克是多少千克 2、比40千克多51是多少千克3、35比40少几分之几4、41减去51的差除以50,结果是多少5、40比35多几分之几6、一个数的21与52的和是152,这个数是多少二、解决问题1. 一辆普通自行车的售价是386元,相当于一辆普通摩托车售价的215 ,这辆摩托车的售价多少元(1) 看作单位“1”的量是( ) (2) 画出线段图(3) 列方程方法计算 (4)算术方法计算2、(1)一种VCD 影碟机原来的价钱是1260元,现在比原来降价154。
