信号与系统周期计算方法
《信号与系统》复习

物理意义:非周期信号可以分解为无数个频率为, 复振幅为[X(j)/2p]d 的虚指数信号ejw t的线性组合。
简述傅氏反变换公式的物理意义?
傅里叶变换性质
F 时移特性 x(t t 0 ) X( j) e jt
0
x(t)
X(j)
展缩特性
1 F x (at) X( j ) a a
(n = 1,2) (n = 1,2)
奇对称周期信号其傅里叶级数只含有正弦项。
周期信号的傅里叶级数 周期信号x(t) 如图 所示,其傅氏级数系数的特点是
偶对称周期信号其傅里叶级数只含有直流项与余弦项 周期信号f(t)如图所示,其直流分量等于_____
周期信号的频谱及特点
Cn是频率的函数,它反映了组成信号各次谐波 的幅度和相位随频率变化的规律,称频谱函数。
《信号与系统》复习
考核方式
平时成绩20% 实验成绩20% 期末成绩60%
题型: 选择题(每题3分,共30分) 填空题(每空2分,共20分) 简答题(每题4分,共20分)
计算题(每题10分,共30分)
第一章:信号与系统分析导论
周期信号平均功率计算 若电路中电阻R=1Ω,流过的电流为周期电流i(t)= 4cos(2πt)+2cos(3πt) A,其平均功率为( ) 系统的数学模型 连续时间系统:系统的输入激励与输出响应都必须为 连续时间信号,其数学模型是微分方程式。 离散时间系统: 系统的输入激励与输出响应都必须 为离散时间信号,其数学模型是差分方程式。
L[ yzs (t )] Yzs ( s) H ( s) L[ x(t )] X ( s)
写出系统函数H (s) 的定义式
简述拉氏变换求解微分方程的过程
信号与系统第4章 周期信号的频域分析(3学时)

T0 /2
0
x(t )sin(n 0t )dt
四、信号对称性与傅里叶系数的关系
3、半波重迭信号
~ x (t ) ~ x (t T0 / 2)
~ x (t )
A t
T0
T0 / 2 0
T0 / 2
T0
特点: 只含有正弦与余弦的偶次谐波分量,而无奇次谐波分量。
四、信号对称性与傅里叶系数的关系
~ x (t )
2 1 -4 -3 -2 -1 1 2 3 4
~ x (t ) ~ x1 (t ) ~ x2 (t )
nπ nπt t~ x (t ) 1.5 Sa ( ) cos( ) 2 2 n 1
~ x1 (t )
2
x 1(t ) 2
1 2 3 4
-4 -3 -2 -1
三、周期信号的功率谱
一、周期信号频谱的概念
连续时间周期信号可以表示为虚指数信号之和,其 中Cn 为傅里叶系数 。
~ x (t )
n =
Cn e
jn0t
1 Cn T0
T0 t 0
t0
~ x (t )e jn 0t dt
问题1:不同信号的傅里叶级数形式是否相同? 相同 问题2:不同信号的傅里叶级数不同表现在哪里? 系数
例3 课本P129
例4 已知连续周期信号的频谱如图,试写出信号的 Fourier级数表示式。 Cn
3 2 1 1 3 4 3 2
9
6
0
3
6
9
n
解: 由图可知 C0 4
C 1 3
C2 1
C 3 2
~ x (t )
信号与系统 陈后金 第二版 课后习题答案(完整版)

(1) f (t) = 3sin 2t + 6 sinπ t
(2) f (t) = (a sin t) 2
(8)
f
(k)
=
cos⎜⎛ ⎝
πk 4
⎟⎞ ⎠
+
sin⎜⎛ ⎝
πk 8
⎟⎞ ⎠
−
2
cos⎜⎛ ⎝
πk 2
⎟⎞ ⎠
解:(1)因为 sin 2t 的周期为π ,而 sin πt 的周期为 2 。
显然,使方程
−∞
0
2-10 已知信号 f (t) 的波形如题 2-10 图所示,绘出下列信号的波形。
f (t)
2
1
−1 0
t 2
题 2-10 图
(3) f (5 − 3t) (7) f ′(t) 解:(3)将 f (t) 表示成如下的数学表达式
(5) f (t)u(1 − t)
由此得
⎧2
f
(t)
=
⎪ ⎨ ⎪ ⎩
f (t)u(1− t) 2
1
0.5
t
−1 0
1
(7)方法 1:几何法。由于 f (t) 的波形在 t = −1处有一个幅度为 2 的正跳变,所以 f ′(t) 在 此处会形成一个强度为 2 的冲激信号。同理,在 t = 0 处 f ′(t) 会形成一个强度为 1 的冲激信 号(方向向下,因为是负跳变),而在 0 < t < 2 的区间内有 f ′(t) = −0.5 (由 f (t) 的表达式可
第 1 页 共 27 页
《信号与系统》(陈后金等编)作业参考解答
(2)显然,该系统为非线性系统。 由于
T{f (t − t0 )}= Kf (t − t0 ) + f 2 (t − t0 ) = y(t − t0 )
张宇-信号与系统各章内容整理48学时【最新】

第一章 信号与系统主要内容重点难点1.信号的描述x[n]、x (t ),两者不同之处2.【了解】 信号的功率和能量3.【掌握】自变量变换(计算题目)、理解变换前后图片的缩放或信号的变化4.【了解】 常见信号:指数(j t j n e e w w 、)、正弦(cos cos t n w w 、)、单位冲激(()[]t n d d 、)、单位阶跃(()[]u t u n 、)5.【掌握】用阶跃函数表示矩形函数;冲激与阶跃信号的关系;冲激信号的提取作用;指数信号和正弦信号的周期性。
6.【了解】系统互联7.【掌握】系统的基本性质:记忆与无记忆性、可逆性、因果性、稳定性、时不变与线性。
对已知系统进行性质判断(掌握)1.3、5、71.00cos j n n e w w 、的周期性判断,是周期的条件,若是周期的,则周期:2.00cos j tt e w w 、的周期:自变量变换的量值确定0cos j n n e w w 、的周期性和频率逆转性。
系统的时不变性与线性等性质的证明2T ωπ=02N mωπ=第二章 线性时不变系统第三章 周期信号的傅里叶级数表示FS本章内容安排基本思路:主要内容难点 ✧ 系统的单位冲激响应容易求出:令 ()()x t t d =,对应的输出即为单位冲激响应() h t ;✧ 将任意信号分解为冲激信号()[]t n d d 、的线性组合[][][]; ()()()k x n x k n k x t x t d d t d t t ¥¥-=-=-=-åò✧ 利用L TI 系统的线性和时不变性,在单位冲激响应[]() h t h n 、已知的情况下,推导连续时间和离散时间系统对任意输入x 的响应:[][][]y n =x n * h n ; y(t)=x(t)* h(t)✧ 利用输入输出的卷积关系,根据单位冲激响应[]() h t h n 、,判断ITI 系统的性质1.【掌握】卷积和2.【掌握】卷积积分3.【掌握】用[]() h t h n 、判断L TI 的性质 4.【理解】 初始松弛 5. 【掌握】任意信号与冲激信号、阶跃函数的卷积性质(对比1章冲激信号抽取作用)卷积运算中,求和或者求积时,上下限的确定本章内容安排基本思路:主要内容难点第四章 连续时间傅里变换CFT✧ L TI 系统对复指数信号st ne z 、响应容易求得:()st H s e 、()n H z z 其中()()s H s h e d t t t +--=ò、()[]kk H z h k z+-=-=å✧ 将周期信号分解为0jk tew 的线性组合,即傅立叶级数表示式:()()()0021jk tjk tTk k k k jk t k Tx t a e a e a x t e dt T πωω+∞+∞=-∞=-∞-⎧==⎪⎪⎨⎪=⎪⎩∑∑⎰✧ 傅立叶级数收敛条件分析✧ 从频域分析系统对信号的作用(3.9、3.10)1.【掌握】连续时间周期信号的傅立叶级数公式,求常见信号的傅立叶级数 2.【掌握】收敛条件、傅立叶截断时的吉伯斯现象3..【理解】滤波和频谱的概念,能够判断信号是否能通过一确定的滤波器 5.【掌握】RC 回路实现的滤波器的滤波特性分析,滤波器设计时的折衷思想。
信号与系统第6讲第3章周期信号的傅里叶级数表示

sin(2 k(1/ 4)) k
sin(k k
/ 2)
根据Example3.5的结果,用性质计算傅里叶级数的系数
分析:原函数为x(t),本函数为g(t)
g (t )
x(t
1)
1 2
,周期方波的参数T
4,T1
1,
如果原函数的系数为ak,x(t 1)的系数为bk
bk
a e jk (2 / 4)1 k
在不连续点上,傅里叶级数的收敛趋势-吉伯斯现象
不连续点上收敛于不连续点的平均值 不连续点附近呈现起伏现象,起伏的峰值不随N增加而降低 峰值为不连续点差值的9%
吉伯斯现象的实际意义
不连续信号的傅里叶级数截断近似在接近不连续点有高频起伏 选择足够大的N,可以保证这些起伏的总能量可以忽略
2024/6/10
2024/6/10
信号与系统-第6讲
19
§3.5 连续时间傅里叶级数性质
(4)Example3.8 计算周期冲激串的傅里叶级数系数 根据性质计算周期方波的系数
周期冲激串可表示为x(t) (t kT ) k
ak
1 T
T / 2 (t)e jk 2t /T dt 1
T / 2
T
周期方波为g (t ),它的导数为q(t )
c0为直流分量, c0 2T1 / T
对照前面 例题验证
结果
20
§3.5 连续时间傅里叶级数性质
(5)Example3.9
1.x(t)是实信号
2.x(t)是周期信号,T 4,傅里叶级数系数ak
3.ak 0,k 1
4.傅里叶系数为bk
e
j
k
/
2
a
的信号是奇信号
信号与系统-学习提纲

jωt
为虚指数信号,是周期信号,模拟角频率= ω ,单位=rad/s
(1). Ae (2).
jωt
= A e jθ × e jωt = A e j (ωt +θ ) ,A 称为复振幅,包含幅度|A|和相位θ
ω > 0 时, 当 t 增大时, 在单位圆上逆时针旋转; ω < 0 呢? e jωt 在复平面上的运动轨迹:
信号与系统--学习指导
Signals and Systems
1/共 32 页
m, n, i, j, k 及大写——作为变量时,一般表示整数
第一章 信号与系统概述 一、判断信号的周期性——P17 的 1-5 1.理解定义: ∀t ∈ ( −∞, ∞), x (t ) = x (t + T ) , ∀k ∈ ( −∞, ∞ ), x ( k ) = x ( k + N ) ; 1.)要求对任意的 t , k 都满足 2.)周期离散信号要求 周期 必须是 整数,连续信号的周期则 无此 要求! 2.最小的正周期 T0 , N 0 称为基本[基波]周期,一般情况下周期指基本[基波]周期 3.若 T , N 是信号的周期,则 mT , mN 也是信号的周期 4.两个周期信号的周期有公倍数时,相加[或相乘]得到的信号 才能是 周期的 5.掌握正弦余弦、 虚指数信号的频率, 如 cos(ω0t + θ ) 、e 根据模拟角频率或数字角频率,判定和计算它们的周期 6.对于 cos (ω0t + θ ) 形式的信号,不妨化成虚指数的形式,判断周期性可以不用考虑它的
可见,复数 A 包含 2 种信息,幅度|A|和相位θ——复数的优点;A=Re+jIm 为另一种表示 1. lim e = 0 的条件是: σ = Re[ s ] < 0
第一章 信号与系统概论(2)

+∞
∫ (1 − x )δ (x )dx = ∫ δ (x )dx = u (t )
t t −∞ −∞
( t ∈ [t , t ]) ( t ∉ [t , t ])
1 2 1 2
6. 符号函数
定义
1 sgn(t) = 0 −1
(t > 0) (t = 0) (t < 0)
sgn(t) 1 0 -1
可用阶跃信号表示
sg ( t) = 2u(t) −1 n
信号的因果和反因果分解
任意信号 f (t ) 有因果反因果分解
at
1.指数信号
实际上,经常遇到的是因果指数衰减信号 因果指数衰减信号
2.正弦信号
正弦信号和余弦信号统称为正弦信号,一 般可表示为: f t = K sin ωt + φ 其中 K 为振幅, 是角频率,φ 称为初 2π 1 = 相位。正弦信号的周期 T = , ω f 其中 f 是频率。 与指数信号相似,正弦信号对时间的微分 或积分仍是正弦信号
∫
t
−∞
δ (τ ) d τ = u ( t )
d dt
u (t ) = δ (t )
∫
+∞ −∞
δ ( t − t 0 ) f ( t ) dt =
∞ −∞
=
∫
f ( t 0 )δ ( t − t 0 ) dt = f ( t 0 )
相乘
f (t )δ (t − t0 ) = f (t0 )δ (t − t0 )
冲激函数的检零性质
当冲激函数应用于非线性函数时,具有 应用于非线性函数时, 应用于非线性函数时 检测其零点,并反映其导数的性质。 检测其零点,并反映其导数的性质 由于函数在其零点 t i ,i=1, 2, …, n 有 f t i = 0 ,使得在其零点领域,有
《信号与系统》教与学第四章
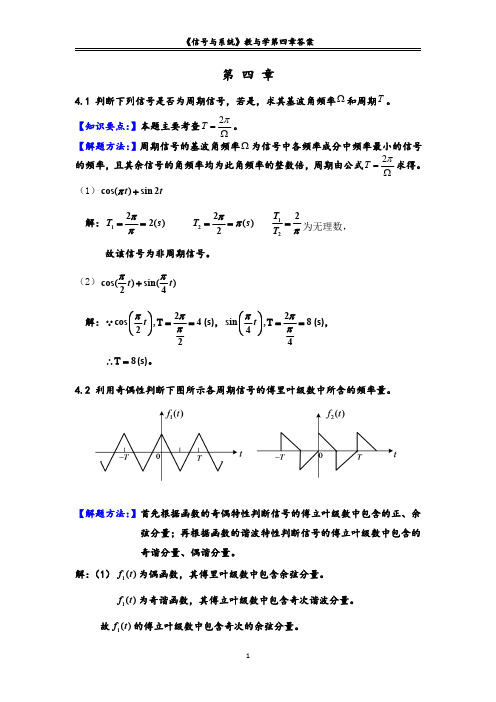
j n e 3
j n
e3
1 n
sin
n 3
,
n
0, 1,
2,
2
《信号与系统》教与学第四章答案
4.4 周期信号 f (t ) 的双边频谱 Fn 如图所示,求其三角函数表达式。
【知识要点:】本题主要考查周期信号的频谱概念,单边谱与双边谱的关系。
(3)计算信号的功率。
【知识要点:】本题主要考查周期信号的频谱概念应用;帕斯瓦尔功率等式应用。
T
2
;
f
t
A0 2
n1
An
cos
nt n
;P
Fn 2 。
n
【解题方法:】利用已知条件观察求出 ,并带入公式计算求出各次谐波分量;
根据单边幅度谱和双边幅度谱的关系、单边相位谱和双边相位谱的关系画出双
边幅度谱和相位谱;最后利用帕斯瓦尔功率等式计算信号的功率。
解:(1)
x
t
16 cos
20
t
4
6
cos
30
t
6
4
cos
40
t
3
10 (rad/s) ,
T
2
2 10
1 (s) , 5
周期信号所含谐波次数为二次,三次,四次;
求得。
(1) cos( t ) sin 2t
解: T1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信号与系统周期计算方法
例1-1 试判断下列各信号f(t)是否为周期信号。
若是,其周期T为多少?
(1) (2)
f(t)=cos2t+sin3t
(3) f(t)=cos10t+sin10t (4) f(t)=sin2t+cos πt
(5) f(t)=t2+1 (6)
f(t)=sin2πt+cos5πt
(7) f(t)=(sin2t)2(8)
(9) f(t)=10cos4πtU(t)
解(1)为周期信号,其周期s
(2) f(t)为两个子信号f1(t)=cos2t与f2(t)=sin3t的和,即f(t)=f1(t)+f2(t),且f1(t)=f1(t-n1T1),f2(t)=f2(t-n2T2),其中n1∈Z,n2∈Z。
则当(n1与n2必须为不可约的整数)时,f(t)即为周期信号,其周期T=n1T1=n2T2。
今子信号cos2t的周期为s,子信号sin3t的周期为s。
故有
由于已为不能再约的整数比,故f(t)为周期信号,其周期T为
(3) 子信号cos10t的周期为,子信号sin10t的周期为。
故有
可见f(t)为一周期信号,其周期T为
此题也可用下述方法判断,即
可见f(t)为周期信号,其周期为。
(4) 子信号sin2t与cos t的周期分别为,。
故有
可见不是整数比,故f(t)不是周期信号。
(5) 不是周期信号。
(6) 子信号与的周期分别为,。
故有
可见f(t)为周期信号,其周期为T=2T1=5T2=2 s。
(7) 因,故f(t)为周期信号,其周期。
(8) 因f(t)的振幅是随时间按指数规律变化的,故f(t)不是周期信号。
(9) 因f(t)不是无始无终的信号,而是有始无终的信号,故不是周期信号。
