材料力学B试题6弯曲变形
材料力学B作业

第一章 绪 论一、选择题1、构件的强度是指_________,刚度是指_________,稳定性是指_________。
A. 在外力作用下构件抵抗变形的能力B. 在外力作用下构件保持其原有的平衡状态的能力C. 在外力作用下构件抵抗破坏的能力2、根据均匀性假设,可认为构件的________在各点处相同。
A. 应力B. 应变C. 材料的弹性常数D. 位移3、下列结论中正确的是________ 。
A. 内力是应力的代数和B. 应力是内力的平均值C. 应力是内力的集度D. 内力必大于应力4、下列说法中,正确的是________ 。
A. 内力随外力的改变而改变。
B. 内力与外力无关。
C. 内力在任意截面上都均匀分布。
D. 内力在各截面上是不变的。
5、图示两单元体虚线表示其受力后的变形情况,两单元体的切应变γ分别为________ 。
A. α,αB. 0,αC. 0,-2αD. α,2α二、计算题1、如图所示,在杆件的斜截面m-m上,任一点A处的应力p=120 MPa,其方位角θ=20°,试求该点处的正应力σ与切应力τ。
2、已知杆内截面上的内力主矢为F R与主矩M如图所示,且均位于x-y平面内。
试问杆件截面上存在哪种内力分量,并确定其大小。
图中之C点为截面形心。
3、板件ABCD的变形如图中虚线A’B’C’D’所示。
试求棱边AB与AD的平均正应变以及A点处直角BAD的切应变。
第二章 拉伸与压缩一、选择题和填空题1、轴向拉伸杆件如图所示,关于应力分布正确答案是_________。
A 1-1、2-2面上应力皆均匀分布;B 1-1面上应力非均匀分布,2-2面上应力均匀分布;C 1-1面上应力均匀分布,2-2面上应力非均匀分布;D 1-1、2-2面上应力皆非均匀分布。
2、图示阶梯杆AD 受三个集中力作用,设AB 、BC 、CD 段的横截面积分别为3A 、2A 、A ,则三段的横截面上 。
A 轴力和应力都相等B 轴力不等,应力相等C 轴力相等,应力不等D 轴力和应力都不等3、在低碳钢拉伸曲线中,其变形破坏全过程可分为4个变形阶段,它们依次是 、 、 、 。
材料力学B试题6弯曲变形
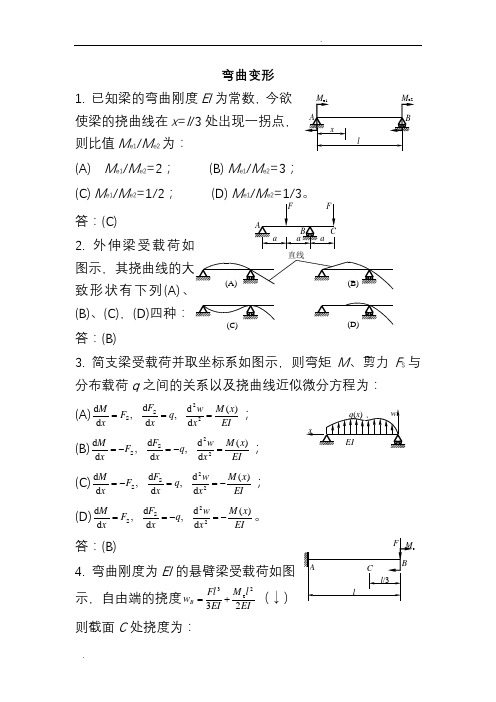
弯曲变形1. 已知梁的弯曲刚度EI 为常数,今欲使梁的挠曲线在x =l /3处出现一拐点,则比值M e1/M e2为:(A) M e1/M e2=2; (B) M e1/M e2=3; (C) M e1/M e2=1/2; (D) M e1/M e2=1/3。
答:(C)2. 外伸梁受载荷如致形状有下列(A)(B)、(C),(D)四种:答:(B)3. 简支梁受载荷并取坐标系如图示,则弯矩M 、剪力F S 与分布载荷q 之间的关系以及挠曲线近似微分方程为: (A)EI x M x w q xF F x M )(d d ,d d ,d d 22SS ===;(B)EI x M xw q x F F xM)(d d ,d d ,d d 22SS =-=-=; (C)EI x M x w q x F F x M )(d d ,d d ,d d 22SS -==-=;(D)EI x M x w q xF F x M )(d d ,d d ,d d 22SS -=-==。
答:(B)4. 弯曲刚度为EI 的悬臂梁受载荷如图示,自由端的挠度EIl M EI Fl w B 232e 3+=(↓)则截面C 处挠度为:(A)2e 3322323⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛l EI M l EI F (↓);(B)233223/323⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛l EI Fl l EI F (↓); (C)2e 3322)3/(323⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛l EI Fl M l EI F (↓);(D)2e 3322)3/(323⎪⎭⎫ ⎝⎛-+⎪⎭⎫⎝⎛l EI Fl M l EI F (↓)。
答:(C)5. 画出(a)、(b)、(c)三种梁的挠曲线大致形状。
答:6.7.(a)、(b)刚度关系为下列中的哪一种: (A) (a)>(b); (B) (a)<(b);(C) (a)=(b); (D) 不一定。
答:(C)8. 试写出图示等截面梁的位移边界条件,并定性地画出梁的挠曲线大致形状。
材料力学课件ppt-6弯曲变形

L 6
(x
a)3 ]
4、求转角
x 0 代入得:
A
1
x0
Fb(L2 b2 ) 6LEI
x L代入得:
B
2
xL
Fab(L 6LEI
a)
目录
5、求 ymax 。
由 dy 0 求得 ymax 的位置值x。
dx
A
Fb(L2 b2 ) 6LEI
0,
C
1
xa
Fab(a b) 3LEI
0( a
例6-4 已知:q、l、 EI,求:yC ,B
目录
w w w
目录
弯曲变形/用叠加法求梁的变形 w
B1
ql3 24 EI
,
wC1
5ql 4 384 EI
w
B3
(ql2 ) l 3EI
ql3
3EI
,
wC 3
3ql 4 48 EI
w
B2
(ql) l2 16 EI
ql3 16 EI
,
wC 2
(ql )l 3 48 EI
则简支梁的转角方程和挠度方程为
AC段 (0 x a)
1(x)
Fb 6LEI
[3x2
(L2
b2
)],
y1 ( x)
Fb 6LEI
[x3
(L2
b2 )x],
BC段 (a x L)
2 ( x)
Fb 6LEI
[3x2
(L2
b2 )]
F(x 2
a)2
,
y2
(x)
Fb 6LEI
[x3
(L2
b2)x
目录
§6-4 用叠加法求弯曲变形 一、叠加法前提
材料力学第六章 弯曲变形

4
2
C
B
)
=
A
( A)q C
l q
( B )q
(b)
B
( wC )q
l
θ B ( θ B )q ( θ B ) M e
+
Me
(c)
Mel ql 24 EI 6 EI
3
A
B
( B ) M e
( A ) MC ( wC ) M
e
e
l
例题3
AB梁的EI为已知,求梁中间C截面挠度.
F1l 2 F2 la 0.4 400 200 B ( ) 16 EI 3 EI 210 1880 16 3 +0.423 10-4 (rad)
F1l a F2a F2a l wC 5.19 106 m 16 EI 3 EI 3 EI wmax w (3)校核刚度: l l
x A
dx
F
x
C' dω
B
d tg dx
二、挠曲线的微分方程
1.纯弯曲时曲率与弯矩的关系
M EI
1
横力弯曲时, M 和 都是x的函数.略去剪力对梁的位移的影 响, 则
1 M ( x) ( x) EI
2.由数学得到平面曲线的曲率
F
1 | w | 3 2 2 ( x) (1 w )
q
A x B
w w F wq
+
w wF wq
例1 已知:EI, F,q .求C点挠度 F q
A
C a a
B
Fa 3 ( wC )F 6 EI
材料力学第6章弯曲变形

M1 EIw1
Fb x1 l
2 x1
" EIw2
Fb M2 x2 F ( x2 a ) l
2 x2 2
EIw1
Fb C1 l 2
x2 a Fb F C2 (i) EIw2 l 2 2
工学院
§6.2 挠曲线的微分方程
纯弯曲情况下,弯矩与曲率 间的关系(5.1):
M EI
1
--(a)
横力弯曲时,梁截面上有弯矩也有剪力,对于跨 度远大于截面高度的梁,剪力对弯曲变形的影响可以 省略,(a)式便可以作为横力弯曲变形的基本方程。其 中,M和1/ρ都是x的函数。
工学院
§6.2 挠曲线的微分方程
(o) (p)
CB段 (a x2 l )
Fb 2 3l 2 2 2 l b 3 x ( x a ) 2 2 6l b Fb 2 l 2 2 3 EIw2 l b x x ( x a ) 2 2 6l b 2 EIw2
车床主轴的变形过大会影响 齿轮的啮合和轴承的配合, 造成磨损不匀,产生噪音, 降低寿命以及影响加工精度。
工学院
§6.1 工程中的弯曲变形问题
吊车梁的变形过大,会 使梁上小车行走困难, 出现爬坡现象,还会引 起较严重的振动。
变形超过允许数值,即 使在弹性范围内,也被 认为是一种失效现象。
工学院
§6.1 工程中的弯曲变形问题
l
2
b
2
3
工学院
§6.3 用积分法求弯曲变形—实例3
7). 讨论
上面得到最大挠度表达式为: 3 1 Fb 2 2 wmax l b 9 3 EIl
《材料力学》弯曲计算-习题

②无均布载荷段弯矩图均为直线。有均布载荷段,弯矩图为
抛物线,其开口与均布载荷方向相同。
(3)弯矩、剪力、载荷集度的关系
①
M '(x) F S (x) F S'(x) q(x)
② FS=0的点是M图的取极值的点,FS=0的段M图是平行
于轴线的直线。
注意: 内力图上要注明控制面值、特殊点纵坐标值。
利用微分关系绘内力图
y
B截面 30.3 +
z
C截面 15.1 z
-
+
69
34.5
(d) 单位:MPa
Engineering Mechanics
四、弯曲 弯曲强度计算
例3 之二
解:(1)求截面形心轴,即中性轴z轴。
yC
( yi Ai ) Ai
170 30 170 30 200 (170 30)
2
2
17030 30 200
解:(1)外力分析,判变形。
10kN
50kN
(a) A
CD
B
z
4m
2m
4m
求得支坐反力
FA 26kN ,FB 34kN
荷载与梁轴垂直,梁将发
26kN 26 16
34kN
生平面弯曲。中性轴z过形心
+ (b)
与载荷垂直,沿水平方向。
FQ(kN)
104 136
34
(2)内力分析,判危险面。剪力
+
(c)
⑤解题步骤:
1)外力分析,判变形、中性轴,求截面的几何性质、支反力。 2)内力分析,判危险面,画剪力图、弯矩图(可只画弯矩图)
3)应力分析,判危险点。 4)强度计算。
材料力学B试题6弯曲变形
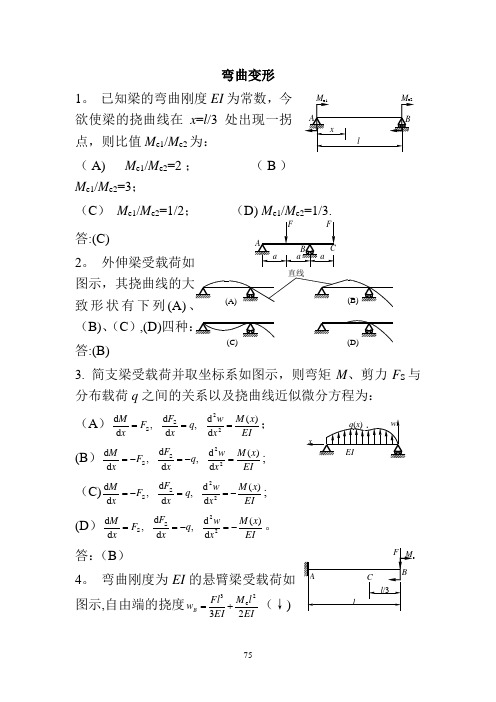
弯曲变形1。
已知梁的弯曲刚度EI 为常数,今欲使梁的挠曲线在x =l /3处出现一拐点,则比值M e1/M e2为:(A) M e1/M e2=2; (B ) M e1/M e2=3;(C ) M e1/M e2=1/2; (D) M e1/M e2=1/3.答:(C)2。
外伸梁受载荷如致形状有下列(A)(B)、(C ),(D)答:(B)3. 简支梁受载荷并取坐标系如图示,则弯矩M 、剪力F S 与分布载荷q 之间的关系以及挠曲线近似微分方程为: (A )EI x M xw q xF FxM )(d d ,d d ,d d 22SS ===;(B )EI x M x w q x F F x M )(d d ,d d ,d d 22S S =-=-=; (C)EI x M xw q x F F x M )(d d ,d d ,d d 22S S -==-=;(D )EI x M xw q x F F x M )(d d ,d d ,d d 22S S -=-==。
答:(B )4。
弯曲刚度为EI 的悬臂梁受载荷如图示,自由端的挠度EIl M EI Flw B 232e3+=(↓)则截面C 处挠度为:(A )2e 3322323⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛l EI M l EI F (↓);(B )233223/323⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛l EI Fl l EI F (↓); (C)2e 3322)3/(323⎪⎭⎫ ⎝⎛++⎪⎭⎫⎝⎛l EI Fl M l EI F (↓);(D)2e 3322)3/(323⎪⎭⎫ ⎝⎛-+⎪⎭⎫⎝⎛l EI Fl M l EI F (↓).答:(C )5. 画出(a )、(b)、(c )三种梁的挠曲线大致形状。
答:6.7.(a )、(b)刚度关系为下列中的哪一种: (A) (a)>(b ); (B) (a)<(b);(C ) (a)=(b ); (D) 不一定. 答:(C)8。
材料力学弯曲变形

压杆稳定计算 1)根据压杆的约束条件确定长度系数 )根据压杆的约束条件确定长度系数µ 2)计算杆件自身的柔度 )计算杆件自身的柔度λ(10.7),判断发生弯曲的平面 , 也可由惯性矩来判断最大、最小刚度平面) (也可由惯性矩来判断最大、最小刚度平面) 3)通过比较 的大小,判断计算临界压力的公式 的大小, )通过比较λ的大小
1. λ1与材料的性能有关,材料不同,λ1的数 与材料的性能有关,材料不同, 值也就不同; 越大,杆件越容易弯曲。 值也就不同;λ越大,杆件越容易弯曲。 2. 满足 1条件的杆件称为细长杆或大柔度杆; 满足λ≥λ 条件的杆件称为细长杆 大柔度杆; 细长杆或 也叫大柔度杆的分界条件。 也叫大柔度杆的分界条件。其临界应力可用欧 拉公式计算。 拉公式计算。 3. λ越大杆件越容易弯曲。 越大杆件越容易弯曲。 越大杆件越容易弯曲 解题步骤: 解题步骤: 1)由截面形状确定最大、最小刚度平面 )由截面形状确定最大、 2)计算柔度,判断欧拉公式是否适用 )计算柔度, 3)计算临界压力和临界应力 )
σ =
P ≤ [σ ] st A
14
图示结构中, 为圆截面杆 直径d=80 mm,A端固 为圆截面杆, 例10.4 图示结构中,AB为圆截面杆,直径 , 端固 端铰支; 是正方形截面杆 边长a=70 mm,C端也为 是正方形截面杆, 定,B端铰支;BC是正方形截面杆,边长 端铰支 , 端也为 铰支; 和 杆可以独自发生弯曲变形而互不影响 杆可以独自发生弯曲变形而互不影响; 铰支;AB和BC杆可以独自发生弯曲变形而互不影响;两杆 的材料是A3钢 的材料是 钢,其λp=104 ,l=3 m,稳定安全系数 st=2.5 ; ,稳定安全系数n 求结构的许可载荷P。 求结构的许可载荷 。
π 2E Pcr = σ cr A = 2 ⋅ A = 269kN λ
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
弯曲变形1. 已知梁的弯曲刚度EI 为常数,今欲使梁的挠曲线在x =l /3处出现一拐点,则比值M e1/M e2为:(A) M e1/M e2=2; (B) M e1/M e2=3; (C) M e1/M e2=1/2; (D) M e1/M e2=1/3。
答:(C)2.致形状有下列(A)(B)、(C),(D)四种: 答:(B)3. 简支梁受载荷并取坐标系如图示,则弯矩M 、剪力F S 与分布载荷q 之间的关系以及挠曲线近似微分方程为: (A)EI x M xw q x F F x M )(d d ,d d ,d d 22SS ===;(B)EI x M x w q x F F x M )(d d ,d d ,d d 22SS =-=-=; (C)EI x M xw q x F F x M )(d d ,d d ,d d 22SS -==-=;(D)EI x M xw q xF F x M )(d d ,d d ,d d 22SS -=-==。
答:(B)4. 弯曲刚度为EI 的悬臂梁受载荷如图示,自由端的挠度EIl M EI Fl w B 232e 3+=(↓)则截面C 处挠度为:(A)2e 3322323⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛l EI M l EI F (↓);(B)233223/323⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛l EI Fl l EI F (↓); (C)2e 3322)3/(323⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛l EI Fl M l EI F (↓);(D)2e 3322)3/(323⎪⎭⎫ ⎝⎛-+⎪⎭⎫⎝⎛l EI Fl M l EI F (↓)。
答:(C)5. 画出(a)、(b)、(c)三种梁的挠曲线大致形状。
答:6. 试画出图示梁的挠曲线大致形状。
(a)(a)(b)(c)7. 正方形截面梁分别按(a)、(b)两种形式放置,则两者间的弯曲刚度关系为下列中的哪一种: (A) (a)>(b); (B) (a)<(b);(C) (a)=(b); (D) 不一定。
答:(C)8. 试写出图示等截面梁的位移边界条件,并定性地画出梁的挠曲线大致形状。
答:x =0, w 1=0,1w '=0;x =2a ,w 2=0,w 3=0;x =a ,w 1=w 2;x =2a ,32w w '='。
9. 试画出图示静定组合梁在集中力F 作用下挠曲线的大致形状。
(a)w ===θw w10. 画出图示各梁的挠曲线大致形状。
答:11. 作图示外伸梁的弯矩图及其挠曲线的大致形状。
12. 弯曲刚度为EI 的等截面外伸梁如图示。
当梁内任一纵向层总长度均不因其自重引起的弯曲而有所改变时,证明两支座间的距离应为l -2a =0.577l 。
⎢⎣⎡=⎰l Δ:提示证:令外伸端长度为a ,内跨长度为2b ,a l b -=2,因对称性,由题意有:⎰⎰⎰⎰⎰=⎪⎭⎫ ⎝⎛-+⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-===b b a l lx x q qbx EI w x qa x x q EI w x x M EI w x l 020202000d 2d 2d 2d )(d Δε得 a 3 + 3a 2b -2b 3 = 0 a 3 + a 2b + 2a 2b -2b 3 = 0 a 2 + 2ba -2b 2 = 0 b a )13(-=a lb -=2a = 0.211l即 l -2a = 0.577l 证毕。
13. 等截面悬臂梁弯曲刚度EI 为已知,梁下有一曲面,方程为w = -Ax 3。
欲使梁变形后与该曲面密合(曲面不受力),试求梁的自由端处应施加的载荷。
解:EIAx w EI x M 6)(-=''= F S (x ) = -6EIA x=l , M = -6EIAlF =6EIA (↑),M e =6EIAl (14. 变截面悬臂梁受均布载荷ql 及弹性模量E 。
试求截面A 的挠度w A 解:x lhb h x b x I 1212)()(303== x h b ql x I x M w E 306)()(-=='' C x hb ql w E +-='2303 D Cx x h b ql Ew ++-=330 由边界条件0,='==w w l x 得3043032,3hb ql D h b ql C -==3042h Eb ql w A -=(↓) ,30338h Eb ql C =θ()15. 在刚性圆柱上放置一长2R 、宽b 、厚h 的钢板,已知钢板的弹性模量为E 。
试确定在铅垂载荷q 作用下,钢板不与圆柱接触部分的长度l 及其中之最大应力。
解:钢板与圆柱接触处有 EIql R 2/12= 故 qREbh RqEIl 623==REhbh R EI bh ql W Mz 26//6/2/222====σ16. 弯曲刚度为EI 的悬臂梁受载荷如图示,试用积分法求梁的最大挠度及其挠曲线方程。
解:30)(6)(x l lqx M w EI --==''C x l l qw EI +--='40)(24D Cx x l lq EIw ++--=50)(120 120,244030l q D l q C -==12024)(120403050l q x l q x l l q EIw -+--=EIl q w 3040max -=(↓)17. 图示梁的左端可以自由上下移动,但不能左右移动及转动。
试用积分法求力F 作用处点A解:Fx Fl w EI -='' 3,03FlD C -==362332Fl x F x Fl EIw --=EIFl w A 33-=(↓)18. 简支梁上自A 至B 的分布载荷q (x )=-Kx 2,K 为常数。
试求挠曲线方程。
解:2)(Kx q x M -=='' 二次积分B Ax x K x M++=412)( x =0, M =0, B =0 x =l , M =0, 123Kl A -=x Kl x K x M w EI 1212)(34-==''C x Kl x K w EI +-='2352460D Cx x Kl x K EIw ++-=33672360x =0, w =0, D =0 x =l , w =0, 36045Kl C -=)45(3605336x l x l x EIKw +--=(↓) 19. 弯曲刚度为EI 的悬臂梁原有微小初曲率,其方程为y =Kx 3。
现在梁B 端作用一集中力,如图示。
当F 力逐渐增面接触。
若作用力为F ,试求: (1)梁与水平面的接触长度; (2)梁B 端与水平面的垂直距离。
解:(1) 受力前C 处曲率Ka a 6)(11=ρ,弯矩M (a )1 = 0受力后C 处曲率0)(12=a ρ,弯矩M (a )2 = -F (l - a )1212)()()(1)(1a M a M a a -=-ρρ EIa l F Ka )(6--=- ⇒EIKF Fla 6+=(2)同理, 受力前x 1截面处0)(),(6d d )(111122111=+=⎪⎪⎭⎫ ⎝⎛=+=x M x a K x y x xa x ρ受力后x 1截面处 )()(,d d )(1121211221x b F x M x y x --==ρEI x b F x a K x y )()(6d d 112112--=+-积分二次D Cx EIFx EI Fbx Kx Kax y +++-+=132131211623C =0,D =0 EIKF EIKla lb 66+=-=231)6()(361EIK F EI EIKl y y bx B +===20. 图示弯曲刚度为EID Cx Bx Ax qx EIw ++++-=23424式中A 、B 、C 、D 为积分常数。
试根据边界条件确定常数A 、B 、C 、D ,并绘制梁的剪力F S 、弯矩M 图。
解:x = 0,w = 0,D = 0 C Bx Ax qx w EI +++-='236230,0,0=='=C w xA qx x F w EI 6)(S +-=='''12,0,2S ql A F l x ===0,='=w l x 代入w '方程242ql B -=21. 已知承受均布载荷q 0的简支梁中点挠度为EIl q w 384540=,则图示受三角形分布载荷作用梁w C = 。
答:EIl q 768540(↓)22. 试用叠加法计算图示梁A 点的挠度w A 。
解:22)2/(3)2/(3)2/(233aEI a F EI a F EI a F w A ++= qlEIFa 48133=(↓)23. 试求图示梁BC 段中点的挠度。
解:EIa q EI a qa EI a qa w 384)2(53)3(3)(21433+⎪⎪⎭⎫ ⎝⎛+=EIqa8394=(↓)24. 已知梁的弯曲刚度EI 。
试用叠加法求图示梁截面C 的挠度w C 。
解:EI a a l q EI a l q EI l a l q EI ql w C 96)2(256)2(96)2(76853434⋅-+-+--= EIa l qa 96)23(222-=(↓)25. 已知梁的弯曲刚度EI 为常数。
试用叠加法求图示梁B 截面的挠度和转角。
)(30244030↓==EIl q w EIl q B B θ解:EIl q EI l q EI l q w B 12011308404040=-=(↓)qB EI l /2l /2aA⎪⎭⎫ ⎝⎛-=a l q 22C 2BEIl q EI l q EI l q B 8246303030=-=θ26. 试用叠加法求图示简支梁跨度中点解:⎢⎣⎡++⎥⎦⎤⎢⎣⎡⨯+=EI l Fl EI l F EI l Fl EI l F w C 3)2/)(8/(16)2/(16)2/)(8/(248)2/(223EIFl l EI Fl EI Fl l EI l Fl 38474643768546)2/)(8/(333=⋅+=⎥⎦⎤+27. 试用叠加法求图示简支梁集中载荷作用点C 的挠度。
解: EIFlEI l F EI l F w w B B C 483)4/(413414333====(↓)28. 已知简支梁在均布载荷作用下跨中的挠度为EIqlw C 38454=,用叠加法求图示梁中点C 的挠度。
解: ()EIl q EIl q w C 76853842/54040=⋅=(↓)q /23q29. 弯曲刚度为EI 的悬臂梁受载荷如图示,试用叠加法求A 端的转角θA 。
