浅谈圆曲线测设方法(DOC)
圆曲线
文献综述一、圆曲线的详细测设在各类线路工程弯道处施工，常常会遇到圆曲线的测设工作。
目前，圆曲线测设的方法已有多种，如偏角法、切线支距法、弦线支距法等。
然而，在实际工作中测设方法的选用要视现场条件、测设数据求算的繁简、测设工作量的大小，以及测设时仪器和工具情况等因素而定。
另外，上述的几种测设方法，都是先根据辅点的桩号（里程）来计算测设数据，然后再到实地放样。
因此，在实际工作中利用上述传统测设方法，有时会因地形条件的限制而无法放样出辅点（如不通视或量距不便等），或放样出的辅点处无法设置标桩。
在本次毕业设计的论文课题中介绍的几种圆曲线测设的新方法，不仅计算简单、测设便捷，而且可在不需要知道曲线上某点里程的情况下进行，从而避免了按预先给定的曲线点反算的测设数据放样不通视而转站的麻烦。
同时，利用本文介绍的新方法，还可以根据线路工程施工进度的要求，灵活地选择性地放样出部分曲线；也可以用于快速地确定曲线上某一加桩的位置；若用于线路验收测量，则更加方便，验测结果更具有代表性、更可靠。
二、全站仪在任意站测设圆曲线及方法交点偏角法测设方法用全站仪任意站测设圆曲线，安置一次仪器就能完成全部工作。
虽然外业计算麻烦，但对于不能设站的转点，可谓方便灵活。
但它的不足之处仍然是计算烦锁，对于不熟悉内业的外业工作者，很难实际操作。
如果利用一些程序计算器，编制输入：AB 的四组坐标和半径、九个数据的程序，可迅速得出放样数据，简化了外业工作。
为了放样工作的便利,可在平面控制网中纳入一些放样点,构成GPS同级全面网。
由于放样点间距离较近,在进行同步环和闭合环检验时可仅考虑各分量的较差,而不考虑相对闭合差。
因为,用相对闭合差来衡量是不合理的。
由于GPS接收机的固定误差,相位中心偏差以及观测时的对中误差均在1mm～5mm之间,对于几十米的短边,其相对闭合差值势必较大。
3)平面控制网的设计主要考虑独立基线的选择以及异步闭合环的设计,要考虑构成尽可能多的闭合图形,并将网中处于边缘的观测点用独立基线连接起来,形成封闭图形。
第六章(4) 曲线测设
（2）坐标计算
xi R sin i
yi R(1 cosi )
i
Li
•180
R
（3）测设方法？ 优点：各点测设相互独立，不产生误差积累 缺点：检核条件少
4、极坐标法 根据仪器点和待测点的坐标，计算距离和方位角，
然后直接测设的方法，是目前应用最广泛的方法。 5、RTK法（坐标转换）
二、复曲线测设 两条或两条以上半径不同的同向圆曲线组成的曲线称为复 曲线。 切基线法 JD1～JD2为切基线，GQ为主副曲线的公切点
8.7 103 mm
4．圆曲线参数方程 坐标系同前：
xi R sin i m yi R(1 cosi ) P
式中：i
180
R
(li
l0 ) 0
0
l0 2R
β、m、p为缓和曲线参数
若αi以弧度表示，并顾及
0
l0 2R
，则有：
i
li
l0 R
0
li
l0 R
l0 2R
li
0.5l0 R
(2n
l 2n2
0
1)!(2 R) 2 n1
(4n
3)
［例］已知某曲线设计时选配的圆曲线半径R = 200 m，
缓和曲线长l0 = 70 m，若n=2试按上式估算坐标计算的截 断误差。
[解]
R3 x
705 4!4004
1000 9
3.0 101 mm
R3 y
706 5!4005
1000 11
DK126+891.92
（三）主点放样 步骤： （1）仪器安于JD点，瞄准线路前进方向的后方，沿视线方向 量切线长T，即得ZY点 （2）同理瞄准前进方向，在视线上量T可得YZ点
圆曲线主点测设(word文档良心出品)
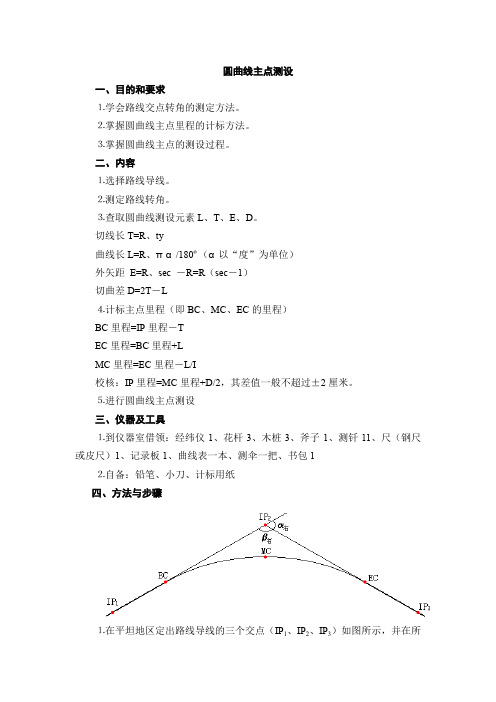
圆曲线主点测设一、目的和要求⒈学会路线交点转角的测定方法。
⒉掌握圆曲线主点里程的计标方法。
⒊掌握圆曲线主点的测设过程。
二、内容⒈选择路线导线。
⒉测定路线转角。
⒊查取圆曲线测设元素L、T、E、D。
切线长T=R、ty曲线长L=R、πα/180º（α以“度”为单位）外矢距E=R、sec －R=R（sec－1）切曲差D=2T－L⒋计标主点里程（即BC、MC、EC的里程）BC里程=IP里程－TEC里程=BC里程+LMC里程=EC里程－L/I校核：IP里程=MC里程+D/2，其差值一般不超过±2厘米。
⒌进行圆曲线主点测设三、仪器及工具⒈到仪器室借领：经纬仪1、花杆3、木桩3、斧子1、测钎11、尺（钢尺或皮尺）1、记录板1、曲线表一本、测伞一把、书包1⒉自备：铅笔、小刀、计标用纸四、方法与步骤⒈在平坦地区定出路线导线的三个交点（IP1、IP2、IP3）如图所示，并在所选点上用木桩标定其位置，导线边要在于80m，目估β右<145°。
⒉在交点IP2、上安置经纬仪，用测回法观测β右，并且计算出转角α。
⒊假定圆曲线半径R=100m，然后根据R和α右，在《公路曲线测投用表》中，查出曲线测设元素T、L、E、D。
⒋计算圆曲线主点的里程（假定IP2的里程已知为K4+296.67）。
IP2K4+ 296.67－）TBC－）LEC－）L/2MC+ D/2IP2（校核）⒌设置圆曲线主点⑴在IP2－－IP1方向线上，自IP2时取切线长T得圆曲线起点BC，插一测钎，作为起始桩。
⑵在IP2－－IP3方向线上，自IP2量取切线长T得圆曲线终点EC，插一测钎，作为终点桩。
⑶用经纬仪设置β右/2的方向线，即角β右的角平分线，在此角分线上自IP2量取外矩E，得圆曲线中点MC，插一测钎作为中点桩。
⒍站在曲线内侧观看BC、MC、EC桩是否有圆曲线的线型，以作为概略检核。
⒎交换工种后再重复5的步骤，看两次设置的主点位置是否重合，如果不重合，而且差得太大，那就查找原因，重新测设，如在容许范围内，则点位即可确定。
圆曲线测设，传统方法讲解
圆曲线测设，传统方法讲解根据线路偏角α、圆曲线半径R计算测设数据进行放样。
测设分两步进行：先测设圆曲线的三个主点（直圆点ZY、曲中点QZ和圆直点YZ），再详细测设圆曲线上按规定桩距各副点(中桩点)。
一、圆曲线测设元素的计算二、圆曲线主点测设1．主点里程的计算注意：YZ=JD+T-D二、圆曲线主点测设1．主点里程的计算2．主点的测设（1）ZY点：将经纬仪置于交点JDi上，望远镜照准后交点JDi-1或此方向上的转点，自交点JDi沿此方向量取切线长T，即得圆曲线起点ZY；量取ZY到最近一个直线桩的距离与两桩号之差比较，不应超过限值，最后打桩。
（2）YZ点：将望远镜照准前交点JDi+1或此方向上的转点，往返量取切线长T，得圆曲线终点，打下YZ桩。
（3）QZ点：沿分角线方向量取外距E，打下QZ桩。
三、圆曲线的详细测设1．圆曲线测设的基本要求详细测设所采用的桩距与曲线半径有关，桩距的要求见表（1）整桩号法：将曲线上靠近ZY的第一个桩的桩号凑整成为l0倍数的整桩号，然后按桩距l0连续向YZ设桩，这样设桩均为整桩号。
（2）整桩距法:从曲线起点和终点开始，分别以桩距l0连续向曲线中点设桩，或从曲线的起点，按桩距l0设桩至终点。
由于这样设置的桩均为零桩号，因此应注意加设百米桩和公里桩。
2.圆曲线详细测设的方法圆曲线详细，最常用的方法有切线支距法、偏角法等。
（1）切线支距法切线支距法是以圆曲线的起点ZY或终点YZ为坐标原点，以切线为x轴，过原点的半径方向为y轴，建立直角坐标。
按曲线上各点坐标x、y设置曲线。
测设步骤①从ZY（或YZ）点开始用钢尺或皮尺沿切线方向量取Pi的横坐标xi ，得垂足Ni 。
②在各垂足Ni上用方向架定出垂直方向，量取纵坐标yi，即可定出Pi点。
③曲线上各点设置完毕后，应量取相邻各桩之间的距离，与相应的桩号之差作比较，且考虑弧弦差的影响，若较差均在限差之内，则曲线测设合格；否则应查明原因，予以纠正。
圆曲线的详细测设
第三节圆曲线的详细测设§11 —3圆曲线的详细测设一、偏角法测设圆曲线圆曲线的主点ZY、QZ、YZ定出后,为在地面上标定出圆曲线的形状，还必须进行曲线的加密工作。
曲线点：对圆曲线进行加密，详细测设定出的曲线上的加密点。
曲线点的间距：一般规定，R> 150 m时曲线点的间距为20m, 50m W R<150m时曲线点的间距为10m 。
R<50m时曲线上每隔5m测设一个细部点；在点上要钉设木桩，在地形变化处还要钉加桩。
曲线测设：设置曲线点的工作，常用的方法有：偏角法和切线支距法。
1.偏角法的测设原理：1 ）偏角：即弦切角2）原理：根据偏角（》）及弦长（c）测设曲线点。
如图11-4 :从ZY点出发，根据偏角3 1及弦长C（ZY-1 ）测设曲线点1；根据偏角及弦长C（ 1 一2）测设曲线点2… 等。
2•偏角及弦长的计算：（1）偏角计算：原理：偏角（弦切角）等于弦所对应的圆心角的一半。
心角：则相应的偏角：K 180 •如图11-4, ZY-1曲线长为K,所对圆= —* --------R 7Tu 舉K 180^爲"竺——•——-2 ZR n当所测曲线各点间的距离相等时，以后各点的偏角则为第一个偏角3的累计倍数。
即:§ =u ⑻)1I 2/?d； = 23】I6y—3*5] .....氏=吃（2）弦长计算（如图11-4）严密计算公式：Jrdi /f(' =2R sin $sin — =C二sin —1 2 R■※弦弧差（弦长与其相对应的曲线长之差）：弦弧差=K i -C i = L i3/（24R2）当R=450m时，20m的弦弧差为2mm ,•••当R>400m时，不考虑弦弧差的影响。
由于铁路曲线半径一般很大，20m的弦长与其相对应的曲线长之差很小，就用弦长代替相应的曲线长进行圆曲线测设。
近似计算：'、"整弦：里程为20m倍数的两相邻曲线点间的弦长（曲线点间距20m对应的弦长）。
圆曲线测设
第四章圆曲线要素计算及测设根据提供资料，=40º20′（右）,R=120米，转角点JD的桩号为K3+135.12，用偏角法测设各桩点（规定桩距为20米）。
切线长：曲线长:外矢距：切曲差：经计算，T=36.73 L=70.40 E=6.53根据JD的桩号为K3+135.12，则：JD桩号 K3+135.12-) T 36.73ZY桩号 K3+098.39+) L 70.40YZ桩号 K3+098.39-) L/2 35.20QZ桩号 K3+133.59+) D/2 1.53JD桩号 K3+135.12所以，经计算交点的里程与校核计算相符。
第一节仪器安置在ZY点上的施测法一、在ZY点上施测法11．计算根据转折角和半径R及交点桩计算三主点的桩号为：ZY： K3+098.39； QZ ：K3+133.59 ；YZ： K3+168.79。
因ZY点的里程为3+098.39，在曲线上，它前面最近的整里程为3+100.00，所以起始弧长=（3+100）-（3+098.39）=1.61（m）。
又因点YZ点的里程为3+168.79，在曲线上，它后面最近的里程为3+160.00，弧长=(3+168.79)-(3+160.00)=8.79（m）。
现将计算的偏角值到列表如表4-1，供测设时使用。
为检查计算有无错误，可与总偏角核对。
本次研究课题中的总偏角为=20º10′00″，与计算之总偏角20º10′05″相差05″，这是因为偏角表计算至秒为止，秒后数值四舍五入所造成的误差，与测量精度无影响，属容许误差。
2、施测方法：如图4-1所示，将仪器安置在ZY点上，全站仪显示对准0º0′0″，后视JD，然后旋转望远镜，拨至第一桩点K3+100.00的偏角0º27′40″，从ZY点起沿此方向量出第一段曲线长 1.61米相应的弦长，定出第一桩点。
再拨至第二桩点K3+120.00的偏角6º11′26″，从第一桩点量出第二段曲线长20米相应的弦长，交出第二桩点。
圆曲线及其主点的测设
第二节圆曲线及其主点的测设§11—2 圆曲线及其主点的测设一、圆曲线概述1．圆曲线半径铁路：我国《新建铁路测量工程规范》和《铁路技术管理规程》中规定：采用的圆曲线半径为：4000、3000、2500、2000、1800、1500、1200、1000、800、700、600、550、500、450、400和350米。
各级铁路曲线的最大半径为4000米。
Ⅰ、Ⅱ级铁路的最小半径：在一般地区分别为1000米和800米，在特殊地段为400米；Ⅲ级铁路的最小半径：在一般地区为600米，在特殊困难地区为350米。
公路：我国《公路工程技术标准》中规定：高速公路的最小半径：在平原微丘区为650米,在山岭重丘区为250米；一级公路在上述两种地区分别为400米和125米；二级公路分别为250米和60米；三级公路分别为125米和30米；四级公路分别为60米和15米。
2．圆曲线主点圆曲线的主点：ZY——直圆点, 即直线与圆曲线的分界点；QZ——曲中点,即圆曲线的中点；YZ——圆直点,即圆曲线与直线的分界点。
圆曲线的控制点：ZY、QZ、YZ、JD。
JD——两直线方向的交点,也是一个重要的点,但不在线路上。
图11-3圆曲线及其主点和要素3．圆曲线要素T——切线长,即交点至直圆点或圆直点的直线长度(JD--ZY,JD—YZ之距离)；见图11-3L——曲线长,即圆曲线的长度(ZY—QZ—YZ圆弧的长度）；E0——外矢距,即交点至曲中点的距离(JD至QZ之距离)；α——转向角,即直线方向转变的水平角；R——圆曲线半径。
T、L、E0总称为圆曲线要素.4、圆曲线要素的计算：α和R分别根据实际测定和线路设计时选定，可按公式法或查表法确定圆曲线的要素T、L、E o1）公式法：切线长曲线长外矢距2）查表法：在《铁路曲线测设用表》（以下简称曲线表）中以α、R为引数，查得相应的圆曲线要素。
[例11-1]：已知α=55o43'24"，R=500 m，求圆曲线各要素T，L，E o。
圆曲线的详细测设
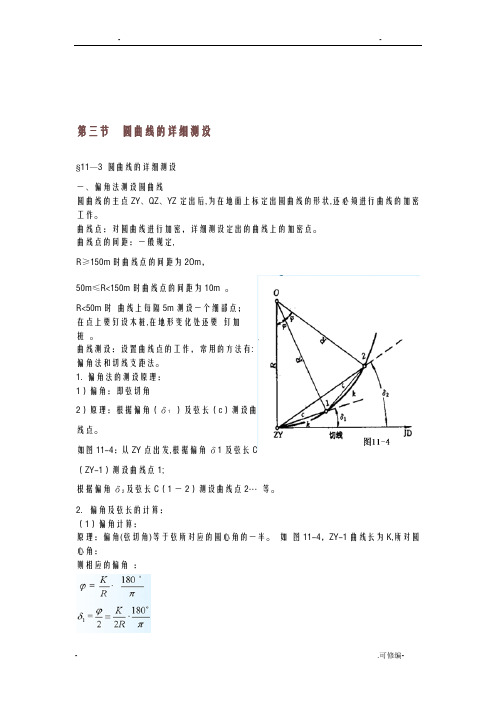
第三节圆曲线的详细测设§11—3 圆曲线的详细测设一、偏角法测设圆曲线圆曲线的主点ZY、QZ、YZ定出后,为在地面上标定出圆曲线的形状,还必须进行曲线的加密工作。
曲线点：对圆曲线进行加密，详细测设定出的曲线上的加密点。
曲线点的间距：一般规定,R≥150m时曲线点的间距为2Om，50m≤R<150m时曲线点的间距为10m 。
R<50m时曲线上每隔5m测设一个细部点；在点上要钉设木桩,在地形变化处还要钉加桩。
曲线测设：设置曲线点的工作，常用的方法有:偏角法和切线支距法。
1. 偏角法的测设原理：1）偏角：即弦切角2）原理：根据偏角（δ1）及弦长（c）测设曲线点。
如图11-4：从ZY点出发,根据偏角δ1及弦长C（ZY-1）测设曲线点1;根据偏角δ2及弦长C（1一2）测设曲线点2…等。
2．偏角及弦长的计算：（1）偏角计算：原理：偏角(弦切角)等于弦所对应的圆心角的一半。
如图11-4，ZY-1曲线长为K,所对圆心角：则相应的偏角：当所测曲线各点间的距离相等时,以后各点的偏角则为第一个偏角δ1的累计倍数。
即：（2）弦长计算(如图11-4)严密计算公式：※弦弧差（弦长与其相对应的曲线长之差）:弦弧差=K i– C i = L i3/ (24R2)当R=450m时，20m的弦弧差为2mm，∴当R>400m时，不考虑弦弧差的影响。
由于铁路曲线半径一般很大, 20m的弦长与其相对应的曲线长之差很小,就用弦长代替相应的曲线长进行圆曲线测设。
近似计算：整弦：里程为20m倍数的两相邻曲线点间的弦长（曲线点间距20m对应的弦长）。
分弦：有一端里程不为20m倍数的两相邻曲线点间的弦长。
（通常要求曲线点设置在整数里程上（如20m的倍数）,即里程尾数为00, 20, 40, 60, 80m等点上，但曲线的ZY点、QZ 点、YZ点常不是整数里程,因此在曲线两端及中间出现分弦）。
例如：在前面例题中，ZY的里程为37+553.24；QZ的里程为37+796.38;YZ的里程为38+039.52,因而曲线两端及中间出现四段分弦。
圆曲线主点的测设
1、偏角法
(A)短弦偏角法 无全站仪时，用经 纬仪配合钢尺测设， 适合于测设场地起 伏不大。
特点： 测点误差积 累。
偏角法测设圆 曲线是以曲线 起点ZY或终点 YZ作为测站， 计δ算出测站至 曲线上任一细 部点i的弦线与 切线的夹角
（弦切角，也 称偏角）和弦 线Ci。据此确定 点的位置。
O
R
QZ
例题：已知交点的桩号为K3+182.76，测得转折角α =25°48′10″ 设计圆曲线半径R=300m。JD，ZD1和ZD2坐标如图。
求：曲线主点和细部点的坐标。
解：由图中数据计算出两条切线及点至点的方位角分别为 计算出主点、圆曲线细部点的坐标列于下表
测设曲线上整桩和加桩称为圆曲线详细最常用的方法有偏角法偏角法又有短弦偏角法和长弦偏角法切线支最常用的方法有偏角法偏角法又有短弦偏角法和长弦偏角法切线支直角坐标法直角坐标法和极坐标法等
平面圆曲线的测设
任务一：偏角法测设平面单圆曲线 任务二：极坐标法测设平面单圆曲线 任务三：切线支距法测设平面单圆曲线
2R sin i或展开为 ci
li
li3 24 R2
宜以QZ 为界，将曲线分两部分进行测设。
平面圆曲线的测设
任务一：偏角法测设平面单圆曲线 任务二：极坐标法测设平面单圆曲线 任务三：切线支距法测设平面单圆曲线
任务二：切线支距法测设平面单圆曲线
切线支距法（也称直角坐标法） 以曲线起点ZY（或终点YZ）为 独立坐标系的原点，切线指向JD 方向为X轴，通过原点的方向为Y 轴，建立局部直角坐标系，计算 出曲线细部点Pi在该独立坐标系 中的坐标（Xi，Yi）进行测设。 一、计算测设数据
后进行详细测设，即再依据 主点测设曲线上每隔一定距 离的里程桩，详细标定曲线 位置。
圆曲线测设—圆曲线加桩(点)测设
O
2.坐标法测设曲线细部点
圆曲线细部点坐标计算(按偏角和长弦)
曲线里程桩号
偏角
方位角α
弦长C (m)
ZY 3+091.05 0°00’00” 52°16’30”
P1 3+100 P2 3+120 QZ 3+133.29
2°08’12” 6°54’41” 10°05’00”
54°24’42” 59°11’11” 62°21’30”
而曲线起点ZY至曲中线点的QZ的偏角为
4
，曲线起点ZY至曲线终点YZ的偏角
为
2
。
1.偏角法(长弦偏角)
根据弦切角为同弧所对圆心角 之半：
0
1 2
0
1
1 2
1
i
1 2
1
(i
1)0
n 1
1 2
n1
同弧所对的弦长为： Ci 2R sin i
根据弦切角和弦长,以切线为起始方向,用极坐标法测设Pi
偏角法具体测设步骤如下：
偏角法具体测设步骤如下：
精度如下规定：
半径方向（路线横向）误差 ±0.1m
切线方向（路线纵向）误差
L 1000
（L为曲线长）
偏角法是一种测设精度较高、灵活性较大的常用方法，适用于地势起伏，视
野开阔的地区。它既能在三个主点上测设曲线，又能在曲线任一点测设曲线，但
其缺点是测点有误差的积累，所以宜在由起点、终点两端向中间测设或在曲线中
8.95 28.88 42.02
P3 3+140 P4 3+160 YZ 3+175.52
11°41’10” 16°27’39” 20°10’00”
浅谈圆曲线测设方法
浅谈圆曲线测设方法前言：在各类线路工程弯道处施工，常常会遇到圆曲线的测设工作。
目前，圆曲线测设的方法已有多种，如偏角法、切线支距法、弦线支距法、坐标法等。
然而，在实际工作中测设方法的选用要视现场条件、测设数据求算的繁简、测设工作量的大小，以及测设时仪器和工具情况等因素而定。
另外，上述的几种测设方法，都是先根据辅点的桩号（里程）来计算测设数据，然后再到实地放样。
单圆曲线简称圆曲线，若按常规方法测设，通常分两步进行，即：圆曲线主点（起控制作用的点）的测设和曲线细部点的测设。
（一）圆曲线要素及计算见图9-10，圆曲线的半径R、偏角α、切线长T、曲线长L、外矢距E、切曲差q，通称为圆曲线要素。
R、α是已知数据。
R是在线路设计中按线路等级及地形条件等因素选定的，α是线路定测时测定的。
（二）圆曲线主点及主点里程的计算圆曲线的主点一般为：直圆点-ZY、曲中点-QZ、圆直点-YZ。
各主点里程的计算：各主点里程依据交点（JD）的里程计算。
设交点里程为JD DK，则各主点的里程为：（9-6）（三）圆曲线主点的测设见图9-11，测设圆曲线各主点的步骤如下：1．在交点JD安置仪器，以线路方向（转点桩或交点桩）定向，即确定切线方向；2．从JD点起沿视线方向量分别取切线长T，确定ZY点和YZ点；3．后视YZ点，用正、倒分中法正拨（右偏）或反拨（左偏）90°~α/2（图中的β角）定出分中点视线方向；4．沿分中点视线方向量取外矢距E，确定QZ点。
图9-11 圆曲线主点测设（四）圆曲线细部点的测设一．偏角法偏角法实质是角度与距离交会的一种方法。
如图9-12所示。
（1）测设元素：给定的点间距l（以直代曲的长度）、曲线点的偏角δi 。
δi（以度为单位）的计算公式如下：（9-7）式中，li——i点至ZY点间的曲线弧长。
由于曲线半径R较大，相邻两个测设点间的弧长所对的圆心角较小，使得弦长（测设时为10m、20m或50m）和弧长之差很小（通常小于量距误差），图9-12 圆曲线细部点测设所以，实际测设时均以弦长代替弧长。
第四讲2、圆曲线
24 图12－
Байду номын сангаас
• 1、要增加曲线测设例题 • 2、极坐标法用例题介绍 • 3、曲线测设技巧和方法
2 1
δ 3 = 3 ⋅ δ1
L
δ n = n ⋅ δ1
•
由于《测规》规定，圆曲线的中桩里程宜为20 m的整倍数，而通常在ZY、QZ、YZ附近的曲 线点与主点间的曲线长不足20 m，则称其所对应的弦为分弦。分弦所对应的偏角可按式（11 －8）来计算。
（二）圆曲线详细测设举例
• • • • •
圆曲线详细测设前，曲线主点ZY、QZ、YZ己测设好，因此通常以ZY为测站，分别测设ZY～ QZ和YZ～QZ曲线段，并闭合于QZ作检核。 以上例资料为依据，举例说明测设的步骤与方法。 1．以ZY为测站 （1）偏角计算 已知ZY里程为DK53+621.56，QZ为DK 53+864.70，R ＝ 500 m，曲线ZY QZ为顺时针转 （图12－20）。偏角资料计算见表12－12。由于偏角值与度盘读数增加方向一致，故称“正 拨”。
左 右
• •
•
R——圆曲线的半径。 α 、R为计算曲线要素的必要资料，是已 知值。α 可由外业直接测出，亦可由纸上 定线求得；R为设计时采用的数据。 圆曲线要素的计算公式，由图12－18得： • α
切线长 曲线长 外矢距 T＝R ⋅ tan π L = R ⋅α ⋅ • o 180 α E0 = R ⋅ sec − R 2 2
（12－7） 图12－18
•
α 式中计算L时， 以度为单位。
（三）圆曲线主点里程计算
• •
•
主点里程计算是根据计算出的曲线要素，由一已知点里程来推算，一般沿里程增加的方向由 ZY QZ Y2进行推算。 如上例己知ZY点的里程为DK53＋621.56，则各主点里程计算如下： • ZY DK53+621.56 • +L/2 243.14 • QZ DK53+864.70 • +L/2 243.14 • YZ DK 54+107.84 若已知交点JD的里程，则需计算出ZY或YZ的里程，由此推算其它主点的里程。
圆曲线主点测设步骤
圆曲线主点测设步骤一、引言圆曲线主点测设是道路设计中的重要环节，用于确定道路中的圆曲线位置和参数，以保证道路的安全性和流畅性。
本文将详细介绍圆曲线主点测设的步骤和方法。
二、测设前的准备工作在进行圆曲线主点测设之前，需要进行以下准备工作：2.1 确定测设范围根据道路设计要求和实际情况，确定需要进行圆曲线主点测设的路段范围。
2.2 准备测量工具和设备准备测量工具和设备，包括测距仪、测角仪、刷墨仪等。
2.3 制定测量方案根据测设范围和测量工具，制定详细的测量方案，包括测点位置、测量顺序、测量方法等。
三、圆曲线主点测设步骤圆曲线主点测设包括以下步骤：3.1 测量起点和终点首先，在测设范围的起点和终点位置进行测量，确定测量起点和终点的坐标。
3.2 确定切线方向在起点和终点位置，使用测角仪确定切线方向，即道路的初始方向和最终方向。
3.3 确定切线长度根据设计要求，确定切线长度，即道路的起点和终点之间的直线距离。
3.4 确定圆曲线半径根据道路设计要求和实际情况，确定圆曲线的半径。
3.5 确定过渡曲线长度根据道路设计要求和实际情况，确定过渡曲线的长度。
3.6 确定过渡曲线起点和终点根据切线方向、切线长度、圆曲线半径和过渡曲线长度，确定过渡曲线的起点和终点位置。
3.7 确定圆曲线主点根据过渡曲线起点和终点位置，使用测距仪和测角仪确定圆曲线主点的坐标和角度。
3.8 标识圆曲线主点在确定圆曲线主点后，使用刷墨仪或其他标识工具，在实地进行标识，以便后续的道路施工。
四、测设精度控制为了保证圆曲线主点测设的精度，需要进行精度控制，包括以下方面：4.1 测量仪器的校准在进行测设之前，需要对测量仪器进行校准，确保其准确性和稳定性。
4.2 测量数据的处理对于测量得到的数据，需要进行处理和分析，排除异常值和误差，保证测量结果的准确性。
4.3 现场实地核对在进行测设之后，需要进行现场实地核对，与设计要求进行对比，确保测设结果与设计一致。
圆曲线测设
偏 角（°′″）
正拨
反拨
0 00 00
360 00 00
0 23 25
359 36 35
0 57 48
359 02 12
1 32 10
358 27 50
2 06 33
357 53 27
2 40 56
357 19 04
3 15 18
356 44 32
3 49 41
356 10 19
4 24 04
355 35 56
（2）偏角法
偏角法测设圆曲线是以
曲线起点ZY或曲线终点
YZ为测站，计算出测站
至曲线上任一点弦线与
切线的夹角（弦切角，
也称偏角）和弦长C，据
此确定点位。 1）计算公式：
偏角：
l 180
2 2R π
弦长：
C 2R sin 2
2R sin
弧弦差：
l
C
l3 24R 2
4、主点放样
（1）用盘左位后视直线上的转点（ZD）， 固定水平制动螺旋，沿视线方向定线，并 用钢尺量出切线长初步定出曲线起点 （ZY），钉下木桩，用铅笔标记点位，并 返测该段距离，当相对误差小于1/2000时， 取两次丈量结果的平均值准确定出ZY点。
（2）用望远镜瞄准另一切线的转点，固定水 平制动螺旋，按上法定出曲线终点（YZ） （打ZY或YZ点桩，用盘左、盘右其中一个盘 位即可）。
（3）把望远镜从切线方向转（180－α ）／2 的角值，定出方向线（分角线），从交点沿 分角线方向量出外矢距E0，初步得曲中点 （QZ），（定下木桩，用铅笔定出点位）再 用另一盘位瞄准切线方向，转（180－α ）／ 2角再定出分角线又得一曲中点位置，取正、 倒镜分中位置钉下小钉作为曲中点QZ。
道路中线测量—圆曲线测设(工程测量课件)
01
交点和转点的测设
02
03
道路中
线测量
04
05
06
08
09
路线转角的测定和里程桩设置
圆曲线测设
圆曲线详细测设的基本要求
虚交点的测设
带有缓和曲线的平曲线测设
回头曲线的测设
道路中线逐桩坐标计算
C
目
录 ONTENTS
1
圆曲线详细测设
2
整桩号法
3
整桩距法
4
特点及适用性
1
圆曲线详细测设
➢ 圆曲线详细测设：
3
整桩距法
➢ 整桩距法：
➢ 从圆曲线起点ZY和终点YZ
开始，分别以桩距 l 0 连续
向圆曲线中点QZ设桩。
例： 已知某JD的里程为K2+968.43，测得转角 =34°1
2‘，圆曲线半径R=200m，若按整桩距法加桩，试确定加
桩桩号。
解：
由前例已知ZY里程=K2+906.9，QZ里程=K2+966.59，
2
圆曲线主点测设
➢ ZY点的测设：
➢ 将仪器置于JD上，望远镜照准
后视JD或此方向上的转点，沿
望远镜视线方向量取切线长T，
得ZY，先插一测钎标志。
➢ 用钢尺丈量ZY至最近一个直线
桩的距离，如两桩号之差等于
所丈量的距离或相差在容许范
围内，即可在测钎处打下ZY桩。
➢ YZ点的测设：
➢ 在ZY点测设完后，转动望远镜
C
目
录 ONTENTS
1
直角坐标系的建立
2
加密桩点坐标的计算
3
测设方法
4
优缺点及适用性
圆曲线主点测设步骤
圆曲线主点测设步骤圆曲线主点测设步骤一、概述圆曲线是公路、铁路等交通工程中常用的一种曲线形式，其具有平滑、连续、美观等特点。
因此，在公路、铁路等交通工程中，圆曲线的测设是非常重要的一项工作。
本文将详细介绍圆曲线主点的测设步骤。
二、前期准备在进行圆曲线主点测设之前，需要进行以下几个方面的准备工作。
1. 地形勘察：对待建道路或铁路的地形进行勘察，确定道路或铁路的纵断面和横断面；2. 设计图纸：根据地形勘察结果和设计要求，编制出道路或铁路的设计图纸；3. 确定基准点：在设计图纸上确定基准点，并进行标注；4. 确定初始控制点：在设计图纸上根据基准点确定初始控制点，并进行标注；5. 准备测量仪器：包括经纬仪、全站仪、水平仪等。
三、圆曲线主点测设步骤1. 建立坐标系首先，在圆曲线上建立坐标系，确定圆心和半径。
一般情况下，圆心位于横断面中央，半径根据设计要求确定。
2. 测量初始控制点在设计图纸上确定初始控制点，并进行标注。
然后，在实地进行测量，使用经纬仪或全站仪进行测量，并记录数据。
3. 测量圆心角在测量初始控制点之后，需要测量圆心角。
使用全站仪或经纬仪进行测量，并记录数据。
4. 计算主点坐标根据测得的数据，可以计算出主点的坐标。
具体计算方法如下：（1）计算弦长：弦长=2×半径×sin（圆心角÷2）（2）计算偏移距离：偏移距离=弦长÷2×tan（偏移角）其中，偏移角为设计要求中规定的值。
（3）计算主点坐标：主点坐标=初始控制点坐标+偏移距离×旋转矩阵其中，旋转矩阵为：cosθ -sinθsinθ cosθ其中，θ为初始控制点与主点所在直线的夹角。
5. 核对和修正计算出主点坐标之后，需要进行核对和修正。
核对时，需要将测得的数据和计算结果进行比较，检查是否存在误差。
如果存在误差，则需要进行修正。
四、总结圆曲线主点的测设是公路、铁路等交通工程中非常重要的一项工作。
建筑施工测量课件子单元10-2 圆曲线测设
单元10 线路施工测量
子单元2 园曲线测设
2. 主点里程计算
圆曲线交点的里程已由设计标定，根据交点的里程和主点测 设元素，可计算各主点的里程，
ZY里程 = JD里程－T QZ里程 = ZY里程＋ L/2 YZ里程 = QZ里程＋ L/2 计算检核： JD里程 = YZ里程－T＋D
单元10 线路施工测量
再根据方位角α2-1和 切线长度T，用坐标正算 公式计算曲线起点坐标 (xZY , yZY)和终点坐标 (xYZ , yYZ)，曲线中点坐 标(xQZ , yQZ)则由分角 线方位角α2-QZ和矢径E 计算得到，其中分角线方 位角α2-QZ也可由第一条 切线的方位角和线路转角 推算得到。
单元10 线路施工测量
单元10 线路施工测量
子单元2 圆曲线测设
一、圆曲线主点 的测设
当道路的平面走向由一个方向转到另一个方 向时，必须用平面曲线来连接。曲线的形式较 多，其中圆曲线是最基本的一种平面曲线。另 一种是缓和曲线。
二、圆曲线的 详细测设
单元10 线路施工测量
子单元2 园曲线测设
确定圆曲线的参数是转角α和半径R，设计时确定，在道路 施工图上有标注。圆曲线上起控制作用的点有三个，一是圆曲 线的起点，简称“直圆点”；二是圆曲线的中点，简称“曲中 点” ；三是圆曲线的终点，简称“圆直点” 。
单元10 线路施工测量
子单元2 园曲线测设
（1）计算圆心坐标
计算第一条切线的方位角α2-1和ZY点坐标（xZY , ZY）， 因ZY点至圆心方向与切线方向垂直，其方位角为 αZY-O=α2-1±90°（式中 “±” 当偏角右偏时取“－”；左 偏时取“＋”。则圆心坐标（xo , yo）为
xo xZY R cos zyo yo yZY R sinzyo
圆曲线的测设步骤
圆曲线的测设步骤
圆曲线的测设步骤一般包括以下几个步骤：
1. 准备工作：确定测设区域，安全标识设置，仪器检查和校准等准备工作。
2. 建立基线：根据需要选择起点和终点，建立一条基线作为测设的起点。
3. 设置测设仪器：根据测设的需求，选择合适的测量仪器，并进行仪器的设置，包括放置测量仪器的位置和高度等。
4. 量测点的布置：在测设区域内按照一定的间距设置测量点，可以使用测量杆或其他标志物进行标记。
5. 进行测量：使用测量仪器进行测量，可以采用全站仪或其他适用的测量工具。
根据测量仪器的说明和操作步骤，进行相应的测量。
6. 数据处理与计算：将测得的数据导入计算机进行数据处理和计算，得到所需的测量结果，包括曲线半径、切线长、圆曲线长度等。
7. 绘制测量图：将测设结果绘制成测量图，包括圆曲线曲线图、水平曲线图和纵断面图等。
8. 检查和验收：对测设结果进行检查和验收，确保测量结果的
准确性和可靠性。
需要注意的是，在进行圆曲线测设时，需要遵循相关的测量规范和标准，保证测量的精度和准确性。
同时，在测设过程中要注意安全，遵守相关的安全操作规范，确保测量人员和周围环境的安全。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
浅谈圆曲线测设方法
前言：
在各类线路工程弯道处施工，常常会遇到圆曲线的测设工作。
目前，圆曲线测设的方法已有多种，如偏角法、切线支距法、弦线支距法、坐标法等。
然而，在实际工作中测设方法的选用要视现场条件、测设数据求算的繁简、测设工作量的大小，以及测设时仪器和工具情况等因素而定。
另外，上述的几种测设方法，都是先根据辅点的桩号（里程）来计算测设数据，然后再到实地放样。
单圆曲线简称圆曲线，若按常规方法测设，通常分两步进行，即：圆曲线主点（起控制作用的点）的测设和曲线细部点的测设。
（一）圆曲线要素及计算
见图9-10，圆曲线的半径R、偏角α、切线长T、曲线长L、外矢距E、切曲差q，通称为圆曲线要素。
R、α是已知数据。
R是在线路设计中按线路等级及地形条件等因素选定的，α是线路定测时测定的。
（二）圆曲线主点及主点里程的计算
圆曲线的主点一般为：直圆点-ZY、曲中点-QZ、圆直点-YZ。
各主点里程的计算：各主点里程依据交点（JD）的里程计算。
设交点里程为JD DK，则各主点的里程为：
（9-6）
（三）圆曲线主点的测设
见图9-11，测设圆曲线各主点的步骤如下：
1．在交点JD安置仪器，以线路方向（转点桩或交点桩）定向，即确定切线方向；
2．从JD点起沿视线方向量分别取切线长T，确定ZY点和YZ点；
3．后视YZ点，用正、倒分中法正拨（右偏）或反拨（左偏）90°~α/2（图中的β角）定出分中点视线方向；
4．沿分中点视线方向量取外矢距E，确定QZ点。
图9-11 圆曲线主点测设
（四）圆曲线细部点的测设
一．偏角法
偏角法实质是角度与距离交会的一种方法。
如图9-12所示。
（1）测设元素：给定的点间距l（以直代曲的长度）、曲线点的偏角δi 。
δi（以度为单位）的计算公式如下：
（9-7）
式中，li——i点至ZY点间的曲线弧长。
由于曲线半径R较大，相邻两个测设点间的弧长所对的圆心角较小，使得弦长（测设时为10m、20m或50m）和弧长之差很小（通常小于量距误差），
图9-12 圆曲线细部点测设
所以，实际测设时均以弦长代替弧长。
（2）测设步骤（见图9-12）
① 在ZY点整置仪器，照准交点JD，度盘置0；
② 拨角δ1（注意：正拨角，还是反拨角），延视线方向量取长l，确定1点，钉木桩并以小钉标志点位；
③ 拨角δ2，从已测设的1点开始，量长l，其端点恰与视线相交，确定2点，钉入木桩并以小钉标志点位；
④ 按上方法进行其它各点的测设，直至QZ点（QZ点也要按此方法放出，用以检查测设质量及调整其它各点）；
（3）检查与调整（见图9-13）
图9-13 圆曲线测设闭合差调整
方法与步骤为：
由于测设时各种误差的累积，致使详细测设时的曲中点-QZ′与主点测设时的QZ点不重合，其距离称为曲线测设的闭合差f。
f沿QZ点切线方向的分量称为纵向闭合差fx，其相对允许值为
1/2000；f沿QZ点向径方向的分量称为横向闭合差fy，其允许值为
±10cm。
若测设满足上述精度要求，则对各点按与距离成正比例关系进行点位调整；否则，应对测设点进行检查，修正粗差点和错误点。
调整的步骤如下：
① 确定调整方向：与QZ′（细部测设）至QZ（主点测设）的方向一致；
② 确定调整量：调整量按与距离成正比例分配。
上面述及的方法为整桩法，各点测设完后一定要注意补齐百米桩。
为防止丢失百米桩，也可采用湊整方法，即对测设的第1点进行里程湊整，但湊整距离不得大于规定的点间距，各点测设方法同整桩法。
见图9-14。
图9-14 圆曲线细部点测设
二．切线支距法
切线支距法：建立以ZY点（或YZ点）为原点，以切线方向（指向JD点）为x轴、向径方向为y轴的独立直角坐标系，并依据点间距l计算各测设点的独立直角坐标，再用支距法实际测设各点位的方法,见图9－15。
这种方法为实现由全站仪、RTK进行坐标放样提供了坐标转换模型基础。
图9-15 切线支距法
1）测设元素：由给定的点间距l（以直代曲的长度），计算各测设点的坐标x、y，即：
（9-8）
2）测设步骤（见图9－16）
（1）在ZY点整置仪器，照准JD点确定切线方向，沿此方向依次量取x1、x2、…，得点1′、2′、…，并临时标定之；
（2）分别在垂足点1′、2′、…整置仪器，照准JD点拨直角，并沿对应视线方向量取y1、y2、…，得测设点1、2、…，钉入木桩并以小钉标志点位；
（3）曲线细部点测设结束，应对点间距予以检查，使其点位误差合乎要求，否则，对误差超限点位，应予重新测设、调整；
（4）在确认各点位正确后，若有百米桩未测设，需要用其邻近的曲线细部点，用直线内插的方法测设，并分别钉入点位桩与标志桩。
图9-16 切线支距法测设示意图
三．坐标法
坐标法的测设数据主要是计算圆曲线主点和细部点的坐标，然后根据控制点和细部点的坐标，利用全站仪或GPS RTK即可测设，不需要计算测设数据。
（1）圆曲线主点坐标计算
以图9-15所示为例，根据路线交点JD及转点ZD1、ZD2的坐标，反算出切线ZD1→JD的方位角为θ1，按路线的转角△，推算出切线JD→ZD2的方位角θ2＝θ1＋△，分角线JD→QZ的方位角θ3＝θ1＋90°＋Δ/2，根据JD点的坐标及方位角θ1、θ2、θ3和切线长T、矢距E，计算出ZY和YZ的坐标，其公式为：
（9-9）
图9-17 坐标法测设圆曲线
（2）圆曲线细部点坐标的计算
根据图中第一条切线的方位角θ1及偏角γi（γi＝φi/2），可知圆曲线起点ZY至细部点Pi点的方位角θPi（θPi＝θ1＋γi），再根据弦长ci 和ZY的坐标计算细部点的坐标，其公式为：
（9-10）
综上所述，三种方法各有优缺点。
随着科技的发展，很多软件程序利用曲线要素都能快速的计算出曲线段内各个点坐标，免去了繁复的计算。
以及全站仪、GPS越来越普遍，坐标法也越来越普及。