第五章 非平稳序列的随机分析
时间序列分析第五章非平稳序列的随机分析

考察差分运算对该序列线性趋势信息的提 取作用
2020/3/12
时间序列分析
差分前后时序图
原序列时序图
差分后序列时序图
2020/3/12
时间序列分析
例5.2
尝试提取1950年——1999年北京市民用 车辆拥有量序列的确定性信息
2020/3/12
时间序列分析
Green函数递推公式
1 1 1 2 1 1 2 2
j 1 j1 pd j pd j
t
2
,
E(
t
s
)
0,
s
t
Exs t 0,s t
2020/3/12
时间序列分析
ARIMA 模型族
d=0 ARIMA(p,d,q)=ARMA(p,q)
P=0 ARIMA(P,d,q)=IMA(d,q)
q=0 ARIMA(P,d,q)=ARI(p,d)
d=1,P=q=0 ARIMA(P,d,q)=random walk model
差分后序列时序图
一阶差分
二阶差分
2020/3/12
时间序列分析
例5.3
差分运算提取1962年1月——1975年12月平均 每头奶牛的月产奶量序列中的确定性信息
2020/3/12
时间序列分析
差分后差分
2020/3/12
时间序列分析
过差分
足够多次的差分运算可以充分地提取原 序列中的非平稳确定性信息
2020/3/12
时间序列分析
随机游走模型( random walk)
模型结构
时间序列分析 第五章-非平稳序列的随机分析
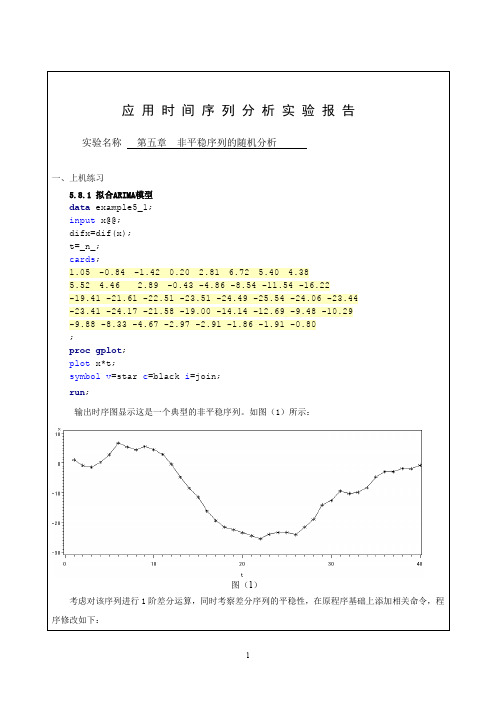
图(1)考虑对该序列进行1阶差分运算,同时考察差分序列的平稳性,在原程序基础上添加相关命令,程序修改如下:图(2)时序图显示差分后序列difx没有明显的非平稳特征。
(2)“identify var=x(1);”,使用该命令可以识别差分后序列的平稳性。
纯随机性和适当的拟合图(6)普通最小二乘估计结果图(8)最终拟合模型输出结果图(9)拟合效果图图(12)带有延迟因变量的回归模型拟合效果图5.8.3拟合GARCH模型SAS系统中AUTOREG过程功能非常强大,不仅可以提供上述的分析功能,还可以提供异方差性检验乃至条件异方差模型建模。
以临时数据集example5_3数据为例,介绍GARCH模型的拟合,相关命令如下:data example5_3;input x@@;t=_n_;cards;10.77 13.30 16.64 19.54 18.97 20.52 24.3623.51 27.16 30.80 31.84 31.63 32.68 34.9033.85 33.09 35.46 35.32 39.94 37.47 35.2433.03 32.67 35.20 32.36 32.34 38.45 38.1732.14 39.70 49.42 47.86 48.34 62.50 63.5667.61 64.59 66.17 67.50 76.12 79.31 78.8581.34 87.06 86.41 93.20 82.95 72.96 61.1061.27 71.58 88.34 98.70 97.31 97.17 91.1780.20 85.12 81.40 70.87 57.75 52.35 67.5087.95 85.46 84.55 98.16 102.42 113.02 119.95122.37 126.96 122.79 127.96 139.20 141.05 140.87137.08 145.53 145.59 134.36 122.54 106.92 97.23110.39 132.40 152.30 154.91 152.69 162.67 160.31142.57 146.54 153.83 141.81 157.83 161.79 142.07139.43 140.92 154.61 172.33 191.78 199.27 197.57189.29 181.49 166.84 154.28 150.12 165.17 170.32;proc gplot data=example5_3;plot x*t=1;symbol1c=black i=join v=start;proc autoreg data=example5_3;model x=t/nlag=5dwprob archtest;model x=t/nlag=2noint garch=(p=1,q=1);output out=out p=p residual=residual lcl=lcl ucl=ucl cev=cev;data out;set out;l95=-1.96*sqrt(51.42515);u95=1.96*sqrt(51.42515);Lcl_GARCH=-1.96*sqrt(cev);Ucl_GARCH=1.96*sqrt(cev);Lcl_p=p-1.96*sqrt(cev);Ucl_p=p+1.96*sqrt(cev);proc gplot data=out;plot residual*t=2 l95*t=3 Lcl_GARCH*t=4 u95*t=3 Ucl_GARCH*t=4/overlay; plot x*t=5 lcl*t=3 LCL_p*t=4 ucl*t=3 UCL_p*t=4/overlay;symbol2c=green i=needle v=none;symbol3v=black i=join c=none w=2l=2;symbol4c=red i=join v=none;symbol5c=green i=join v=none;run;该序列输出时序图如图(13)所示。
时 间 序 列 分 析 实 验 报 告实例

应用时间序列分析实验报告实验名称第五章非平稳序列的随机分析专业班级姓名学号一、上机练习程序及其结果分析:data ex3_1;input x@@;time=_n_;cards;0.30 -0.45 0.36 0.00 0.17 0.45 2.154.42 3.48 2.99 1.74 2.40 0.11 0.960.21 -0.10 -1.27 -1.45 -1.19 -1.47 -1.34-1.02 -0.27 0.14 -0.07 0.10 -0.15 -0.36-0.50 -1.93 -1.49 -2.35 -2.18 -0.39 -0.52-2.24 -3.46 -3.97 -4.60 -3.09 -2.19 -1.210.78 0.88 2.07 1.44 1.50 0.29 -0.36-0.97 -0.30 -0.28 0.80 0.91 1.95 1.771.80 0.56 -0.11 0.10 -0.56 -1.34 -2.470.07 -0.69 -1.96 0.04 1.59 0.20 0.391.06 -0.39 -0.162.07 1.35 1.46 1.500.94 -0.08 -0.66 -0.21 -0.77 -0.52 0.05;procgplot data=ex3_1;plot x*time=1;symbol1c=red I=join v=star;run;结果分析:上图是数据对应的时序图,从图上曲线分析来看,数据并没有周期性或者趋向性规律,因而可以初步判断这是平稳数列。
procarima data=ex3_1;identifyVar=x nlag=8;run;结果分析:本过程中,我们建立了8阶自回归分析模型,图上依次是变量的描述性统计量、样本自相关图、样本逆相关图和样本偏自相关图。
由于本次实验探究的是平稳序列,因而样本逆相关图先不作分析。
从自相关图来看,自相关系数趋于0的速度是比较快的,再结合时序图来看,可以确定这组数列是属于平稳数列。
【2019年整理】时间序列分析--第五章非平稳序列的随机分析

尝试提取1950年——1999年北京市民用 车辆拥有量序列的确定性信息
4/8/2019
时间序列分析
差分后序列时序图
一阶差分
二阶差分
4/8/2019
时间序列分析
例5.3
差分运算提取1962年1月——1975年12月平均 每头奶牛的月产奶量序列中的确定性信息
4/8/2019
时间序列分析
差分后序列时序图
4/8/2019
时间序列分析
差分方式的选择
序列蕴含着显著的线性趋势,一阶差分 就可以实现趋势平稳 序列蕴含着曲线趋势,通常低阶(二阶 或三阶)差分就可以提取出曲线趋势的 影响 对于蕴含着固定周期的序列进行步长为 周期长度的差分运算,通常可以较好地 提取周期信息
时间序列分析
4/8/2019
例5.1
时间序列分析
ARIMA模型建模步骤
获 得 观 察 值 序 列 平稳性 检验 N 差分 运算 Y 白噪声 检验 N 拟合 ARMA 模型
时间序列分析
Y
分 析 结 束
4/8/2019
例5.6
对1952年——1988年中国农业实际国民 收入指数序列建模
4/8/2019
时间序列分析
一阶差分序列时序图
第五章
非平稳序列的随机分析
4/8/2019
时间序列分析
本章结构
差分运算 ARIMA模型 Auto-Regressive模型 异方差的性质 方差齐性变化 条件异方差模型
4/8/2019
时间序列分析
5.1 差分运算
差分运算的实质 差分方式的选择 过差分
时间序列分析--第五章非平稳序列的随机分析

50
乘积季节模型
使用场合
序列的季节效应、长期趋势效应和随机波动之间有着复 杂地相互关联性,简单的季节模型不能充分地提取其中 的相关关系
构造原理
短期相关性用低阶ARMA(p,q)模型提取
季节相关性用以周期步长S为单位的ARMA(P,Q)模型提取
假设短期相关和季节效应之间具有乘积关系,模型结构
3
差分运算的实质
差分方法是一种非常简便、有效的确定 性信息提取方法
Cramer分解定理在理论上保证了适当阶 数的差分一定可以充分提取确定性信息
差分运算的实质是使用自回归的方式提 取确定性信息
d
d xt (1 B)d xt (1)i Cdi xti i0
5/10/2019
模型中有部分系数省缺了,那么该模型 称为疏系数模型。
5/10/2019
课件
34
疏系数模型类型
如果只是自相关部分有省缺系数,那么该疏系 数模型可以简记为ARIMA(( p1,, pm ), d, q)
p1,, pm 为非零自相关系数的阶数
如果只是移动平滑部分有省缺系数,那么该疏 系数模型可以简记为 ARIMA( p, d, (q1,, qn ))
26
建模
定阶
ARIMA(0,1,1)
参数估计
(1 B)xt 4.99661 (1 0.70766 B) t
Var(t ) 56.48763
模型检验
模型显著 参数显著
5/10/2019
课件
27
ARIMA模型预测
原则
最小均方误差预测原理
Green函数递推公式
一阶差分
非平稳时间序列解析

动态乘子的比较
趋势平稳过程 动态乘子:
xt t+( B) t
xt s t
2 趋势平稳过程满足 j 0 j , 所以
xt s lims 0. t
单整序列
差分一次变为平稳过程,记为I(1) 平稳过程记为I(0) 如果差分n-1次不平稳,差分n次平稳,称 为n阶单整的,记为I(n)
趋势平稳过程和单位根过程比较
预测比较
H 0 : xt xt 1 t H1 : xt t ( xt 1 t ) t ,| | 1
包含一个确定性趋势和一个随机趋势
单位根过程
满足下面表达式的过程成为单位根过程
(1 B) xt t 1 t 1
其中
(B) t
(1) 0, j 0 2 j , (u ) 0根在单位圆外.
单位根过程对时间序列的增量进行刻画,增 量平稳,但水平变量不平稳。
2.方差有界并且不随时间变化,是常数. 称为方差齐性
平稳ARMA模型, 可表示为
xt t 1 t 1
,
i 0
| i |
t WN (0, )
2
此类模型的特点 3. 长期预测趋于无条件均值 4. 预测误差的方差有界
序列分解
xt l t l 1 t l 1 et (l )
预测误差
l 1 t 1 l t l 1 t 1 ˆt (l ) x
预测值
ˆ (l ) E ( xt l xt , xt 1 , ) x Var ( xt l xt , xt 1 , ) Var[et (l )]
第5章非平稳序列的确定性分析

拟合效果图
图 5-4
移动平均法
移动平均方法是一种常用的修匀方法。它 最早于1870年由法国数学家 De forest提出,19 世纪晚期已经广泛应用于商业和保险精算行业。 商人使用移动平均方法消除随机波动和季节性 影响,得到商品的价格变动趋势。精算师采用 移动平均方法来修匀死亡率,得到消除随机波 动的生命表。目前股市中普遍采用的5日均线、 10日均线、30日均线、60日均线等指标,实际 上都是移动平均估计值。
1987Q4 1988Q1 1988Q2 11325 10698 11624
10515.5 10658 10703.5 10758.5 10775.25 10773 10864
11008.25 11081 11174.75
10586.75 10680.75 10731 10766.88 10744.13 10818.5 10936.13 11044.63 11127.88 11183.25
459.2
415.12
422.2
460.12
524.7
530.86
524.4
612.88
723.8
741.52
869.3
883
1065.4 1025.92
1232.1 1136.78
1239
1238.7
1278.1 1317.66
1378.9 1335.68
1460.2 1367.02
1322.2 1445.84
1802.5 1879.7 1979.5 2047.9 1956.3 2272.8 2548.1 2809 2821 3010 3251 3186 3383 3791 3881.31 4804.8 5177.9 5345.1 5825 6012.7
时间序列分析--第五章非平稳序列的随机分析

非平稳序列的随机分析
2020/6/14
课件
1
本章结构
差分运算 ARIMA模型 Auto-Regressive模型 异方差的性质 方差齐性变化 条件异方差模型
2020/6/14
课件
2
5.1 差分运算
差分运算的实质 差分方式的选择 过差分
2020/6/14
课件
3
差分运算的实质
方差大
Var(xt ) Var(at at1)
2 2
Var(2xt ) Var(at 2at1 at2 )
6 2
2020/6/14
课件ቤተ መጻሕፍቲ ባይዱ
14
5.2 ARIMA模型
ARIMA模型结构 ARIMA模型性质 ARIMA模型建模 ARIMA模型预测 疏系数模型 季节模型
2020/6/14
1 1 1 2 1 1 2 2
j 1 j1 pd j pd j
2020/6/14
课件
28
预测值
xtl ( tl 1 tl1 l1 t1) ( l t l1 t1 )
et (l)
xˆt (l)
E[et (l)] 0
Var[et (l)]
(1
2 1
2 l 1
)
2
2020/6/14
课件
29
例5.7
已知ARIMA(1,1,1)模型为
(1 0.8B)(1 B)xt (1 0.6B) t
且 xt1 4.5
xt 5.3
t 0.8
2
1
求 xt3 的95%的置信区间
2020/6/14
课件
30
预测值
等价形式
(11.8B 0.8B2 )xt (1 0.6B)t xt 1.8xt1 0.8xt2 t 0.6t1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
本章结构
1.
差分运算
2.
ARIMA模型
3.
Auto-Regressive模型
4.
异方差的性质
5.
方差齐性变换
6.
条件异方差模型
青岛大学经济学院时间序列分析第五章2
差分前后时序图
•原序列时序图•差分后序列时序图
青岛大学经济学院时间序列分析第五章7
例5.2
•尝试提取1950年——1999年北京市民用车辆拥有量序列的确定性信息
青岛大学经济学院时间序列分析第五章8
差分后序列时序图
•一阶差分•二阶差分
青岛大学经济学院时间序列分析第五章9
例5.3
•差分运算提取1962年1月——1975年12月平均每头奶牛的月产奶量序列中的确定性信息
青岛大学经济学院时间序列分析第五章10
差分后序列时序图
•一阶差分•1阶-12步差分
青岛大学经济学院时间序列分析第五章11
本章结构
1.
差分运算
2.
ARIMA模型
3.
Auto-Regressive模型
4.
异方差的性质
5.
方差齐性变换
6.
条件异方差模型
青岛大学经济学院时间序列分析第五章15
ARIMA模型的平稳性
•ARIMA(p,d,q)模型共有p+d个特征根,其中p个在单位圆内,d个在单位圆上。
所以当
时ARIMA(p,d,q)模型非平稳。
•例5.5
ARIMA(0,1,0)时序图
d
青岛大学经济学院时间序列分析第五章20
例5.6
•对1952年——1988年中国农业实际国民收入指数序列建模
青岛大学经济学院时间序列分析第五章23
一阶差分序列时序图
青岛大学经济学院时间序列分析第五章24
一阶差分序列自相关图
青岛大学经济学院时间序列分析第五章25
拟合ARMA模型
•偏自相关图
青岛大学经济学院时间序列分析第五章27
青岛大学经济学院
时间序列分析 第五章
28
建模
•定阶
–ARIMA(0,1,1)
•参数估计
模型检验
t
t B x B ε)70766.01(99661.4)1(++=-48763
.56)(=t Var ε残差白噪声检验
参数显著性检验
延迟阶数
统计量
P值待估参数t 统计量P值6 3.630.6036 2.390.0223127.860.7262-5.58
<0.0001
18
11.03
0.8552
μ
2χ1
θ
例5.6续:对中国农业实际国民收入指数序列的预测
青岛大学经济学院时间序列分析第五章34
例5.8
•对1917年-1975年美国23岁妇女每万人生育率序列建模
青岛大学经济学院时间序列分析第五章37
一阶差分
青岛大学经济学院时间序列分析第五章38
自相关图
青岛大学经济学院时间序列分析第五章39
偏自相关图
青岛大学经济学院时间序列分析第五章40
例5.9
•拟合1962——1991年德国工人季度失业率序列
青岛大学经济学院时间序列分析第五章44
差分平稳
•对原序列作一阶差分消除趋势,再作4步差分消除季节效应的影响,差分后序列的时序图如下
青岛大学经济学院时间序列分析第五章45
差分后序列自相关图
青岛大学经济学院时间序列分析第五章47
差分后序列偏自相关图
青岛大学经济学院时间序列分析第五章48。
