随机变量方差的概念及性质
随机变量方差的概念及性质

= ( n 2 n) p 2 + np.
D( X ) = E ( X 2 ) [ E ( X )]2
= ( n 2 n) p 2 + np ( np )2
= np(1 p ) ).
3. 泊松分布
设 X ~ π(λ ), 且分布律为
P{ X = k } =
λk
k!
e λ , k = 0,1,2,
π π 2 = 3π + 24 2 4 16
4 2
2
= 20 2π 2 .
2 0 例4 设 X ~ 1 1 3 2
1 3 , 求 D( 2 X 3 + 5). 1 1 12 12
解
D( 2 X 3 + 5) = D( 2 X 3 ) + D( 5)
= 4 D( X )
= E[ X E ( X )]2 + E[Y E (Y )]2 ± 2 E {[ X E ( X )][Y E (Y )]}
= D( X ) + D(Y ).
推广 若 X 1 , X 2 ,
D( X1 ± X 2 ±
, X n 相互独立 , 则有 + D( X n ).
± X n ) = D( X1 ) + D( X 2 ) +
= C E {[ X E ( X )] }
2 2
= C 2 D( X ).
(3) 设 X, Y 相互独立, D(X), D(Y) 存在, 则
D( X ± Y ) = D( X ) + D(Y ).
证明
D( X ± Y ) = E {[( X ± Y ) E ( X ± Y )]2 } = E {[ X E ( X )] ± [Y E (Y )]}2
随机变量方差的定义及性质

02
CATALOGUE
方差的性质
方差的非负性
总结词
方差具有非负性,即对于任何随机变量X,其方差Var(X)总是非负的。
详细描述
方差的独立性
要点一
总结词
如果两个随机变量X和Y是独立的,那么Var(X+Y) = Var(X) + Var(Y)。
要点二
详细描述
这是方差的一个重要性质,表明如果两个随机变量相互独 立,那么它们的和的方差等于它们各自方差的和。这个性 质在概率论和统计学中非常重要,因为它允许我们通过独 立随机变量的方差来计算复合随机变量的方差。
度。
方差主要关注数据点的离散程度 ,而峰态则关注数据点的集中趋
势。
如果数据分布更加尖锐,即数据 点更加集中在平均值附近,则方 差可能会减小,因为数据点之间
的差异较小。
THANKS
感谢观看
方差还可以表示为
Var(X)=E(X^2)-[E(X)]^2。这个公式可以用来计算方差,其中E(X^2)表示随机变量X的平方的期望值 ,E(X)表示随机变量X的期望值。
方差与期望值的关系
方差的大小与期望值有关。如果一个随机变量的期望值越大,其方差也越大;如果一个随机变量的期望值越小,其方差也越 小。
03
CATALOGUE
方差的应用
方差在统计学中的应用
描述数据分散程度
方差是衡量随机变量取值分散程度的量,用于描述数 据的离散程度。
检验假设
在统计学中,方差分析(ANOVA)等方法用于检验 多个总体均值是否相等,从而判断假设是否成立。
随机变量的方差和标准差

0
2
0
xe
x2 2a2
dx
2a
2
e
x2 2a2
d
0
x2 2a2
2a
2
e
x2 2a2
0
2a2
;
DX EX 2 EX 2a2 πa2 a2 (4 π).
22
DXY EX 2Y 2 (EXY )2 EX 2EY 2 (EX )2 (EY )2 [DX (EX )2 ][DY (EY )2 ] (EX )2 (EY )2
证明 事实上,有 其中
二、切贝绍夫不等式
1
2
xi
( X EX )2 P
X xi
DX 2
,
1
2
xi EX
( X EX )2 P
X xi
P X EX PX xi xi EX
证明 (1) 设X是非负离散 型随机变量,其一切可能 值为{Xi},
则对于任意ε>0,有
设随机变量X的数学期望和方差都存在,则对于任意ε>0, 事件{|X-EX|≥ε}的概率有如下估计式——切贝绍夫不等式:
其中前两个和式∑表示对于满足| xi -EX|≥ε的X 的一切可能 值xi求和,后一个和式∑表示对于X 的一切可能值xi求和.
设X 是连续型随机变量,其概率密度
P
| x EX |
f
|xEX |
( x)dx
1 2
(x
EX )2
例为f (4fx.)(1dx1x) ,设则D随X2机 变 量 X 的 数 学 期 望 为 μ ,
方差为
,则由切
贝绍夫不等式,有
PX E X
P
3
X
3
连续型随机变量的数学期望与方差
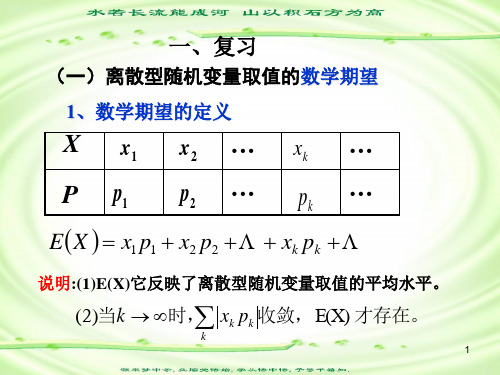
(1)D( )
E[
E( )]2
[x
E( )]2
p( x)dx
(2)方差的简便计算公式
D( )=E( 2) E(2 )
x2 p(x)dx
x p( x)dx
例2 随机变量的概率密度函数
6x(1 x),当0 x 1
p(x)
0
当x 0或x 1时
求随机变量的方差。
12
4、方差的性质 设 k ,b,c均为常数,则有
E( ) xp(x)dx
15
2、数学期望的性质
(1)EaX b aEX b
(2)EaX aEX
(3)EX b EX b
(4)Eb b
(5)EX Y EX EY
(6)E( f ( )) f (x)p(x)dx
(6)E f ( ) f (xk )PK
k
16
(二)连续型随机变量ξ取值的方差
(1)D(c) 0
(2)D(k ) k 2D( ) (3)D( b) D( )
(4)D(k b) k 2D( )
13
下页
三、练习
• 课本第90页 第6题
14
四、小结 (一)连续型随机变量ξ取值的数学期望
1、连续型随机变量的数学期望的定义 p(x) 设连续型随机变量 的密度函数为
若积分 xp(x绝)d对x 收敛,则 的数学期望为:
x0 x1 x2 L xn
xi xi1 xi
b i
【xi
,
xi
)
+1
y p(x)
o
x0b0 x1 xi bi xi1
xn x
6
连续型随机变量ξ的概率分布
ξ 【x0 , x1)【x1, x2)
高斯随机变量的均值和方差

高斯随机变量的均值和方差高斯随机变量的均值和方差概述:高斯随机变量是一种常见的概率分布,也被称为正态分布。
它在各个科学领域中都有广泛的应用,具有很强的实用价值。
均值和方差是高斯随机变量的两个重要统计特征,对于了解它的分布特性和应用具有重要意义。
一、高斯随机变量的定义和性质高斯随机变量的定义是指数学上服从正态分布的随机变量。
它的概率密度函数可以表示为一个钟形曲线,呈现出对称性和峰值集中的特点。
正态分布的概率密度函数可由均值和方差唯一确定。
1. 对称性:高斯随机变量的概率密度函数关于均值对称,即曲线在均值处达到峰值。
2. 峰值集中:均值是高斯随机变量的分布特征之一,它确定了曲线的中心位置。
方差则衡量了数据相对于均值的离散程度,决定了曲线的宽窄。
二、高斯随机变量的均值均值是一个概率分布的集中趋势的度量标准,对于高斯分布来说,均值是分布的中心位置。
1. 数学期望:高斯随机变量的均值也被称为数学期望,表示了随机变量的平均值。
对于高斯分布,其数学期望即为分布的均值。
2. 均值的性质:高斯随机变量的均值具有线性性质,即对于两个独立的高斯随机变量X和Y,它们的线性组合aX + bY的均值就是a和b的加权平均值。
三、高斯随机变量的方差方差是用来衡量数据的离散程度,对于高斯分布来说,方差决定了数据的分布宽度。
1. 方差的定义:高斯随机变量的方差是其概率分布关于均值的平均偏离程度的度量。
方差的数学定义为随机变量与均值的差的平方的期望。
2. 方差的性质:高斯随机变量的方差有以下几个性质:(1)方差非负,即方差的值大于等于0。
(2)方差为0表示所有数据都是相同的,即没有离散度。
(3)方差具有线性性质,对于两个独立的高斯随机变量X和Y,它们的线性组合aX + bY的方差为a^2Var(X) + b^2Var(Y)。
结论:高斯随机变量的均值和方差是衡量它分布特性的重要统计量。
均值决定了分布的中心位置,方差则表征了对中心位置的离散程度。
3.2随机变量的方差

一样的,还必须考虑这两个班级学生的两极分
化情况.为了反映随机变量的这种离散程度,我
们引入方差概念.
一、方差的概念
1.定义1 定义3.2.1 设 是一个随机变量,数学期望 E
2 为随机 存在,则称 E ( E ) E ( E ) 存在,如果
2
变量的方差,并记为. D 或Var
这个结论的充分性是显然的,下面证明必要性:
1 1 D 0 P( E 0) P( E ) P( E ) 0 n n 1 n n 1 1 2 n 1 ( ) n
由此知
P( E ) 0
更一般地,若 1 , 2
, n 两两独立,则
D1 n D1 D n
性质4 对任意的常数 C E ,则有 D E( C) 2 事实上 E ( C )2 E ( E E C ) 2
E ( E ) 2 2( E C ) E ( E ) ( E C ) 2 D ( E C ) 2 .
E 2
a
2 2 x a ab b x 2 p ( x)dx 4(b a ) a 3 2 2 2
(b a ) D E ( E ) . 12
7) 指数分布 设 ~ E( ) ,已知 E , 因为
E x p( x)dx x e dx x 2d (e x )
契贝晓夫不等式也可以表示成
P( a ) 1 D
2
由切比雪夫不等式看出, D 越小,事件 发生的概率越小, 越是集中在 的附近取值.由
此可见,方差刻划了随机变量取值的离散程度.
方差概念及计算公式

trapz梯形法定积分
cumtrapz梯形法区间积分
sum等宽矩阵法定积分
cumsum等宽矩阵法区间积分
fnint样条的不定积分
多重数值积分
dblquad('fun',inmin,inmax,outmin,outmax,tol,method) 定积分
问题1:函数f(x)在什么条件下可以表示成幂级数 ;
问题2:如果f(x)能表示成如上形式的幂级数,那末系数cn(n=0,1,2,3,…)怎样确定?
下面我们就来学习这两个问题。
泰勒级数
我们先来讨论第二个问题.假定f(x)在a的邻区内能表示成 这种形式的幂级数,其中a是事先给定某一常数,我们来看看系数cn与f(x)应有怎样的关系。
积分限为函数时 先求G(y)={x2(y),x1(y)}f(x,y)dx 再求I={y2,y1}G(y)dy 这里用{}表示豆芽符
数值微分
多项式求导 polyder
差分算积分 diff(X)
6.符号微积分
约定变量x 系数a,b
极限
limit(f,x,a)求x->a时f值、
limit(f,x,a,'right') 右极限 limit(f,x,a,'left')左极限
超定求最小二乘解 用A\B %基于奇异值分解;用pinv(A)*B %基于householder变换
欠定由qr分解求得
非负最小二乘解 X=nnls(A,b,TOL) TOL指定误差,可缺省
零点法求解方程
fzero一元 fsolve多元
x=fzero(fun,x0)
[x,fval,exitflag]=fzero(fun,x0,options,P1,P2,...)
一随机变量方差的定义及性质

(1p)/ p2
ab ab 2 (ba)2 12
0
1/
1 / 2
μ,σ0
μ
σ2
分布
Gamma分布
参数 , 0
数学期望
/
方差
/2
三、例题讲解
例1 设随机变量X 具有概率密度
求D(X).
1 x, 1 x 0, p(x) 1 x, 0 x 1,
2(X),即 D(X) 2(X) E{[XE(X)]2}.
称 D(X)为标准差或均,记 方为 差σ(X).
2. 方差的意义
方差描述了随机变量X取值对于数学 期望的分散程度.如果D(X)值大, 表示X 取 值分散程度大, E(X)的代表性差;而如果 D(X) 值小, 则表示X 的取值比较集中,以 E(X)作为随机变量的代表性好.
k
则有
0p1.
EX k n 0kk npk(1p)nknp
E (X 2 ) E [X (X 1 ) X ]
E [X (X 1 ) ] E (X )
n
k(k1)Cn kpk(1p)nknp
k0
nk(k1)n!pk(1p)nknp k0k!(nk)!
xexdx
0
1/.
D (X ) E (X 2 ) [E (X )2]
0 x2exdx1/2
2/21/2
1 2 指 数 分 布 的 期 望 分和 别方 1为 /差和1/2.
6. 正态分布
设X~N(μ,σ2),其概率密度为
f(x )1e (x 2 σ μ 2 )2, σ 0 , x . 2 σ
D (X ) E (X 2 ) [E (X )2]
bx2 1 dxab2 a ba 2 ((bb aa)2 .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
σ 0, x .
先求标准正态变量 Z x μ 的数学期望和方差. σ
Z的概率密度为 (t) 1 et2 2,
2π
于是 E(Z ) 1 tet2 2 d t 1 et2 2 0,
2π
2π
D(Z ) E(Z 2 )
1 t 2et2 2 d t
2π
1 tet2 2 1 et2 2 d t
求D( X ).
解 E( X ) 0 (1 p) 1 p p, E( X 2 ) 02 (1 p) 12 p p,
由(2.4)式 D( X ) E( X 2 ) [E( X )]2 p p2 p(1 p).
例3 设 X ~ π( ), 求D( X ).
解 X 的分布律为
2π
2π
1,
因 X Z,
即得 E( X ) E( Z ) μ.
D( X ) D( Z ) D(Z ) 2D(Z ) σ 2.
正态分布的期望和方差分别为两个参数 μ 和 σ2.
若X i
~
N
(
i
,
2 i
),
i
1,2,
, n,
且它们相互独
立,则它们的线性组合:C1 X1 C2 X2 Cn Xn
D( X C ) E{[X C E( X C)]2} E{[X E( X )]2} D( X ).
3 设 X ,Y 是两个随机变量,则有 D( X Y ) D( X ) D(Y ) 2E{(X E( X ))(X E(Y ))}.
若 X ,Y 相互独立, 则有 D( X Y ) D( X ) D(Y ).
第二节 方 差
一、随机变量方差的概念及性质 二、重要概率分布的方差 三、例题讲解 四、小结
一、随机变量方差的概念及性质
1. 概念的引入
方差是一个常用来体现随机变量取值分散程度 的量. 实例 有两批灯泡,其平均寿命都是 E(X)=1000小时.
•
• • • • • •• • •
O
1000
x
• •• • •
2E{(X E( X ))(X E(Y ))} 2E{XY XE(Y ) YE( X ) E( X )E(Y )}
2{E( XY ) E( X )E(Y ) E(Y )E( X ) E( X )E(Y )}
2{E( XY ) E( X )E(Y )}.
若 X ,Y 相互独立,由数学期望的性质4 知道上 式右端为0,于是
E
X
2
1
2 E[( X
)2]
2 2
1.
X X ,
则 E( X ) 1 E( X ) 1 [E( X ) ] 0;
D( X ) E( X 2 ) [E( X )]2
E
X
2
1
2 E[( X
)2]
2 2
1.
例2 设随机变量X 具有(0 1)分布,其分布律为 P{X 0} 1 p, P{X 1} p.
D( X Y ) D( X ) D(Y ). 这一性质可以推广到任意有限多个相互独立的随 机变量之和的情况.
推广 若 X1, X2, , Xn 相互独立, 则有
D( X1 X2 Xn )D( X1) D( X2 ) D( Xn ).
(4) D( X ) 0 的充要条件是 X 以概率1 取常数 C,
(n2 n) p2 np (np)2
np(1 p).
3. 泊松分布
设 X ~ π( ), 且分布律为
P{X k} k e , k 0,1,2, , 0.
k! 则有
E(X
)
k
k0
k
k!
e
e
k 1
k1 (k 1)!
e e .
E( X 2 ) E[ X ( X 1) X ]
3. 方差的意义
按定义, 随机变量 X 的方差表达了X 的取值与 其数学期望的偏离程度. 若 D( X )较小意味着X 的 取值比较集中在E( X )的附近, 反之, 若 D( X )较大 则表示 X 的取值较分散. 因此, D( X )是刻画X 取 值分散程度的一个量,它是衡量X 取值分散程度 的一个尺度.
a
2
b
2
(b a)2 . 12
例5 设随机变量 X 服从指数分布, 其概率密度为
1 ex θ , x 0,
f (x) θ
0,
x 0.
其中θ 0, 求E( X ), D( X ).
解 E( X ) xf ( x)d x x 1 ex θ d x
0θ
xex θ ex θ d x θ. 00
设随机变量 X 服从指数分布,其概率密度为
则有
1 ex θ , x 0,
f (x) θ
0,
x 0.
E( X ) xf ( x)d x x 1 ex θ d x
0θ
xe x θ 0
ex θ d x θ.
0
E( X 2 ) x2 f ( x)d x
x2 1 e x θ d x
(2) 利用公式计算
D( X ) E( X 2 ) [E( X )]2. 证 D( X ) E{[X E( X )]2}
E{X 2 2XE( X ) [E( X )]2} E( X 2 ) 2E( X )E( X ) [E( X )]2 E( X 2 ) [E( X )]2
泊松分布的期望和方差相等, 都等于参数 .
例4 设 X ~ U (a,b), 求( X ).
解 X 的概率密度为
f (x)
1, ba
0,
a x b, 其他.
上节例7已算得 E( X ) a b , 方差为 2
D( X ) E( X 2 ) [E( X )]2
b a
x
2
b
1
a
d
x
E[X ( X 1)] E( X )
k(k 1) k e
k0
k!
2e
k 2
k2 (k 2)!
2e e
2
.
所以 D( X ) E( X 2 ) [E( X )]2 2 2 .
泊松分布的期望和方差都等于参数 .
4. 均匀分布
设 X ~ U(a,b), 其概率密度为
5. 方差的性质
1 设 C 是常数,则D(C ) 0.
证 D(C) E{[C E(C)]2} 0. 2 设 X 是一个随机变量,C是常数,则有 D(CX ) C 2D( X ), D( X C) D( X ).
证 D(CX ) E{[CX E(CX )]2} C 2E{[X E( X )]2} C 2D( X ).
k0
n
n k(k 1)n!pk (1 p)nk np
k0 k!(n k)!
n
n(n 1) p2
(n 2)! pk2 (1 p)(n2)(k2)
k2 (n k)!(k 2)!
np
n(n 1) p2[ p (1 p)]n2 np
(n2 n) p2 np.
D( X ) E( X 2 ) [E( X )]2
E( X 2 ) x2 f ( x)d x x2 1 ex θ d x
0
θ
x2e x θ 2 xe x θ d x θ 2 . 00
于是 D( X ) E( X 2 ) [E( X )]2 2θ2 θ2 θ2 .
即有 E( X ) θ, D( X ) θ2 .
例6 设 X ~ b(n, p), 求E( X ), D( X ).
解 由二项分布的定义知,随机变量X 是 n重伯 努利试验中事件A发生的次数, 且在每次试验中A 发生的概率为p . 引入随机变量
Xk
1, 0,
A在第k次试验发生, k A在第k次试验不发生,
1,2,
4. 随机变量方差的计算
(1) 利用定义计算
对于离散型随机变量
D( X ) [ xk E( X )]2 pk ,
k 1
其中 P{X xk } pk , k 1,2, 是 X 的分布律. 对于连续型随机变量
D( X ) [ x E( X )]2 f ( x)d x,
其中 f ( x) 为X的概率密度.
0
θ
x2e x θ 2 xe x θ d x
0
0
θ2.
D( X ) E( X 2 ) [E( X )]2 2θ2 θ2 θ2 .
指数分布的期望和方差分别为θ 和 θ2.
6. 正态分布
设 X ~ N ( μ,σ2 ), 其概率密度为
f (x)
1 e ,
(
x μ 2σ2
)2
2πσ
E(Z ) 2 1 3 2 4, D(Z ) D(2X 3Y ) 4D( X ) 9D(Y ) 48.
故有Z ~ N (4,48).
分布 两点分布 二项分布
泊松分布 均匀分布 指数分布 正态分布
参数
0 p1 n 1,
0 p1
0
ab
θ0 μ,σ 0
数学期望 方差
p
p(1 p)
证 D( X Y ) E{[(X Y ) E( X Y )]2} E{[X E( X )] [Y E(Y )]}2 E[X E( X )]2 E[Y E(Y )]2
2E{[X E( X )][Y E(Y )]} D( X ) D(Y ) 2E{(X E( X ))(X E(Y ))}. 上式右端第三项:
f (x)
1, ba
0,
a x b, 其他.
则有E( X )
b1
xf ( x)d x
xd x
aba
1 (a b). 2
结论 均匀分布的数学期望位于区间的中点.
D( X ) E( X 2 ) [E( X )]2
