哈夫曼编码讲解58页PPT
霍夫曼编码PPT课件
对于各值（码值）的代码（码字）就是从根节点出发到底层节点所经历 的分支序列。如a4的代码（码字）为00，a6的码字为111... ...通常a4和 a6等称为码值，00和111等称为码字。所有码值和码字对应关系如下表 所示：
Your company slogan
（三）霍夫曼表
将所有码值和码字的关系整理成一张表，为了整字 节输出码字，表中还含有各码字的长度。这种表就称 为霍夫曼表。本例霍夫曼表如表所示：
Your company slogan
进行压缩编码时，只要将码值用码字代替即可。所 以源符a1 a1 a2 a2 a3 a3 a3 a4 a4 a4 a4 a5 a5 a5 a6 a6 a6 a7 a7 a8编码为： 01001001101110110110100000000110110 11010000100001001。
Your company slogan
四、霍夫曼编码
（一）霍夫曼编码过程
设信息源空间为[A*P]:{A:a1 a2 ……an}{P(A):P(a1) P(a2)P(a3)……P(an)}其中∑ P(ak)=1,先用r个码的号码符 号集X:{x1,x2,……xr}对信源A中的每一个符号ak进行编码。 编码过程如下： 把信源符号ai按其出现的概率的大小顺序排列起来； 把最末两个具有最小概率的元素之概率加起来； 把该概率之和同其余概率由大到小排队，然后再把两个最 小概率加起来，再排队； 重复步骤 (2) 、 (3), 直到概率和达到 1 为止 ; 在每次合并消息时，将被合并的消息赋以1和0或0和1； 寻找从每个信源符号到概率为1处的路径，记录下路径上 的1和0； 对每个符号写出"1"、"0"序列（从码数的根到终节点）。 创建霍夫曼表。 压缩编码时，将码值用码字代替。
哈夫曼编码PPT课件
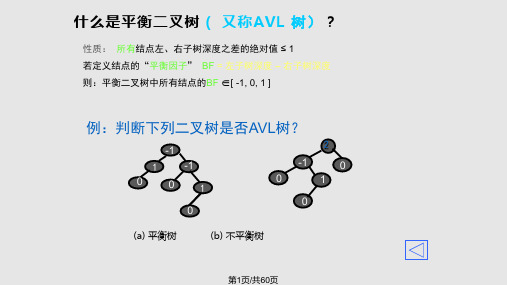
Huffman编码举例
例1【严题集6.26③】：假设用于通信的电文仅由8个字母 {a, b, c, d, e, f, g, h} 构成， 它们在电文中出现的概率分别为{ 0.07, 0.19, 0.02, 0.06, 0.32, 0.03, 0.21, 0.10 }，试 为这8个字母设计哈夫曼编码。如果用0～7的二进制编码方案又如何？ 【类同P148 例2】
建议2： Huffman树的存储结构可采用顺序存储结构： 将整个Huffman树的结点存储在一个数组HT[1..n..m]中;
各叶子结点的编码存储在另一“复合”数组HC[1..n]中。
第16页/共60页
Huffman树和Huffman树编码的存储表示：
typedef struct{ unsigned int weight；//权值分量（可放大取整） unsigned int parent，lchild，rchild； //双亲和孩子分量 }HTNode，*HuffmanTree；//用动态数组存储Huffman树 typedef char**HuffmanCode； //动态数组存储Huffman编码表
HT[s1].parent=i; HT[s2].parent=i; HT[i].lchild=s1; HT[i].rchild=s2; HT[i].weight=HT[s1].weight+ HT[s2].weight;}
第18页/共60页
(续前)再求出n个字符的Huffman编码HC
HC=(HuffmanCode)malloc((n+1)*sizeof(char*)); //分配n个字符编码的头指针 向量（一维数组） cd=(char*) malloc(n*sizeof(char)); //分配求编码的工作空间(n)
哈夫曼编码和译码
哈夫曼树的构造算法: 哈夫曼树的构造算法: 个结点的一维数组, (1)初始化哈夫曼树的 )初始化哈夫曼树的2n-1个结点的一维数组, 个结点的一维数组 即将各结点中的各个域均置0; 即将各结点中的各个域均置 ; 个权值存放到一维数组的前n个单元中 (2)读入 个权值存放到一维数组的前 个单元中, )读入n个权值存放到一维数组的前 个单元中, 它们即为初始森林中的n个只含根结点的权值 个只含根结点的权值; 它们即为初始森林中的 个只含根结点的权值; (3)对森林中的二叉树进行合并,产生 个新 )对森林中的二叉树进行合并,产生n-1个新 结点,依次存放到一维数组的第n+1个开始的单元中, 个开始的单元中, 结点,依次存放到一维数组的第 个开始的单元中 在这个过程中要注意对每个结点双亲域, 在这个过程中要注意对每个结点双亲域,左右孩子 域以及权值的修改. 域以及权值的修改.
13
s1=maxval;s2= maxval;/ 设maxval为float类型最大值 ; ;/*设 ;/ 为 类型最大值 */ for(j =1;j<=i;j+ +) ( ; ; ) if (ht[j].parent = =0) /*判断是否为根结点 判断是否为根结点*/ 判断是否为根结点 if (ht[j].weight<s1) { s2=s1;s1= ht[j].weight; p2=p1;p1=j; } ; ; ; ; else if (ht[j].weight <s2) { s2= ht[j].weight; p2=j; } ; ; ht[p1].parent=i;ht[p2].parent=i; ; ; ht[i].lchild =p1;ht[i].rchild=p2; ; ; ht[i].weight= ht[pl].weight+ht[p2].weight; ; } return (ht);} ;
哈夫曼编码与解码C语言知识讲解
哈夫曼编码与解码C语言#include "stdio.h" /*I/O函数*/#include"stdlib.h" /*其他库函数声明*/int num;/*记录结点数*/int codenum=0;/*已经获得的编码个数*/char filename[20]=""; /*存储文件名*/typedef struct /*哈夫曼结点存储结构*/{char ch; /*结点字符*/int w; /*结点权值*/int lchild,rchild; /*左右孩子的数组下标*/}HafuNode,*HafuTree;HafuTree ht;/*声明一个指向树结点到指针*/typedef struct{char ch; /*叶子结点字符*/char codestr[20]; /*字符编码*/}HafuCode;HafuCode code[27];/*用于存放对应字符到哈夫曼编码*/void InitHafuArry(){ /*导入文件计算权值，生成只含有叶子结点的HafuNode数组*/int j,i,k;HafuNode tmpht;FILE *fp; /*定义一指向打开文件的指针*/char ch;/*用于存储一个字母*/char location[30]="D:\\";ht=(HafuTree)malloc(53*sizeof(HafuNode)); /*为哈夫曼数分配内存空间*/ if(ht==NULL) return ;for(i=0;i<53;i++) /*初始化所以的数据单元，每个单元自成一棵树*/ {ht[i].w=0; /*权值初始化为0*/ht[i].lchild=ht[i].rchild=-1; /*左右子为空*/}num=0;printf("File name:");scanf("%s",filename);strcat(location,filename);fp=fopen(location,"r");if(!fp) /*返回1时即存在文件*/{printf("Open Error");return;}while(!feof(fp))/*没到结尾时返回0*/{ch=fgetc(fp);if(ch==' '||ch<='z'&&ch>='a'||ch<='Z'&&ch>='A'){printf("%c",ch);if(ch==' ') ch='#';for(j=0;j<num;j++){if(ht[j].ch==ch){break;}}if(j==num) /*找到新字符*/{ht[num].ch=ch; /*将新字符存入并将权值加1*/ht[num].w++;num++;}else{ht[j].w++; /*将已有字符权值加1*/}}}fclose(fp);printf("\n");for(i=0;i<num;i++) /*对叶子结点按权值进行升序排序*/{k=i;for(j=i+1;j<num;j++){if(ht[j].w<ht[k].w)/*如果后面发现权值比i小的则将其下标记录下来，循环完之后找到最小的*/k=j;}if(k!=i) /*如果权值最小的不是第i个元素则交换位置，将小的放到前面*/ {tmpht=ht[i];ht[i]=ht[k];ht[k]=tmpht;}}}int CreateHafuman(HafuTree ht){ /*在数组ht中生成哈夫曼数，返回根节点下标*/int i,k,j,root;HafuNode hfnode;codenum=0;for(i=0;i<num-1;i++){ /*需生成num-1个结点*/k=2*i+1; /*每次取最前面两个结点，其权值必定最小*/hfnode.w=ht[k].w+ht[k-1].w;hfnode.lchild=k-1;hfnode.rchild=k;for(j=num+i;j>k;j--) /*将新结点插入有序数组中*/{if(ht[j].w>hfnode.w){ht[j+1]=ht[j];}else break;}ht[j]=hfnode;root=j;/*一直跟随新生成的结点，最后新生成的结点为根结点*/}return root;}void GetHafuCode(HafuTree ht,int root,char *codestr){ /*ht是哈夫曼树，root是根结点下标，codestr是来暂时存放叶子结点编码的，一开始为空*/FILE *out;int len,i;FILE *fp; /*定义一指向打开文件的指针*/char ch;/*用于存储一个字母*/char location[30]="D:\\";if(ht[root].lchild==-1){/*遇到递归终点是叶子结点记录叶子结点的哈夫曼编码*/code[codenum].ch=ht[root].ch;strcpy(code[codenum].codestr,codestr);codenum++;}else /*不是终点则继续递归*/{len=strlen(codestr);codestr[len]='0'; /*左分支编码是0*/codestr[len+1]=0; /*向左孩子递归之前调整编码序列末尾加0,相当于加了个‘\0’（null）其十进制值是0，以便下次循环时添加字符，否则会被覆盖掉*/GetHafuCode(ht,ht[root].lchild,codestr); /*向左递归*/len=strlen(codestr);codestr[len-1]='1';/*右分支编码为1，想右递归之前末尾编码0改为1*/ GetHafuCode(ht,ht[root].rchild,codestr); /*向右递归*/len=strlen(codestr);codestr[len-1]=0; /*左右孩子递归返回后，删除编码标记末尾*/}strcat(location,filename);fp=fopen(location,"r");if(!fp) /*返回1时即存在文件*/{printf("Open Error");return;}out=fopen("D:\\code.txt","w+") ;if(!out){/*printf("Write Error"); */return;}while(!feof(fp))/*没到结尾时返回0*/{ch=fgetc(fp); /*再打开源文件，对照哈夫曼编码译成编码*/if(ch==' '||ch<='z'&&ch>='a'||ch<='Z'&&ch>='A'){ if(ch==' ') ch='#'; /*如果是空格就用#号代替*/for(i=0;i<codenum;i++){ /*找到字符所对应到哈夫曼编码*/if(ch==code[i].ch){ /*将所得哈夫曼编码输出到文件中*/fputs(code[i].codestr,out);}}}}fclose(fp); /*关闭打开到两个文件*/fclose(out);}void decodeHafuCode(HafuTree ht,int root) /*将哈夫曼编码翻译为明文*/ {FILE *fp2; /*定义一指向打开文件的指针*/char ch;/*用于存储一个字母*/int curr=root;/*当前结点到下标*/char filename2[20]="";/*获得文件名*/char location[30]="D:\\";printf("File name:");scanf("%s",filename);strcat(location,filename);fp2=fopen(location,"r");if(!fp2) /*返回1时即存在文件*/{printf("Open Error2");return;}printf("Code:");while(!feof(fp2))/*没到结尾时返回0*/{ch=fgetc(fp2);if(ch>='0'&&ch<='1')/*将编码过滤出来*/{printf("%c",ch); /*将密文输出显示*/}}printf("\n");rewind(fp2); /*将文件指针位置定位在开头*/while(!feof(fp2))/*没到结尾时返回0*/{ch=fgetc(fp2);if(ch>='0'&&ch<='1')/*将编码过滤出来*/{if(ch=='0') /*如果为0则当前结点向左走*/{if(ht[curr].lchild!=-1){curr=ht[curr].lchild;/*若有左子则去左子*/}else{curr=root; /*没有则返回根结点*/}}if(ch=='1') /*如果为1则当前结点向右走*/{if(ht[curr].rchild!=-1){curr=ht[curr].rchild;/*若有右子则去右子*/}else{curr=root; /*没有则返回根结点*/}}if(ht[curr].lchild==-1&&ht[curr].rchild==-1)/*若为叶子结点则打印输出*/ {printf("%c",ht[curr].ch=='#'?' ':ht[curr].ch);curr=root; /*回到根结点继续索引*/}}}fclose(fp2);}void main(){ int root;int i;char codestr[20]="";int control;/*显示菜单可选择编码、译码还是退出*/printf("================Menu==============\n");printf("chose 1:encode\n");printf("chose 2:decode\n");printf("chose 3:exit\n");scanf("%d",&control);while(control!=3) /*只有没有选择退出就一直循环*/{if(control==1) /*选择编码选项*/{FILE *output;char ch;InitHafuArry(); /*初始化结点*/root=CreateHafuman(ht); /*造一棵哈夫曼树*/GetHafuCode(ht,root,codestr);/*根据哈夫曼树将明文译成密码*/ printf("Code:");output=fopen("D:\\CODE.TXT","r");if(!output) /*返回1时即存在文件*/{printf("Open Error3");continue;}while(!feof(output))/*没到结尾时返回0*/{ch=fgetc(output);if(ch>='0'&&ch<='1')/*将编码过滤出来*/{printf("%c",ch); /*将密文输出显示*/}}fclose(output);/*将打开文件关闭*/}if(control==2) /*如果选择译码，则调用译码函数*/{decodeHafuCode(ht,root);}if(control==3) /*如果选择3则退出程序*/{exit(0);}/*若没有退出则继续打印菜单提示供选择*/printf("\n\n================Menu==============\n"); printf("chose 1:encode\n");printf("chose 2:decode\n");printf("chose 3:exit\n");getch();scanf("%d",&control);}}。
数据结构哈夫曼树PPT课件
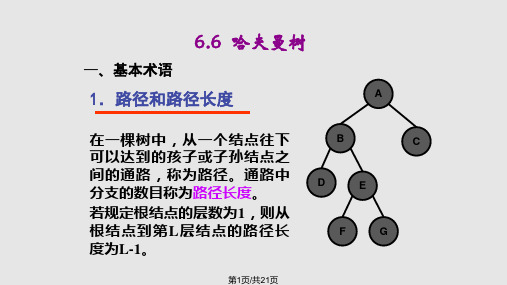
例：
W（权）={2,4,2,3,3}，叶子结点个数,m=5 试设计Huffman树。
14
6
3
3
8
4
4
22
构造的 Huffman树
第12页/共21页
三、哈夫曼树的应用(哈夫曼编码)
在远程通讯中，要将待传字符转换成由二进制组成 的字符串：
设要传送的字符为： 若编码为：A—00 (等长) B—01
重码 000011010
关键：要设计长度不等的编码，则必须使任一字符的编码都不 是另一个字符的编码的前缀。这种编码称作最优前缀编码。
第14页/共21页
设要传送的字符为：
若编码为 ：A—0
B—110
C用二叉树设 计二进制前缀
编码
0
1
C0
1
BD
第15页/共21页
ABACCDA
C—10 D---11
ABACCDA
若将编码设计为长度不等的二进制编码，即让待传字符串中出 现次数较多的字符采用尽可能短的编码，则转换的二进制字符 串便可能减少。
第13页/共21页
设要传送的字符为：ABACCDA 若编码为： A—0
B—00 C—1 D---01
ABACCDA
但： 0000 AAAA ABA BB
二、构造哈夫曼树 1．哈夫曼树的定义
在一棵二叉树中，若带权路径长度达到最小，称这样的 二叉树为最优二叉树，也称为哈夫曼树(Huffman tree)。
第3页/共21页
例 有4个结点，权值分别为7，5，2，4，构造有4个叶子结点的二叉树
4d
a 7
n
c
2
WPL
WK LK
k 1
数据结构哈夫曼树和哈夫曼编码PPT课件
C
AB
AC
BC
ABC
第27页/共55页
回朔策略—求幂集
000
000
100
000
010
100
110
000
001
010
011 100 101 110
111
第28页/共55页
回朔策略—求幂集
void powerSet(int num){ if (num<=len-1) { for (int i=0; i<2; i++){ if (i = = 0) mask[num]=1; else mask[num]=0; powerSet(num+1);} } else{ for (int j=0; j<len; j++){ if (mask[j]==1) printf("%c",set[j]);} printf("\n");}
}
第29页/共55页
回朔策略—求幂集
int len=3; int mask[]={0,0,0}; char set[]={'A','B','C'}; int main(int argc, char* argv[]) {
powerSet(0); return 0; }
第30页/共55页
章末复习
1. 熟练掌握二叉树的结构特性，了解相应的证 明方法。 2. 熟悉二叉树的各种存储结构的特点及适用范 围。 3. 遍历二叉树是二叉树各种操作的基础。实现 二叉树遍历的具体算法与所采用的存储结构有 关。掌握各种遍历策略的递归算法，灵活运用 遍历算法实现二叉树的其它操作。层次遍历是 按另一种搜索策略进行的遍历。
哈夫曼编码---PPT
12
结果：
结果：
谢 谢
15
哈夫曼编码实现文件压缩与解压
小组成员：刘 勇 吴风松 张艳芬
1
信源编码的基本途径有两个：
使序列中的各个符号尽可能地互相独立， 即解除相关性；使编码中各个符号源自现的概率尽可能地相 等，即概率均匀化。
2
哈夫曼码为最佳无失真码 哈夫曼编码原理： 哈夫曼编码使用变长编码表对源符号（如文 件中的一个字母）进行编码，可以使编码 之后的字符串的平均长度、期望值降低， 从而达到无损压缩数据的目的。 特点：1.出现机率高的字母使用较短的编 码，反之出现机率低的则使用较长的编码 2.一个短的元素的编码不会成为其他长 3 编码的前缀
5
哈夫曼编码的建模：
为什么要用二叉树的结构来实 现哈夫曼编码？
6
例子说明：
0.4 0.2 0.2 0.1 0.1 0.4 0.2 0.2 0.2 0.4 0.4 0.2
0 1
0.6 0 0.4 1
1.0
0 1
0 1
7
对英文文本文件：
8
霍夫曼树的构造：
9
压缩：
10
解压：
11
程序实现框架：
哈夫曼编码方法
(1)将信源消息符号按其出现的概率大小依次 排列， p1 p2 pn (2)取两个概率最小的字母分别配以0和1两个 码元，并将这两个概率相加作为一个新字 母的概率，与未分配的二进符号的字母重 新排队。
4
(3)对重排后的两个概率最小符号重复步骤 (2) 的过程。
(4) 不断继续上述过程，直到最后两个符号配 以0和1为止。 (5) 从最后一级开始，向前返回得到各个信源 符号所对应的码元序列，即相应的码字。
哈夫曼编码资料讲解
P
0.22 0.20 0.18 0.15 0.10 0.08 0.05 0.02
码字 1 2 3 00 01 02 030 031
例•5-信9 源输出2个符号，概率分布为P=（0.9,0.1)，信 源熵H（X）=H（0.9)=0.469。采用二进制哈夫曼编 码。 L=1, 1=1bit/符号； L=2,P’=(0.81,0.09,0.09,0.01), 2=0.645bit/符号； L=3, K 3=0.533bit/符号； L=4, 4=0.493bit/符号。 随着序K列长度L的增加，平均码长迅速降低，接近 信息源熵值，K 编码效率接近于1.
K
一般情况下，信源符号以恒速输出，信道也是恒速传 输的。通过编码后，会造成编码输出每秒的比特数 不是常量，因而不能直接由信道来传送。为了适应 信道，必须增加缓冲寄存器。将编码输出暂存在缓 冲器中，然后再由信道传输，使输入和输出的速率 保持平衡。
溢出：当信源连续输出低概率符号时，因为码长较长， 有可能使缓冲器存不下而溢出。
0110 4
0111 4
该哈夫曼编码的平均码长
7
K p(ai)Ki 2.72码元/符号 i1
信息传输速率
RH(X)2.610.96Bit/码元 K 2.72
哈夫曼编码方法得到的码并非唯一的
1 每次对信源缩减时，赋予信源最后两个概率最小的符号， 用0和1是可以任意的，所以可以得到不同的哈夫曼码，但 不会影响码字的长度。
编码过程
0.4
0.4
0.6 0 1.0
0.2
0.4 0 0.4 1
0.2 0
0.2 1
0.2 1
码字 码长
1
1
01 2
000 3