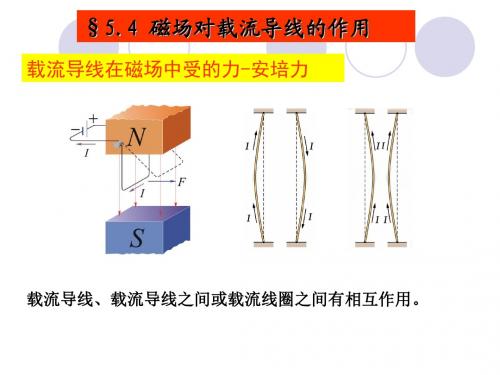
洛伦兹力及安培力的计算
5 .5安培力、洛伦兹力
Fab
l1
b
B
Fbc
l 2 o'
ˆ n Pm
考虑方向: M P m B
Pm B sin
上述结论具有普遍 意义(也适用于带电
粒子沿任意闭合回路 的运动或自旋磁矩在 磁场中受的力矩) 。
Pm 右旋 力矩方向为:四指从 到 B ,大拇指指向。
§5.5 洛仑兹力 霍尔效应 1. 洛仑兹力
R
dl Rd
Fx
0
IB cos Rd 0
IB sinRd IB2R
0
例2 计算半径为R的半圆导线在均匀磁场 B中所受的力。
半径为R的半圆导线的安培力: 大小: F BI 2R
B
I
F
R
方向: 沿平面竖直向上
等效于长度为2R,电流为I的直导线所 (起点和终点重合)受的力 推广: 任何载流导线在均匀磁场中受力等效 于一直导线(起点和终点重合)所受 的力
IB VH h B
+
I
VH
定量分析:
h b
A - - - - + + + + + B
B
I
+ VH
A -
f B B
-
-
+
v
+
q
-
B
fE
+
+
I
运动电荷 所受洛仑兹力:
U A U B EH b v Bb f B qv B q e I nqv S nev bh 电场力: f E qEH I 二者平衡时: vb neh qv B qEH
安培力、洛伦兹力

安培力洛伦兹力教学内容安培力洛伦兹力教学目标1.知道安培力的概念。
知道通电导线在磁场中所受安培力的方向与电流、磁场方向都垂直时,它的方向的判断----左手定则。
知道左手定则的内容,会用左手定则熟练地判定安培力的方向,并会用它解答有关问题.2.会用安培力公式F=BIL解答有关问题. 知道电流方向与磁场方向平行时,电流受的安培力最小,等于零;电流方向与磁场方向垂直时,电流受的安培力最大,等于BIL.3.了解磁电式电流表的内部构造和原理。
4. 知道什么是洛伦兹力.利用左手定则判断洛伦兹力的方向.5.知道洛伦兹力大小的推理过程.6.了解v和B垂直时的洛伦兹力大小及方向判断.理解洛伦兹力对电荷不做功.7.了解电视显像管的工作原理.教学重点难点重点:1.安培力的方向确定和大小的计算。
2.利用左手定则会判断洛伦兹力的方向.3.掌握垂直进入磁场方向的带电粒子,受到洛伦兹力大小的计算难点:1.左手定则的运用(尤其是当电流和磁场不垂直时,左手定则如何变通使用)。
2.洛伦兹力对带电粒子不做功.3.洛伦兹力方向的判断.教学过程第1课时导入让学生回忆在在第二节中通电导线在磁场中受力大小与什么因素有关。
知识要点一、安培力的方向通电导线在磁场中受到的力叫安培力,安培力的方向可以用左手定则判断:左手定则:伸开左手,使大拇指跟其余四个手指垂直,并且跟手掌在同一个平面内,把手放人磁场中,让磁感线垂直穿人手心,并使伸开的四指指向电流方向,那么,拇指所指的方向,就是通电导线在磁场中的受力方向.说明:电流和磁场可以不垂直,但安培力必然和电流方向垂直,也和磁场方向垂直,用左手定则时,磁场不一定垂直穿过手心,只要不从手背传过就行。
二、安培力的大小通电导线(电流为I、导线长为L)和磁场(B)方向垂直时,通电导线所受的安培力的大小:F = BIL(最大)两种特例:即F = ILB(I⊥B)和F = 0(I∥B)。
一般情况:当磁感应强度B的方向与导线成θ角时,有F = ILBsinθ还应该注意的是:尽管公式F=ILB是从公式B=F/IL变形而得的,但两者的物理意义却有不同。
高二物理安培力知识点

高二物理安培力知识点安培力(Ampere Force),又称真空中的洛伦兹力(Lorentz Force),是指一个电荷在磁场中所受到的力。
在高二物理学习中,我们需要了解并掌握安培力的计算方法、性质以及与电流、磁场等相关的知识点。
本文将为大家介绍高二物理中与安培力相关的知识点。
一、安培力的计算公式安培力的计算公式为F = qvBsinθ,其中F表示安培力的大小,q表示电荷的大小,v表示电荷的速度,B表示磁感应强度,θ表示电荷速度与磁场方向之间的夹角。
二、安培力的性质1. 安培力与电荷的关系安培力与电荷的大小成正比,即当电荷q增加时,安培力F也相应增加。
2. 安培力与电流的关系电流是单位时间内通过导体横截面的电荷量,安培力与电流的大小成正比。
设导线长度为l,电荷在导线中的速度为v,电荷密度为ρ,则电流I = ρvl。
因此,安培力F与电流I也成正比。
3. 安培力与磁场的关系安培力与磁场的大小成正比,即当磁感应强度B增加时,安培力F也相应增加。
4. 安培力与速度的关系安培力与电荷的速度v的大小成正比,即当电荷速度v增加时,安培力F也相应增加。
5. 安培力的方向安培力的方向遵循右手定则:将右手从电荷正方向握住导线,在磁场方向上升的情况下,手指弯曲的方向即为安培力的方向。
6. 安培力的性质总结安培力与电荷、电流、磁场强度、速度之间有着一定的数学关系,根据具体情况可以通过计算公式来求解安培力的大小和方向。
三、安培力与磁场的应用1. 高斯枪高斯枪是利用安培力的原理来实现粒子的加速和磁聚焦。
通过在导弹中引入磁场,使得导弹内部飞行的粒子受到安培力的作用,从而达到加速的效果。
2. 电磁铁电磁铁是将电能转化为磁能的一种装置。
当电流通过电磁铁的线圈时,线圈周围会产生强磁场,而磁感应强度B与电流I成正比。
通过控制电流的大小,可以调节磁场的强度,从而实现对物体的吸附和释放。
3. 涡流制动涡流制动是一种利用安培力原理制动运动金属物体的方法。
(完整word版)安培力与洛伦兹力

安培力与洛伦兹力一、安培力定义:通电导线在磁场中所受的力。
大小:1、磁场与电流垂直时,F=BIL2、磁场与电流平行时,F=03、磁场与电流成b角时,F=BILsin b理解:1、公式适用于匀强磁场,若为非匀强,则需要用到积分。
2、公式中的夹角为磁场与导线的夹角.3、磁场有垂直电流方向的分量才对电流产生力的作用,平行电流方向对电流不产生力的作用。
因此,如果知道一段导线的受力,我们只可以确定磁场垂直电流方向的分量,换句话说,我们只可以确定场强的最小值。
4、对于一段导线有效长度的确定.直导线:本身长度*sin b(磁场与导线的夹角)弯曲导线:在导线所在平面垂直于磁场方向的前提下,有效长度为两端点的连线.5、对于闭合线圈,其有效长度一定为0.因此,对于完全处于匀强磁场中的闭合线圈,其所受的磁场力合力一定为零。
方向:左手定则(判断磁场方向——右手、判断受力方向——左手)同时垂直与电流方向和磁场方向。
注意:不管电流方向与磁场方向是否垂直,安培力方向总垂直与电流方向与磁场方向决定的平面。
二、洛伦兹力定义:运动电荷在磁场中所受的力.大小:1、v//B或v=0时,F=0。
2、v垂直于B时,F=qvb。
3、v与B的夹角为ɑ时,F=Bqvsin ɑ。
4、B、ɑ、v均为粒子运动过程中的瞬时量。
方向:1、使用左手定则进行判定(判断磁场用右手,判断受力用左手)。
2、四指指向一定是正电荷的运动方向,是负电荷的反方向.(四指指向电流方向)。
3、洛伦兹力的方向和电荷运动方向与磁场方向都垂直(不做功)。
理解:1、洛伦兹力与速度成正比,并且与速度的方向有关,同样的速度,垂直磁场入射的时候,洛伦兹力最大。
2、洛伦兹力始终和速度方向垂直,根据W=FSsinɑ,ɑ=90知,W=0.也就是说洛仑兹力始终不做功.3、做功为0,根据功能关系,能量不改变,洛伦兹力不改变速度的大小。
由牛顿第一定律,力可以改变物体运动状态,洛伦兹力改变速度大小。
三、安培力与洛伦兹力的内在关系由安培力F=BIL推导洛伦兹力F=qvB设:导体的横截面积为S,单位体积的电荷数为n,自由电荷的电荷量为q,电荷定向移动的速度大小为v。
安培力和洛伦兹力

B
FE e H
I
v
E
b
d
■
9
1. 霍尔效应:在磁场中,载流导体或半导 体上出现横向电势差的现象。
1879年美国物理 学家霍尔发现
2.霍尔电压:1)定义:霍尔效应中产生的电势差。
上图中导体上下两端面出现电势差
IB VH Bb nqd
霍尔系数
1 / nq
10
■
2)公式: ①运动电荷受洛仑兹力 f m qB ②在霍尔电场中,电荷受电力 f e qEH
§6.4 安培力和洛伦兹力
§6.4 .1 安培力
*§6.4 .2
§6.4 .3
磁场对载流线圈的作用力矩 磁矩
洛仑兹力
§6.4.4
* §6.4.5
带电粒子在磁场中运动
霍尔效应
1
§6.4 .3 洛仑兹力 1.洛仑兹力:
磁场对运动电荷施以的磁场力叫洛仑兹力。
2.公式:
3.说明: 1)各量的含义:
f m q B
Id l d F
B
dF
B
Id l
2.整个载流导线受力 F Idl B
l
注意:先化成标量再积分。 ■
15
二、安培力与洛仑兹力的关系 1.推导: 安培力 df Idl B 而
I qns df qnsdl B
v//
h
B
2)粒子运动:螺旋运动 粒子在垂直磁场的平面里做圆周运动 同时又沿磁场方向匀速运动 ■
7
①螺旋半径 ②螺距
m0 m0 sin R qB qB
■
2πm0 cos h T0 cos qB
安培力与洛伦兹力

安培力与洛伦兹力安培力和洛伦兹力是电磁力学中两个重要的力的概念。
它们在解释电荷在磁场中的运动和相互作用方面起着关键的作用。
本文将介绍安培力和洛伦兹力的概念、公式及其应用。
一、安培力安培力是由电流产生的磁场对电荷的作用力。
根据安培力定律,当电流通过一段导线时,会产生一个磁场,而这个磁场会对附近的其他电荷施加力。
安培力的大小与电流的大小和方向以及电荷所处位置有关。
安培力的公式可以表示为:F = BILsinθ,其中F是安培力的大小,B是磁场的强度,I是电流的大小,L是电流所在导线的长度,θ是电流和磁场的夹角。
当电流和磁场垂直时,安培力达到最大值;而当电流和磁场平行时,安培力为零。
这一规律为我们解释电流在磁场中的运动提供了重要的依据。
安培力在许多实际应用中发挥着重要的作用。
例如,电动机、发电机和变压器等电器设备都是基于安培力的工作原理。
此外,MRI(磁共振成像)技术也是利用安培力来实现对人体内部结构的图像获取。
二、洛伦兹力洛伦兹力是电荷在磁场中所受到的力。
它是由电荷的运动状态和磁场的作用相互耦合产生的。
根据洛伦兹力定律,当带电粒子在磁场中运动时,会受到一个垂直于其速度方向且大小与速度、电荷量和磁场强度有关的力。
洛伦兹力的公式可以表示为:F = qvBsinθ,其中F是洛伦兹力的大小,q是电荷量,v是电荷的速度,B是磁场的强度,θ是速度和磁场的夹角。
洛伦兹力的方向垂直于速度和磁场的平面,并遵循左手螺旋定则。
当速度与磁场平行或反平行时,洛伦兹力为零;而当速度与磁场垂直时,洛伦兹力达到最大值。
洛伦兹力在许多领域都有着广泛的应用。
在粒子物理学中,加速器通过电磁铁产生磁场,通过对带电粒子施加洛伦兹力来加速粒子。
在药物输送和生物学研究中,利用洛伦兹力可以对带电颗粒进行操控和定位。
三、安培力与洛伦兹力的关系安培力和洛伦兹力在形式上非常相似,但它们的作用对象不同。
安培力作用于电流所携带的电荷,而洛伦兹力则作用于运动的电荷。
洛伦兹力和安培力

三、 磁场力的功
载流线圈或导线在磁场中受到磁场力(安培力) 载流线圈或导线在磁场中受到磁场力(安培力) 或磁力矩作用,因此,当导线或线圈位置改变时, 或磁力矩作用,因此,当导线或线圈位置改变时, 磁场力就做了功。下面从一些特殊情况出发, 磁场力就做了功。下面从一些特殊情况出发,建立 磁场力做功的一般公式。 磁场力做功的一般公式。 1. 载流导线在磁场中运动时磁力所作的功
r r r dF = Idl × B
一段任意形状载流导线受到的安培力
r F =
∫
L
r dF =
∫
L
v v Id l × B
安培力的微观解释 载流导线受到的安培力的微观实质是载流导线中大 量载流子受到洛仑兹力的结果。 量载流子受到洛仑兹力的结果。简单证明如下 r 在载流导线上任取一电流元 Idl 其中电荷dq沿导线速度为 其中电荷 沿导线速度为 r r 电流元长 dl = vdt 则 dq = Idt 在电流元所在的微小空间区域, 在电流元所在的微小空间区域,磁场可看作匀强的 按照洛仑兹力公式 洛仑兹力公式, ,按照洛仑兹力公式,可得电流元所受磁场力 r r r r r dl r d F = d q v × B = Id t d t × B = I d l × B 这就是电流元在磁场中受到的安培力
这一推一吸的合力便驱使列车高速前进。 这一推一吸的合力便驱使列车高速前进。强大的磁力 可使列车悬浮1 10cm 与轨道脱离接触, cm, 可使列车悬浮 1~ 10cm, 与轨道脱离接触 , 消除了列 车运行时与轨道的摩擦阻力,使列车速度可达 400km/s 400km/s
电磁驱动力原理图
二、磁场对载流线圈的作用
Fy = ∫ IBdx = IBL
0
安培力与洛伦兹力的计算

安培力与洛伦兹力的计算安培力和洛伦兹力是电磁学中重要的概念,它们描述了电荷在电磁场中所受到的力的性质和计算方法。
在本文中,我们将详细介绍安培力和洛伦兹力的计算,并探讨它们在物理学和工程学中的应用。
一、安培力的计算安培力是由电流所产生的力,它的方向垂直于电流方向和磁场方向。
安培力的大小可以通过以下公式计算:F = BIL sinθ其中,F表示安培力的大小,B是磁场的大小,I是电流的大小,L是电流所在导线的长度,θ是电流方向与磁场方向之间的夹角。
例如,假设有一根长度为L的导线,通过它的电流大小为I,置于磁场中。
如果电流与磁场的夹角为θ,磁场的大小为B,那么安培力F可以通过上述公式进行计算。
二、洛伦兹力的计算洛伦兹力是由带电粒子在磁场中所受到的力,它的方向垂直于粒子的速度方向和磁场方向。
洛伦兹力的大小可以通过以下公式计算:F = qvB sinθ其中,F表示洛伦兹力的大小,q是带电粒子的电荷大小,v是粒子的速度大小,B是磁场的大小,θ是速度方向与磁场方向之间的夹角。
举例来说,假设有一个带电粒子,电荷大小为q,速度大小为v,它沿着某一方向运动,并置于磁场中。
如果速度与磁场的夹角为θ,磁场的大小为B,那么洛伦兹力F可以通过上述公式进行计算。
三、安培力和洛伦兹力的应用安培力和洛伦兹力在物理学和工程学中有着广泛的应用。
1. 电动机和发电机:安培力和洛伦兹力是电动机和发电机的基本原理。
电动机利用洛伦兹力,将电能转化为机械能;而发电机则利用安培力,将机械能转化为电能。
2. 电磁铁:电磁铁是利用安培力的一个典型例子。
当电流通过电磁铁的线圈时,产生的安培力使得铁芯产生磁性,从而形成强大的磁场。
3. 粒子加速器:在粒子加速器中,电荷粒子通过磁场加速运动。
洛伦兹力起着关键作用,使得粒子能够沿着特定的轨道加速运动。
4. 磁悬浮列车:磁悬浮列车利用洛伦兹力来实现无接触的悬浮和推动。
通过在轨道上设置磁场,与列车上的磁性装置相互作用,产生洛伦兹力,从而使列车悬浮并运动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
M max Bpm
a(b) n
Fab
B
Fcd
BIS a(b)
d (c)
Fab
(2) = 0 时线圈受到的磁力矩为零
----稳定的平衡位置
线圈稍受扰动,就会回到平衡位置。
Fcd d (c) B
a(b) Fab
(3) = 时线圈所受力矩为零
----不稳定的平衡位置 线圈稍受扰动,就会离开平衡位置。
解: 线圈磁矩
pm NISn
1 NI R2n
2
R
I
600 B
n
磁力 矩 M pm B
磁力矩大小为
M pmB sin 600
R
I
600 B
n
1 NIR2B 3 3 NIBR 2
2
24
磁力矩方向竖直向上。
线圈俯视的转动方向为逆时针。
α
线圈从该位置 由60o 减小为 0。
转到平衡位置时, BS
A I2
b
导线右侧磁场方向如图。
导线 AB 所受力:
dFAB BI 2dl
I1
B
a
C
0 2
I1 b
I2dl
各电流元所受安倍
力的方向相同,
dF
A I2
b
FAB
dFAB
0 I1I 2 2
a b
方向向左。
导线 BC 所受力:
r
dFBC BI 2dl
I1
B
a
C
0 2
I1 r
I 2 dr
M pm B
该式只适用于匀强磁场。
例:下列平面线圈与磁感应线平 行,求它所受磁力矩的大小及转动 方向。
R
I
B
分析:电流元受力情况如何?
解:
M pm B
M pmB R2I B
M 的方向向上。
线圈俯视的转动方向为逆时针。
R
I
B
M pm B
§11-9 平行载流导线间的相互作用力
A I I(2 1)
NI (B R2 cos 0 B R2 cos 60 )
2
2
1 NIBR2
4
R
磁力矩作正功,它使夹 I 角减少到零。
600 B n
§12-1 磁介质
一、磁介质
若某种物质放在磁场中,出现磁化
现象,从而改变原来磁场的分布,这
种物质称为磁介质。
A1
A2
R
螺线管内的磁场是增强 还是减弱?
a(b) n
M
Fab
l1 sin
2
Fcd
l1 2
Fab
sin
Il1l2Bsin ISB sin
力矩方向竖直向上。 (M
r
F
)
而M力 矩的pm大小B和方IS向n可 B用 下式F表cd 示:B
M pm B
d (c)
说明: 对N 匝线圈,
定义磁矩
pm NISn
a(b) n
Fab
M NISB sin
平衡时 evB eEH EH vB
2. 载流子为正电荷时的霍耳效应
哪端电势高? 上端电势高。
B1
EH
FLvI
V
Fe
2
半导体的霍耳效应:
n 型半导体:载流子以电子为主
p 型半导体:以带正电的空穴为主
霍耳效应的应用: 测量磁感应强度、压力、转速
等。
应用于自动控制和计算机技术。
§11-8 磁场对载流导线的作用
Fab a(b) Fcd d (c)
B
2. 非匀强磁场中载流线圈所受力 和力矩
在非匀强磁场中,载流线圈所受合 力一般不为零,线圈将发生平动,还 可能发生转动。
I
F
F
合力水平向
左,线圈向磁场
强的方向平动。
I1
B
a
C
Idl
一 般 情 况 下 载 d
流线圈所受力矩较
FA
I2
为复杂。不能用下
式计算,
dF2
I2dl
B1
I2
方向垂直指向导线 1 。
单位长度受力为
F2
dF2 dl
0 2
I1I 2 d
同理可导出导线 1单位长度所受力 大小与其相同,但方向相反。两导线
相互吸引。
dF2
0 I1I 2 2d
dl
二、电流强度单位“安培”的定义
真空中相距 1 m 的两无限长平行 细直导线中载有相等的电流时 ,若每 米长度导线上的相互作 用力正好等于
一、平行载流导线间的相互作用力
求导线单位长度 1 d 2
所受力。
导线1在导线2处 所产生的磁感应强
度大小为
B1
0 I1 2d
I1
B1
I2
方向垂直纸面向内。
对导线 2上 任 一电流元的作用力
dF2 I2dl B1
1d2
大小为
dF2 I2B1dl 0I1I2 dl 2d
I1
I
B
I
y Idl
dF B
0 x
取电解流:元建I立dl如,图它坐所标受系安,培力大小
dF IBdl sin 90 IBdl
方向沿径向向外。
dF Idl B
I
y
dFy
Idl
ddBFFx
0 x
由 dF 分布的对称性可知,合力方
向沿 y 轴正向,
F Fy
L dFy
B
n
Fab
线圈转动d , 磁力矩作元功 B S
dA Md
Fcd
B
BIS sin d
BISd (cos)
Id (BS cos)
Id
Fab
n
d
从1转到2 , 磁力矩作功
A
2 1
Id
I
(2
1)
I
A I
该结果对均匀磁场中任意形状平面 载流线圈都适用。
例:半径为R,载流 I的半圆形闭 合线圈共有N 匝,当均匀外磁场方向 与线圈法向成60o角时,求线圈的磁 矩; 此时线圈所受磁力矩;从该位 置转到平衡位置,磁力矩所作的功。
螺距
h
v//T
2 mv//
qB
R mv qB T 2m qB
2. 带电粒子在非均匀磁场中的运动 在会聚磁场中形成磁镜。
B
R mv 向右B 增大,R变小。 qB
F
B
FB
力的水平分量使粒子水平运动减速, 最后反转,形成磁镜。
应用:等离子体磁约束装置
I
I
地球上空的范艾 仑辐射带和极光
M ISBsin
方向竖直向上
M
NISn
B
pm
B
M pm B
上式适用于均匀磁场中任意形状的 平面线圈。
均匀磁场中的载流线圈所受合力 为零,但力矩不为零(除平衡位置), 线圈会发生转动而不会平动。
讨论:
M
pm B
Fcd
B
d (c)
M ISBsin
(1) = /2,3π/2 时
pm
,方
向总是与外磁场 B相0 反。与电子轨道
运动方向无关。
分子中,各个电子附加磁矩的和 为分子总的附加磁矩,方向总是与外 磁场相反。
3. 抗磁质的磁化 抗磁质的分子总磁矩为零,即
电子的轨道磁矩和自旋磁矩的矢量 和等于零。
外磁场对电子轨道运动作用的 结果,产生与外磁场反向的附加磁 场(附加磁矩的方向为进动圆电流 中心的磁场方向),使介质内的磁 场弱于外磁场。
抗磁质 B与B0反向
B
B0
B'
B0
r 1
铁磁质 B与B0同向,B' B0
B B0 B' B0 r 1
顺磁质和抗磁质为弱磁质:
r 1106 1 0
铁磁质为强磁质: r 102 104
二、磁介质磁化的微观解释
1. 分子电流和分子磁矩 分子电流:分子(或原子)中,由
于电子的绕核运动和自旋,对外产生 磁效应的总和,可用一个等效的圆电 流表示。
§11-7 霍耳效应
一、霍耳效应
霍耳效应:载流导体薄板放入与
板面垂直的磁场中,板上下端面间产
生电势差的现象。
d
B1
哪一端电势高? b
I
V
2
二、霍耳效应的微观解释
1. 载流子为电子
下 端电势 高, FL ev B Fe eEH
B1
EHv
FL I
Fe
n
2
V
即 FL evB 方向向上
Fe eEH 方向向下
分子磁矩:分子电流的磁矩。
分子磁矩等于电子轨道运动的磁 矩和自旋磁矩的矢量和。
2. 在外磁场中电子的进动和相应 的附加磁矩
B0
pm
电子运动是两种运动的合成:绕核 运动和绕外磁场方向为轴线的进动。
Pm
L
pm
L
Pm
B0
pm
B0
电子角动量 L 进动的转向总是与
B0 的方向成右手螺旋关系。
电子进动产生附加磁矩
R mv qB
v
B
O
R
F
周期 T 2 R 2 m T 与 v 无关。
v qB
v
v
与 v
B
斜交
v//
B
v// v cos ----平行于磁场匀速运动
v vsin ----垂直于磁场作匀速圆
周运动
运动轨迹为螺旋线。
v
v
v//
B
h
回旋半径 R mv qB
以矩F形ad 载流d线圈B说明:
