微专题34 传送带模型的能量分析
“传送带”模型问题专题分析

“传送带”模型问题专题分析一.模型特点:1.水平传送带情景一物块可能运动情况:(1)可能一直加速(2)可能先加速后匀速情景二(1)v0>v时,可能一直减速,也可能先减速再匀速(2)v0<v时,可能一直加速,也可能先加速再匀速情景三(1)传送带较短时,滑块一直减速达到左端(2)传送带较长时,滑块还要被传送带传回右端。
其中v0>v返回时速度为v,当v0<v返回时速度为v02倾斜传送带。
情景一(1)可能一直加速(2)可能先加速后匀速情景二(1)可能一直加速(2)可能先加速后匀速(3)可能先以a1加速后以a2加速二.思路方法:(1)水平传送带问题:求解关键在于对物体所受摩擦力进行正确的分析判断。
进一步分析物体的运动情况,物体的速度与传送带速度相等的时刻摩擦力发生突变。
(2)倾斜传送带问题:求解关键在于认真分析物体与传送带的相对运动情况。
进一步分析物体所受摩擦力的情况及运动情况。
当物体速度与传送带速度相等时,物体所受摩擦力可能发生突变。
例1.如图所示,水平传送带以5m/s的恒定速度运动,传送带长l=2.5m,今在其左端A处将一工件轻轻放在上面,工件被带动,传送到右端B处,已知工件与传送带间的动摩擦因数μ=0.5,试求:工件经多少时间由传送带左端A 运动到右端B?(g取10m/s2)答案:1s2.(多选)(2017·锦州模拟)如图所示,水平传送带A、B两端相距s=3.5m,物体与传送带间的动摩擦因数μ=0.1,物体滑上传送带A端的瞬时速度vA=4m/s,到达B端的瞬时速度设为vB。
下列说法中正确的是()A.若传送带不动,vB=3m/sB.若传送带逆时针匀速转动,vB一定等于3m/sC.若传送带顺时针匀速转动,vB一定等于3m/sD.若传送带顺时针匀速转动,vB有可能等于3m/s【解析】选A、B、D总结:(一)受力分析:传送带模型中要注意摩擦力的突变(发生在v物与v带相同的时刻),对于倾斜传送带模型要分析mgsinθ与f的大小与方向。
传送带模型中的能量问题全解

1 2 A.等于 mv 2 C .大于 μ mgs
1 2 B.小于 mv 2 D.小于μ mgs
答案 C
THANK YOU
A
v
B
答案: (1)
(2)t=1s (3)0.5m (4)2.5s (5)4J
Ff 4 N
a 1m / s 2
2.如图所示,水平传送带AB逆时针匀速转动,一个质量为
M=1.0 kg的小物块以某一初速度由传送带左端滑上,通过速度
传感器记录下物块速度随时间的变化关系如图所示(图中取向左为
传送带装置示意图,绷紧的传送带AB始终保持v=1m/s的恒定速率运行. 一质量为m=4kg的行 李无初速度地放在A处,传送带对行李的滑动摩擦力使行李开始做匀加速直线运动,随后行李又 以与传送带相等的速率做匀速直线运动 . 设行李与传送带间的动摩擦因数 μ =0.1,AB间的距离 l=2m,g=10m/s2. 求: (1)求行李刚开始运动时所受的滑动摩擦力大小与加速度大小 (2)求行李做匀加速运动的时间 (3)行李在传送带上形成的划迹的长度 (4)行李从A运动到B的时间 (5)电机带动传送带匀速传动输出的总能量。
不打滑,质量为0.1kg的小物块与传送带间的动摩擦因数为μ = 3 。
当传送带沿逆时针方向以 v 1 =3m/s 的速度匀速运动时,将小物块 无初速地放在A点后,它会运动至B点。(g取10m/s2) (1)求物体刚放在A点的加速度? (2)物体从A到B约需多长时间? (3)整个过程中摩擦产生的热量?
0.5.设皮带足够长.取g=10 m/s2,在邮件与皮带发生相对滑 动的过程中,求 (1)邮件滑动的时间t; (2)邮件对地的位移大小x; (3)邮件与皮带间的摩擦力对皮带做的功W.
传送带模型中的能量问题概述课件

➢ (2)邮件对地的位移大小x;
➢ (3)邮件与皮带间的摩擦力对皮带做的功W.
➢ (1)0.2 s ➢ (2)0.1 m ➢ (3)-2 J
➢ 3.如图所示,水平传送带长为s,以速度v始终保持匀速运动,把质量为m 的货物放到A点,货物与传送带间的动摩擦因数为μ,当货物从A点运动到 B点的过程中,摩擦力对货物做的功不可能是( )
生的
、因放上物体而使电动机多消耗的电能等,常依据功能关系或
定律求解.
预学案
➢ 2.传送带模型问题中的功能关系分析
➢ (1)功能关系分析:W=ΔEk+ΔEp+Q.
➢ (2)对Q的理解:产生的内能Q=
.
探究案
➢ 1.水平传送带被广泛的应用于机场和火车站,用于对旅客的行李进行安全检查. 如图为一水平 传送带装置示意图,绷紧的传送带AB始终保持v=1m/s的恒定速率运行. 一质量为m=4kg的行 李无初速度地放在A处,传送带对行李的滑动摩擦力使行李开始做匀加速直线运动,随后行李又 以与传送带相等的速率做匀速直线运动. 设行李与传送带间的动摩擦因数μ=0.1,AB间的距离 l=2m,g=10m/s2. 求:
A.等于 1mv2 2
C.大于μmgs
B.小于 1mv2 2
D.小于μmgs
➢ 答案 C
THANK YOU
➢ (1)小木块的位移; ➢ (2)传送带转过的路程; ➢ (3)小木块获得的动能; ➢ (4)摩擦过程产生的摩擦热;
(1) v2 (2)v2 (3)1mv2 (4)1mv2
2μg μg 2
2
➢ 2.某快递公司分拣邮件的水平传输装置示意如图.皮带在电动机 的带动下保持v=1 m/s的恒定速度向右运动.现将一质量为m =2 kg的邮件轻放在皮带上.邮件和皮带间的动摩擦因数μ= 0.5.设皮带足够长.取g=10 m/s2,在邮件与皮带发生相对滑 动的过程中,求
传送带模型中的能量问题

高三物理传送带模型中的能量问题1.如图所示,比较长的传送带与水平方向的夹角θ=37°,在电动机带动下以v 0=4 m/s 的恒定速率顺时针方向运行.在传送带底端P 处有一离传送带很近的固定挡板,可将传送带上的物体挡住.在距P 距离为L =9 m 的Q 处无初速度地放一质量m =1 kg 的物体,它与传送带间的动摩擦因数μ=0.5,物体与挡板的碰撞能量损失及碰撞时间不计,取g =10 m/s 2,sin37°=0.6,求物体从静止释放到第一次返回上升至最高点的过程中:(1)相对传送带发生的位移;(2)系统因摩擦产生的热量;(3)传送带多消耗的电能;(4)物体的最终状态及该状态后电动机的输出功率.【解析】(1)要分上和下两个过程处理,注意相对路程和相对位移是不一样的。
解法1:力和运动法.物体由静止释放,沿传送带向下加速运动,相对传送带亦向下滑,受力如图1所示,有mgsin θ-μmgcos θ=ma 1,得a 1=2 m/s 2 与P 碰前速度v 1=2a 1L =6 m/s设物体从Q 到P 的时间为t 1,则t 1=v 1a 1=3 s 设物体对地位移为x 1,可知x 1=L =9 m ,相对传送带向下的位移Δx 1=x 1+v 0t 1=21 m物体与挡板碰撞后,以速度v 1反弹,向上做减速运动,因v 1>v 0,物体相对传送带向上滑,设速度减小到与传送带速度相等的时间为t 2,此过程受力如图2所示,有mgsin θ+μmgcos θ=ma 2得a 2=10 m/s 2,t 2=v 1-v 0a 2=0.2 s 在t 2时间内物体对地向上的位移x 2=v 1+v 02t 2=1 m 相对传送带向上的位移Δx 2=x 2-v 0t 2=0.2 m 物体速度与传送带速度相等后,由于mgsin θ>μmgcos θ物体不能匀速,将相对传送带向下滑,对地向上做加速度大小为a 3=a 1=2 m/s 2的减速运动,设速度减小到零的时间为t 3,t 3=v 0a 3=2 s 此过程中物体对地向上的位移x 3=v 02t 3=4 m 相对传送带向下的位移Δx 3=v 0t 3-x 3=4 m整个过程中两者相对滑动位移为Δx =Δx 1-Δx 2+Δx 3=24.8 m.解法2:相对运动法.以传送带为参考系,在求出相对初速度和相对加速度后,三个阶段物体相对传送带的位移分别为Δx 1=v 0t 1+12a 1t 21=21 m Δx 2=(v 1-v 0)t 2-12a 2t 22=0.2m Δx 3=12a 3t 23=4 m 第二阶段物体相对传送带向上运动,两者相对滑动总位移为Δx =Δx 1-Δx 2+Δx 3=24.8 m.解法3:图象法.设沿传送带向上为正方向,画出如图3所示物体和传送带运动的v -t 图象,直接用物体和传送带v -t 图线所夹的面积表示相对发生的位移:Δx 1=(v 0+v 0+v 1)t 12=21 m ,Δx 2=(v 1-v 0)t 22=0.2 m Δx 3=12v 0t 3=4 m 两者相对滑动的总位移为Δx =Δx 1-Δx 2+Δx 3=24.8 m.(2)系统因摩擦产生的热量,是由于一对滑动摩擦力作用点移动的不同导致做功不等而造成的,产生的热量不是与传送带和物体间的相对移动的位移而是与相对移动的距离有关(如图4所示阴影部分面积):Q =Q 1+Q 2+Q 3=F f ·Δl =μmgcos θ(Δx 1+Δx 2+Δx 3)=100.8 J.出现相对来回的情况时,热量要用相对路程而不能用相对位移(3)传送带消耗的电能是因为传送带要克服摩擦力做功,这与传送带对地运动位移有关(如图5所示阴影部分面积),在物体向下加速和相对传送带向下运动的减速阶段,摩擦力对传送带做负功消耗电能,在物体相对传送带向上运动的减速阶段,摩擦力对传送带做正功,减少电能损耗.ΔE 电=-F f (x 传送带1-x 传送带2+x 传送带3)=-μmgcos θ(v 0t 1-v 0t 2+v 0t 3)=-76.8 J即传送带多消耗的电能为76.8 J.可由功能关系处理,从开始到回到最高点过程中,系统增加了热能100.8 J ,减少了重力势能mgxsin θ,x=x1-x2-x3=4m, mgxsin θ=24j,系统动能就有变,系统总的增加了100.8-24=76.8j 所以传送带多消耗的电能是76.8j(4)物体返回上升到最高点时速度为零,以后将重复上述过程,且每次碰后反弹速度、上升高度依次减小,最终达到一个稳态:稳态的反弹速度大小应等于传送带速度4 m/s ,此后受到的摩擦力总是斜向上,加速度为gsin θ-μgcos θ=2 m/s 2,方向斜向下,物体相对地面做往返“类竖直上抛”运动,对地上升的最大位移为x m =v 202a 1=4 m ,往返时间为T =2v 0a 1=4 s 传送带受到的摩擦力大小始终为F f =μmgcos θ,稳态后方始终斜向下,故电动机的输出功率稳定为P =F f v 0=μmgcos θ×v 0=16 W.传送带受到物体的摩擦力方向向下,电动机对传送带的力要向上,这样,电动机的输出功率用力和时间的积就可以求出了。
高中物理传送带模型(最新)
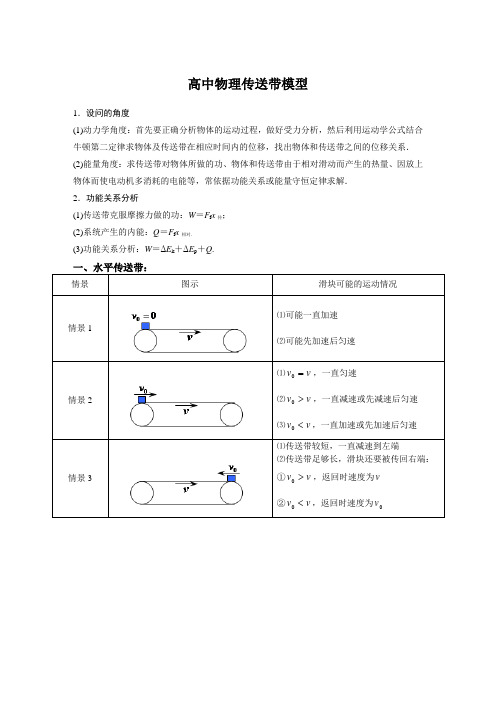
高中物理传送带模型1.设问的角度(1)动力学角度:首先要正确分析物体的运动过程,做好受力分析,然后利用运动学公式结合牛顿第二定律求物体及传送带在相应时间内的位移,找出物体和传送带之间的位移关系.(2)能量角度:求传送带对物体所做的功、物体和传送带由于相对滑动而产生的热量、因放上物体而使电动机多消耗的电能等,常依据功能关系或能量守恒定律求解.2.功能关系分析(1)传送带克服摩擦力做的功:W=F f x传;(2)系统产生的内能:Q=F f x相对.(3)功能关系分析:W=ΔE k+ΔE p+Q.一、水平传送带:情景图示滑块可能的运动情况情景1⑴可能一直加速⑵可能先加速后匀速情景2 ⑴vv=,一直匀速⑵vv>,一直减速或先减速后匀速⑶vv<,一直加速或先加速后匀速情景3 ⑴传送带较短,一直减速到左端⑵传送带足够长,滑块还要被传回右端:①vv>,返回时速度为v②vv<,返回时速度为v二、倾斜传送带:情景图示滑块可能的运动情况情景1 ⑴可能一直加速⑵可能先加速后匀速⑶可能从左端滑落情景2 ⑴可能一直加速⑵可能先加速后匀速⑶可能先以1a加速,后以2a加速情景3 ⑴可能一直加速⑵可能一直匀速⑶可能先加速后匀速⑷可能先减速后匀速⑸可能先以1a加速,后以2a加速情景4 ⑴可能一直加速⑵可能一直减速⑶可能先减速到0,后反向加速例1(多选)如图所示为某建筑工地所用的水平放置的运输带,在电动机的带动下运输带始终以恒定的速度v0=1 m/s顺时针传动.建筑工人将质量m=2 kg的建筑材料静止地放到运输带的最左端,同时建筑工人以v0=1 m/s的速度向右匀速运动.已知建筑材料与运输带之间的动摩擦因数为μ=0.1,运输带的长度为L=2 m,重力加速度大小为g=10 m/s2.以下说法正确的是()A.建筑工人比建筑材料早到右端0.5 sB.建筑材料在运输带上一直做匀加速直线运动C.因运输建筑材料电动机多消耗的能量为1 JD.运输带对建筑材料做的功为1 J答案AD解析 建筑工人匀速运动到右端,所需时间t 1=Lv 0=2 s ,假设建筑材料先加速再匀速运动,加速时的加速度大小为a =μg =1 m/s 2,加速的时间为t 2=v 0a =1 s ,加速运动的位移为x 1=v 02t 2=0.5 m<L ,假设成立,因此建筑材料先加速运动再匀速运动,匀速运动的时间为t 3=L -x 1v 0=1.5 s ,因此建筑工人比建筑材料早到达右端的时间为Δt =t 3+t 2-t 1=0.5 s ,A 正确,B 错误;建筑材料与运输带在加速阶段摩擦生热,该过程中运输带的位移为x 2=v 0t 2=1 m ,则因摩擦而生成的热量为Q =μmg (x 2-x 1)=1 J ,由动能定理可知,运输带对建筑材料做的功为W =12m v 02=1 J ,则因运输建筑材料电动机多消耗的能量为2 J ,C 错误,D 正确.例2 如图所示,绷紧的传送带与水平面的夹角θ=30°,传送带在电动机的带动下,始终保持v 0=2 m/s 的速率运行,现把一质量为m =10 kg 的工件(可视为质点)轻轻放在传送带的底端,经过时间t =1.9 s ,工件被传送到h =1.5 m 的高处,g 取10 m/s 2,求:(1)工件与传送带间的动摩擦因数; (2)电动机由于传送工件多消耗的电能. 答案 (1)32(2)230 J 解析 (1)由题图可知,传送带长x =hsin θ=3 m 工件速度达到v 0前,做匀加速运动,有x 1=v 02t 1工件速度达到v 0后,做匀速运动, 有x -x 1=v 0(t -t 1)联立解得加速运动的时间t 1=0.8 s 加速运动的位移x 1=0.8 m 所以加速度大小a =v 0t 1=2.5 m/s 2由牛顿第二定律有μmg cos θ-mg sin θ=ma 解得μ=32. (2)由能量守恒定律知,电动机多消耗的电能用于增加工件的动能、势能以及克服传送带与工件之间发生相对位移时摩擦力做功产生的热量. 在时间t 1内,传送带运动的位移 x 传=v 0t 1=1.6 m在时间t 1内,工件相对传送带的位移 x 相=x 传-x 1=0.8 m在时间t 1内,摩擦产生的热量 Q =μmg cos θ·x 相=60 J最终工件获得的动能E k =12m v 02=20 J工件增加的势能E p =mgh =150 J 电动机多消耗的电能 E =Q +E k +E p =230 J.例3如图所示,绷紧的传送带,始终以2 m/s 的速度匀速斜向上运行,传送带与水平方向间的夹角︒=30θ. 现把质量为10 kg 的工件轻轻地放在传送带底端P 处,由传送带传送至顶端Q 处.已知P 、Q 之间的距离为4 m ,工件与传送带间的动摩擦因数23=μ,取2/10s m g = (1)通过计算说明工件在传送带上做什么运动;(2)求工件从P 点运动到Q 点所用的时间.答案:⑴工件先以2/5.2s m 的加速度匀加速运动0.8m ,之后匀速;⑵时间s t t t 4.221=+=例4如图甲所示,绷紧的水平传送带始终以恒定速率v 1运行.初速度大小为v 2的小物块从与传送带等高的光滑水平地面上的A 处滑上传送带.若从小物块滑上传送带开始计时,小物块在传送带上运动的v -t 图象(以地面为参考系)如图乙所示.已知v 2>v 1,则( )A .t 2时刻,小物块离A 处的距离达到最大B .t 2时刻,小物块相对传送带滑动的距离最大C .0~t 2时间内,小物块受到的摩擦力方向先向右后向左D .0~t 3时间内,小物块始终受到大小不变的摩擦力作用 答案:B例5如图所示,水平地面上有一长L =2 m 、质量M =1 kg 的长板,其右端上方有一固定挡板.质量m =2 kg 的小滑块从长板的左端以v 0=6 m/s 的初速度向右运动,同时长板在水平拉力F 作用下以v =2 m/s 的速度向右匀速运动,滑块与挡板相碰后速度为0,长板继续匀速运动,直到长板与滑块分离.已知长板与地面间的动摩擦因数μ1=0.4,滑块与长板间的动摩擦因数μ2=0.5,重力加速度g 取10 m/s 2.求:(1)滑块从长板的左端运动至挡板处的过程,长板的位移x ; (2)滑块碰到挡板前,水平拉力大小F ;(3)滑块从长板的左端运动至与长板分离的过程,系统因摩擦产生的热量Q . 答案 (1)0.8 m (2)2 N (3)48 J 解析 (1)滑块在板上做匀减速运动, a =μ2mg m =μ2g解得:a =5 m/s 2根据运动学公式得:L =v 0t -12at 2解得t =0.4 s (t =2.0 s 舍去)碰到挡板前滑块速度v 1=v 0-at =4 m/s>2 m/s ,说明滑块一直匀减速 板移动的位移x =v t =0.8 m (2)对板受力分析如图所示,有:F +F f2=F f1其中F f1=μ1(M +m )g =12 N ,F f2=μ2mg =10 N 解得:F =2 N(3)法一:滑块与挡板碰撞前,滑块与长板因摩擦产生的热量: Q 1=F f2·(L -x ) =μ2mg (L -x )=12 J滑块与挡板碰撞后,滑块与长板因摩擦产生的热量:Q 2=μ2mg (L -x )=12 J 整个过程中,长板与地面因摩擦产生的热量: Q 3=μ1(M +m )g ·L =24 J 所以,系统因摩擦产生的热量: Q =Q 1+Q 2+Q 3=48 J法二:滑块与挡板碰撞前,木板受到的拉力为F 1=2 N (第二问可知) F 1做功为W 1=F 1x =2×0.8=1.6 J 滑块与挡板碰撞后,木板受到的拉力为:F2=F f1+F f2=μ1(M+m)g+μ2mg=22 NF2做功为W2=F2(L-x)=22×1.2 J=26.4 J 碰到挡板前滑块速度v1=v0-at=4 m/s滑块动能变化:ΔE k=20 J所以系统因摩擦产生的热量:Q=W1+W2+ΔE k=48 J.。
传送带模型中的动力学及能量观点的综合问题(解析版)-高中物理

传送带模型中的动力学及能量观点的综合问题学校:_________班级:___________姓名:_____________模型概述1.传送带的特点:传送带运输是利用货物和传送带之间的摩擦力将货物运送到其他地方,物体(视为质点)放在传送带上,由于物体和传送带相对滑动(或有相对运动趋势)而产生摩擦力,根据物体和传送带间的速度关系,摩擦力可能是动力,也可能是阻力。
2.传送带问题的解题关键:抓住v物=v传的临界点,当v物=v传时,摩擦力发生突变,物体的加速度发生突变。
3.传送带问题中位移的区别1)物体位移:以地面为参考系,单独对物体由运动学公式求得的位移。
2)物体相对传送带的位移(划痕长度)Δx①若有一次相对运动:Δx=x传-x物或Δx=x物-x传。
②若有两次相对运动:两次相对运动方向相同,则Δx=Δx1+Δx2(图甲);两次相对运动方向相反,则Δx等于较长的相对位移大小(图乙)。
4.传送带问题的基本类型有水平传送带和倾斜传送带两种基本模型.1)水平传送带常见类型及滑块运动情况类型滑块运动情况①可能一直加速②可能先加速后匀速①v0>v时,可能一直减速,也可能先减速再匀速②v0=v时,一直匀速③v0<v时,摩擦力为动力,可能一直加速,也可能先加速再匀速①传送带较短时,摩擦力为阻力,滑块一直减速到达左端②传送带足够长时,摩擦力先为阻力,滑块先向左减速,减速到零后摩擦力再为动力,物体反向加速运动回到右端。
2)倾斜传送带常见类型及滑块运动情况类型滑块运动情况①可能一直加速②可能先加速后匀速①可能一直加速②可能先加速后匀速③可能先以a 1加速再以a 2加速5.传送带问题分析的基本思路求解的关键在于根据物体和传送带之间的相对运动情况,确定摩擦力的大小和方向.当物体的速度与传送带的速度相等时,物体所受的摩擦力有可能发生突变,速度相等前后对摩擦力的分析是解题的关键.1)动力学分析:首先要正确分析物体的运动过程,做好受力分析,然后利用运动学公式结合牛顿第二定律求物体及传送带在相应时间内的位移,找出物体和传送带之间的位移关系.2)功能关系分析①功能关系分析:电机所做的功W =ΔE k (+ΔE P )+Q ②对W 和Q 的理解:Ⅰ、因放上物体而使电动机多消耗的电能:W Ⅱ、传送带克服摩擦力做的功:W f =F f ⋅x 传;Ⅲ、产生的内能:Q =W f =-F f ⋅x 相对.典题攻破1.水平传送带1.(2024·河南郑州·三模)(多选)如图所示,足够长的水平传送带以恒定速率v 1=2m/s 向右运动,一质量为m =1kg 的滑块从传送带右端以水平向左的速率v 2=4m/s 滑上传送带,经过时间t =9s ,最终滑块又返回至传送带的右端。
传送带中的能量能量分析

传送带中的能量能量分析象山中学 李铁林传送带作为一种运输工具,其能量的转化主要考虑两个方面:①、增加物体的机械能(动能和势能)②、增加系统的内能(即由于物体和皮带之间发生相对运动因摩擦而产生的热量)例1. 如图,电机带动传送带以速度v 匀速传动,一质量为m 的小木块由静止放在传送带上(传送带足够长)若小木 块与传送带之间的动摩擦因数为µ,当小木块与传送带相对静止时,求:⑴、小木块的位移。
⑵、传送带经过的路程。
⑶、小木块获得的动能。
⑷、摩擦过程产生的热量。
⑸电机带动传送带匀速转动输出的总能量。
分析:木块刚放上时速度为零,必然受到传送带的滑动摩擦力作用做匀加速直线运动,达到与传送带有共同速度后不再有相对运动,整个过程中木块获得一定的动能,系统要产生摩擦热。
对木块:相对滑动时,a=µg,达到相对静止所用的时间为t=v g μ,木块的位移21122v s vt gμ==,传送带的位移22v s vt g μ==,木块相对传送带的位移2212v s s s gμ=-=,小木块获得的动能212k E mv =,产生的热量221211()()2Q fs f s s mg s s mv μ==-=-=,电动机输出的总能量转化为小木块的动能和系统产生的热量2k E E Q mv =+=注意:当木块的初速为零时,木块经过的位移和木块相对皮带的位移恰好相等,这一特点要记住,在解题中很有用处。
2.如图,已知传送带两轮的半径r =1m ,传动中传送带不打滑,质量为1kg 的物体从光滑轨道A 点无初速下滑(A 点比B 点高h =5m ),物体与传送带之间的动摩擦因数2.0=μ,当传送带静止时,物体恰能在C 点离开传送带,则(1)BC 两点间距离为多少?(2)若要使物体从A 点无初速释放后能以最短时间到达C 点,轮子转动的角速度大小应满足什么条件?(3)当传送带两轮以12rad/s 的角速度顺时针转动时,物体仍从A 点无初速释放,在整个过程中物体与皮带系统增加的内能为多少?解:(1)设物体质量为m ,在C 点时运动速度为C v ,BC 间距离为s 。
“传送带”模型中的能量问题教学总结

“传送带”模型中的能量问题微专题训练14 “传送带”模型中的能量问题1.(单选)如图1所示,质量为m 的物体在水平传送带上由静止释放,传送带由电动机带动,始终保持以速度v 匀速运动,物体与传送带间的动摩擦因数为μ,物体在滑下传送带之前能保持与传送带相对静止,对于物体从静止释放到与传送带相对静止这一过程,下列说法中正确的是( ).图1A .电动机多做的功为12m v 2B .物体在传送带上的划痕长v 2μgC .传送带克服摩擦力做的功为12m v 2D .电动机增加的功率为μmg v解析 小物块与传送带相对静止之前,物体做匀加速运动,由运动学公式知x 物=v2t ,传送带做匀速运动,由运动学公式知x 传=v t ,对物块根据动能定理μmgx 物=12m v 2,摩擦产生的热量Q =μmgx 相=μmg (x 传-x 物),四式联立得摩擦产生的热量Q =12m v 2,根据能量守恒定律,电动机多做的功一部分转化为物块的动能,一部分转化为热量,故电动机多做的功等于m v 2,A项错误;物体在传送带上的划痕长等于x 传-x 物=x 物=v 22μg,B 项错误;传送带克服摩擦力做的功为μmgx 传=2μmgx 物=m v 2,C 项错误;电动机增加的功率也就是电动机克服摩擦力做功的功率为μmg v ,D 项正确. 答案 D2.(单选)如图2所示,水平传送带两端点A 、B 间的距离为l ,传送带开始时处于静止状态.把一个小物体放到右端的A 点,某人用恒定的水平力F 使小物体以速度v 1匀速滑到左端的B 点,拉力F 所做的功为W 1、功率为P 1,这一过程物体和传送带之间因摩擦而产生的热量为Q 1.随后让传送带以v 2的速度匀速运动,此人仍然用相同的恒定的水平力F 拉物体,使它以相对传送带为v 1的速度匀速从A 滑行到B ,这一过程中,拉力F 所做的功为W 2、功率为P 2,物体和传送带之间因摩擦而产生的热量为Q 2.下列关系中正确的是( ).图2A .W 1=W 2,P 1<P 2,Q 1=Q 2B .W 1=W 2,P 1<P 2,Q 1>Q 2C .W 1>W 2,P 1=P 2,Q 1>Q 2D .W 1>W 2,P 1=P 2,Q 1=Q 2解析 因为两次的拉力和拉力方向的位移不变,由功的概念可知,两次拉力做功相等,所以W 1=W 2,当传送带不动时,物体运动的时间为t 1=lv 1;当传送带以v 2的速度匀速运动时,物体运动的时间为t 2=lv 1+v 2,所以第二次用的时间短,功率大,即P 1<P 2;一对滑动摩擦力做功的绝对值等于滑动摩擦力与相对路程的乘积,也等于转化的内能,第二次的相对路程小,所以Q 1>Q 2. 答案 B3.(2013·西安模拟)如图3甲所示,一倾角为37°的传送带以恒定速度运行.现将一质量m =1 kg 的小物体抛上传送带,物体相对地面的速度随时间变化的关系如图乙所示,取沿传送带向上为正方向,g =10 m/s 2,sin 37°=0.6,cos 37°=0.8.求:图3(1)0~8 s 内物体位移的大小; (2)物体与传送带间的动摩擦因数;(3)0~8 s 内物体机械能增量及因与传送带摩擦产生的热量Q .解析 (1)从图乙中求出物体位移x =-2×2×12 m +4×4×12 m +2×4 m =14 m(2)由图象知,物体相对传送带滑动时的加速度a =1 m/s 2 对此过程中物体受力分析得μmg cos θ-mg sin θ=ma 得μ=0.875(3)物体被送上的高度h =x sin θ=8.4 m 重力势能增量ΔE p =mgh =84 J 动能增量ΔE k =12m v 22-12m v 21=6 J机械能增加ΔE =ΔE p +ΔE k =90 J 0~8 s 内只有前6 s 发生相对滑动. 0~6 s 内传送带运动距离x 1=4×6 m =24 m 0~6 s 内物体位移x 2=6 m产生的热量Q =μmg cos θ·Δx =μmg cos θ(x 1-x 2)=126 J 答案 (1)14 m (2)0.875 (3)90 J 126 J4.如图4所示,质量为m 的滑块,放在光滑的水平平台上,平台右端B 与水平传送带相接,传送带的运行速度为v 0,长为L ,今将滑块缓慢向左压缩固定在平台上的轻弹簧,到达某处时突然释放,当滑块滑到传送带右端C 时,恰好与传送带速度相同.滑块与传送带间的动摩擦因数为μ.图4(1)试分析滑块在传送带上的运动情况;(2)若滑块离开弹簧时的速度大于传送带的速度,求释放滑块时,弹簧具有的弹性势能; (3)若滑块离开弹簧时的速度大于传送带的速度,求滑块在传送带上滑行的整个过程中产生的热量.解析 (1)若滑块冲上传送带时的速度小于传送带的速度,则滑块在传送带上由于受到向右的滑动摩擦力而做匀加速运动;若滑块冲上传送带时的速度大于传送带的速度,则滑块受到向左的滑动摩擦力而做匀减速运动.(2)设滑块冲上传送带时的速度为v ,在弹簧弹开过程中,由机械能守恒:E p =12m v 2①设滑块在传送带上做匀减速运动的加速度大小为a ,则 由牛顿第二定律得μmg =ma② 由运动学公式得v 2-v 20=2aL③联立①②③得E p =12m v 20+μmgL .(3)设滑块在传送带上运动的时间为t ,则t 时间内传送带的位移s =v 0t ④ v 0=v -at⑤ 滑块相对传送带滑动的路程Δs =L -s ⑥ 相对滑动产生的热量Q =μmg ·Δs⑦联立②③④⑤⑥⑦得Q =μmgL -m v 0(v 20+2μgL -v 0).答案 (1)见解析 (2)12m v 20+μmgL(3)μmgL -m v 0(v 20+2μgL -v 0)5.如图5所示,一质量为m =2 kg 的滑块从半径为R =0.2 m 的光滑四分之一圆弧轨道的顶端A 处由静止滑下,A 点和圆弧对应的圆心O 点等高,圆弧的底端B 与水平传送带平滑相接.已知传送带匀速运行的速度为v 0=4 m/s ,B 点到传送带右端C 的距离为L =2 m .当滑块滑到传送带的右端C 时,其速度恰好与传送带的速度相同.(g =10 m/s 2)求:图5(1)滑块到达底端B 时对轨道的压力; (2)滑块与传送带间的动摩擦因数μ;(3)此过程中,由于滑块与传送带之间的摩擦而产生的热量Q . 解析 (1)滑块由A 到B 的过程中,由机械能守恒定律得: mgR =12m v 2B① 物体在B 点,由牛顿第二定律得:F B -mg =m v 2BR②由①②两式得:F B =60 N由牛顿第三定律得滑块到达底端B 时对轨道的压力大小为60 N ,方向竖直向下. (2)方法一 滑块在从B 到C 运动过程中,由牛顿第二定律得:μmg =ma③ 由运动学公式得:v 20-v 2B =2aL④ 由①③④三式得:μ=0.3⑤方法二 滑块在从A 到C 整个运动过程中,由动能定理得:mgR +μmgL =12m v 20-0解得μ=0.3(3)滑块在从B 到C 运动过程中,设运动时间为t 由运动学公式得:v 0=v B +at ⑥ 产生的热量:Q =μmg (v 0t -L )⑦由①③⑤⑥⑦得:Q =4 J答案 (1)60 N ,方向竖直向下 (2)0.3 (3)4 J。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
微专题34 传送带模型的能量分析【核心要点提示】传送带模型能量分析的问题主要包括以下两个核心问题(1)摩擦系统内摩擦热的计算:依据Q =F f ·x 相对,找出摩擦力与相对路程大小即可。
要注意的问题是公式中的x 相对并不是指的是相对位移大小。
特别是相对往返运动中,x 相对为多过程相对位移大小之和。
(2)由于传送物体而多消耗的电能:一般而言,有两种思路:①运用能量守恒,多消耗的电能等于系统能量的增加的能量。
以倾斜向上运动传送带传送物体为例,多消耗的电能k E E E Q =∆+∆+重摩擦②运用功能关系,传送带克服阻力做的功等于消耗的电能E fS =传 【微专题训练】如图所示,水平传送带长为s ,以速度v 始终保持匀速运动,把质量为m 的货物放到A 点,货物与传送带间的动摩擦因数为μ,当货物从A 点运动到B 点的过程中,摩擦力对货物做的功不可能是( )A .等于12mv 2B .小于12mv 2C .大于μmgsD .小于μmgs【解析】货物在传送带上相对地面的运动可能先加速后匀速,也可能一直加速,而货物的最终速度应小于等于v ,根据动能定理知摩擦力对货物做的功可能等于12mv 2,可能小于12mv 2,可能等于μmgs ,可能小于μmgs ,故选C. 【答案】C(2016·湖北省部分高中高三联考)如图所示,质量为m 的物体在水平传送带上由静止释放,传送带由电动机带动,始终保持以速度v 匀速运动,物体与传送带间的动摩擦因数为μ,物体过一会儿能保持与传送带相对静止,对于物体从静止释放到相对静止这一过程,下列说法正确的是( )A .电动机多做的功为mv 2/2B .物体在传送带上的划痕长v 2/2μgC .传送带克服摩擦力做的功为mv 2/2D .电动机增加的功率为μmgv【解析】电动机多做的功转化成了物体的动能和内能,物体在这个过程中获得的动能就是12mv 2,所以电动机多做的功一定要大于12mv 2,故A 错误;物体在传送带上的划痕长等于物体在传送带上的相对位移,物体达到速度v 所需的时间t =v μg ,在这段时间内物体的位移x 1=v 22μg ,传送带的位移x 2=vt =v 2μg ,则物体相对位移x =x 2-x 1=v 22μg ,故B 正确;传送带克服摩擦力做的功就为电动机多做的功,所以由A 的分析可知,C 错误;电动机增加的功率即为克服摩擦力做功的功率,大小为fv =μmgv ,所以D 正确。
【答案】BD如图所示,在匀速转动的电动机带动下,足够长的水平传送带以恒定速率v 1匀速向右运动,一质量为m 的滑块从传送带右端以水平向左的速率v 2(v 2>v 1)滑上传送带,最后滑块返回传送带的右端.关于这一过程的下列判断,正确的有( )A .滑块返回传送带右端的速率为v 1B .此过程中传送带对滑块做功为12mv 21-12mv 22 C .此过程中电动机对传送带做功为12mv 21-12mv 22 D .此过程中滑块与传送带间摩擦产生的热量为12m (v 1+v 2)2【解析】 滑块向左运动过程中,运动方向受到皮带的阻力,到达最左端,对地速度为零,由动能定理可知,-fx 1=0-12mv 22,其后在皮带摩擦力的作用下,摩擦力为动力,使滑块加速,假设加速至v 1,则有fx 1=12mv 21-0,以上两式中可知x 2<x 1,说明滑块返回传送带右端的速率能够达到v 1,A 选项正确;此过程中传送带对滑块做功,由动能定理可知,为12mv 21-12mv 22,B 选项正确;此过程中电动机对传送带做功,分为两部分,一部分为木块增加的动能12mv 21-12mv 22,另一部分产生内能Q ,C 选项错误;此过程中滑块与传送带间摩擦产生的热量为摩擦力与相对路程的乘积,分两个过程考虑,第一过程为滑块从右端滑至最左端至对地速度为零,假设运动时间为t 1,则t 1=0-v 2-μg =v 2μg ,t 1时间内皮带对地向右的位移x 3=v 1t 1=v 1v 2μg ,fx 3=mv 1v 2,即第一过程产生的热量为f (x 1+x 3)=12mv 21+mv 1v 2,第二过程中由于物块对地加速的位移为x 2,与物块、皮带间的相对滑动距离相等,故第二阶段产生的热量为12mv 22,此过程中滑块与传送带间摩擦产生的热量为12mv 21+mv 1v 2+12mv 22=12m (v 1+v 2)2,D 选项正确. 【答案】 ABD(2017·东北三省三校一模)在大型物流货场,广泛应用着传送带搬运货物。
如图甲所示,与水平面成θ角倾斜的传送带以恒定速率运动,皮带始终是绷紧的,将m =1 kg 的货物放在传送带上的A 处,经过1.2 s 到达传送带的B 端。
用速度传感器测得货物与传送带的速度v 随时间t 变化图象如图乙所示,已知重力加速度g =10 m/s 2,由v -t 图可知( )A .A 、B 两点的距离为2.4 mB .货物与传送带间的动摩擦因数为0.5C .货物从A 运动到B 过程中,传送带对货物做功大小为12.8 JD .货物从A 运动到B 过程中,货物与传送带摩擦产生的热量为11.2 J【解析】由题图乙可知,货物在前0.2 s 运动的距离L 1=0.2 m ,在0.2~1.2 s 内移动的距离L 2=3 m ,所以A 、B 两点距离L =L 1+L 2=3.2 m ,A 错误;从图象上看,前0.2 s 货物的加速度a 1=10 m/s 2,0.2~1.2 s 内货物的加速度a 2=2 m/s 2,根据受力情况,可知ma 1=mg sin θ+μmg co θ,ma 2=mg sin θ-μmg cos θ,解得μ=0.5,B 正确;同时还解得摩擦力F f =μmg cos θ=4 N ,前0.2 s 摩擦力做功W 1=F f L 1=0.8 J ,在0.2~1.2 s 内摩擦力做功W 2=-F f L 2=-12J ,摩擦力对货物做的总功W 1+W 2=-11.2 J ,C 错误;从图象可求得相对位移L 相=1.2 m ,摩擦产生的热量Q =1.2×4 J =4.8 J ,D 错误。
【答案】B(2015·邯郸市高三月考)一条长12 m 的传送带,倾角为30°,它能够将工件从地面送到卡车上,每个工件的质量为25 kg ,传送带每分钟可传送16个工件,不考虑传送带对工件的加速,g =10 m/s 2,下列说法正确的是( ) A .传送带每分钟对工件做的总功是2.4×104 JB .摩擦力每分钟对工件做的总功是1.2×104 JC .传送带的传送功率为100 WD .传送带的传送功率为200 W【解析】传送工件时不计加速,则工件随传送带一起匀速上升,即摩擦力F f =mg sin θ,传送带对工件做功实质是传送带的摩擦力F f 对工件做功,所以W =nF f ·l =16×mg sin 30°×l =2.4×104J ,A 项正确,B 项错误;由功率定义P =W t =2.4×10460W =400 W ,知C 、D 项错误。
【答案】A【新乡市2017届高三上学期模拟考试能力提升训练】在一水平向右匀速传输的传送带的左端A 点,每隔T 的时间,轻放上一个相同的工件,已知工件与传送带间动摩擦因素为,工件质量均为m ,经测量,发现后面那些已经和传送带达到相同速度的工件之间的距离为x ,下列判断正确的有( )A.传送带的速度为xTB.传送带的速度为22gx μC.每个工件与传送带间因摩擦而产生的热量为12mgx μ D.在一段较长的时间内,传送带因为传送工件而将多消耗的能量为23mtx T【答案】AD【解析】工件在传送带上先做匀加速直线运动,然后做匀速直线运动,每个工件滑上传送带后运动的规律相同,可知x=vT ,解得传送带的速度v=xT.故A 正确.设每个工件匀加速运动的位移为x ,根据牛顿第二定律得,工件的加速度为μg ,则传送带的速度v =s 与x 的关系.故B 错误.工件与传送带相对滑动的路程为:2222222v v v x x v g g g gT μμμμ⋅-===,则摩擦产生的热量为:Q=μmg △x =222mx T .故C 错误.根据能量守恒得,传送带因传送一个工件多消耗的能量xx22212mx E mv mg x T μ=+=,在时间t 内,传送工件的个数tn T=,则多消耗的能量23mtx E nE T'==.故D 正确.故选AD.如图所示,甲、乙两种粗糙面不同的传送带,倾斜于水平地面放置,以同样恒定速率v 向上运动.现将一质量为m 的小物体(视为质点)轻轻放在A 处,小物体在甲传送带上到达B 处时恰好达到传送带的速率v ;在乙传送带上到达离B 竖直高度为h 的C 处时达到传送带的速率v .已知B 处离地面的高度皆为H .则在小物体从A 到B 的过程中( )A .两种传送带与小物体之间的动摩擦因数相同B .将小物体传送到B 处,两种传送带消耗的电能相等C .两种传送带对小物体做功相等D .将小物体传送到B 处,两种系统产生的热量相等【解析】小物体在两种传送带均做初速度为零的匀加速直线运动,加速度大小a =μg cos θ-g sin θ,在速度达到v 的过程中,小物体在甲传送带上的位移s 较大,根据公式a =v 22s ,可知小物体在甲传送带上时的加速度较小,根据a =μg cos θ-g sin θ,可得μ=ag cos θ+tan θ,即小物体与甲传送带间的动摩擦因数较小,选项A 错误;在小物体从A 到B 的过程中,根据功能关系可知,传送带对小物体做的功等于小物体机械能的增加量,选项C 正确;在小物体从A 到B 的过程中,只有小物体相对传送带发生滑动时,即只有在加速过程中,系统才发生“摩擦生热”,根据公式Q =fs 相对计算系统产生的热量,可选取做匀速运动的传送带为惯性参考系,小物体在惯性参考系里做初速度大小为v ,加速度大小为a =μg cos θ-g sin θ,末速度为零的匀减速直线运动,可求出s 相对=v 22a ,可见,s 相对等于小物体相对于地面速度从0加速到v 过程中的位移,即系统产生的热量等于小物体加速过程中摩擦力对小物体做的功,对于甲传送带,在加速过程中摩擦力做正功设为W 1,克服重力做功为mgH ,动能改变量为12mv 2,根据动能定理可求得W 1=12mv 2+mgH ,同理可求出小物体在乙传送带上加速过程中摩擦力做的功为W 2=12mv 2+mg (H -h ),显然W 1>W 2,所以Q 1>Q 2,即甲系统产生的热量多,选项D 错误;在将小物体传送到B 处的过程中,传送带消耗的电能等于系统增加的机械能和产生的内能,两种系统增加的机械能相等,产生的内能不等,所以消耗的电能不等,选项B 错误. 【答案】C如图所示,与水平面夹角θ=30°的倾斜传送带始终绷紧,传送带下端A 点与上端B 点间的距离L =4 m ,传送带以恒定的速率v =2 m/s 向上运动.现将一质量为1 kg 的物体无初速度地放于A 处,已知物体与传送带间的动摩擦因数μ=32,取g =10 m/s 2,求:(1)物体从A 运动到B 共需多长时间? (2)电动机因传送该物体多消耗的电能.【解析】(1)物体无初速度地放在A 处后,因mg sin θ<μmg cos θ 故物体斜向上做匀加速直线运动. 加速度a =μmg cos θ-mg sin θm =2.5 m/s 2物体达到与传送带同速所需的时间t 1=va =0.8 st 1时间内物体的位移x 1=v2t 1=0.8 m之后物体以速度v 做匀速运动,运动的时间 t 2=L -x 1v=1.6 s物体运动的总时间t =t 1+t 2=2.4 s(2)解法1:前0.8 s 内物体相对传送带的位移Δx =vt 1-x 1=0.8 m 因摩擦而产生的内能E 内=μmg cos θ·Δx =6 J 整个过程中多消耗的电能E 电=E k +E p +E 内=12mv 2+mgL sin θ+E 内=28 J解法2:电动机多消耗的电能在数值上等于两个过程克服摩擦力所做的功,E 电=W f1+W f2 传送带在加速过程的位移x 1′=vt 1=1.6 m W f1=μmgx 1′cos θ=12 J传送带在匀速过程的位移x 2′=vt 2=3.2 m W f2=mgx 2′sin θ=16 J 所以E 电=28 J【答案】(1)2.4 s (2)28 J一质量为M =2 kg 的小物块随足够长的水平传送带一起运动,被一水平向左飞来的子弹击中,子弹从物块中穿过,如图5甲所示,地面观察者记录了小物块被击穿后的速度随时间的变化关系,如图乙所示(图中取向右运动的方向为正方向),已知传送带的速度保持不变,g 取10 m/s 2.(1)指出传送带的速度v 的方向及大小,说明理由. (2)计算物块与传送带间的动摩擦因数.(3)计算物块对传送带总共做了多少功?系统有多少能量转化为内能?【解析】(1)由题图可知,物块被击中后先向左做匀减速运动,速度为零后,又向右做匀加速运动,当速度等于2 m/s 以后随传送带一起匀速运动,所以传送带的速度方向向右,大小为2 m/s.(2)由题图可知,a =Δv Δt =42 m/s 2=2 m/s 2由牛顿第二定律得,滑动摩擦力F f =Ma ,其中 F f =μF N ,F N =Mg ,所以物块与传送带间的动摩擦因数 μ=a g =210=0.2. (3)由题图可知,传送带与物块存在摩擦力的时间只有3 s ,传送带在这段时间内的位移 x =vt =2×3 m =6 m所以物块对传送带所做的功为 W =-F f x =-4×6 J =-24 J选传送带为参考系,物块相对于传送带通过的路程 x ′=v ′2t =62×3 m =9 m ,所以转化为内能E Q =F f x ′=4×9 J =36 J.【答案】(1)2 m/s ,方向向右 理由见解析 (2)0.2 (3)-24 J 36 J如图所示,在大型超市的仓库中,要利用皮带运输机将货物由平台D 运送到高为h =2.5 m 的平台C 上.为了便于运输,仓储员在平台D 与皮带间放了一个14圆周的光滑轨道ab ,轨道半径为R =0.8 m ,轨道最低点与皮带接触良好.已知皮带和水平面间的夹角为θ=37°,皮带和货物间的动摩擦因数为μ=0.75,运输机的皮带以v 0=1 m/s 的速度沿顺时针方向匀速运动(皮带和轮子之间不打滑).现仓储员将质量为m =200 kg 的货物放于轨道的a 端(g =10 m/s 2).求:(1)货物到达圆轨道最低点b 时对轨道的压力; (2)货物沿皮带向上滑行多远才能相对皮带静止; (3)皮带将货物由A 运送到B 需对货物做多少功.【解析】(1)货物由a 到b ,由机械能守恒定律得mgR =12mv 2解得v =2gR =2×10×0.8 m/s =4 m/s 在最低点b ,由F 合=ma 得F -mg =m v 2RF =m ⎝⎛⎭⎫v 2R +g =200×⎝⎛⎭⎫420.8+10 N =6×103 N 由牛顿第三定律可知货物到达圆轨道最低点时对轨道的压力F ′=F =6×103 N. (2)货物在皮带上运动时,由动能定理得: -mgx sin37°-fx =12mv 20-12mv 2且f =μmg cos37° 解得:x =v 2-v 202g+μ=0.625 m.(3)由于tan37°=μ,则货物减速到v 0后便和皮带一起匀速向上运动货物由平台D 运送到平台C 的过程中,由功能关系知,皮带对货物做的功为W =mg (h -R )+12mv 20=3 500 J. 【答案】(1)6×103 N (2)0.625 m (3)3 500 J飞机场上运送行李的装置为一水平放置的环形传送带,传送带的总质量为M ,其俯视图如图所示,现开启电动机,传送带达到稳定运行的速度v 后,将行李依次轻轻放到传送带上,若有n 件质量均为m 的行李需通过传送带运送给旅客.假设在转弯处行李与传送带无相对滑动,忽略皮带轮、电动机损失的能量.求从电动机开启到运送完行李需要消耗的电能为多少?【解析】 设行李与传送带间的动摩擦因数为μ,则行李与传送带间由于摩擦而产生的总热量Q =nμmg Δx由运动学公式,得Δx =x 带-x 行=vt -12vt =12vt又v =at =μgt ,联立解得Q =12nmv 2由能量守恒,得E =Q +12Mv 2+12nmv 2故电动机消耗的电能为E =12Mv 2+nmv 2【答案】 12Mv 2+nmv 2(2014·江苏单科)如图所示,生产车间有两个相互垂直且等高的水平传送带甲和乙,甲的速度为v 0。
