信号与系统证明题
信号与系统考题参考解答(完整版)

《信号与系统》作业参考解答第一章(P16-17)1-3 设)(1t f 和)(2t f 是基本周期分别为1T 和2T 的周期信号。
证明)()()(21t f t f t f +=是周期为T 的周期信号的条件为T nT mT ==21 (m ,n 为正整数) 解:由题知)()(111t f mT t f =+ )()(222t f mT t f =+要使)()()()()(2121t f t f T t f T t f T t f +=+++=+则必须有21nT mT T == (m ,n 为正整数) 1-5 试判断下列信号是否是周期信号。
若是,确定其周期。
(1)t t t f πsin 62sin 3)(+= (2)2)sin ()(t a t f =(8)⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=2cos 28sin 4cos )(k k k k f πππ解:(1)因为t 2sin 的周期为π,而t πsin 的周期为2。
显然,使方程n m 2=π (m ,n 为正整数)成立的正整数m ,n 是不存在的,所以信号t t t f πsin 62sin 3)(+=是非周期信号。
(2)因为)2cos 1()sin ()(22t a t a t f -==所以信号2)sin ()(t a t f =是周期π=T 的周期信号。
(8)由于)4/cos(k π的周期为8)4//(21==ππN ,)8/sin(k π的周期为16)8//(22==ππN ,)2/cos(k π的周期为4)2//(23==ππN ,且有16412321=⨯=⨯=⨯N N N所以,该信号是周期16=N 的周期信号。
1-10 判断下列系统是否为线性时不变系统,为什么?其中)(t f 、][k f 为输入信号,)(t y 、][k y 为零状态响应。
(1))()()(t f t g t y = (2))()()(2t f t Kf t y += 解:(1)显然,该系统为线性系统。
信号与系统习题答案第三章

第三章习题基础题3.1 证明cos t , cos(2)t , …, cos()nt (n 为正整数),在区间(0,2)π的正交集。
它是否是完备集?解:(积分???)此含数集在(0,2)π为正交集。
又有sin()nt 不属于此含数集02sin()cos()0nt mt dt π=⎰,对于所有的m 和n 。
由完备正交函数定义所以此函数集不完备。
3.2 上题的含数集在(0,)π是否为正交集?解:由此可知此含数集在区间(0,)π内是正交的。
3.3实周期信号()f t 在区间(,)22T T-内的能量定义为222()TT E f t dt -=⎰。
如有和信号12()()f t f t +(1)若1()f t 与2()f t 在区间(,)22T T-内相互正交,证明和信号的总能量等于各信号的能量之和;(2)若1()f t 与2()f t 不是相互正交的,求和信号的总能量。
解:(1)和信号f(t)的能量为[]222222222221212222()12()()()()()()T T T T T T T T T T E f t dt dtf t dt f t dt f t f t dtf t f t -----===+++⎰⎰⎰⎰⎰(少乘以2)由1()f t 与2()f t 在区间内正交可得2122()()0T T f t f t dt -=⎰则有 22221222()()T T T T E f t dt f t dt --=+⎰⎰即此时和信号的总能量等于各信号的能量之和。
和信号的能量为(2)[]222222222221212222()12()()()()()()T T T T T T T T T T E f t dt dtf t dt f t dt f t f t dtf t f t -----===+++⎰⎰⎰⎰⎰(少乘以2吧?)由1()f t 与2()f t 在区间(,)22T T-内不正交可得2122()()0T T f t f t dt K -=≠⎰则有2222222212122222()()()()T T T T T T T T E f t dt f t dt K f t dt f t dt ----=++≠+⎰⎰⎰⎰即此时和信号的总能量不等于各信号的能量之和。
信号与系统练习题(带答案)

信号与系统练习题(带答案)1. 信号f(t)的波形如图所示。
分别画出信号(24),(24),(24)f t f t f t '''-+-+-+的波形,并且写出其表达式。
答案:2. 信号f ( t )的图形如下所示,对(a)写出f ' ( t )的表达式,对(b)写出f " ( t )的表达式,并分别画出它们的波形。
解 (a)20,21≤≤tf ' (t)= δ(t -2), t = 2-2δ(t -4), t = 4(b) f " (t ) = 2δ(t ) - 2δ(t -1)-2δ(t -3)+2δ(t -4)3. 已知f(5-2t)的波形如图所示,试画出f(t)的波形。
52:()(2)(2)(52)5252252:(52)(2)(2)()f t f t f t f t t tf t f t f t f t −−−→−−−→-−−−→---=-∴-→-→→ 压缩反转平移左移反转拉伸分析()右移求解过程55[52()]2,22t t t t -+=-∴+ 以代替而求得-2t ,即f(5-2t)左移(52)(2)f t f t -−−−→-时移由(2)反转:f(-2t)中以-t 代替t ,可求得f(2t),表明f(-2t)的波形 以t =0的纵轴为中心线对褶,注意()t δ是偶数,故112()2()22t t δδ--=+(2)(2)f t f t -−−−→反褶由(3)尺度变换:以12t 代替f(2t)中的t ,所得的f(t)波形将是f(2t)波形在时间轴上扩展两倍。
4. 求序列{}12[]1,2,1,0,1,2[][1cos()][]2f n n f n n u n π===+和的卷积和。
解:{}112222[]1,2,1[]2[1][2][]*[][]2[1][2]f n n n n f n f n f n f n f n δδδ==+-+-=+-+-5. 试求下列卷积。
奥本海姆《信号与系统》(第2版)配套模拟试题及详解(上册)

奥本海姆《信号与系统》(第2版)配套模拟试题及详解一、单项选择题(本大题共5小题,每题3分,共15分;在每小题列出的四个选项中只有一个是符合题目要求的,错选、多选或未选均无分。
)1.用下列差分方程描述的系统为线性系统的是______。
A.B.C.D.【答案】C查看答案【解析】A项,方程右边出现常数3,是非线性关系。
B项,出现y(k-1)y(k-2)项,是非线性关系。
D项,出现|f(k)|,是非线性关系。
2.单边Z变换的原序列,f(k)等于______。
【答案】A查看答案【解析】3.系统的幅频特性和相频特性如图1(a)、(b)所示,则下列信号通过该系统时,不产生失真的是______。
图1A.B.C.D.【答案】B查看答案【解析】由系统的幅频特性和相频特性可知:若输入信号的频率均处于w=-5~5之间,既不产生幅度失真又不产生相位失真。
只有B满足这一条件。
4.试确定序列是否为周期序列。
若是,其周期N为______。
A.不是周期序列B.是,N=24C.是,N=12D.是,N=8【答案】B查看答案【解析】因为,得,得。
又因为是有理数,因此是周期序列。
设共同周期为N,则有。
5.信号f(t)的傅里叶变换为,则的傅里叶变换为______。
【答案】B查看答案【解析】因为,由傅里叶变换的时移性质,有,由傅里叶变换的频移性质,有二、填空题(本大题共5小题,每题3分;共15分。
)1.对连续时间信号,按采样频率采样得到的离散时间信号=______。
【答案】查看答案【解析】,其中,为离散域的频率,为连续域的频率,。
2.周期性方波x(t)如图2所示,T=2,它的四次谐波频率=______rad/s。
图2【答案】查看答案【解析】基波频率,则四次谐波频率为。
3.周期矩形信号f(t)的波形如图3,则该信号的谱线间隔为0.1Hz,其中,直流分量为______。
图3【答案】0.4查看答案【解析】由f(t)波形可知T=l0S,基波频率即谱线间隔为0.1Hz。
信号与系统题库(完整版)

信号与系统题目部分,(卷面共有200题,0.0分,各大题标有题量和总分) 一、选择题(7小题,共0.0分)[1]题图中,若h '(0)=1,且该系统为稳定的因果系统,则该系统的冲激响应()h t 为。
A 、231()(3)()5tt h t e e t ε-=+- B 、32()()()tt h t e e t ε--=+C 、3232()()55tt e t e t εε--+D 、3232()()55tt e t e t εε--+-[2]已知信号x[n]如下图所示,则x[n]的偶分量[]e x n 是。
[3]波形如图示,通过一截止角频率为50rad sπ,通带内传输值为1,相移为零的理想低通滤波器,则输出的频率分量为() A 、012cos 20cos 40C C t C t ππ++ B 、012sin 20sin 40C C t C t ππ++ C 、01cos 20C C t π+ D 、01sin 20C C t π+[4]已知周期性冲激序列()()T k t t kT δδ+∞=-∞=-∑的傅里叶变换为()δωΩΩ,其中2TπΩ=;又知111()2(),()()2T T f t t f t f t f t δ⎛⎫==++⎪⎝⎭;则()f t 的傅里叶变换为________。
A 、2()δωΩΩ B 、24()δωΩΩ C 、2()δωΩΩ D 、22()δωΩΩ[5]某线性时不变离散时间系统的单位函数响应为()3(1)2()kkh k k k εε-=--+,则该系统是________系统。
A 、因果稳定B 、因果不稳定C 、非因果稳定D 、非因果不稳定 [6]一线性系统的零输入响应为(23kk --+)u(k), 零状态响应为(1)2()k k u k -+,则该系统的阶数A 、肯定是二阶B 、肯定是三阶C 、至少是二阶D 、至少是三阶 [7]已知某系统的冲激响应如图所示则当系统的阶跃响应为。
信号与系统第四版习题解答精选全文完整版

可编辑修改精选全文完整版《信号与系统》(第四版)习题解析高等教育2007年8月目录第1章习题解析1第2章习题解析5第3章习题解析14第4章习题解析21第5章习题解析29第6章习题解析39第7章习题解析47第8章习题解析52第1章习题解析1-1题1-1图示信号中,哪些是连续信号?哪些是离散信号?哪些是周期信号?哪些是非周期信号?哪些是有始信号?(c) (d)题1-1图解(a)、(c)、(d)为连续信号;(b)为离散信号;(d)为周期信号;其余为非周期信号;(a)、(b)、(c)为有始(因果)信号。
1-2给定题1-2图示信号f( t ),试画出下列信号的波形。
[提示:f( 2t )表示将f( t )波形压缩,f (2t)表示将f ( t )波形展宽。
](a) 2 f (t - 2 ) (b) f ( 2t )(c)f (2t )(d)f (-t +1 )题1-2图解以上各函数的波形如图p1-2所示。
图p1-21-3 如图1-3图示,R 、L 、C 元件可以看成以电流为输入,电压为响应的简单线性系统S R 、S L 、S C ,试写出各系统响应电压与激励电流函数关系的表达式。
S RS LS C题1-3图解各系统响应与输入的关系可分别表示为)()(t i R t u R R ⋅= tt i Lt u L L d )(d )(= ⎰∞-=tC C i C t u ττd )(1)(1-4 如题1-4图示系统由加法器、积分器和放大量为-a 的放大器三个子系统组成,系统属于何种联接形式?试写出该系统的微分方程。
题1-4图解系统为反馈联接形式。
设加法器的输出为x ( t ),由于)()()()(t y a t f t x -+=且)()(,d )()(t y t x t t x t y '==⎰故有)()()(t ay t f t y -='即)()()(t f t ay t y =+'1-5已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|,试判定该系统是否为线性时不变系统?解设T 为系统的运算子,则可以表示为)()]([)(t f t f T t y ==不失一般性,设f ( t ) = f 1( t ) +f 2( t ),则)()()]([111t y t f t f T ==)()()]([222t y t f t f T ==故有)()()()]([21t y t f t f t f T =+=显然)()()()(2121t f t f t f t f +≠+即不满足可加性,故为非线性时不变系统。
信号和系统试题及答案

信号和系统试题及答案一、选择题(每题4分,共20分)1. 信号的频谱分析中,傅里叶变换的物理意义是什么?A. 信号的时域表示B. 信号的频域表示C. 信号的相位信息D. 信号的幅度信息答案:B2. 在线性时不变系统中,系统的输出与输入的关系是什么?A. 线性关系B. 非线性关系C. 时变关系D. 随机关系答案:A3. 下列哪个函数不是周期函数?A. sin(t)B. cos(2t)C. e^(-t)D. cos(2πt)答案:C4. 系统稳定性的判定可以通过什么方法?A. 奈奎斯特准则B. 伯德图C. 相位裕度D. 所有以上答案:D5. 系统函数H(s)的零点和极点分别代表什么?A. 系统输入和输出B. 系统稳定性和不稳定性C. 系统增益和衰减D. 系统频率响应答案:B二、填空题(每题4分,共20分)1. 连续时间信号的傅里叶变换定义为:X(jω) = ____________。
答案:∫x(t)e^(-jωt)dt2. 如果一个系统的冲激响应h(t)是因果的,则系统的零状态响应y(t)与输入x(t)的关系为:y(t) = ____________。
答案:∫h(t-τ)x(τ)dτ3. 一个线性时不变系统的特性可以用其系统函数H(s)来描述,其中s 是复频域变量,代表的是 ____________。
答案:拉普拉斯变换4. 如果一个系统的频率响应H(jω)在ω=ω0处有极点,则在时域中对应的响应h(t)将具有 ____________。
答案:振荡特性5. 系统的因果性意味着系统的输出不会在输入之前出现,这可以用系统的冲激响应h(t)满足的条件来表示:h(t) = ____________。
答案:0,t < 0三、简答题(每题10分,共30分)1. 请简述傅里叶级数与傅里叶变换的区别。
答案:傅里叶级数适用于周期信号,是将周期信号分解为正弦和余弦函数的和,而傅里叶变换适用于非周期信号,是将信号分解为复指数函数的积分。
奥本海姆《信号与系统(第二版)》习题参考答案
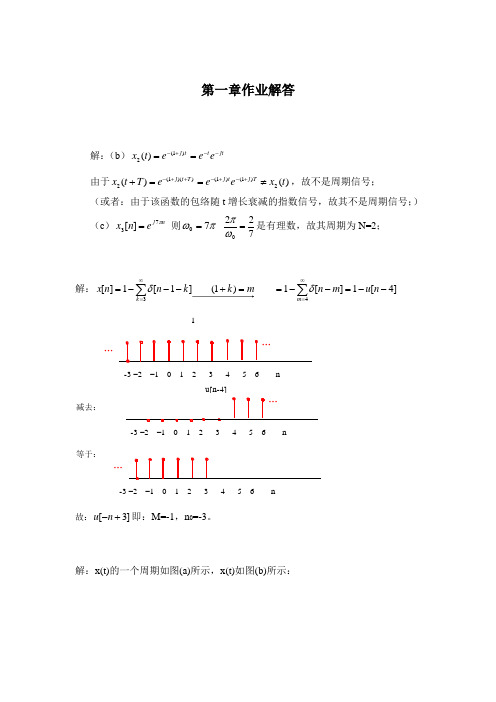
第一章作业解答解:(b )jt t t j e e e t x --+-==)1(2)(由于)()(2)1()1())(1(2t x e e e T t x T j t j T t j ≠==++-+-++-,故不是周期信号;(或者:由于该函数的包络随t 增长衰减的指数信号,故其不是周期信号;) (c )n j e n x π73][= 则πω70= 7220=ωπ是有理数,故其周期为N=2;解:]4[1][1)1(]1[1][43--=--==+---=∑∑∞=∞=n u m n mk k n n x m k δδ-3 –2 –1 0 1 2 3 4 5 6 n1…减去:-3 –2 –1 0 1 2 3 4 5 6 nu[n-4]等于:-3 –2 –1 0 1 2 34 5 6 n…故:]3[+-n u 即:M=-1,n 0=-3。
解:x(t)的一个周期如图(a)所示,x(t)如图(b)所示:而:g(t)如图(c)所示……dtt dx )(如图(d )所示:……故:)1(3)(3)(--=t g t g dtt dx 则:1t ,0t 3,32121==-==;A A 1.15解:该系统如下图所示: 2[n](1)]4[2]3[5]2[2]}4[4]3[2{21]}3[4]2[2{]3[21]2[][][1111111222-+-+-=-+-+-+-=-+-==n x n x n x n x n x n x n x n x n x n y n y即:]4[2]3[5]2[2][-+-+-=n x n x n x n y(2)若系统级联顺序改变,该系统不会改变,因为该系统是线性时不变系统。
(也可以通过改变顺序求取输入、输出关系,与前面做对比)。
解:(a )因果性:)(sin )(t x t y =举一反例:当)0()y(,0int s x t =-=-=ππ则时输出与以后的输入有关,不是因果的;(b )线性:按照线性的证明过程(这里略),该系统是线性的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信号与系统可能出现证明题的知识点总结
1、因果系统:非线性时不变系统的因果系统的证明 △
线性时不变系统的因果系统的证明 ☆
☆证明:为何h (t )=0,t <0(h (n )=0,n <0)时,则为因果系统。
(给定具体系统,判别其因果性)
2、稳定系统:非线性时不变系统的稳定性的证明 △
线性时不变系统的稳定性的证明 ☆
☆证明:为何∫|ℎ(t )|dt <M ∞−∞(∑|ℎ(n )|<M ∞n=0)系统稳定。
(给定具体系统,判别其稳定性)
3、线性时不变系统的证明☆(考查方法:给定具体系统,根据定义证明)见上册P21,1.8
4、卷积性质的证明
证明:对于线性时不变系统,零状态响应()r t ,激励为()e t ,系统的单位冲激函数为()h t ,证明: ()()()r t e t h t =*
5、傅里叶变换性质的证明
证明 狄利克雷条件为非周期信号存在傅里叶变换的充分条件
6、帕塞瓦尔定理的证明
7、证明:为什么右边信号的收敛域为()00Re ,s z r σ>>,左边信号的变换域为()Re s σ<, z r <
8、S 变换性质的证明
9、证明:()()000n n z z z h n H z z =*=⋅,()()000
s t s t s s e h t H s e =*=⋅ ()()()()()000cos cos w w w t h t H jw w t w ϕϕϕ=+*=⋅++,
其中()()()j w H jw H jw e ϕ=⋅ ,为()h t 的傅里叶变换
10、时域抽样定理的证明
11、Z 变换的性质的证明
12、连续信号的拉普拉斯变换与对应信号取样得到的理想取样信号的Z变换之间的关系,见下册 P71
13、理想取样的S变换与其对应的离散序列的Z变换之间的关系,见下册P70
14、证明式(8-43),见信号与系统书
15、式(9-36a),(9-36b),(9-38a)的证明
16、证明 A矩阵的特征根为系统的特征根。
