信号与系统练习题
(完整word版)信号与系统练习题——第5章
信号与系统练习题 第5章一、选择题1、系统函数()H s 与激励信号()f t 之间的关系是（B)A 、反比关系B 、没有关系C 、线性关系D 、不确定2、信号)()(2t e t f t ε-=的单边拉普拉斯变换=)(s F （D ） A 、2)2(1+s B 、 2)2(+s sC 、 2+s sD 、21+s3、已知某系统的框图如下，则此系统的系统函数表示为（C)A 、21()23H s s s =++ B 、2()23s H s s s =++C 、243()23s H s s s +=++ D 、241()23s H s s s +=-+4、已知某LTI 系统的系统函数()H s ，唯一决定该系统的冲激响应()h t 函数形式的是（B ）A 、()H s 的零点B 、()H s 的极点C 、系统的激励D 、激励与()H s 的极点 5、2(2)()(1)(2)s s H s s s +=+-，属于其零点的是(C)A 、—1B 、2C 、-2D 、1 6、2(2)()(1)(2)s s H s s s +=+-,属于其极点的是（C ）A 、0B 、—2C 、2D 、1 7、已知22()22sF s s s =++,则(0)f +=（C ）8、已知2()22F s s s =++，则()f ∞=（A) A 、0 B 、—2 C 、2 D 、不确定 9、信号2(1)()()t f t e t ε--=的单边拉普拉斯变换=)(s F （A ）A 、2()2e F s s =+B 、2()2s F s s =+ C 、1()2F s s =+ D 、()2s F s s =+10、信号2(1)()(1)t f t e t ε--=-的单边拉普拉斯变换=)(s F (A ）A 、()2s e F s s -=+B 、2()2e F s s =+ C 、1()2F s s =+ D 、()2s F s s =+11、已知信号()cos(2)f t t =的单边拉普拉斯变换2()4s F s s =+，则()[cos(2)]dy t t dt=的单边拉普拉斯变换()Y s =(B ）A 、2se s -+ B 、244s -+ C 、224s s + D 、24s s +12、已知信号()cos(2)f t t =的单边拉普拉斯变换2()4s F s s =+,则()[cos(2)()]dy t t t dtε=的单边拉普拉斯变换()Y s =（C ）A 、2se s -+ B 、244s -+ C 、224s s + D 、24s s +13、已知信号()f t 的单边拉普拉斯变换为()F s ，则()[()]dy t f t dt=的单边拉普拉斯变换()Y s =（A ） A 、()(0)sF s f -- B 、()(0)sF s f -+ C 、()sF s D 、()F s s14、已知信号()f t 的单边拉普拉斯变换为()F s ，则()[()()]dy t f t t dtε=的单边拉普拉斯变换()Y s =（C ）A 、()(0)sF s f --B 、()(0)sF s f -+C 、()sF sD 、()F s s15、已知223()21s F s s s +=++，则(0)f +=(C ）A 、0B 、-2C 、2D 、不确定 16、已知223()21s F s s s +=++，则()f ∞=（A ）A 、0B 、—2C 、2D 、不确定 17、已知1()1F s s =+，则(0)f +=(C ）18、已知()1F s s =+，则()f ∞=（A ） A 、0 B 、—1 C 、3 D 、不确定 19、信号5(1)()t f t e --=的单边拉普拉斯变换=)(s F (A)A 、5()5e F s s =+B 、5()5s F s s =+ C 、1()5F s s =+ D 、()5s F s s =+二、填空题1、某LTI 连续系统的系统函数为235)(2+++=s s s s H ，描述该系统的微分方程为)(5)()(2)(3)(''''t f t f t y t y t y +=++。
信号与系统练习及答案
信号与系统练习及答案一、单项选择题1．已知信号f (t )的波形如题1图所示，则f （t ）的表达式为（ ） A ．tu(t) B ．(t-1)u(t-1) C ．tu(t-1) D ．2(t-1)u(t-1) 2．积分式⎰-δ+δ++4422)]dt-(t 2(t))[23(t t的积分结果是（ ）A ．14B ．24C ．26D ．283．已知f(t)的波形如题3（a ）图所示，则f (5-2t)的波形为（ ）4．周期矩形脉冲的谱线间隔与（ ） A ．脉冲幅度有关 B ．脉冲宽度有关 C ．脉冲周期有关D ．周期和脉冲宽度有关5．若矩形脉冲信号的宽度加宽，则它的频谱带宽（ ）A ．不变B ．变窄C ．变宽D ．与脉冲宽度无关6．如果两个信号分别通过系统函数为H （j ω）的系统后，得到相同的响应，那么这两个信号（）A ．一定相同B ．一定不同C ．只能为零D ．可以不同7．f(t)=)(t u e t的拉氏变换为F （s ）=11-s ，且收敛域为（ ）A ．Re[s]>0B ．Re[s]<0C ．Re[s]>1D ．Re[s]<18．函数⎰-∞-δ=2t dx)x ()t (f 的单边拉氏变换F （s ）等于（ ）A ．1B ．s1 C ．e -2sD ．s1e -2s9．单边拉氏变换F （s ）=22++-s e)s (的原函数f(t)等于（ ）A ．e -2t u(t-1)B ．e -2(t-1)u(t-1)C ．e -2t u(t-2)D ．e -2(t-2)u(t-2)答案: BCCCBDCDA二．填空题1．如果一线性时不变系统的单位冲激响应为h(t)，则该系统的阶跃响应g(t)为_________。
2．已知x(t)的傅里叶变换为X （j ω），那么x (t-t 0)的傅里叶变换为_________________。
3．如果一线性时不变系统的输入为f(t)，零状态响应为y f (t )=2f (t-t 0)，则该系统的单位冲激响应h(t)为_________________。
(完整word版)信号与系统专题练习题及答案
信号与系统专题练习题一、选择题1．设当t 〈3时，x(t)=0，则使)2()1(t x t x -+-=0的t 值为 C 。
A t>-2或t>-1 B t=1和t=2 C t>—1 D t 〉-22．设当t 〈3时，x （t)=0，则使)2()1(t x t x -⋅-=0的t 值为 D 。
A t>2或t 〉-1 B t=1和t=2 C t>—1 D t>—23．设当t<3时，x(t ）=0，则使x （t/3)=0的t 值为 C 。
A t>3 B t=0 C t<9 D t=34．信号)3/4cos(3)(π+=t t x 的周期是 C 。
A π2 B π C 2/π D π/2 5．下列各表达式中正确的是 BA. )()2(t t δδ= B 。
)(21)2(t t δδ= C. )(2)2(t t δδ= D 。
)2(21)(2t t δδ=6. 已知系统的激励e(t)与响应r(t)的关系为:)1()(t e t r -= 则该系统为 B . A 线性时不变系统 B 线性时变系统 C 非线性时不变系统 D 非线性时变系统 7。
已知 系统的激励e(t ）与响应r （t)的关系为:)()(2t e t r = 则该系统为 C .A 线性时不变系统B 线性时变系统C 非线性时不变系统D 非线性时变系统8。
⎰∞-=t d ττττδ2sin )( A 。
A 2u （t ） B )(4t δ C 4 D 4u （t) 10. dt t t )2(2cos 33+⋅⎰-δπ等于 B 。
A 0 B —1 C 2 D —211．线性时不变系统输出中的自由响应的形式由 A 决定A 系统函数极点的位置；B 激励信号的形式;C 系统起始状态；D 以上均不对。
12．若系统的起始状态为0，在x （t)的激励下，所得的响应为 D . A 强迫响应;B 稳态响应；C 暂态响应;D 零状态响应。
信号与系统第1章习题
人口数为上述三部分之和，即
y(k)=y(k－1)+(α－β)y(k－1)+f(k)
整理得
y(k)-(1+α－β)y(k－1)=f(k)
这是一个一阶差分方程。
63
第1章 信号与系统的基本概念
1.15 某经济开发区计划每年投入一定资金，设这批资金 在投入后第二年度的利润回报率为α%，第三年度开始年度的
号。因sint的周期T1=2π s, sin2t的周期T2=π s，且T1/T2=2为有 cosπt的周期T2=2 s, 且T1/T2=π/2 理数, 故f1(t)是周期信号,它的周期为2π s。 (2) 因sin2t的周期T1=π s, 为无理数， 故f2(t)是非周期信号。
(3) 因cost的周期为T1=2π s,
题解图 1.5-2
18
第1章 信号与系统的基本概念
(3) 由于x(2-t)=x［-(t-2)］,故可将x(t)波形“翻转”后，再 右移2个单位,画出题(3)波形如题解图1.5-3中的f3(t)所示。
题解图 1.5-3
19
第1章 信号与系统的基本概念
(4) 按照“展缩-平移”方式，将x(t)波形“压缩”
34
第1章 信号与系统的基本概念
题解图 1.6-3
35
第1章 信号与系统的基本概念
(4) 先画出y(k)、y(-k)图形，然后进行相减运算，得到题 (4)序列图形如题解图1.6-4所示。
题解图 1.6-4
36
第1章 信号与系统的基本概念
(5) 和序列图形如题解图1.6-5所示。
题解图 1.6-5
第1章 信号与系统的基本概念
y(k)的一阶后向差分:
y(k)的迭分:
信号与系统练习题题库
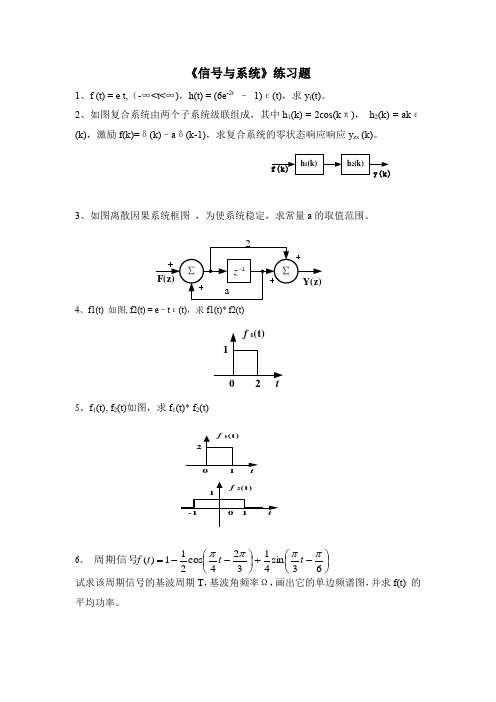
《信号与系统》练习题1、f (t) = e t,（-∞<t<∞)，h(t) = (6e -2t – 1)ε(t)，求y f (t)。
2、如图复合系统由两个子系统级联组成，其中h 1(k) = 2cos(k π)， h 2(k) = ak ε(k)，激励f(k)=δ(k)–a δ(k-1)，求复合系统的零状态响应响应y zs (k)。
3、如图离散因果系统框图 ，为使系统稳定，求常量a 的取值范围。
4、f1(t) 如图, f2(t) = e –t ε(t)，求f1(t)* f2(t)5、f 1(t), f 2(t)如图，求f 1(t)* f 2(t)6、 试求该周期信号的基波周期T ，基波角频率Ω，画出它的单边频谱图，并求f(t) 的平均功率。
⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-+--=63sin 41324cos 211)(ππππt t t f 周期信号7、若描述某系统的差分方程为y(k)+ 4y(k – 1) + 4y(k – 2) = f(k)已知初始条件y(0)=0，y(1)= – 1；激励f(k)=2k ，k ≥0。
求方程的全解。
8、某系统，已知当输入f(k)=(– 1/2)k ε(k)时，其零状态响应 求系统的单位序列响应h(k)和描述系统的差分方程。
9、某系统，已知当输入f(t)=e -t ε(t)时，其零状态响应如下 求系统的单位冲激响应h(k)和描述系统的微分方程。
10、如图复合系统由三个子系统组成，其中h1(k) = ε(k)， h2(k) = ε(k – 5)，求复合系统的单位序列响应h (k)11、如图电路，R=1Ω，C=1F ，以uC(t)为输出，求其h(t)C (t)12、已知信号信号流图如图，求其系统函数（利用梅森公式）。
13、如图所示电路，已知uS(t) = (t) V ，iS(t) =δ(t)，起始状态uC(0-) =1V ，iL(0-) = 2A ，求电压u(t)。
信号与系统练习题——第6章
信号与系统练习题 第6章一、选择题1、()k δ的Z 变换是（A ）A 、1B 、()δωC 、2()πδωD 、2π 2、已知一序列的Z 变换的收敛域为2z >，则该序列为（D ）A 、有限长序列B 、反因果序列C 、双边序列D 、因果序列 3、序列1()4(1)()()4kkh k k k εε=--+的z 变换收敛域为 (C) A 、14z >B 、4z >C 、144z << D 、4z < 4、象函数()1ZF Z Z=-（1Z <）的原序列为（B ）。
A 、(1)k ε--- B 、(1)k ε-- C 、()k ε- D 、()k ε 5、某LTI 离散时间系统的系统函数为65)(2+-=Z Z ZZ H ，该系统的单位响应=)(k h （F ）。
A 、(23)(1)kkk ε--- ； B 、(23)()kkk ε-；C 、(32)(1)kkk ε---；D 、)()23(k kk ε-6、某因果序列()f k 的Z 变换为()5ZF Z Z =- （5Z >），则(0)f =（B ）。
A 、 0 ； B 、 1 ； C 、 5 ； D 、 -0.2。
7、已知126)(22-+=z z z z F 5.0>z ，则原函数=)(k f （B ） A 、 )(])1(2)5.0[(k kkε-⋅+- B 、)(])1(25.0[k kkε-⋅+C 、 )(]25.0[k kε+ D 、)(]2)5.0[(k kε+-8、已知223()2z F z z z =+- 2z > ，则原函数=)(k f （A ）。
A 、 [2(2)1]()kk ε-+ B 、)(])1(25.0[k kk ε-⋅+C 、 [0.51]()kk ε+ D 、[(2)1]()kk ε-+9、序列1()()2kf k =的z 变换及收敛域为（A ） A 、3()(21)(2)z F z z z =-- ，21<z <2 B 、3()(21)(2)F z z z -=-- ，z >2C 、3()(21)(2)z F z z z =--，z >2 D 、3()(21)(2)z F z z z -=-- ，21<z <210、已知一序列的Z 变换的收敛域为2z <，则该序列为（B ）A 、有限长序列B 、反因果序列C 、双边序列D 、因果序列 11、已知一序列的Z 变换的收敛域为122z <<，则该序列为（C ） A 、有限长序列 B 、反因果序列 C 、双边序列 D 、因果序列 12、已知因果信号()f k 的单边Z 变换为()F z ，则信号(1)f k -的单边Z 变换为（C ） A 、1()(1)z F z f -+- B 、1()(1)z F z f --- C 、1()z F z - D 、()zF z13、已知信号()f k 的单边Z 变换为()F z ，则信号(1)f k -的单边Z 变换为（A ）1()(1)z F z f -+- B 、1()(1)z F z f --- C 、1()z F z - D 、()zF z二、填空题1、离散信号)(2)(k k f kε-=的单边z 变换=)(z F 5.0z z-。
信号与系统练习题附答案
A、因果不稳定系统
B、非因果稳定系统
C、因果稳定系统
D、非因果不稳定系统
21 设连续时间线性系统的单位冲激响应为 h(t)，系统的频率特性为 H ( j) H ( j) e j () ，信号通
过线性系统不失真的条件是（ ）
A. H ( j) 可以为任意函数，() t0
B. H ( j) 和() 都可以为任意函数
1 D. 2 (5 ) j
17.若收敛坐标落于原点，S 平面有半平面为收敛区，则（ ）
A. 该信号是有始有终信号
B. 该信号是按指数规律增长的信号
C. 该信号是按指数规律衰减的信号
D. 该信号的幅 度既不增长也不衰减而等于稳定值，或随时间 t，t n 成比例增长的信号
18.
F (s)
s(s 2
A．系统是线性的 B。系统是时不变的 C。系统是因果的 D。系统是稳定的
37．对于信号 f (t) sin 2t 的最小取样频率是 （ ）
A．1 Hz
B。2 Hz
38．理想低通滤波器是（ ）
A．因果系统
C。4 Hz
B。物理可实现系统
D。8 Hz
C。非因果系统
D。响应不超前于激励发生的系统
39．长度为 M 的序列 x1[n] 与长度为 N 的序列 x2[n] 的卷积和 x1[n] * x2[n] 的序列的长度为(
C． e3t (t 1)
D。 e3t (t 3)
50．已知信号 f (t) 的傅氏变换为 F ( j), 则 f (3 t ) 的傅氏变换为（ ） 2
A． 2F ( j2)e j3
B。 2F ( j2)e j3
C． 2F ( j2)e j6
D。 2F ( j2)e j6
信号与系统练习题
练习题一、 单项选择题（共35题）1.下列信号中为周期信号的是【 B 】(A) t t t f πsin 2cos )(+= (B) t t t f 3cos 2sin )(+=(C) t t t f πsin 2cos 3)(+=(D))(cos )(t t t f επ=2. 积分dt t t e t ∫∞∞−−+)]()(['2δδ等于【 D 】(A) -1 (B)1 (C) 2 (D) 3 3. 卷积积分)()(t t t εε∗等于【 C 】(A) )(2t t ε (B) )(t t ε (C) )(212t t ε (D) )(2t t ε4. 卷积和)]1()([)(−−∗k k k δδε等于【 A 】(A) )(k δ (B) )1(−k δ (C) )2(−k δ (D) )(k ε5. 信号)()(2t e t f t ε−=的频谱函数)(ωj F 等于【 B 】(A)ωj 1 (B) ωj +21 (C) ωj −21 (D) ωj +−21 6. 系统的幅频特性|H (j ω)|和相频特性如图(a)(b)所示，则下列信号通过该系统时，不产生失真的是【 B 】(A) f (t ) = cos(t ) + cos(8t ) (B) f (t ) = sin(2t ) + sin(4t ) (C) f (t ) = sin(2t ) sin(4t ) (D) f (t ) = cos 2(4t )7. 象函数ses F −+=11)(的原函数)(t f 是t=0接入的有始周期信号，其第一个周期（0<t<T ）的时间函数表达式=)(0t f 【 D 】(A) )(t δ (B) )1(−t δ (C) )1()(−+t t δδ (D) )1()(−−t t δδ8.函数)]()[sin()(22t t dt d t f επ=的拉普拉斯变换=)(s F 【 C 】(A) 222π+s s (B) 22ππ+s (C) 222ππ+s s (D) 22ππ+s s 9. 序列)1(2)(2)(−−+=−k k k f k k εε的双边Z 变换=)(z F 【 B 】 (A)221,)2)(12(3<<−−z z z z (B) 221,)2)(12(3<<−−−z z z z(C)21,)2)(12(3>−−−z z z z (D) 2,)2)(12(3<−−−z z z z10. 象函数)2)(1()(2−+=z z z z F 其收敛域为2>z ，则其原序列=)(k f 【 A 】(A) )(])2(32)1(31[k k k ε+− (B) )(])2(3231[k k ε+(C) )(])2(32)1(31[k k k ε−+− (D) )1(])2(32)1(31[−−+−k k k ε11. 积分dt t t )(4sin(91δπ∫−−等于【 B 】(A)22(B) 22− (C) 2 (D) 2− 12. 卷积积分)()(t t εε∗等于【 C 】(A) )(2t ε (B) )(t ε (C) )(t t ε (D) 1 13. 卷积和)1()1(−∗−k k δε等于【 A 】(A) )2(−k ε (B) )(k ε (C) )1(−k δ (D) )2(−k δ 14. 信号t t f 2cos )(=的频谱函数)(ωj F 等于【 D 】(A) )1()1(++−ωδωδ (B) )]1()1([++−ωδωδπ (C))2()2(++−ωδωδ (D) )]2()2([++−ωδωδπ15. 已知)()(ωj F t f ↔，则函数)()2(t f t −的频谱函数为【 C 】(A))(2)(ωωωj F d j dF − (B) )(2)(ωωωj F d j dF +(C) )(2)(ωωωj F d j dF j− (D) )(2)(ωωωj F d j dF j + 16. 信号)1()()(−−=t t t f εε的拉普拉斯变换等于【 D 】(A))1(se − (B))1(1s e s − (C) )1(se −− (D) )1(1s e s−− 17. 象函数)1(1)(2s e s s F −+=的原函数)(t f 是t=0接入的有始周期信号，其第一个周期（0<t<T ）的时间函数表达式=)(0t f 【 D 】(A) )(t ε (B) )2(−t ε (C))2()(−+t t εε (D))2()(−−t t εε18. 序列)()1()(k k k f ε+=的双边Z 变换=)(z F 【 A 】(A) 1,)1(22>−z z z (B) 1,)1(22>+z z z(C) 1,)1(22<−z z z (D) 1,)1(22<+z z z 19. 象函数)2)(1()(2−+=z z z z F 其收敛域为1<z ，则其原序列=)(k f 【 D 】(A) )(])2(32)1(31[k k k ε+− (B) )(])2(32)1(31[k k k ε−−−(C))1(])2(32)1(31[−−+−k k k ε (D) )1(])2(32)1(31[−−−−−k k k ε20.)]([)1(t e dtdt t δ−−等于【 A 】 (A) )()('t t δδ+ (B) )()('t t δδ−(C) )(2)('t t δδ+ (D) )(2)('t t δδ−21.积分dt t t )1()4sin(03−−∫−δπ等于【 B 】(A) 1 (B) 0 (C)2 (D)322.)]([2t e dtdt ε−等于【 C 】(A) )()(2t et tεδ−− (B) )()(2t et tεδ−+ (C) )(2)(2t et tεδ−− (D) )(2)(2t et tεδ−+23. 积分dt t t ∫∞∞−−)('2)2(δ等于【 D 】 (A) 1 (B)2 (C) 3 (D) 424. 积分dt t t t ∫∞∞−)()2sin(δ等于【 B 】 (A) 1 (B)2 (C) 3 (D) 425. 卷积积分)]2()([)(−−∗t t t εεε等于【 D 】(A) )2()(−−t t t t εε (B) )2()(−+t t t t εε (C) )2()2()(−−+t t t t εε (D) )2()2()(−−−t t t t εε 26. 卷积积分)(')(t t δε∗等于【 C 】(A) )(2t δ (B) )(2t δ− (C) )(t δ (D) )(t δ− 27. 卷积积分)1()1(+∗−t t εε等于【 A 】(A) )(t t ε (B) )()1(t t ε− (C) )()2(t t ε− (D) )()1(t t ε+ 28. 卷积和)2()1(−∗−k k δδ等于【 D 】(A) )2(−k δ (B) )(k δ (C) )1(−k δ (D) )3(−k δ29. 已知卷积和)()1()()(k k k k εεε+=∗，则)4()3(−∗−k k εε等于【 B】(A) )6()6(−−k k ε (B) )7()6(−−k k ε (C) )6()7(−−k k ε (D) )7()7(−−k k ε 30.)]()2[cos(t t dtdε 的拉普拉斯变换等于【 C 】 (A)442+s (B) 442+−s(C)422+ss (D) 422+−ss31. 信号)()(t t t f ε=的拉普拉斯变换等于【 D 】(A)22s− (B)22s (C)21s− (D)21s32. 序列)(3)(2)(k k k f εδ+=的双边Z 变换=)(z F 【 A 】(A) 1,132>−+z z z (B) 1,132>−−z z z(C) 1,132>−+−z z z (D) 1,132>−−−z z z33. 序列)()(k k k f ε=的双边Z 变换=)(z F 【 A 】(A)1,)1(2>−z z z (B) 1,)1(2>+z z z(C) 1,)1(22>−z z z (D) 1,)1(22>+z z z 34. 象函数)3)(2(1)(−−=z z z F 其收敛域为3>z ，则其原序列=)(k f 【 C 】(A) )()32()(61k k k k εδ−− (B) )()32()(61k k k k εδ−+(C) )()32()(6111k k k k εδ−−−− (D) )()32()(6111k k k k εδ−−−+35. 序列)(])1(1[21)(k k f k ε−+=的双边Z 变换=)(z F 【 C 】(A)1,12>−z z z (B)1,12>+z z z(C) 1,122>−z z z (D) 1,122>+z z z二．填空题（共23题）：1. 已知信号)(t f 的波形如图所示，画出信号)2(t f −的波形为 )2(t f −O t2. 周期信号623sin(41)324cos(211)(ππππ−+−−=t t t f 的基波角频率=Ω s rad /.12π3. 信号11)(+=jt t f 的傅里叶变换等于 . 4. 频谱函数)3cos(2)(ωω=j F 的傅里叶逆变换=)(t f .)3()3(−++t t δδ5.信号)1()]1(sin[)()sin()(−−−=t t t t t f επεπ的拉普拉斯变换=)(s F . 22)1(ππ+−−s e s 6. 已知信号)(t f 的波形如图所示，画出信号)42(−t f的波形为 )42(−t fO t7. 序列)5.0cos()43sin()(k k k f ππ+=的周期为 . 88. 信号t tt f sin )(=的傅里叶变换等于 . )(2ωπg9.信号)1()()1(−=−−t et f t ε的拉普拉斯变换=)(s F .1+−s e s10.已知信号)(t f 的波形如图所示，则)(t f 的傅里叶变换等于 . )(2)(2ωωπδSa −11.若信号)(t f 的频谱函数为)(ωj F ，则)(b at f −的频谱函数为 ， 其中a 为非零常数。
信号与系统练习题——第1-3章
信号与系统练习题——第1-3章信号与系统练习题（第1-3章）一、选择题1、下列信号的分类方法不正确的是（A ）A 、数字信号和离散信号B 、确定信号和随机信号C 、周期信号和非周期信号D 、连续信号和离散信号2、下列离散序列中，哪个不是周期序列? （D ）A 、165()3cos()512f k k ππ=+ B 、2211()5cos()712f k k ππ=+ C 、33()9sin()5f k k π= D 、433()7sin()45f k k π=+ 3、下列哪一个信号是周期性的？（C ）。
A 、()3cos 2sin f t t t π=+；B 、()cos()()f t t t πε=；C 、()sin()76f k k ππ=+； D 、1()cos()53f k k π=+。
4、周期信号()sin6cos9f t t t =+的周期为（D ）A 、πB 、2πC 、12π D 、23π5、周期信号()sin3cos f t t t π=+的周期为（C ）。
A 、πB 、2πC 、无周期D 、13π 6、以下序列中，周期为5的是（D ） A. 3()cos()58f k k π=+ B. 3()sin()58f k k π=+ C. 2()58()j k f k eπ+= D. 2()58()j k f k e ππ+=7、下列说法正确的是（D ）A 、两个周期信号()x t ，()y t 的和信号()()x t y t +一定是周期信号B 、两个周期信号()x t ，()y t 的周期分别为2()()x t y t +是周期信号C 、两个周期信号()x t ，()y t 的周期分别为2和π，则信号()()x t y t +是周期信号D 、两个周期信号()x t ，()y t 的周期分别为2和3，则信号()()x t y t +是周期信号8、下列说法不正确的是（A ）A 、两个连续周期信号的和一定是连续周期信号B 、两个离散周期信号的和一定是离散周期信号C 、连续信号()sin(),(,)f t t t ω=∈-∞+∞一定是周期信号D 、两个连续周期信号()x t ，()y t 的周期分别为2和3，则信号()()x t y t +是周期信号9、(52)f t -是如下运算的结果（C ）A 、(2)f t -右移5B 、(2)f t -左移5C 、(2)f t -右移25 D 、(2)f t -左移25 10、将信号()f t 变换为（A ）称为对信号()f t 的平移。
信号与系统练习题——第1-3章
信号与系统练习题（第1-3章）一、选择题1、下列信号的分类方法不正确的是（A ）A 、数字信号和离散信号B 、确定信号和随机信号C 、周期信号和非周期信号D 、连续信号和离散信号 2、下列离散序列中，哪个不是周期序列? （D ） A 、165()3cos()512f k k ππ=+ B 、2211()5cos()712f k k ππ=+C 、33()9sin()5f k k π= D 、433()7sin()45f k k π=+ 3、下列哪一个信号是周期性的？（C ）。
A 、()3cos 2sin f t t t π=+；B 、()cos()()f t t t πε=；C 、()sin()76f k k ππ=+； D 、1()cos()53f k k π=+。
4、周期信号()sin6cos9f t t t =+的周期为（D ）A 、πB 、2πC 、12π D 、23π 5、周期信号()sin3cos f t t t π=+的周期为（C ）。
A 、πB 、2πC 、无周期D 、13π 6、以下序列中，周期为5的是（D ）A. 3()cos()58f k k π=+ B. 3()sin()58f k k π=+ C.2()58()j k f k eπ+= D. 2()58()j k f k eππ+=7、下列说法正确的是（D ）A 、两个周期信号()x t ，()y t 的和信号()()x t y t +一定是周期信号B 、两个周期信号()x t ，()y t 的周期分别为2()()x t y t +是周期信号C 、两个周期信号()x t ，()y t 的周期分别为2和π，则信号()()x t y t +是周期信号D 、两个周期信号()x t ，()y t 的周期分别为2和3，则信号()()x t y t +是周期信号 8、下列说法不正确的是（A ）A 、两个连续周期信号的和一定是连续周期信号B 、两个离散周期信号的和一定是离散周期信号C 、连续信号()sin(),(,)f t t t ω=∈-∞+∞一定是周期信号D 、两个连续周期信号()x t ，()y t 的周期分别为2和3，则信号()()x t y t +是周期信号 9、(52)f t -是如下运算的结果（C ）A 、(2)f t -右移5B 、(2)f t -左移5C 、(2)f t -右移25 D 、(2)f t -左移2510、将信号()f t 变换为（A ）称为对信号()f t 的平移。
信号与系统练习题附答案
12.连续信号)(t f 与)(0t t -δ的乘积，即=-)()(0t t t f δ（ ）.A.)()(00t t t f -δ B. )(0t t f - C. )(t δ D. )()(0t t f δ13.已知系统响应()y t 与激励()f t 的关系为（ ）2(51)()()5()[()]t y t ty t y t f t '''-++=则该系统是( )系统。
A. 线性非时变B. 非线性非时变C. 线性时变D. 非线性时变14. 下列系统那个是因果、线性、时不变的连续系统( )。
A ．)()(2)(3)(t f t y t y t y '=+'+''B.)()()(3)(t f t f t y t y ='+''C ．)()()(3)(t f t ty t y t y =+'+''D ．)(2)1(3)(t f t y t y =+-'+''15.若对连续时间信号进行频域分析，则需对该信号进行（ ）. A. LT B. FT C. Z 变换 D. 希尔伯特变换16.)()52(t etj ε+-的频谱函数为（ ）A.ωj e j 521- B. ωj e j 521+ C.j )5(21ω++ D.j)5(21ω++-17.若收敛坐标落于原点，S 平面有半平面为收敛区，则（ ）A. 该信号是有始有终信号B. 该信号是按指数规律增长的信号C. 该信号是按指数规律衰减的信号D. 该信号的幅 度既不增长也不衰减而等于稳定值，或随时间nt t ，成比例增长的信号 18. )22(3)(2+++=s s s s s F ，则根据终值定理有=∞)(f （ ） A. 0 B. 1.5 C. ∞0 D. 119.信号)2(4sin 3)2(4cos 2)(++-=t t t f ππ与冲激函数)2(-t δ之积为（ ）A 、2B 、2)2(-t δC 、3)2(-t δD 、5)2(-t δ，则该系统是（）＞－系统的系统函数．已知2]Re[,651)(LTI 202s s s s s H +++=A 、因果不稳定系统B 、非因果稳定系统C 、因果稳定系统D 、非因果不稳定系统21 设连续时间线性系统的单位冲激响应为h(t)，系统的频率特性为)()()(ωϕωωj e j H j H =，信号通过线性系统不失真的条件是（ ）A. )(ωj H 可以为任意函数，0)(t ωωϕ-=B.)(ωj H 和)(ωϕ都可以为任意函数C. h(t)为常数D.)(ωj H 为常数，0)(t ωωϕ-=22. 系统的幅频特性|H (ω)|和相频特性如图2(a)(b)所示，则下列信号通过该系统时，不产生失真的是（ ）。
信号与系统练习题-第4章
信号与系统练习题 第4章一、选择题1、周期信号的频谱具有的特点是〔D 〕A 、离散性B 、收敛性C 、谐波性D 、以上都对 2、以下表达正确的选项是〔D 〕。
A 、)(t f 为周期偶函数，其傅立叶级数只有偶次谐波；B 、)(t f 为周期偶函数，其傅立叶级数只有余弦偶次谐波分量；C 、)(t f 为周期奇函数，其傅立叶级数只有奇次谐波；D 、)(t f 为周期奇函数，其傅立叶级数只有正弦分量。
3、某连续系统的系统函数ωωj j H -=)(，那么输入为t j e t f 2)(=时，系统的零状态响应()zs y t =〔B 〕A 、)j(2t e B 、)2-j(2t e2πC 、 )j(2t e2 D 、 )2-j(2t eπ4、频谱函数11)(+=ωωj j F 的傅里叶反变换=)(t f 〔A 〕A 、 )(t e t ε-B 、 )(t te t ε-C 、 )(t e t εD 、 )(t te t ε 5、假设矩形脉冲信号的宽度加宽，那么它的频谱带宽(B)。
A 、 不变 ；B 、变窄 ；C 、 变宽；D 、与脉冲宽度无关 6、假设()f t 是实偶信号，以下说法正确的选项是〔A 〕 A 、该信号的频谱是实偶函数；B 、该信号的频谱是虚奇函数C 、该信号的频谱是奇函数；D 、该信号的频谱的实部实偶函数，虚部是奇函数7、某一周期函数，在其频谱分量中，仅含有正弦基波分量和正弦奇次谐波分量，该函数属于〔D 〕。
A 、奇函数 B 、偶函数 C 、既是偶函数又是奇谐函数 D 、既是奇函数又是奇谐函数 8、关于抽样信号sin ()tSa t t=，以下说法错误的选项是〔A 〕。
A 、()Sa t 信号是奇函数 B 、 ()Sa t 信号在t=0时取最大值1 C 、()0Sa t =时，t n π=±〔n 为自然数〕 D 、()()Sa t Sa t =-9、带限信号)(t f 的最高角频率为m ω，现对)(t f 进行理想冲激取样，得到取样信号()s f t ，为了能从()s f t 中恢复出原信号，那么取样角频率s ω需满足〔B 〕A 、s m ωω≥B 、2s m ωω≥C 、m s ωω≥D 、2m s ωω≥10、频谱函数1()2F j j ωω=+的傅里叶反变换=)(t f 〔A 〕。
(完整版)信号与系统练习及答案
信号与系统练习及答案一、单项选择题1．已知信号f (t )的波形如题1图所示，则f （t ）的表达式为（ ）A ．tu(t)B ．(t-1)u(t-1)C ．tu(t-1)D ．2(t-1)u(t-1)2．积分式⎰-δ+δ++4422)]dt -(t 2(t))[23(t t 的积分结果是（ ） A ．14 B ．24 C ．26 D ．283．已知f(t)的波形如题3（a ）图所示，则f (5-2t)的波形为（ ）4．周期矩形脉冲的谱线间隔与（ ）A ．脉冲幅度有关B ．脉冲宽度有关C ．脉冲周期有关D ．周期和脉冲宽度有关 5．若矩形脉冲信号的宽度加宽，则它的频谱带宽（ ） A ．不变 B ．变窄 C ．变宽D ．与脉冲宽度无关 6．如果两个信号分别通过系统函数为H （j ω）的系统后，得到相同的响应，那么这两个信号（）A ．一定相同 B ．一定不同 C ．只能为零 D ．可以不同7．f(t)=)(t u e t 的拉氏变换为F （s ）=11-s ，且收敛域为（ ） A ．Re[s]>0B ．Re[s]<0C ．Re[s]>1D ．Re[s]<1 8．函数⎰-∞-δ=2t dx )x ()t (f 的单边拉氏变换F （s ）等于（ ） A ．1 B ．s 1 C ．e -2s D ．s1e -2s 9．单边拉氏变换F （s ）=22++-s e )s (的原函数f(t)等于（ ） A ．e -2t u(t-1) B ．e -2(t-1)u(t-1) C ．e -2t u(t-2)D ．e -2(t-2)u(t-2)答案: BCCCBDCDA二．填空题1．如果一线性时不变系统的单位冲激响应为h(t)，则该系统的阶跃响应g(t)为_________。
2．已知x(t)的傅里叶变换为X （j ω），那么x (t-t 0)的傅里叶变换为_________________。
3．如果一线性时不变系统的输入为f(t)，零状态响应为y f (t )=2f (t-t 0)，则该系统的单位冲激响应h(t)为_________________。
(完整版)信号与系统练习及答案
信号与系统练习及答案一、单项选择题1．已知信号f (t )的波形如题1图所示，则f （t ）的表达式为（ ）A ．tu(t)B ．(t-1)u(t-1)C ．tu(t-1)D ．2(t-1)u(t-1)2．积分式⎰-δ+δ++4422)]dt -(t 2(t))[23(t t 的积分结果是（ ） A ．14 B ．24 C ．26 D ．283．已知f(t)的波形如题3（a ）图所示，则f (5-2t)的波形为（ ）4．周期矩形脉冲的谱线间隔与（ ）A ．脉冲幅度有关B ．脉冲宽度有关C ．脉冲周期有关D ．周期和脉冲宽度有关 5．若矩形脉冲信号的宽度加宽，则它的频谱带宽（ ） A ．不变 B ．变窄 C ．变宽D ．与脉冲宽度无关 6．如果两个信号分别通过系统函数为H （j ω）的系统后，得到相同的响应，那么这两个信号（）A ．一定相同 B ．一定不同 C ．只能为零 D ．可以不同7．f(t)=)(t u e t 的拉氏变换为F （s ）=11-s ，且收敛域为（ ） A ．Re[s]>0B ．Re[s]<0C ．Re[s]>1D ．Re[s]<1 8．函数⎰-∞-δ=2t dx )x ()t (f 的单边拉氏变换F （s ）等于（ ） A ．1 B ．s 1 C ．e -2s D ．s1e -2s 9．单边拉氏变换F （s ）=22++-s e )s (的原函数f(t)等于（ ） A ．e -2t u(t-1) B ．e -2(t-1)u(t-1) C ．e -2t u(t-2)D ．e -2(t-2)u(t-2)答案: BCCCBDCDA二．填空题1．如果一线性时不变系统的单位冲激响应为h(t)，则该系统的阶跃响应g(t)为_________。
2．已知x(t)的傅里叶变换为X （j ω），那么x (t-t 0)的傅里叶变换为_________________。
3．如果一线性时不变系统的输入为f(t)，零状态响应为y f (t )=2f (t-t 0)，则该系统的单位冲激响应h(t)为_________________。
信号与系统练习题(带答案)
信号与系统练习题（带答案）1. 信号f(t)的波形如图所示。
分别画出信号(24),(24),(24)f t f t f t '''-+-+-+的波形，并且写出其表达式。
答案：2. 信号f ( t )的图形如下所示，对(a)写出f ' ( t )的表达式，对(b)写出f " ( t )的表达式，并分别画出它们的波形。
解 (a)20,21≤≤tf ' (t)= δ(t -2)， t = 2-2δ(t -4)， t = 4(b) f " (t ) = 2δ(t ) - 2δ(t -1)-2δ(t -3)+2δ(t -4)3. 已知f(5-2t)的波形如图所示，试画出f(t)的波形。
52:()(2)(2)(52)5252252:(52)(2)(2)()f t f t f t f t t tf t f t f t f t −−−→−−−→-−−−→---=-∴-→-→→ 压缩反转平移左移反转拉伸分析（）右移求解过程55[52()]2,22t t t t -+=-∴+ 以代替而求得－2t ，即f(5-2t)左移(52)(2)f t f t -−−−→-时移由（2）反转：f(-2t)中以-t 代替t ，可求得f(2t),表明f(-2t)的波形 以t ＝0的纵轴为中心线对褶，注意()t δ是偶数，故112()2()22t t δδ--=+(2)(2)f t f t -−−−→反褶由（3）尺度变换：以12t 代替f(2t)中的t ，所得的f(t)波形将是f(2t)波形在时间轴上扩展两倍。
4. 求序列{}12[]1,2,1,0,1,2[][1cos()][]2f n n f n n u n π===+和的卷积和。
解：{}112222[]1,2,1[]2[1][2][]*[][]2[1][2]f n n n n f n f n f n f n f n δδδ==+-+-=+-+-5. 试求下列卷积。
信号与系统试题信号与系统试题附答案
信号与系统试题信号与系统试题附答案信号与系统试题信号与系统试题附答案信号与系统复习参考练习题一、单项选择题：14、已知连续时间信号f (t ) =sin 50(t -2)100(t -2) , 则信号f (t ) ·cos 104t 所占有的频带宽度为（）A ．400rad ／sB 。
200 rad／sC 。
100 rad／sD 。
50 rad／s15、已知信号f (t ) 如下图（a ）所示，其反转右移的信号f 1(t) 是（）16、已知信号f 1(t ) 如下图所示，其表达式是（）A 、ε（t ）＋2ε(t－2) －ε(t－3)B 、ε(t－1) ＋ε(t－2) －2ε(t－3)C 、ε(t)＋ε(t－2) －ε(t－3)D 、ε(t－1) ＋ε(t－2) －ε(t－3)17、如图所示：f （t ）为原始信号，f 1(t)为变换信号，则f 1(t)的表达式是（）A 、f(－t+1)B 、f(t+1)C 、f(－2t+1)D 、f(－t/2+1)18、若系统的冲激响应为h(t),输入信号为f(t),系统的零状态响应是（）19。
信号f (t ) =2cos π4(t -2) +3sin π4(t +2) 与冲激函数δ(t -2) 之积为（）A 、2B 、2δ(t -2)C 、3δ(t -2)D 、5δ(t -2)20．已知LTI 系统的系统函数H (s ) =s +1, Re[s ]＞－2，则该系统是（） s 2+5s +6A 、因果不稳定系统B 、非因果稳定系统C 、因果稳定系统D 、非因果不稳定系统21、线性时不变系统的冲激响应曲线如图所示，该系统微分方程的特征根是（）A 、常数B 、实数C 、复数 D、实数+复数22、线性时不变系统零状态响应曲线如图所示，则系统的输入应当是（）A 、阶跃信号B 、正弦信号C 、冲激信号 D、斜升信号∞23. 积分-∞?f (t ) δ(t ) dt 的结果为( )A f (0)B f (t ) C. f (t ) δ(t ) D. f (0) δ(t )24. 卷积δ(t ) *f (t ) *δ(t ) 的结果为( )A. δ(t )B. δ(2t )C. f (t )D. f (2t )25. 零输入响应是( )A. 全部自由响应B. 部分自由响应C. 部分零状态响应D. 全响应与强迫响应之差 2A 、eB 、eC 、eD 、127. 信号〔ε(t)－ε(t－2) 〕的拉氏变换的收敛域为 ( )A.Re[s]>0B.Re[s]>2C. 全S 平面D. 不存在28．已知连续系统二阶微分方程的零输入响应y zi (t ) 的形式为Ae -t -13-3+Be -2t ，则其2个特征根为( )A 。
信号与系统考试题及答案
信号与系统考试题及答案第一题：问题描述：什么是信号与系统？答案：信号与系统是电子工程和通信工程中重要的基础学科。
信号是信息的传递载体，可以是电流、电压、声音、图像等形式。
系统是对信号进行处理、传输和控制的装置或网络。
信号与系统的研究内容包括信号的产生、变换、传输、处理和控制等。
第二题：问题描述：信号的分类有哪些？答案：信号可以根据多种特征进行分类。
按照时间域和频率域可以将信号分为连续时间信号和离散时间信号；按照信号的能量和功率可以分为能量信号和功率信号；按照信号的周期性可以分为周期信号和非周期信号；按照信号的波形可以分为正弦信号、方波信号、脉冲信号等。
第三题：问题描述：什么是线性时不变系统？答案：线性时不变系统是信号与系统领域中重要的概念。
线性表示系统满足叠加性原理，即输入信号的线性组合经过系统后，输出信号也是输入信号的线性组合。
时不变表示系统的性质不随时间变化而改变。
线性时不变系统具有许多重要的性质和特点，可以通过线性时不变系统对信号进行处理和分析。
第四题：问题描述：系统的冲激响应有什么作用？答案：系统的冲激响应是描述系统特性的重要参数。
当输入信号为单位冲激函数时，系统的输出即为系统的冲激响应。
通过分析冲激响应可以得到系统的频率响应、幅频特性、相频特性等，从而对系统的性能进行评估和优化。
冲激响应还可以用于系统的卷积运算和信号的滤波等应用。
第五题：问题描述：如何对信号进行采样？答案：信号采样是将连续时间信号转换为离散时间信号的过程。
常用的采样方法包括周期采样和非周期采样。
周期采样是将连续时间信号按照一定的时间间隔进行等间隔采样；非周期采样是在信号上选取一系列采样点，采样点之间的时间间隔可以不相等。
采样频率和采样定理是采样过程中需要考虑的重要因素。
第六题：问题描述：什么是离散傅里叶变换（DFT）？答案：离散傅里叶变换是对离散时间信号进行频域分析的重要工具。
通过计算离散傅里叶变换可以将离散时间信号转换为复数序列，该复数序列包含了信号的频率成分和相位信息。
信号与系统1-2单元练习题
一、填空题1、如图1所示信号，则信号f(t)的数学表示式为。
2、设：两信号f1(t)和f2(t)如图2所示，则：f1(t)与f2(t)间变换关系为。
3、写出下列表达式的值：（3）f(t)*δ(t) = (4）f(t)*δ(t-t0) =4、写出卷积的定义式。
5、周期是6、=二．综合题1．判断信号是否为周期信号，并计算它的能量或平均功率。
2．已知信号f(t)波形如图所示，试绘出下列函数的波形。
（1）（2）；3．已知描述系统的传输算子为：，求系统的冲激响应。
4．信号f1(t), f2(t)波形如图所示，（1）写出信号f1(t), f2(t)的数学表达式；（2）利用卷积的微分积分性质求卷积f(t)=f1(t)*f2(t)；（3）利用图解法求卷积f(t)=f1(t)*f2(t)并绘出所得结果的波形；f(0)=？5.已知系统的微分方程为，若系统的初始条件y(0-)=y’(0-)=1，输入f(t)=e-3tε(t)，求系统的零输入响应y zi(t)，零状态响应y zs(t)和完全响应y(t)。
6、右图所示电路，235553)(223++--+=ppppppH)(3)('2)(2)('3)("tftftytyty+=++(1)()()(2)()()f t t f t t tδδ=-=。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第一章绪论1、选择题1.1、f （5-2t ）是如下运算的结果 CA 、 f （-2t ）右移5B 、 f （-2t ）左移5C 、 f （-2t ）右移25 D 、 f （-2t ）左移251.2、f （t 0-a t ）是如下运算的结果 C 。
A 、f （-a t ）右移t 0；B 、f （-a t ）左移t 0 ；C 、f （-a t ）右移a t 0；D 、f （-a t ）左移at0 1.3、已知 系统的激励e(t)与响应r(t)的关系为：)()()(t u t e t r = 则该系统为 B 。
A 、线性时不变系统；B 、线性时变系统；C 、非线性时不变系统；D 、非线性时变系统 1.4、已知 系统的激励e(t)与响应r(t)的关系为：)()(2t e t r = 则该系统为 C 。
A 、线性时不变系统 B 、线性时变系统 C 、非线性时不变系统 D 、非线性时变系统 1.5、已知 系统的激励e(t)与响应r(t)的关系为：)1()(t e t r -= 则该系统为 B 。
A 、线性时不变系统B 、线性时变系统C 、非线性时不变系统D 、非线性时变系统1.6、已知 系统的激励e(t)与响应r(t)的关系为：)2()(t e t r = 则该系统为 B A 、线性时不变系统 B 、线性时变系统 C 、非线性时不变系统 D 、非线性时变系统 1.7.信号)34cos(3)(π+=t t x 的周期为 C 。
A 、π2 B 、π C 、2π D 、π21.8、信号)30cos()10cos(2)(t t t f -=的周期为： B 。
A 、15π B 、5π C 、π D 、10π1.9、dt t t )2(2cos 33+⎰-δπ等于 B 。
A.0 B.-1 C.2 D.-21.10、 若)(t x 是己录制声音的磁带,则下列表述错误的是： BA. )(t x -表示将此磁带倒转播放产生的信号B. )2(t x 表示将此磁带放音速度降低一半播放C. )(0t t x -表示将此磁带延迟0t 时间播放D. )(2t x 表示将磁带的音量放大一倍播放 1.11.=⋅)]([cos t u t dtdA A ．)()(sin t t u t δ+⋅- B. t sin - C. )(t δ D.t cos1.12．信号t t t x o 2cos 4)304cos(3)(++=的周期为 B 。
A π2 B π C π5.0 D π/2 1.13．如果a>0，b>0，则f (b-a t )是如下运算的结果 C 。
A f (-a t )右移bB f (-a t )左移bC f (-a t )右移b/aD f (-a t )左移b/a 1.14．线性时不变系统的响应，下列说法错误的是 C 。
A 零状态响应是线性时不变的 B 零输入响应是线性时不变的 C 全响应是线性时不变的 D 强迫响应是线性时不变的 2、填空题与判断题2.1、=+t t 0cos )1(ωδ0cos )1(ωδ+t =⋅t t cos )(δ()t δ =--)2()cos 1(πδt t ()2t πδ- =⋅-at e t )(δ()t δ=-⋅)(cos )(0τωδt t 0cos()()t ωτδ⎰∞∞--=dt e t at )(δ 1=--⎰∞∞-dt t t )2()cos 1(πδ 1⎰+∞∞-=⋅tdt t cos )(δ 1⎰+∞∞-=tdt t 0cos )(ωδ 1 ⎰∞-=td ττωτδ0cos )(()u t⎰+∞∞-=+tdt t 0cos )1(ωδ0cos ω⎰∞-=+td ττωτδ0cos )1(0cos (1)u t ω+⎰∞--=td e ττδτ)(()u t⎰∞∞--=--dt t et t)1(][22δ21e --⎰∞∞--=dt e t at )(δ 1 ，2.2、任一信号f(t)与单位冲激信号)(t δ的关系为 ⎰∞∞--=dx t x x f t f )()()(δ， 单位阶跃信号u(t)与单位冲激信号)(t δ的关系为u(t)=⎰∞-td ττδ)(。
2.3、 任何信号都可以分解为偶分量与奇分量之和。
（√） 2.4、偶函数加上直流后仍为偶函数。
（√） 2.5、两个周期信号之和一定是周期信号 （×） 2.6．)cos()3sin()(t t t y π+=是周期信号。
(×) 2.7．冲激响应为)2()(+=t t h δ的系统是线性时不变因果系统。
（×）3、作图题3.1、绘出函数)]3()2([)(---=t u t u t t f 的波形。
2313.2、绘出函数)1()1()(--=t u t t f 的波形。
1-13.3、绘出函数)1()(-=t tu t f 的波形。
123.4、画出微分方程)()()()()(10012t e dtdb t e b t r a t r dt d a t r dt d +=++的仿真框图。
b3.5、画出系统)()()()(2122t e t r a t r dt da t r dtd =++仿真框图。
3.6．画出微分方程)(6)(5)(4)(3)(2)(2233t e t e dtdt r t r dt d t r dt d t r dt d +=+++的仿真框图。
解：引入辅助函数)(t q ，得：)()(4)(3)(2)(2233t e t q t q dtdt q dt d t q dt d =+++)(6)(5)(t q t q dtdt r += ⎰⎰∑∑⎰e(t)r(t)''q 'q '''q -3-465-23.7．画出信号f (t )= 0.5(t+1)[u(t+1)-u(t-1)]的波形以及偶分量f e (t )与奇分量f o (t)波形。
f （t ）-111 t3.8．画出信号f (t )= 0.25(t+2)[u(t+2)-u(t-2)]的波形以及偶分量f e (t )与奇分量f o (t)波形。
t2-2 1f （t ）第二章连续时间系统的时域分析1、选择题2．若系统的起始状态为0，在e(t)的激励下，所得的响应为 D 。
A 强迫响应 B 稳态响应 C 暂态响应 D 零状态响应 3．线性系统响应满足以下规律 a 。
A)、若起始状态为零，则零输入响应为零。
B)、若起始状态为零，则零状态响应为零。
C)、若系统的零状态响应为零，则强迫响应也为零。
D)、若系统的起始状态为零，则系统的自由响应为零； 4．线性时不变系统输出中的自由响应的形式由 A 决定。
A 系统函数极点的位置B 激励信号的形式C 系统起始状态D 以上均不对。
5．线性时不变系统输出中的自由响应的形式由 B 决定。
A 激励信号B 齐次微分方程的特征根C 系统起始状态D 以上均不对 6．线性时不变稳定系统的自由响应是 C 。
A 零状态响应B 零输入响应C 瞬态响应D 稳态响应 7．对线性时不变系统的响应，下列说法错误的是 B 。
A 零状态响应是线性的B 全响应是线性的C 零输入响应是线性的D 零输入响应是自由响应一部分8．线性时不变系统的响应，下列说法错误的是 C 。
A 零状态响应是线性时不变的B 零输入响应是线性时不变的C 全响应是线性时不变的D 强迫响应是线性时不变的 2、判断题2.1线性常系数微分方程表示的系统，方程的齐次解称之自由响应，特解称之强迫响应。
（√）2.2．不同的系统具有不同的数学模型。
(×) 2.3若系统起始状态为零，则系统的零状态响应就是系统的强迫响应 （ × ） 2.4 零输入响应就是由输入信号产生的响应。
（ × ） 2.5零状态响应是自由响应的一部分。
（×） 2.6．零输入响应称之为自由响应，零状态响应称之为强迫响应。
(×) 2.7当激励为冲激信号时，系统的全响应就是冲激响应。
（×） 2.8．当激励为阶跃信号时，系统的全响应就是阶跃响应。
(×) 2.9．已知f 1(t)=u(t+1)-u(t-1)，f 2(t)=u(t-1)-u(t-2)，则f 1(t)*f 2(t)的非零值区间为(0,3)。
( √ ) 2.10．若f(t)=f 1(t)*f 2(t)，则有f(t)=f 1(2t)*f 2(2t)。
(×) 2.11．若)(*)()(t h t e t r =，则有)(*)()(000t t h t t e t t r --=-。
(×) 2.12．线性时不变系统的全响应是线性的。
(× ) 2.14．线性常系数微分方程表示的系统，方程的齐次解称为自由响应。
(√)2.15．线性时不变系统的响应具有可分解性。
(√) 2.16．系统的零输入响应等于该系统的自由响应。
(×) 2.17．因果系统没有输入就没有输出，因而因果系统的零输入响应为零。
(×) 2.18．线性时不变系统的零状态响应是线性时不变的。
(√) 2.19．卷积的方法只适用于线性时不变系统的分析。
(√) 2.20 如果)(1t f 和)(2t f 均为奇函数，则)(*)(21t f t f 为偶函数。
(√)3、填空题3.1已知一连续LTI 系统的单位阶跃响应为)()(3t u e t g t -=，则该系统的单位冲激响应为：h(t)=)(3)(3t u e t t --δ。
3.2=)](*)([t u t u dt d ()u t =*)]()([t tu t u dt d ()tu t =⎥⎦⎤⎢⎣⎡⎰∞-t d u t u dt d λλ)(*)(()tu t=-)](*)([t u t u e dtd t()t e u t - =-)(cos *)(0τωδt t 0cos ()t ωτ- =-t e t *)(δt e - =+t t 0cos *)1(ωδ0cos (1)t ω+3.3 一起始储能为零的系统，当输入为 u (t)时，系统响应为3()t e u t -，则当输入为δ（t ）时，系统的响应为3()3()t t e u t δ--。
已知系统的单位阶跃响应为)1(10)()1(-=--t u e t g t ，则激励)1(2)(-=t t f δ的零状态响应=)(t rz s )3(10)3(20)3(-----t u e t t δ_。
4计算题例2-8 已知系统微分方程为)(3)(3)(t e t r t r dt d =+，若起始状态为23)0(=-r ，激励信号)()(t u t e =，求系统的自由响应和强迫响应、零输入响应和零状态响应。