《平行线的特征》课件
平行线的特征数学公开课课件

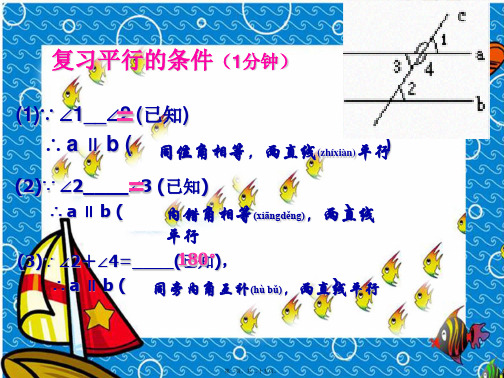
同位角相等,两直线平行 如图, 直线a、b被直线c所截,当 内错角相等,两直线平行 满足_______条件时, a∥b。 c
由 角 定 线
同旁内角互补,两直线平行
1
由“角”的数量关系(相等或互 补) 你能说出 3
a
角的关系
几个? 定“线”的位置关系(平行)4 2
平行关系
b
如图,直线a,b被c所截且a∥b
问题1:找出图中的同位角,a 并猜测它们有何关系?你能想办 b 法验证你的想法吗? 同位角相等 问题2:利用问题1的结论, 你能否得出具有其它位置关系的 角之间的大小? 内错角相等 同旁内角互补
c 1 3
2 1 4 5 7 6 8
由 此 你 想 到 了 什 么 ?
平行线的特征
两条平行直线被第三条直线所截,同位角相等,内 错角相等,同旁内角互补。
同理可得∠C= 180°-∠D=70 °
B
C 桃子
草莓
西瓜
香蕉
杨梅
苹果
桔子
பைடு நூலகம்梨子
桔子题:
如图:在墙面上安装一管道需经两次拐弯,拐 弯后的管道与拐弯前的管道平行。若第一个弯 道处∠B=142°,那么第二个弯道处∠C为多少 度?为什么? B A 解:∵AB∥CD ∴∠C=∠B=142° C D (两直线平行,内错角相等) 苹果 香蕉
苹果 草莓
梨子 桃子
香蕉
桔子
西瓜
杨梅
苹果题:
如图,要在一座房子的两侧铺设 平行管道,如果房子一侧铺设的 角度为120° ,那么,为了使管 道对接,另一侧应以什么角度铺 设?为什么? 解:60° ;两直线平行,同旁内 角互补.
120°
苹果 香蕉
平行线的特征

平行线的特征平行线是几何学中重要的概念之一。
在二维欧几里得空间中,如果两条直线永远不相交,那么它们被称为平行线。
本文将介绍平行线的特征及相关的性质。
1. 平行线的定义给定二维欧几里得空间中的两条直线L1和L2,如果它们满足以下条件,则称L1和L2为平行线:•L1和L2不相交。
•L1和L2存在公共的平面。
2. 平行线的性质2.1 平行线的判定已知两条直线L1和L2,判断它们是否平行的方法有多种,这里介绍两种常见的判定方法:方法一:使用线性方程判断如果直线L1的斜率等于直线L2的斜率,那么L1和L2是平行线。
方法二:使用向量判断设直线L1上一点为点A,直线L2上一点为点B。
如果向量AB与L1的方向向量平行,则L1和L2是平行线。
2.2 平行线与夹角平行线之间不存在交点,因此它们之间的夹角为0度。
即使将两条平行线延长,无论延长多远,它们之间的夹角始终保持不变。
2.3 平行线与平行四边形平行线之间的性质与平行四边形的性质密切相关。
平行四边形是有四条边都平行的四边形。
性质一:对边平行平行四边形的对边是平行的。
即如果ABCD是一个平行四边形,那么线段AB和线段CD是平行线,线段AC和线段BD是平行线。
性质二:邻边互补平行四边形的邻边是互补的。
即如果ABCD是一个平行四边形,那么角A和角C是互补角,角B和角D是互补角。
性质三:对角线等长平行四边形的对角线等长。
即如果ABCD是一个平行四边形,那么线段AC和线段BD的长度相等。
2.4 平行线与转角当两条直线相交时,会形成四个角。
其中,相邻的两个角称为相邻角,非相邻的两个角称为转角。
如果两条直线分别与一条横穿它们的其他线相交,并且转角为等量,则这两条直线是平行线。
3. 平行线的应用平行线在几何学中有广泛的应用,下面简要介绍其中的几个应用领域。
3.1 地理学在地理学中,平行线常用于地图投影中的经纬度线。
地球上的纬线是平行于赤道的圆环状线,而经线是与纬线相交在地球上的两极的直线。
人教版小学数学四年级上册《平行与垂直》课件(共15张PPT)

汉字中的垂直和平行现象。
直王
找一找下面图形各有几组平行线和垂线?
_2_组平行线 _4_组垂线
_2_组平行线 _0_组垂线
_1_组平行线 _2_组垂线
摆一摆
1、先任意摆第一根小棒,然后再拿两根小 棒,把它们摆成和第一根小棒平行。
2、先任意摆第一根小棒,然后再拿两根小 棒,把它们摆成和第一根小棒垂直。
平行与垂直
一、直线有哪些特征?
二、猜一猜 下列哪些点在直线 a 上
B
aE
A
C D
①
②
①
①
②
③
④
⑤
⑥
⑦
a b
①
⑦
平 行 线(互相平行)
a
b
在同一个平面内不相交的两条直线叫做
平行线,也可以说这两条直线互相平行。
记作: a ∥b
c∥d
符号“∥”表示平行
相交
②
④ ⑤
③ ⑥
a
垂足
垂线
下课! 同学们再见!
授课老师: 时间:2024年9月1日
b
垂线
如果两条直线相交成直角,
就说这两条直线互相垂直。
记作:
a ⊥b c ⊥ d
符号“⊥”表示垂直
判断下面两条线是否平行。
(√ )
( × ) ( ×)
(× ) (√ )
( ×) (×)
通过验证,看哪组直线是互相垂直的,在序号上打上勾。
1
2
3
4
5
数学运算符号中的垂直和平行现象。
+=
英文字母中的平行和垂直现象。
平行线的性质 课件(共22张PPT)

3
∴∠2=∠3(两直线平行,同位角相等),
∵∠1=∠3(对顶角相等),
∴∠1=∠2(等量代换).
你发现了什么?
两条平行直线被第三条直线所截,内错角相等. 简写成:两直线平行,内错角相等. 表达方式:如图,
∵a∥b(已知),
∴∠1=∠2(两直线平行,内错角相等).
如图,直线a∥b,直线a、b被直线c所截
试一试
翻开你的数学练习横格本,每一页上都有许多如图所示的互 相平行的横线条,随意画一条斜线与这些横线条相交, 找出其中 任意一对同位角.观察或用量角器度量这对同位角,你有什么发现?
∠1=∠2
那么,一般情况下,如图,如果直线a与直线b平行,直线l与 直线a、b分别交于点O和点P,其中的同位角∠1与∠2也必定相等吗?
A.65°
B.55°
C.45°
D.35°
课堂小结
知识点 平行线的性质
1.两直线平行,同位角 相等 . 2.两直线平行,内错角 相等 . 3.两直线平行,同旁内角 互补 .
已知
同位角相等 内错角相等 同旁内角互补
得到
判定 性质
得到 两直线平行
已知
(2)从∠1=110o可以知道 ∠3是多少度?为什么?
(3)从 ∠1=110 o可以知道∠4 是多少度?为什么?B
D
解:(1)∠2=110o 理由:两直线平行,内错角相等;
(2)∠3=110o 理由:两直线平行,同位角相等;
(3)∠4=70o 理由:两直线平行,同旁内角互补.
C 2E 43
2.如图,直线a∥b,∠1=50°,∠2=40°,则∠3的度数为 ( B )
例3 将如左图所示的方格图中的图形向右平行移动4格,再向上 平行移动3格,画出平行移动后的图形.
七年级数学下册 2.3.1 平行线的特征课件
(2)图中有几对内错角?它们的大小有什么
关系?为什么 ? shén me)
(shén me)
c
2对
∠3与∠5 ∠4与∠ 6
a2 1
34
b
6
8
∵∠4=∠2,∠2=∠6,
∴ ∠4=∠6。
同理: ∠3=∠5
第五页,共二十五页。
(3)图中有几对同旁内角?它们(tā men)的大小
有什么关系?为什么?
c
2对
道处∠B=142o,
那么第二个弯道处∠C 为多少度?为什么?
A
B
C
解:由平行线的性质(xìngzhì)得:∠B=∠C=142°.
第二十页,共二十五页。
变式:一学员在广场上练习驾驶汽车,两次拐 弯后,行驶的方向(fāngxiàng)与原来的方向(fāngxiàng)
相同,这两次拐弯的角度可能A是( )
2 、如 1 图 2 , 3 1 , 3 , 5 那 4 _ 135么 _ 0 __
1
a
3
24bຫໍສະໝຸດ 第十二页,共二十五页。3、如图:AB,CD被EF所截,AB∥CD
若∠1=1200,则∠2= _1_20o
( 两直线(zhíxiàn)平行,内错角相等)
∠3= 180-o ∠1 =__60_o
AC
如图:AB,CD被EF所截,AB∥CD。4.(1)如果(rúguǒ)AD//BC,根据。110°
)。3、
Image
12/10/2021
第二十五页,共二十五页。
115° 110°
B
C
解: ∵AD//BC ,∠A=115° ∴∠A+∠B=180 °(两直线(zhíxiàn)平行,同旁内角互补) ∴∠B=180°- ∠A=65°
《平行线的特征》课件2(34张PPT)(冀教版七年级下)

易将“平行线的性质定理” 与“平行线的判定定理”混
淆。
区分平行线的性质定理与判定定理 。
返回
我校学生是大多来自农村,学习一般刻苦用功, 但相对沉闷呆板一些。他们往往习惯于被动听讲做 笔记。我校学生一般难以在家上网,接触的新奇教 学资源很少。故对“远教”、“网络”等心甚向往, 充满好奇,渴望接受“这种新形式的课堂教学。
从以上图形的变化中,你发现了什么规律吗?
A
B
1
C2
3
(图甲) D
E
A1
B
A 1
2
(图乙)
3
D
A
21
2
(图丙) 3 4
D
3 (图丁)
E D4
B E B
E
训练发散思维,培养创新意识。初步 接触了辅助线的添加,激发自主探索 的兴趣,找寻规律以及培养联想的能 力!
学有余力的学生的能 力得以进一步提高, 不同的人在数学中得 到不同的发展!
角 ∠1 ∠2 ∠3 ∠4
21
34
l1
65
78
l2
度数
l3
角 ∠5 ∠6 ∠7 ∠8
度数
各对同位角、内错角、同旁内角的度数之间有什么
关系?大胆的去猜想,试着说一说!
如图,请选取条格纸上的任意两条
平行直线l1、l2,画一条直线l3与这两条 平行线相交,标出这些角。
21
34
l1
度量这些角,把结果填入下表:
平行线的性质:
21 34 65 78
定理1.∵ l1∥l2 ,
l1
∴∠1=∠5 .(两直线平行,同位角相等)
l2
定理2.∵ l1∥l2 , ∴∠3=∠5 .(两直线平行,内错角相等)
(小学课件)认识平行线

目录
• 平行线基本概念 • 平行线判定方法 • 平行线性质探究 • 平行线在几何图形中应用 • 平行线与相交线关系 • 课堂小结与拓展延伸
01
平行线基本概念
定义与性质
定义
在同一平面内,不相交的两条直线 叫做平行线。
性质
平行线具有传递性,即如果直线a 平行于直线b,直线b平行于直线c, 那么直线a也平行于直线c。
平行四边形的面积可以通过其一组对边和它们之间的高来计算,即面积=底×高,其 中底和高都是平行线。
梯形中平行线应用
梯形有一组对边平行,这是梯形的基 本特征,也是平行线在梯形中的最直 接应用。
在等腰梯形中,两腰相等且与底边平 行,这也是平行线在等腰梯形中的一 个重要应用。
梯形的面积可以通过其上下底和它们 之间的高来计算,即面积=(上底+下 底)×高÷2,其中上下底和高都与平行 线有关。
挑战题
已知三条直线a、b、c在同一平面内,且a与b平行,b与c平行。那么,a与c是 否一定平行?请说明理由。
THANKS
其他几何图形中平行线应用
在长方形中,对边平行且相等,相邻边互相垂直。这些性质都与平行线有关。
在正方形中,所有边都相等且互相平行,对角线互相平分且垂直。这些性质也都与平行线有 关。
在一些复杂的几何图形中,如多边形、圆等,也可能存在平行线的应用。例如,在多边形中, 如果有一组对边平行,则该多边形可以被划分成若干个平行四边形或梯形进行计算。在圆中, 平行线可以用于描述圆的切线、割线等性质。
艺术创作
在绘画、雕塑和其他艺术形式中,艺术家经常运用平行线和相交线来创 造视觉效果和表达空间关系。例如,在透视画中,平行线会汇聚到一个 或多个消失点,从而营造出三维空间的错觉。
平行线的特征

A
∠1=∠2 , ∠3 =∠4 D C
F
1
2
3
4
B
E
(1)∠1和 (1)∠1和∠3的大小关系? ∠2和∠4呢? 的大小关系? (2)反射光线BD、EF平行吗? (2)反射光线BD、EF平行吗? 反射光线BD 平行吗
互相交流这节课 你学到了什么…… 你学到了什么
性质) 二平行直线的特征(性质)
两条平行直线被第三条直线直线所截, 两条平行直线被第三条直线直线所截, 同位角相等,内错角相等,同旁内角互补。 同位角相等,内错角相等,同旁内角互补。
简记为: 简记为: 重点内容
两直线平行,同位角相等。 两直线平行,同位角相等。 两直线平行,内错角相等。 两直线平行,内错角相等。 两直线平行,同旁内角互补。 两直线平行,同旁内角互补。
三星堆遗址
位于中国四川省广汉市南兴镇北的三 星堆遗址,属于古蜀国文明。 星堆遗址,属于古蜀国文明。遗址分布范 围达12平方公里,距今4800年至2800 12平方公里 4800年至2800年 围达12平方公里,距今4800年至2800年, 延续时间近2000 2000年 延续时间近2000年。 出土了各种文物:金器、玉器、石器、 出土了各种文物:金器、玉器、石器、 陶器、青铜器...等数千件。 ...等数千件 陶器、青铜器...等数千件。其中有享誉 中外的金杖、金面罩、青铜人像、头像、 中外的金杖、金面罩、青铜人像、头像、 人立像、画具等精品文物1000多件。 1000多件 人立像、画具等精品文物1000多件。
如图, 如图,是举世闻名的三星堆考古中发掘出 的一个梯形残缺玉片, 的一个梯形残缺玉片,工作人员从玉片上已经 量得∠A=115° D=100° 量得∠A=115°,∠D=100°。已知梯形的两底 AD//BC, AD//BC,请你求出另外两个角的度数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a 2 1 (1)测量同位角∠1和∠5的 测量同位角∠ 4 3 大小,它们有什么关系? 大小,它们有什么关系? 相等: 1=∠ 相等:∠1=∠5。 b 6 图中还有其它同位角吗? 图中还有其它同位角吗? 还有三对 8 它们的大小有什么关系? 同位角。 它们的大小有什么关系? 同位角。 2=∠ 3=∠ 4=∠ ∠2=∠6、∠3=∠7、 ∠4=∠8; 图中有几对内错角?它们的大小有什么关系?为什么? (2)图中有几对内错角?它们的大小有什么关系?为什么? 4=∠ 有两对内错角: 3=∠ 有两对内错角: 3=∠5、 ∠4=∠6; ∠ ∵∠4=∠ 2=∠ 4=∠ 同理: 3=∠ ∵∠4=∠2,∠2=∠6, ∴ ∠4=∠6。 同理: ∠3=∠5
思考: 思考:
1、判定定理与性质定理的 条件与结论有什么关系? 互换。 条件与结论有什么关系? 互换。 使用判定定理时是 2、使用判定定理时是 已知 角的相等或互补 ,说明 二直线平行 ; 使用性质定理时是 使用性质定理时是 已知 二直线平行 ,说明 角的相等或互补 。
做一做 做一做
如图:一束平行光线AB和DE射向一个水平镜面后 AB和 如图:一束平行光线AB DE射向一个水平镜面后 ∠1=∠2 ∠3=∠4 被反射, 此时∠ 被反射, 此时∠1=∠2 , ∠3=∠4 。 (1 )∠1,∠3的大小有什么关系?∠2与∠4呢? 的大小有什么关系?∠2与 D C F 你知道理由吗? 你知道理由吗? A 两直线平行
本节课初步学习了如何混合应用平行线的判定与 性质进行计算和说理(证明) 性质进行计算和说理(证明). 要懂得几何中的计算往往要说理, 要懂得几何中的计算往往要说理,要熟悉几何里 计算题的格式; 计算题的格式; 还要懂得几何中常常可以由“已知” 还要懂得几何中常常可以由“已知”的条件推得 一系列新的结论,在这个过程中,要能清楚每一步推 一系列新的结论,在这个过程中, 理的依据,并初步了解解答这类问题的格式和要求. 理的依据,并初步了解解答这类问题的格式和要求.
五、作业
作业
教材p.55 习题2.4 教材p.55 习题2.4 第 1、2 、3 题。
两条平行直线被第三条直线直线所截, 两条平行直线被第三条直线直线所截, 同位角相等,内错角相等,同旁内角互补。 同位角相等,内错角相等,同旁内角互补。
简记为: 简记为:
两直线平行,同位角相等。 两直线平行,同位角相等。 两直线平行,内错角相等。 两直线平行,内错角相等。 两直线平行,同旁内角互补。 两直线平行,同旁内角互补。
做一做
再找一组平行线,说明你的理由。 再找一组平行线,说明你的理由。 做一做
B C D
如图2 如图2—8,三个相 同的三角尺拼成一个图 形,请找出图中的一组 平行线,并说明你的理由。 平行线,并说明你的理由。
A
AC与DE是平行的。 AC与DE是平行的 是平行的。
因为∠EDC与 因为∠EDC与∠ACB 是同位角, 是同位角, 而且又相等。 而且又相等。
② 不共顶点的角: 不共顶点的角:
回顾与思考
回顾 & 思考 ☞
二、判断两直线平行
l a b
同位角相等,两直线平行 两直线平行. 两直线平行. 内错角 相等 ,两直线平行
两直线平行. 同旁内角 互补,两直线平行
考察两直线是否有平行关系, 考察两直线是否有平行关系,我们往往用第三直线 作为沟通这两直线的桥梁—— 作为沟通这两直线的桥梁—— 考察(被第三直线截成的八个角中) 考察(被第三直线截成的八个角中)不共顶点的两个 角, 是否满足某种数量关系 . 抓住被考察的两直线、寻找第三线; 抓住被考察的两直线、寻找第三线; 找出不共顶点的两个角及其数量关系, 找出不共顶点的两个角及其数量关系, 是判定两直线平行的必要途径。 是判定两直线平行的必要途径。
本节课学习了平行线的三个性质,总结了平行线的判定 本节课学习了平行线的三个性质, 质的区别. 与性 质的区别. 这里的关键之一是要搞清“已知”了什么, 这里的关键之一是要搞清“已知”了什么,得到的是什么样 结论” 这样才能确保正确的应用,不发生错误. 的“结论”.这样才能确保正确的应用,不发生错误.
3
回顾 & 思考 ☞ 一、直线交成的角 回顾与思考一 回顾与思考
2 两直线相交形成 4 个角,从数量关系 个角, 1 上讲, 上讲, ∠1与∠2形成 互补的 角, 3 从位置关系上讲, 从位置关系上讲, ∠2与∠4形成 对顶 角; 4 对顶的两角 相等 。
在“三线八角”中, 三线八角” C 7 4 A 8 F 2 6 3 E 1 5
平行: 平行:
∵ ∠2=∠4 2=∠
你知道理由吗? ∴ BC∥EF 。 你知道理由吗? BC∥
随堂练习 三、随堂练习
p 60
1、如图所示,AB∥CD,AC∥BD。 如图所示,AB∥CD,AC∥BD。 分别找出与∠ 相等或互补的角。 分别找出与∠1相等或互补的角。
9 12
解: ,与∠1相等的角有: 如图, 相等的角有: 如图
∠1与∠7形成 对顶 角, ∠5与∠7形成 互为补 角, (1) 同位角有 4 对: 同位角有 ∠1和∠2, D ∠5和∠6, ∠7和∠8. ∠3和∠4, 内错角有 B (2) 内错角有 2 对: ∠7和∠2, ∠5和∠4. (3) 同旁内角有 2 对: 同旁内角有 ∠7和∠4, ∠5和∠2
① 共顶点的角: 共顶点的角:
两类定理的比较
两条平行直线被第三条直线直线所截, 两条平行直线被第三条直线直线所截, 判定定理
条件 结论
性质定理
条件 结论
同位角相等, 两直线平行,同位角相等。 同位角相等, 两直线平行 两直线平行,同位角相等。 内错角相等, 两直线平行,内错角相等。 内错角相等, 两直线平行 两直线平行,内错角相等。 同旁内角互补, 两直线平行, 同旁内角互补,两直线平行 两直线平行,同旁内角互补
∠3, ∠3, ∠5, ∠7, ∠9, 11, 13, 15; ∠11, ∠13, ∠15; 与∠1互补的角有: 互补的角有: ∠ 2, ∠ 4, ∠ 6, ∠ 8, 10, 12, 14, ∠10, ∠12, ∠14, ∠16 ;
16
B
13
10 5 8 2 7
A
15 4
14 1
D
6
C
3
四、本节课你的收获是什么? 本节课你的收获是什么?
(3)图中有几对同旁内角?它们的大小有什么关系?为什么? 图中有几对同旁内角?它们的大小有什么关系?为什么? 有两对同旁内角: 4+∠5=180° 有两对同旁内角: ∠4+∠5=180°, ∠3+∠6=180°。 3+∠6=180°
从中,你发现了什么规律吗? 从中,你发现了什么规律吗?
二平行直线的特征 性质) (性质)
相等:∠3=∠4; 相等: 3=∠4; ∠2 =∠4 。
同位角相等 同位角相等 两直线平行
1 B
2
3 E
4
∵AB∥DE ∴∠1=∠3。 AB∥ ∴∠1=∠ 2=∠ 1=∠ 3=∠ 又 ∠1=∠2 ,∠3=∠4 ∴ ∠2=∠4。 (2 )反射光线BC与EF也平行吗? 反射光线BC EF也平行吗 BC与 也平行吗?
他选谁为第三线? AC 他选谁为第三线? 用的是什么角? 内错角。 用的是什么角? 内错角。 你知道这一步的理由吗? 你知道这一步的理由吗? 内错角相等, 内错角相等, 两直线平行。 两直线平行。
新知探索:
二直线平行后到什么? 二直线平行后得到什么?
c
如图:直线 a 与b 直线平行。 直线平行。 如图:
图2—8 我是这样想的: 我是这样想的: BCA=∠ ∠BCA=∠EAC, BD∥AE。 BD∥
E
你看得懂她的意识吗? 你看得懂她的意识吗? 她选的第三线是谁? 她选的第三线是谁?
选BD作第三线, BD作第三线 作第三线, 用三角尺的60 60° 用三角尺的60°角相等 说明“同位角相等” 说明“同位角相等”, 同位角相等两直线平行” 用“同位角相等两直线平行” BD∥AE。 来说明 BD∥AE。
