横向稳定杆的设计
螺旋弹簧横向稳定杆减振器设计指南

减振器储油缸直径 Dc = (1.35 ~ 1.57)D ,工作缸与储油缸壁厚一般取 1.5~2.0 mm 。
选择减振器尺寸时主要考虑一下两点:在工作速度范围内油液压力适当,能够得到稳定的阻力值,
8
容易保证油封的可靠性;减振器具有足够的散热面积,防止因温度过高引起阻力衰减或减振器早期失效。 作缸径的确定:
可根据减振器最大拉伸阻力和最大允许压力近似求出工作缸径。
( ) D = 4Fmax (mm) πp 1 − λ2 式中: D -作缸径, mm ; p -工作缸允许最大压力,一般为 3~4 N / mm2 ; F max -减振器最大拉伸阻力, N ; λ -减振器杆直径与工作缸之比,双筒减振器为 0.4~0.5,单筒减振器为 0.3~0.35。
Cϕb
=
1 2
⋅
P f
L2
=
3 EIL2
(6)
l l 2⎢⎣⎡
3 − a3 + L (a + b)2 + 4
1
2
2 2
(b
+
c
)⎥⎦⎤
当角钢度给定时,可求得所需要的稳定杆直径 d 为
l l d
=
4
128 3π
⋅
Cϕb L2 E
⎡ ⎢⎣
3 − a3 + 1 (a + b)2 + 4
1
2
2 2
(b
+
c
)⎥⎦⎤
(7) 按弹簧指数 C = Dm / d 及 K ' 的表达式(见式 24 下的说明求得 K ' ,运用式(24)求出载荷 P1 ,
稳定杆设计计算

7 横向稳定杆为了降低偏频和改善行驶平顺性,乘用车悬架的垂直刚度和侧倾角刚度设计得较低,在转弯时可能产生较大侧倾,影响行驶稳定性。
为同时获得较大的静挠度和侧倾角刚度,在汽车中广泛地采用了横向稳定杆,如图8。
53所示。
另外,在前、后悬架上采用横向稳定杆,还可以调整前、后悬架的侧倾角刚度之比,获得需要的转向特性。
但是当汽车在坑洼不平的路面上行驶时,左、右车轮垂直位移不同,横向稳定杆被扭转,加强了左、右车轮之间的运动联系,对行驶平顺性不利。
图8。
53 横向稳定杆的安装示意图为了缓冲、隔振、降低噪音,横向稳定杆与悬架和车身(车架)的连接处均有橡胶支承(图8.53中A、T、C处)。
由于布置上的原因,横向稳定杆通常做成比较复杂的形状,但为简化计算,一般认为横向稳定杆是等臂梯形,同时假定在车身侧倾时力臂的变化可忽略不计。
如图8。
54所示,设在车身侧倾时,在横向稳定杆的一个端点作用力F,在其另一个端点作用有大小相等、方向相反的力。
下面推导在F作用下横向稳定杆端点的位移f。
c汽车设计·228· ·228·(a ) 横向稳定杆尺寸示意图 (b ) 车轮位移与横向稳定杆位移图图8。
54 横向稳定杆安装尺寸及位移图图8。
55为横向稳定杆半边的弯矩图。
在力F 作用下横向稳定杆发生弹性变形,F 作的功与横向稳定杆中总的变形位能相等。
图8.55 横向稳定杆半边弯矩图横向稳定杆变形位能的计算公式如下: (1) T l 段的扭转位能.2T1p=4F l U GJ (8—110) 式中,p J 为横向稳定杆的截面极惯性矩;G 为材料剪切弹性模量;T l 为横向稳定杆直线段长度。
(2) 1l 段的弯曲位能.2312 =6F l U EJ(8—111)式中,J 为横向稳定杆的截面惯性矩;E 为材料弹性模量.(3) 0l 段的弯曲位能。
002222322233200002()()1=d d ()2212l l F l l x M x F U x x l l l EJ EJl EJ ⎡⎤⋅+==⋅+⋅⎢⎥⎣⎦⎰⎰ (8-112) 其中,x 轴的原点在横向稳定杆的对称中心。
横向稳定杆的参数计算与设计报告
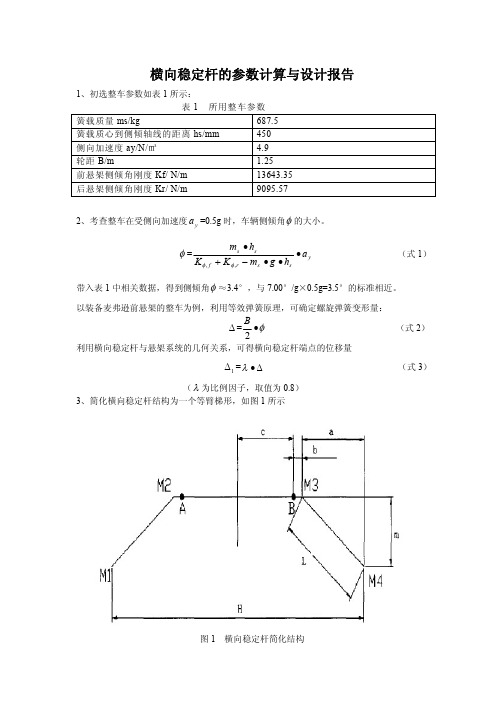
稳定杆安装位置到对称面距离 c/mm 稳定杆安装位置到拐点距离 b/mm 未注中心线弯曲半径 /mm
由图 1 中稳定杆各参数间的几何关系和表 2 的相关数据,可确定稳定杆端点到拐点距离
H L= c b m 2 ;夹角 =PI-arcsin(m/L) 2
横向稳定杆的材料多选用 50CrVA,其相关应力参数如表 3 所示 表 3 材料参数 弹性模量 E/GPa 剪切弹性模量 G/GPa 许用扭转应力 [ ]/MPa 泊松比μ 206 79 740 0.29
稳定杆端点受力 F=2K 1 。 至此,确定横向稳定杆的 H、L、 、b、c、m,完成稳定杆的几何尺寸设计计算工作。
横向稳定杆的参数计算与设计报告
1、初选整车参数如表 1 所示: 表1 簧载质量 ms/kg 簧载质心到侧倾轴线的距离 hs/mm 侧向加速度 ay/N/㎡ 轮距 B/m 前悬架侧倾角刚度 Kf/ N/m 后悬架侧倾角刚度 Kr/ N/m 所用整车参数 687.5 450 4.9 1.25 13643.35 9095.57
=
B 2
(式 2)
利用横向稳定杆与悬架系统的几何关系,可得横向稳定杆端点的位移量
1 =
( 为比例因子,取值为 0.பைடு நூலகம்) 3、简化横向稳定杆结构为一个等臂梯形,如图 1 所示
(式 3)
图1
横向稳定杆简化结构
表2 稳定杆横向跨度 H/mm 稳定杆纵向跨度 m/mm
所需横向稳定杆参数 1049.1 213.6 315.5 51.6 30
F 1 U 1 2U 2 U 3 2
F m2 2(c b) 2F 2 L3 =
4G Jp
F2 H c 2c 6 E J 12 E J 2
FSC横向稳定杆设计及有限元分析

AUTOMOBILE DESIGN 丨汽车设计
D 时代汽车
图4 横向稳定杆側倾刚度计算程序
结构简化为一半,同时也可以减小网格划分 的数量,缩短求解时间,如图6所示。
图6 横向稳定杆ANSYS分析简化模型
. . - Z 中、一一
图3 横向稳定杆模型简化图 I
则此时横向稳定杆的侧倾角刚度的侧倾 角刚度计算公式[5]为 :
设计横向稳定杆时,除了要考虑整车总 的侧倾角刚度外,还应考虑前后悬架的侧倾角 刚度之比。赛车设计中根据车手的驾驶习惯不 同,常常会将前后悬都装上稳定杆,调节到略 微 转 向 过 度 (就个人驾驶习惯而言)。最理想
图1 横向稳定杆位置布置
的状态是把横向稳定杆所提供的侧倾角刚度控 制在悬架的总侧倾角刚度的20%~50%之间。
其 次 ,当汽车过弯时,在侧向加速度的 作用下,由于各轴质量的大小和重心高度不 一 致 ,悬架的布置也会有一定的差异,于是
便导致了各轴所承受的力矩也就不一样。如 果此时不能使在前后轴的侧倾力矩保持一 致 ,那 么 ,车身就会受到一个额外的附加力
矩 ,这往往是我们不希望看到的。所 以 ,为 了保持车身在各轴处的侧倾角相等,那么整
K = (3*EI (l-2*ll*cos ( 0 ) A2) ) / (6* (1+ U ) *l*l l A2*sin ( 0 ) A2+2*11A3) (2)
其 中 :E为弹性模量;I 为截面惯性矩; P 为泊松比。
观 察 公 式 不 难 发 现 ,影 响 到 横 向稳 定 杆 的侧倾角刚度的主要因素为:所选材料的弹 性 模 量 、泊 松 比 、杆 身 长 度 、摆 臂 长 度 、截 面 极 惯 性 矩 (若 为 圆 管 ,则为圆管的内外 径 )、杆身与摆臂的夹角等。
悬架弹簧,横向稳定杆设计报告【FSAE技术组资料】

1悬架设计本车参数:偏频 , 杠杆比簧下质量 9 7kg 整车质量 280kg 簧上质量估算240kg 轴距L 1580mm 前轮距 1240mm 后轮距 1200mm 质心到前轴距a 869mm 质心到后轴距b 711mm 质心高度h 300mm 质心到侧倾轴线距离H 242mm 前悬静态侧倾中心高度R FZ 54mm 后悬静态侧倾中心高度R RZ57mm 侧倾增益度/Ay φ1 10.5/0.5*711*240/158054smlf smrf sm m m bm l Kg ==== (3 3) 后轴左右车轮簧上质量:0.5/0.5*869*240/158066smlr smrr sm m m am l Kg ==== (3 4) 乘适刚度是指轮胎接地点相对车架或车身单位垂直位移时所受到的垂向力。
前轴单侧悬架乘适刚度:2222244*3.5*5426114.97/RF F smlf K f m N m ===ππ (3 5) 后轴单侧悬架乘适刚度:m N m f K smlr R RR /18.2345066*0.3*442222===ππ (3 6)由TW R K K K111+= (3 7) 式中:R K :乘适刚度WK :悬架刚度(车轮中心刚度)T K :轮胎刚度车轮中心刚度是指车轮中心相对车架或车身单位垂直位移时所受到的垂向力。
已知轮胎刚度T K =100719 36N/m 前悬架车轮中心刚度: 100719.36*26114.9735256.4/100719.3626114.97T RF WF T RF K K K N m K K ===-- (3 8)后悬架车轮中心刚度: m N K K K K K RR T RR T WR /00.3056718.2345036.10071918.23450*36.100719=-=-=(3 9)弹簧刚度SK 与悬架刚度WK 的关系如下:2*MR K K W S = (3 10) 式中:MR :杠杆比;前悬架的弹簧刚度:1 ibs/in=175 4N/m(3 11)后悬架的弹簧刚度:3(3 12)侧倾角刚度是指车架或车身侧倾单位转角时悬架系统给车架或车身总的弹性恢复力矩。
基于CATIA的汽车横向稳定杆的参数化设计

FOCUS 技术聚焦
设计·创新
基于 CATIA 的汽车横向 稳定杆的参数化设计
李群 何耀华 (武汉理工大学汽车工程学院)
摘要:参数化设计在产品的优化设计中发挥着重要作用。为完成汽车横向稳定杆的参数化设计,文章推导出横向 稳定杆尺寸参数的约束公式,并在此基础上建立基于 CATIA 的稳定杆参数化模型,将模型与 Excel 表格相关联, 实现参数驱动横向稳定杆的自动重构,完成横向稳定杆的参数化设计。运用 Abaqus 软件建立横向稳定杆有限元 模型,校核结果验证了稳定杆参数化设计的正确性。 关键词:汽车;横向稳定杆;CATIA;参数化设计
1
((N·m) ((N·m) ms/kg 倾 轴 线 度 ay/ (° )
/(°)) /(°))
的 距 离 (m/s2)
角 θ/ 线 弯 点 位 向 跨 向 跨 置到对 装 位 同 侧 拐 E/Pa 模 量 应 力
rad 曲 半 移 度 度 称面距 置 到 点距离
G/Pa [τ]/Pa
径 线刚 d/m 度 K/
模型 Join 到一起;
加大小为 1 084.4 N,方向相反的 z 向载荷。对横向
5)转换到 Part Design 模块生成杆的实体模型, 稳定杆做静力学分析,得到横向稳定杆应力云图,如
即稳定杆的参数化基础模型,如图 4 所示。
图 6 所示。可以看出最大应力集中在拐角处编号为
11 130 的节点上,最大值 544.4 MPa,该材料的扭转
Parametric Design of Automotive Stabilizer Bar Based on CATIA
Abstract: Parametric design plays an important role in product optimized design. In order to complete the parametric design of stabilizer bar, the constraint formula of stabilizer bar parameters is derived, and parametric model of stabilizer bar is established based on CATIA, which is associated with the Excel table, the automatic reconstruction of stabilizer bar by parameter—driven is achieved, the parametric design of stabilizer bar is completed. Based on Abaqus software, the finite element model of stabilizer bar is established, the checking results verified the correctness of parametric design of stabilizer bar. Key words: Automobile; Stabilizer bar; CATIA; Parametric design
巴哈赛车横向稳定杆的设计与性能验证

Science and Technology &Innovation ┃科技与创新2020年第08期·5·文章编号:2095-6835(2020)08-0005-03巴哈赛车横向稳定杆的设计与性能验证侯小舸,杨云珍,王琦(武汉理工大学汽车工程学院,湖北武汉430070)摘要:设计了一套匹配巴哈赛车底盘特性的横向稳定杆,通过提高悬架系统的侧倾角刚度提高整车的抗侧倾能力,从而增强赛车的横向稳定性。
建立横向稳定杆的数学模型;分析稳定杆的各参数对横向稳定杆所能提供的侧倾角刚度的影响;对悬架系统进行仿真分析,得出横向稳定杆的特性曲线;并进行实车的稳态回转试验与跑动测试,进一步验证了横向稳定杆的抗侧倾性能。
关键词:横向稳定杆;巴哈赛车;悬架;侧倾角刚度中图分类号:U463.33文献标识码:ADOI :10.15913/ki.kjycx.2020.08.003大学生巴哈赛车是一种发动机中置、后驱的小型全地形车,具有独特的防滚架结构和与之相匹配的斜置单纵臂后悬架系统,独特的悬架布置导致其在高速入弯时,会产生较大的侧倾和横向振动,导致轮胎侧偏严重,影响赛车的操控稳定性及平顺性[1]。
因此设计出一款匹配巴哈赛车底盘布置的横向稳定系统,建立出横向稳定杆的理论模型;并对悬架系统进行运动仿真分析;最后通过实车跑动测试,更为真实地验证了横向稳定杆的性能。
1建立横向稳定杆的数学模型1.1横向稳定杆的布置横向稳定杆的布置如图1所示。
图1横向稳定杆的布置示意图当整车发生侧倾时,一侧轮胎相对于车架有一段垂向位移量∆1,车轮处的跳动量传递到稳定杆臂末端的跳动量为∆2,设∆2与∆1的比值为横向稳定杆的传动比ε,两轮间距为D 。
稳定杆的抗侧倾性能的评价指标并不是稳定杆自身的侧倾角刚度,而是稳定杆传递到车轮处的等效侧倾角刚度。
1.2横向稳定杆侧倾刚度的计算设稳定杆长度为n ,稳定杆臂的长度为a ,稳定杆直径为d ,稳定杆与稳定杆臂的夹角为θ,稳定杆臂末端端点的距离为L ,稳定杆与稳定杆臂通过螺栓连接,稳定杆上有两处橡胶衬套用以固定稳定杆。
横向稳定杆的参数计算与设计报告

2、考查整车在受侧向加速度 a y =0.5g 时,车辆侧倾角 的大小。
=
K , f
m s hs ay K , r m s g hs
(式 1)
带入表 1 中相关数据,得到侧倾角 ≈3.4°,与 7.00°/g×0.5g=3.5°的标准相近。 以装备麦弗逊前悬架的整车为例,利用等效弹簧原理,可确定螺旋弹簧变形量:
横向稳定杆的参数计算与设计报告
1、初选整车参数如表 1 所示: 表1 簧载质量 ms/kg 簧载质心到侧倾轴线的距离 hs/mm 侧向加速度 ay/N/㎡ 轮距 B/m 前悬架侧倾角刚度 Kf/ N/m 后悬架侧倾角刚度 Kr/ N/m 所用整车参数 687.5 450 4.9 1.25 13643.35 9095.57
F 1 U 1 2U 2 U 3 2
F m2 2(c b) 2F 2 L3 =
4G Jp
F2 H c 2c 6 E J 12 E J 2
2
(式 4)
设车身在侧倾时受到横向稳定杆所产生的阻力距为 T,侧倾角为 ,有
d=
c) 2 2c 2
B 3E 0.8 2
2
稳定杆线刚度 K=
3E J
2 3 H H H 2 2 2 3
2
设在车身侧倾时,在横向稳定杆的一个端点作用一个力 F,在其另外一个端点作用有一个大 小相等、方向相反的力。在力 F 作用下要发生弹性变形,F 作的功与横向稳定杆中总的变形 位能相等。横向稳定杆半边的变形位能包括: M 2 M 3 段的扭转位能 U 1 ; M 3 M 4 段的弯曲 位能 U 2 ; AB 段的弯曲位能 U 3 。 根据位能相等原理有,F 所做的功与横向稳定杆中总的变形位能相等。
