2019年山东省菏泽市中考试题含答案解析
2019年山东省菏泽市中考数学试卷以及答案

2019年山东省菏泽市中考数学试卷一、选择题(本大题共8个小题,每小题3分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.点P(﹣2,1)在平面直角坐标系中所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限2.在算式()□()的□中填上运算符号,使结果最大,这个运算符号是()A.加号B.减号C.乘号D.除号3.如果用□表示1个立方体,用表示两个立方体叠加,用■表示三个立方体叠加,那么下面图是由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是( )A .B .C .D .4.已知⎩⎨⎧==12y x 是二元一次方程组81mx ny nx my +=⎧⎨-=⎩的解,则n m -2的算术平方根为( )A .±2B . 2C .2D . 45.下列图形中是中心对称图形是( )A .B .C .D .6.反比例函数2y x =的两个点为11(,)x y 、22(,)x y ,且12x x >,则下式关系成立的是( )A .12y y >B .12y y <C .12y y =D .不能确定7.我市今年6月某日部分区县的最高气温如下表:区县牡丹区东明鄄城郓城巨野定陶开发区曹县成武单县最高气温(℃)32 32 30 32 30 32 32 32 30 29则这10个区县该日最高气温的众数和中位数分别是()A.32,32B.32,30C.30,32D.32,318.已知二次函数2y ax bx c=++的图像如图所示,那么一次函数y bx c=+和反比例函数ayx=在同一平面直角坐标系中的图像大致是()A .B .C .D .二、填空题(本大题共6个小题,每小题4分,共24分.把答案填在题中的横线上.)9.已知线段AB=8cm ,在直线AB 上画线段BC ,使它等于3cm ,则线段AC= cm .10.若不等式组3x x m >⎧⎨>⎩的解集是3x >,则m 的取值范围是 .11.如图,PA ,PB 是⊙O 是切线,A ,B 为切点,AC 是⊙O 的直径,若∠P=46°,则∠BAC= 度.12.口袋内装有大小、质量和材质都相同的红色1号、红色2号、黄色1号、黄色2号、黄色3号的5个小球,从中摸出两球,这两球都是红色的概率是 .13.将4个数a b c d ,,,排成2行、2列,两边各加一条竖直线记成a b c d ,定义a b c dad bc =-,上述记号就叫做2阶行列式.若 1 181 1x xx x +-=-+,则x = .14.一个自然数的立方,可以分裂成若干个连续奇数的和.例如:32,33和34分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即3235=+;337911=++;3413151719=+++;……;若36也按照此规律来进行“分裂”,则36“分裂”出的奇数中,最大的奇数是 .三、解答题(本大题共7个小题,共72分.解答应写出文字说明、证明过程或演算步骤.)15.(1)先化简,再求代数式的值.222()111a a a a a ++÷++-,其中2012(1)tan 60a ︒=-+.16.(1)如图,∠DAB=∠CAE,请补充一个条件:,使△ABC∽△ADE.17.(1)如图,一次函数2y=23x -+的图象分别与x 轴、y 轴交于点A 、B ,以线段AB 为边在第一象限内作等腰Rt△ABC,∠BAC=90°.求过B 、C 两点直线的解析式.(2)我市某校为了创建书香校园,去年购进一批图书.经了解,科普书的单价比文学书的单价多4元,用12000元购进的科普书与用8000元购进的文学书本数相等.今年文学书和科普书的单价和去年相比保持不变,该校打算用10000元再购进一批文学书和科普书,问购进文学书550本后至多还能购进多少本科普书?18.如图,在边长为1的小正方形组成的格中,△ABC和△DEF 的顶点都在格点上,P1,P2,P3,P4,P5是△DEF边上的5个格点,请按要求完成下列各题:(1)试证明三角形△ABC为直角三角形;(2)判断△ABC和△DEF是否相似,并说明理由;(3)画一个三角形,使它的三个顶点为P1,P2,P3,P4,P5中的3个格点并且与△ABC相似(要求:用尺规作图,保留痕迹,不写作法与证明).19.某中学举行数学知识竞赛,所有参赛学生分别设有一、二、三等奖和纪念奖,获奖情况已绘制成如图所示的两幅不完整的统计图.根据图中所给出的信息解答下列问题:(1)二等奖所占的比例是多少?(2)这次数学知识竞赛获得二等奖的人数是多少?(3)请将条形统计图补充完整;(4)若给所有参赛学生每人发一张卡片,各自写上自己的名字,然后把卡片放入一个不透明的袋子里,摇匀后任意摸出一张,求摸出的卡片上是写有一等奖学生名字的概率.20.牡丹花会前夕,我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销.经过调查,得到如下数据:销售单价x(元/件)…20 30 40 50 60 …每天销售量(y件)…500 400 300 200 100 …(1)把上表中x、y的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式;(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价﹣成本总价)(3)菏泽市物价部门规定,该工艺品销售单价最高不能超过35元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?21.如图,在平面直角坐标系中放置一直角三角板,其顶点为A(0,1),B(2,0),O(0,0),将此三角板绕原点O逆时针旋转90°,得到△A′B′O.(1)一抛物线经过点A′、B′、B,求该抛物线的解析式;(2)设点P是在第一象限内抛物线上的一动点,是否存在点P,使四边形PB′A′B的面积是△A′B′O面积4倍?若存在,请求出P的坐标;若不存在,请说明理由.(3)在(2)的条件下,试指出四边形PB′A′B是哪种形状的四边形?并写出四边形PB′A′B的两条性质.答案解析一、选择题(本大题共8个小题,每小题3分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(2018菏泽)点P(﹣2,1)在平面直角坐标系中所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限考点:点的坐标。
2019山东省菏泽市中考试题解析

2019年山东省菏泽市中考试题解析(满分120分,考试时间120分钟)一、选择题(本大题共8小题,每小题3分,共24分)1.(2019山东菏泽,1,3分)下列各数中,最大的数是( )A .−12B .14C .0D .﹣2【答案】B【解析】解:﹣2<−12<0<14,则最大的数是14,故选B . 【知识点】有理数大小比较2. (2019山东菏泽,2,3分)下列图形中,既是轴对称图形,又是中心对称图形的是( )【答案】C【解析】解:A 、不是轴对称图形,是中心对称图形,故此选项错误;B 、是轴对称图形,不是中心对称图形,故此选项错误;C 、是轴对称图形,也是中心对称图形,故此选项正确;D 、不是轴对称图形,是中心对称图形,故此选项错误,故选C .【知识点】轴对称图形;中心对称图形3. (2019山东菏泽,3,3分)下列运算正确的是( )A .(﹣a 3)2=﹣a 6B .a 2•a 3=a 6C .a 8÷a 2=a 4D .3a 2﹣2a 2=a 2 【答案】D【解析】解:A 、原式=a 6,不符合题意;B 、原式=a 5,不符合题意;C 、原式=a 6,不符合题意;D 、原式=a 2,符合题意,故选D .【知识点】合并同类项;同底数幂的乘法;幂的乘方与积的乘方;同底数幂的除法4. (2019山东菏泽,4,3分)一个几何体的三视图如图所示,则这个几何体的表面积是( )A .5cm 2B .8cm 2C .9cm 2D .10cm 2【答案】D【解析】解:由题意推知几何体是长方体,长、宽、高分别1cm 、1cm 、2cm ,所以其面积为:2×(1×1+1×2+1×2)=10(cm 2),故选D .【知识点】由三视图判断几何体5. (2019山东菏泽,5,3分))已知{x =3y =−2是方程组{ax +by =2bx +ay =−3的解,则a +b 的值是( ) A .﹣1B .1C .﹣5D .5 【答案】A【解析】解:将{x =3y =−2代入{ax +by =2bx +ay =−3, 可得:{3a −2b =23b −2a =−3, 两式相加:a +b =﹣1,故选A .【知识点】二元一次方程组的解6.(2019山东菏泽,6,3分)如图,AB 是⊙O 的直径,C ,D 是⊙O 上的两点,且BC 平分∠ABD ,AD 分别与BC ,OC 相交于点E ,F ,则下列结论不一定成立的是( )A .OC ∥BDB .AD ⊥OC C .△CEF ≌△BED D .AF =FD【答案】C【解析】解:∵AB 是⊙O 的直径,BC 平分∠ABD ,∴∠ADB =90°,∠OBC =∠DBC ,∴AD ⊥BD ,∵OB =OC ,∴∠OCB =∠OBC ,∴∠DBC =∠OCB ,∴OC ∥BD ,选项A 成立;∴AD⊥OC,选项B成立;∴AF=FD,选项D成立;∵△CEF和△BED中,没有相等的边,∴△CEF与△BED不全等,选项C不成立,故选C.【知识点】圆周角定理7.(2019山东菏泽,7,3分)在平面直角坐标系中,一个智能机器人接到的指令是:从原点O出发,按“向上→向右→向下→向右”的方向依次不断移动,每次移动1个单位长度,其移动路线如图所示,第一次移动到点A1,第二次移动到点A2……第n次移动到点A n,则点A2019的坐标是()A.(1010,0)B.(1010,1)C.(1009,0)D.(1009,1)【答案】C【解析】解:A1(0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,1),A6(3,1),…,2019÷4=504…3,所以A2019的坐标为(504×2+1,0),则A2019的坐标是(1009,0),故选C.【知识点】点的坐标规律8.(2019山东菏泽,8,3分)如图,正方形ABCD的边长为2cm,动点P,Q同时从点A出发,在正方形的边上,分别按A→D→C,A→B→C的方向,都以1cm/s的速度运动,到达点C运动终止,连接PQ,设运动时间为xs,△APQ的面积为ycm2,则下列图象中能大致表示y与x的函数关系的是()【答案】A【解析】解:①当0≤x ≤2时,∵正方形的边长为2cm ,∴y =S △APQ =12AQ •AP =12x 2;②当2≤x ≤4时,y =S △APQ =S 正方形ABCD ﹣S △CP ′Q ′﹣S △ABQ ′﹣S △AP ′D ,=2×2−12(4﹣x )2−12×2×(x ﹣2)−12×2×(x ﹣2)=−12x 2+2x∴y 与x 之间的函数关系可以用两段二次函数图象表示,纵观各选项,只有A 选项图象符合.故选A .【知识点】动点问题的函数图象二、填空题(本大题共6小题,每小题3分,共18分)9.(2019山东菏泽,9,3分)计算(12)﹣1﹣(﹣3)2的结果是_________ 【答案】﹣7【解析】解:原式=2﹣9=﹣7.【知识点】实数运算;有理数的乘方;有理数的减法;负整数指数幂10. (2019山东菏泽,10,3分)已知x =√6+√2,那么x 2﹣2√2x 的值是_________【答案】4.【解析】解:∵x −√2=√6,∴x 2﹣2√2x +2=6,∴x 2﹣2√2x =4.【知识点】二次根式的化简求值11. (2019山东菏泽,11,3分)如图,AD ∥CE ,∠ABC =100°,则∠2﹣∠1的度数是_________【答案】80° 【解析】解:作BF ∥AD ,∵AD ∥CE ,∴AD ∥BF ∥EC ,∴∠1=∠3,∠4+∠2=180°,∠3+∠4=100°,∴∠1+∠4=100°,∠2+∠4=180°,∴∠2﹣∠1=80°.故答案为:80°.【知识点】平行线的性质12. (2019山东菏泽,12,3分)一组数据4,5,6,x 的众数与中位数相等,则这组数据的方差是_________ 【答案】12【解析】解:若众数为4,则数据为4,4,5,6,此时中位数为4.5,不符合题意;若众数为5,则数据为4,5,5,6,中位数为5,符合题意,此时平均数为4+5+5+64=5,方差为14[(4﹣5)2+(5﹣5)2+(5﹣5)2+(6﹣5)2]=12; 若众数为6,则数据为4,5,6,6,中位数为5.5,不符合题意, 故答案为12. 【知识点】中位数;众数;方差13. (2019山东菏泽,13,3分)如图,E ,F 是正方形ABCD 的对角线AC 上的两点,AC =8,AE =CF =2,则四边形BEDF 的周长是 .【答案】85【解析】解:如图,连接BD 交AC 于点O ,∵四边形ABCD 为正方形,∴BD ⊥AC ,OD =OB =OA =OC ,∵AE=CF=2,∴OA﹣AE=OC﹣CF,即OE=OF,∴四边形BEDF为平行四边形,且BD⊥EF,∴四边形BEDF为菱形,∴DE=DF=BE=BF,∵AC=BD=8,OE=OF=8−42=2,由勾股定理得:DE=√OD2+OE2=√42+22=2√5,∴四边形BEDF的周长=4DE=4×2√5=8√5,故答案为:85.【知识点】全等三角形的判定与性质;正方形的性质14.(2019山东菏泽,14,3分)如图,直线y=−34x﹣3交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是.【答案】(−73,0)或P(−173,0).【解析】解:∵直线y=−34x﹣3交x轴于点A,交y轴于点B,∴令x=0,得y=﹣3,令y=0,得x=﹣4,∴A(﹣4,0),B(0.﹣3),∴OA=4,OB=3,∴AB=5,设⊙P与直线AB相切于D,连接PD,则PD⊥AB,PD=1,∵∠ADP=∠AOB=90°,∠P AD=∠BAO,∴△APD∽△ABO,∴PDOB=APAB,∴13=AP 5, ∴AP =53,∴OP =73或OP =173,∴P (−73,0)或P (−173,0), 故答案为:(−73,0)或P (−173,0).【知识点】一次函数的图象;切线的判定与性质; 相似三角形的判定和性质三、解答题(本大题共8小题,满分78分,各小题都必须写出解答过程)15. (2019山东菏泽,15,6分)解不等式组:{x −3(x −2)≥−4,x −1<2x+13. 【思路分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.【解题过程】解:解不等式x ﹣3(x ﹣2)≥﹣4,得:x ≤5,解不等式x ﹣1<2x+13,得:x <4, 则不等式组的解集为x <4.【知识点】解一元一次不等式组16.(2019山东菏泽,16,6分)先化简,再求值:1x−y (2y x+y −1)÷1y 2−x 2,其中x =y +2019.【思路分析】根据分式的减法和乘除法可以化简题目中的式子,然后将x =y +2019代入化简后的式子即可解答本题.【解题过程】解:1x−y (2y x+y −1)÷1y 2−x 2 =1x−y ⋅2y−(x+y)x+y⋅(y +x)(y −x) =﹣(2y ﹣x ﹣y )=x ﹣y ,∵x =y +2019,∴原式=y +2019﹣y =2019.【知识点】分式的化简求值17.(2019山东菏泽,17,6分)如图,四边形ABCD是矩形.(1)用尺规作线段AC的垂直平分线,交AB于点E,交CD于点F(不写作法,保留作图痕迹);(2)若BC=4,∠BAC=30°,求BE的长.【思路分析】(1)根据线段的垂直平分线的作图解答即可;(2)利用含30°的直角三角形的性质解答即可.【解题过程】解:(1)如图所示:(2)∵四边形ABCD是矩形,EF是线段AC的垂直平分线,∴AE=EC,∠CAB=∠ACE=30°,∴∠ECB=60°,∴∠ECB=30°,∵BC=4,∴BE=4√3 3.【知识点】矩形的性质;线段垂直平分线的性质;作图18.(2019山东菏泽,18,6分)列方程(组)解应用题:德上高速公路巨野至单县段正在加速建设,预计2019年8月竣工.届时,如果汽车行驶高速公路上的平均速度比在普通公路上的平均速度提高80%,那么行驶81千米的高速公路比行驶同等长度的普通公路所用时间将会缩短36分钟,求该汽车在高速公路上的平均速度.【思路分析】设汽车行驶在普通公路上的平均速度是x千米/分钟,则汽车行驶在高速公路上的平均速度是1.8x 千米/分钟,根据“行驶81千米的高速公路比行驶同等长度的普通公路所用时间将会缩短36分钟”列出方程并解答.【解题过程】解:设汽车行驶在普通公路上的平均速度是x千米/分钟,则汽车行驶在高速公路上的平均速度是1.8x千米/分钟,由题意,得811.8x+36=81x.解得x=1.经检验,x=1是所列方程的根,且符合题意.所以1.8x=1.8(千米/分钟).答:汽车行驶在高速公路上的平均速度是1.8千米/分钟.【知识点】分式方程的应用19.(2019山东菏泽,19,7分)由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达A处时,测得小岛B位于它的北偏东30°方向,且与航母相距80海里再航行一段时间后到达C处,测得小岛B位于它的西北方向,求此时航母与小岛的距离BC的长.【思路分析】过点C作CD⊥AB于点D,根据题意得到∠BAD=60°,∠BCD=45°,AC=80,解直角三角形即可得到结论.【解题过程】解:过点C作CD⊥AB于点D,由题意,得:∠BAD=60°,∠BCD=45°,AC=80,在Rt△ADB中,∠BAD=60°,∴tan60°=BDAD=√3,∴AD=BD √3,在Rt△BCD中,∠BCD=45°,∴tan45°=BDCD=1,∴BD=CD,∴AC=AD+CD=BD√3+BD=80,∴BD=120﹣40√3,∴BC=√2BC=120√2−40√6,答:BC的距离是(120√2−40√6)海里.【知识点】解直角三角形的应用﹣方向角问题20. (2019山东菏泽,20,7分)如图,▱ABCD 中,顶点A 的坐标是(0,2),AD ∥x 轴,BC 交y 轴于点E ,顶点C 的纵坐标是﹣4,▱ABCD 的面积是24.反比例函数y =k x的图象经过点B 和D ,求:(1)反比例函数的表达式;(2)AB 所在直线的函数表达式.【思路分析】(1)根据题意得出AE =6,结合平行四边形的面积得出AD =BC =4,继而知点D 坐标,从而得出反比例函数解析式;(2)先根据反比例函数解析式求出点B 的坐标,再利用待定系数法求解可得.【解题过程】解:(1)∵顶点A 的坐标是(0,2),顶点C 的纵坐标是﹣4,∴AE =6,又▱ABCD 的面积是24,∴AD =BC =4,则D (4,2)∴k =4×2=8,∴反比例函数解析式为y =8x ;(2)由题意知B 的纵坐标为﹣4,∴其横坐标为﹣2,则B (﹣2,﹣4),设AB 所在直线解析式为y =kx +b ,将A (0,2)、B (﹣2,﹣4)代入,得:{b =2−2k +b =−4, 解得:{k =3b =2, 所以AB 所在直线解析式为y =3x +2.【知识点】待定系数法求一次函数解析式;反比例函数系数k 的几何意义;平行四边形的性质21.(2019山东菏泽,21,10分)4月23日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”我市某中学响应号召,鼓励师生利用课余时间广泛阅读,该校文学社发起了“读书感悟•分享”比赛活动根据参赛学生的成绩划分为A,B,C,D四个等级,并绘制了下面不完整的统计图表,根据图表中提供的信息解答下列问题;频数频率A4BC a0.3D16b(1)求a,b的值;(2)求B等级对应扇形圆心角的度数;(3)学校要从A等级的学生中随机选取2人参加市级比赛,求A等级中的学生小明被选中参加市级比赛的概率.【思路分析】(1)根据A等级有4人,所占的百分比是10%即可求得总人数,然后求得a和b的值;(2)首先计算出B等级频数,再利用360°乘以对应的百分比即可求得B等级所对应的圆心角度数;(3)利用列举法求得选中A等级的小明的概率.【解题过程】解:(1)总人数:4÷10%=40,a=40×0.3=12,b=1640=0.4;(2)B的频数:40﹣4﹣12﹣16=8,B等级对应扇形圆心角的度数:840×360°=72°;(3)用a表示小明,用b、c、d表示另外三名同学.则选中小明的概率是:612=12.【知识点】扇形统计图;频数(率)分布表;概率22.(2019山东菏泽,22,10分)如图,BC是⊙O的直径,CE是⊙O的弦,过点E作⊙O的切线,交CB的延长线于点G,过点B作BF⊥GE于点F,交CE的延长线于点A.(1)求证:∠ABG=2∠C;(2)若GF=3√3,GB=6,求⊙O的半径.【思路分析】(1)连接OE,根据切线的性质得到OE⊥EG,推出OE∥AB,得到∠A=∠OEC,根据等腰三角形的性质得到∠OEC=∠C,求得∠A=∠C,根据三角形的外角的性质即可得到结论;(2)根据勾股定理得到BF=√BG2−GF2=3,根据相似三角形的性质即可得到结论.【解题过程】解:(1)证明:连接OE,∵EG是⊙O的切线,∴OE⊥EG,∵BF⊥GE,∴OE∥AB,∴∠A=∠OEC,∵OE=OC,∴∠OEC=∠C,∴∠A=∠C,∵∠ABG=∠A+∠C,∴∠ABG=2∠C;(2)解:∵BF⊥GE,∴∠BFG=90°,∵GF=3√3,GB=6,∴BF=√BG2−GF2=3,∵BF∥OE,∴△BGF∽△OGE,∴BFOE=BGOG,∴3OE=66+OE,∴OE=6,∴⊙O的半径为6.【知识点】圆周角定理;切线的性质;相似三角形的判定和性质;等腰三角形的判定和性质23.(2019山东菏泽,23,10分)如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°.(1)如图1,连接BE,CD,BE的廷长线交AC于点F,交CD于点P,求证:BP⊥CD;(2)如图2,把△ADE绕点A顺时针旋转,当点D落在AB上时,连接BE,CD,CD的延长线交BE于点P,若BC=6√2,AD=3,求△PDE的面积.【思路分析】(1)根据等腰直角三角形的性质得到AD=AE,AB=AC,∠BAC﹣∠EAF=∠EAD﹣∠EAF,求得∠BAE=∠DAC,根据全等三角形的性质得到∠ABE=∠ACD,根据余角的性质即可得到结论;(2)根据全等三角形的性质得到∠ABE=∠ACD,BE=CD,求得∠EPD=90°,得到DE=3√2,AB=6,求得BD=6﹣3=3,CD=√AD2+AC2=3√5,根据相似三角形的性质得到PD=√55,PB=6√55根据三角形的面积公式即可得到结论.【解题过程】解:(1)∵△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°.∴AD=AE,AB=AC,∠BAC﹣∠EAF=∠EAD﹣∠EAF,即∠BAE=∠DAC,在△ABE与△ADC中,{AB=AC∠BAE=∠CAD AE=AD,∴△ABE≌△ADC(SAS),∴∠ABE=∠ACD,∵∠ABE+∠AFB=∠ABE+∠CFP=90°,∴∠CPF=90°,∴BP⊥CD;(2)在△ABE与△ACD中,{AE=AD∠EAB=∠CAB=90°AB=AC,∴△ABE≌△ACD(SAS),∴∠ABE=∠ACD,BE=CD,∵∠PDB=∠ADC,∴∠BPD=∠CAB=90°,∴∠EPD=90°,BC=6√2,AD=3,求△PDE的面积.∵BC=6√2,AD=3,∴DE=3√2,AB=6,∴BD=6﹣3=3,CD=√AD2+AC2=3√5,∵△BDP∽△CDA,∴BDCD=PDAD=PBAC,∴33√5=PD3=PB6,∴PD=3√55,PB=6√55∴PE=3√5−6√55=9√55,∴△PDE的面积=12×9√55×3√55=2710.【知识点】全等三角形的判定与性质;等腰直角三角形;旋转的性质;相似三角形的判定和性质;勾股定理24.(2019山东菏泽,24,10分)如图,抛物线与x轴交于A,B两点,与y轴交于点C(0,﹣2),点A的坐标是(2,0),P为抛物线上的一个动点,过点P作PD⊥x轴于点D,交直线BC于点E,抛物线的对称轴是直线x=﹣1.(1)求抛物线的函数表达式;(2)若点P 在第二象限内,且PE =14OD ,求△PBE 的面积.(3)在(2)的条件下,若M 为直线BC 上一点,在x 轴的上方,是否存在点M ,使△BDM 是以BD 为腰的等腰三角形?若存在,求出点M 的坐标;若不存在,请说明理由.【思路分析】(1)点A (2,0)、点B (﹣4,0),则函数的表达式为:y =a (x ﹣2)(x +4)=a (x 2+2x ﹣8),即可求解;(2)PE =14OD ,则PE =(14x 2+12x ﹣2−12x +2)=14(﹣x ),求得:点D (﹣5,0),利用S △PBE =12PE ×BD =12(14x 2+12x ﹣2−12x +2)(﹣4﹣x ),即可求解; (3)BD =1=BM ,则y M =﹣BM sin ∠ABC =﹣1×1√5=−√55,即可求解. 【解题过程】解:(1)点A 的坐标是(2,0),抛物线的对称轴是直线x =﹣1,则点B (﹣4,0), 则函数的表达式为:y =a (x ﹣2)(x +4)=a (x 2+2x ﹣8),即:﹣8a =﹣2,解得:a =14,故抛物线的表达式为:y =14x 2+12x ﹣2;(2)将点B 、C 的坐标代入一次函数表达式:y =mx +n 并解得:直线BC 的表达式为:y =−12x ﹣2,则tan ∠ABC =12,则sin ∠ABC =1√5, 设点D (x ,0),则点P (x ,14x 2+12x ﹣2),点E (x ,12x ﹣2), ∵PE =14OD ,∴PE =(14x 2+12x ﹣2−12x +2)=14(﹣x ), 解得:x =0或﹣5(舍去x =0),即点D (﹣5,0)S △PBE =12×PE ×BD =12(14x 2+12x ﹣2−12x +2)(﹣4﹣x )=58; (3)由题意得:△BDM 是以BD 为腰的等腰三角形,只存在:BD =BM 的情况,BD=1=BM,则y M=﹣BM sin∠ABC=﹣1×1√5=−√55,则x M=−20+2√55,故点M(−20+2√55,−√55).【知识点】二次函数综合题;数形结合;函数思想;二次函数的解析式;。
2019年度菏泽市中考语文试卷及答案解析

卷I型:A参考答案注意事项:1. 本试题共三个大题,22个小题,满分120分,考试时间120分钟。
2. 用黑色、蓝色水笔或钢笔答卷。
答题前将密封线内的项目填写清楚。
一、古诗文积累(30分)一经典诗文积累1、默写唐代诗人王昌龄的《采莲曲》一诗。
(4分)__________________________,__________________________。
__________________________,__________________________。
2、依据课文填空。
(4分)①__________________________,必先苦其心志。
(孟子《生于忧患,死于安乐》)②此中有真意,_________________。
(陶渊明《饮酒》)③___________,____________,和风细雨不须归。
(张志和《渔父》)3、根据提示默写。
(4分)①李商隐《夜雨寄北》中想象将来与亲友团聚、剪烛夜话的句子:__________________________,__________________________。
②陆游《卜算子·咏梅》中描写梅花即使被碾压成泥,也依旧保持清香的句子:__________________________,__________________________。
(二)阅读下面诗歌,完成第4-5题。
(4分)雨后池上(宋)刘攽一雨池塘水面平,淡磨明镜照薝楹。
东风忽起垂杨舞,更作荷心万点声。
注释:①薝楹:薝廊。
②更:又。
4、诗题为《雨后池上》,那么,诗中从哪些方面表现了“雨后”二字?(2分)5、请简要赏析第二段加点词语的妙处。
(2分)(三)阅读下文,完成第6-10题。
(14分)【甲】潭中鱼可百许头,皆若空游无所依。
日光下澈,影布石上,佁然不动;俶尔远逝,往来翕忽,似与游者相乐。
潭西南而望,斗折蛇行,明灭可见。
其岸势犬牙差互,不可知其源。
坐潭上,四面竹树环合,寂寥无人,凄神寒骨,悄怆幽邃。
山东省菏泽市2019年中考物理真题试题(含解析)

山东省菏泽市2019年中考物理真题试题(2019·菏泽中考)【答案】D【解析】本题考查导体和绝缘体的辨析。
橡胶棒、玻璃棒和陶瓷筷子都属于绝缘体;湿木棒属于导体,故选D。
需要注意的是导体和绝缘体并没有绝对的界限,干木棒属于绝缘体。
(2019·菏泽中考)【答案】B【解析】本题考查对用电器的工作原理以及对电流热效应的认识。
电风扇工作时,把电能转化为机械能;电暖气工作时,把电能转化为内能;电视机工作时,主要是把电能转化为了光能、声能、内能等;电磁继电器工作时,主要是把电能转化为磁场能。
而电流的热效应指的是当用电器工作时,电能转化为内能的现象,故选B。
(2019·菏泽中考)【答案】C【解析】本题考查对惯性的理解。
汽车紧急刹车时,乘客的下身随车要减速至停止运动,但由于乘客具有惯性,其上身仍将保持原的运动状态继续向前运动,因此乘客会从座位上向前冲,故选C。
(2019·菏泽中考)【答案】B【解析】本题考查三种摩擦现象的辨析。
刹车时,自行车的钢圈与刹车闸皮之间的摩擦是滑动摩擦,故A错误;滑冰时,冰刀与冰面之间的摩擦是滑动摩擦,故B正确;人在正常行走时,脚与地面之间的摩擦是静摩擦,故C错误;划火柴时,火柴头和砂纸之间的摩擦是滑动摩擦,故D错误;故选B。
(2019·菏泽中考)【答案】A【解析】本题考查对声现象及其传播规律的认识。
声音的响度取决于声振动幅度的大小;同时响度与发声体的远近有关,距离发声体越近,响度就越大,距离发声体越远,响度就越小。
因此A说法错误。
(2019·菏泽中考)【答案】D【解析】本题考查对安全用电原则的理解及安全用电常识的认识。
当用电器电线绝缘皮破损后,极易发生触电事故,因此不能再继续使用,故D选项不符合安全用电原则。
(2019·菏泽中考)【答案】C【解析】本题考查滑动变阻器阻值的调节。
A选项中导线连接的是滑杆两端的接线柱,此时滑动变阻器接入电路阻值为零,故A错误;B、D选项中导线虽然连接的是“上、下”两个接线柱,但当滑片向b端移动时,滑动变阻器接入电路的阻值是变小的,故B、D错误;C 选项中导线连接的也是“上、下”两个接线柱,并且当滑片向b端移动时,滑动变阻器接入电路的阻值是变大的,故C正确。
2019年山东菏泽中考数学试卷及详细答案解析(word版)
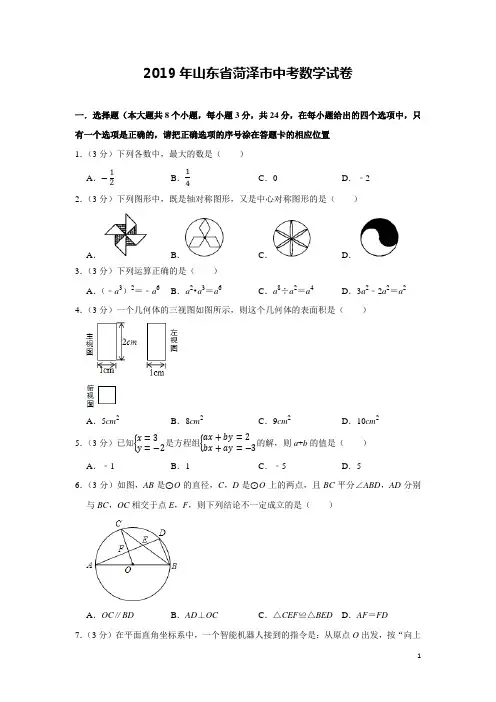
2019年山东省菏泽市中考数学试卷一.选择题(本大题共8个小题,每小题3分,共24分,在每小题给出的四个选项中,只有一个选项是正确的,请把正确选项的序号涂在答题卡的相应位置 1.(3分)下列各数中,最大的数是( ) A .−12B .14C .0D .﹣22.(3分)下列图形中,既是轴对称图形,又是中心对称图形的是( )A .B .C .D .3.(3分)下列运算正确的是( ) A .(﹣a 3)2=﹣a 6B .a 2•a 3=a 6C .a 8÷a 2=a 4D .3a 2﹣2a 2=a 24.(3分)一个几何体的三视图如图所示,则这个几何体的表面积是( )A .5cm 2B .8cm 2C .9cm 2D .10cm 25.(3分)已知{x =3y =−2是方程组{ax +by =2bx +ay =−3的解,则a +b 的值是( )A .﹣1B .1C .﹣5D .56.(3分)如图,AB 是⊙O 的直径,C ,D 是⊙O 上的两点,且BC 平分∠ABD ,AD 分别与BC ,OC 相交于点E ,F ,则下列结论不一定成立的是( )A .OC ∥BDB .AD ⊥OCC .△CEF ≌△BED D .AF =FD7.(3分)在平面直角坐标系中,一个智能机器人接到的指令是:从原点O 出发,按“向上→向右→向下→向右”的方向依次不断移动,每次移动1个单位长度,其移动路线如图所示,第一次移动到点A 1,第二次移动到点A 2……第n 次移动到点A n ,则点A 2019的坐标是( )A .(1010,0)B .(1010,1)C .(1009,0)D .(1009,1)8.(3分)如图,正方形ABCD 的边长为2cm ,动点P ,Q 同时从点A 出发,在正方形的边上,分别按A →D →C ,A →B →C 的方向,都以1cm /s 的速度运动,到达点C 运动终止,连接PQ ,设运动时间为xs ,△APQ 的面积为ycm 2,则下列图象中能大致表示y 与x 的函数关系的是( )A .B .C .D .二、填空题(本大题共6个小题,每小题3分,共18分,只要求把最后结果填写在答题卡的相应区域内.)9.(3分)计算(12)﹣1﹣(﹣3)2的结果是 .10.(3分)已知x =√6+√2,那么x 2﹣2√2x 的值是 .11.(3分)如图,AD ∥CE ,∠ABC =100°,则∠2﹣∠1的度数是 .12.(3分)一组数据4,5,6,x的众数与中位数相等,则这组数据的方差是.13.(3分)如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是.14.(3分)如图,直线y=−34x﹣3交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是.三、解答题(本题共78分,把解答或证明过程写在答题卡的相应区域内)15.(6分)解不等式组:{x−3(x−2)≥−4,x−1<2x+13.16.(6分)先化简,再求值:1x−y (2yx+y−1)÷122,其中x=y+2019.17.(6分)如图,四边形ABCD是矩形.(1)用尺规作线段AC的垂直平分线,交AB于点E,交CD于点F(不写作法,保留作图痕迹);(2)若BC=4,∠BAC=30°,求BE的长.18.(6分)列方程(组)解应用题:德上高速公路巨野至单县段正在加速建设,预计2019年8月竣工.届时,如果汽车行驶高速公路上的平均速度比在普通公路上的平均速度提高80%,那么行驶81千米的高速公路比行驶同等长度的普通公路所用时间将会缩短36分钟,求该汽车在高速公路上的平均速度.19.(7分)由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达A处时,测得小岛B位于它的北偏东30°方向,且与航母相距80海里再航行一段时间后到达C处,测得小岛B位于它的西北方向,求此时航母与小岛的距离BC的长.20.(7分)如图,▱ABCD中,顶点A的坐标是(0,2),AD∥x轴,BC交y轴于点E,顶点C的纵坐标是﹣4,▱ABCD的面积是24.反比例函数y=kx的图象经过点B和D,求:(1)反比例函数的表达式;(2)AB所在直线的函数表达式.21.(10分)4月23日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”我市某中学响应号召,鼓励师生利用课余时间广泛阅读,该校文学社发起了“读书感悟•分享”比赛活动根据参赛学生的成绩划分为A,B,C,D四个等级,并绘制了下面不完整的统计图表,根据图表中提供的信息解答下列问题;频数频率A4BC a0.3D16b(1)求a,b的值;(2)求B等级对应扇形圆心角的度数;(3)学校要从A等级的学生中随机选取2人参加市级比赛,求A等级中的学生小明被选中参加市级比赛的概率.22.(10分)如图,BC是⊙O的直径,CE是⊙O的弦,过点E作⊙O的切线,交CB的延长线于点G,过点B作BF⊥GE于点F,交CE的延长线于点A.(1)求证:∠ABG=2∠C;(2)若GF=3√3,GB=6,求⊙O的半径.23.(10分)如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°.(1)如图1,连接BE,CD,BE的廷长线交AC于点F,交CD于点P,求证:BP⊥CD;(2)如图2,把△ADE绕点A顺时针旋转,当点D落在AB上时,连接BE,CD,CD 的延长线交BE于点P,若BC=6√2,AD=3,求△PDE的面积.24.(10分)如图,抛物线与x轴交于A,B两点,与y轴交于点C(0,﹣2),点A的坐标是(2,0),P为抛物线上的一个动点,过点P作PD⊥x轴于点D,交直线BC于点E,抛物线的对称轴是直线x=﹣1.(1)求抛物线的函数表达式;(2)若点P在第二象限内,且PE=14OD,求△PBE的面积.(3)在(2)的条件下,若M为直线BC上一点,在x轴的上方,是否存在点M,使△BDM是以BD为腰的等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.2019年山东省菏泽市中考数学试卷答案解析一.选择题(本大题共8个小题,每小题3分,共24分,在每小题给出的四个选项中,只有一个选项是正确的,请把正确选项的序号涂在答题卡的相应位置 1.(3分)下列各数中,最大的数是( ) A .−12B .14C .0D .﹣2【解答】解:﹣2<−12<0<14, 则最大的数是14,故选:B .2.(3分)下列图形中,既是轴对称图形,又是中心对称图形的是( )A .B .C .D .【解答】解:A 、不是轴对称图形,是中心对称图形,故此选项错误; B 、是轴对称图形,不是中心对称图形,故此选项错误; C 、是轴对称图形,也是中心对称图形,故此选项正确; D 、不是轴对称图形,是中心对称图形,故此选项错误; 故选:C .3.(3分)下列运算正确的是( ) A .(﹣a 3)2=﹣a 6B .a 2•a 3=a 6C .a 8÷a 2=a 4D .3a 2﹣2a 2=a 2【解答】解:A 、原式=a 6,不符合题意; B 、原式=a 5,不符合题意; C 、原式=a 6,不符合题意; D 、原式=a 2,符合题意, 故选:D .4.(3分)一个几何体的三视图如图所示,则这个几何体的表面积是( )A .5cm 2B .8cm 2C .9cm 2D .10cm 2【解答】解:由题意推知几何体是长方体,长、宽、高分别1cm 、1cm 、2cm , 所以其面积为:2×(1×1+1×2+1×2)=10(cm 2). 故选:D .5.(3分)已知{x =3y =−2是方程组{ax +by =2bx +ay =−3的解,则a +b 的值是( )A .﹣1B .1C .﹣5D .5【解答】解:将{x =3y =−2代入{ax +by =2bx +ay =−3,可得:{3a −2b =23b −2a =−3,两式相加:a +b =﹣1, 故选:A .6.(3分)如图,AB 是⊙O 的直径,C ,D 是⊙O 上的两点,且BC 平分∠ABD ,AD 分别与BC ,OC 相交于点E ,F ,则下列结论不一定成立的是( )A .OC ∥BDB .AD ⊥OCC .△CEF ≌△BED D .AF =FD【解答】解:∵AB 是⊙O 的直径,BC 平分∠ABD , ∴∠ADB =90°,∠OBC =∠DBC , ∴AD ⊥BD , ∵OB =OC , ∴∠OCB =∠OBC , ∴∠DBC =∠OCB ,∴OC∥BD,选项A成立;∴AD⊥OC,选项B成立;∴AF=FD,选项D成立;∵△CEF和△BED中,没有相等的边,∴△CEF与△BED不全等,选项C不成立;故选:C.7.(3分)在平面直角坐标系中,一个智能机器人接到的指令是:从原点O出发,按“向上→向右→向下→向右”的方向依次不断移动,每次移动1个单位长度,其移动路线如图所示,第一次移动到点A1,第二次移动到点A2……第n次移动到点A n,则点A2019的坐标是()A.(1010,0)B.(1010,1)C.(1009,0)D.(1009,1)【解答】解:A1(0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,1),A6(3,1),…,2019÷4=504…3,所以A2019的坐标为(504×2+1,0),则A2019的坐标是(1009,0).故选:C.8.(3分)如图,正方形ABCD的边长为2cm,动点P,Q同时从点A出发,在正方形的边上,分别按A→D→C,A→B→C的方向,都以1cm/s的速度运动,到达点C运动终止,连接PQ,设运动时间为xs,△APQ的面积为ycm2,则下列图象中能大致表示y与x的函数关系的是()A .B .C .D .【解答】解:①当0≤x ≤2时, ∵正方形的边长为2cm , ∴y =S △APQ =12AQ •AP =12x 2; ②当2≤x ≤4时, y =S △APQ=S 正方形ABCD ﹣S △CP ′Q ′﹣S △ABQ ′﹣S △AP ′D ,=2×2−12(4﹣x )2−12×2×(x ﹣2)−12×2×(x ﹣2) =−12x 2+2x所以,y 与x 之间的函数关系可以用两段二次函数图象表示,纵观各选项,只有A 选项图象符合. 故选:A .二、填空题(本大题共6个小题,每小题3分,共18分,只要求把最后结果填写在答题卡的相应区域内.)9.(3分)计算(12)﹣1﹣(﹣3)2的结果是 ﹣7 .【解答】解:原式=2﹣9=﹣7. 故答案为:﹣7.10.(3分)已知x =√6+√2,那么x 2﹣2√2x 的值是 4 . 【解答】解:∵x −√2=√6,∴x 2﹣2√2x +2=6, ∴x 2﹣2√2x =4, 故答案为:411.(3分)如图,AD ∥CE ,∠ABC =100°,则∠2﹣∠1的度数是 80° .【解答】解:作BF ∥AD , ∵AD ∥CE , ∴AD ∥BF ∥EC ,∴∠1=∠3,∠4+∠2=180°,∠3+∠4=100°, ∴∠1+∠4=100°,∠2+∠4=180°, ∴∠2﹣∠1=80°. 故答案为:80°.12.(3分)一组数据4,5,6,x 的众数与中位数相等,则这组数据的方差是12.【解答】解:若众数为4,则数据为4,4,5,6,此时中位数为4.5,不符合题意; 若众数为5,则数据为4,5,5,6,中位数为5,符合题意, 此时平均数为4+5+5+64=5,方差为14[(4﹣5)2+(5﹣5)2+(5﹣5)2+(6﹣5)2]=12;若众数为6,则数据为4,5,6,6,中位数为5.5,不符合题意; 故答案为12.13.(3分)如图,E ,F 是正方形ABCD 的对角线AC 上的两点,AC =8,AE =CF =2,则四边形BEDF 的周长是 8√5 .【解答】解:如图,连接BD交AC于点O,∵四边形ABCD为正方形,∴BD⊥AC,OD=OB=OA=OC,∵AE=CF=2,∴OA﹣AE=OC﹣CF,即OE=OF,∴四边形BEDF为平行四边形,且BD⊥EF,∴四边形BEDF为菱形,∴DE=DF=BE=BF,∵AC=BD=8,OE=OF=8−42=2,由勾股定理得:DE=√OD2+OE2=√42+22=2√5,∴四边形BEDF的周长=4DE=4×2√5=8√5,故答案为:8√5.14.(3分)如图,直线y=−34x﹣3交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是(−73,0)或P(−173,0).【解答】解:∵直线y =−34x ﹣3交x 轴于点A ,交y 轴于点B , ∴令x =0,得y =﹣3,令y =0,得x =﹣4, ∴A (﹣4,0),B (0.﹣3), ∴OA =4,OB =3, ∴AB =5,设⊙P 与直线AB 相切于D , 连接PD ,则PD ⊥AB ,PD =1,∵∠ADP =∠AOB =90°,∠P AD =∠BAO , ∴△APD ∽△ABO , ∴PD OB =AP AB,∴13=AP 5,∴AP =53, ∴OP =73或OP =173, ∴P (−73,0)或P (−173,0), 故答案为:(−73,0)或P (−173,0).三、解答题(本题共78分,把解答或证明过程写在答题卡的相应区域内) 15.(6分)解不等式组:{x −3(x −2)≥−4,x −1<2x+13.【解答】解:解不等式x ﹣3(x ﹣2)≥﹣4,得:x ≤5, 解不等式x ﹣1<2x+13,得:x <4, 则不等式组的解集为x <4.16.(6分)先化简,再求值:1x−y (2yx+y−1)÷1y2−x2,其中x=y+2019.【解答】解:1x−y (2yx+y−1)÷1y2−x2=1x−y⋅2y−(x+y)x+y⋅(y+x)(y−x)=﹣(2y﹣x﹣y)=x﹣y,∵x=y+2019,∴原式=y+2019﹣y=2019.17.(6分)如图,四边形ABCD是矩形.(1)用尺规作线段AC的垂直平分线,交AB于点E,交CD于点F(不写作法,保留作图痕迹);(2)若BC=4,∠BAC=30°,求BE的长.【解答】解:(1)如图所示:(2)∵四边形ABCD是矩形,EF是线段AC的垂直平分线,∴AE=EC,∠CAB=∠ACE=30°,∴∠ECB=60°,∴∠ECB=30°,∵BC=4,∴BE=4√3 3.18.(6分)列方程(组)解应用题:德上高速公路巨野至单县段正在加速建设,预计2019年8月竣工.届时,如果汽车行驶高速公路上的平均速度比在普通公路上的平均速度提高80%,那么行驶81千米的高速公路比行驶同等长度的普通公路所用时间将会缩短36分钟,求该汽车在高速公路上的平均速度.【解答】解:设汽车行驶在普通公路上的平均速度是x千米/分钟,则汽车行驶在高速公路上的平均速度是1.8x千米/分钟,由题意,得811.8x+36=81x.解得x=1.经检验,x=1是所列方程的根,且符合题意.所以1.8x=1.8(千米/分钟).答:汽车行驶在高速公路上的平均速度是1.8千米/分钟.19.(7分)由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达A处时,测得小岛B位于它的北偏东30°方向,且与航母相距80海里再航行一段时间后到达C处,测得小岛B位于它的西北方向,求此时航母与小岛的距离BC的长.【解答】解:过点C作CD⊥AB于点D,由题意,得:∠BAD=60°,∠BCD=45°,AB=80,在Rt△ADB中,∠BAD=60°,∴AD=12AB=40,BD=√32AB=40√3,在Rt△BCD中,∠BCD=45°,∴BD=CD=40√3,∴BC=√2BD=40√6,答:BC的距离是40√6海里.20.(7分)如图,▱ABCD 中,顶点A 的坐标是(0,2),AD ∥x 轴,BC 交y 轴于点E ,顶点C 的纵坐标是﹣4,▱ABCD 的面积是24.反比例函数y =kx的图象经过点B 和D ,求: (1)反比例函数的表达式; (2)AB 所在直线的函数表达式.【解答】解:(1)∵顶点A 的坐标是(0,2),顶点C 的纵坐标是﹣4, ∴AE =6,又▱ABCD 的面积是24, ∴AD =BC =4, 则D (4,2) ∴k =4×2=8,∴反比例函数解析式为y =8x ;(2)由题意知B 的纵坐标为﹣4, ∴其横坐标为﹣2, 则B (﹣2,﹣4),设AB 所在直线解析式为y =kx +b ,将A (0,2)、B (﹣2,﹣4)代入,得:{b =2−2k +b =−4,解得:{k =3b =2,所以AB 所在直线解析式为y =3x +2.21.(10分)4月23日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”我市某中学响应号召,鼓励师生利用课余时间广泛阅读,该校文学社发起了“读书感悟•分享”比赛活动根据参赛学生的成绩划分为A,B,C,D四个等级,并绘制了下面不完整的统计图表,根据图表中提供的信息解答下列问题;频数频率A4BC a0.3D16b(1)求a,b的值;(2)求B等级对应扇形圆心角的度数;(3)学校要从A等级的学生中随机选取2人参加市级比赛,求A等级中的学生小明被选中参加市级比赛的概率.【解答】解:(1)总人数:4÷10%=40,a=40×0.3=12,b=1640=0.4;(2)B的频数:40﹣4﹣12﹣16=8,B等级对应扇形圆心角的度数:840×360°=72°;(3)用a表示小明,用b、c、d表示另外三名同学.则选中小明的概率是:612=1 2.22.(10分)如图,BC是⊙O的直径,CE是⊙O的弦,过点E作⊙O的切线,交CB的延长线于点G,过点B作BF⊥GE于点F,交CE的延长线于点A.(1)求证:∠ABG=2∠C;(2)若GF=3√3,GB=6,求⊙O的半径.【解答】(1)证明:连接OE,∵EG是⊙O的切线,∴OE⊥EG,∵BF⊥GE,∴OE∥AB,∴∠A=∠OEC,∵OE=OC,∴∠OEC=∠C,∴∠A=∠C,∵∠ABG=∠A+∠C,∴∠ABG=2∠C;(2)解:∵BF⊥GE,∴∠BFG=90°,∵GF=3√3,GB=6,∴BF=√BG2−GF2=3,∵BF∥OE,∴△BGF∽△OGE,∴BFOE =BGOG,∴3OE =66+OE,∴OE=6,∴⊙O的半径为6.23.(10分)如图,△ABC 和△ADE 是有公共顶点的等腰直角三角形,∠BAC =∠DAE =90°.(1)如图1,连接BE ,CD ,BE 的廷长线交AC 于点F ,交CD 于点P ,求证:BP ⊥CD ; (2)如图2,把△ADE 绕点A 顺时针旋转,当点D 落在AB 上时,连接BE ,CD ,CD 的延长线交BE 于点P ,若BC =6√2,AD =3,求△PDE 的面积.【解答】解:(1)∵△ABC 和△ADE 是有公共顶点的等腰直角三角形,∠BAC =∠DAE =90°.∴AD =AE ,AB =AC ,∠BAC ﹣∠EAF =∠EAD ﹣∠EAF , 即∠BAE =∠DAC ,在△ABE 与△ADC 中,{AB =AC∠BAE =∠CAD AE =AD ,∴△ABE ≌△ADC (SAS ), ∴∠ABE =∠ACD ,∵∠ABE +∠AFB =∠ABE +∠CFP =90°, ∴∠CPF =90°, ∴BP ⊥CD ;(2)在△ABE 与△ACD 中,{AE =AD∠EAB =∠CAB =90°AB =AC ,∴△ABE ≌△ACD (SAS ), ∴∠ABE =∠ACD ,BE =CD , ∵∠PDB =∠ADC , ∴∠BPD =∠CAB =90°,∴∠EPD =90°,BC =6√2,AD =3,求△PDE 的面积.∵BC =6√2,AD =3, ∴DE =3√2,AB =6,∴BD =6﹣3=3,CD =√AD 2+AC 2=3√5, ∵△BDP ∽△CDA , ∴BD CD =PD AD =PB AC , ∴3√5=PD 3=PB6,∴PD =3√55,PB =6√55 ∴PE =3√5−6√55=9√55, ∴△PDE 的面积=12×9√55×3√55=2710.24.(10分)如图,抛物线与x 轴交于A ,B 两点,与y 轴交于点C (0,﹣2),点A 的坐标是(2,0),P 为抛物线上的一个动点,过点P 作PD ⊥x 轴于点D ,交直线BC 于点E ,抛物线的对称轴是直线x =﹣1.(1)求抛物线的函数表达式;(2)若点P 在第二象限内,且PE =14OD ,求△PBE 的面积.(3)在(2)的条件下,若M 为直线BC 上一点,在x 轴的上方,是否存在点M ,使△BDM 是以BD 为腰的等腰三角形?若存在,求出点M 的坐标;若不存在,请说明理由. 【解答】解:(1)点A 的坐标是(2,0),抛物线的对称轴是直线x =﹣1,则点B (﹣4,0),则函数的表达式为:y =a (x ﹣2)(x +4)=a (x 2+2x ﹣8), 即:﹣8a =﹣2,解得:a =14,故抛物线的表达式为:y =14x 2+12x ﹣2;(2)将点B 、C 的坐标代入一次函数表达式:y =mx +n 并解得: 直线BC 的表达式为:y =−12x ﹣2,则tan ∠ABC =12,则sin ∠ABC =5, 设点D (x ,0),则点P (x ,14x 2+12x ﹣2),点E (x ,12x ﹣2),∵PE =14OD ,∴PE =(14x 2+12x ﹣2−12x +2)=14(﹣x ),解得:x =0或﹣5(舍去x =0),即点D (﹣5,0)S △PBE =12×PE ×BD =12(14x 2+12x ﹣2−12x +2)(﹣4﹣x )=58;(3)由题意得:△BDM 是以BD 为腰的等腰三角形,①当BD =BM 时,过点M 作MH ⊥x 轴于点H ,BD =1=BM ,则MH =y M =BM sin ∠ABC =1×1√5=√55,则x M =20+2√55,故点M (−20+2√55,−√55);②当BD =DM (M ′)时,同理可得:点M′(−235,45);故点M坐标为(−20+2√55,−√55)或(−235,45).。
2019年山东省菏泽市中考数学试题及答案(word版)

2019年山东省菏泽市中考数学试题及答案2019年山东省菏泽市中考数学试题及答案一、选择题(本大题共8个小题,每小题3分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(2018菏泽)点P(﹣2,1)在平面直角坐标系中所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限考点:点的坐标。
解答:解:点P(﹣2,1)在第二象限.故选B.2.(2018菏泽)在算式()□()的□中填上运算符号,使结果最大,这个运算符号是()A.加号B.减号C.乘号D.除号考点:实数的运算;实数大小比较。
解答:解:当填入加号时:()+()=﹣;当填入减号时:()﹣()=0;当填入乘号时:()×()=;当填入除号时:()÷()=1.∵1>>0>﹣,∴这个运算符号是除号.故选D.3.(2018菏泽)如果用□表示1个立方体,用表示两个立方体叠加,用■表示三个立方体叠加,那么下面图是由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是()A .B .C .D .考点:简单组合体的三视图。
解答:解:从正前方观察,应看到长有三个立方体,且中间的为三个立方体叠加;高为两个立方体,在中间且有两个立方体叠加.故选B .4.(2018菏泽)已知是二元一次方程组的解,则的算术平方根为( )A .±2B . 2C .2D . 4考点:二元一次方程组的解;算术平方根。
解答:解:∵是二元一次方程组的解, ∴, 解得:,∴2m ﹣n=4,∴的算术平方根为2.故选C .5.(2018菏泽)下列图形中是中心对称图形是( )A .B .C .D .考点:中心对称图形。
解答:解:A 、不是中心对称图形,故本选项错误;B 、不是中心对称图形,故本选项错误;C 、不是中心对称图形,故本选项错误; ⎩⎨⎧==12y x 81mx ny nx my +=⎧⎨-=⎩n m -2⎩⎨⎧==12y x ⎩⎨⎧=-=+18my nx ny mx 2821m n n m +=⎧⎨-=⎩32m n =⎧⎨=⎩n m -2D 、是中心对称图形,故本选项正确.故选D .6.(2018菏泽)反比例函数的两个点为、,且,则下式关系成立的是( )A .B .C .D .不能确定考点:反比例函数图象上点的坐标特征。
2019年山东省菏泽市中考地理试题(Word版,含解析)
2019年山东省菏泽市中考地理试卷一、本大题包括20个小题每小题2分,共20分.在每小题所列的四个选项中,只有一项最符合题目要求.1.台湾省是我国地震多发区,2019年4月18日花莲县附近(北纬24.13度,东经121.52度)发生6.1级左右地震。
据此并结合图完成1~2题。
有关台湾岛自然地理特点的叙述,正确的是()A.平原主要分布在岛屿东部B.西部是迎风坡,比东部降水多C.河流水流湍急,水能丰富D.全年高温多雨,森林资源丰富2.台湾省是我国地震多发区,2019年4月18日花莲县附近(北纬24.13度,东经121.52度)发生6.1级左右地震。
据此并结合图完成1~2题。
台湾省地震多发频发,主要因为其位于()A.太平洋的大洋中脊B.印度洋大陆架附近C.欧亚板块的内部D.板块与板块交界附近3.如图三幅图是东北地区地理事物分布图。
读图完成3~4题。
东北地区的城市主要分布在()A.交通干线沿线地区B.森林资源丰富的地区C.蒙古族集中分布区D.纬度较高的山谷地区4.如图三幅图是东北地区地理事物分布图。
读图完成3~4题。
赫哲族和鄂伦春族的集中分布区分别是()A.长白山山林地带和辽河平原B.三江平原和大、小兴安岭山林地带C.松嫩平原和三江平原D.辽河平原和大、小兴安岭山林地带5.随着西部大开发的逐步深入,国家加大了支持新疆发展力度。
读“新疆地形图”,完成5~6题。
新疆经济发展方向不合理的是()A.山地牧场广阔,多优良畜种,大力发展畜牧业B.石油资源丰富,发展石油开采和加工工业C.邻国众多,河网稠密,发展内河航运,促进商贸流通D.光照强,昼夜温差大,水果优质,发展水果种植与加工业6.随着西部大开发的逐步深入,国家加大了支持新疆发展力度。
读“新疆地形图”,完成5~6题。
关于新疆主要地形的叙述,正确的是()A.①盆地是我国海拔最高的盆地B.②山脉的南侧是青藏高原C.③山脉是阴山,呈东西走向D.④盆地东邻黄土高原7.读“辽中南地区示意图”和“珠江三角洲地区示意图”,完成7~8题。
山东省菏泽市2019年中考物理试卷(含答案解析)
山东省菏泽市2019年中考物理试卷一、单选题(共12题;共24分)1.通常情况下,下列物品属于导体的是()A. 橡胶棒B. 玻璃棒C. 陶瓷筷子D. 湿木棒2.下列电器中,利用电流热效应工作的是()A. 电风扇B. 电暖气C. 电视机D. 电磁继电器3.公共汽车紧急刹车时,乘客从座位上向前冲的原因是()A. 乘客没坐稳B. 乘客没抓好扶手C. 乘客具有惯性D. 乘客的座位太光滑4.下列关于摩擦的说法中,正确的是()A. 自行车的钢圈与刹车闸皮之间的摩擦是滚动摩擦B. 滑冰时,冰刀与冰面间的摩擦是滑动摩擦C. 人在正常行走时,脚与地面之间的摩擦是滑动摩擦D. 划火柴时,火柴头和砂纸之间的摩擦是滚动摩擦5.下列说法中,错误的是()A. 声音的响度与发声体振动的快慢有关B. 声音在不同介质中传播的速度一般不相同C. 利用超声波清洗眼镜,说明声波可以传递能量D. 真空不能传播声音6.下列各项操作中,不符合安全用电原则的是()A. 更换电灯泡时,要断开电源开关B. 使用验电笔时,手要接触验电笔后端的金属部分C. 在家庭电路的前端安装空气开关D. 电器电线绝缘皮破损了,仍然继续使用7.当滑动变阻器的滑片向b端滑动时,下列四种接法中,变阻器阻值变大的是()A. B.C. D.8.下列对于科学研究的方法,说法错误的是()A. 在研究光现象时,引入“光线”的概念--类比法B. 牛顿第一运动定律--实验+推理C. 在研究串联电路的电阻时,引入“总电阻”的概念--等效法D. 在研究磁场时,根据小磁针的指向判断磁场方向--转换法9.下列电路中两个灯泡都能够独立工作的是()A. B.C. D.10.人们常用“生沉熟浮”来判断饺子是否煮熟,煮熟后的饺子会漂起来的原因是()A. 饺子的重力减小了B. 饺子的重力和浮力都增大了C. 饺子的重力不变,浮力增大D. 饺子的重力和浮力都减小了11.如图所示,关于家用插座说法中,正确的是()A. 开关串联在干路中,指示灯与各组插孔并联在电路中B. 开关、指示灯和各组插孔并联在电路中C. 开关、指示灯和各组插孔串联在电路中D. 各组插孔串联在一起与指示灯并联在电路中12.如图所示电路(电源电压保持不变),闭合开关S,当滑动变阻器的滑片向右端移动时,下列说法正确的是()A. 电压表示数不变,电流表示数变大B. 电压表示数变大,电流表示数变小C. 电压表示数变小,电流表示数变小D. 电压表示数变大,电阻R1的电功率变大二、填空题(共5题;共5分)13.小明站在穿衣镜前1.5m处,他看到自己在镜中的像是一个等大的________像(选填“实”或“虚”),他的像与他之间的距离是________m.(玻璃厚度忽略不计)14.中美经贸摩擦实质上是科技实力的较量。
2019年菏泽市中考语文试卷与答案
卷I 型:A参考答案注意事项:1. 本试题共三个大题,22 个小题,满分120 分, 考试时间120 分钟。
2. 用黑色、蓝色水笔或钢笔答卷。
答题前将密封线内的项目填写清楚。
一、古诗文积累(30 分)一经典诗文积累1、默写唐代诗人王昌龄的《采莲曲》一诗。
( 4 分)__________________________,__________________________ 。
__________________________,__________________________ 。
2、依据课文填空。
( 4 分)①__________________________ ,必先苦其心志。
(孟子《生于忧患,死于安乐》)②此中有真意,_________________。
(陶渊明《饮酒》)③___________,____________,和风细雨不须归。
(张志和《渔父》)3、根据提示默写。
( 4 分)①李商隐《夜雨寄北》中想象将来与亲友团聚、剪烛夜话的句子:__________________________,__________________________ 。
②陆游《卜算子·咏梅》中描写梅花即使被碾压成泥,也依旧保持清香的句子:__________________________,__________________________ 。
(二)阅读下面诗歌,完成第4-5 题。
(4 分)雨后池上(宋)刘攽一雨池塘水面平,淡磨明镜照薝楹。
东风忽起垂杨舞,更作荷心万点声。
注释:①薝楹:薝廊。
②更:又。
4、诗题为《雨后池上》,那么,诗中从哪些方面表现了“雨后”二字?( 2 分)5、请简要赏析第二段加点词语的妙处。
( 2 分)(三)阅读下文,完成第6-10 题。
(14 分)远尔【甲】潭中鱼可百许头,皆若空游无所依。
日光下澈,影布石上,佁然不动;俶逝,往来翕忽,似与游者相乐。
潭西南而望,斗折蛇行,明灭可见。
山东省菏泽市中考英语试题(word版,含解析)
山东省菏泽市2019年中考英语试题选择题(共80分)一、听力(共四节,满分7.5分)做题时,先将答案标在试卷上,录音内容结束后,请将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题 1.5分,满分7.5分)听下面5个句子每个句子后有三幅图画,每个句子仅读一遍。
请你从每题所给的A、B、C三个选项中选出与句子内容相符的图画,并标在试卷的相应位置。
1.(1.5分)2.(1.5分)3.(1.5分)4.(1.5分)5.(1.5分)第二节(共5小题;每小题 1.5分,满分7.5分)听下面5个句子,每个句子后有一道小题,每个句子读两遍,请你听完句子的第二遍朗读后,从每题所给的A、B、C三个选项中选出最佳答语并标在试卷的相应位置。
6.(1.5分)A.You're welcome.B.It doesn't matter.C.Sorry to hear that.7.(1.5分)A.Yes,I can.B.No,I can't.C.Sorry,I won't.8.(1.5分)A.I want to be a teacher.B.I'm 12 years old.C.I'd like some noodles.9.(1.5分)A.It's very beautiful.B.Yes,I have.C.Sounds good.10.(1.5分)A.Enjoy the full moon.B.Watch the boat races.C.Make snowmen.第三节(共1小题;每小题7.5分,满分7.5分) 听下面5段对话,每段对话后有一道小题,每段对话和问题读两遍,请你听完对话和问题的第二遍朗读后,从每题所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
11.(7.5分)(1)How much is the red hat?A.It's five dollars.B.It's ten dollars.C.It's fifteen dollars.(2)Why can't Tim come to the party?A.He has to do the dishes.B.He has to clean his room.C.He has to study for a test.(3)Why can't Tim come to the party?A.He has to do the dishes.B.He has to clean his room.C.He has to study for a test.(4)What should Peter do?A.Write to David and say thanks.B.Call David and say sorry.C.Email David and say hello.(5)Who probably answered the telephone just now?A.Rick.B.Lucy.C.Lucy's mother.第四节(共1小题;每小题7.5分,满分7.5分) 听下面一段短文,短文后有五道小题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019年山东省菏泽市中考试题解析(满分120分,考试时间120分钟)一、选择题(本大题共8小题,每小题3分,共24分)1.(2019山东菏泽,1,3分)下列各数中,最大的数是( )A .−12B .14C .0D .﹣2【答案】B【解析】解:﹣2<−12<0<14,则最大的数是14,故选B . 【知识点】有理数大小比较2. (2019山东菏泽,2,3分)下列图形中,既是轴对称图形,又是中心对称图形的是( )【答案】C【解析】解:A 、不是轴对称图形,是中心对称图形,故此选项错误;B 、是轴对称图形,不是中心对称图形,故此选项错误;C 、是轴对称图形,也是中心对称图形,故此选项正确;D 、不是轴对称图形,是中心对称图形,故此选项错误,故选C .【知识点】轴对称图形;中心对称图形3. (2019山东菏泽,3,3分)下列运算正确的是( )A .(﹣a 3)2=﹣a 6B .a 2•a 3=a 6C .a 8÷a 2=a 4D .3a 2﹣2a 2=a 2 【答案】D【解析】解:A 、原式=a 6,不符合题意;B 、原式=a 5,不符合题意;C 、原式=a 6,不符合题意;D 、原式=a 2,符合题意,故选D .【知识点】合并同类项;同底数幂的乘法;幂的乘方与积的乘方;同底数幂的除法4. (2019山东菏泽,4,3分)一个几何体的三视图如图所示,则这个几何体的表面积是( )A .5cm 2B .8cm 2C .9cm 2D .10cm 2【答案】D【解析】解:由题意推知几何体是长方体,长、宽、高分别1cm 、1cm 、2cm ,所以其面积为:2×(1×1+1×2+1×2)=10(cm 2),故选D .【知识点】由三视图判断几何体5. (2019山东菏泽,5,3分))已知{x =3y =−2是方程组{ax +by =2bx +ay =−3的解,则a +b 的值是( ) A .﹣1B .1C .﹣5D .5 【答案】A【解析】解:将{x =3y =−2代入{ax +by =2bx +ay =−3, 可得:{3a −2b =23b −2a =−3, 两式相加:a +b =﹣1,故选A .【知识点】二元一次方程组的解6.(2019山东菏泽,6,3分)如图,AB 是⊙O 的直径,C ,D 是⊙O 上的两点,且BC 平分∠ABD ,AD 分别与BC ,OC 相交于点E ,F ,则下列结论不一定成立的是( )A .OC ∥BDB .AD ⊥OC C .△CEF ≌△BED D .AF =FD【答案】C【解析】解:∵AB 是⊙O 的直径,BC 平分∠ABD ,∴∠ADB =90°,∠OBC =∠DBC ,∴AD ⊥BD ,∵OB =OC ,∴∠OCB =∠OBC ,∴∠DBC =∠OCB ,∴OC ∥BD ,选项A 成立;∴AD⊥OC,选项B成立;∴AF=FD,选项D成立;∵△CEF和△BED中,没有相等的边,∴△CEF与△BED不全等,选项C不成立,故选C.【知识点】圆周角定理7.(2019山东菏泽,7,3分)在平面直角坐标系中,一个智能机器人接到的指令是:从原点O出发,按“向上→向右→向下→向右”的方向依次不断移动,每次移动1个单位长度,其移动路线如图所示,第一次移动到点A1,第二次移动到点A2……第n次移动到点A n,则点A2019的坐标是()A.(1010,0)B.(1010,1)C.(1009,0)D.(1009,1)【答案】C【解析】解:A1(0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,1),A6(3,1),…,2019÷4=504…3,所以A2019的坐标为(504×2+1,0),则A2019的坐标是(1009,0),故选C.【知识点】点的坐标规律8.(2019山东菏泽,8,3分)如图,正方形ABCD的边长为2cm,动点P,Q同时从点A出发,在正方形的边上,分别按A→D→C,A→B→C的方向,都以1cm/s的速度运动,到达点C运动终止,连接PQ,设运动时间为xs,△APQ的面积为ycm2,则下列图象中能大致表示y与x的函数关系的是()【答案】A【解析】解:①当0≤x ≤2时,∵正方形的边长为2cm ,∴y =S △APQ =12AQ •AP =12x 2;②当2≤x ≤4时,y =S △APQ =S 正方形ABCD ﹣S △CP ′Q ′﹣S △ABQ ′﹣S △AP ′D ,=2×2−12(4﹣x )2−12×2×(x ﹣2)−12×2×(x ﹣2)=−12x 2+2x∴y 与x 之间的函数关系可以用两段二次函数图象表示,纵观各选项,只有A 选项图象符合.故选A .【知识点】动点问题的函数图象二、填空题(本大题共6小题,每小题3分,共18分)9.(2019山东菏泽,9,3分)计算(12)﹣1﹣(﹣3)2的结果是_________ 【答案】﹣7【解析】解:原式=2﹣9=﹣7.【知识点】实数运算;有理数的乘方;有理数的减法;负整数指数幂10. (2019山东菏泽,10,3分)已知x =√6+√2,那么x 2﹣2√2x 的值是_________【答案】4.【解析】解:∵x −√2=√6,∴x 2﹣2√2x +2=6,∴x 2﹣2√2x =4.【知识点】二次根式的化简求值11. (2019山东菏泽,11,3分)如图,AD ∥CE ,∠ABC =100°,则∠2﹣∠1的度数是_________【答案】80° 【解析】解:作BF ∥AD ,∵AD ∥CE ,∴AD ∥BF ∥EC ,∴∠1=∠3,∠4+∠2=180°,∠3+∠4=100°,∴∠1+∠4=100°,∠2+∠4=180°,∴∠2﹣∠1=80°.故答案为:80°.【知识点】平行线的性质12. (2019山东菏泽,12,3分)一组数据4,5,6,x 的众数与中位数相等,则这组数据的方差是_________ 【答案】12【解析】解:若众数为4,则数据为4,4,5,6,此时中位数为4.5,不符合题意;若众数为5,则数据为4,5,5,6,中位数为5,符合题意,此时平均数为4+5+5+64=5,方差为14[(4﹣5)2+(5﹣5)2+(5﹣5)2+(6﹣5)2]=12; 若众数为6,则数据为4,5,6,6,中位数为5.5,不符合题意, 故答案为12. 【知识点】中位数;众数;方差13. (2019山东菏泽,13,3分)如图,E ,F 是正方形ABCD 的对角线AC 上的两点,AC =8,AE =CF =2,则四边形BEDF 的周长是 .【答案】【解析】解:如图,连接BD 交AC 于点O ,∵四边形ABCD 为正方形,∴BD ⊥AC ,OD =OB =OA =OC ,∵AE=CF=2,∴OA﹣AE=OC﹣CF,即OE=OF,∴四边形BEDF为平行四边形,且BD⊥EF,∴四边形BEDF为菱形,∴DE=DF=BE=BF,∵AC=BD=8,OE=OF=8−42=2,由勾股定理得:DE=√OD2+OE2=√42+22=2√5,∴四边形BEDF的周长=4DE=4×2√5=8√5,故答案为:【知识点】全等三角形的判定与性质;正方形的性质14.(2019山东菏泽,14,3分)如图,直线y=−34x﹣3交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是.【答案】(−73,0)或P(−173,0).【解析】解:∵直线y=−34x﹣3交x轴于点A,交y轴于点B,∴令x=0,得y=﹣3,令y=0,得x=﹣4,∴A(﹣4,0),B(0.﹣3),∴OA=4,OB=3,∴AB=5,设⊙P与直线AB相切于D,连接PD,则PD⊥AB,PD=1,∵∠ADP=∠AOB=90°,∠P AD=∠BAO,∴△APD∽△ABO,∴PDOB=APAB,∴13=AP 5, ∴AP =53,∴OP =73或OP =173,∴P (−73,0)或P (−173,0), 故答案为:(−73,0)或P (−173,0).【知识点】一次函数的图象;切线的判定与性质; 相似三角形的判定和性质三、解答题(本大题共8小题,满分78分,各小题都必须写出解答过程)15. (2019山东菏泽,15,6分)解不等式组:{x −3(x −2)≥−4,x −1<2x+13. 【思路分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.【解题过程】解:解不等式x ﹣3(x ﹣2)≥﹣4,得:x ≤5,解不等式x ﹣1<2x+13,得:x <4, 则不等式组的解集为x <4.【知识点】解一元一次不等式组16.(2019山东菏泽,16,6分)先化简,再求值:1x−y (2y x+y −1)÷1y 2−x 2,其中x =y +2019.【思路分析】根据分式的减法和乘除法可以化简题目中的式子,然后将x =y +2019代入化简后的式子即可解答本题.【解题过程】解:1x−y (2y x+y −1)÷1y 2−x 2 =1x−y ⋅2y−(x+y)x+y⋅(y +x)(y −x) =﹣(2y ﹣x ﹣y )=x ﹣y ,∵x =y +2019,∴原式=y +2019﹣y =2019.【知识点】分式的化简求值17.(2019山东菏泽,17,6分)如图,四边形ABCD是矩形.(1)用尺规作线段AC的垂直平分线,交AB于点E,交CD于点F(不写作法,保留作图痕迹);(2)若BC=4,∠BAC=30°,求BE的长.【思路分析】(1)根据线段的垂直平分线的作图解答即可;(2)利用含30°的直角三角形的性质解答即可.【解题过程】解:(1)如图所示:(2)∵四边形ABCD是矩形,EF是线段AC的垂直平分线,∴AE=EC,∠CAB=∠ACE=30°,∴∠ECB=60°,∴∠ECB=30°,∵BC=4,∴BE=4√3 3.【知识点】矩形的性质;线段垂直平分线的性质;作图18.(2019山东菏泽,18,6分)列方程(组)解应用题:德上高速公路巨野至单县段正在加速建设,预计2019年8月竣工.届时,如果汽车行驶高速公路上的平均速度比在普通公路上的平均速度提高80%,那么行驶81千米的高速公路比行驶同等长度的普通公路所用时间将会缩短36分钟,求该汽车在高速公路上的平均速度.【思路分析】设汽车行驶在普通公路上的平均速度是x千米/分钟,则汽车行驶在高速公路上的平均速度是1.8x 千米/分钟,根据“行驶81千米的高速公路比行驶同等长度的普通公路所用时间将会缩短36分钟”列出方程并解答.【解题过程】解:设汽车行驶在普通公路上的平均速度是x千米/分钟,则汽车行驶在高速公路上的平均速度是1.8x千米/分钟,由题意,得811.8x+36=81x.解得x=1.经检验,x=1是所列方程的根,且符合题意.所以1.8x=1.8(千米/分钟).答:汽车行驶在高速公路上的平均速度是1.8千米/分钟.【知识点】分式方程的应用19.(2019山东菏泽,19,7分)由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达A处时,测得小岛B位于它的北偏东30°方向,且与航母相距80海里再航行一段时间后到达C处,测得小岛B位于它的西北方向,求此时航母与小岛的距离BC的长.【思路分析】过点C作CD⊥AB于点D,根据题意得到∠BAD=60°,∠BCD=45°,AC=80,解直角三角形即可得到结论.【解题过程】解:过点C作CD⊥AB于点D,由题意,得:∠BAD=60°,∠BCD=45°,AC=80,在Rt△ADB中,∠BAD=60°,∴tan60°=BDAD=√3,∴AD=BD √3,在Rt△BCD中,∠BCD=45°,∴tan45°=BDCD=1,∴BD=CD,∴AC=AD+CD=BD3+BD=80,∴BD=120﹣40√3,∴BC=√2BC=120√2−40√6,答:BC的距离是(120√2−40√6)海里.【知识点】解直角三角形的应用﹣方向角问题20. (2019山东菏泽,20,7分)如图,▱ABCD 中,顶点A 的坐标是(0,2),AD ∥x 轴,BC 交y 轴于点E ,顶点C 的纵坐标是﹣4,▱ABCD 的面积是24.反比例函数y =k x的图象经过点B 和D ,求:(1)反比例函数的表达式;(2)AB 所在直线的函数表达式.【思路分析】(1)根据题意得出AE =6,结合平行四边形的面积得出AD =BC =4,继而知点D 坐标,从而得出反比例函数解析式;(2)先根据反比例函数解析式求出点B 的坐标,再利用待定系数法求解可得.【解题过程】解:(1)∵顶点A 的坐标是(0,2),顶点C 的纵坐标是﹣4,∴AE =6,又▱ABCD 的面积是24,∴AD =BC =4,则D (4,2)∴k =4×2=8,∴反比例函数解析式为y =8x ;(2)由题意知B 的纵坐标为﹣4,∴其横坐标为﹣2,则B (﹣2,﹣4),设AB 所在直线解析式为y =kx +b ,将A (0,2)、B (﹣2,﹣4)代入,得:{b =2−2k +b =−4, 解得:{k =3b =2, 所以AB 所在直线解析式为y =3x +2.【知识点】待定系数法求一次函数解析式;反比例函数系数k 的几何意义;平行四边形的性质21.(2019山东菏泽,21,10分)4月23日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”我市某中学响应号召,鼓励师生利用课余时间广泛阅读,该校文学社发起了“读书感悟•分享”比赛活动根据参赛学生的成绩划分为A,B,C,D四个等级,并绘制了下面不完整的统计图表,根据图表中提供的信息解答下列问题;频数频率A4BC a0.3D16b(1)求a,b的值;(2)求B等级对应扇形圆心角的度数;(3)学校要从A等级的学生中随机选取2人参加市级比赛,求A等级中的学生小明被选中参加市级比赛的概率.【思路分析】(1)根据A等级有4人,所占的百分比是10%即可求得总人数,然后求得a和b的值;(2)首先计算出B等级频数,再利用360°乘以对应的百分比即可求得B等级所对应的圆心角度数;(3)利用列举法求得选中A等级的小明的概率.【解题过程】解:(1)总人数:4÷10%=40,a=40×0.3=12,b=1640=0.4;(2)B的频数:40﹣4﹣12﹣16=8,B等级对应扇形圆心角的度数:840×360°=72°;(3)用a表示小明,用b、c、d表示另外三名同学.则选中小明的概率是:612=12.【知识点】扇形统计图;频数(率)分布表;概率22.(2019山东菏泽,22,10分)如图,BC是⊙O的直径,CE是⊙O的弦,过点E作⊙O的切线,交CB的延长线于点G,过点B作BF⊥GE于点F,交CE的延长线于点A.(1)求证:∠ABG=2∠C;(2)若GF=3√3,GB=6,求⊙O的半径.【思路分析】(1)连接OE,根据切线的性质得到OE⊥EG,推出OE∥AB,得到∠A=∠OEC,根据等腰三角形的性质得到∠OEC=∠C,求得∠A=∠C,根据三角形的外角的性质即可得到结论;(2)根据勾股定理得到BF=√BG2−GF2=3,根据相似三角形的性质即可得到结论.【解题过程】解:(1)证明:连接OE,∵EG是⊙O的切线,∴OE⊥EG,∵BF⊥GE,∴OE∥AB,∴∠A=∠OEC,∵OE=OC,∴∠OEC=∠C,∴∠A=∠C,∵∠ABG=∠A+∠C,∴∠ABG=2∠C;(2)解:∵BF⊥GE,∴∠BFG=90°,∵GF=3√3,GB=6,∴BF=√BG2−GF2=3,∵BF∥OE,∴△BGF∽△OGE,∴BFOE=BGOG,∴3OE=66+OE,∴OE=6,∴⊙O的半径为6.【知识点】圆周角定理;切线的性质;相似三角形的判定和性质;等腰三角形的判定和性质23.(2019山东菏泽,23,10分)如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°.(1)如图1,连接BE,CD,BE的廷长线交AC于点F,交CD于点P,求证:BP⊥CD;(2)如图2,把△ADE绕点A顺时针旋转,当点D落在AB上时,连接BE,CD,CD的延长线交BE于点P,若BC=6√2,AD=3,求△PDE的面积.【思路分析】(1)根据等腰直角三角形的性质得到AD=AE,AB=AC,∠BAC﹣∠EAF=∠EAD﹣∠EAF,求得∠BAE=∠DAC,根据全等三角形的性质得到∠ABE=∠ACD,根据余角的性质即可得到结论;(2)根据全等三角形的性质得到∠ABE=∠ACD,BE=CD,求得∠EPD=90°,得到DE=3√2,AB=6,求得BD=6﹣3=3,CD=√AD2+AC2=3√5,根据相似三角形的性质得到PD=√55,PB=6√55根据三角形的面积公式即可得到结论.【解题过程】解:(1)∵△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°.∴AD=AE,AB=AC,∠BAC﹣∠EAF=∠EAD﹣∠EAF,即∠BAE=∠DAC,在△ABE与△ADC中,{AB=AC∠BAE=∠CAD AE=AD,∴△ABE≌△ADC(SAS),∴∠ABE=∠ACD,∵∠ABE+∠AFB=∠ABE+∠CFP=90°,∴∠CPF=90°,∴BP⊥CD;(2)在△ABE与△ACD中,{AE=AD∠EAB=∠CAB=90°AB=AC,∴△ABE≌△ACD(SAS),∴∠ABE=∠ACD,BE=CD,∵∠PDB=∠ADC,∴∠BPD=∠CAB=90°,∴∠EPD=90°,BC=6√2,AD=3,求△PDE的面积.∵BC=6√2,AD=3,∴DE=3√2,AB=6,∴BD=6﹣3=3,CD=√AD2+AC2=3√5,∵△BDP∽△CDA,∴BDCD=PDAD=PBAC,∴3√5=PD3=PB6,∴PD=3√55,PB=6√55∴PE=3√5−6√55=9√55,∴△PDE的面积=12×9√55×3√55=2710.【知识点】全等三角形的判定与性质;等腰直角三角形;旋转的性质;相似三角形的判定和性质;勾股定理24.(2019山东菏泽,24,10分)如图,抛物线与x轴交于A,B两点,与y轴交于点C(0,﹣2),点A的坐标是(2,0),P为抛物线上的一个动点,过点P作PD⊥x轴于点D,交直线BC于点E,抛物线的对称轴是直线x=﹣1.(1)求抛物线的函数表达式;(2)若点P 在第二象限内,且PE =14OD ,求△PBE 的面积.(3)在(2)的条件下,若M 为直线BC 上一点,在x 轴的上方,是否存在点M ,使△BDM 是以BD 为腰的等腰三角形?若存在,求出点M 的坐标;若不存在,请说明理由.【思路分析】(1)点A (2,0)、点B (﹣4,0),则函数的表达式为:y =a (x ﹣2)(x +4)=a (x 2+2x ﹣8),即可求解;(2)PE =14OD ,则PE =(14x 2+12x ﹣2−12x +2)=14(﹣x ),求得:点D (﹣5,0),利用S △PBE =12PE ×BD =12(14x 2+12x ﹣2−12x +2)(﹣4﹣x ),即可求解; (3)BD =1=BM ,则y M =﹣BM sin ∠ABC =﹣1×5=−√55,即可求解. 【解题过程】解:(1)点A 的坐标是(2,0),抛物线的对称轴是直线x =﹣1,则点B (﹣4,0), 则函数的表达式为:y =a (x ﹣2)(x +4)=a (x 2+2x ﹣8),即:﹣8a =﹣2,解得:a =14,故抛物线的表达式为:y =14x 2+12x ﹣2;(2)将点B 、C 的坐标代入一次函数表达式:y =mx +n 并解得:直线BC 的表达式为:y =−12x ﹣2,则tan ∠ABC =12,则sin ∠ABC =5, 设点D (x ,0),则点P (x ,14x 2+12x ﹣2),点E (x ,12x ﹣2), ∵PE =14OD ,∴PE =(14x 2+12x ﹣2−12x +2)=14(﹣x ), 解得:x =0或﹣5(舍去x =0),即点D (﹣5,0)S △PBE =12×PE ×BD =12(14x 2+12x ﹣2−12x +2)(﹣4﹣x )=58; (3)由题意得:△BDM 是以BD 为腰的等腰三角形,只存在:BD =BM 的情况,BD=1=BM,则y M=﹣BM sin∠ABC=﹣15=−√55,则x M=−20+2√55,故点M(−20+2√55,−√55).【知识点】二次函数综合题;数形结合;函数思想;二次函数的解析式;。
