江苏省南京市鼓楼区2015-2016学年八年级上学期期中数学试卷
2015-2016人教版八年级数学第一学期期末考试试卷及答案
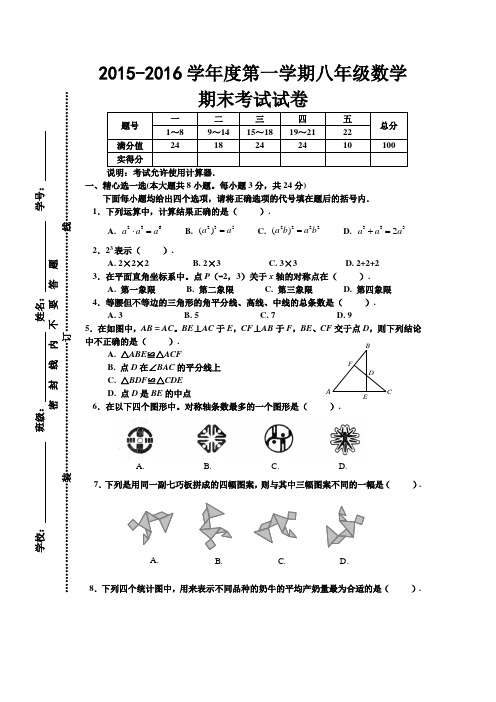
2015-2016学年度第一学期八年级数学期末考试试卷一、精心选一选(本大题共8小题。
每小题3分,共24分)下面每小题均给出四个选项,请将正确选项的代号填在题后的括号内. 1.下列运算中,计算结果正确的是( ).A. 236a a a ⋅=B. 235()a a =C. 2222()a b a b =D. 3332a a a += 2.23表示( ).A. 2×2×2B. 2×3C. 3×3D. 2+2+2 3.在平面直角坐标系中。
点P (-2,3)关于x 轴的对称点在( ).A. 第一象限B. 第二象限C. 第三象限D. 第四象限 4.等腰但不等边的三角形的角平分线、高线、中线的总条数是( ).A. 3B. 5C. 7D. 95.在如图中,AB = AC 。
BE ⊥AC 于E ,CF ⊥AB 于F ,BE 、CF 交于点D ,则下列结论中不正确的是( ). A. △ABE ≌△ACFB. 点D 在∠BAC 的平分线上C. △BDF ≌△CDED. 点D 是BE的中点 6.在以下四个图形中。
对称轴条数最多的一个图形是( ).7.下列是用同一副七巧板拼成的四幅图案,则与其中三幅图案不同的一幅是( ).D.C.B.A.8.下列四个统计图中,用来表示不同品种的奶牛的平均产奶量最为合适的是( ).FEDC BAA. B. C. D.二、细心填一填(本大题共6小题,每小题3分,共18分)9.若单项式23m a b 与n ab -是同类项,则22m n -= .l0.中国文字中有许多是轴对称图形,请你写出三个具有轴对称图形的汉字 . 11.如图是由三个小正方形组成的图形,请你在图中补画一个小正方形,使补画后的图形为轴对称图形.12.如图,已知方格纸中的每个小方格都是相同的正方形.∠AOB 画在方格纸上,请在小方格的顶点上标出一个点P 。
使点P 落在∠AOB 的平分线上.BOA13.数的运算中有一些有趣的对称,请你仿照等式“12×231=132×21”的形式完成:(1)18×891 = × ;(2)24×231 = × .14.下列图案是由边长相等的灰白两色正方形瓷砖铺设的地面,则按此规律可以得到:(1)第4个图案中白色瓷砖块数是 ; (2)第n 个图案中白色瓷砖块数是 .第1个图案 第2个图案 第3个图案三、耐心求一求(本大题共4小题.每小题6分。
八年级上期中数学试卷含答案解析

八年级上学期期中数学试卷一、选择题(本大题共6小题,每小题2分,共计12分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项的序号填涂在答题纸上)1.在下列常见的手机软件小图标中,是轴对称图形的是()A. B. C.D.2.下列几组数中,能构成直角三角形三边的是()A.2,3,5 B.3,4,4 C.32,42,52D.6,8,103.下列说法正确的是()A.全等三角形是指形状相同的两个三角形B.全等三角形的周长和面积分别相等C.全等三角形是指面积相等的两个三角形D.所有的等边三角形都是全等三角形4.如图,在△ABC中,AB=AC,AD是BC边上中线.若AB=10,AD=8,则△ABC的周长是()A.26 B.28 C.32 D.365.如图,点O是△ABC的两外角平分线的交点,下列结论:①OB=OC;②点O到AB、AC的距离相等;③点O到△ABC的三边的距离相等;④点O在∠A的平分线上.其中结论正确的个数是()A.1 B.2 C.3 D.46.如图,在△ABC中,AB=BC,∠ACB=90°,点D、E在AB上,将△ACD、△BCE分别沿CD、CE翻折,点A、B分别落在点A′、B′的位置,再将△A′CD、△B′CE分别沿A′C、B′C翻折,点D 与点E恰好重合于点O,则∠A′OB′的度数是()A.90°B.120°C.135°D.150°二、填空题(本大题共10小题,每小题2分,共20分.不需写出解答过程,请把答案直接填写在答题纸相应位置上)7.如图,△ABC中,∠ACB=90°,以它的各边为边向外作三个正方形,面积分别为S1,S2,S3,已知S1=15,S3=25,则S2=.8.已知等腰三角形一个外角等于80°,则这个等腰三角形的顶角的度数是.9.如图,已知∠BAC=∠DAC,请添加一个条件:,使△ABC≌△ADC(写出一个即可).10.如图,OC是∠AOB的平分线,PD⊥DA,垂足为D,PD=2,则点P到OB的距离是.11.如图,在△ABC中,∠B与∠C的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E.若AB=9,AC=7,则△ADE的周长是.12.如图,△ABC为等边三角形,以AC为直角边作等腰直角三角形ACD,∠ACD=90°,则∠CBD=°.13.如图,△ABC≌△BDE,点B、C、D在一条直线上,AC、BE交于点O,若∠AOE=95°,则∠BDE=°.14.如图,在△ABC中,∠ACB=90°,∠CAB=30°.以AB长为一边作△ABD,且AD=BD,∠ADB=90°,取AB中点E,连DE、CE、CD.则∠EDC=°.15.已知直角三角形斜边长为10cm,周长为22cm,则此直角三角形的面积为.16.如图,在2×2方格纸中,有一个以格点为顶点的△ABC,请你找出方格纸中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有个.三、解答题(本大题共9小题,共68分.请在答题纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)17.已知:如图,AB=AD,∠C=∠E,∠BAE=∠DAC.求证:△ABC≌△ADE.18.已知:如图,在△ABC中,DE∥BC,AD=AE.求证:AB=AC.19.如图,在边长为1的小正方形组成的方格纸中,有一个以格点为顶点的△ABC.(1)试根据三角形三边关系,判断△ABC的形状;(2)在方格纸中利用直尺分别画出AB、BC的垂直平分线,交点为O.观察点O的位置,你能得出怎样的结论?20.如图,将边长为a与b、对角线长为c的长方形纸片ABCD,绕点C顺时针旋转90°得到长方形FGCE,连接AF.通过用不同方法计算梯形ABEF的面积可验证勾股定理,请你写出验证的过程.21.如图,在△ABC中,∠C=90°,∠A>∠B.(1)用直尺和圆规作AB的垂直平分线,交AB与D,交BC于E;(不写作法,保留作图痕迹)(2)在(1)的条件下,若CE=DE,求∠A,∠B的度数.22.2015~2016学年度八年级某班数学实验课安排测量操场上旗杆的高度.小聪同学经过认真思考,研究出了一个可行的测量方案:在某一时刻测得旗杆AB的影长BC和∠ACB的大小,然后在操场上画∠MDN,使得∠MDN=∠ACB,在边DM上截取线段DE=BC,再利用三角形全等的知识求出旗杆的高度,请完成小聪同学的测量方案,并把图形补画完整,说明方案可行的理由.23.(1)如图(1),在△ABC,AB=AC,O为△ABC内一点,且OB=OC,求证:直线AO垂直平分BC.以下是小明的证题思路,请补全框图中的分析过程.(2)如图(2),在△ABC中,AB=AC,点D、E分别在AB、AC上,且BD=CE.请你只用无刻度的直尺画出BC边的垂直平分线(不写画法,保留画图痕迹).(3)如图(3),在五边形ABCDE中,AB=AE,BC=DE,∠B=∠E,请你只用无刻度的直尺画出CD边的垂直平分线,并说明理由.其中、为正整数,且>.(1)观察表格,当m=2,n=1时,此时对应的a、b、c的值能否为直角三角形三边的长?说明你的理由.(2)探究a,b,c与m、n之间的关系并用含m、n的代数式表示:a=,b=,c=.(3)以a,b,c为边长的三角形是否一定为直角三角形?如果是,请说明理由;如果不是,请举出反例.25.(1)如图(1),在△ABC中,AB>AC>BC,∠ACB=80°,点D、E分别在线段BA、AB的延长线上,且AD=AC,BE=BC,则∠DCE=;(2)如图(2),在△ABC中,AB>AC>BC,∠ACB=80°,点D、E分别在边AB上,且AD=AC,BE=BC,求∠DCE的度数;(3)在△ABC中,AB>AC>BC,∠ACB=80°,点D、E分别在直线AB上,且AD=AC,BE=BC,则∠求DCE的度数(直接写出答案);(4)如图(3),在△ABC中,AB=14,AC=15,BC=13,点D、E在直线AB上,且AD=AC,BE=BC.请根据题意把图形补画完整,并在图形的下方直接写出△DCE的面积.(如果有多种情况,图形不够用请自己画出,各种情况用一个图形单独表示).江苏省南京市鼓楼区2015~2016学年度八年级上学期期中数学试卷参考答案与试题解析一、选择题(本大题共6小题,每小题2分,共计12分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项的序号填涂在答题纸上)1.在下列常见的手机软件小图标中,是轴对称图形的是()A. B. C.D.【考点】轴对称图形.【分析】根据轴对称图形的概念求解.【解答】解:A、是轴对称图形,故正确;B、不是轴对称图形,故错误;C、不是轴对称图形,故错误;D、不是轴对称图形,故错误.故选A.【点评】本题考查了轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合.2.下列几组数中,能构成直角三角形三边的是()A.2,3,5 B.3,4,4 C.32,42,52D.6,8,10【考点】勾股定理的逆定理.【分析】欲求证是否为直角三角形,这里给出三边的长,只要验证两小边的平方和等于最长边的平方即可.【解答】解:A、32+22≠52,不能构成直角三角形,故此选项错误;B、42+32≠42,不能构成直角三角形,故此选项错误;C、(32)2+(42)2≠(52)2,不能构成直角三角形,故此选项错误;D、62+82=102,能构成直角三角形,故此选项正确.故选D.【点评】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.3.下列说法正确的是()A.全等三角形是指形状相同的两个三角形B.全等三角形的周长和面积分别相等C.全等三角形是指面积相等的两个三角形D.所有的等边三角形都是全等三角形【考点】全等三角形的应用.【分析】依据全等三角形的定义:能够完全重合的两个三角形.即可求解.【解答】解:A、全等三角形的形状相同,但形状相同的两个三角形不一定是全等三角形.故该选项错误;B、全等三角形是指能够完全重合的两个三角形,则全等三角形的周长和面积一定相等,故B正确;C、全等三角形面积相等,但面积相等的两个三角形不一定是全等三角形.故该选项错误;D、两个等边三角形,形状相同,但不一定能完全重合,不一定全等.故错误.故选B.【点评】本题主要考查全等三角形的定义,全等是指形状相同,大小相同,两个方面必须同时满足.4.如图,在△ABC中,AB=AC,AD是BC边上中线.若AB=10,AD=8,则△ABC的周长是()A.26 B.28 C.32 D.36【考点】等腰三角形的性质.【分析】由等腰三角形的三线合一性质得出AD⊥BC,BD=CD=BC,由勾股定理求出BD,得出BC,即可得出结果.【解答】解:∵AB=AC,AD是BC边上中线,∴AD⊥BC,BD=CD=BC,∴BD===6,∴BC=2BD=12,∴△ABC的周长=AB+AC+BC=10+10+12=32;故选:C.【点评】本题考查了等腰三角形的性质、勾股定理;熟练掌握等腰三角形的三线合一性质,由勾股定理求出BD是解决问题的关键.5.如图,点O是△ABC的两外角平分线的交点,下列结论:①OB=OC;②点O到AB、AC的距离相等;③点O到△ABC的三边的距离相等;④点O在∠A的平分线上.其中结论正确的个数是()A.1 B.2 C.3 D.4【考点】角平分线的性质.【分析】过点O作OE⊥AB于E,作OF⊥BC于F,作OG⊥AC于G,根据角平分线上的点到角的两边的距离相等可得OE=OF=OG,再根据到角的两边距离相等的点在角的平分线上解答.【解答】解:如图,过点O作OE⊥AB于E,作OF⊥BC于F,作OG⊥AC于G,∵点O是△ABC的两外角平分线的交点,∴OE=OG,OF=OG,∴OE=OF=OG,∴点O在∠B的平分线上,故②③④正确,只有点G是AC的中点时,BO=CO,故①错误,综上所述,说法正确的是②③④.故选C.【点评】本题考查了角平分线上的点到角的两边的距离相等的性质,到角的两边距离相等的点在角的平分线上,熟记性质并作出辅助线是解题的关键6.如图,在△ABC中,AB=BC,∠ACB=90°,点D、E在AB上,将△ACD、△BCE分别沿CD、CE翻折,点A、B分别落在点A′、B′的位置,再将△A′CD、△B′CE分别沿A′C、B′C翻折,点D 与点E恰好重合于点O,则∠A′OB′的度数是()A.90°B.120°C.135°D.150°【考点】翻折变换(折叠问题).【分析】如图所示,延长CO到F,由翻折的性质可知:∠A′CF=,,∠CA′O=∠DA′O=∠A=45°,∠OB′C=∠CB′E=∠ECB=45°,最后利用三角形外角的性质可求得∠A′OB′的度数.【解答】解:如图所示:延长CO到F.∵AB=BC,∠ACB=90°,∴∠A=∠B=45°.由翻折的性质可知:∠A′CF=,,∠CA′O=∠DA′O=∠A=45°,∠OB′C=∠CB′E=∠ECB=45°.∴∠A′CB′=∠A′CF+∠B′CF==30°.∴∠A′OB′=∠A′CB′+∠CA′O+∠OB′C=30°+45°+45°=120°.故选:B.【点评】本题主要考查的是翻折的性质,利用翻折的性质求得∠A′CB′=30°,∠CA′O=45°,∠OB′C=45°是解题的关键.二、填空题(本大题共10小题,每小题2分,共20分.不需写出解答过程,请把答案直接填写在答题纸相应位置上)7.如图,△ABC中,∠ACB=90°,以它的各边为边向外作三个正方形,面积分别为S1,S2,S3,已知S1=15,S3=25,则S2=10.【考点】勾股定理.【分析】由勾股定理得出AC2+BC2=AB2,得出S1+S2=S3,得出S2=S3﹣S1,即可得出结果.【解答】解:∵∠ACB=90°,∴AC2+BC2=AB2,∴S1+S2=S3,∴S2=S3﹣S1=25﹣15=10;故答案为:10.【点评】本题考查了勾股定理、正方形面积的计算;熟练掌握勾股定理,由勾股定理得出正方形的面积关系是解决问题的关键.8.已知等腰三角形一个外角等于80°,则这个等腰三角形的顶角的度数是100°.【考点】等腰三角形的性质.【分析】三角形内角与相邻的外角和为180°,三角形内角和为180°,等腰三角形两底角相等,100°只可能是顶角.【解答】解:等腰三角形一个外角为80°,那相邻的内角为100°三角形内角和为180°,如果这个内角为底角,内角和将超过180°,所以100°只可能是顶角.故答案为:100°.【点评】本题主要考查三角形外角性质、等腰三角形性质及三角形内角和定理;判断出80°的外角只能是顶角的外角是正确解答本题的关键.9.如图,已知∠BAC=∠DAC,请添加一个条件:AB=AD,使△ABC≌△ADC(写出一个即可).【考点】全等三角形的判定.【专题】开放型.【分析】添加AB=AD,再加上条件∠BAC=∠DAC,公共边AC,可利用SAS定理判定△ABC≌△ADC.【解答】解:添加:AB=AD,在△ABC和△ADC中,,∴△ABC≌△ADC(SAS).故答案为:AB=AD.【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.10.如图,OC是∠AOB的平分线,PD⊥DA,垂足为D,PD=2,则点P到OB的距离是2.【考点】角平分线的性质.【分析】过点P作PE⊥OB,由角平分线的性质可得PD=PE,进而可得出结论.【解答】解:如图,过点P作PE⊥OB,∵OC是∠AOB的平分线,点P在OC上,且PD⊥OA,PE⊥OB,∴PE=PD,又PD=2,∴PE=PD=2.故答案为2.【点评】本题考查了角平分线的性质,要熟练掌握角平分线的性质,即角平分线上的点到角两边的距离相等是解答此题的关键.11.如图,在△ABC中,∠B与∠C的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E.若AB=9,AC=7,则△ADE的周长是16.【考点】等腰三角形的判定与性质;平行线的性质.【分析】先根据角平分线的定义及平行线的性质证明△BDO和△CEO是等腰三角形,再由等腰三角形的性质得BD=DO,CE=EO,则△ADE的周长=AB+AC,从而得出答案.【解答】解:∵BO平分∠ABC,∴∠DBO=∠CBO,∵DE∥BC,∴∠CBO=∠DOB,∴∠DBO=∠DOB,∴BD=DO,同理OE=EC,∴△ADE的周长=AD+AE+ED=AB+AC=9+7=16,故答案为16.【点评】本题考查等腰三角形的性质,平行线的性质及角平分线的性质.有效的进行线段的等量代换是正确解答本题的关键.12.如图,△ABC为等边三角形,以AC为直角边作等腰直角三角形ACD,∠ACD=90°,则∠CBD= 15°.【考点】等腰三角形的性质;等边三角形的性质;等腰直角三角形.【分析】由△ABC为等边三角形,得到AB=BC=AC,∠ABC=∠ACB=60°,由△ACD是等腰直角三角形,得到AC=CD,等量代换得到BC=CD,根据等腰三角形的性质得到∠CBD=∠CDB,根据三角形的内角和即可得到结论.【解答】解:∵△ABC为等边三角形,∴AB=BC=AC,∠ABC=∠ACB=60°,∵△ACD是等腰直角三角形,∴AC=CD,∴BC=CD,∴∠CBD=∠CDB,∵∠BCD=∠ACB+∠ACD=150°,∴∠CBD=15°,故答案为:15°.【点评】此题考查了等边三角形的性质,等腰三角形的判定和性质,等腰直角三角形的性质,熟练掌握等腰三角形的性质是解题的关键.13.如图,△ABC≌△BDE,点B、C、D在一条直线上,AC、BE交于点O,若∠AOE=95°,则∠BDE= 95°.【考点】全等三角形的性质.【分析】根据全等得出∠A=∠EBD,∠ABC=∠BDE,求出∠BDE=∠ABC=∠ABO+∠EBD=∠ABO+∠A,即可求出答案.【解答】解:∵△ABC≌△BDE,∴∠A=∠EBD,∠ABC=∠BDE,∵∠AOE=95°,∴∠BDE=∠ABC=∠ABO+∠EBD=∠ABO+∠A=180°﹣∠AOB=180°﹣(180°﹣95°)=95°,故答案为:95.【点评】本题考查了三角形内角和定理,全等三角形的性质的应用,能根据全等得出∠A=∠EBD和∠ABC=∠BDE是解此题的关键.14.如图,在△ABC中,∠ACB=90°,∠CAB=30°.以AB长为一边作△ABD,且AD=BD,∠ADB=90°,取AB中点E,连DE、CE、CD.则∠EDC=75°.【考点】直角三角形斜边上的中线.【分析】根据在直角三角形中,斜边上的中线等于斜边的一半得到EC=EA=EB=AB,根据三角形的外角的性质求出∠CEB=60°,根据直角三角形的性质得到ED=EC,根据三角形内角和定理计算即可.【解答】解:∵∠ACB=90°,点E是AB中点,∴EC=EA=EB=AB,∴∠ECA=∠CAB=30°,∴∠CEB=60°,∵AD=BD,点E是AB中点,∴DE⊥AB,即∠AED=90°,∴∠DEC=180°﹣90°﹣60°=30°,∵∠ADB=90°,点E是AB中点,∴DE=AB,∴ED=EC,∴∠EDC=75°,故答案为:75.【点评】本题考查的是直角三角形的性质、等腰三角形的性质,掌握在直角三角形中,斜边上的中线等于斜边的一半、等腰三角形的三线合一是解题的关键.15.已知直角三角形斜边长为10cm,周长为22cm,则此直角三角形的面积为11cm2.【考点】勾股定理.【分析】设一条直角边为xcm,另一条直角边bcm,再根据勾股定理求出2ab的值,根据三角形的面积公式即可得出结论.【解答】解:∵直角三角形斜边长为10cm,周长为22cm,∴设一条直角边为acm,另一条直角边为bcm,∴a+b=22﹣10=12(cm),a2+b2=102=100,∴(a+b)2=a2+b2+2ab=12×12=144,∴2ab=144﹣(a2+b2)=144﹣100=44,∴ab=11.∴此三角形的面积为11cm2.故答案为:11cm2.【点评】本题考查的是勾股定理、三角形面积的计算方法;熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.16.如图,在2×2方格纸中,有一个以格点为顶点的△ABC,请你找出方格纸中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有5个.【考点】利用轴对称设计图案.【分析】根据轴对称图形的定义:如果一个图形沿着一条直线对折,两侧的图形能完全重合,这个图形就是轴对称图形进行画图即可.【解答】解:如图:与△ABC成轴对称且也以格点为顶点的三角形有△ABD、△BCD、△FBE、△HCE,△AFG,共5个.故答案为:5.【点评】本题考查轴对称图形的定义,以及利用轴对称设计图案,利用轴对称设计图案关键是要熟悉轴对称的性质,利用轴对称的作图方法来作图,通过变换对称轴来得到不同的图案.三、解答题(本大题共9小题,共68分.请在答题纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)17.已知:如图,AB=AD,∠C=∠E,∠BAE=∠DAC.求证:△ABC≌△ADE.【考点】全等三角形的判定.【专题】证明题.【分析】先证出∠BAC=∠DAE,再由AAS证明△ABC≌△ADE即可.【解答】证明:∵∠BAE=∠DAC,∴∠BAE+∠EAC=∠DAC+∠EAC,即∠BAC=∠DAE,在△ABC和△ADE中,,∴△ABC≌△ADE(AAS).【点评】本题考查了全等三角形的判定;熟练掌握全等三角形的判定方法,并能进行推理论证是解决问题的关键.18.已知:如图,在△ABC中,DE∥BC,AD=AE.求证:AB=AC.【考点】等腰三角形的判定与性质;平行线的性质.【专题】证明题.【分析】根据平行线的性质得到∠ADE=∠B,∠AED=∠C,根据等腰三角形的性质得到∠ADE=∠AED,等量代换得到∠B=∠C,于是得到结论.【解答】证明:∵DE∥BC,∴∠ADE=∠B,∠AED=∠C,∵AD=AE,∴∠ADE=∠AED,∴∠B=∠C,∴AB=AC.【点评】本题考查了等腰三角形的判定和性质,平行线的性质,熟练掌握等腰三角形的判定和性质是解题的关键.19.如图,在边长为1的小正方形组成的方格纸中,有一个以格点为顶点的△ABC.(1)试根据三角形三边关系,判断△ABC的形状;(2)在方格纸中利用直尺分别画出AB、BC的垂直平分线,交点为O.观察点O的位置,你能得出怎样的结论?【考点】勾股定理;线段垂直平分线的性质;勾股定理的逆定理.【专题】作图题.【分析】(1)根据勾股定理求得该三角形的三条边的长度,然后结合勾股定理的逆定理判定该三角形为直角三角形;(2)根据题意得到图形,由此可以得到点P位于斜边BC上.【解答】解:(1)如图所示,AB2=42+42=32,BC2=62+22=40,AC2=22+22=8,所以AB2+AC2=BC2.所以△ABC是直角三角形;(2)如图所示,点P是△ABC的外心,且在斜边BC上.【点评】本题考查了勾股定理,勾股定理逆定理,线段垂直平分线的性质.注意:勾股定理应用于直角三角形中.20.如图,将边长为a与b、对角线长为c的长方形纸片ABCD,绕点C顺时针旋转90°得到长方形FGCE,连接AF.通过用不同方法计算梯形ABEF的面积可验证勾股定理,请你写出验证的过程.【考点】勾股定理的证明.=S△ABC+S△CEF+S△ACF,利用三角形以及梯形的面积公式即可证明.【分析】根据S梯形ABEF=(EF+AB)•BE=(a+b)•(a+b)=(a+b)2,【解答】证明:∵S梯形ABEF∵Rt△CDA≌Rt△CGF,∴∠ACD=∠CFG,∵∠CFG+∠GCF=90°,∴∠ACD+∠GCF=90°,即∠ACF=90°,=S△ABC+S△CEF+S△ACF,∵S梯形ABEF=ab+ab+c2,∴S梯形ABEF∴(a+b)2=ab+ab+c2∴a2+2ab+b2=2ab+c2,∴a2+b2=c2.【点评】本题考查了用数形结合来证明勾股定理,证明勾股定理常用的方法是利用面积证明,本题锻炼了同学们的数形结合的思想方法.21.如图,在△ABC中,∠C=90°,∠A>∠B.(1)用直尺和圆规作AB的垂直平分线,交AB与D,交BC于E;(不写作法,保留作图痕迹)(2)在(1)的条件下,若CE=DE,求∠A,∠B的度数.【考点】作图—基本作图;线段垂直平分线的性质.【专题】作图题.【分析】(1)利用基本作图(作线段的垂直平分线)作出DE;(2)先利用角平分线性质定理的逆定理得到AE平分∠DAC,即∠CAE=∠BAE,再根据线段垂直平分线的性质定理得到EA=EB,则∠B=∠BAE,所以∠BAC=2∠B,再利用互余得到∠B+∠BAC=90°,于是得到∠B=30°,∠BAC=60°.【解答】解:(1)如图,DE为所作;(2)连结AE,如图,∵EC⊥AC,ED⊥AD,CE=DE,∴AE平分∠DAC,即∠CAE=∠BAE,∵ED垂直平分AB,∴EA=EB,∴∠B=∠BAE,∴∠BAC=2∠B,∵∠B+∠BAC=90°,∴∠B=30°,∠BAC=60°.【点评】本题考查了基本作图有:作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线.22.2015~2016学年度八年级某班数学实验课安排测量操场上旗杆的高度.小聪同学经过认真思考,研究出了一个可行的测量方案:在某一时刻测得旗杆AB的影长BC和∠ACB的大小,然后在操场上画∠MDN,使得∠MDN=∠ACB,在边DM上截取线段DE=BC,再利用三角形全等的知识求出旗杆的高度,请完成小聪同学的测量方案,并把图形补画完整,说明方案可行的理由.【考点】全等三角形的应用.【分析】利用全等三角形的判定与性质得出AB=EG,进而得出答案.【解答】解:如图所示:过点E作GE⊥DM,垂足为E,此时EG=AB,理由:在△ACB和△GDE中,∴△ACB≌△GDE(ASA),∴AB=EG,即可以得出旗杆高度.【点评】此题主要考查了全等三角形的应用,根据题意得出全等三角形是解题关键.23.(1)如图(1),在△ABC,AB=AC,O为△ABC内一点,且OB=OC,求证:直线AO垂直平分BC.以下是小明的证题思路,请补全框图中的分析过程.(2)如图(2),在△ABC中,AB=AC,点D、E分别在AB、AC上,且BD=CE.请你只用无刻度的直尺画出BC边的垂直平分线(不写画法,保留画图痕迹).(3)如图(3),在五边形ABCDE中,AB=AE,BC=DE,∠B=∠E,请你只用无刻度的直尺画出CD边的垂直平分线,并说明理由.【考点】作图—复杂作图;线段垂直平分线的性质.【专题】作图题.【分析】(1)根据线段垂直平分线的性质定理的逆定理,只要AB=AC,OB=OC即可说明直线AO 垂直平分BC;(2)连结BE、CD相交于点O,则直线AO为BC边的垂直平分线;(3)连结BD、CE相交于点O,则直线AO为CD边的垂直平分线.先证明ABC≌△AED得到AC=AD,∠ACB=∠ADE,根据等腰三角形的性质得∠ACD=∠ADC,所以∠BCD=∠EDC,再证明△BCD≌△ECD,则∠BDC=∠ECD,所以OD=OC,于是根据线段垂直平分线定理的逆定理即可判断直线AO为CD边的垂直平分线.【解答】解:(1)(2)如图(2),AO为所作;(3)如图(3),AO为所作.在△ABC和△AED中,∴△ABC≌△AED,∴AC=AD,∠ACB=∠ADE,∴∠ACD=∠ADC,∴∠BCD=∠EDC,在△BCD和△EDC中,,∴△BCD≌△ECD,∴∠BDC=∠ECD,∴OD=OC,∴AO垂直平分CD.【点评】本题考查了作图﹣复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此题得关键是运用线段垂直平分线定理的逆定理.其中、为正整数,且>.(1)观察表格,当m=2,n=1时,此时对应的a、b、c的值能否为直角三角形三边的长?说明你的理由.(2)探究a,b,c与m、n之间的关系并用含m、n的代数式表示:a=m2+n2,b=2mn,c= m2﹣n2.(3)以a,b,c为边长的三角形是否一定为直角三角形?如果是,请说明理由;如果不是,请举出反例.【考点】勾股定理的逆定理.【分析】(1)计算出a、b、c的值,根据勾股定理的逆定理判断即可;(2)根据给出的数据总结即可;(3)分别计算出a2、b2、c2,根据勾股定理的逆定理进行判断.【解答】解:(1)当m=2,n=1时,a=5、b=4、c=3,∵32+42=52,∴a、b、c的值能为直角三角形三边的长;(2)观察得,a=m2+n2,b=2mn,c=m2﹣n2;(3)以a,b,c为边长的三角形一定为直角三角形,∵a2=(m2+n2)2=m4+2m2n2+n4,b2+c2=m4﹣2m2n2+n4+4m2n2=m4+2m2n2+n4,∴a2=b2+c2,∴以a,b,c为边长的三角形一定为直角三角形.【点评】本题考查的是勾股定理的逆定理,掌握如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解题的关键.25.(1)如图(1),在△ABC中,AB>AC>BC,∠ACB=80°,点D、E分别在线段BA、AB的延长线上,且AD=AC,BE=BC,则∠DCE=130°;(2)如图(2),在△ABC中,AB>AC>BC,∠ACB=80°,点D、E分别在边AB上,且AD=AC,BE=BC,求∠DCE的度数;(3)在△ABC中,AB>AC>BC,∠ACB=80°,点D、E分别在直线AB上,且AD=AC,BE=BC,则∠求DCE的度数(直接写出答案);(4)如图(3),在△ABC中,AB=14,AC=15,BC=13,点D、E在直线AB上,且AD=AC,BE=BC.请根据题意把图形补画完整,并在图形的下方直接写出△DCE的面积.(如果有多种情况,图形不够用请自己画出,各种情况用一个图形单独表示).【考点】等腰三角形的性质.【分析】(1)根据等腰三角形的性质得到∠ACD=∠D,∠BCE=∠E,由三角形的内角和得到∠CAB+∠CBA=100°,根据三角形的外角的性质得到∠CDA+∠BCE=(∠CAB+∠CBA)=50°,即可得到结论;(2)根据三角形的内角和和外角的性质即可得到结论;(3)点D、E分别在直线AB上,除去(1)(2)两种情况,还有两种情况,如图3,由(1)知,∠D=CAB,由(2)知∠CEB=,列方程即可求得结果.(4)在△ABC中,AB=14,AC=15,BC=13,过C作CF⊥AB与F,根据勾股定理求得AB边上的高CF=12,然后根据三角形的面积公式即可强大的结论.【解答】解:(1)∵AD=AC,BE=BC,∴∠ACD=∠D,∠BCE=∠E,∵∠ACB=80°,∴∠CAB+∠CBA=100°,∴∠CDA+∠BCE=(∠CAB+∠CBA)=50°,∴∠DCE=130°,故答案为:130°.(2)∵∠ACB=80°,∴∠A+∠B=100°,∵AD=AC,BE=BC,∴∠ACD=∠ADC,∠BEC=∠BCE,∴∠ADC=,∠BEC=,∴∠ADC+∠BEC=180°﹣(∠A+∠B)=130°,∴∠DCE=50°;(3)点D、E分别在直线AB上,除去(1)(2)两种情况,还有两种情况,如图3,由(1)知,∠D=CAB,由(2)知∠CEB=,∴∠CEB=∠D+∠DCE,∴=CAB+∠DCE,∴∠DCE=40°,如图4,同理∠DCE=40°;(4)在△ABC中,AB=14,AC=15,BC=13,过C作CF⊥AB与F,则AC2﹣AF2=BC2﹣BF2,即152﹣AF2=132﹣(14﹣AF)2,解得:AF=9,∴CF=12,①如图1,DE=AB+AC+BC=42,∴S△CDE=×42×12=252;②如图2,DE=AC+BC﹣AB=14,∴S△CDE=×14×12=84;③如图3,DE=AC+AB﹣BC=16,∴S△CDE=×16×12=96;④如图4,DE=AB+BC﹣AC=12,∴S△CDE=×12×12=72.【点评】本题考查了等腰三角形的性质,勾股定理,三角形的面积,熟练掌握等腰三角形的性质是解题的关键.。
南京市鼓楼区2015-2016学年第一学期九年级数学期末试卷

ADE九年级(上)期末试卷数 学注意事项:本试卷共6页.全卷满分120分.考试时间为120分钟.考生答题全部答在答题卡上,答在本试卷上无效.一、选择题(本大题共6小题,每小题2分,共12分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题纸相应位置.......上) 1.从单词“happy ”中随机抽取一个字母,抽中p 的概率为( )A .15B .14C .25D .122.一元二次方程x 2+x -2=0的根的情况是( )A .有两个不相等的实数根B .有两个相等的实数根C .只有一个实数根D .没有实数根 3.若x 1,x 2是一元二次方程2x 2-7x +5=0的两根,则x 1+x 2的值是( )A .52B .72C .- 72 D .-74.下列哪一个函数,其图形与x 轴有两个交点( ) A .y =17(x +50)2+2016B . y =17(x -50)2+2016C .y =-17(x +50)2+2016D .y =-17(x -50)2-2016 5.如图,⊙O 的内接四边形ABCD 中,∠A =115°,则∠BOD 等于( ) A .57.5° B .65°C .115°D .130°6.已知二次函数y =x 2-x +a (a >0),当自变量x 取m 时,其相应的函数值小于0,那么下列结论中正确的是( )A . m -1>0B .m -1<0C .m -1=0D .m -1与0的大小关系不确定二、填空题(本大题共10小题,每小题2分,共20分.不需写出解答过程,请把答案直接填写在答题..纸相应位置.....上) 7.已知⊙O 的半径为5cm .圆心O 到直线l 的距离为4cm ,则直线l 与⊙O 的位置关系是 . 8.如图,在△ABC 中,D 、E 分别是AB 、AC 上的点,且DE //BC , 若AD :AB =4:9,则S △ADE :S △ABC= .9.若线段AB =6cm ,点C 是线段AB 的一个黄金分割点(AC >BC ),则AC 的长为 cm (结果保留根号).10.若一个圆锥的侧面展开图是一个半径为6cm ,圆心角为120°的扇形,则该圆锥的高为 cm . 11.已知正六边形的边长为4cm ,分别以它的三个不相邻的顶点为圆心,边长为半径画弧(如图),则所得到的三条弧的长度之和为 cm .(结果保留π)12.如图,电线杆上的路灯距离地面8m ,身高1.6m 的小明(AB )站在距离电线杆的底部(点O )20m 的y(第5题)A 处, 则小明的影子AM 长为 m .13.某菜农搭建了一个横截面为抛物线的大棚,尺寸如图,若菜农身高为1.8m ,他在不弯腰的情况下,在棚内的横向活动范围是 m . 14.AB 为半圆O 的直径,现将一块等腰直角三角板如图放置,锐角顶点P 在半圆上,斜边过点B ,一条直角边交该半圆于点Q .若AB =2,则线段BQ 的长为 .15.若二次函数y =ax 2+bx +c 的图象如图所示,则不等式a (x -2)2+b (x -2)+c <0的解集为.16.如图,在⊙O 中,AD 是直径,BC 是弦,D 为BC ︵的中点,直径AD 交BC 于点E ,AE =5,ED =1,则BC 的长是 m .三、解答题(本大题共11小题,共88分.请在答题纸指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤) 17.(9分)(1)解方程2x 2-4x -6=0.(2)①直接写出函数y =2x 2-4x -6的图像与x 轴交点坐标;②求函数y =2x 2-4x -6的图像的顶点坐标.18.(6分)九(2)班组织了一次朗读比赛,甲、乙两队各10人的比赛成绩(10分制)如下表(单位:分):(第12题)(第16题)D(第11题)(1)甲队成绩的中位数是 ▲ 分,乙队成绩的众数是 ▲ 分; (2)计算乙队成绩的平均数和方差;(3)成绩较为整齐的是 ▲ 队.19.(7分)如图,G 是边长为8的正方形ABCD 的边BC 上的一点,矩形DEFG 的边EF 过点A ,GD =10.(1)求FG 的长;(2)直接写出图中与△ BHG 相似的所有三角形.20.(7分)一个不透明的袋子中装有3个红球和1个白球,这些球除颜色外都相同.(1)从中随机摸出1个球,记录颜色后放回,搅匀,再摸出1个球.摸出的两个球中,1个为红球,1个为白球的概率为 ▲ ;(2)从中随机摸出1个球,记录颜色后不放回,再摸出1个球.求摸出的两个球中,1个为红球,1个为白球的概率.21.(7分)在淘宝一年一度的“双十一”活动中,某电商在2014年销售额为2500万元,要使 2016年“双十一”的销售额达到3600万元,平均每年“双十一”销售额增长的百分率是多少?(第19题)22.(8分)在作二次函数y1=ax2+bx+c与一次函数y2=kx+m的图象时,先列出下表:请你根据表格信息回答下列问题,(1)二次函数y1=ax2+bx+c的图像与y轴交点坐标为▲ ;(2)当y1>y2时,自变量x的取值范围是▲ ;(3)请写出二次函数y1=ax2+bx+c的三条不同的性质.23.(8分)请探究两个等腰三角形相似的条件,用文字语言直接写出....探究的结果即可.24.(7分)(1)如图(1),已知射线OP与线段OH,在射线OP上取点D、E、F,且OD=DE=EF,用尺规..作出..OH的三等分点M、N;(不写作法,保留作图痕迹)(2)请用尺规..在图(2)中∠BAC的内部作出一点O,使点O到AB的距离等于点O到AC的距离的2倍. (不写作法,保留作图痕迹)25.(9分)如图,在矩形ABCD 中,点O 是对角线AC 上一点,以OC 为半径的⊙O 与CD 交于点M ,且∠BAC =∠DAM . (1)求证:AM 与⊙O 相切;(2)若AM =3DM ,BC =2,求⊙O 的半径.26.(10分)某家禽养殖场,用总长为110 m 的围栏靠墙(墙长为22 m )围成如图所示的三块矩形区域,矩形AEHG 与矩形CDEF 面积都等于矩形BFHG 面积的一半,设AD 长为x m ,矩形区域ABCD 的面积为y m 2.(1)求y 与x 之间的函数关系式,并写出自变量x 的取值范围; (2)当x 为何值时,y 有最大值?最大值是多少?27.(10分)如图(1),在矩形ABCD 中,AB =3,BC =4,连接BD .现将一个足够大的直角三角板的直角顶点P 放在BD 所在的直线上,一条直角边过点C ,另一条直角边与AB 所在的直线交于点G . (1)是否存在这样的点P ,使点P 、C 、G 为顶点的三角形与△GCB 全等?若存在,画出图形,并直接在图形下方写出BG 的长.(如果你有多种情况,请用①、②、③、…表示,每种情况用一个图形单独表示,如果图形不够用,请自己画图)(第25题)(第24题 )(1)(2)ABCADH(第26题)AD(2)如图(2),当点P 在BD 的延长线上时,以P 为圆心、PB 为半径作圆分别交BA 、BC 延长线于点E 、F ,连EF ,分别过点G 、C 作GM ⊥EF ,CN ⊥EF ,M 、N 为垂足.试探究PM 与FN 的关系.数学试题参考答案及评分标准说明:本评分标准每题给出了一种或几种解法供参考,如果考生的解法与本解答不同,参照本评分标准的精神给分.一、选择题(本大题共6小题,每小题2分,共12分.)二、填空题(本大题共10小题,每小题2分,共20分.)7. 相交 8.16:81 9.35-3 10.4 2 11.8π 12.5 13.3 14. 2 15.x <3或x >5 16.2 527题(2)BFNP MEGDCA三、解答题(本大题共11小题,共88分.) 17.(9分)(1)解方程2x 2-4x -6 =0解: x 2-2x -3=0x 2-2x +1=4(x -1)2=4 ……2分 x -1=±2x 1=3 x 1=-1 ……4分(2)①函数y =2x 2-4x -6的图像与x 轴交点坐标(3 ,0),(-1,0);……6分②y =2(x 2-2x ) -6=2(x 2-2x +1-1)-6 ……7分=2(x -1)2-8 ……8分 所以 顶点(1,-8) ……9分18.(6分)(1)中位数是 9.5 分, …………………1分众数是 10 分; …………………2分(2) 乙x 9分,2乙S =1分2; ……………………5分(3) 乙 队. ……………………6分 19.(7分)(1)在正方形ABCD 和矩形DEFG 中,∠E =∠C =90°,∠EDA 与∠CDG 均为∠ADG 的余角, ∠EDA =∠CDG∴△DEA ∽△DCG , ………………………………………………2分 ∴ED CD =ADGD∵ED =FG , ∴FG CD =ADGD……………………………………………………3分 由已知GD =10,AD =CD =8, ∴FG 8=810,∴ FG =6.4 ………………………………………………………4分 (2)△AFH 、△DCG 、∽△DEA . …………………………………7分 20.(7分)(1)38; …………………………3分(2)编号,或列表或画树状图或枚举正确, ………………………5分共有12种可能出现的结果,它们出现的可能性相同.摸出“1个是红球,1个白球”(记为事件B )的结果有6种, ……………………………6分所以P (B ) =12. ……………………………………………………………………7分21.(7分)解:设平均每年“双十一”销售额增长的百分率是x ,根据题意得2500(1+x )2=3600 …………………………………………………………4分 (1+x )2=3625 …………………………………………………………5分1+x =±65x 1=15=20%,x 2=-115(不合题意,舍去)……………………………………………6分答:平均每年“双十一”销售额增长的百分率是20%.………………………………7分22.(8分)(1)(0,-3);…………………………………………………………2分(2)x <-1或x >5 …………………………………………………………4分(3)答案不惟一,下列解法供参考:该函数的图像开口向上;当x =1时,函数有最大值;当x <1时,y 随x 的增大而减小,当x ≥1时,y 随x 的增大而增大;顶点坐标为(1,-4);对称轴为直线x =1. …………………………………………………………8分 (每少或错1条扣1分) 23.(8分)①顶角相等的两个等腰三角形相似; ②底角相等的两个等腰三角形相似; ③腰和底成比例的两个等腰三角形相似. 正确写出1个得3分、2个6分、3个8分. 24.(7分).(1) (2)点M 、N 为所求作的三等分点. 点O 为所求作的点. ……………………………4分 ……………………………7分25.(9分) (1)证明:连接OM .在矩形ABCD 中,AB ∥DC ,∠D =90°NABCMO∴∠BAC =∠DCA ∵OM =OC , ∴∠OMC =∠OCM . ∵∠BAC =∠DAM ,∴∠DAM =∠OMC . ………………2分 ∴∠OMC +∠DMA =∠DAM +∠DMA . 在△DAM 中,∠D =90°,∴∠DAM +∠DMA =180°-90°=90°. ∴∠OMC +∠DMA =90°.∴∠AMO =90°, ∴AM ⊥MO . ……………………………4分 点M 在⊙O 上,OM 是⊙O 的半径,∴AM 与⊙O 相切. ……………………………5分 (2)在△BAC 与△DAM 中,∵∠BAC =∠DAM ,∠B =∠D ,∴△BAC ∽△DAM ……………………………6分 ∴BC DM =AC AM ,∴BC AC =DMAM. ∵AM =3DM ,∴AC =3BC .BC =2,AC =6. ……………………………7分 在△DAM 中,DM 2+AD 2=AM 2即DM 2+22=(3DM )2解得DM =22.AM =322. ……………………………8分 在△AMO 中,AM 2+MO 2=AO 2即(322)2+ MO 2=(6-MO )2.解得MO =218. ……………………………9分26.(10分)解:(1)∵ 矩形AEHG 与矩形CDEF 面积都等于矩形BFHG 面积的一半,∴ 矩形AEFB 面积是矩形CDEF 面积的3倍,∴ AD =3DE .∵AD =x ,∴GH =34x . ……………………………2分∵ 围栏总长为110 m , ∴ 2x +34x +2CD =110.∴CD =55-118x . ……………………………3分∴y =x (55-118x )=-118x 2+55x . ……………………………5分自变量x 的取值范围为:24≤x <40. ……………………………6分(2)∵y =-118x 2+55x =-118( x 2-40 x ) =-118( x -20) 2+550, …………8分∵自变量x 的取值范围为:24≤x <40,且二次项系数为-118<0,∴当x =24时,y 有最大值,最大值为528平方米. …………10分27.(10分)(1)说明:①②③④图形正确、答案正确,给出1个得3分、2个得5分、3个或4个得7分.(以下推导过程供参考)①当点P 与点D 重合时,△GCB ≌△CGP , BG =CP =3.②当点P 在BD 的延长线上,PC =BC 时, 由HL 得,△GCB ≌△GCP , ∴BG =PG ,BC =PC .∴点G 、C 在BP 的垂直平分线上. ∴GC 是BP 的垂直平分线.∴∠BGC +∠GBD =90°,∠CBD +∠GBD =90°. ∴∠BGC =∠CBD .又∵∠GBC =∠BCD =90°,∴ GCB ∽△BDC . ∴ BG BC = BCCD . ∵ BC =4,CD =3,∴ BG 4 = 4 3 ,∴ BG = 163.③当点P 在线段BD 上(不包括端点),PG =BC 时,△GCB ≌△GCP , ∵△GCB ≌△CGP ,∴CB =GP , BG =PC ,∠BCG =∠PGC . ∴△GPB ≌△CBP .∴∠GBP =∠CPB . ∵∠GBP +∠CPB +∠POB =180°, ∠BCG +∠PGC +∠GOC =180°,∴∠GBP +∠CPB +∠POB =∠BCG +∠PGC +∠GOC . 又∵∠POB =∠GOC , ∴∠GBP =∠PGC ,∴ BD ∥GC . ∵BG ∥CD ,∴ 四边形BGCD 是平行四边形. ∴BG =CD =3.④当点P 与点B 重合,BG >0.(2)由(1)可知,此时△GBC ≌△GPC ,且BG = 16 3.∵△GBC ≌△GPC ,∴∠GPC =∠GBC =90°. ∵GM ⊥EF ,CN ⊥EF ,∴∠GMP =∠PNC =90°,∠GNP +∠GPM =90°.AB ( P )CDG ABCDP G OABCDPGA (G )BCD (P )word 格式-可编辑-感谢下载支持∵∠GPC =90°,∴∠GPM +∠NPC =90°,∴∠MGP =∠NPC .∴△PGM ∽△CPN ,∴ PM CN = PG CP. ∵△GBC ≌△GPC ,∴CP =CB =4,PG =BG = 16 3. ∴ PM CN = 16 3 4 = 4 3 ,∴PM = 4 3CN . .........................................................................8分 ∵PB =PF ,∴∠F =∠PBC ,又∵∠FNC =∠BCD =90°,∴△FNC ∽△BCD ,∴ FN BC = CN DC. ∵BC =4,DC =3,∴ FN 4 = CN 3 ,∴FN = 4 3CN ....................................................9分 ∵PM = 4 3 CN ,FN = 4 3CN ,∴PM =FN .....................................................................10分B F NPMEGD C A。
2022-2023学年江苏省南京市鼓楼区第二十九中学、鼓实四校八年级上学期期中考数学试卷带讲解

A.12B.15C.12或15D.18
【答案】B
【解析】
【分析】根据题意,要分情况讨论:①、3是腰;②、3是底.必须符合三角形三边的关系,任意两边之和大于第三边.
【详解】解:①若3是腰,则另一腰也是3,底是6,但是3+3=6,
∴不构成三角形,舍去.
故选:C.
【点睛】此题考查了勾股定理的逆定理,在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.
2.下列剪纸作品都是轴对称图形.其中对称轴条数最多的作品是()
A. B. C. D.
【答案】D
【解析】
【分析】根据对称轴的概念求解.
20.己知:如图, , 相交于点E.求证: .
【答案】见解析
【解析】
【分析】由全等三角形的性质得到 ,利用等角对等边推出 ,进一步计算即可得到 .
【详解】证明: ,
∴ ,
∴ ,
∴ ,
∴ .
【点睛】本题考查了全等三角形的性质,等角对等边,掌握“全等三角形的对应边相等、对应角相等”是解题的关键.
21.如图,已知线段a,h,用直尺和圆规按下列要求分别作一个等腰三角形ABC(保留作图痕迹,写出必要的文字说明).
6.如图,在 中, ,点D是 上的一点,且 ,则 的值为()
A.4B.9C.16D.25
【答案】C
【解析】
【分析】在 中,得到 ①,在 中,得到 ②,① ②即可求解.【详解】解:在 中, ①,
在 中, ②,
① ②得:
故选:C.
【点睛】本题考查了勾股定理的应用,掌握勾股定理的内容是解题的关键.
江苏省南京市钟英中学2015-2016学年八年级(上)第二次段考数学试卷(解析版)

2015-2016学年江苏省南京市钟英中学八年级(上)第二次段考数学试卷一、选择题(本大题共8小题,每小题2分,共16分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卷相应位置上)1.9的平方根是()A.±3 B.3 C.﹣3 D.±2.下面有4个汽车标志图案,其中是轴对称图形的有()A.1个B.2个C.3个D.4个3.下列各数:3.14159,,π,,1.010010001…(从左向右每两个1之间依次增加一个0)中,无理数的个数有()A.1个B.2个C.3个D.4个4.下列各组数据分别是三角形的三边长,其中能构成直角三角形的是()A.2cm、4cm、5cm B.1cm、1cm、cm C.1cm、2cm、2cm D.cm、2cm、cm5.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是()A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°6.点P(m+3,m+1)在x轴上,则点P的坐标为()A.(2,0)B.(0,﹣2)C.(4,0)D.(0,﹣4)7.若等腰三角形的两边长分别是3和6,则这个三角形的周长是()A.12 B.15 C.12或15 D.98.如图,在矩形ABCD中,AB=2,AD=3,点E是BC边上靠近点B的三等分点,动点P 从点A出发,沿路径A→D→C→E运动,则△APE的面积y与点P经过的路径长x之间的函数关系用图象表示大致是()A.B.C.D.二、填空题(本大题共10小题,每小题2分,共20分.不需写出解答过程,请把答案直接填写在答题卷相应位置上)9.计算的结果为.10.用四舍五入法把9.456精确到百分位,得到的近似值是.11.比较大小:47.(填“>”、“=”、“<”)12.函数y=kx+b(k≠0)的图象平行于直线y=2x+3,且交y轴于点(0,﹣1),则其解析式是.13.点P(3,a)与点q(b,2)关于y轴对称,则a+b=,14.如图,已知函数y=2x+1和y=﹣x﹣2的图象交于点P,根据图象,可得方程组的解为.15.函数是y关于x的正比例函数,则m=.16.如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D 重合,折痕为MN,则线段BN的长为.17.如图,在等边△ABC中,AB=2,N为AB上一点,且AN=1,∠BAC的平分线交BC 于点D,M是AD上的动点,连结BM、MN,则BM+MN的最小值是.18.已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为.三、解答题(本大题共8题,共64分.请在答题卷指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)19.(1)计算:2﹣1+﹣+()0(2)求(x﹣3)2=16中x的值.20.如图:点C、D在AB上,且AC=BD,AE=FB,DE=FC.求证:AE∥BF.21.如图,在∠AOB内找一点P,使得点P到∠AOB的两边距离相等,且使点P到点C的距离最短(尺规作图,请保留作图痕迹).22.图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,点A和点B在小正方形的顶点上.(1)在图1中画出△ABC(点C在小正方形的顶点上),使△ABC为直角三角形(画一个即可);(2)在图2中画出△ABD(点D在小正方形的顶点上),使△ABD为等腰三角形(画一个即可).23.已知一次函数y=kx+b的图象经过点(﹣1,﹣2),且与正比例函数y=x的图象相交于点(2,a).(1)求a、b、k的值;(2)在图中画出这两个函数图象,并求这两个函数图象与x轴所围成的三角形面积.24.小丁每天从报社以每份0.5元买进报纸200份,然后以每份1元卖给读者,报纸卖不完,当天可以退回报社,但报社只按每份0.3元退给小丁,如果小丁平均每天卖出报纸x份,纯收入为y元.(1)求y关于x的函数表达式并写出自变量x的取值范围;(2)如果以每月30天计算,小丁每天至少要卖多少份报纸才能保证每月收入不低于2000元?25.如图,△ABC是等边三角形,点D、E分别是BC、CA的延长线上的点,且CD=AE,DA的延长线交BE于点F.(1)求证:AD=BE;(2)求∠BFD的度数.26.一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,匀速运动.快车离乙地的路程y1(km)与行驶的时间x(h)之间的函数关系,如图中线段AB所示.慢车离甲地的路程y2(km)与行驶的时间x(h)之间的函数关系,如图中线段AC所示.根据图象进行以下研究.解读信息:(1)甲、乙两地之间的距离为km;(2)线段AB的解析式为;两车在慢车出发小时后相遇;问题解决:(3)设快、慢车之间的距离为y(km),求y与慢车行驶时间x(h)的函数关系式,并画出函数的图象.2015-2016学年江苏省南京市钟英中学八年级(上)第二次段考数学试卷参考答案与试题解析一、选择题(本大题共8小题,每小题2分,共16分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卷相应位置上)1.9的平方根是()A.±3 B.3 C.﹣3 D.±【考点】平方根.【分析】根据平方与开平方互为逆运算,可得一个正数的平方根.【解答】解:±,故选:A.2.下面有4个汽车标志图案,其中是轴对称图形的有()A.1个B.2个C.3个D.4个【考点】轴对称图形.【分析】根据轴对称图形的概念结合4个汽车标志图案的形状求解.【解答】解:由轴对称图形的概念可知第1个,第2个,第3个都是轴对称图形.第4个不是轴对称图形,是中心对称图形.故是轴对称图形的有3个.故选C.3.下列各数:3.14159,,π,,1.010010001…(从左向右每两个1之间依次增加一个0)中,无理数的个数有()A.1个B.2个C.3个D.4个【考点】无理数.【分析】根据无理数是无限不循环小数,可得答案.【解答】解:π,1.010010001…(从左向右每两个1之间依次增加一个0)是无理数,故选:B.4.下列各组数据分别是三角形的三边长,其中能构成直角三角形的是()A.2cm、4cm、5cm B.1cm、1cm、cm C.1cm、2cm、2cm D.cm、2cm、cm【考点】勾股定理的逆定理.【分析】由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方即可.【解答】解:A、因为22+42≠52,不能构成直角三角形,此选项错误;B、因为12+12=2,能构成直角三角形,此选项正确;C、因为12+22≠22,不能构成直角三角形,此选项错误;D、因为2+22≠2,不能构成直角三角形,此选项错误.故选B.5.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是()A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°【考点】全等三角形的判定.【分析】本题要判定△ABC≌△ADC,已知AB=AD,AC是公共边,具备了两组边对应相等,故添加CB=CD、∠BAC=∠DAC、∠B=∠D=90°后可分别根据SSS、SAS、HL能判定△ABC≌△ADC,而添加∠BCA=∠DCA后则不能.【解答】解:A、添加CB=CD,根据SSS,能判定△ABC≌△ADC,故A选项不符合题意;B、添加∠BAC=∠DAC,根据SAS,能判定△ABC≌△ADC,故B选项不符合题意;C、添加∠BCA=∠DCA时,不能判定△ABC≌△ADC,故C选项符合题意;D、添加∠B=∠D=90°,根据HL,能判定△ABC≌△ADC,故D选项不符合题意;故选:C.6.点P(m+3,m+1)在x轴上,则点P的坐标为()A.(2,0)B.(0,﹣2)C.(4,0)D.(0,﹣4)【考点】点的坐标.【分析】根据x轴上点的纵坐标为0列出方程求解得到m的值,然后解答即可.【解答】解:∵点P(m+3,m+1)在x轴上,∴m+1=0,∴m=﹣1,∴点P(m+3,m+1)的坐标为(2,0).故选:A.7.若等腰三角形的两边长分别是3和6,则这个三角形的周长是()A.12 B.15 C.12或15 D.9【考点】等腰三角形的性质.【分析】根据题意,要分情况讨论:①、3是腰;②、3是底.必须符合三角形三边的关系,任意两边之和大于第三边.【解答】解:①若3是腰,则另一腰也是3,底是6,但是3+3=6,∴不构成三角形,舍去.②若3是底,则腰是6,6.3+6>6,符合条件.成立.∴C=3+6+6=15.故选B.8.如图,在矩形ABCD中,AB=2,AD=3,点E是BC边上靠近点B的三等分点,动点P 从点A出发,沿路径A→D→C→E运动,则△APE的面积y与点P经过的路径长x之间的函数关系用图象表示大致是()A.B.C.D.【考点】动点问题的函数图象.【分析】求出CE的长,然后分①点P在AD上时,利用三角形的面积公式列式得到y与x﹣S△ADP﹣S△CEP列式整理得到y 的函数关系;②点P在CD上时,根据S△APE=S梯形AECD与x的关系式;③点P在CE上时,利用三角形的面积公式列式得到y与x的关系式,然后选择答案即可.【解答】解:∵在矩形ABCD中,AB=2,AD=3,∴CD=AB=2,BC=AD=3,∵点E是BC边上靠近点B的三等分点,∴CE=×3=2,①点P在AD上时,△APE的面积y=x•2=x(0≤x≤3),②点P在CD上时,S△APE=S﹣S△ADP﹣S△CEP,梯形AECD=(2+3)×2﹣×3×(x﹣3)﹣×2×(3+2﹣x),=5﹣x+﹣5+x,=﹣x+,∴y=﹣x+(3<x≤5),③点P在CE上时,S△APE=×(3+2+2﹣x)×2=﹣x+7,∴y=﹣x+7(5<x≤7),故选:A.二、填空题(本大题共10小题,每小题2分,共20分.不需写出解答过程,请把答案直接填写在答题卷相应位置上)9.计算的结果为﹣3.【考点】立方根.【分析】利用立方根的定义计算即可.【解答】解:=﹣3,故答案为:﹣3.10.用四舍五入法把9.456精确到百分位,得到的近似值是9.46.【考点】近似数和有效数字.【分析】把千分位上的数字6进行四舍五入即可.【解答】解:9.456≈9.46(精确到百分位).故答案为9.46.11.比较大小:4<7.(填“>”、“=”、“<”)【考点】实数大小比较.【分析】根据平方的幂越大底数越大,可得答案.【解答】解:(4)2=48,72=49,∴,故答案为:<.12.函数y=kx+b(k≠0)的图象平行于直线y=2x+3,且交y轴于点(0,﹣1),则其解析式是y=2x﹣1.【考点】两条直线相交或平行问题;待定系数法求一次函数解析式.【分析】根据一次函数的特点,两直线平行,则一次项系数相同,可确定k的值,把点(0,﹣1)代入求出b.【解答】解:∵函数y=kx+b(k≠0)的图象平行于直线y=2x+3,∴k=2;把点(0,﹣1)代入得b=﹣1,∴其解析式是:y=2x﹣1.13.点P(3,a)与点q(b,2)关于y轴对称,则a+b=﹣1,【考点】关于x轴、y轴对称的点的坐标.【分析】平面直角坐标系中任意一点P(x,y),关于y轴的对称点的坐标是(﹣x,y),即关于纵轴的对称点,纵坐标不变,横坐标变成相反数;这样就可以求出A的对称点的坐标.求出a,b以及a+b的值.【解答】解:点P(3,a)与点q(b,2)关于y轴对称则a=2,b=﹣3那么a+b=﹣1.14.如图,已知函数y=2x+1和y=﹣x﹣2的图象交于点P,根据图象,可得方程组的解为.【考点】一次函数与二元一次方程(组).【分析】根据两直线的交点坐标即为方程组的解解答.【解答】解:由图可知,方程组的解为.故答案为:.15.函数是y关于x的正比例函数,则m=1.【考点】正比例函数的定义.【分析】根据正比例函数的定义列式求解即可.【解答】解:由题意得,m2=1且m+1≠0,解得m=±1且m≠﹣1,所以,m=1.故答案为:1.16.如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D 重合,折痕为MN,则线段BN的长为4.【考点】翻折变换(折叠问题).【分析】设BN=x,则由折叠的性质可得DN=AN=9﹣x,根据中点的定义可得BD=3,在Rt△BND中,根据勾股定理可得关于x的方程,解方程即可求解.【解答】解:设BN=x,由折叠的性质可得DN=AN=9﹣x,∵D是BC的中点,∴BD=3,在Rt△BND中,x2+32=(9﹣x)2,解得x=4.故线段BN的长为4.故答案为:4.17.如图,在等边△ABC中,AB=2,N为AB上一点,且AN=1,∠BAC的平分线交BC于点D,M是AD上的动点,连结BM、MN,则BM+MN的最小值是.【考点】轴对称-最短路线问题;等边三角形的性质.【分析】要求BM+MN的最小值,需考虑通过作辅助线转化BM,MN的值,从而找出其最小值求解.【解答】解:连接CN,与AD交于点M.则CN就是BM+MN的最小值.取BN中点E,连接DE.∵等边△ABC的边长为2,AN=1,∴BN=AC﹣AN=2﹣1=1,∴BE=EN=AN=1,又∵AD是BC边上的中线,∴DE是△BCN的中位线,∴CN=2DE,CN∥DE,又∵N为AE的中点,∴M为AD的中点,∴MN是△ADE的中位线,∴DE=2MN,∴CN=2DE=4MN,∴CM=CN.在直角△CDM中,CD=BC=1,DM=AD=,∴CM=,∴CN==.∵BM+MN=CN,∴BM+MN的最小值为.故答案为18.已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为(2,4)或(3,4)或(8,4).【考点】矩形的性质;坐标与图形性质;等腰三角形的性质.【分析】分PD=OD(P在右边),PD=OD(P在左边),OP=OD三种情况,根据题意画出图形,作PQ垂直于x轴,找出直角三角形,根据勾股定理求出OQ,然后根据图形写出P的坐标即可.【解答】解:当OD=PD(P在右边)时,根据题意画出图形,如图所示:过P作PQ⊥x轴交x轴于Q,在直角三角形DPQ中,PQ=4,PD=OD=OA=5,根据勾股定理得:DQ=3,故OQ=OD+DQ=5+3=8,则P1(8,4);当PD=OD(P在左边)时,根据题意画出图形,如图所示:过P作PQ⊥x轴交x轴于Q,在直角三角形DPQ中,PQ=4,PD=OD=5,根据勾股定理得:QD=3,故OQ=OD﹣QD=5﹣3=2,则P2(2,4);当PO=OD时,根据题意画出图形,如图所示:过P作PQ⊥x轴交x轴于Q,在直角三角形OPQ中,OP=OD=5,PQ=4,根据勾股定理得:OQ=3,则P3(3,4),综上,满足题意的P坐标为(2,4)或(3,4)或(8,4).故答案为:(2,4)或(3,4)或(8,4)三、解答题(本大题共8题,共64分.请在答题卷指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)19.(1)计算:2﹣1+﹣+()0(2)求(x﹣3)2=16中x的值.【考点】实数的运算;平方根;零指数幂;负整数指数幂.【分析】(1)原式第一项利用负整数指数幂法则计算,第二项利用算术平方根定义计算,第三项利用立方根定义计算,最后一项利用零指数幂法则计算即可得到结果;(2)方程开方即可求出解.【解答】解:(1)原式=+2﹣2+1=;(2)开方得:x﹣3=±4,解得:x=7或x=﹣1.20.如图:点C、D在AB上,且AC=BD,AE=FB,DE=FC.求证:AE∥BF.【考点】全等三角形的判定与性质.【分析】由AC=BD,利用等式的性质得到AD=BC,利用SSS得到三角形AED与三角形FBC全等,利用全等三角形的对应角相等得到一对内错角相等,利用内错角相等两直线平行即可得证.【解答】证明:∵AC=BD,∴AC+CD=BD+CD,即AD=BC,在△ADE和△BCF中,,∴△ADE≌△BCF(SSS),∴∠A=∠B,∴AE∥BF.21.如图,在∠AOB内找一点P,使得点P到∠AOB的两边距离相等,且使点P到点C的距离最短(尺规作图,请保留作图痕迹).【考点】作图—复杂作图;垂线段最短;角平分线的性质.【分析】使P到∠AOB的两边的距离相等,即画它的角平分线,使点P到点C的距离最短,即过C点作∠AOB的角平分线垂线,垂足就是点P的位置.【解答】解:作∠AOB平分线,过点C作∠AOB平分线的垂线)交点P即为所求.22.图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,点A和点B在小正方形的顶点上.(1)在图1中画出△ABC(点C在小正方形的顶点上),使△ABC为直角三角形(画一个即可);(2)在图2中画出△ABD(点D在小正方形的顶点上),使△ABD为等腰三角形(画一个即可).【考点】作图—应用与设计作图.【分析】(1)利用网格结构,过点A的竖直线与过点B的水平线相交于点C,连接即可,或过点A的水平线与过点B的竖直线相交于点C,连接即可;(2)根据网格结构,作出BD=AB或AB=AD,连接即可得解.【解答】解:(1)如图1,①、②,画一个即可;(2)如图2,①、②,画一个即可.23.已知一次函数y=kx+b的图象经过点(﹣1,﹣2),且与正比例函数y=x的图象相交于点(2,a).(1)求a、b、k的值;(2)在图中画出这两个函数图象,并求这两个函数图象与x轴所围成的三角形面积.【考点】两条直线相交或平行问题.【分析】(1)根据凡是函数图象经过的点必能满足解析式把(2,a)代入y=x可得a的值,然后再利用待定系数法计算出k、b的值即可;(2)首先画出图象,然后再计算出一次函数y=x﹣1与x轴的交点,再求面积即可.【解答】解:(1)∵y=x的图象过(2,a),∴a=1,∵y=kx+b的图象经过点(﹣1,﹣2),(2,1),∴,解得:,∴a=1、b=﹣1、k=1;(2)y=x﹣1与x轴的交点为(1,0),S=×1×1=.24.小丁每天从报社以每份0.5元买进报纸200份,然后以每份1元卖给读者,报纸卖不完,当天可以退回报社,但报社只按每份0.3元退给小丁,如果小丁平均每天卖出报纸x份,纯收入为y元.(1)求y关于x的函数表达式并写出自变量x的取值范围;(2)如果以每月30天计算,小丁每天至少要卖多少份报纸才能保证每月收入不低于2000元?【考点】一次函数的应用.【分析】(1)根据纯收入=卖出的份数×每份的利润﹣剩下的份数×赔掉的钱,可列出y关于x的函数关系式,结合每天只购进200份报纸可得出自变量x的取值范围;(2)结合(1)的关系式与每月收入不低于2000元,可列出关于x的一元一次不等式,解不等式即可得出结论.【解答】解:(1)根据题意可知:y=(1﹣0.5)x﹣(0.5﹣0.3)=0.7x﹣10(0≤x≤200,且x为整数).(2)根据题意得:30(0.7x﹣40)≥2000,解得:x≥152.故小丁每天至少要卖153份报纸才能保证每月收入不低于2000元.25.如图,△ABC是等边三角形,点D、E分别是BC、CA的延长线上的点,且CD=AE,DA的延长线交BE于点F.(1)求证:AD=BE;(2)求∠BFD的度数.【考点】全等三角形的判定与性质.【分析】(1)利用等边三角形的性质,可得AB=AC,∠BAE=∠ACD,从而证得△BAE≌△ACD,即可得到AD=BE;(2)由△BAE≌△ACD可得∠DAC=∠EBA,又由∠DAC=∠EAF,可得∠EAF=∠EBA,再由等边三角形的性质得到∠BAC=60°,可得∠BAE=∠EAF+∠BAF=120°,再利用三角形的内角和即可得到∠BFD的度数.【解答】解:(1)∵△ABC是等边三角形,∴AB=AC,∠BAC=∠ACB,∵∠BAE+∠BAC=180°,∠ACD+∠ACB=180°∴∠BAE=∠ACD,在△BAE与△ACD中,,∴△BAE≌△ACD(SAS),∴AD=BE;(2)∵△BAE≌△ACD,∴∠DAC=∠EBA,∵∠DAC=∠EAF,∴∠EAF=∠EBA,∵△ABC是等边三角形,∴∠BAC=60°,∴∠BAE=120°,即∠EAF+∠BAF=120°,∴∠EBA+∠BAF=120°∴∠BFD=60°.26.一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,匀速运动.快车离乙地的路程y1(km)与行驶的时间x(h)之间的函数关系,如图中线段AB所示.慢车离甲地的路程y2(km)与行驶的时间x(h)之间的函数关系,如图中线段AC所示.根据图象进行以下研究.解读信息:(1)甲、乙两地之间的距离为450km;(2)线段AB的解析式为1=450﹣150x;两车在慢车出发2小时后相遇;问题解决:(3)设快、慢车之间的距离为y(km),求y与慢车行驶时间x(h)的函数关系式,并画出函数的图象.【考点】一次函数的应用.【分析】(1)由一次函数的图象可以直接得出结论为450km;(2)设一次函数的解析式y1=k1x+b1,利用待定系数法解答即可,根据路程、时间和速度的关系解答;(3)根据题意得出函数解析式,画出函数的图象即可.【解答】解:(1)由图象可得:甲、乙两地之间的距离为450km;(2)设一次函数的解析式y1=k1x+b1,可得;,解得:,故线段AB的解析式为y1=450﹣150x (0≤x≤3);设两车在慢车出发x小时后相遇,可得:450÷()=x,解得:x=2,答两车在慢车出发2小时后相遇;故答案为:(1)450;(2)y1=450﹣150x;2;(3)根据题意得出y与慢车行驶时间x(h)的函数关系式如下:,其图象为折线图.2016年4月30日。
人教版八年级上学期期中考试数学试卷共五套(含答案)

人教版八年级上学期期中考试数学试卷(一)一、选择题(本大题共10小题,每小题2分,共20分)1.(2分)下列图形中,不是轴对称图形的是()A. B.C. D.2.(2分)点(﹣2,3)关于y轴对称的点的坐标是()A.(2,﹣3)B.(2,3)C.(﹣2,﹣3)D.(3,﹣2)3.(2分)下列运算中,错误的是()A.2a﹣3a=﹣a B.(﹣ab)3=﹣a3b3 C.a6÷a2=a4D.a•a2=a24.(2分)如图:已知∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=6,则PD=()A.6 B.4 C.3 D.25.(2分)若(﹣x+a)(x﹣3)的积不含x的一次项,则a的值为()A.3 B.﹣3 C.D.6.(2分)若9x2+mxy+16y2是一个完全平方式,那m的值是()A.±12 B.﹣12 C.±24 D.﹣247.(2分)如图,AB=AC,AD=AE,∠B=50°,∠AEC=120°,则∠DAC的度数等于()A.120°B.70°C.60°D.50°8.(2分)如图,BE⊥AC于点D,且AD=CD,BD=ED.若∠ABC=72°,则∠E等于()A.18°B.36°C.54°D.72°9.(2分)已知a、b、c是三角形的三边,则代数式a2﹣2ab+b2﹣c2的值()A.不能确定B.大于0 C.等于0 D.小于010.(2分)如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:①EF=BE+CF;②∠BOC=90°+∠A;③点O到△ABC各边的距离相等;④设OD=m,AE+AF=n,则S=mn.△AEF其中正确的结论是()A.①②③B.①②④C.②③④D.①③④二.填空题(本题共8小题;每小题3分,共24分.)11.(3分)计算:(6x2﹣3x)÷3x= .12.(3分)计算:20152﹣2014×2016= .13.(3分)若a m=2,a n=3,则a2m+n= .14.(3分)已知a+=4,则a2+= .15.(3分)当x 时,(x﹣3)0=1.16.(3分)如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧,分别交AB,AC于点M和N,再分别以点M,N为圆心,大于MN长的一半为半径画弧,两弧交于点P,连结AP并延长,交BC于点D,则下列说法中,正确的有.(填写序号)①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC :S△ABC=1:3.17.(3分)如图,等腰△ABC中,AB=AC,∠DBC=15°,AB的垂直平分线MN交AC于点D,则∠A的度数是.18.(3分)如图,在Rt△ABC中,D,E为斜边AB上的两个点,且BD=BC,AE=AC,则∠DCE的大小为(度).三.解答题(本大题共8小题,共56分)19.(8分)计算:(1)(x+4)2﹣(x+3)(x﹣3)(2)(x+2y﹣3)(x﹣2y+3)20.(12分)因式分解:(1)2a3﹣12a2b+18ab2(2)﹣4(x+2y)2+9(2x﹣y)2(3)x4﹣16(4)(x﹣1)(x﹣3)﹣8.21.(4分)如图,在Rt△ABC中,∠C=90°,∠A=15°.(1)在AC边上求作点D,使得DA=DB.(尺规作图,不写作法,保留作图痕迹).= .(2)在(1)的基础上,连接BD,若BC=1,则S△ABD22.(5分)化简求值:已知[(x﹣2y)2﹣4y2+2xy]÷2x,其中 x=1,y=2.23.(5分)如图,已知△ABC中,∠C=90°,AD平分∠BAC交BC于D,DE⊥AB 于E,点F在AC上,且BD=FD,求证:AE﹣BE=AF.24.(6分)如图,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.(1)证明:AD=BE;(2)求∠AEB的度数.25.(8分)如图,在△ABC中,点D为边BC的中点,过点A作射线AE,过点C 作CF⊥AE于点F,过点B作BG⊥AE于点G,连接FD并延长,交BG于点H (1)求证:DF=DH;(2)若∠CFD=120°,求证:△DHG为等边三角形.26.(8分)如图所示:△ABC是等腰直角三角形,BC=AC,直角顶点C在x轴上,一锐角顶点B在y轴上(1)如图1所示,若C的坐标是(2,0),点A的坐标是(﹣2,﹣2),求:点B的坐标;(2)如图2,若y轴恰好平分∠ABC,AC与y轴交于点D,过点A作AE⊥y轴于E,问BD与AE有怎样的数量关系,并说明理由;(3)如图3角边BC在两坐标轴上滑动,使点A在第四象限内,过A点作AF⊥y 轴于F,在滑动的过程中,两个结论①为定值;②为定值,只有一个结论成立,请你判断正确的结论加以证明,并求出定值.参考答案与试题解析一、选择题(本大题共10小题,每小题2分,共20分)1.(2分)下列图形中,不是轴对称图形的是()A. B.C. D.【解答】解:A、是轴对称图形,不符合题意;B、不是轴对称图形,符合题意;C、是轴对称图形,不符合题意;D、是轴对称图形,不符合题意;故选:B.2.(2分)点(﹣2,3)关于y轴对称的点的坐标是()A.(2,﹣3)B.(2,3)C.(﹣2,﹣3)D.(3,﹣2)【解答】解:点(﹣2,3)关于y轴对称的点的坐标是(2,3),故选:B.3.(2分)下列运算中,错误的是()A.2a﹣3a=﹣a B.(﹣ab)3=﹣a3b3 C.a6÷a2=a4D.a•a2=a2【解答】解:A、2a﹣3a=﹣a,正确,不合题意;B、(﹣ab)3=﹣a3b3,正确,不合题意;C、a6÷a2=a4,正确,不合题意;D、a•a2=a3,错误,故此选项符合题意.故选:D.4.(2分)如图:已知∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=6,则PD=()A.6 B.4 C.3 D.2【解答】解:过P作PE⊥OB于E,∵∠AOP=∠BOP,PD⊥OA,∴PE=PD,∵PC∥OA,∴∠CPO=∠POA=15°=∠BOP,∴∠ECP=∠BOP+∠CPO=30°,∵∠PEC=90°,∴PE=PC=×6=3,即PD=PE=3.故选:C.5.(2分)若(﹣x+a)(x﹣3)的积不含x的一次项,则a的值为()A.3 B.﹣3 C.D.【解答】解:∵(﹣x+a)(x﹣3)=﹣x2+(3+a)x﹣3a,∴3+a=0,解得:a=﹣3,故选:B.6.(2分)若9x2+mxy+16y2是一个完全平方式,那m的值是()A.±12 B.﹣12 C.±24 D.﹣24【解答】解:∵9x2+mxy+16y2是一个完全平方式,∴m=±24,故选:C.7.(2分)如图,AB=AC,AD=AE,∠B=50°,∠AEC=120°,则∠DAC的度数等于()A.120°B.70°C.60°D.50°【解答】解:∵AB=AC,AD=AE,∠B=50°,∠AEC=120°,∴∠AED=∠ADE=60°,∠EAC=60°﹣∠C=60°﹣50°=10°,∴∠DAC=60°+10°=70°.故选:B.8.(2分)如图,BE⊥AC于点D,且AD=CD,BD=ED.若∠ABC=72°,则∠E等于()A.18°B.36°C.54°D.72°【解答】解:∵BE⊥AC,AD=DC,∴BA=BC,∴∠ABD=∠CBD=∠ABC=36°,在△ADB和△CDE中,,∴△ADB≌△CDE,∴∠E=∠ABD=36°,故选:B.9.(2分)已知a、b、c是三角形的三边,则代数式a2﹣2ab+b2﹣c2的值()A.不能确定B.大于0 C.等于0 D.小于0【解答】解:a2﹣2ab+b2﹣c2=(a﹣b)2﹣c2=(a+c﹣b)[a﹣(b+c)].∵a,b,c是三角形的三边.∴a+c﹣b>0,a﹣(b+c)<0.∴a2﹣2ab+b2﹣c2<0.故选:D.10.(2分)如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:①EF=BE+CF;②∠BOC=90°+∠A;③点O到△ABC各边的距离相等;④设OD=m,AE+AF=n,则S=mn.△AEF其中正确的结论是()A.①②③B.①②④C.②③④D.①③④【解答】解:∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴∠OBC=∠ABC,∠OCB=∠ACB,∠A+∠ABC+∠ACB=180°,∴∠OBC+∠OCB=90°﹣∠A,∴∠BOC=180°﹣(∠OBC+∠OCB)=90°+∠A;故②正确;∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴∠OBC=∠OBE,∠OCB=∠OCF,∵EF∥BC,∴∠OBC=∠EOB,∠OCB=∠FOC,∴∠EOB=∠OBE,∠FOC=∠OCF,∴BE=OE,CF=OF,∴EF=OE+OF=BE+CF,故①正确;过点O作OM⊥A B于M,作ON⊥BC于N,连接OA,∵在△AB C中,∠ABC和∠ACB的平分线相交于点O,∴ON=OD=OM=m,∴S△AEF =S△AOE+S△AOF=AE•OM+AF•OD=OD•(AE+AF)=mn;故④错误;∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴点O到△ABC各边的距离相等,故③正确.故选:A.二.填空题(本题共8小题;每小题3分,共24分.)11.(3分)计算:(6x2﹣3x)÷3x= 2x﹣1 .【解答】解:(6x2﹣3x)÷3x,=6x2÷3x﹣3x÷3x,=2x﹣1.故答案为:2x﹣1.12.(3分)计算:20152﹣2014×2016= 1 .【解答】解:20152﹣2014×2016=20152﹣(2015﹣1)×(2015+1)=20152﹣(20152﹣1)=20152﹣20152+1=1.故答案是:1.13.(3分)若a m=2,a n=3,则a2m+n= 12 .【解答】解:∵a m=2,a n=3,∴a2m+n=a2m•a n=(a m)2•a n=22×3=12.故答案为:12.14.(3分)已知a+=4,则a2+= 14 .【解答】解:∵a+=4,∴(a+)2=16,∴a2+2+=16,∴a2+=14.故答案为14.15.(3分)当x ≠3 时,(x﹣3)0=1.【解答】解:由题意得:x﹣3≠0,解得:x≠3,故答案为:≠3.16.(3分)如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧,分别交AB,AC于点M和N,再分别以点M,N为圆心,大于MN长的一半为半径画弧,两弧交于点P,连结AP并延长,交BC于点D,则下列说法中,正确的有①②③④.(填写序号)①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC :S△ABC=1:3.【解答】①证明:连接NP,MP,在△ANP与△AMP中,∵,∴△ANP≌△AMP,则∠CAD=∠BAD,故AD是∠BAC的平分线,故此选项正确;②证明:∵在△ABC中,∠C=90°,∠B=30°,∴∠CAB=60°.∵AD是∠BAC的平分线,∴∠1=∠2=∠CAB=30°,∴∠3=90°﹣∠2=60°,∠ADC=60°,故此选项正确;③证明:∵∠1=∠B=30°,∴AD=BD,∴点D在AB的中垂线上,故此选项正确;④证明:∵在Rt△ACD中,∠2=30°,∴CD=AD,∴BC=BD+CD=AD+AD=AD,S△DAC=AC•CD=AC•AD,∴S△ABC=AC•BC=AC•AD=AC•AD,∴S△DAC :S△ABC=1:3,故此选项正确;故答案为:①②③④.17.(3分)如图,等腰△ABC中,AB=AC,∠DBC=15°,AB的垂直平分线MN交AC于点D,则∠A的度数是50°.【解答】解:∵MN是AB的垂直平分线,∴AD=BD,∴∠A=∠ABD,∵∠DBC=15°,∴∠ABC=∠A+15°,∵AB=AC,∴∠C=∠ABC=∠A+15°,∴∠A+∠A+15°+∠A+15°=180°,解得∠A=50°.故答案为:50°.18.(3分)如图,在Rt△ABC中,D,E为斜边AB上的两个点,且BD=BC,AE=AC,则∠DCE的大小为45 (度).【解答】解:设∠DCE=x,∠ACD=y,则∠ACE=x+y,∠BCE=90°﹣∠ACE=90°﹣x ﹣y.∵AE=AC,∴∠ACE=∠AEC=x+y,∵BD=BC,∴∠BDC=∠BCD=∠BCE+∠DCE=90°﹣x﹣y+x=90°﹣y.在△DCE中,∵∠DCE+∠CDE+∠DEC=180°,∴x+(90°﹣y)+(x+y)=180°,解得x=45°,∴∠DCE=45°.故答案为:45.三.解答题(本大题共8小题,共56分)19.(8分)计算:(1)(x+4)2﹣(x+3)(x﹣3)(2)(x+2y﹣3)(x﹣2y+3)【解答】解:(1)(x+4)2﹣(x+3)(x﹣3)=x2+8x+16﹣(x2﹣9)=8x+25;(2)(x+2y﹣3)(x﹣2y+3)=[x+(2y﹣3)][x﹣(2y﹣3)]=x2﹣(2y﹣3)2=x2﹣4y2+12y﹣9.20.(12分)因式分解:(1)2a3﹣12a2b+18ab2(2)﹣4(x+2y)2+9(2x﹣y)2(3)x4﹣16(4)(x﹣1)(x﹣3)﹣8.【解答】解:(1)原式=2a(a2﹣6a+9b2)=2a(a﹣3b)2;(2)原式=[3(2x﹣y)+2(x+2y)][3(2x﹣y)﹣2(x+2y)]=(8x+y)(4x ﹣7y);(3)原式=(x2+4)(x2﹣4)=(x2+4)(x+2)(x﹣2);(4)原式=x2﹣4x﹣5=(x﹣5)(x+1).21.(4分)如图,在Rt△ABC中,∠C=90°,∠A=15°.(1)在AC边上求作点D,使得DA=DB.(尺规作图,不写作法,保留作图痕迹).= 1 .(2)在(1)的基础上,连接BD,若BC=1,则S△ABD【解答】解:(1)如图所示:此时DA=DB;(2)如图所示:∵∠C=90°,∠A=15°,AD=BD,∴∠A=∠ABD=15°,∴∠CDB=30°,∵BC=1,∴AD=BD=2,∴S=×1×2=1.△ABD故答案为:1.22.(5分)化简求值:已知[(x﹣2y)2﹣4y2+2xy]÷2x,其中 x=1,y=2.【解答】解:原式=(x2﹣4xy+4y2﹣4y2+2xy)÷2x=(x2﹣2xy)÷2x=x﹣y当x=1,y=2时,原式=﹣2=﹣23.(5分)如图,已知△ABC中,∠C=90°,AD平分∠BAC交BC于D,DE⊥AB 于E,点F在AC上,且BD=FD,求证:AE﹣BE=AF.【解答】证明:∵AD平分∠BAC交BC于D,DE⊥AB于E,∠C=90°,∴DC=DE,在Rt△ACD和Rt△AED中,,∴Rt△ACD≌Rt△AED(HL),同理可得Rt△FCD和Rt△BED,∴AC=AE,CF=BE,∴AE﹣BE=AF.24.(6分)如图,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.(1)证明:AD=BE;(2)求∠AEB的度数.【解答】解:(1)∵△ACB和△DCE均为等边三角形,∴CA=CB,CD=CE,∠ACB=∠DCE=60°,∴∠ACD=60°﹣∠CDB=∠BCE.在△ACD和△BCE中,,∴△ACD≌△BCE(SAS).∴AD=BE.(2)∵△ACD≌△BCE,∴∠ADC=∠BEC.∵△DCE为等边三角形,∴∠CDE=∠CED=60°.∵点A,D,E在同一直线上,∴∠BEC=120°.∴∠AEB=∠BEC﹣∠CED=60°.25.(8分)如图,在△ABC中,点D为边BC的中点,过点A作射线AE,过点C 作CF⊥AE于点F,过点B作BG⊥AE于点G,连接FD并延长,交BG于点H (1)求证:DF=DH;(2)若∠CFD=120°,求证:△DHG为等边三角形.【解答】证明:(1)∵CF⊥AE,BG⊥AE,∴∠BGF=∠CFG=90°,∴∠1+∠GMB=∠2+∠CME,∵∠GMB=∠CME,∴∠1=∠2,∵点D为边BC的中点,∴DB=CD,在△BHD和△CED中,,∴△BHD≌△CED(ASA),∴DF=DH;(2)∵∠CFD=120°,∠CFG=90°,∴∠GFH=30°,∵∠BGM=90°,∵△HGF是直角三角形,HD=DF,∴DG=HF=DH,∴△DHG为等边三角形.26.(8分)如图所示:△ABC是等腰直角三角形,BC=AC,直角顶点C在x轴上,一锐角顶点B在y轴上(1)如图1所示,若C的坐标是(2,0),点A的坐标是(﹣2,﹣2),求:点B的坐标;(2)如图2,若y轴恰好平分∠ABC,AC与y轴交于点D,过点A作AE⊥y轴于E,问BD与AE有怎样的数量关系,并说明理由;(3)如图3角边BC在两坐标轴上滑动,使点A在第四象限内,过A点作AF⊥y 轴于F,在滑动的过程中,两个结论①为定值;②为定值,只有一个结论成立,请你判断正确的结论加以证明,并求出定值.【解答】解:(1)过点B作BD⊥OD,∵∠DAC+∠ACD=90°,∠ACD+∠BCD=90°,∴∠BCD=∠DAC,在△ADC和△COB中,,∴△ADC≌△COB(AAS),∴AD=OC,CD=OB,∴点B坐标为(0,4);(2)延长BC,AE交于点F,∵AC=BC,AC⊥BC,∴∠BAC=∠ABC=45°,∵BD平分∠ABC,∴∠COD=22.5°,∠DAE=90°﹣∠ABD﹣∠BAD=22.5°,在△ACF和△BCD中,,∴△ACF≌△BCD(ASA),∴AF=BD,在△ABE和△FBE中,,∴△ABE≌△FBE(ASA),∴AE=EF,∴BD=2AE;(3)作AE⊥OC,则AF=OE,∵∠CBO+∠OCB=90°,∠OCB+∠ACO=90°,∴∠ACO=∠CBO,在△BCO和△ACE中,,∴△BCO≌△ACE(AAS),∴CE=OB,∴OB+AF=OC.∴=1.人教版八年级上学期期中考试数学试卷(二)一、选择题(每小题3分,共30分)1.(3分)下列图形分别是桂林、湖南、甘肃、佛山电视台的台徽,其中为轴对称图形的是()A.B.C.D.2.(3分)若等腰三角形底角为72°,则顶角为()A.108°B.72°C.54°D.36°3.(3分)对于任意三角形的高,下列说法不正确的是()A.锐角三角形有三条高B.直角三角形只有一条高C.任意三角形都有三条高D.钝角三角形有两条高在三角形的外部4.(3分)一个三角形的两边长为3和8,第三边长为奇数,则第三边长为()A.5或7 B.7或9 C.7 D.95.(3分)在△ABC和△DEF中,AB=DE,∠B=∠E,如果补充一个条件后不一定能使△ABC≌△DEF,则补充的条件是()A.BC=EF B.∠A=∠D C.AC=DF D.∠C=∠F6.(3分)如图,∠B=∠D=90°,CB=CD,∠1=30°,则∠2=()A.30°B.40°C.50°D.60°7.(3分)下列各组数可能是一个三角形的边长的是()A.1,2,4 B.4,5,9 C.4,6,8 D.5,5,118.(3分)已知等腰三角形其中一个内角为70°,那么这个等腰三角形的顶角度数为()A.70°B.70°或55°C.40°或55°D.70°或40°9.(3分)点M(3,2)关于y轴对称的点的坐标为()A.(﹣3,2)B.(﹣3,﹣2)C.(3,﹣2)D.(2,﹣3)10.(3分)已知△ABC≌△DEF,∠A=80°,∠E=40°,则∠F等于()A.80°B.40°C.120°D.60°二、填空题(每小题4分,共24分)11.(4分)如果△ABC和△DEF全等,△DEF和△GHI全等,则△ABC和△GHI 全等,如果△ABC和△DEF不全等,△DEF和△GHI全等,则△ABC和△GHI全等.(填“一定”或“不一定”或“一定不”)12.(4分)点P(﹣1,2)关于x轴对称点P的坐标为.113.(4分)如图,已知△ABC≌△ADE,若∠BAE=120°,∠BAD=40°,则∠DAC= .14.(4分)如图,已知AO=OB,若增加一个条件,则有△AOC≌△BOC.15.(4分)如图,△ABC中,∠C=90°,AD平分∠CAB交BC于D,DE⊥AB于E,且CD=3cm,则ED长为.16.(4分)如图,在△ABC中,AD=DE, AB=BE,∠A=92°,则∠CED= .三、计算题(本大题7小题,共66分)17.(8分)在等腰三角形ABC中,已知它的两边分别为3cm和7cm,试求三角形ABC的周长.18.(8分)一个等腰三角形的周长为18cm.(1)已知腰长是底边长的2倍,求各边长.(2)已知其中一边长为4cm,求另两边长.19.(8分)已知:点B、E、C、F在同一直线上,AB=DE,∠A=∠D,AC∥DF.求证:(1)△ABC≌△DEF;(2)BE=CF.20.(10分)如图,AE是∠BAC的平分线,AB=AC.若点D是AE上任意一点,请证明:△ABD≌△ACD.21.(10分)已知:如图,点D在△ABC的边BC上,AB=AC=CD,AD=BD,求△ABC 各内角的度数.22.(10分)如图,AF=DB,BC=EF,AC=DE,求证:BC∥EF.23.(12分)△ABC在平面直角坐标系中的位置如图所示A、B、C三点在格点上.(1)作出△ABC关于x轴对称的△A1B1C1,并写出点C1的坐标;(2)作出△ABC关于y对称的△A2B2C2,并写出点C2的坐标.(3)求△ABC的面积.参考答案与试题解析一、选择题(每小题3分,共30分)1.(3分)下列图形分别是桂林、湖南、甘肃、佛山电视台的台徽,其中为轴对称图形的是()A.B.C.D.【解答】解:A、不是轴对称图形,故错误;B、不是轴对称图形,故错误;C、不是轴对称图形,故错误;D、是轴对称图形,故正确.故选:D.2.(3分)若等腰三角形底角为72°,则顶角为()A.108°B.72°C.54°D.36°【解答】解:∵等腰三角形底角为72°∴顶角=180°﹣(72°×2)=36°故选:D.3.(3分)对于任意三角形的高,下列说法不正确的是()A.锐角三角形有三条高B.直角三角形只有一条高C.任意三角形都有三条高D.钝角三角形有两条高在三角形的外部【解答】解:A、锐角三角形有三条高,说法正确,故本选项不符合题意;B、直角三角形有三条高,说法错误,故本选项符合题意;C、任意三角形都有三条高,说法正确,故本选项不符合题意;D、钝角三角形有两条高在三角形的外部,说法正确,故本选项不符合题意;故选:B.4.(3分)一个三角形的两边长为3和8,第三边长为奇数,则第三边长为()A.5或7 B.7或9 C.7 D.9【解答】解:根据三角形的三边关系,得第三边大于8﹣3=5,而小于两边之和8+3=11.又第三边应是奇数,则第三边等于7或9.故选:B.5.(3分)在△ABC和△DEF中,AB=DE,∠B=∠E,如果补充一个条件后不一定能使△ABC≌△DEF,则补充的条件是()A.BC=EF B.∠A=∠D C.AC=DF D.∠C=∠F【解答】解:A、添加BC=EF,可利用SAS判定△ABC≌△DEF,故此选项错误;B、添加∠A=∠D,可利用ASA判定△ABC≌△DEF,故此选项错误;C、添加AC=DF,不能判定△ABC≌△DEF,故此选项正确;D、添加∠C=∠F,可利用AAS判定△ABC≌△DEF,故此选项错误;故选:C.6.(3分)如图,∠B=∠D=90°,CB=CD,∠1=30°,则∠2=()A.30°B.40°C.50°D.60°【解答】解:∵∠B=90°,∠1=30°,∴∠3=90°﹣∠1=90°﹣30°=60°,在Rt△ABC和Rt△ADC中,,∴Rt△ABC≌Rt△ADC(HL),∴∠2=∠3=60°.故选:D.7.(3分)下列各组数可能是一个三角形的边长的是()A.1,2,4 B.4,5,9 C.4,6,8 D.5,5,11【解答】解:A、因为1+2<4,所以本组数不能构成三角形.故本选项错误;B、因为4+5=9,所以本组数不能构成三角形.故本选项错误;C、因为4+6>8,所以本组数可以构成三角形.故本选项正确;D、因为5+5<11,所以本组数不能构成三角形.故本选项错误;故选:C.8.(3分)已知等腰三角形其中一个内角为70°,那么这个等腰三角形的顶角度数为()A.70°B.70°或55°C.40°或55°D.70°或40°【解答】解:分两种情况:当70°的角是底角时,则顶角度数为40°;当70°的角是顶角时,则顶角为70°.故选:D.9.(3分)点M(3,2)关于y轴对称的点的坐标为()A.(﹣3,2)B.(﹣3,﹣2)C.(3,﹣2)D.(2,﹣3)【解答】解:点M(3,2)关于y轴对称的点的坐标为(﹣3,2),故选:A.10.(3分)已知△ABC≌△DEF,∠A=80°,∠E=40°,则∠F等于()A.80°B.40°C.120°D.60°【解答】解:∵△ABC≌△DEF,∴∠D=∠A=80°,∵∠E=40°,∴∠F=180°﹣∠D﹣∠E=180°﹣80°﹣40°=60°.故选:D.二、填空题(每小题4分,共24分)11.(4分)如果△ABC和△DEF全等,△DEF和△GHI全等,则△ABC和△GHI 一定全等,如果△ABC和△DEF不全等,△DEF和△GHI全等,则△ABC和△GHI 一定不全等.(填“一定”或“不一定”或“一定不”)【解答】解:根据全等三角形的传递性,△ABC和△GHI一定全等,三者有一对不重合则△ABC和△GHI一定不重合,则二者不全等.故结果分别为一定,一定不.的坐标为(﹣1,﹣2).12.(4分)点P(﹣1,2)关于x轴对称点P1【解答】解:点P(﹣1,2)关于x轴对称点P的坐标为(﹣1,﹣2),1故答案为:(﹣1,﹣2).13.(4分)如图,已知△ABC≌△ADE,若∠BAE=120°,∠BAD=40°,则∠DAC=【解答】解:∵△ABC≌△ADE,∴∠DAE=∠BAC,∵∠CAD=∠BAC﹣∠BAD=∠DAE﹣∠CAE,∴∠BAD=∠CAE=40°,∵∠BAE=120°,∠BAD=40°,∴∠DAC=BAE﹣∠BAD﹣∠CAE=120°﹣40°﹣40°=40°.故答案为40°.14.(4分)如图,已知AO=OB,若增加一个条件∠1=∠2 ,则有△AOC≌△BOC.【解答】解:∵AO=OB,∠1=∠2,OC=OC,∴△AOC≌△BOC.故答案为:∠1=∠2.15.(4分)如图,△ABC中,∠C=90°,AD平分∠CAB交BC于D,DE⊥AB于E,且CD=3cm,则ED长为3cm .【解答】解:∵AD平分∠CAB,∠C=90°,DE⊥AB于点E,∵CD=3cm,∴DE=3cm.故答案为3cm.16.(4分)如图,在△ABC中,AD=DE,AB=BE,∠A=92°,则∠CED= 88°.【解答】解:∵在△ABD和△EBD中,∴△ABD≌△EBD(SSS),∴∠BED=∠A=92°,∴∠CED=180°﹣∠DEB=88°,故答案为:88°.三、计算题(本大题7小题,共66分)17.(8分)在等腰三角形ABC中,已知它的两边分别为3cm和7cm,试求三角形ABC的周长.【解答】解:当3cm是腰时,3+3<7cm,不符合三角形三边关系,故舍去;当7cm是腰时,周长=7+7+3=17cm.故该三角形的周长为17cm.18.(8分)一个等腰三角形的周长为18cm.(1)已知腰长是底边长的2倍,求各边长.(2)已知其中一边长为4cm,求另两边长.【解答】解:(1)设底边BC=acm,则AC=AB=2acm,∵三角形的周长是18cm,∴2a+2a+a=18,∴a=,2a=.答:等腰三角形的三边长是cm, cm, cm.(2)当4cm为腰,设底边为xcm,可得:4+4+x=18,解得:x=10,三角形的三边长是4cm,4m,10cm,不符合三角形的三边关系定理,当4cm为底,设腰为xcm,可得:x+4+x=18,解得:x=7,三角形的三边长是7cm,7cm,4cm,符合三角形的三边关系定理,所以另两边长7cm,7cm.19.(8分)已知:点B、E、C、F在同一直线上,AB=DE,∠A=∠D,AC∥DF.求证:(1)△ABC≌△DEF;(2)BE=CF.【解答】证明:(1)∵AC∥DF∴∠ACB=∠F在△ABC与△DEF中,∴△ABC≌△DEF(2)∵△ABC≌△DEF∴BC=EF∴BC﹣EC=EF﹣EC即BE=CF20.(10分)如图,AE是∠BAC的平分线,AB=AC.若点D是AE上任意一点,请证明:△ABD≌△ACD.【解答】证明:∵AE是∠BA C的平分线,∴∠BAD=∠CAD,在△ABD和△ACD中,,∴△BAD≌△CAD(SAS)21.(10分)已知:如图,点D在△ABC的边BC上,AB=AC=CD,AD=BD,求△ABC 各内角的度数.【解答】解:设∠B=α∵AB=AC,∴∠C=α,∵BD=BA,∴∠BAD=α,∵∠ADC为△ABC外角,∴∠ADC=2α,∵AC=DC,∴∠CAD=2α,∴∠BAC=3α,∴在△ABC中∠B+∠C+∠BAC=5α=180°,∴α=36°,∴∠B=∠C=36°,∴∠CAB=108°.22.(10分)如图,AF=DB,BC=EF,AC=DE,求证:BC∥EF.【解答】证明:∵AF=DB,∴AF+FB=DB+FB,∴AB=DF,在△ACB和△DEF中,,∴△ACB≌△DEF(SSS),∴∠ABC=∠EFD,∴CB∥EF.23.(12分)△ABC在平面直角坐标系中的位置如图所示A、B、C三点在格点上.(1)作出△ABC关于x轴对称的△A1B1C1,并写出点C1的坐标;(2)作出△ABC关于y对称的△A2B2C2,并写出点C2的坐标.(3)求△ABC的面积.【解答】解:(1)如图,△A1B1C1即为所求;点C1的坐标(3,﹣2)(2)如图,△A2B2C2即为所求;点C2的坐标(﹣3,2).(3)S△ABC=2×3﹣×1×2﹣×1×2﹣×1×3=2.5.人教版八年级上学期期中考试数学试卷(三)一、选择题(共10小题,每小题3分,共30分.)1.(3分)下列图形分别是桂林、湖南、甘肃、佛山电视台的台徽,其中为轴对称图形的是()A.B.C.D.2.(3分)点(﹣4,﹣2)关于y轴对称的点的坐标是()A.(4,2)B.(4,﹣2)C.(﹣4,﹣2)D.(﹣4,2)3.(3分)对于任意三角形的高,下列说法不正确的是()A.锐角三角形有三条高B.直角三角形只有一条高C.任意三角形都有三条高D.钝角三角形有两条高在三角形的外部4.(3分)一个三角形的两边长为3和8,第三边长为奇数,则第三边长为()A.5或7 B.7或9 C.7 D.95.(3分)等腰三角形的一个角是80°,则它的底角是()A.50°B.80°C.50°或80°D.20°或80°6.(3分)如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是()A.三角形的稳定性B.两点之间线段最短C.两点确定一条直线D.垂线段最短7.(3分)如图,∠B=∠D=90°,CB=CD,∠1=30°,则∠2=()A.30°B.40°C.50°D.60°8.(3分)如图,△ABC中,AB=AC,D为BC的中点,以下结论:(1)△ABD≌△ACD;(2)AD⊥BC;(3)∠B=∠C;(4)AD是△ABC的角平分线.其中正确的有()A.1个B.2个C.3个D.4个9.(3分)如图所示,△ABC中,AC=AD=BD,∠DAC=80°,则∠B的度数是()A.40°B.35°C.25°D.20°10.(3分)如图,点A的坐标是(2,2),若点P在x轴或y轴上且△APO是等腰三角形,这样的点P共有()个.A.6 B.7 C.8 D.9二、填空题(本大题共6小题,每小题3分,共18分.)11.(3分)三角形的外角和等于度.12.(3分)直线CD是线段AB的垂直平分线,点P在直线CD上,如果PA=5,则PB= .13.(3分)如图,∠1+∠2+∠3+∠4+∠5+∠6+∠7= °.14.(3分)如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线交AB于点D,交AC于点E,连接BE,则∠CBE的度数为.15.(3分)如图,等边三角形ABC中,BD是AC边上的中线,BD=BE,则∠EDA= 度.16.(3分)如图,△ABC是等边三角形,D为AB的中点,DE⊥AC垂足为点E,EF∥AB,AE=1,则△EFC的周长= .三、作图题:(每题8分,共16分)17.(8分)如图,在平面直角坐标系xoy中,A(1,2),B(3,1),C(﹣2,﹣1).(1)在图中作出△ABC关于y轴的对称图形△A1B1C1.(2)写出点A1,B1,C1的坐标(直接写答案).A 1B1.C118.(8分)如图,在5×5的正方形网格中,每个小正方形的边长均为1,线段AB的端点在格点上,按要求画出格点三角形,并求其面积.(1)在图①中画出一个以AB为腰的等腰三角形ABC,其面积为.(2)在图②中画出一个以AB为底的等腰三角形ABC,其面积为.四、解答题(每题8,共32分)19.(8分)已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB ⊥BE,垂足为B,DE⊥BE,垂足为E,且AB=DE,AC=DF.求证:BF=CE.20.(8分)如图,在△ABC中,AB=AC,BD垂直AC,垂足为D,∠A=40°,求∠DBC的度数.21.(8分)如图∠BAC=30°,D为角平分线上一点,DE⊥AC于E,DF∥AC且交AB于F.(1)求证:△ADF是等腰三角形.(2)若DF=10cm,求DE的长.22.(8分)如图,已知△ABC和△BED都是等边三角形,且A、E、D在一条直线上,且DC=4,BD=2,求AD的长度?五、解答题:(每题12分,共24分)23.(12分)如图:在等边三角形ABC中,AE=CD,(1)求证:△ABE≌△CAD;(2)过B点作BQ⊥AD于Q,求证:BP=2PQ.24.(12分)实验与探究:(1)由图观察易知A(0,2)关于直线l的对称点A′的坐标为(2,0),请在图中分别标明B(5,3)、C(﹣2,5)关于直线l的对称点B′、C′的位置,并写出他们的坐标:B′、C′;归纳与发现:(2)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点P'的坐标为(不必证明);运用与拓广:(3)已知两点D(1,﹣3)、E(﹣1,﹣4),试在直线l上确定一点Q,使点Q 到D、E两点的距离之和最小.(要有必要的画图说明,并保留作图痕迹)参考答案与试题解析一、选择题(共10小题,每小题3分,共30分.)1.(3分)下列图形分别是桂林、湖南、甘肃、佛山电视台的台徽,其中为轴对称图形的是()A.B.C.D.【解答】解:A、不是轴对称图形,故错误;B、不是轴对称图形,故错误;C、不是轴对称图形,故错误;D、是轴对称图形,故正确.故选:D.2.(3分)点(﹣4,﹣2)关于y轴对称的点的坐标是()A.(4,2)B.(4,﹣2)C.(﹣4,﹣2)D.(﹣4,2)【解答】解:点(﹣4,﹣2)关于y轴对称的点的坐标是(4,﹣2),故选:B.3.(3分)对于任意三角形的高,下列说法不正确的是()A.锐角三角形有三条高B.直角三角形只有一条高C.任意三角形都有三条高D.钝角三角形有两条高在三角形的外部【解答】解:A、锐角三角形有三条高,说法正确,故本选项不符合题意;B、直角三角形有三条高,说法错误,故本选项符合题意;C、任意三角形都有三条高,说法正确,故本选项不符合题意;D、钝角三角形有两条高在三角形的外部,说法正确,故本选项不符合题意;故选:B.4.(3分)一个三角形的两边长为3和8,第三边长为奇数,则第三边长为()A.5或7 B.7或9 C.7 D.9【解答】解:根据三角形的三边关系,得第三边大于8﹣3=5,而小于两边之和8+3=11.又第三边应是奇数,则第三边等于7或9.故选:B.5.(3分)等腰三角形的一个角是80°,则它的底角是()A.50°B.80°C.50°或80°D.20°或80°【解答】解:①当顶角是80°时,它的底角=(180°﹣80°)=50°;②底角是80°.所以底角是50°或80°.故选:C.6.(3分)如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是()A.三角形的稳定性B.两点之间线段最短C.两点确定一条直线D.垂线段最短【解答】解:构成△AOB,这里所运用的几何原理是三角形的稳定性.故选:A.7.(3分)如图,∠B=∠D=90°,CB=CD,∠1=30°,则∠2=()A.30°B.40°C.50°D.60°【解答】解:∵∠B=90°,∠1=30°,∴∠3=90°﹣∠1=90°﹣30°=60°,在Rt△ABC和Rt△ADC中,,∴Rt△ABC≌Rt△ADC(HL),∴∠2=∠3=60°.故选:D.8.(3分)如图,△ABC中,AB=AC,D为BC的中点,以下结论:(1)△ABD≌△ACD;(2)AD⊥BC;(3)∠B=∠C;(4)AD是△ABC的角平分线.其中正确的有()A.1个B.2个C.3个D.4个【解答】解:∵AB=AC,∴∠B=∠C,∴(3)正确,∵D为BC的中点,∴AD⊥BC,∠BAD=∠CAD,∴(2)(4)正确,在△ABD和△ACD中∴△ABD≌△ACD(SSS),∴(1)正确,∴正确的有4个,故选:D.9.(3分)如图所示,△ABC中,AC=AD=BD,∠DAC=80°,则∠B的度数是()A.40°B.35°C.25°D.20°【解答】解:∵AD=AC,∠DAC=80°,∴∠ADC==50°,又∵AD=BD,∴∠B=∠BAD,∵∠B+∠BAD=∠ADC,∴2∠B=∠ADC,∴∠B=∠ADC=25°,故选:C.10.(3分)如图,点A的坐标是(2,2),若点P在x轴或y轴上且△APO是等腰三角形,这样的点P共有()个.A.6 B.7 C.8 D.9【解答】解:如图,满足条件的点P有8个,故选:C.二、填空题(本大题共6小题,每小题3分,共18分.)11.(3分)三角形的外角和等于360 度.【解答】解:三角形的外角和等于360°.故答案是:360.12.(3分)直线CD是线段AB的垂直平分线,点P在直线CD上,如果PA=5,则PB= 5 .【解答】解:∵直线CD是线段AB的垂直平分线,P为直线CD上的一点,∴PB=PA,而已知线段PA=5,∴PB=5.故答案是:5.13.(3分)如图,∠1+∠2+∠3+∠4+∠5+∠6+∠7= 540 °.【解答】解:如图,∵∠1+∠2+γ=180°①,∠3+∠4+β+θ=360°②,∠5+∠6+∠7+α=360°③,∴①+②+③得,∠1+∠2+∠3+∠4+∠5+∠6+∠7+α+β+γ+θ=900°,∵α+β=180°,γ+θ=180°,∴∠1+∠2+∠3+∠4+∠5+∠6+∠7,=900°﹣180°﹣180°,=540°.故答案为:540.14.(3分)如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线交AB于点D,交AC于点E,连接BE,则∠CBE的度数为30°.【解答】解:∵AB=AC,∠A=40°,∴∠ABC=∠C=70°,∵DE是AB的垂直平分线,∴EA=EB,∴∠EBA=∠A=40°,∴∠CBE=∠ABC﹣∠EBA=30°,故答案为:30°.15.(3分)如图,等边三角形ABC中,BD是AC边上的中线,BD=BE,则∠EDA= 15 度.【解答】解:∵等边三角形ABC中,BD是AC边上的中线,∴∠ABD=ABC=30°,∠ADB=90°,∵BD=BE,∴∠BDE=∠BED==75°,∴∠EDA=15°.故答案为:15.16.(3分)如图,△ABC是等边三角形,D为AB的中点,DE⊥AC垂足为点E,EF∥AB,AE=1,则△EFC的周长= 9 .【解答】解:在Rt△ADE中,∠A=60°,∴∠A DE=30°,又AE=1,∴AD=2AE=2,∵D为AB的中点,∴AB=AC=4,∴CE=AC﹣AE=4﹣1=3,∵EF∥AB,∴∠EFC=∠B=60°,又∠C=60°,∴△EFC为等边三角形,∴EF=FC=EC=3,∴△EFC的周长=3+3+3=9.三、作图题:(每题8分,共16分)17.(8分)如图,在平面直角坐标系xoy中,A(1,2),B(3,1),C(﹣2,﹣1).(1)在图中作出△ABC关于y轴的对称图形△A1B1C1.(2)写出点A1,B1,C1的坐标(直接写答案).A1(﹣1,2)B1(﹣3,1)C1(2,﹣1).【解答】解:(1)所作图形如下所示:(2)A1,B1,C1的坐标分别为:(﹣1,2),(﹣3,1),(2,﹣1).故答案为:(﹣1,2),(﹣3,1),(2,﹣1).18.(8分)如图,在5×5的正方形网格中,每个小正方形的边长均为1,线段AB的端点在格点上,按要求画出格点三角形,并求其面积.(1)在图①中画出一个以AB为腰的等腰三角形ABC,其面积为4或5或3 .(2)在图②中画出一个以AB为底的等腰三角形ABC,其面积为3,2.5 .【解答】解:(1)以AB为腰的等腰三角形的面积:×2×3=3;面积为:4或5或3;(2)以AB为底的等腰三角形的面积:2×3﹣×3×1﹣×1×2×2=2.5,故答案为3,2.5.四、解答题(每题8,共32分)19.(8分)已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB ⊥BE,垂足为B,DE⊥BE,垂足为E,且AB=DE,AC=DF.求证:BF=CE.【解答】证明:∵AB⊥BE,DE⊥BE,∴∠B=∠E=90°.在Rt△ABC和△RtDEF中,,∴△RtABC≌Rt△DEF,∴BC=EF,∴BC﹣CF=EF﹣CF,即:BF=CE.20.(8分)如图,在△ABC中,AB=AC,BD垂直AC,垂足为D,∠A=40°,求∠DBC的度数.【解答】解:∵在△ABC中,AB=AC,∠A=40°,∴∠ABC=∠ACB=(180°﹣40°)÷2=70°;又∵BD⊥AC垂足为D,∴∠DBC=90°﹣∠ACB=90°﹣70°=20°.21.(8分)如图∠BAC=30°,D为角平分线上一点,DE⊥AC于E,DF∥AC且交AB于F.(1)求证:△ADF是等腰三角形.(2)若DF=10cm,求DE的长.【解答】(1)证明:∵∠BAC=30°,D为角平分线上一点,∴∠BAD=∠CAD,∵DF∥AC,∴∠CAD=∠FDA,∴∠BAD=∠FDA,∴FA=FD,即△ADF是等腰三角形;(2)解:作DH⊥AB于H,∵DF∥AC,∴∠BFD=∠BAC=30°,∴DH=DF=5,∵D为角平分线上一点,DE⊥AC,DH⊥AB,∴DE=DH=5cm.22.(8分)如图,已知△ABC和△BED都是等边三角形,且A、E、D在一条直线上,且DC=4,BD=2,求AD的长度?【解答】解:∵△ABC和△BED都是等边三角形,∴AB=BC,BE=BD,∠ABC=∠EBD=60°,∴∠ABE=∠CBD=60°﹣∠CBE,在△ABE和△CBD中,∴△ABE≌△CBD(SAS),∴AE=CD=4,∵△BED是等边三角形,。
2020-2021学年江苏省南京市鼓楼区四校联考八年级(上)期中数学试卷 (解析版)
2020-2021学年江苏省南京市鼓楼区四校联考八年级第一学期期中数学试卷一、选择题(共6小题).1.(2分)下列倡导节约的图案中是轴对称图形的是()A.B.C.D.2.(2分)下列各式正确的是()A.B.|3.14﹣π|=π﹣3.14C.D.3.(2分)如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是()A.带①去B.带②去C.带③去D.带①和②去4.(2分)小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是()A.角的内部到角的两边的距离相等的点在角的平分线上B.角平分线上的点到这个角两边的距离相等C.三角形三条角平分线的交点到三条边的距离相等D.以上均不正确5.(2分)如图所示,△ABC中,AB=BC=AC,BD=CE,AD与BE相交于点P,则∠APE的度数是()A.45°B.55°C.75°D.60°6.(2分)如图的方格纸中每一个小方格都是边长为1的正方形,A、B两点都在小方格的格点(顶点)上,请在图中找一个格点C,使△ABC为等腰三角形,这样的格点的个数有()A.8个B.9个C.10个D.11个二、填空题(共10小题).7.(2分)比较大小:2.8.(2分)角是轴对称图形,是它的对称轴.9.(2分)已知实数a、b互为相反数,c、d互为倒数,e是的整数部分,f是的小数部分,求代数式﹣+e﹣f=.10.(2分)等腰三角形的一个内角为70°,另外两个内角的度数为.11.(2分)如图,要为一段高5米,长13米的楼梯铺上红地毯,至少需要红地毯米.12.(2分)如图,在△ABC中,DE是AC的垂直平分线,AE=3,△BCD的周长为13,则△ABC的周长是.13.(2分)如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为.14.(2分)如图,在△ABC中,AB=AC=5,BC=6,点M为BC中点,MN⊥AC于点N,则MN的长是.15.(2分)如图,∠ACD是△ABC的外角,∠BAC=80°,∠ABC和∠ACD的平分线相交于点E,连接AE,则∠CAE的度数是.16.(2分)如图,∠AOB=30°,点P为∠AOB内一点,OP=8.点M、N分别在OA、OB上,则△PMN周长的最小值为.三、解答题(共8小题,共68分.)17.(8分)计算(1)(﹣2)2+;(2)+(π﹣3)0﹣|1﹣|.18.(10分)求下列各式中的x:(1)(x+2)2=4;(2)1+(x﹣1)3=﹣7.19.(8分)如图,已知直线l及直线l外一点P.(1)求作:直线PQ,使得PQ⊥l.(保留作图痕迹)(2)证明:PQ⊥l.20.(8分)如图,点D,E分别是三角形△ABC边BC上的点,若AB=AC,BE=CD,求证:AD=AE.21.(6分)已知:△ABC和△ECD是等腰直角三角形,∠ACB=∠DCE=90°,点D在AB的延长线上.求证:AE2+AD2=ED2.22.(6分)如图为一个广告牌支架的示意图,其中AB=13m,AD=12m,BD=5m,AC=15m,求图中△ABC的周长和面积.23.(10分)如图,△ABC中,∠ACB=90°,AB=5cm,BC=4cm,若点P从点A出发,以每秒2cm的速度沿折线A﹣B﹣C﹣A运动,设运动时间为t秒(t>0).(1)若点P在BC上且满足PA=PB,则此时t=.(2)若点P恰好在∠ABC的角平分线上,求此时t的值;(3)在点P运动过程中,若△ACP为等腰三角形,则此时t=.24.(12分)阅读理解:课外兴趣小组活动时,老师提出了如下问题:在△ABC中,AB=9,AC=5,BC边上的中线AD的取值范围.(1)小明在组内经过合作交流,得到了如下的解决方法(如图1):①延长AD到Q使得DQ=AD;②再连接BQ,把AB、AC、2AD集中在△ABQ中;③利用三角形的三边关系可得4<AQ<14,则AD的取值范围是.感悟:解题时,条件中若出现“中点”“中线”等条件,可以考虑倍长中线,构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形中.(2)请写出图1中AC与BQ的位置关系并证明;(3)思考:已知,如图2,AD是△ABC的中线,AB=AE,AC=AF,∠BAE=∠FAC =90°,试探究线段AD与EF的数量和位置关系,并加以证明.参考答案一、选择题(共6小题).1.(2分)下列倡导节约的图案中是轴对称图形的是()A.B.C.D.解:A、不是轴对称图形,故此选项错误;B、是轴对称图形,故此选项正确;C、不是轴对称图形,故此选项错误;D、不是轴对称图形,故此选项错误;故选:B.2.(2分)下列各式正确的是()A.B.|3.14﹣π|=π﹣3.14C.D.解:A、=9,故本选项错误;B、正确;C、=2,故本选项错误;D、已是最简形式,并且不是同类项,不用计算,故本选项错误.故选:B.3.(2分)如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是()A.带①去B.带②去C.带③去D.带①和②去解:A、带①去,仅保留了原三角形的一个角和部分边,不能得到与原来一样的三角形,故A选项错误;B、带②去,仅保留了原三角形的一部分边,也是不能得到与原来一样的三角形,故B选项错误;C、带③去,不但保留了原三角形的两个角还保留了其中一条边,符合ASA判定,故C选项正确;D、带①和②去,仅保留了原三角形的一个角和部分边,同样不能得到与原来一样的三角形,故D选项错误.故选:C.4.(2分)小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是()A.角的内部到角的两边的距离相等的点在角的平分线上B.角平分线上的点到这个角两边的距离相等C.三角形三条角平分线的交点到三条边的距离相等D.以上均不正确解:(1)如图所示:过两把直尺的交点P作PE⊥AO,PF⊥BO,∵两把完全相同的长方形直尺,∴PE=PF,∴OP平分∠AOB(角的内部到角的两边的距离相等的点在这个角的平分线上),故选:A.5.(2分)如图所示,△ABC中,AB=BC=AC,BD=CE,AD与BE相交于点P,则∠APE的度数是()A.45°B.55°C.75°D.60°解:在△ABD和△BCE中,,∴△ABD≌△BCE(SAS),∴∠BAD=∠CBE,∵∠APE=∠ABE+∠BAD,∠ABE+∠CBE=60°,∴∠APE=∠ABC=60°.故选:D.6.(2分)如图的方格纸中每一个小方格都是边长为1的正方形,A、B两点都在小方格的格点(顶点)上,请在图中找一个格点C,使△ABC为等腰三角形,这样的格点的个数有()A.8个B.9个C.10个D.11个解:图中的黑点为C点所在位置,这样的C点共有9个.故选:B.二、填空题(共10小题).7.(2分)比较大小:>2.解:=9,23=8,∵9>8,∴>2.故答案为:>.8.(2分)角是轴对称图形,角平分线所在的直线是它的对称轴.解:角的对称轴是“角平分线所在的直线”.故答案为:角平分线所在的直线.9.(2分)已知实数a、b互为相反数,c、d互为倒数,e是的整数部分,f是的小数部分,求代数式﹣+e﹣f=4﹣.解:∵实数a、b互为相反数,∴a+b=0,∵c、d互为倒数,∴cd=1,∵3<<4,∴的整数部分为3,e=3,∵2<<3,∴的小数部分为﹣2,即f=﹣2,∴﹣+e﹣f=﹣+3﹣(﹣2)=0﹣1+3﹣+2=4﹣,故答案为:4﹣.10.(2分)等腰三角形的一个内角为70°,另外两个内角的度数为55°,55°或70°,40°.解:分情况讨论:(1)若等腰三角形的顶角为70°时,另外两个内角=(180°﹣70°)÷2=55°;(2)若等腰三角形的底角为70°时,它的另外一个底角为70°,顶角为180°﹣70°﹣70°=40°.故填55°,55°或70°,40°.11.(2分)如图,要为一段高5米,长13米的楼梯铺上红地毯,至少需要红地毯17米.解:根据勾股定理,楼梯水平长度为=12米,则红地毯至少要12+5=17米长,故答案为:17.12.(2分)如图,在△ABC中,DE是AC的垂直平分线,AE=3,△BCD的周长为13,则△ABC的周长是19.解:∵DE是AC的垂直平分线,AE=3,∴DA=DC,AC=2AE=6,∵△BCD的周长为13,∴BC+BD+CD=13,∴BC+BD+DA=BC+AB=13,∴△ABC的周长=BC+AB+AC=13+6=19,故答案为:19.13.(2分)如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为4.解:设BN=x,由折叠的性质可得DN=AN=9﹣x,∵D是BC的中点,∴BD=3,在Rt△BND中,x2+32=(9﹣x)2,解得x=4.故线段BN的长为4.故答案为:4.14.(2分)如图,在△ABC中,AB=AC=5,BC=6,点M为BC中点,MN⊥AC于点N,则MN的长是.解:连接AM,∵AB=AC,点M为BC中点,∴AM⊥CM(三线合一),BM=CM,∵AB=AC=5,BC=6,∴BM=CM=3,在Rt△ABM中,AB=5,BM=3,∴根据勾股定理得:AM===4,又S△AMC=MN•AC=AM•MC,∴MN==.15.(2分)如图,∠ACD是△ABC的外角,∠BAC=80°,∠ABC和∠ACD的平分线相交于点E,连接AE,则∠CAE的度数是50°.解:过点E作EN⊥BD,垂足为N,作EM⊥AC,垂足为M,作EF⊥AB,交BA的延长线于F,∵BE平分∠ABC,CE平分∠ACD,∴EF=EN=EM,∴E点在∠FAC的角平分线上,∴∠CAE=∠CAF,∵∠CAF+∠BAC=180°,∠BAC=80°,∴∠CAF=100°,∴∠CAE=50°.16.(2分)如图,∠AOB=30°,点P为∠AOB内一点,OP=8.点M、N分别在OA、OB上,则△PMN周长的最小值为8.解:分别作点P关于OA、OB的对称点P1、P2,连P1、P2,交OA于M,交OB于N,连接OP,则OP1=OP=OP2,∠P1OA=∠POA,∠POB=∠P2OB,MP=P1M,PN=P2N,则△PMN的周长的最小值=P1P2∴∠P1OP2=2∠AOB=60°,∴△OP1P2是等边三角形.△PMN的周长=P1P2,∴P1P2=OP1=OP2=OP=8.故答案为:8.三、解答题(本大题共8小题,共68分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)17.(8分)计算(1)(﹣2)2+;(2)+(π﹣3)0﹣|1﹣|.解:(1)原式=4+4﹣2=6;(2)原式=+1﹣(﹣1)=﹣.18.(10分)求下列各式中的x:(1)(x+2)2=4;(2)1+(x﹣1)3=﹣7.解:(1)x+2=±2,∴x+2=2或x+2=﹣2,∴x=0或﹣4;(2)(x﹣1)3=﹣8,x﹣1=﹣2,∴x=﹣1.19.(8分)如图,已知直线l及直线l外一点P.(1)求作:直线PQ,使得PQ⊥l.(保留作图痕迹)(2)证明:PQ⊥l.【解答】(1)解:如图,直线PQ即为所求.(2)证明:由作图可知,PC=PD,CQ=QD,∴PQ垂直平分线段CD,∴PQ⊥直线l.20.(8分)如图,点D,E分别是三角形△ABC边BC上的点,若AB=AC,BE=CD,求证:AD=AE.【解答】证明:∵AB=AC,∴∠B=∠C,在△ABE和△ACD中,,∴△ABE≌△ACD(SAS),∴AD=AE.21.(6分)已知:△ABC和△ECD是等腰直角三角形,∠ACB=∠DCE=90°,点D在AB的延长线上.求证:AE2+AD2=ED2.【解答】证明:∵BC=AC,∴∠ACB=90°,∴∠ABC=∠CAB=45°.∵△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,∴BC=CA,CD=CE,∠BCD=∠ECA,在△ACE和△BCD中,,∴△ACE≌△BCD(SAS).∴∠CAE=∠CBD=135°,∴∠DAE=∠CAE﹣∠CAB=90°,∴AD2+AE2=ED2.22.(6分)如图为一个广告牌支架的示意图,其中AB=13m,AD=12m,BD=5m,AC=15m,求图中△ABC的周长和面积.解:在△ABD中,∵AB=13m,AD=12m,BD=5m,∴AB2=AD2+BD2,∴AD⊥BC,在Rt△ADC中,∵AD=12m,AC=15m,∴DC==9(m),∴△ABC的周长为:AB+AC+BC=13+15+5+9=42m,△ABC的面积为:×BC×AD=×14×12=84m2.23.(10分)如图,△ABC中,∠ACB=90°,AB=5cm,BC=4cm,若点P从点A出发,以每秒2cm的速度沿折线A﹣B﹣C﹣A运动,设运动时间为t秒(t>0).(1)若点P在BC上且满足PA=PB,则此时t=.(2)若点P恰好在∠ABC的角平分线上,求此时t的值;(3)在点P运动过程中,若△ACP为等腰三角形,则此时t=或或或3.解:(1)如图,设PB=PA=x,则PC=4﹣x,∵∠ACB=90°,AB=5cm,BC=4cm,∴AC=3cm,在Rt△ACP中,AC2+PC2=AP2,∴32+(4﹣x)2=x2,解得x=,∴BP=,∴t===.故答案为:.(2)如图,过P作PD⊥AB于D,∵BP平分∠ABC,∠C=90°,∴PD=PC,BC=BD=4,∴AD=5﹣4=1,设PD=PC=y,则AP=3﹣y,在Rt△ADP中,AD2+PD2=AP2,∴12+y2=(3﹣y)2,解得y=,∴CP=,∴t===,当点P与点B重合时,点P也在∠ABC的角平分线上,此时,t==.综上所述,点P恰好在∠ABC的角平分线上,t的值为或.(3)分四种情况:①如图,当P在AB上且AP=CP时,∠A=∠ACP,而∠A+∠B=90°,∠ACP+∠BCP=90°,∴∠B=∠BCP,∴CP=BP,∴P是AB的中点,即AP=AB=,∴t==.②如图,当P在AB上且AP=CA=3时,t==.③如图,当P在AB上且AC=PC时,过C作CD⊥AB于D,则CD==,∴Rt△ACD中,AD=,∴AP=2AD=,∴t==.④如图,当P在BC上且AC=PC=3时,BP=4﹣3=1,∴t===3.综上所述,当t=或或或3时,△ACP为等腰三角形.故答案为:或或或3.24.(12分)阅读理解:课外兴趣小组活动时,老师提出了如下问题:在△ABC中,AB=9,AC=5,BC边上的中线AD的取值范围.(1)小明在组内经过合作交流,得到了如下的解决方法(如图1):①延长AD到Q使得DQ=AD;②再连接BQ,把AB、AC、2AD集中在△ABQ中;③利用三角形的三边关系可得4<AQ<14,则AD的取值范围是2<AD<7.感悟:解题时,条件中若出现“中点”“中线”等条件,可以考虑倍长中线,构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形中.(2)请写出图1中AC与BQ的位置关系并证明;(3)思考:已知,如图2,AD是△ABC的中线,AB=AE,AC=AF,∠BAE=∠FAC =90°,试探究线段AD与EF的数量和位置关系,并加以证明.解:(1)延长AD到Q使得DQ=AD,连接BQ,∵AD是△ABC的中线,∴BD=CD,在△QDB和△ADC中,,∴△QDB≌△ADC(SAS),∴BQ=AC=5,在△ABQ中,AB﹣BQ<AQ<AB+BQ,∴4<AQ<14,∴2<AD<7,故答案为:2<AD<7;(2)AC∥BQ,理由:由(1)知,△QDB≌△ADC,∴∠BQD=∠CAD,∴AC∥BQ;(3)EF=2AD,AD⊥EF,理由:如图2,延长AD到Q使得DQ=AD,连接BQ,由(1)知,△BDQ≌△CDA(SAS),∴∠DBQ=∠ACD,BQ=AC,∵AC=AF,∴BQ=AF,在△ABC中,∠BAC+∠ABC+∠ACB=180°,∴∠BAC+∠ABC+∠DBQ=180°,∴∠BAC+ABQ=180°,∵∠BAE=∠FAC=90°,∴∠BAC+∠EAF=180°,∴∠ABQ=∠EAF,在△ABQ和△EAF中,,∴△ABQ≌△EAF,∴AQ=EF,∠BAQ=∠AEF,延长DA交EF于P,∵∠BAE=90°,∴∠BAQ+∠EAP=90°,∴∠AEF+∠EAP=90°,∴∠APE=90°,∴AD⊥EF,∵AD=DQ,∴AQ=2AD,∵AQ=EF,∴EF=2AD,即:EF=2AD,AD⊥EF.。
2019-2020学年江苏省南京市鼓楼区八年级上学期期中数学试卷 (学生版+解析版)
2019-2020学年江苏省南京市鼓楼区八年级(上)期中数学试卷一、选择题(共8小题).1.有些国家的国旗设计成了轴对称图形,观察如图代表国旗的图案,你认为是轴对称图形的有()A.4个B.3个C.2个D.1个2.在实数﹣,,0,﹣,2.161161161…,中,无理数有()A.1个B.2个C.3个D.4个3.等腰三角形两边长分别为4和8,则这个等腰三角形的周长为()A.16B.18C.20D.16或204.以下列数组为边长的三角形中,能构成直角三角形的是()A.5,12,13B.8,15,16C.9,16,25D.12,15,20 5.下列说法中,正确的有()A.只有正数才有平方根B.27的立方根是±3C.立方根等于﹣1的实数是﹣1D.1的平方根是16.如图,AD是△ABC的角平分线,DE⊥AB,垂足为E,S△ABC=7,DE=2,AB=4,则AC长是()A.6B.5C.4D.37.如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠BCD的角平分线,则图中的等腰三角形有()A.5个B.4个C.3个D.2个8.如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x﹣y=2,③2xy+4=49,④x+y=9.其中说法正确的是()A.①②B.①②③C.①②④D.①②③④二、填空题(共10小题,每小题2分,共20分)9.由四舍五入法得到的近似数2.5×103精确到位.10.16的平方根为;(﹣4)3的立方根是.11.若,则x﹣y=.12.如图中有6个条形方格图,图上由实线围成的图形与(1)是全等形的有.13.如图,△ABC中,DE是AC的垂直平分线,AB=5,BC=7,则△ABD的周长是.14.已知等腰三角形的一个外角等于110°,则它的顶角是°.15.如图,在3×3的正方形网格中,则∠1+∠2+∠3+∠4=°.16.如图,在△ABC中,边AB、AC的垂直平分线分别交BC于点E、点D.若∠BAC=130°,那么∠EAD=.17.如图,在四边形ABCD中,AB=AC=BD,AC与BD相交于O,且AC⊥BD.①AB∥CD;②△ABD≌△BAC;③AB2+CD2=AD2+CB2;④∠ACB+∠BDA=135°.其中结论正确的是(填序号).18.如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为.三、解答题(共9小题,共64分)19.计算:(1)﹣(2)()2+|1﹣|+()0.20.求下列各式中的x的值(1)4x2﹣9=0(2)64(x+1)3=﹣125.21.已知:如图,C是AB的中点,AE=BD,∠A=∠B.求证:∠ACE=∠BCD.22.如图,在△ABC中,AB=5,AC=13,AD是边BC上的中线,E在AD的延长线上,AD=ED=6,求△ABC的面积.23.如图,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.(1)证明:AD=BE;(2)求∠AEB的度数.24.如图(1)是用硬板纸做成的两个全等的直角三角形,两直角边的长分别为a和b,斜边长为c,请你开动脑筋,将它们拼成一个能证明勾股定理的图形.(1)画出拼成的这个图形的示意图,并用这个图形证明勾股定理;(2)假设图(1)中的直角三角形有若干个,你能运用图(1)中所给的直角三角形拼出另一种能证明勾股定理的图形吗?请画出拼后的示意图(无需证明)25.阅读理解:求的近似值.小明的方法:设=10+x,其中0<x<1,则105=(10+x)2,即105=100+20x+x2.∵0<x<1∴0<x2<1,∴105≈100+20x,解之得x≈0.25,即的近似值为10.25,小莉的方法:设=11﹣y,其中0<y<1,则105=(11﹣y)2,即105=121﹣22y+y2,∵0<y<1∴0<y2<1,∴105≈121﹣22y,解之得y≈0.73,即的近似值为10.27.【反思比较】你认为的方法更接近.(填“小明”或“小莉”)【深入思考】下面关于x与y之间的数量关系A.x+y>1 B.x+y=1 C.x+y<1 D.无法确定你认为正确的是.请说明理由.26.(1)我们已经如道:在△ABC中,如果AB=AC,则∠B=∠C,下面我们继续研究:如图①,在△ABC中,如果AB>AC,则∠B与∠C的大小关系如何?为此,我们把AC 沿∠BAC的平分线翻折,因为AB>AC,所以点C落在AB边的点D处,如图②所示,然后把纸展平,连接DE.接下来,你能推出∠B与∠C的大小关系了吗?试写出说理过程.(2)如图③,在△ABC中,AE是角平分线,且∠C=2∠B.求证:AB=AC+CE.(3)在(2)的条件下,若点P,F分别为AE、AC上的动点,且S△ABC=15,AB=8,则PF+PC的最小值为.27.如图,已知等边△ABC,点D为△ABC内的一点,连接DA、DB、DC,∠ADB=120°.以CD为边向CD上方作等边△CDE,连接AE(0°<∠ACE<60°).(1)求证:△BDC≌△AEC.(2)若DC=2n,AD=AE,则△ADE的面积为.(3)若DA=n2+1,DB=n2﹣1,DC=2n(n为大于1的整数).求证:DA2+DC2=AC2.参考答案一、选择题(共8小题,每小题2分,共16分)1.有些国家的国旗设计成了轴对称图形,观察如图代表国旗的图案,你认为是轴对称图形的有()A.4个B.3个C.2个D.1个解:根据轴对称的概念可知:加拿大国旗、瑞士国旗是轴对称图形,符合题意;澳大利亚国旗、乌拉圭国旗都不是轴对称图形,不符合题意.故选:C.2.在实数﹣,,0,﹣,2.161161161…,中,无理数有()A.1个B.2个C.3个D.4个解:在实数﹣,,0,﹣,2.161161161…,中,无理数有﹣,﹣,一共2个.故选:B.3.等腰三角形两边长分别为4和8,则这个等腰三角形的周长为()A.16B.18C.20D.16或20解:①当4为腰时,4+4=8,故此种情况不存在;②当8为腰时,8﹣4<8<8+4,符合题意.故此三角形的周长=8+8+4=20.故选:C.4.以下列数组为边长的三角形中,能构成直角三角形的是()A.5,12,13B.8,15,16C.9,16,25D.12,15,20解:A、∵52+122=132,∴A正确;B、∵82+152≠162,∴B错误;C、∵92+162≠252,∴C错误;D、∵122+152≠202,∴D错误;故选:A.5.下列说法中,正确的有()A.只有正数才有平方根B.27的立方根是±3C.立方根等于﹣1的实数是﹣1D.1的平方根是1解:A、只有正数才有平方根,错误,0的平方根是0,故本选项错误;B、27的立方根是3,故本选项错误;C、立方根等于﹣1的实数是﹣1正确,故本选项正确;D、1的平方根是±1,故本选项错误.故选:C.6.如图,AD是△ABC的角平分线,DE⊥AB,垂足为E,S△ABC=7,DE=2,AB=4,则AC长是()A.6B.5C.4D.3解:过点D作DF⊥AC于F,∵AD是△ABC的角平分线,DE⊥AB,∴DE=DF=2,∴S△ABC=×4×2+AC×2=7,解得AC=3.故选:D.7.如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠BCD的角平分线,则图中的等腰三角形有()A.5个B.4个C.3个D.2个解:共有5个.(1)∵AB=AC∴△ABC是等腰三角形;(2)∵BD、CE分别是∠ABC、∠BCD的角平分线∴∠EBC=∠ABC,∠ECB=∠BCD,∵△ABC是等腰三角形,∴∠EBC=∠ECB,∴△BCE是等腰三角形;(3)∵∠A=36°,AB=AC,∴∠ABC=∠ACB=(180°﹣36°)=72°,又BD是∠ABC的角平分线,∴∠ABD=∠ABC=36°=∠A,∴△ABD是等腰三角形;同理可证△CDE和△BCD是等腰三角形.故选:A.8.如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x﹣y=2,③2xy+4=49,④x+y=9.其中说法正确的是()A.①②B.①②③C.①②④D.①②③④解:由题意,①﹣②得2xy=45 ③,∴2xy+4=49,①+③得x2+2xy+y2=94,∴(x+y)2=94,∴①②③正确,④错误.故选:B.二、填空题(共10小题,每小题2分,共20分)9.由四舍五入法得到的近似数2.5×103精确到百位.解:2.5×103精确到百位.故答案是:百.10.16的平方根为±4;(﹣4)3的立方根是﹣4.解:16的平方根为±4;(﹣4)3的立方根是﹣4.故答案为:±4、﹣4.11.若,则x﹣y=5.解:根据题意得,x﹣3=0,y+2=0,解得x=3,y=﹣2,x﹣y=3﹣(﹣2)=3+2=5.故答案为:5.12.如图中有6个条形方格图,图上由实线围成的图形与(1)是全等形的有(2),(3),(6).解:由图可知,图上由实线围成的图形与(1)是全等形的有(2),(3),(6),故答案为:(2),(3),(6),13.如图,△ABC中,DE是AC的垂直平分线,AB=5,BC=7,则△ABD的周长是12.解:∵DE是AC的垂直平分线,∴DA=DC.∵AB=5,BC=7,∴△ABD的周长=AB+BD+DA=AB+BD+DC=AB+BC=12,故答案为:12.14.已知等腰三角形的一个外角等于110°,则它的顶角是70或40°.解:①若110°是顶角的外角,则顶角=180°﹣110°=70°;②若110°是底角的外角,则底角=180°﹣110°=70°,那么顶角=180°﹣2×70°=40°.故它的顶角是70°或40°.故答案为:70或40.15.如图,在3×3的正方形网格中,则∠1+∠2+∠3+∠4=180°.解:∵∠1和∠4所在的三角形全等,∴∠1+∠4=90°,∵∠2和∠3所在的三角形全等,∴∠2+∠3=90°,∴∠1+∠2+∠3十∠4=180°.故答案为:180.16.如图,在△ABC中,边AB、AC的垂直平分线分别交BC于点E、点D.若∠BAC=130°,那么∠EAD=80°.解:∵∠BAC=130°,∴∠B+∠C=50°,∵DA=DB,EA=EC,∴∠DAB=∠B,∠EAC=∠C,∴∠DAE=∠BAC﹣(∠DAB+∠EAC)=∠BAC﹣(∠B+∠C)=80°.故答案为:80°17.如图,在四边形ABCD中,AB=AC=BD,AC与BD相交于O,且AC⊥BD.①AB∥CD;②△ABD≌△BAC;③AB2+CD2=AD2+CB2;④∠ACB+∠BDA=135°.其中结论正确的是③④(填序号).解:在四边形ABCD中,∠ABD与∠BAC不一定相等,故①AB∥CD;②△ABD≌△BAC都不一定成立,∵AC⊥BD,∴Rt△CDH中,CD2=DH2+CH2;Rt△ABH中,AB2=AH2+BH2;Rt△ADH中,AD2=DH2+AH2;Rt△BCH中,BC2=CH2+BH2;∴AB2+CD2=AD2+CB2,故③正确;∵AC⊥BD,∴∠ABH+∠BAH=90°,又∵AB=AC=BD,∴等腰△ABC中,∠ACB=(180°﹣∠BAC),等腰△ABD中,∠ADB=(180°﹣∠ABD),∴∠ACB+∠BDA=(180°﹣∠BAC)+(180°﹣∠ABD)=180°﹣(∠ABH+∠BAH)=180°﹣45°=135°,故④正确.故答案为:③④.18.如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为 4.8.解:设CD与BE交于点G,∵四边形ABCD是矩形,∴∠D=∠A=∠C=90°,AD=BC=6,CD=AB=8,由折叠的性质可知△ABP≌△EBP,∴EP=AP,∠E=∠A=90°,BE=AB=8,在△ODP和△OEG中,,∴△ODP≌△OEG(ASA),∴OP=OG,PD=GE,∴DG=EP,设AP=EP=x,则PD=GE=6﹣x,DG=x,∴CG=8﹣x,BG=8﹣(6﹣x)=2+x,根据勾股定理得:BC2+CG2=BG2,即62+(8﹣x)2=(x+2)2,解得:x=4.8,∴AP=4.8,故答案为:4.8.三、解答题(共9小题,共64分)19.计算:(1)﹣(2)()2+|1﹣|+()0.解:(1)原式=5﹣(﹣3)=5+3=8;(2)原式=3+﹣1+1=3+.20.求下列各式中的x的值(1)4x2﹣9=0(2)64(x+1)3=﹣125.解:(1)移项4x2=9,系数化为1,x2=,x=±;(2)(x+1)3=﹣,x+1=﹣,x=﹣.21.已知:如图,C是AB的中点,AE=BD,∠A=∠B.求证:∠ACE=∠BCD.【解答】证明:∵C是AB的中点,∴AC=BC,在△ACE和△BCD中,,∴△ACE≌△BCD(SAS),∴∠ACE=∠BCD.22.如图,在△ABC中,AB=5,AC=13,AD是边BC上的中线,E在AD的延长线上,AD=ED=6,求△ABC的面积.解:∵AD是边BC上的中线,∴BD=CD,在△ABD和△ECD中,,∴△ABD≌△ECD(SAS),∴AB=CE=5,∵AE=AD+ED=12,AC=13,CE=5,∴AE2+CE2=AC2,∴△ACE是直角三角形,∴△ABC的面积=△ACE的面积=×5×12=30.23.如图,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.(1)证明:AD=BE;(2)求∠AEB的度数.解:(1)∵△ACB和△DCE均为等边三角形,∴CA=CB,CD=CE,∠ACB=∠DCE=60°,∴∠ACD=60°﹣∠CDB=∠BCE.在△ACD和△BCE中,,∴△ACD≌△BCE(SAS).∴AD=BE.(2)∵△ACD≌△BCE,∴∠ADC=∠BEC.∵△DCE为等边三角形,∴∠CDE=∠CED=60°.∵点A,D,E在同一直线上,∴∠ADC=120°,∴∠BEC=120°.∴∠AEB=∠BEC﹣∠CED=60°.24.如图(1)是用硬板纸做成的两个全等的直角三角形,两直角边的长分别为a和b,斜边长为c,请你开动脑筋,将它们拼成一个能证明勾股定理的图形.(1)画出拼成的这个图形的示意图,并用这个图形证明勾股定理;(2)假设图(1)中的直角三角形有若干个,你能运用图(1)中所给的直角三角形拼出另一种能证明勾股定理的图形吗?请画出拼后的示意图(无需证明)【解答】解解:(1)如图所示,是梯形;由上图我们根据梯形的面积公式可知,梯形的面积=(a+b)(a+b).从上图我们还发现梯形的面积=三个三角形的面积,即ab+ab+c2.两者列成等式化简即可得:a2+b2=c2;(2)画边长为(a+b)的正方形,如图,其中a、b为直角边,c为斜边.25.阅读理解:求的近似值.小明的方法:设=10+x,其中0<x<1,则105=(10+x)2,即105=100+20x+x2.∵0<x<1∴0<x2<1,∴105≈100+20x,解之得x≈0.25,即的近似值为10.25,小莉的方法:设=11﹣y,其中0<y<1,则105=(11﹣y)2,即105=121﹣22y+y2,∵0<y<1∴0<y2<1,∴105≈121﹣22y,解之得y≈0.73,即的近似值为10.27.【反思比较】你认为小明的方法更接近.(填“小明”或“小莉”)【深入思考】下面关于x与y之间的数量关系A.x+y>1 B.x+y=1 C.x+y<1 D.无法确定你认为正确的是B.请说明理由.解:我认为小明的方法更接近.故答案为小明.因为10+x=11﹣y,所以x+y=1,故答案为B.26.(1)我们已经如道:在△ABC中,如果AB=AC,则∠B=∠C,下面我们继续研究:如图①,在△ABC中,如果AB>AC,则∠B与∠C的大小关系如何?为此,我们把AC 沿∠BAC的平分线翻折,因为AB>AC,所以点C落在AB边的点D处,如图②所示,然后把纸展平,连接DE.接下来,你能推出∠B与∠C的大小关系了吗?试写出说理过程.(2)如图③,在△ABC中,AE是角平分线,且∠C=2∠B.求证:AB=AC+CE.(3)在(2)的条件下,若点P,F分别为AE、AC上的动点,且S△ABC=15,AB=8,则PF+PC的最小值为.解:(1)∠C>∠B,理由如下:∵点C落在AB边的点D处,∴∠ADE=∠C,∵AC沿∠BAC的平分线翻折,∠ADE为△EDB的一个外角,∴∠ADE=∠B+∠DEB,∴∠ADE>∠B,即:∠C>∠B;(2)如图3,在AB上截取AD=AC,连接DE,∵AE是角平分线,∴∠BAE=∠CAE.在△ADE和△ACE中,∴△ADE≌△ACE(SAS),∴∠ADE=∠C,DE=CE.∵∠ADE=∠B+∠DEB,且∠C=2∠B.∴∠B=∠DEB,∴DB=DE,∵AB=AD+DB,AD=AC,DB=DE=CE.∴AB=AC+CE.(3)如图4,在AB上截取AH=AF,连接CH,∵AH=AF,∠HAP=∠F AP,AP=AP,∴△AHP≌△AFP(SAS),∴HP=PF,∴PF+PC=PH+PC,∴点P在线段CH上,且CH⊥AB时,PF+PC的值最小,∵S△ABC=15=×AB×CH,AB=8,∴CH=,∴PF+PC的最小值为,故答案为:.27.如图,已知等边△ABC,点D为△ABC内的一点,连接DA、DB、DC,∠ADB=120°.以CD为边向CD上方作等边△CDE,连接AE(0°<∠ACE<60°).(1)求证:△BDC≌△AEC.(2)若DC=2n,AD=AE,则△ADE的面积为n2.(3)若DA=n2+1,DB=n2﹣1,DC=2n(n为大于1的整数).求证:DA2+DC2=AC2.解:(1)∵△ABC是等边三角形,∴∠ACB=60°,BC=AC,∵△CDE是等边三角形,∴∠DCE=60°,CD=CE,∴∠BCA=∠DCE=60°,∴∠BCD=∠ACE,∴△BDC≌△AEC(SAS);(2)如图,由(1)知,△BDC≌△AEC,∴∠CBD=∠CAE,BD=AE,∵AE=AD,∴BD=AD,∴∠ABD=∠BAD,∵∠ADB=120°,∴∠ABD=∠BAD=30°,∵△ABC是等边三角形,∴∠BAC=∠ABC=60°,∴∠CBD=∠ABC﹣∠ABD=30°,∠CAD=∠BAC﹣∠DAB=30°,∴∠CAE=∠CBD=30°,∴∠DAE=∠CAD+∠CAE=60°,∵AD=AE,∴△ADE是等边三角形,∴AD=DE,∠ADE=60°,∵△CDE是等边三角形,∴DE=CD=2n,∴AD=2n,过点E作EF⊥AD于F,在Rt△DEF中,DF=DE=n,根据勾股定理得,EF==n,∴S△ADE=AD•EF=×2n×n=n2,故答案为:n2;(3)∵△CDE是等边三角形,∴∠CED=60°,DE=DC=2n∵△BDC≌△AEC,∴∠AEC=∠BDC,AE=DB,EC=DC,∵DB=n2﹣1,∴AE=n2﹣1,∴AE2+DE2=(n2﹣1)2+(2n)2=n4﹣2n2+1+4n2=n4+2n2+1=(n2+1)2=DA2,∴△ADE是以AD为斜边的直角三角形,∴∠AED=90°,∴∠AEC=∠AED+∠CED=150°,∴∠BDC=∠AEC=150°,∵∠ADB=120°,∴∠ADC=360°﹣∠ADB﹣∠BDC=90°,在Rt△ACD中,AD2+CD2=AC2.。
2015-2016学年度上学期期末考试八年级数学试卷(含答案)
2015—2016学年度上学期期末考试八年级数学试题注意事项:1.本卷满分120分,考试时间120分钟。
2.本卷是试题卷,不能答题。
答题必须写在答题卡上。
解题中的辅助线和需标注的角、字母、符号等务必添在答题卡的图形上。
3.在答题卡上答题,选择题必须用2B铅笔填涂,非选择题必须用0.5毫米黑色签字笔或黑色墨水钢笔作答。
★祝考试顺利★一、选择题(每小题3分,共30分)1.下列图形中轴对称图形是()ABCD2,.已知三角形的三边长分别是3,8,x,若x的值为偶数,则x的值有( )A.6个B.5个C.4个D.3个3.一个多边形截去一个角后,形成的多边形的内角和是2520°,则原多边形的边数是( )A.15或16B.16或17C.15或17D.15.16或174.如图,△ACB≌△A'CB',∠BCB'=30°,则∠ACA'的度数为( )A.20°B.30°C.35°D.40°5, 等腰三角形的两边长分别为5cm 和10cm,则此三角形的周长是()A.15cmB. 20cmC. 25cmD.20cm或25cm6.如图,已知∠CAB=∠DAB,则添加下列一个条件不能使△ABC≌△ABD的是( )A.AC=ADB.BC=BDC.∠C=∠DD.∠ABC=∠ABD7.如图,已知在△ABC中,CD是AB边上的高,BE平分∠ABC,交CD于点E,BC=5,DE =2,则△BCE的面积等于( )A.10B.7C.5D.4第9题图 8.若()22316m x x+-+是完全平方式,则m 的值等于( )A. 3B. -5C.7D. 7或-19.如图,在△ABC 中,AB =AC ,BE=CD ,BD =CF ,则∠EDF 的度数为 ( ) A .1452A ︒-∠ B .1902A ︒-∠ C .90A ︒-∠ D .180A ︒-∠第10题 10.如上图,等腰Rt △ABC 中,∠BAC =90°,AD ⊥BC 于点D ,∠ABC 的平分线分别交AC 、AD 于E 、F 两点,M 为EF 的中点,AM 的延长线交BC 于点N ,连接DM ,下列结论:① DF =DN ;② △DMN 为等腰三角形;③ DM 平分∠BMN ;④ AE =32EC ;⑤ AE =NC ,其中正确结论的个数是( )A .2个B .3个C .4个D .5个二、填空题(每小题3分,共24分)11.计算:()()312360.1250.2522⨯-⨯⨯- = 12,在实数范围内分解因式:3234a ab - = 13.若2,3,mn xx ==则2m nx+=14.若A (x ,3)关于y 轴的对称点是B (﹣2,y ),则x=__________,y=__________,点A 关于x 轴的对称点的坐标是__________.15,如图,△ABC 中,DE 是AC 的垂直平分线,AE =3 cm ,△ABD 的周长是13 cm ,则△ABC 的周长为 _________第15题图 第17题图16,已知等腰三角形一腰的垂直平分线与另一腰所在直线的夹角为40°,求此等腰三角形的顶角为17.如图,∠AOB =30°,点P 为∠AOB 内一点,OP =8.点M 、N 分别在OA 、OB 上,则△PMN 周长的最小值为__________2第18题图18. 如图所示,在△ABC 中,∠A =80°,延长BC 到D ,∠ABC 与∠ACD 的平分线相交于A 1点,∠A 1BC 与∠A 1CD 的平分线相交于A 2点,依此类推,∠A 4BC 与∠A 4CD 的平分线相交于A 5点,则∠A 5的度数是 。
八年级上册数学期中考试试题
北大附中2015-2016学年度第一学期期中考试初二年级数学试卷班级________姓名_________考号(学号)_________考生须知1.本试卷共4页,共三道大题,23道小题,满分100分.考试时间90分钟.2.在试卷和答题卡上认真填写班级、姓名和考号.3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效.4.在答题卡上,选择题、作图题用2B铅笔作答,其他试题用黑色字迹签字笔作答.一、选择题:(下列各题的四个选项中,有且只有一个是正确的,每题3分,共30分)1.下列图形中,不是..轴对称图形的是()A B C D2. 在平面直角坐标系中,点P(-3,5)关于x轴的对称点的坐标是()A.(3,5)B.(3,-5)C.(5,-3)D.(-3,-5)3.下列运算中正确的是()A.532aaa=⋅B.()532aa=C.326aaa=÷D.10552aaa=+4.已知等腰三角形的一边长为4,另一边长为8,则它的周长是()A.12 B.16 C.20 D.16或205. 如图,BC⊥AC,BD⊥AD,且BC=BD,则利用()可说明ABC∆∆与全等.A. SASB. AASC. SSAD. HL6.下列式子可用平方差公式计算的式子是()A.()()abba--B.()()11-+-xx C.()()baba+---D.()()11+--xx7.下列各式不能分解因式的是()A.224x x-B.214x x++C.229x y+ D.21m-8. 若x m+与2x-的乘积中不含x的一次项,则实数m的值为()A.2-B.2C.0D.19.若一个三角形一条边的中点到其他两边的距离相等,那么那个三角形是()A.等边三角形B.等腰三角形C.不等边三角形D.直角三角形10. 如图(1)是长方形纸带,α=∠DEF,将纸带沿EF折叠成图(2),再沿BF折叠成图CDABFGEGFFEEDDDCCC BBBAAA(3),则图(3)中的CFE ∠的度数是( )图(1) 图(2) 图(3)A .α2B . α290+︒C .α2180-︒D . α3180-︒ 二、填空题:(本题共20分,每小题4分)11. 若关于x 的二次三项式2x +kx b +因式分解为()()31+-x x ,则k+b 的值为__________;12. 已知49)(,5)(22=-=+y x y x ,则xy 的值为__________;13. 已知:如图,△ABC 是等边三角形,E 是AC 上一点,D 是BC 延长线上一点,连接BE 和DE ,若∠ABE =40°,BE =DE ,求∠CED 的度数为__________; 14.如图,在△ABC 中,边AB 的垂直平分线别离交BC 于点D ,交AB 于点E . 若AE =3,△ADC 的周长为8,则△ABC 的周长为 ;第13题图 第14题图 第15题图15. 如图,动点P 从(0,3)起身,沿所示方向运动,每当碰着长方形的边时反弹,反弹时角度均为45°,当点P 第2次碰着长方形的边时,点P 的坐标为__________;当点P 第2015次碰着长方形的边时,点P 的坐标为__________. 三、解答题:(本大题共小8题,共50分)16. (5分)已知:如图, A 、B 、C 、D 四点在同一直线上, AB =CD ,AE ∥BF 且AE =BF .求证: EC =FD .17. (5分)先化简,再求当2a =,1b =时,代数式()()()b a b b a b a ++-+22的值.18.(5分) 已知0242=+-x x ,求代数式()()()2232y y x y x x --+--的值.19.(每题5分,共10分)把下列多项式分解因式.(1)33312a b ab - (2) a a a 1812223-+-E ACDF DE CAB20.(5分)已知:如图,线段AB和射线BM交于点B.(1)利用尺规..完成以下作图,并保留作图痕迹.(不要求写作法)①在射线BM上求作一点C,使AC=AB;②在线段AB上求作一点D,使点D到BC,AC的距离相等;(2)在(1)所作的图形中,若∠ABM=72°,则图中与BC相等的线段是.21.(7分)在乘法公式的学习中,咱们采纳了构造几何图形的方式研究问题,借助直观、形象的几何模型,加深对乘法公式的熟悉和明白得,从中感悟数形结合的思想方式,感悟几何与代数内在的统一性.依照课堂学习的体会,解决下列问题:(1)如图①,边长为(k+3)的正方形纸片,剪去一个边长为k的正方形以后,剩余部份可剪拼成一个长方形(不重叠无裂痕),则那个长方形的面积是(用含k的式子表示);(2)有3张边长为a的正方形纸片,4张边长别离为a,b (a <b) 的长方形纸片,5张边长为b的正方形纸片,现从其中掏出若干张纸片(每种纸片至少取一张),拼成一个正方形(不重叠无裂痕),则所拼成的正方形的边长最长能够为;A.a+b B.2a+b C.3a+b D.a+2b(3)一个大正方形和4个大小完全相同的小正方形按图②,图③两种方式摆放,求图③中,大正方形中未被4个小正方形覆盖部份的面积(用含m,n的式子表示).22.(7分)在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E.点M是线段CA上的一个动点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏省南京市鼓楼区2015年八年级上学期期中数学试卷
一、选择题(本大题共6小题,每小题2分,共计12分.在每小题所给出的四个选项中,恰.
有一项
...是符合题目要求的,请将正确选项的序号填涂在答题纸
...上)
1.在下列常见的手机软件小图标中,是轴对称图形的是
A.B.C.D.
2.下列几组数中,能构成直角三角形三边的是
A.2,3,5 B.3,4,4 C.32,42,52 D.6,8,10
3.下列说法正确的是
A.全等三角形是指形状相同的两个三角形
B.全等三角形的周长和面积分别相等
C.全等三角形是指面积相等的两个三角形
D.所有的等边三角形都是全等三角形
4.如图,在△ABC中,AB=AC,AD是BC边上中线.若AB=10,AD=8,则△ABC的周长是
A.26 B.28 C.32 D.36
5.如图,点O是△ABC的两外角平分线的交点,下列结论:①OB=OC;②点O到AB、AC 的距离相等;③点O到△ABC的三边的距离相等;④点O在∠A的平分线上.其中结论正确的个数是
A.1 B.2 C.3 D.4
6.如图,在△ABC中,AB=BC,∠ACB=90°,点D、E在AB上,将△ACD、△BCE分别沿CD、CE翻折,点A、B分别落在点A′、B′的位置,再将△A′CD、△B′CE分别沿A′C、B′C翻折,点D与点E恰好重合于点O,则∠A′OB′的度数是
A.90°B.120°C.135°D.150°
二、填空题(本大题共10小题,每小题2分,共20分.不需写出解答过程,请把答案直接填写在答题纸
...相应位置上)
7.如图,△ABC中,∠ACB=90°,以它的各边为边向外作三个正方形,面积分别为S1,S2,A
(第4题)
D C
(第5题)
A
C
B
O
B
A
A′
B′
D
E
O
(第6题)
S 3,已知S 1=15,S 3=25,则S 2= ▲ .
8.已知等腰三角形一个外角等于80°,则这个等腰三角形的顶角的度数是 ▲ .
9.如图,已知∠BAC =∠DAC ,请添加一个条件: ▲ ,使△ABC ≌△ADC (写出一个即可). 10.如图,OC 是∠AOB 的平分线,PD ⊥DA ,垂足为D ,PD =2,则点P 到OB 的距离是 ▲ . 11.如图,在△ABC 中,∠B 与∠C 的平分线交于点O ,过点O 作DE ∥BC ,分别交AB 、AC 于点D 、E .若AB =9,AC =7,则△ADE 的周长是 ▲ .
12.如图,△ABC 为等边三角形,以AC 为直角边作等腰直角三角形ACD ,∠ACD =90°,则∠CBD = ▲ °.
13.如图,△ABC ≌△BDE ,点B 、C 、D 在一条直线上,AC 、BE 交于点O ,若∠AOE =95°,则∠BDE = ▲ °.
14.如图,在△ABC 中,∠ACB =90°,∠CAB =30°.以AB 长为一边作△ABD ,且AD =BD ,∠ADB =90°,取AB 中点E ,连DE 、CE 、CD .则∠EDC = ▲ °. 15.已知直角三角形斜边长为10 cm ,周长为22 cm ,则此直角三角形的面积为 ▲ .
16.如图,在2×2方格纸中,有一个以格点为顶点的△ABC ,请你找出方格纸中所有与△ABC
三、解答题(本大题共9小题,共68分.请在答题纸指定区域内作答,解答时应写出文字说
A
B
(第9题)
C
A
O
B
P
C
D
(第10题)
A
B
C
S 3
S 1 S 2 (第7题)
(第14题)
A
D
C
E A
(第16题)
C
B
A
B
D E
(第13题)
O (第12题)
A
D
明、证明过程或演算步骤)
17.(6分)已知:如图,AB =AD ,∠C =∠E ,∠BAE =∠DAC .
求证:△ABC ≌△ADE .
18.(6分)已知:如图,在△ABC 中,DE ∥BC ,AD =AE . 求证:AB =AC .
19.(7分)如图,在边长为1的小正方形组成的方格纸中,有一个以格点为顶点的△ABC . (1)试根据三角形三边关系,判断△ABC 的形状;
(2)在方格纸中利用直尺分别画出AB 、BC 的垂直平分线,交点为O .观察点O 的位置, 你能得出怎样的结论?
(第17题)
A
B
C
D
E
D E
B
C
(第18题)
A
A
B
C
(第19题)
20.(7分)如图,将边长为a 与b 、对角线长为c 的长方形纸片ABCD ,绕点C 顺时针旋转
90°得到长方形EFCG ,连接AE .通过用不同方法计算梯形ABGE 的面积可验证勾股定理,请你写出验证的过程.
21.(8分)如图,在△ABC 中,∠C =90°,∠A >∠B .
(1)用直尺和圆规.....作.AB 的垂直平分线,交AB 与D ,交BC 于E ;
(不写作法,保留作图痕迹)
(2)在(1)的条件下,若CE =DE ,求∠A ,∠B 的度数.
22.(8分)八年级某班数学实验课安排测量操场上旗杆的高度.小聪同学经过认真思考,研
究出了一个可行的测量方案:在某一时刻测得旗杆AB 的影长BC 和∠ACB 的大小,然后在操场上画∠MDN ,使得∠MDN =∠ACB ,在边DM 上截取线段DE =BC ,再利用三角形全等的知识求出旗杆的高度.请完成小聪同学的测量方案,并说明方案可行的理由.
(第21题)
A
C
(第20题)
A
B
C
G
E F
D
a
a b b c
c
(第22题)
23.(8分)(1)如图(1),在△ABC 中,AB =AC ,O 为△ABC 内一点,且OB =OC . 求证:直线AO 垂直平分BC .
以下是小明的证题思路,请补全框图中的分析过程.
(2)如图(2),在△ABC 中,AB =AC ,点D 、E 分别在AB 、AC 上,且BD =CE .请你
只用无刻度的直尺画出BC 的垂直平分线(不写画法,保留画图痕迹).
(3)如图(3),五边形ABCDE 中,AB =AE ,BC =DE ,∠B =∠E .请你只用无刻度的直
尺画出CD 边的垂直平分线,并说明理由.
24.(8分)在一次“构造勾股数”的探究学习课中,老师给出了下表:
其中m 、n 为正整数,且m >n .
(1)观察表格,当m =2,n =1时,此时对应的a 、b 、c 的值能否作为直角三角
形三边的长?说明你的理由.
(2)探究a 、b 、c 与m 、n 之间的关系,并用含m 、n 的代数式表示: a = ▲ ,
b = ▲ ,
c = ▲ .
(3)以a 、b 、c 为三边长的三角形是否一定是直角三角形?如果是,请说明理由;
如果不是,请举出反例.
(第23题)
(1)
(2) A
B D
C
E
(3)
25. (10分)(1)如图(1),在△ABC 中,AB >AC >BC ,∠ACB =80°,点D 、
E 线段BA 、AB 的延长线上,且AD =AC ,BE =B C ,则∠DCE = ▲ °;
(2)如图(2),在△ABC 中,AB >AC >BC ,∠ACB =80°,点D 、E 在边AB 上,且AD =AC ,BE =BC ,求∠DCE 的度数;
B A
E
C
D (第25题(1))
C
A
D
E
B
(3)。
