大学物理(第四版)课后习题及答案 动量
大学物理 动量和角动量习题思考题及答案
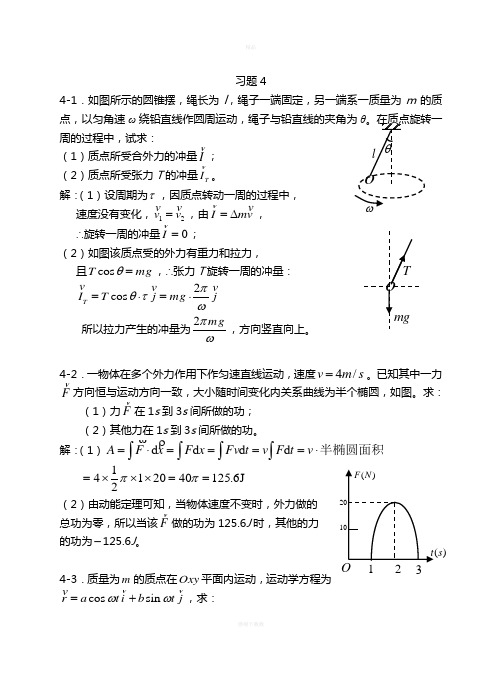
)s 习题44-1.如图所示的圆锥摆,绳长为l ,绳子一端固定,另一端系一质量为m 的质点,以匀角速ω周的过程中,试求:(1)质点所受合外力的冲量I v ;(2)质点所受张力T 的冲量T I v。
解:(1)设周期为τ,因质点转动一周的过程中, 速度没有变化,12v v =v v,由I mv =∆vv, ∴旋转一周的冲量0I =v;(2)如图该质点受的外力有重力和拉力, 且cos T mg θ=,∴张力T 旋转一周的冲量:2cos T I T j mg j πθτω=⋅=⋅v v v所以拉力产生的冲量为2mgπω,方向竖直向上。
4-2.一物体在多个外力作用下作匀速直线运动,速度4/v m s =。
已知其中一力F v方向恒与运动方向一致,大小随时间变化内关系曲线为半个椭圆,如图。
求:(1)力F v在1s 到3s 间所做的功;(2)其他力在1s 到3s 间所做的功。
解:(1)半椭圆面积⋅====⋅=⎰⎰⎰⎰v t F v t Fv x F x F A d d d d ρϖJ 6.12540201214==⨯⨯⨯=ππ(2)由动能定理可知,当物体速度不变时,外力做的 总功为零,所以当该F v做的功为125.6J 时,其他的力 的功为-125.6J 。
4-3.质量为m 的质点在Oxy 平面内运动,运动学方程为cos sin r a t i b t j ωω=+v v v,求:(1)质点在任一时刻的动量;(2)从0=t 到ωπ/2=t 的时间内质点受到的冲量。
解:(1)根据动量的定义:P mv =v v,而d r v dt==v v sin cos a t i b t j ωωωω-+v v , ∴()(sin cos )P t m a t i b t j ωωω=--v v v ;(2)由2()(0)0I mv P P m b j m b j πωωω=∆=-=-=v v v v v v ,所以冲量为零。
大学物理(第四版)课后习题及答案 波动

第十四章波动14-1 一横波再沿绳子传播时得波动方程为。
(1)求波得振幅、波速、频率及波长;(2)求绳上质点振动时得最大速度;(3)分别画出t=1s 和t=2s时得波形,并指出波峰和波谷。
画出x=1.0m处质点得振动曲线并讨论其与波形图得不同。
14-1分析(1)已知波动方程(又称波函数)求波动的特征量(波速、频率、振幅A及彼长 等),通常采用比较法。
将已知的波动方程按波动方程的一般形式书写,然后通过比较确定各特征量(式中前“-”、“+”的选取分别对应波沿x轴正向和负向传播)。
比较法思路清晰、求解简便,是一种常用的解题方法。
(2)讨论波动问题,要理解振动物理量与波动物理量之间的内在联系与区别。
例如区分质点的振动速度与波速的不同,振动速度是质点的运动速度,即;而波速是波线上质点运动状态的传播速度(也称相位的传播速度、波形的传播速度或能量的传播速度),其大小由介质的性质决定。
介质不变,彼速保持恒定。
(3)将不同时刻的t值代人已知波动方程,便可以得到不同时刻的波形方程,从而作出波形图。
而将确定的x值代入波动方程,便可以得到该位置处质点的运动方程,从而作出振动图。
解(1)将已知波动方程表示为与一般表达式比较,可得则(2)绳上质点的振动速度则(3) t=1s和 t=2s时的波形方程分别为波形图如图14-1(a)所示。
x=1.0m处质点的运动方程为振动图线如图14-1(b)所示。
波形图与振动图虽在图形上相似,但却有着本质的区别前者表示某确定时刻波线上所有质点的位移情况,而后者则表示某确定位置的时间变化的情况。
14-2 波源作简谐运动,其运动方程为,它所形成得波形以30m/s的速度沿一直线传播。
(1)求波的周期及波长;(2)写出波的方程。
14-2分析 已知彼源运动方程求波动物理量及波动方程,可先将运动方程与其一般形式进行比较,求出振幅地角频率及初相,而这三个物理量与波动方程的一般形式中相应的三个物理量是相同的。
大学物理(第四版)课后习题及答案 波动(2020年7月整理).pdf

第十四章波动14-1 一横波再沿绳子传播时得波动方程为[]x m t s m y )()5.2(cos )20.0(11−−−=ππ。
(1)求波得振幅、波速、频率及波长;(2)求绳上质点振动时得最大速度;(3)分别画出t=1s 和t=2s 时得波形,并指出波峰和波谷。
画出x=1.0m 处质点得振动曲线并讨论其与波形图得不同。
14-1 ()[]x m t s m y )(5.2cos )20.0(11−−−=ππ分析(1)已知波动方程(又称波函数)求波动的特征量(波速u 、频率ν、振幅A 及彼长 等),通常采用比较法。
将已知的波动方程按波动方程的一般形式⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛=0cos ϕωu x t A y 书写,然后通过比较确定各特征量(式中前“-”、“+”的选取分别对应波沿x 轴正向和负向传播)。
比较法思路清晰、求解简便,是一种常用的解题方法。
(2)讨论波动问题,要理解振动物理量与波动物理量之间的内在联系与区别。
例如区分质点的振动速度与波速的不同,振动速度是质点的运动速度,即dt dy v =;而波速是波线上质点运动状态的传播速度(也称相位的传播速度、波形的传播速度或能量的传播速度),其大小由介质的性质决定。
介质不变,彼速保持恒定。
(3)将不同时刻的t 值代人已知波动方程,便可以得到不同时刻的波形方程)(x y y =,从而作出波形图。
而将确定的x 值代入波动方程,便可以得到该位置处质点的运动方程)(t y y =,从而作出振动图。
解(1)将已知波动方程表示为()()[]115.25.2cos )20.0(−−⋅−=s m x t s m y π 与一般表达式()[]0cos ϕω+−=u x t A y 比较,可得0,5.2,20.001=⋅==−ϕs m u m A则 m v u Hz v 0.2,25.12====λπω(2)绳上质点的振动速度()()()[]1115.25.2sin 5.0−−−⋅−⋅−==s m x t s s m dt dy v ππ 则1max 57.1−⋅=s m v(3) t=1s 和 t =2s 时的波形方程分别为()[]x m m y 115.2cos )20.0(−−=ππ()[]x m m y 125cos )20.0(−−=ππ波形图如图14-1(a )所示。
大学物理第三章-动量守恒定律和能量守恒定律-习题及答案

F外 dt=dP
力的效果 关系 适用对象 适用范围 解题分析
*动量定理与牛顿定律的关系 牛顿定律 动量定理 力的瞬时效果 力对时间的积累效果 牛顿定律是动量定理的 动量定理是牛顿定律的 微分形式 积分形式 质点 质点、质点系 惯性系 惯性系 必须研究质点在每时刻 只需研究质点(系)始末 的运动情况 两状态的变化 0
因而
Fx 2mv cos / t
Fy 0
代入数据,得
Fx 2 0.2 6 cos 60 0 / 0.03 40 N
根据牛顿第三定律,球对墙壁的作用力为 40N,方向向左。 二、质点系的动量定理 1.两个质点的情况 设系统内有两个质点 1 和 2,质量分别 为 m1 和 m2,作用在质点上的外力分别为 F1 和 F2, 而两质点之间的相互作用力为 F12 和 F21,根据动量定理,在Δt=t2-t1 时间内, 两质点的动量的增量分别为
dv 1) F m dt dv 2) F m dt
F ma Fdt mdv dmv ——动量定理 dv dv dr 1 m mv mdr mv dv d mv 2 动能定理 dr dt dr 2
大学物理《力学4·动量》复习题及答案

( )选坐标系如图:有动量守恒定律 1
x方向:mu 5m v2 cosq
y方向: mv1 5mv2 sinq 0
解(1)、 )式得: (2 v2 u / 5 cosq(1) Nhomakorabea( 2)
B
y
u
u u / 5 1 sin2q 4
q
v2
x
A
v1 3u / 4
v1
(2).A球碰前后动能变化:
9.体重相同的甲乙两人,分别用双手握住 跨过无摩擦滑轮的绳子两端,当他们由同 一高度向上爬时,相对于绳子,甲的速度 是乙的两倍,则到达顶点情况是
(A)甲先到达。 (B)乙先到达。 (C)同时到达。 (D)谁先到达不能确定。
[ ]
• 动量选择题答案:CCCDADACC
10.质量为 M=2.0 kg 的物体(不考虑体 积),用一根长 l =1.0 m 为的细绳悬挂在天 花板上,今有一质量为 m=20 g 的子弹以 v0=600 m/s 的水平速度射穿物体,刚射出物 体时子弹的速度大小 v0 = 30 m/s, 设穿透 时间极短,求:
14. 光滑斜面与水平面的夹角为,轻质弹簧 上端固定,今在弹簧的另一端轻轻地挂上质 量为 M=1.0kg 的木块,则木块沿斜面向下 滑动。当木块向下滑 x =30 cm 时,恰好有 一质量 m = 0.01 kg 的子弹,沿水平方向以 速度 v = 200 m/s 射中木块并陷在其中,设 弹簧的倔强系数 k=25 N/m 为,求子弹打入 木块后它们的共同速度。 k M m 解:( )木块下滑中,以 1 x 木块、弹簧、 地球为系统。
v2 M v1 mv cos / M m
0.89(m/s)
方向向上。
大学物理课后习题及答案(1-4章)含步骤解

,根据流量守恒
,
(2)当
(3)当
时,
时,
−
,整理可得:
可得
,即
,
图1-34所示为输液的装置。设吊瓶的截面积为1 ,针孔的截面积为2 ,且1 ≫ 2 ,开始时( = 0),吊瓶内上下
液面距针孔的高度分别为ℎ1 和ℎ2 ,求吊瓶内药液全部输完时需要的时间。
,则针孔的流量为
液体总体积为
Ԧ =
= 2Ԧ − 2 Ԧ = −2Ԧ
1s末和2s末质点的速度为: 1 = 2Ԧ − 2Ԧ(m ∙ s−1 ),2 = 2Ԧ − 4Ԧ(m ∙ s −1 );
1s末和2s末质点的加速度相等:Ԧ = −2Ԧ (m ∙ s−2 )
已知一质点做直线运动,其加速度Ԧ = 4 + 3 m ∙ s−2 , 开始运动时,0 = 5 m,
= 0.06(m)
(2)设弹簧最大压缩量为∆′ , 与碰撞粘在一起的速度为 ′,0 = ( +
) ′,代入已知条件可得 ′ = 4Τ11, + 压缩弹簧的过程中,机械能守恒,则
1
(
2
1
+ ) 2 = 2 ∆′2 ,得∆′ =
+
≈ 0.04(m)
(1)角加速度 =
由 =
∆
∆
=
0−2×1500÷60
50
由 =
=
2×1500
60
= 50 (rad ∙ s −1 )
= − (rad ∙ s−2 )
= −,得 = −,两边进行积分
得到 − 50 = − − 0,
大学物理第四版下册答案

大学物理第四版下册答案【篇一:大学物理(上海交通大学)课后习题答案(第四版)】已知质点位矢随时间变化的函数形式为其中?为常量.求:(1)质点的轨道;(2)速度和速率。
消去t可得轨道方程x?y?r 2)v?222dr1-2. 已知质点位矢随时间变化的函数形式为r?4ti?(3?2t)j,式中r的单位为m,t的单位为s.求:(1)质点的轨道;(2)从t?0到t?1秒的位移;(3)t?0和t?1秒两时刻的速度。
解:1)由r?4ti?(3?2t)j可知22x?4t2 y?3?2t消去t得轨道方程为:x?(y?3) 2)v?2dr?8ti?2j dt113)v(0)?2jv(1)?8i?2j1-3. 已知质点位矢随时间变化的函数形式为r?ti?2tj,式中r的单位为2(1)任一时刻的速度和加速度;(2)任一时刻的切向加速m,t的单位为s.求:度和法向加速度。
解:1)v?dr?2ti?2j dta?dv?2i dt22)v?[(2t)?4]?2(t2?1)at?dv?dt2tt?12an??1-4. 一升降机以加速度a上升,在上升过程中有一螺钉从天花板上松落,升降机的天花板与底板相距为d,求螺钉从天花板落到底板上所需的时间。
解:以地面为参照系,坐标如图,升降机与螺丝的运动方程分别为 12at(1)图 21y2?h?v0t?gt2 (2)2y1?v0t?1-4y1?y2 (3)解之t?1-5. 一质量为m的小球在高度h处以水平抛出,求:(1)小球的运动方程;(2)小球在落地之前的轨迹方程;(3)落地前瞬时小球的初速度v0drdvdv,,. dtdtdt解:(1) x?v0t 式(1)1y?h?gt2 式(2)21r(t)?v0ti?(h-gt2)j2gx2(2)联立式(1)、式(2)得 y?h?22v0(3)dr?v0i-gtj而落地所用时间t?dt2h g所以drdv?v0i-2ghj??gj dtdt22v?v2v0?(?gt)2 x?vy?g2tdv??[v2?(gt)2]01-6. 路灯距地面的高度为h1,一身高为h2的人在路灯下以匀速v1沿直线行走。
(完整版)《大学物理》习题册题目及答案第2单元 动量守恒定律

第2单元 动量守恒定律序号 学号 姓名 专业、班级一 选择题[ B ]1. 力i F t 12=(SI)作用在质量m =2 kg 的物体上,使物体由原点从静止开始运动,则它在3秒末的动量应为:(A) -54i kg ⋅m ⋅s -1(B) 54i kg ⋅m ⋅s -1(C) -27i kg ⋅m ⋅s -1 (D) 27i kg ⋅m ⋅s-1[ C ]2. 如图所示,圆锥摆的摆球质量为m ,速率为v ,圆半径为R ,当摆球在轨道上运动半周时,摆球所受重力冲量的大小为:(A) mv 2 (B)()()22/2v R mg mv π+(C)vRmgπ (D) 0[ A ]3 .粒子B 的质量是粒子A 的质量的4倍。
开始时粒子A 的速度为()j i ϖϖ43+,粒子B 的速度为(j i ϖϖ72-)。
由于两者的相互作用,粒子A 的速度为()j i ϖϖ47-,此时粒子B 的速度等于:(A) j i 5- (B) j i ϖϖ72- (C) 0 (D) j i ϖϖ35-[ C ]4. 水平冰面上以一定速度向东行驶的炮车,向东南(斜向上)方向发射一炮弹,对于炮车和炮弹这一系统,在此过程中(忽略冰面摩擦及空气阻力) (A )总动量守恒(B )总动量在炮身前进的方向上的分量守恒,其它方向动量不守恒 (C) 总动量在水平面上任意方向的分量守恒,竖直方向分量不守恒 (D )动量在任何方向的分量均不守恒二 填空题1. 一颗子弹在枪筒里前进时所受的合力大小为t F 31044005⨯-=(SI),子弹从枪口射出的速率为3001s m -⋅。
假设子弹离开枪口时合力刚好为零,则(1) 子弹走完枪筒全长所用的时间 t = 0.003 s ,(2) 子弹在枪筒中所受的冲量 I = s N 6.0⋅ , (3) 子弹的质量 m = 2 ×10-3 kg 。
2. 质量m 为10kg 的木箱放在地面上,在水平拉力F 的作用下由静止开始沿直线运动,其拉力随时间的变化关系如图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
题3.1:质量为m 的物体,由水平面上点O 以初速为0v 抛出,0v 与水平面成仰角α。
若不计空气阻力,求:(1)物体从发射点O 到最高点的过程中,重力的冲量;(2)物体从发射点到落回至同一水平面的过程中,重力的冲量。
题3.1分析:重力是恒力,因此,求其在一段时间内的冲量时,只需求出时间间隔即可。
由抛体运动规律可知,物体到达最高点的时间g v t αsin 01=∆,物体从出发到落回至同一水平面所需的时间是到达最高点时间的两倍。
这样,按冲量的定义即可求出结果。
另一种解的方法是根据过程的始、末动量,由动量定理求出。
解1:物体从出发到达最高点所需的时间为g v t αsin 01=∆ 则物体落回地面的时间为gv t t αsin 22012=∆=∆ 于是,在相应的过程中重力的冲量分别为 j j F I αsin d 0111mv t mg t t -=∆-==⎰∆j j F I αsin 2d 0222mv t mg t t -=∆-==⎰∆解2:根据动量定理,物体由发射点O 运动到A 、B 的过程中,重力的冲量分别为j j j I αsin 00y Ay 1mv mv mv -=-= j j j I αsin 200y By 2mv mv mv -=-=题3.2:高空作业时系安全带是必要的,假如质量为51.0kg 的人不慎从高空掉下来,由于安全带的保护,使他最终被悬挂起来。
已知此时人离原处的距离为2米,安全带的缓冲作用时间为0.50秒。
求安全带对人的平均冲力。
题3.2解1:以人为研究对象,在自由落体运动过程中,人跌落至2 m 处时的速度为ghv 21= (1)在缓冲过程中,人受重力和安全带冲力的作用,根据动量定理,有()12mv mv t -=∆+P F (2)由(1)式、(2)式可得安全带对人的平均冲力大小为 ()N 1014.123⨯=∆+=∆∆+=tgh m mg t mv mg F解2:从整个过程来讨论,根据动量定理有N 1014.1/23⨯=+∆=mg g h tmgF 题 3.3:如图所示,在水平地面上,有一横截面2m 20.0=S 的直角弯管,管中有流速为1s m 0.3-⋅=v 的水通过,求弯管所受力的大小和方向。
题3.3解:在t ∆时间内,从管一端流入(或流出)水的质量为t vS m ∆=∆ρ,弯曲部分AB 的水的动量的增量则为()()A B A B v v t vS v v m p -∆=-∆=∆ρ依据动量定理p I ∆=,得到管壁对这部分水的平均冲力()A B v v IF -=∆=Sv tρ 从而可得水流对管壁作用力的大小为N 105.2232⨯-=-=-='Sv F F ρ作用力的方向则沿直角平分线指向弯管外侧。
题3.4:一作斜抛运动的物体,在最高点炸裂为质量相等的两块,最高点距离地面为m 6.19。
爆炸s 00.1后,第一块落到爆炸点正下方的地面上,此处距抛出点的水平距离为m 1000.12⨯。
问第二块落在距抛出点多远的地面上?(设空气的阻力不计)题3.4解:取如图示坐标,根据抛体运动的规律,爆炸前,物体在最高点A 的速度的水平分量为hg x t x v 21010x ==(1) 物体爆炸后,第一块碎片竖直落下的运动方程为21121gt t v h y --= 当该碎片落地时,有11,0t t y ==,则由上式得爆炸后第一块碎片抛出的速度121121t gt h v -=(2) 又根据动量守恒定律,在最高点处有2x 0x 21mv mv =(3) 2y 121210mv mv +-=(4)联立解式(1)、(2)、(3)和(4),可得爆炸后第二块碎片抛出时的速度分量分别为 110x 2x s m 100222-⋅===hgx v v 11211y 2s m 7.1421-⋅=-==t gt h v v 爆炸后,第二块碎片斜抛运动,其运动方程为 222y 22x 21221gt t v h y t v x x -+=+= 落地时,02=y ,由(5)、(6)可解得第二块碎片落地点的水平位置 m 5002=x题3.5:A 、B 两船在平静的湖面上平行逆向航行,当两船擦肩相遇时,两船各自向对方平稳地传递kg 50的重物,结果是A 船停了下来,而B 船以1s m 4.3-⋅的速度继续向前驶去。
A 、B 两船原有质量分别为kg 105.03⨯和kg 100.13⨯,求在传递重物前两船的速度。
(忽略水对船的阻力)题3.5分析:由于两船横向传递的速度可略去不计,则对搬出重物后的船A 与从船B 搬入的重物所组成的系统I 来讲,在水平方向上无外力作用,因此,它们相互作用的过程中应满足动量守恒;同样,对搬出重物后的船B 与从船A 搬入的重物所组成的系统II 亦是这样。
由此,分别列出系统I 、II 的动量守恒方程即可解出结果。
解:设A 、B 两船原有的速度分别以v A 、v B 表示,传递重物后船的速度分别以v 'A 、v 'B 表示,被搬运重物的质量以m 表示。
分别对上述系统I 、II 应用动量守恒定律,则有()AA B A A v m mv v m m '=+- (1) ()BB A B B v m mv v m m '=+-(2) 由题意知v 'A = 0,v 'B = 3.4 m ⋅s -1代入数据后,可解得()()12A B BB A s m 40.0-⋅-=---'-=m m m m m v m m v ()()()12B A BB A B s m 6.3-⋅=---'-=m m m m m v m m m v也可以选择不同的系统,例如,把A 、B 两船(包括传递的物体在内)视为系统,同样能满足动量守恒,也可以列出相应的方程求解。
题3.6:质量为m '的人手里拿着一个质量为m 的物体,此人用与水平面成α角的速率0v 向前跳去。
当他达到最高点时,他将物体以相对于人为u 的水平速率向后抛出。
问:由于人抛出物体,他跳跃的距离增加了多少?(假设人可视为质点)题3.6解:取如图所示坐标。
把人与物体视为一系统,当人跳跃到最高点处,在向左抛物过程中,满足动量守恒,故有 ()()u v m v m v m m -+'='+αcos 0式中v 为人抛物后相对地面的水平速度,v -u 为抛出物对地面的水平速度。
得u mm mv v +'+=αcos 0 人的水平速度的增量为u mm mv v v +'=-=∆αcos 0 而人从最高点到地面的运动时间为g v t αsin 0= 所以,人跳跃后增加的距离()u gm m mv vt x +'=∆=∆αsin 0题3.7:铁路上有一静止的平板车,其质量为m ',设平板车可无摩擦地在水平轨道上运动。
现有N 个人从平板车的后端跳下,每个人的质量均为m ,相对平板车的速度均为u 。
问:在下列两种情况下,(1)N 个人同时跳离;(2)一个人、一个人地跳离,平板车的末速是多少?所得的结果为何不同,其物理原因是什么?题3.7解:取平板车及N 个人组成的系统,以地面为参考系,平板车的运动方向为正方向,系统在该方向上满足动量守恒。
考虑N 个人同时跳车的情况,这跳车后平板车的速度为v ,则由动量守恒定律得 ()u v Nm v m -+'=0u Nmm Nmv +'=(1)又考虑N 个人一个接一个的跳车的情况。
设当平板车上尚有n 个人时的速度为v n ,跳下一人后车速为v n -1,在这一次跳车过程中,根据动量守恒有()()()u v m mv n v m v nm m -+-+'=+'---1n 1n 1n n 1(2)由式(2)可解得递推公式 u nmm mv v +'+=-n 1n (3)显然,当车上有N 个人时(即n = N ),因尚未有人跳离平板车,故v N = 0;而车上N 个人全跳完时,车速为v 0。
根据(3)有u Nmm mv +'+=-01N()u mN m mv v N 112N -+'+=--……u mm mv v +'+=10 将上述各等式的两侧分别相加,整理后得 ∑=+'=Nn u nmm mv 10由于N n Nm m nm m ,,3,2,1 =+'≤+'故有 v v >0即N 个人一个接一个地跳车时,平板车的末速v 0大于N 个人同时跳下时平板车的末速v 。
这是因为在N 个人逐一跳离车时,车队地的速度逐次增加,导致跳车者相对地面的速度也在逐次增大,并对平板车所作的功也相应增大,因而平板车得到的能量也大,其车速也大。
题3.8:如图所示,一绳索跨过无摩擦的滑轮,系在质量为kg 00.1的物体上,起初物体静止在无摩擦的水平面上。
若用N 00.5的恒力作用在绳索的另一端,使物体向右加速运动,当系在物体上的绳索从水平面成 30角变为 37角时,力对物体所作的功为多少?已知滑轮与水平面之间的距离为1m 。
题3.8分析:该题中虽施以“恒力”,但是,作用在物体上的力的方向在不断变化。
需按功的矢量定义式⎰⋅=s F d W 来求解。
解:取图示坐标,绳索拉力对物体所作的功为J 69.1d d cos d 212=+-==⋅=⎰⎰⎰x x x xd Fx x F W θx F题 3.9:一物体在介质中按规律3ct x =作直线运动,c 为一常量。
设介质对物体的阻力正比于速度的平方。
试求物体由00=x 运动到l x =时,阻力所作的功。
(已知阻力系数为k )题3.9解:由运动学方程3ct x =,可得物体的速度 23d d ct txv ==按题意及上述关系,物体所受阻力的大小为 3/43/242299x kc t kc kv F === 则阻力的功为3/73/203/43/200727d 9d 180cos d l kc x x kc x F W lll-=-==⋅=⎰⎰⎰ x F题 3.10:一人从m 0.10深的井中提水,起始桶中装有kg 0.10的水,由于水桶漏水,每升高m 00.1要漏去kg 20.0的水。
求水桶被匀速地从井中提到井口,人所作的功。
题3.10解:水桶在匀速上提过程中,a = 0,拉力与水桶重力平衡,有 0=+P F在图示所取坐标下,水桶重力随位置的变化关系为 agy mg P -=其中a = 0.2 kg/m ,人对水桶的拉力的功为 ()J 882d d m 100m 100=-=⋅=⎰⎰y agy mg W y F题3.11:一质量为kg 20.0的球,系在长为m 00.2的细绳上,细绳的另一端系在天花板上。
