游戏算法整理(贴图完整版)
3D游戏常用技巧NormalMapping(法线贴图)原理解析——基础篇

3D游戏常⽤技巧NormalMapping(法线贴图)原理解析——基础篇1、法线贴图基本概念 在制作3D游戏时,常常遇到这样⼀个问题:⼀个平⾯,这个平⾯在现实中并不是⼀个“平”⾯,例如砖墙的表⾯带有⽯质浮雕等等。
这种情况下如果只是简单的做⼀个平⾯,则让⼈感觉严重失真,如图1所⽰;⽽如果⽤很密集的三⾓形去表⽰这类略有凹凸的表⾯,则性能上⼤⼤下降。
研究⼈员发现,⼈眼对物体的凹凸感觉,很⼤程度上取决于表⾯的光照明暗变化,如果能通过⼀张贴图在⼀个平⾯上表现出由凹凸造成的明暗变化,则可以让⼈眼感觉这个平⾯是凹凸不平的(虽然这个平⾯还是平的)。
法线贴图正是为了这个⽬的⽽产⽣的。
图1 不同细节程度的蜡烛 准确的说,法线贴图是Bump Mapping(凹凸贴图)的其中⼀种。
第⼀个Bump Mapping由Blinn在1978年提出,⽬的是以低代价给予计算机⼏何体以更丰富的表⾯信息。
30年来,这项技术不断延展,尤其是计算机图形学成熟以后,相继出现了不少算法变体,法线贴图就是其中很重要的⼀种。
研究⼈员对法线贴图进⼀步改进,出现了Parallax Mapping(视差贴图), Relief Mapping等技术,实现了更逼真的效果。
本⽂仅针对法线贴图进⾏介绍。
⼀条法线是⼀个三维向量,⼀个三维向量由x, y, z等3个分量组成,在法线贴图中,把(x, y, z)当作RGB3个颜⾊的值存储(如图2),并将其每个分量映射到[-1, 1]。
例如,对于x, y, z各有8位的纹理,[0, 128, 255]表⽰法向量(-1, 0, 1)。
图2 利⽤彩⾊通道存储法线贴图2、切线空间 法线贴图中存储的法线最初是定义在世界空间中,但在实际中,这种⽅式很少见,因为只要物体移动,法线贴图则不再有效。
另⼀种⽅式就是将法线存储在物体的局部空间中,物体可以进⾏刚体变换(平移,旋转,缩放),法线贴图依旧有效,但是这种⽅法并不能应对任何⽅式的变换,并且法线贴图不能在不同物体进⾏复⽤,增加了美⼯的负担。
游戏算法整理

游戏算法整理算法一:A*寻路初探译者序:很久以前就知道了A*算法,但是从未认真读过相关的文章,也没有看过代码,只是脑子里有个模糊的概念。
这次决定从头开始,研究一下这个被人推崇备至的简单方法,作为学习人工智能的开始。
这篇文章非常知名,国内应该有不少人翻译过它,我没有查找,觉得翻译本身也是对自身英文水平的锻炼。
经过努力,终于完成了文档,也明白的A*算法的原理。
毫无疑问,作者用形象的描述,简洁诙谐的语言由浅入深的讲述了这一神奇的算法,相信每个读过的人都会对此有所认识(如果没有,那就是偶的翻译太差了 --b)。
现在是2005年7月19日的版本,应原作者要求,对文中的某些算法细节做了修改。
原文链接:/reference/articles/article2003.asp 原作者文章链接:/games/aStarTutorial.htm 以下是翻译的正文。
会者不难,A*(念作A星)算法对初学者来说的确有些难度。
这篇文章并不试图对这个话题作权威的陈述。
取而代之的是,它只是描述算法的原理,使你可以在进一步的阅读中理解其他相关的资料。
最后,这篇文章没有程序细节。
你尽可以用任意的计算机程序语言实现它。
如你所愿,我在文章的末尾包含了一个指向例子程序的链接。
压缩包包括C++和Blitz Basic两个语言的版本,如果你只是想看看它的运行效果,里面还包含了可执行文件。
我们正在提高自己。
让我们从头开始。
序:搜索区域假设有人想从A点移动到一墙之隔的B点,如下图,绿色的是起点A,红色是终点B,蓝色方块是中间的墙。
[图1]你首先注意到,搜索区域被我们划分成了方形网格。
像这样,简化搜索区域,是寻路的第一步。
这一方法把搜索区域简化成了一个二维数组。
数组的每一个元素是网格的一个方块,方块被标记为可通过的和不可通过的。
路径被描述为从A到B我们经过的方块的集合。
一旦路径被找到,我们的人就从一个方格的中心走向另一个,直到到达目的地。
这些中点被称为“节点”。
游戏设计-第07章 2D游戏算法

pDC->SelectObject(pOldBrush1);
CBrush brush2(RGB(84+(64*i)%255,204+(64*i)%255,24+(64*i)%255));
CBrush*pOldBrush2=pDC->SelectObject(&brush2);
pDC->Ellipse(300,250,350,300);
游戏设计概论(第二版)
//在不同位置画四个不同颜色的圆
CBrush brush1(RGB(20+(64*i)%255,140+(64*i)%255,210+(64+i)%255));
CBrush*pOldBrush1=pDC->SelectObject(&brush1);
pDC->Ellipse(300,200,350,250); //Pie
void CMy1_1View::OnTimer(UINT nIDEvent)
{
// TODO: Add your message handler code here and/or
call default
//获取指针pdc
CDC *pDC=GetDC();
//调用OnDraw(pDC)重画
OnDraw(pDC);
return -1;
// TODO: Add your specialized creation code here
//设置更新时间
SetTimer(1, 750, NULL);
return 0;
}
游戏设计概论(第二版)
e. 完成。
位变
游戏设计概论(第二版)
游戏开发中经常用到的算法详解

游戏开发中经常用到的算法详解作为游戏开发人员,算法是我们必须掌握的技能之一。
无论是小型独立游戏还是大型 AAA 游戏,算法都扮演了至关重要的角色。
在这篇文章中,我将为大家详细介绍游戏开发中经常用到的算法,帮助大家深入掌握游戏开发的核心技术。
一、碰撞检测算法碰撞检测算法是游戏开发中常用的一种算法,它可以判断两个物体是否相互接触。
在游戏中,我们需要不断地检测物体之间的碰撞,以保证游戏场景的正常运作。
最常用的碰撞检测算法包括了 AABB 碰撞检测算法、圆形碰撞检测算法、多边形碰撞检测算法等。
其中,AABB 碰撞检测算法是最简单的一种算法,它通过对物体的包围盒进行检测来判断物体是否相互接触。
如果两个物体的包围盒相交,那么这两个物体就存在碰撞。
圆形碰撞检测算法则是通过计算两个圆心之间的距离来判断两个圆形是否相交。
多边形碰撞检测算法则是通过计算两个多边形边之间的相对位置来判断两个多边形是否相交。
二、路径搜索算法路径搜索算法是游戏中常用的一种算法,它可以帮助我们找到两个地点之间最短的路径。
在游戏中,我们经常需要让角色沿着特定的路径移动,这时就需要使用到路径搜索算法。
最常用的路径搜索算法包括了 A* 算法、Dijkstra 算法等。
其中,A* 算法比较常用,它采用启发式函数来估算当前节点到目标节点的距离,以此来选择下一个要遍历的节点。
三、随机数生成算法在游戏开发中,我们经常需要生成随机数来实现一些功能,比如道具掉落、怪物生成、随机地图等。
随机数生成算法是这种情况下必不可少的。
目前常用的随机数生成算法包括了 Linear Congruential Generator(线性同余法)、Mersenne Twister 等。
其中,Mersenne Twister 算法是目前被广泛使用和认可的一种算法,它有着优秀的随机性和均匀性。
同时,需要注意的是,在游戏中使用随机数时,我们需要遵循一定的规则,以保证游戏的可玩性和公平性。
游戏数据策划常用公式(仅供边缘参考)

游戏数据策划常用公式(仅供边缘参考)对于公式的使用,没有严格的规定。
比如,升级公式,没有人说一定要用XXX公式,这个是灵活的。
但是,作为新手,了解一些现存的公式会对以后自己设计公式的时候起到帮助作用,可以帮助新手解决在数值分析的时候,遇到公式问题就一筹莫展的现象。
以下是我通过各种方法收集,了解到的一些公式和说明:(1)***公式 (攻+修正a)*修正b-((防+修正a)*修正b)=损失最终损失=(损失+修正a)*修正b这个公式是“龟派的刘勇”给别人讲课时候说的一个公式(2)RPGmaker 里面的内建战斗计算公式集普通***伤害值:(A***B)伤害值=(A攻/2)-(B防/4)数值为80%~120%之间*「必杀」伤害X3*「强力防御」伤害/4普通***命中率:(A***B)命中率(%)=100-(100-A之武器命中率)X<1(B速度/A速度-1)/2> *武器有「无视於敌方闪躲率」的场合,其基本命中率同现在之不变*命中率会随装备改变*当B装备「提升物理***闪躲率」之防具的情况,命中率会有25%之差异*当B为无法行动之状况,命中率无条件成为100%特殊技能效果量:(A***B)效果量=基本效果量(A***力X打击关系度20)(A精神力X精神关系度/40)*数值分散度1会产生-5%(50~-50%)的变动*特殊技能中设定「无视防御」的场合,效果量以下列公式降低: (B防X打击关系度/40)(B精神力X精神关系度/80)*当B为防御的场合会减半,强力防御则/4*使用回复战斗不能的技能时,效果量等於生命的回复率(%)特殊技能成功率:成功率(%)=基本成功率*具有多种效果的技能,其效果由成功率的计算判断*状态变化技的场合,角色的状态有效度为基础配合异常发生率(特殊技能的成功率为50%,状态的异常发生率为50%之时,产生变化机率为25%)*失败时讯息为「…躲开了」的场合,物理***的技能适用於「普通***的命中率」算式*使生命或法力降低的技能失败时,别的能力值及状态***也随之无效逃走成功率:逃走成功率(%)=【1.5-(所有敌方角色的平均速度/所有我方角色的平均速度)】X100*若双方平均速度相同时,逃走成功率为50%*每逃走失败一次,逃走成功率提升10%*先制***的场合,可以无条件逃走(3)海天英雄传的一些公式名望公式:3^n*100-100任务等级获得的名望:n*n*n*10门派武功学习需要的忠诚度:(3^(n-1))*100-100任务等级获得的门派忠诚度:(2^n)*n*10任务等级获得的钱:n2=n1+50*n, n3=n2+50*n ……(4)三国志英杰传里面的一些公式***力=((4000÷(140-武力)+兵种基本***力×2+士气)×(等级+10)÷10)×(100+宝物***加成)÷100防御力=((4000÷(140-统御力)+兵种基本防御力×2+士气)×(等级+10)÷10×(100+宝物防御加成)÷100最大兵力=兵种基本兵力+兵种兵力增幅×(等级-1)最大策略值=(等级+10)×智力×5÷200***伤害:1)第一步:当***方兵种克制防御方兵种(骑兵系***步兵系、步兵系***弓兵系、弓兵系***骑兵系)时,防御力修正值=防御方防御力-防御方防御力÷4当***方兵种被防御方兵种克制(骑兵系***弓兵系、弓兵系***步兵系、步兵系***骑兵系)时,防御力修正值=防御方防御力+防御方防御力÷4当***方兵种和防御方兵种不存在生克关系时防御力修正值=防御方防御力2)第二步:基本物理杀伤=(***方***力-防御力修正值÷2)×(100-地形杀伤修正)÷100【地形杀伤修正】森林20 山地30 村庄 5草原 5 鹿寨30 兵营103)第三步:如果是反击***伤害=基本物理杀伤÷2如果是正常******伤害=基本物理杀伤4)第四步:如果***伤害<=0,则***伤害=1。
2048游戏核心算法

2048游戏核⼼算法2048 游戏核⼼算法 架构显⽰(界⾯)与控制(算法)分离控制台PyQtPyGame 算法1. ⾼内聚: 上下移动 -矩阵转置-> 左右移动 向左移动 --> 合并数据 --> 零元素后移 向右移动 -翻转-> 合并数据 --> 零元素后移2. 降维思想: 将⼆维列表的操作,改为对⼀维列表的操作.list_merge = None# 1. 定义函数 zero_to_end()# [2,0,2,0] --> [2,2,0,0]# [2,0,0,2] --> [2,2,0,0]# [2,4,0,2] --> [2,4,2,0]def zero_to_end():"""零元素向后移动思想:从后向前判断,如果是0则删除,在末尾追加."""for i in range(len(list_merge) - 1, -1, -1): if list_merge[i] == 0: del list_merge[i] list_merge.append(0)# zero_to_end()# print(list_merge)# 2. 定义函数 merge()# [2,0,2,0] -->[2,2,0,0] --> [4,0,0,0]# [2,0,0,2] -->[2,2,0,0] --> [4,0,0,0]# [4,4,4,4] --> [8,8,0,0]# [2,0,4,2] --> [2,4,2,0]def merge():"""合并数据核⼼思想:零元素后移,判断是否相邻相同。
如果是则合并."""zero_to_end()for i in range(len(list_merge) - 1): if list_merge[i] == list_merge[i + 1]: list_merge[i] += list_merge[i + 1] del list_merge[i + 1] list_merge.append(0)# merge()# print(list_merge)# 3. 向左移动map = [[2, 0, 0, 2],[4, 2, 0, 2],[0, 4, 0, 4],]def move_left():"""向左移动map思想:获取每⾏,交给list_merge,在通知merge()进⾏合并:return:"""global list_mergefor line in map: list_merge = line merge()# move_left()# print(map)# 4. 向右移动 move_rightdef move_right():"""向左移动map思想:获取每⾏,交给list_merge,在通知merge()进⾏合并:return:"""global list_merge for line in map:# 从右向左获取数据形成新列表 list_merge = line[::-1]# 处理数据 merge()# 将处理后的数据再从右向左还给map line[::-1] = list_merge# move_right()# print(map)# 5. 向上移动 move_up 转置 move_left 转置def square_matrix_transposition(): """ ⽅阵转置(列转换为⾏) :param map: 需要转置的⽅阵 :return: """for c in range(1, len(map)): # 1 2 3 for r in range(c, len(map)): map[r][c - 1], map[c - 1][r] = map[c - 1][r], map[r][c - 1] def move_up(): """ 向上移动 思想:转置 move_left 转置 """square_matrix_transposition()move_left()square_matrix_transposition()def move_down(): """ 向下移动 思想: 转置 move_right 转置 :return: """square_matrix_transposition() move_right()square_matrix_transposition()# move_up()move_down()print(map)。
游戏开发常用算法

游戏开发常⽤算法转⾃:要使计算机能完成⼈们预定的⼯作,⾸先必须为如何完成预定的⼯作设计⼀个算法,然后再根据算法编写程序。
计算机程序要对问题的每个对象和处理规则给出正确详尽的描述,其中程序的数据结构和变量⽤来描述问题的对象,程序结构、函数和语句⽤来描述问题的算法。
算法数据结构是程序的两个重要⽅⾯。
算法是问题求解过程的精确描述,⼀个算法由有限条可完全机械地执⾏的、有确定结果的指令组成。
指令正确地描述了要完成的任务和它们被执⾏的顺序。
计算机按算法指令所描述的顺序执⾏算法的指令能在有限的步骤内终⽌,或终⽌于给出问题的解,或终⽌于指出问题对此输⼊数据⽆解。
通常求解⼀个问题可能会有多种算法可供选择,选择的主要标准是算法的正确性和可靠性,简单性和易理解性。
其次是算法所需要的存储空间少和执⾏更快等。
算法设计是⼀件⾮常困难的⼯作,经常采⽤的算法设计技术主要有迭代法、穷举搜索法、递推法、贪婪法、回溯法、分治法、动态规划法等等。
另外,为了更简洁的形式设计和藐视算法,在算法设计时⼜常常采⽤递归技术,⽤递归描述算法。
⼀、迭代法迭代法是⽤于求⽅程或⽅程组近似根的⼀种常⽤的算法设计⽅法。
设⽅程为f(x)=0,⽤某种数学⽅法导出等价的形式x=g(x),然后按以下步骤执⾏:(1)选⼀个⽅程的近似根,赋给变量x0;(2)将x0的值保存于变量x1,然后计算g(x1),并将结果存于变量x0;(3)当x0与x1的差的绝对值还⼩于指定的精度要求时,重复步骤(2)的计算。
若⽅程有根,并且⽤上述⽅法计算出来的近似根序列收敛,则按上述⽅法求得的x0就认为是⽅程的根。
上述算法⽤C程序的形式表⽰为:【算法】迭代法求⽅程的根{ x0=初始近似根;do {x1=x0;x0=g(x1); /*按特定的⽅程计算新的近似根*/} while ( fabs(x0-x1)>Epsilon);printf(“⽅程的近似根是%f\n”,x0);}迭代算法也常⽤于求⽅程组的根,令X=(x0,x1,…,xn-1)设⽅程组为:xi=gi(X) (I=0,1,…,n-1)则求⽅程组根的迭代算法可描述如下:【算法】迭代法求⽅程组的根{ for (i=0;i x=初始近似根;do {for (i=0;i y=x;for (i=0;i x=gi(X);for (delta=0.0,i=0;i if (fabs(y-x)>delta) delta=fabs(y-x);} while (delta>Epsilon);for (i=0;i printf(“变量x[%d]的近似根是 %f”,I,x);printf(“\n”);}具体使⽤迭代法求根时应注意以下两种可能发⽣的情况:(1)如果⽅程⽆解,算法求出的近似根序列就不会收敛,迭代过程会变成死循环,因此在使⽤迭代算法前应先考察⽅程是否有解,并在程序中对迭代的次数给予限制;(2)⽅程虽然有解,但迭代公式选择不当,或迭代的初始近似根选择不合理,也会导致迭代失败。
unity3d贴图说明
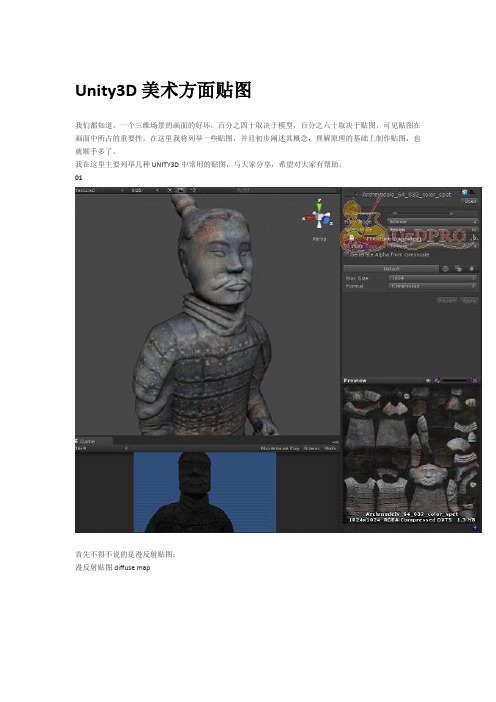
Unity3D美术方面贴图我们都知道,一个三维场景的画面的好坏,百分之四十取决于模型,百分之六十取决于贴图,可见贴图在画面中所占的重要性。
在这里我将列举一些贴图,并且初步阐述其概念,理解原理的基础上制作贴图,也就顺手多了。
我在这里主要列举几种UNITY3D中常用的贴图,与大家分享,希望对大家有帮助。
01首先不得不说的是漫反射贴图:漫反射贴图diffuse map漫反射贴图在游戏中表现出物体表面的反射和表面颜色。
换句话说,它可以表现出物体被光照射到而显出的颜色和强度。
我们通过颜色和明暗来绘制一幅漫反射贴图,在这张贴图中,墙的砖缝中因为吸收了比较多的光线,所以比较暗,而墙砖的表面因为反射比较强,所以吸收的光线比较少。
上面的这张图可以看出砖块本身是灰色的,而砖块之间的裂缝几乎是黑色的。
刨去那些杂糅的东西,我们只谈明显的,漫反射贴图表现了什么?列举一下,物体的固有色以及纹理,贴图上的光影。
前面的固有色和纹理我们很容易理解,至于后面的光影,我们再绘制漫反射贴图的时候需要区别对待,比如我们做一堵墙,每一块砖都是用模型做出来的,那么我们就没有必要绘制砖缝,因为这个可以通过打灯光来实现。
可是我们如果用模型只做了一面墙,上面的砖块是用贴图来实现,那么就得绘制出砖缝了。
从美术的角度,砖缝出了事一条单独的材质带外,还有就是砖缝也是承接投影的,所以在漫反射图上,绘制出投影也是很有必要的,如下图:没有什么物体能够反射出跟照到它身上相同强度的光。
因此,让你的漫反射贴图暗一些是一个不错的想法。
通常,光滑的面只有很少的光会散射,所以你的漫反射贴图可以亮一些。
漫反射贴图应用到材质中去是直接通过DiffuseMap的。
再命名规范上它通常是再文件的末尾加上“_d”来标记它是漫反射贴图。
凹凸贴图Bump maps凸凹贴图可以给贴图增加立体感。
它其实并不能改变模型的形状,而是通过影响模型表面的影子来达到凸凹效果的。
再游戏中有两种不同类型的凸凹贴图,法线贴图(normalmap)和高度贴图(highmap)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
算法一:A*寻路初探译者序:很久以前就知道了A*算法,但是从未认真读过相关的文章,也没有看过代码,只是脑子里有个模糊的概念。
这次决定从头开始,研究一下这个被人推崇备至的简单方法,作为学习人工智能的开始。
这篇文章非常知名,国内应该有不少人翻译过它,我没有查找,觉得翻译本身也是对自身英文水平的锻炼。
经过努力,终于完成了文档,也明白的A*算法的原理。
毫无疑问,作者用形象的描述,简洁诙谐的语言由浅入深的讲述了这一神奇的算法,相信每个读过的人都会对此有所认识。
原文链接:/reference/articles/article2003.asp以下是翻译的正文。
(由于本人使用ultraedit编辑,所以没有对原文中的各种链接加以处理(除了图表),也是为了避免未经许可链接的嫌疑,有兴趣的读者可以参考原文。
会者不难,A*(念作A星)算法对初学者来说的确有些难度。
这篇文章并不试图对这个话题作权威的陈述。
取而代之的是,它只是描述算法的原理,使你可以在进一步的阅读中理解其他相关的资料。
最后,这篇文章没有程序细节。
你尽可以用任意的计算机程序语言实现它。
如你所愿,我在文章的末尾包含了一个指向例子程序的链接。
压缩包包括C++和Blitz Basic两个语言的版本,如果你只是想看看它的运行效果,里面还包含了可执行文件。
我们正在提高自己。
让我们从头开始。
序:搜索区域假设有人想从A点移动到一墙之隔的B点,如图,绿色的是起点A,红色是终点B,蓝色方块是中间的墙。
[图1]你首先注意到,搜索区域被我们划分成了方形网格。
像这样,简化搜索区域,是寻路的第一步。
这一方法把搜索区域简化成了一个二维数组。
数组的每一个元素是网格的一个方块,方块被标记为可通过的和不可通过的。
路径被描述为从A到B我们经过的方块的集合。
一旦路径被找到,我们的人就从一个方格的中心走向另一个,直到到达目的地。
这些中点被称为“节点”。
当你阅读其他的寻路资料时,你将经常会看到人们讨论节点。
为什么不把他们描述为方格呢?因为有可能你的路径被分割成其他不是方格的结构。
他们完全可以是矩形,六角形,或者其他任意形状。
节点能够被放置在形状的任意位置-可以在中心,或者沿着边界,或其他什么地方。
我们使用这种系统,无论如何,因为它是最简单的。
开始搜索正如我们处理上图网格的方法,一旦搜索区域被转化为容易处理的节点,下一步就是去引导一次找到最短路径的搜索。
在A*寻路算法中,我们通过从点A开始,检查相邻方格的方式,向外扩展直到找到目标。
我们做如下操作开始搜索:1,从点A开始,并且把它作为待处理点存入一个“开启列表”。
开启列表就像一张购物清单。
尽管现在列表里只有一个元素,但以后就会多起来。
你的路径可能会通过它包含的方格,也可能不会。
基本上,这是一个待检查方格的列表。
2,寻找起点周围所有可到达或者可通过的方格,跳过有墙,水,或其他无法通过地形的方格。
也把他们加入开启列表。
为所有这些方格保存点A作为“父方格”。
当我们想描述路径的时候,父方格的资料是十分重要的。
后面会解释它的具体用途。
3,从开启列表中删除点A,把它加入到一个“关闭列表”,列表中保存所有不需要再次检查的方格。
在这一点,你应该形成如图的结构。
在图中,暗绿色方格是你起始方格的中心。
它被用浅蓝色描边,以表示它被加入到关闭列表中了。
所有的相邻格现在都在开启列表中,它们被用浅绿色描边。
每个方格都有一个灰色指针反指他们的父方格,也就是开始的方格。
[图2]接着,我们选择开启列表中的临近方格,大致重复前面的过程,如下。
但是,哪个方格是我们要选择的呢?是那个F值最低的。
路径评分:选择路径中经过哪个方格的关键是下面这个等式:F =G + H这里:* G = 从起点A,沿着产生的路径,移动到网格上指定方格的移动耗费。
* H = 从网格上那个方格移动到终点B的预估移动耗费。
这经常被称为启发式的,可能会让你有点迷惑。
这样叫的原因是因为它只是个猜测。
我们没办法事先知道路径的长度,因为路上可能存在各种障碍(墙,水,等等)。
虽然本文只提供了一种计算H的方法,但是你可以在网上找到很多其他的方法。
我们的路径是通过反复遍历开启列表并且选择具有最低F值的方格来生成的。
文章将对这个过程做更详细的描述。
首先,我们更深入的看看如何计算这个方程。
正如上面所说,G表示沿路径从起点到当前点的移动耗费。
在这个例子里,我们令水平或者垂直移动的耗费为10,对角线方向耗费为14。
我们取这些值是因为沿对角线的距离是沿水平或垂直移动耗费的的根号2(别怕),或者约1.414倍。
为了简化,我们用10和14近似。
比例基本正确,同时我们避免了求根运算和小数。
这不是只因为我们怕麻烦或者不喜欢数学。
使用这样的整数对计算机来说也更快捷。
你不就就会发现,如果你不使用这些简化方法,寻路会变得很慢。
既然我们在计算沿特定路径通往某个方格的G值,求值的方法就是取它父节点的G值,然后依照它相对父节点是对角线方向或者直角方向(非对角线),分别增加14和10。
例子中这个方法的需求会变得更多,因为我们从起点方格以外获取了不止一个方格。
H 值可以用不同的方法估算。
我们这里使用的方法被称为曼哈顿方法,它计算从当前格到目的格之间水平和垂直的方格的数量总和,忽略对角线方向,然后把结果乘以 10。
这被成为曼哈顿方法是因为它看起来像计算城市中从一个地方到另外一个地方的街区数,在那里你不能沿对角线方向穿过街区。
很重要的一点,我们忽略了一切障碍物。
这是对剩余距离的一个估算,而非实际值,这也是这一方法被称为启发式的原因。
想知道更多?你可以在这里找到方程和额外的注解。
F的值是G和H的和。
第一步搜索的结果可以在下面的图表中看到。
F,G和H的评分被写在每个方格里。
正如在紧挨起始格右侧的方格所表示的,F被打印在左上角,G在左下角,H则在右下角。
[图3]现在我们来看看这些方格。
写字母的方格里,G = 10。
这是因为它只在水平方向偏离起始格一个格距。
紧邻起始格的上方,下方和左边的方格的G值都等于10。
对角线方向的G值是14。
H 值通过求解到红色目标格的曼哈顿距离得到,其中只在水平和垂直方向移动,并且忽略中间的墙。
用这种方法,起点右侧紧邻的方格离红色方格有3格距离,H值就是30。
这块方格上方的方格有4格距离(记住,只能在水平和垂直方向移动),H值是40。
你大致应该知道如何计算其他方格的H值了~。
每个格子的F值,还是简单的由G和H相加得到继续搜索为了继续搜索,我们简单的从开启列表中选择F值最低的方格。
然后,对选中的方格做如下处理:4,把它从开启列表中删除,然后添加到关闭列表中。
5,检查所有相邻格子。
跳过那些已经在关闭列表中的或者不可通过的(有墙,水的地形,或者其他无法通过的地形),把他们添加进开启列表,如果他们还不在里面的话。
把选中的方格作为新的方格的父节点。
6,如果某个相邻格已经在开启列表里了,检查现在的这条路径是否更好。
换句话说,检查如果我们用新的路径到达它的话,G值是否会更低一些。
如果不是,那就什么都不做。
另一方面,如果新的G值更低,那就把相邻方格的父节点改为目前选中的方格(在上面的图表中,把箭头的方向改为指向这个方格)。
最后,重新计算F和G的值。
如果这看起来不够清晰,你可以看下面的图示。
好了,让我们看看它是怎么运作的。
我们最初的9格方格中,在起点被切换到关闭列表中后,还剩8格留在开启列表中。
这里面,F值最低的那个是起始格右侧紧邻的格子,它的F值是40。
因此我们选择这一格作为下一个要处理的方格。
在紧随的图中,它被用蓝色突出显示。
[图4]首先,我们把它从开启列表中取出,放入关闭列表(这就是他被蓝色突出显示的原因)。
然后我们检查相邻的格子。
哦,右侧的格子是墙,所以我们略过。
左侧的格子是起始格。
它在关闭列表里,所以我们也跳过它。
其他4格已经在开启列表里了,于是我们检查G值来判定,如果通过这一格到达那里,路径是否更好。
我们来看选中格子下面的方格。
它的G值是14。
如果我们从当前格移动到那里,G值就会等于20(到达当前格的G值是10,移动到上面的格子将使得G值增加10)。
因为G值20大于14,所以这不是更好的路径。
如果你看图,就能理解。
与其通过先水平移动一格,再垂直移动一格,还不如直接沿对角线方向移动一格来得简单。
当我们对已经存在于开启列表中的4个临近格重复这一过程的时候,我们发现没有一条路径可以通过使用当前格子得到改善,所以我们不做任何改变。
既然我们已经检查过了所有邻近格,那么就可以移动到下一格了。
于是我们检索开启列表,现在里面只有7格了,我们仍然选择其中F值最低的。
有趣的是,这次,有两个格子的数值都是54。
我们如何选择?这并不麻烦。
从速度上考虑,选择最后添加进列表的格子会更快捷。
这种导致了寻路过程中,在靠近目标的时候,优先使用新找到的格子的偏好。
但这无关紧要。
(对相同数值的不同对待,导致不同版本的A*算法找到等长的不同路径。
)那我们就选择起始格右下方的格子,如图。
[图5]这次,当我们检查相邻格的时候,发现右侧是墙,于是略过。
上面一格也被略过。
我们也略过了墙下面的格子。
为什么呢?因为你不能在不穿越墙角的情况下直接到达那个格子。
你的确需要先往下走然后到达那一格,按部就班的走过那个拐角。
(注解:穿越拐角的规则是可选的。
它取决于你的节点是如何放置的。
)这样一来,就剩下了其他5格。
当前格下面的另外两个格子目前不在开启列表中,于是我们添加他们,并且把当前格指定为他们的父节点。
其余3格,两个已经在开启列表中(起始格,和当前格上方的格子,在表格中蓝色高亮显示),于是我们略过它们。
最后一格,在当前格的左侧,将被检查通过这条路径,G值是否更低。
不必担心,我们已经准备好检查开启列表中的下一格了。
我们重复这个过程,知道目标格被添加进开启列表,就如在下面的图中所看到的。
[图6]注意,起始格下方格子的父节点已经和前面不同的。
之前它的G值是28,并且指向右上方的格子。
现在它的G值是20,指向它上方的格子。
这在寻路过程中的某处发生,当应用新路径时,G值经过检查变得低了-于是父节点被重新指定,G和F值被重新计算。
尽管这一变化在这个例子中并不重要,在很多场合,这种变化会导致寻路结果的巨大变化。
那么,我们怎么确定这条路径呢?很简单,从红色的目标格开始,按箭头的方向朝父节点移动。
这最终会引导你回到起始格,这就是你的路径!看起来应该像图中那样。
从起始格A移动到目标格B只是简单的从每个格子(节点)的中点沿路径移动到下一个,直到你到达目标点。
就这么简单。
[图7]A*方法总结好,现在你已经看完了整个说明,让我们把每一步的操作写在一起:1,把起始格添加到开启列表。
2,重复如下的工作:a) 寻找开启列表中F值最低的格子。
我们称它为当前格。
b) 把它切换到关闭列表。
c) 对相邻的8格中的每一个?* 如果它不可通过或者已经在关闭列表中,略过它。
