双向板计算
双向板挠度计算

双向板挠度计算
双向板挠度计算
双向板挠度计算是结构工程中常用的一种计算方法,用于评估板材在受力时的弯曲程度。
本文将介绍双向板挠度计算的基本原理和计算方法。
## 原理
双向板挠度计算基于材料力学的基本原理,即弹性模量和截面惯性矩。
弹性模量指的是材料的弹性变形能力,截面惯性矩则是描述材料抵抗扭曲变形的能力。
在板材受力时,其挠度与施加的力和板材的尺寸有关。
## 计算方法
双向板挠度计算可以采用多种方法,其中最常用的是杨氏公式。
该公式将板材的挠度与施加的力、板材的长度、宽度和厚度以及弹性模量和截面惯性矩等参数
联系起来。
具体地,双向板挠度计算的公式如下:
δ = (qL^4)/(8EI)
其中,δ表示板材的挠度,q表示施加在板材上的力,L表示板材的长度,E表示板材的弹性模量,I表示板材的截面惯性矩。
在实际计算中,需要根据具体的板材尺寸和力的大小确定各参数的数值。
其中,弹性模量和截面惯性矩可以通过材料力学实验获得,也可以从相关手册中查找。
## 应用范围
双向板挠度计算广泛应用于建筑、机械制造、航空航天等领域。
在建筑领域,双向板挠度计算通常用于评估楼板结构的强度和稳定性,以确保建筑物的安全性。
在机械制造和航空航天领域,双向板挠度计算则用于设计和制造各种复杂的机械和飞行器。
## 结论
双向板挠度计算是结构工程中重要的计算方法之一,可以帮助工程师评估板材的弯曲程度和稳定性。
在实际应用中,需要根据具体的情况选择合适的计算方法和参数,以确保计算结果的准确性和可靠性。
池壁双向板计算示例
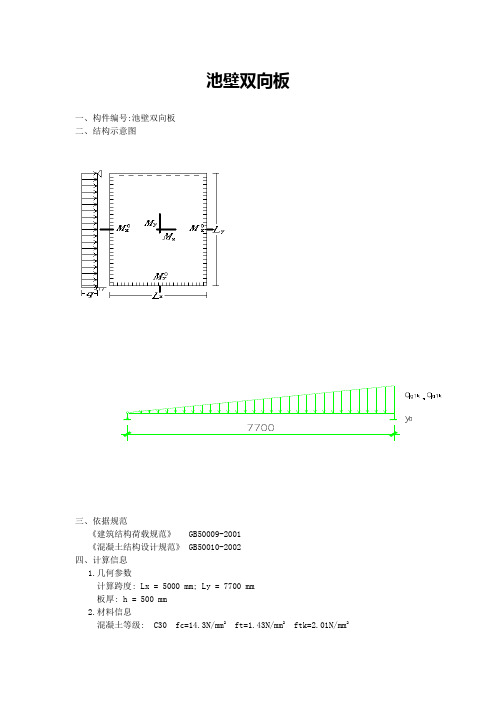
池壁双向板一、构件编号:池壁双向板二、结构示意图三、依据规范《建筑结构荷载规范》 GB50009-2001《混凝土结构设计规范》 GB50010-2002四、计算信息1.几何参数计算跨度: Lx = 5000 mm; Ly = 7700 mm板厚: h = 500 mm2.材料信息混凝土等级: C30 fc=14.3N/mm2 ft=1.43N/mm2 ftk=2.01N/mm2 Ec=3.00×104N/mm2钢筋种类: HRB335 fy = 300 N/mm2Es = 2.0×105 N/mm2最小配筋率: ρ= 0.215%纵向受拉钢筋合力点至近边距离: as = 40mm保护层厚度: c = 30mm3.荷载信息(均布荷载)永久荷载分项系数: γG = 1.200可变荷载分项系数: γQ = 1.300准永久值系数: ψq = 0.500永久荷载标准值: qgk = 1.000kN/m2可变荷载标准值: qqk = 80.000kN/m24.计算方法:弹性板5.边界条件(上端/下端/左端/右端):简支/固定/固定/固定6.设计参数结构重要性系数: γo = 1.00泊松比:μ = 0.200五、计算参数:1.计算板的跨度: Lo = 5000 mm2.计算板的有效高度: ho = h-as=500-40=460 mm六、配筋计算(lx/ly=5000/7700=0.649<2.000 所以按双向板计算):1.X向底板钢筋1) 确定X向板底弯矩Mx = 表中系数(γG*qgk+γQ*qqk)*Lo2= (0.0371+0.0116*0.200)*(1.200*1.000+1.300*80.000)*52 = 56.197 kN*m2) 确定计算系数αs = γo*Mx/(α1*fc*b*ho*ho)= 1.00*56.197×106/(1.00*14.3*1000*460*460)= 0.0193) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.019) = 0.0194) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*14.3*1000*460*0.019/300 = 411mm25) 验算最小配筋率ρ = As/(b*h) = 411/(1000*500) = 0.082%ρ<ρmin = 0.215% 不满足最小配筋要求所以取面积为As = ρmin*b*h = 0.215%*1000*500 = 1075 mm2采取方案d20@200, 实配面积1571 mm22.Y向底板钢筋1) 确定Y向板底弯矩My = 表中系数(γG*qgk+γQ*qqk)*Lo2= (0.0116+0.0371*0.200)*(1.200*1.000+1.300*80.000)*52 = 27.089 kN*m2) 确定计算系数αs = γo*Mx/(α1*fc*b*ho*ho)= 1.00*27.089×106/(1.00*14.3*1000*460*460)= 0.0093) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.009) = 0.0094) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*14.3*1000*460*0.009/300 = 197mm25) 验算最小配筋率ρ = As/(b*h) = 197/(1000*500) = 0.039%ρ<ρmin = 0.215% 不满足最小配筋要求所以取面积为As = ρmin*b*h = 0.215%*1000*500 = 1075 mm2采取方案d20@200, 实配面积1571 mm23.X向支座左边钢筋1) 确定左边支座弯矩M o x = 表中系数(γG*qgk+γQ*qqk)*Lo2= 0.0796*(1.200*1.000+1.300*80.000)*52= 113.463 kN*m2) 确定计算系数αs = γo*Mx/(α1*fc*b*ho*ho)= 1.00*113.463×106/(1.00*14.3*1000*460*460)= 0.0373) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.037) = 0.0384) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*14.3*1000*460*0.038/300 = 838mm25) 验算最小配筋率ρ = As/(b*h) = 838/(1000*500) = 0.168%ρ<ρmin = 0.215% 不满足最小配筋要求所以取面积为As = ρmin*b*h = 0.215%*1000*500 = 1075mm2采取方案d20@100, 实配面积3142 mm24.X向支座右边钢筋1) 确定右边支座弯矩M o x = 表中系数(γG*qgk+γQ*qqk)*Lo2= 0.0796*(1.200*1.000+1.300*80.000)*52= 113.463 kN*m2) 确定计算系数αs = γo*Mx/(α1*fc*b*ho*ho)= 1.00*113.463×106/(1.00*14.3*1000*460*460)= 0.0373) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.037) = 0.0384) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*14.3*1000*460*0.038/300= 838mm25) 验算最小配筋率ρ = As/(b*h) = 838/(1000*500) = 0.168%ρ<ρmin = 0.215% 不满足最小配筋要求所以取面积为As = ρmin*b*h = 0.215%*1000*500 = 1075 mm2采取方案d20@100, 实配面积3142 mm25.Y向下边支座钢筋1) 确定下边支座弯矩M o y = 表中系数(γG*qgk+γQ*qqk)*Lo2= 0.0572*(1.200*1.000+1.300*80.000)*52= 81.508 kN*m2) 确定计算系数αs = γo*Mx/(α1*fc*b*ho*ho)= 1.00*81.508×106/(1.00*14.3*1000*460*460)= 0.0273) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.027) = 0.0274) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*14.3*1000*460*0.027/300= 599mm25) 验算最小配筋率ρ = As/(b*h) = 599/(1000*500) = 0.120%ρ<ρmin = 0.215% 不满足最小配筋要求所以取面积为As = ρmin*b*h = 0.215%*1000*500 = 1075 mm2采取方案d20@100, 实配面积3142 mm2七、跨中挠度计算:Mk -------- 按荷载效应的标准组合计算的弯矩值Mq -------- 按荷载效应的准永久组合计算的弯矩值1.计算荷载效应Mk = Mgk + Mqk= (0.0371+0.0116*0.200)*(15.000+30.000)*52 = 44.366 kN*mMq = Mgk+ψq*Mqk= (0.0371+0.0116*0.200)*(15.000+0.500*30.000)*52 = 29.577 kN*m 2.计算受弯构件的短期刚度 Bs1) 计算按荷载荷载效应的标准组合作用下,构件纵向受拉钢筋应力σsk = Mk/(0.87*ho*As) (混凝土规范式 8.1.3-3)= 44.366×106/(0.87*460*1571) = 70.567 N/mm2) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积: Ate = 0.5*b*h = 0.5*1000*500= 250000mm2ρte = As/Ate (混凝土规范式 8.1.2-4)= 1571/250000 = 0.628%3) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ = 1.1-0.65*ftk/(ρte*σsk) (混凝土规范式 8.1.2-2)= 1.1-0.65*2.01/(0.628%*70.567) = -1.846因为ψ不能小于最小值0.2,所以取ψ = 0.24) 计算钢筋弹性模量与混凝土模量的比值αEαE = Es/Ec = 2.0×105/3.00×104 = 6.6675) 计算受压翼缘面积与腹板有效面积的比值γf矩形截面,γf=06) 计算纵向受拉钢筋配筋率ρρ = As/(b*ho)= 1571/(1000*460) = 0.342%7) 计算受弯构件的短期刚度 BsBs = Es*As*ho2/[1.15ψ+0.2+6*αE*ρ/(1+ 3.5γf')](混凝土规范式8.2.3--1) = 2.0×105*1571*4602/[1.15*0.200+0.2+6*6.667*0.342%/(1+3.5*0.0)]= 1.173×105 kN*m23.计算受弯构件的长期刚度B1) 确定考虑荷载长期效应组合对挠度影响增大影响系数θ当ρ'=0时,θ=2.0 (混凝土规范第 8.2.5 条)2) 计算受弯构件的长期刚度 BB = Mk/(Mq*(θ-1)+Mk)*Bs (混凝土规范式 8.2.2)= 44.366/(29.577*(2.0-1)+44.366)*1.173×105= 7.040×104 kN*m24.计算受弯构件挠度f max = f*(q gk+q qk)*Lo4/B= 0.00240*(15.000+30.000)*54/7.040×104= 0.959mm5.验算挠度挠度限值fo=Lo/200=5000/200=25.000mmfmax=0.959mm≤fo=25.000mm,满足规范要求!八、裂缝宽度验算:1.跨中X方向裂缝1) 计算荷载效应Mx = 表中系数(qgk+qqk)*Lo2= (0.0371+0.0116*0.200)*(15.000+30.000)*52= 44.366 kN*m2) 带肋钢筋,所以取值v i=1.03) 计算按荷载荷载效应的标准组合作用下,构件纵向受拉钢筋应力σsk=Mk/(0.87*ho*As) (混凝土规范式 8.1.3-3)=44.366×106/(0.87*460*1571)=70.567N/mm4) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*500=250000 mm2ρte=As/Ate (混凝土规范式 8.1.2-4)=1571/250000 = 0.0063因为ρte=0.0063 < 0.01,所以让ρte=0.015) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsk) (混凝土规范式 8.1.2-2)=1.1-0.65*2.010/(0.0100*70.567)=-0.751因为ψ=-0.751 < 0.2,所以让ψ=0.26) 计算单位面积钢筋根数nn=1000/dist = 1000/200=57) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=5*20*20/(5*1.0*20)=208) 计算最大裂缝宽度ωmax=αcr*ψ*σsk/Es*(1.9c+0.08*Deq/ρte) (混凝土规范式 8.1.2-1) =2.1*0.200*70.567/2.0×105*(1.9*30+0.08*20/0.0100)=0.0322mm ≤ 0.30, 满足规范要求2.跨中Y方向裂缝1) 计算荷载效应My = 表中系数(qgk+qqk)*Lo2= (0.0116+0.0371*0.200)*(15.000+30.000)*52= 21.386 kN*m2) 带肋钢筋,所以取值v i=1.03) 计算按荷载荷载效应的标准组合作用下,构件纵向受拉钢筋应力σsk=Mk/(0.87*ho*As) (混凝土规范式 8.1.3-3)=21.386×106/(0.87*460*1571)=34.015N/mm4) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*500=250000 mm2ρte=As/Ate (混凝土规范式 8.1.2-4)=1571/250000 = 0.0063因为ρte=0.0063 < 0.01,所以让ρte=0.015) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsk) (混凝土规范式 8.1.2-2)=1.1-0.65*2.010/(0.0100*34.015)=-2.741因为ψ=-2.741 < 0.2,所以让ψ=0.26) 计算单位面积钢筋根数nn=1000/dist = 1000/200=57) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=5*20*20/(5*1.0*20)=208) 计算最大裂缝宽度ωmax=αcr*ψ*σsk/Es*(1.9c+0.08*Deq/ρte) (混凝土规范式 8.1.2-1) =2.1*0.200*34.015/2.0×105*(1.9*30+0.08*20/0.0100)=0.0155mm ≤ 0.30, 满足规范要求3.支座下方向裂缝1) 计算荷载效应M o y = 表中系数(qgk+qqk)*Lo2= 0.0572*(15.000+30.000)*52= 64.349 kN*m2) 带肋钢筋,所以取值v i=1.03) 计算按荷载荷载效应的标准组合作用下,构件纵向受拉钢筋应力σsk=Mk/(0.87*ho*As) (混凝土规范式 8.1.3-3)=64.349×106/(0.87*460*3142)=51.175N/mm4) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*500=250000 mm2ρte=As/Ate (混凝土规范式 8.1.2-4)=3142/250000 = 0.01265) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsk) (混凝土规范式 8.1.2-2)=1.1-0.65*2.010/(0.0126*51.175)=-0.931因为ψ=-0.931 < 0.2,所以让ψ=0.26) 计算单位面积钢筋根数nn=1000/dist = 1000/100=107) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=10*20*20/(10*1.0*20)=208) 计算最大裂缝宽度ωmax=αcr*ψ*σsk/Es*(1.9c+0.08*Deq/ρte) (混凝土规范式 8.1.2-1) =2.1*0.200*51.175/2.0×105*(1.9*30+0.08*20/0.0126)=0.0198mm ≤ 0.30, 满足规范要求4.支座左方向裂缝1) 计算荷载效应M o x = 表中系数(qgk+qqk)*Lo2= 0.0796*(15.000+30.000)*52= 89.576 kN*m2) 带肋钢筋,所以取值v i=1.03) 计算按荷载荷载效应的标准组合作用下,构件纵向受拉钢筋应力σsk=Mk/(0.87*ho*As) (混凝土规范式 8.1.3-3)=89.576×106/(0.87*460*3142)=71.238N/mm4) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*500=250000 mm2ρte=As/Ate (混凝土规范式 8.1.2-4)=3142/250000 = 0.01265) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsk) (混凝土规范式 8.1.2-2)=1.1-0.65*2.010/(0.0126*71.238)=-0.359因为ψ=-0.359 < 0.2,所以让ψ=0.26) 计算单位面积钢筋根数nn=1000/dist = 1000/100=107) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=10*20*20/(10*1.0*20)=208) 计算最大裂缝宽度ωmax=αcr*ψ*σsk/Es*(1.9c+0.08*Deq/ρte) (混凝土规范式 8.1.2-1) =2.1*0.200*71.238/2.0×105*(1.9*30+0.08*20/0.0126)=0.0276mm ≤ 0.30, 满足规范要求5.支座右方向裂缝1) 计算荷载效应M o x = 表中系数(qgk+qqk)*Lo2= 0.0796*(15.000+30.000)*52= 89.576 kN*m2) 带肋钢筋,所以取值v i=1.03) 计算按荷载荷载效应的标准组合作用下,构件纵向受拉钢筋应力σsk=Mk/(0.87*ho*As) (混凝土规范式 8.1.3-3)=89.576×106/(0.87*460*3142)=71.238N/mm4) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*500=250000 mm2ρte=As/Ate (混凝土规范式 8.1.2-4)=3142/250000 = 0.01265) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsk) (混凝土规范式 8.1.2-2)=1.1-0.65*2.010/(0.0126*71.238)=-0.359因为ψ=-0.359 < 0.2,所以让ψ=0.26) 计算单位面积钢筋根数nn=1000/dist = 1000/100=107) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=10*20*20/(10*1.0*20)=208) 计算最大裂缝宽度ωmax=αcr*ψ*σsk/Es*(1.9c+0.08*Deq/ρte) (混凝土规范式 8.1.2-1) =2.1*0.200*71.238/2.0×105*(1.9*30+0.08*20/0.0126)=0.0276mm ≤ 0.30, 满足规范要求。
双向板计算步骤

LB-1 矩形板计算一、构件编号: LB-1二、示意图三、依据规范《建筑结构荷载规范》GB50009-2001《混凝土结构设计规范》GB50010-2010四、计算信息1. 几何参数计算跨度: Lx = 3000 mm; Ly = 4600 mm 板厚: h = 120 mm2. 材料信息混凝土等级: C25 fc=11.9N/mm ft=1.27N/mm ftk=1.78N/mm42Ec=2.80 x 104N/mrnQ C Q 钢筋种类: HRB400 fy = 360 N/mm 2 Es = 2.0 x105 N/mm2最小配筋率:p = 0.200%纵向受拉钢筋合力点至近边距离: as = 40mm保护层厚度: c = 20mm3. 荷载信息(均布荷载)永久荷载分项系数:丫G = 1.200 可变荷载分项系数:丫Q = 1.400 准永久值系数:如q = 1.000永久荷载标准值:q gk = 4.100kN/m可变荷载标准值:q qk = 2.000kN/m4. 计算方法: 弹性板5. 边界条件(上端/ 下端/ 左端/ 右端): 固定/ 简支/ 简支/ 简支6. 设计参数结构重要性系数:丫o = 1.00泊松比:卩=0.200五、计算参数:1. 计算板的跨度: Lo = 3000 mm2. 计算板的有效高度: ho = h-as=120-40=80 mm六、配筋计算(lx/ly=3000/4600=0.652<2.000 所以按双向板计算):1. X 向底板钢筋1) 确定X 向板底弯矩2Mx = 表中系数(丫G*q gk+丫Q*q qk)*Lo= (0.0634+0.0307*0.200)*(1.200*4.100+1.400*2.000)*3 = 4.829kN*m2) 确定计算系数a s = 丫o*Mx/( a 1*fc*b*ho*ho)=1.00*4.829 X 10 6/(1.00*11.9*1000*80*80)= 0.0633) 计算相对受压区高度E= 1 -sqrt(1- 2* a s) = 1 -sqrt(1-2*0.063) = 0.0664) 计算受拉钢筋面积As = a 1*fc*b*ho* E /fy = 1.000*11.9*1000*80*0.066/360 = 173mm5) 验算最小配筋率p = As/(b*h) = 173/(1000*120) = 0.144%p <p min = 0.200% 不满足最小配筋要求所以取面积为As = p min*b*h = 0.200%*1000*120 = 240 mm 采取方案?8@200, 实配面积251 mm 22. Y 向底板钢筋1) 确定Y 向板底弯矩My = 表中系数(丫G*q gk+丫Q*q qk)*Lo 2= (0.0307+0.0634*0.200)*(1.200*4.100+1.400*2.000)*3= 3.012 kN*m2) 确定计算系数a s = 丫o*My/( a 1*fc*b*ho*ho)=1.00*3.012 X 10 6/(1.00*11.9*1000*80*80) = 0.0403) 计算相对受压区高度E = 1 -sqrt(1- 2*a s) = 1 -sqrt(1-2*0.040) = 0.0404) 计算受拉钢筋面积As = a 1*fc*b*ho* E /fy = 1.000*11.9*1000*80*0.040/360= 107mm 5) 验算最小配筋率p = As/(b*h) = 107/(1000*120) = 0.089%p < p min = 0.200% 不满足最小配筋要求所以取面积为As = p min*b*h = 0.200%*1000*120 = 240 mm 采取方案?8@200, 实配面积251 mm 23. Y 向上边支座钢筋1) 确定上边支座弯矩表中系数(丫G*q gk+丫Q*q q k)*Lo= 0.1131*(1.200*4.100+1.400*2.000)*3= 7.861 kN*m2) 确定计算系数a s = 丫o*M o y/( a 1*fc*b*ho*ho)=1.00*7.861 X 10 6/(1.00*11.9*1000*80*80) = 0.1033) 计算相对受压区高度E = 1 -sqrt(1- 2* a s) = 1 -sqrt(1-2*0.103) = 0.1094) 计算受拉钢筋面积As = a 1*fc*b*ho* E /fy = 1.000*11.9*1000*80*0.109/360= 289mm 25) 验算最小配筋率p = As/(b*h) = 289/(1000*120) = 0.241%p>p min = 0.200% 满足最小配筋要求采取方案?8@160, 实配面积314 mm 2七、跨中挠度计算:Mk ------- 按荷载效应的标准组合计算的弯矩值Mq ------- 按荷载效应的准永久组合计算的弯矩值1. 计算荷载效应Mk = Mgk + Mqk2= (0.0634+0.0307*0.200)*(4.100+2.000)*3 2 = 3.816 kN*mMq = Mgk+山q*Mqk2 = (0.0634+0.0307*0.200)*(4.100+1.0*2.000)*3 2 = 3.816 kN*m2. 计算受弯构件的短期刚度Bs1) 计算按荷载荷载效应的两种组合作用下,构件纵向受拉钢筋应力=3.816 X 10*0.87*80*251) = 218.438 N/mm=3.816 X 107(0.87*80*251) = 218.438 N/mm2) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率2矩形截面积: Ate = 0.5*b*h = 0.5*1000*120= 60000mm 2= 251/60000 = 0.418%3) 计算裂缝间纵向受拉钢筋应变不均匀系数如= 1.1-0.65*1.78/(0.418%*218.438) = -0.166因为如不能小于最小值0.2,所以取如k = 0.2= 1.1-0.65*1.78/(0.418%*218.438) = -0.166因为如不能小于最小值0.2,所以取如q = 0.24) 计算钢筋弹性模量与混凝土模量的比值aE54a E = Es/Ec = 2.0 X10 5/2.80 X104 = 7.1435) 计算受压翼缘面积与腹板有效面积的比值Y矩形截面,丫f=06) 计算纵向受拉钢筋配筋率pp = As/(b*ho)= 251/(1000*8 0) = 0.314%7) 计算受弯构件的短期刚度Bs2Bsk = Es*As*ho 2522.0 X 105*251*80 2/[1.15*-0.166+0.2+6*7.143*0.314%/(1+3.5*0.0)]22= 5.692 X102 kN*m2Bsq = Es*As*ho522.0X105*251*80 2/[1.15*-0.166+0.2+6*7.143*0.314%/(1+3.5*0.0)]22= 5.692 X102 kN*m23. 计算受弯构件的长期刚度B1) 确定考虑荷载长期效应组合对挠度影响增大影响系数92) 计算受弯构件的长期刚度B2 = 3.816/(3.816*(2.0- 1)+3.816)*5.692 X10 222= 2.846 X102 kN*m22= 5.692 X102/2.022= 2.846 X102 kN*m2B = min(Bk,Bq)= min(284.588,284.588)= 284.5884. 计算受弯构件挠度f max = f*(q gk+q qk)*Lo 4/B42=0.00677*(4.100+2.000)*3 72.846 X 102= 11.749mm5. 验算挠度挠度限值fo=Lo/200=3000/200=15.000mm fmax=11.749mn^fo=15.000mm,满足规范要求八、裂缝宽度验算:1. 跨中X 方向裂缝1) 计算荷载效应2Mx = 表中系数(q gk+^q qk)*Lo= (0.0634+0.0307*0.200)*(4.100+1.00*2.000)*3= 3.816 kN*m2) 光面钢筋, 所以取值v i=0.73) 因为C > 65,所以取C = 654) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力=3.816X106/(0.87*80*251)=218.438N/mm5) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积, Ate=0.5*b*h=0.5*1000*120=60000 mm 2=251/60000 = 0.0042因为p te=0.0042 < 0.01, 所以让p te=0.016) 计算裂缝间纵向受拉钢筋应变不均匀系数如=1.1-0.65*1.780/(0.0100*218.438)=0.5707) 计算单位面积钢筋根数nn=1000/dist = 1000/200=58) 计算受拉区纵向钢筋的等效直径d eq2d eq= ( En i*d i )/( ”n i*V i*d i)=5*8*8/(5*0.7*8)=119) 计算最大裂缝宽度=1.9*0.570*218.438/2.0 X 10 5*(1.9*20+0.08*11/0.0100)=0.1532mm< 0.30, 满足规范要求2. 跨中Y方向裂缝1) 计算荷载效应My = 表中系数(q gk+^q qk)*Lo= (0.0307+0.0634*0.200)*(4.100+1.00*2.000)*3= 2.380 kN*m2) 光面钢筋, 所以取值V i=0.73) 因为C > 65,所以取C = 654) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力=2.380X106/(0.87*80*251)=136.228N/mm5) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*120=60000 mm 2 =251/60000 = 0.0042因为p te=0.0042 < 0.01, 所以让p te=0.016) 计算裂缝间纵向受拉钢筋应变不均匀系数如=1.1-0.65*1.780/(0.0100*136.228)=0.2517) 计算单位面积钢筋根数nn=1000/dist = 1000/200=58) 计算受拉区纵向钢筋的等效直径d eq2d eq= ( En i*d i )/( ”n i*V i*d i)=5*8*8/(5*0.7*8)=119) 计算最大裂缝宽度5 =1.9*0.251*136.228/2.0 X 105*(1.9*20+0.08*11/0.0100)=0.0420mm< 0.30, 满足规范要求3. 支座上方向裂缝1) 计算荷载效应M o y =表中系数((q gk+^q qk)*Lo 2)2 = 0.1131*(4.100+1.00*2.000)*3 2= 6.211 kN*m2) 光面钢筋, 所以取值v i =0.73) 因为C > 65 ,所以取C = 654) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力=6.211 X 106/(0.87*80*314)=284.215N/mm5) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率2矩形截面积,Ate=0.5*b*h=0.5*1000*120=60000 mm 2 =314/60000 = 0.0052因为p te=0.0052 < 0.01, 所以让p te=0.016) 计算裂缝间纵向受拉钢筋应变不均匀系数如=1.1-0.65*1.780/(0.0100*284.215)=0.6937) 计算单位面积钢筋根数nn=1000/dist = 1000/160=68) 计算受拉区纵向钢筋的等效直径d eq2d eq= ( En i*d i )/( En i*V i*d i)=6*8*8/(6*0.7*8)=119) 计算最大裂缝宽度5=1.9*0.693*284.215/2.0 X10 5*(1.9*20+0.08*11/0.0100)0.2421mm < 0.30, 满足规范要求。
双向板计算

(一)双向板按弹性理论的计算方法1.单跨双向板的弯矩计算为便于应用,单跨双向板按弹性理论计算,已编制成弯矩系数表,供设计者查用。
在教材的附表中,列出了均布荷载作用下,六种不同支承情况的双向板弯矩系数表。
板的弯矩可按下列公式计算:M = 弯矩系数×(g+p)l x2式中M 为跨中或支座单位板宽内的弯矩(kN·m/m);g、p为板上恒载及活载设计值(kN/m2);l x为板的跨度(m)。
错误!未找到引用源。
错误!未找到引用源。
2.多跨连续双向板的弯矩计算(1)跨中弯矩双向板跨中弯矩的最不利活载位置图多跨连续双向板也需要考虑活载的最不利位置。
当求某跨跨中最大弯矩时,应在该跨布置活载,并在其前后左右每隔一区格布置活载,形成如上图(a)所示棋盘格式布置。
图(b)为A-A剖面中第2、第4区格板跨中弯矩的最不利活载位置。
为了能利用单跨双向板的弯矩系数表,可将图(b)的活载分解为图(c)的对称荷载情况和图(d)的反对称荷载情况,将图(c)与(d)叠加即为与图(b)等效的活载分布。
在对称荷载作用下,板在中间支座处的转角很小,可近似地认为转角为零,中间支座均可视为固定支座。
因此,所有中间区格均可按四边固定的单跨双向板计算;如边支座为简支,则边区格按三边固定、一边简支的单跨双向板计算;角区格按两邻边固定、两邻边简支的单跨双向板计算。
在反对称荷载作用下,板在中间支座处转角方向一致,大小相等接近于简支板的转角,所有中间支座均可视为简支支座。
因此,每个区格均可按四边简支的单跨双向板计算。
将上述两种荷载作用下求得的弯矩叠加,即为在棋盘式活载不利位置下板的跨中最大弯矩。
错误!未找到引用源。
错误!未找到引用源。
(2)支座弯矩支座弯矩的活载不利位置,应在该支座两侧区格内布置活载,然后再隔跨布置,考虑到隔跨活载的影响很小,可假定板上所有区格均满布荷载(g+p)时得出的支座弯矩,即为支座的最大弯矩。
这样,所有中间支座均可视为固定支座,边支座则按实际情况考虑,因此可直接由单跨双向板的弯矩系数表查得弯矩系数,计算支座弯距。
双向板按弹性理论的计算方法

(一)双向板按弹性理论的计算方法1.单跨双向板的弯矩计算为便于应用,单跨双向板按弹性理论计算,已编制成弯矩系数表,供设计者查用。
在教材的附表中,列出了均布荷载作用下,六种不同支承情况的双向板弯矩系数表。
板的弯矩可按下列公式计算:M = 弯矩系数×(g+p)l x2{M=αmp(g+p)l x2 αmp为单向连续板(αmb为连续梁)考虑塑性内力重分布的弯矩系数。
}式中M 为跨中或支座单位板宽内的弯矩(kN·m/m);g、p为板上恒载及活载设计值(kN/m2);l x为板的计算跨度(m)。
2.多跨连续双向板的弯矩计算(1)跨中弯矩双向板跨中弯矩的最不利活载位置图多跨连续双向板也需要考虑活载的最不利位置。
当求某跨跨中最大弯矩时,应在该跨布置活载,并在其前后左右每隔一区格布置活载,形成如上图(a)所示棋盘格式布置。
图(b)为A-A剖面中第2、第4区格板跨中弯矩的最不利活载位置。
为了能利用单跨双向板的弯矩系数表,可将图(b)的活载分解为图(c)的对称荷载情况和图(d)的反对称荷载情况,将图(c)与(d)叠加即为与图(b)等效的活载分布。
在对称荷载作用下,板在中间支座处的转角很小,可近似地认为转角为零,中间支座均可视为固定支座。
因此,所有中间区格均可按四边固定的单跨双向板计算;如边支座为简支,则边区格按三边固定、一边简支的单跨双向板计算;角区格按两邻边固定、两邻边简支的单跨双向板计算。
在反对称荷载作用下,板在中间支座处转角方向一致,大小相等接近于简支板的转角,所有中间支座均可视为简支支座。
因此,每个区格均可按四边简支的单跨双向板计算。
将上述两种荷载作用下求得的弯矩叠加,即为在棋盘式活载不利位置下板的跨中最大弯矩。
(2)支座弯矩支座弯矩的活载不利位置,应在该支座两侧区格内布置活载,然后再隔跨布置,考虑到隔跨活载的影响很小,可假定板上所有区格均满布荷载(g+p)时得出的支座弯矩,即为支座的最大弯矩。
(整理)(一)双向板按弹性理论的计算方法.

(一)双向板按弹性理论的计算方法1.单跨双向板的弯矩计算为便于应用,单跨双向板按弹性理论计算,已编制成弯矩系数表,供设计者查用。
在教材的附表中,列出了均布荷载作用下,六种不同支承情况的双向板弯矩系数表。
板的弯矩可按下列公式计算:M = 弯矩系数×(g+p)l x2式中M 为跨中或支座单位板宽内的弯矩(kN·m/m);g、p为板上恒载及活载设计值(kN/m2);l x为板的跨度(m)。
显示更多隐藏2.多跨连续双向板的弯矩计算(1)跨中弯矩双向板跨中弯矩的最不利活载位置图多跨连续双向板也需要考虑活载的最不利位置。
当求某跨跨中最大弯矩时,应在该跨布置活载,并在其前后左右每隔一区格布置活载,形成如上图(a)所示棋盘格式布置。
图(b)为A-A剖面中第2、第4区格板跨中弯矩的最不利活载位置。
为了能利用单跨双向板的弯矩系数表,可将图(b)的活载分解为图(c)的对称荷载情况和图(d)的反对称荷载情况,将图(c)与(d)叠加即为与图(b)等效的活载分布。
在对称荷载作用下,板在中间支座处的转角很小,可近似地认为转角为零,中间支座均可视为固定支座。
因此,所有中间区格均可按四边固定的单跨双向板计算;如边支座为简支,则边区格按三边固定、一边简支的单跨双向板计算;角区格按两邻边固定、两邻边简支的单跨双向板计算。
在反对称荷载作用下,板在中间支座处转角方向一致,大小相等接近于简支板的转角,所有中间支座均可视为简支支座。
因此,每个区格均可按四边简支的单跨双向板计算。
将上述两种荷载作用下求得的弯矩叠加,即为在棋盘式活载不利位置下板的跨中最大弯矩。
(2)支座弯矩支座弯矩的活载不利位置,应在该支座两侧区格内布置活载,然后再隔跨布置,考虑到隔跨活载的影响很小,可假定板上所有区格均满布荷载(g+p)时得出的支座弯矩,即为支座的最大弯矩。
这样,所有中间支座均可视为固定支座,边支座则按实际情况考虑,因此可直接由单跨双向板的弯矩系数表查得弯矩系数,计算支座弯距。
双向板配筋计算
双向板配筋计算双向板是指钢筋混凝土板的两个方向都需要配筋的一种板,也就是需要在水平和竖直方向同时进行配筋。
在建筑工程中,双向板的使用非常普遍,因为它可以承受更大的荷载和分布载荷。
但是,双向板的设计和计算也比较复杂,需要进行严密的计算和分析。
本文将介绍双向板配筋计算的相关知识。
一、双向板的结构特点双向板是一种承载能力强、刚度高、变形小的板,它的结构特点主要有以下几点:1. 双向板的厚度相对较小,一般在100mm以下,但是它的面积比较大,通常用于大跨度的建筑结构中。
2. 双向板需要在两个方向上同时进行配筋,以保证其在水平和竖直方向上的承载能力。
3. 双向板一般采用钢筋混凝土结构,其钢筋主要分布在两个方向上,以增强板的承载能力。
二、双向板的配筋计算双向板的配筋计算一般分为以下几个步骤:1. 确定板的几何尺寸和荷载首先需要确定板的几何尺寸和荷载,包括板的长度、宽度、厚度和所承受的荷载。
这些参数将直接影响到双向板的承载能力和配筋量。
2. 确定板的截面特性根据板的几何尺寸和荷载,可以计算出板的截面特性,包括面积、惯性矩、受拉区高度和压力区高度等。
这些参数将用于后续的配筋计算。
3. 计算受拉区和压力区的面积根据板的截面特性,可以计算出受拉区和压力区的面积,以确定钢筋的布置方式和数量。
4. 确定钢筋的布置方式和数量根据受拉区和压力区的面积,可以确定钢筋的布置方式和数量。
一般来说,双向板的钢筋需要按照正交方向布置,以保证其在两个方向上的承载能力。
5. 检查钢筋的受力状态确定钢筋的布置方式和数量后,需要进行钢筋的受力状态检查,以保证钢筋的受力状态符合设计要求。
检查内容主要包括钢筋的受拉和受压状态、钢筋的弯曲和剪切状态等。
6. 进行验算和调整最后需要进行验算和调整,以保证双向板的承载能力和配筋量符合设计要求。
如果发现问题,需要进行相应的调整和优化。
三、双向板配筋计算注意事项在进行双向板配筋计算时,需要注意以下几点:1. 双向板的配筋计算需要进行详细的分析和计算,不能简单粗暴地进行估算。
双向板的弹性计算法
双向板的弹性计算法双向板的弹性计算法双向板的受力特点前已述及。
双向板常用于工业建筑楼盖、公共建筑门厅部分以及横隔墙较多的民用房屋。
当民用房屋横隔墙间距较小时(如住宅),可将板直接支承于四周的砖墙上,以减少楼盖的结构高度。
1.双向板的计算双向板的内力计算有弹性计算法和塑性计算法两种,本书仅介绍双向板内力的弹性计算法。
弹性计算法是以弹性薄板理论为依据而进行计算的一种方法,由于这种方法内力分析比较复杂,为简化计算,通常是直接应用根据弹性薄板理论编制的弯矩系数表(附表)进行计算。
(1)单跨双向板的计算单跨双向板按其四边支承情况的不同,在楼盖中常会遇到如下六种情况:四边简支(图1a);一边固定三边简支(图1b);两对边固定、两对边简支(图1c);两邻边固定、两邻边简支(图1d);三边固定、一边简支(图7.1.38e);四边固定(图7.1.38f)。
(a)(b)(c)(d)(e)(f)图1 双向板的六种四边支承情况根据不同支承情况,可从附表中查出弯矩系数,即可求得弯矩:M=表中系数×ql2(1)式中M ——跨中或支座单位板宽内的弯矩;q ——均布荷载(kN /m2)l ——板的较小跨度(m)。
附表中给出了图1所示六种边界条件的单跨板在均布荷载作用下的挠度系数、支座弯矩系数以及泊松比μ =0时的跨中弯矩系数。
钢筋混凝土结构的泊松比μ=1/6,故对跨中弯矩应按下式计算:M x(μ )=M X +μM y(2)M y (μ)=M y+μM X (3)式中M X、M y——按附表查得的板跨中弯矩系数计算得到的跨中弯矩值。
【例1】某砖混结构卫生间的现浇板l1×l2=3600mm×6000mm,四周与圈梁整体现浇,现浇板厚h=90mm,墙体厚240 mm,板承受恒载设计值g=3.6KN/m,活载设计值q=2.8KN/m,采用C20砼,受力钢筋HPB235。
试确定该现浇板受力钢筋用量。
【解】长边与短边之比l2/l1=6000/3600=1.67<2,按双向板计算。
双向板设计与计算
当求某区格跨中最大弯矩时,其活荷载的最不利布置,如图3-49所示即 在该区格及其左右前后每隔一区格布置活荷载,通常称为棋盘形荷载布置。
,
②荷载等效
将板上永久荷载g和活荷载q分成为对称荷载和反对称荷载两 种情况,取
对称荷载
g’=g+q/2
反对称荷载
q’=±q/2
,③对称型荷载作用下
近似认为板的中间支座处转角为零
3 折线形楼梯的计算与构造要点 (1)计算要点 为满足建筑使用要求,在房屋中有时需要采用折线形楼梯。 折线形楼梯梁(板)的计算与普通梁(板)式楼梯一样,一 般将斜梯段上的荷载化为沿水平长度方向分布的荷载,然后再按
简支梁计算 M max及Vmax 值。
(2)构造要求 由于折线形楼梯在梁(板)曲折处形成内折角,在配筋时, 若钢筋沿内折角连续配置,则此处受拉钢筋将产生较大的向外的 合力,可能使该处砼保护层崩落,钢筋被拉出而失去作用(图 7.3.19a)。 因此,在内折角处,配筋时应采取将钢筋断开并分别予以锚 固的措施(见图 7.3.19b)。在梁的内折角处,箍筋应适应加密。
M max
1 (g 8
q)l
2 0
g 、q ——作用于梯段板上的沿水平投影方向的
恒载及活载设计值;
l0 ——梯段板的计算跨度。
简支斜板(梁)在竖向均布荷载作用下的最大剪力为:
Vmax
双向板 - 计算步骤
双向板 - 计算步骤双向板计算LB-1矩形板计算一、构件编号: LB-1 二、示意图三、依据规范《建筑结构荷载规范》 GB50009-2001 《混凝土结构设计规范》 GB50010-2021 四、计算信息 1.几何参数计算跨度: Lx = 3000 mm; Ly = 4600 mm 板厚: h = 120 mm 2.材料信息混凝土等级: C25 fc=11.9N/mm2 ft=1.27N/mm2 ftk=1.78N/mm2 钢筋种类: HRB400 fy = 360 N/mm2 Es = 2.0×105 N/mm2最小配筋率: ρ= 0.200%纵向受拉钢筋合力点至近边距离: as = 40mm 保护层厚度: c = 20mm 3.荷载信息(均布荷载)永久荷载分项系数: γG = 1.200 可变荷载分项系数: γQ = 1.400 准永久值系数: ψq = 1.000永久荷载标准值: qgk = 4.100kN/m2可变荷载标准值: qqk = 2.000kN/m24.计算方法:弹性板5.边界条件(上端/下端/左端/右端):固定/简支/简支/简支6.设计参数结构重要性系数: γo = 1.00 泊松比:μ = 0.200 五、计算参数:1.计算板的跨度: Lo = 3000 mmEc=2.80×104N/mm2第1页,共6页双向板计算2.计算板的有效高度: ho = h-as=120-40=80 mm六、配筋计算(lx/ly=3000/4600=0.652<2.000 所以按双向板计算): 1.X向底板钢筋1) 确定X向板底弯矩Mx = 表中系数(γG*qgk+γQ*qqk)*Lo2= (0.0634+0.0307*0.200)*(1.200*4.100+1.400*2.000)*32= 4.829 kN*m 2) 确定计算系数αs = γo*Mx/(α1*fc*b*ho*ho)= 1.00*4.829×106/(1.00*11.9*1000*80*80) = 0.0633) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.063) = 0.066 4) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*11.9*1000*80*0.066/360= 173mm25) 验算最小配筋率ρ = As/(b*h) = 173/(1000*120) = 0.144% ρ所以取面积为As = ρmin*b*h = 0.200%*1000*120 = 240 mm2采取方案?8@200, 实配面积251 mm2 2.Y向底板钢筋1) 确定Y向板底弯矩My = 表中系数(γG*qgk+γQ*qqk)*Lo2= (0.0307+0.0634*0.200)*(1.200*4.100+1.400*2.000)*32= 3.012 kN*m 2) 确定计算系数αs = γo*My/(α1*fc*b*ho*ho)= 1.00*3.012×106/(1.00*11.9*1000*80*80) = 0.0403) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.040) = 0.040 4) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*11.9*1000*80*0.040/360= 107mm25) 验算最小配筋率ρ = As/(b*h) = 107/(1000*120) = 0.089% ρ所以取面积为As = ρmin*b*h = 0.200%*1000*120 = 240 mm2采取方案?8@200, 实配面积251 mm2 3.Y向上边支座钢筋 1) 确定上边支座弯矩Moy = 表中系数(γG*qgk+γQ*qqk)*Lo2= 0.1131*(1.200*4.100+1.400*2.000)*32第2页,共6页双向板计算= 7.861 kN*m 2) 确定计算系数αs = γo*Moy/(α1*fc*b*ho*ho)= 1.00*7.861×106/(1.00*11.9*1000*80*80) = 0.1033) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.103) = 0.109 4) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*11.9*1000*80*0.109/360= 289mm25) 验算最小配筋率ρ = As/(b*h) = 289/(1000*120) = 0.241% ρ≥ρmin = 0.200% 满足最小配筋要求采取方案?8@160, 实配面积314 mm2 七、跨中挠度计算:Mk -------- 按荷载效应的标准组合计算的弯矩值 Mq -------- 按荷载效应的准永久组合计算的弯矩值 1.计算荷载效应 Mk = Mgk + Mqk= (0.0634+0.0307*0.200)*(4.100+2.000)*32= 3.816 kN*m Mq = Mgk+ψq*Mqk= (0.0634+0.0307*0.200)*(4.100+1.0*2.000)*32= 3.816 kN*m 2.计算受弯构件的短期刚度 Bs1) 计算按荷载荷载效应的两种组合作用下,构件纵向受拉钢筋应力σsk = Mk/(0.87*ho*As) 混规(7.1.4-3)= 3.816×106/(0.87*80*251) = 218.438 N/mm σsq = Mq/(0.87*ho*As) 混规(7.1.4-3)= 3.816×106/(0.87*80*251) = 218.438 N/mm2) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积: Ate = 0.5*b*h = 0.5*1000*120= 60000mm2ρte = As/Ate 混规(7.1.2-4) = 251/60000 = 0.418%3) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψk = 1.1-0.65*ftk/(ρte*σsk) 混规(7.1.2-2) = 1.1-0.65*1.78/(0.418%*218.438) = -0.166 因为ψ不能小于最小值0.2,所以取ψk = 0.2ψq = 1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2) = 1.1-0.65*1.78/(0.418%*218.438) = -0.166 因为ψ不能小于最小值0.2,所以取ψq = 0.2 4) 计算钢筋弹性模量与混凝土模量的比值αEαE = Es/Ec = 2.0×105/2.80×104= 7.143 5) 计算受压翼缘面积与腹板有效面积的比值γf 矩形截面,γf=06) 计算纵向受拉钢筋配筋率ρ第3页,共6页双向板计算ρ = As/(b*ho)= 251/(1000*80) = 0.314% 7) 计算受弯构件的短期刚度 Bs2Bsk = Es*As*ho/[1.15ψk+0.2+6*αE*ρ/(1+ 3.5γf')](混规(7.2.3-1))52= 2.0×10*251*80/[1.15*-0.166+0.2+6*7.143*0.314%/(1+3.5*0.0)]22= 5.692×10 kN*m2Bsq = Es*As*ho/[1.15ψq+0.2+6*αE*ρ/(1+ 3.5γf')](混规(7.2.3-1))52= 2.0×10*251*80/[1.15*-0.166+0.2+6*7.143*0.314%/(1+3.5*0.0)]= 5.692×102 kN*m23.计算受弯构件的长期刚度B1) 确定考虑荷载长期效应组合对挠度影响增大影响系数θ当ρ'=0时,θ=2.0 混规(7.2.5) 2) 计算受弯构件的长期刚度 BBk = Mk/(Mq*(θ-1)+Mk)*Bs (混规(7.2.2-1))= 3.816/(3.816*(2.0-1)+3.816)*5.692×102= 2.846×102 kN*m2Bq = Bsq/θ (混规(7.2.2-2))= 5.692×102/2.0= 2.846×102 kN*m2B = min(Bk,Bq)= min(284.588,284.588) = 284.588 4.计算受弯构件挠度f = f*(q4maxgk+qqk)*Lo/B= 0.00677*(4.100+2.000)*34/2.846×102= 11.749mm 5.验算挠度挠度限值fo=Lo/200=3000/200=15.000mmfmax=11.749mm≤fo=15.000mm,满足规范要求! 八、裂缝宽度验算: 1.跨中X方向裂缝 1) 计算荷载效应Mx = 表中系数(qgk+ψqqk)*Lo2= (0.0634+0.0307*0.200)*(4.100+1.00*2.000)*32= 3.816 kN*m2) 光面钢筋,所以取值vi=0.7 3) 因为C > 65,所以取C = 654) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=3.816×106/(0.87*80*251) =218.438N/mm5) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*120=60000 mm2ρte=As/Ate 混规(7.1.2-4) =251/60000 = 0.0042第4页,共6页双向板计算因为ρte=0.0042 < 0.01,所以让ρte=0.01 6) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2) =1.1-0.65*1.780/(0.0100*218.438) =0.5707) 计算单位面积钢筋根数n n=1000/dist = 1000/200 =58) 计算受拉区纵向钢筋的等效直径deqd2eq= (∑ni*di)/(∑ni*vi*di) =5*8*8/(5*0.7*8)=11 9) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1)=1.9*0.570*218.438/2.0×105*(1.9*20+0.08*11/0.0100) =0.1532mm ≤ 0.30, 满足规范要求2.跨中Y方向裂缝 1) 计算荷载效应My = 表中系数(qgk+ψqqk)*Lo2= (0.0307+0.0634*0.200)*(4.100+1.00*2.000)*32= 2.380 kN*m2) 光面钢筋,所以取值vi=0.7 3) 因为C > 65,所以取C = 654) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=2.380×106/(0.87*80*251) =136.228N/mm5) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*120=60000 mm2ρte=As/Ate 混规(7.1.2-4) =251/60000 = 0.0042因为ρte=0.0042 < 0.01,所以让ρte=0.01 6) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ft k/(ρte*σsq) 混规(7.1.2-2) =1.1-0.65*1.780/(0.0100*136.228) =0.2517) 计算单位面积钢筋根数n n=1000/dist = 1000/200 =58) 计算受拉区纵向钢筋的等效直径deqd= (∑n2eqi*di)/(∑ni*vi*di) =5*8*8/(5*0.7*8)=11 9) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1)=1.9*0.251*136.228/2.0×105*(1.9*20+0.08*11/0.0100)第5页,共6页双向板计算=0.0420mm ≤ 0.30, 满足规范要求 3.支座上方向裂缝 1) 计算荷载效应Moy = 表中系数((qgk+ψqqk)*Lo2)= 0.1131*(4.100+1.00*2.000)*32= 6.211 kN*m2) 光面钢筋,所以取值vi=0.7 3) 因为C > 65,所以取C = 654) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=6.211×106/(0.87*80*314) =284.215N/mm5) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*120=60000 mm2ρte=As/Ate 混规(7.1.2-4) =314/60000 = 0.0052因为ρte=0.0052 < 0.01,所以让ρte=0.01 6) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2) =1.1-0.65*1.780/(0.0100*284.215) =0.6937) 计算单位面积钢筋根数n n=1000/dist = 1000/160 =68) 计算受拉区纵向钢筋的等效直径deqd*d2eq= (∑nii)/(∑ni*vi*di) =6*8*8/(6*0.7*8)=11 9) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1)=1.9*0.693*284.215/2.0×105*(1.9*20+0.08*11/0.0100) =0.2421mm ≤ 0.30, 满足规范要求第6页,共6页感谢您的阅读,祝您生活愉快。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作用在板上的荷载
永久荷载标准值:
0.60(kN/m2)水泥砂浆面层自重= 厚度×20
6.25(kN/m2)钢筋混凝土板自重= h×25
0.34(kN/m2)混合砂浆天棚抹灰自重= 厚度×17
qGk= 6.85(kN/m2)永久荷载标准值qGk
可变荷载标准值:
qQk= 2.50(kN/m2)可变荷载标准值qQk
基本组合(支座最大负弯矩):
qg1=11.72(kN/m2)可变荷载效应组合qg1=1.2qGk+1.4qQk
qg2=11.70(kN/m2)永久荷载效应组合qg2=1.35qGk+1.4*0.7qQk qg=11.72(kN/m2)qg=max(qg1,qg2)
基本组合(跨中最大正弯矩):
g1=9.97(kN/m2)可变荷载效应组合g1=1.2qGk+1.4qQk/2
g2=10.47(kN/m2)永久荷载效应组合g2=1.35qGk+1.4*0.7qQk/2 q1= 1.75(kN/m2)q1=1.4qQk/2
q2= 1.23(kN/m2)q2=1.4*0.7qQk/2
g=10.47(kN/m2)g=max(g1,g2)
q= 1.75(kN/m2)q=max(q1,q2)
标准组合(支座最大负弯矩):
qgKK9.35(kN/m2)qgKK=qGk+qQk
标准组合(跨中最大正弯矩):
gKK=8.10(kN/m2)gKK=qGk+qQk/2
qKK= 1.25(kN/m2)qKK=qQk/2
准永久组合(支座最大负弯矩):
qgQQ=8.10(kN/m2)qgQQ=qGk+0.5qQk
准永久组合(跨中最大正弯矩):
gQQ=7.48(kN/m2)gQQ=qGK+0.5qQk/2
qQQ=0.63(kN/m2)qQQ=0.5qQk/2
永久荷载标准值:
由板传-2
α^2
+α^3)×(qGk×lcy)=
15.64(kN/m)由板传
长边梁x×(hx -h)×25/1000000= 2.63(kN/m)短边梁长边梁0×(hx -h)×20/1000000=
0.28(kN/m)短边梁qxGk =18.26(kN/m)
可变荷载标准值:由板传来
qxQk =(1-2α^2+α^3)×(qQk ×lcy)= 5.71(kN/m)基本组合:
.
由可变荷载效应控制qgx1=1.2qxGk+1.4qxQk =29.91(kN/m)由永久荷载效应控制
qgx2=1.35qxGk+1.4*0.7qxQk =
30.25(kN/m)qgx =max(qgx1,qgx2)=
30.25(kN/m)标准组合:qgxK =qxGk+qxQk =23.97(kN/m)准永久组合:
qgxQ =qxGk+0.5qxQk =
21.12(kN/m)
作用在长边梁上的荷载
作用在短边梁上的荷载
永久荷载标准值:
(5/8)×(qGk×lcy)=12.84(kN/m)
y×(hy-h)×25/1000000= 5.63(kN/m)
0×(hy-h)×20/1000000=0.60(kN/m)
qyGk=18.47(kN/m)
可变荷载标准值:
由板传来qyQk=(5/8)×(qQk×lcy)= 4.69(kN/m)
基本组合:.
由可变荷载效应控制qgy1=1.2qyGk+1.4qyQk=28.73(kN/m)由永久荷载效应控制qgy2=1.35qyGk+1.4*0.7qyQk=29.53(kN/m)
qgy=max(qgy1,qgy2)=29.53(kN/m)标准组合:qgyK=qyGk+qyQk =23.16(kN/m)准永久组合:qgyQ=qyGk+0.5qyQk=20.81(kN/m)。
