空间几何体试题和答案解析
高一数学空间几何体的表面积与体积试题答案及解析

高一数学空间几何体的表面积与体积试题答案及解析1. 已知正方体的棱长为1,且其顶点都在一个球面上,则该球的表面积为( ) A .π B .2π C .3π D .4π【答案】C.【解析】正方体的对角线长为外接球的直径,因此,,因此.【考点】球的表面积公式.2. 如图,在四边形ABCD 中,∠DAB =90°,∠ADC =135°,AB =5,CD =2,AD =2,求四边形ABCD 绕AD 旋转一周所成几何体的表面积及体积.【答案】S 表面=(60+4)π.V =π.【解析】该图形旋转后是一个圆台除去一个倒放的圆锥, 则S 表面=S 下底面+S 台侧面+S 锥侧面 , 设圆台上,下地面半径是r 1,r 2,则 S 表面=π×r 22+π×(r 2+r 1)×5+π×r 1×CDV =V 台-V 锥=π(+r 1r 2+)AE -πr 2DE ,将数据代入计算即可。
试题解析:如图,设圆台上,下地面半径是r 1,r 2,过C 点作CF ⊥AB ,由∠ADC =135°,CE ⊥AD, CD=2得∠EDC =45°,r 1=" CE=" 2,则CF=4,BF=3,CF ⊥AB ,得BC=5,r 2=" AB=" 5, ∴S 表面=S 下底面+S 台侧面+S 锥侧面 =π×r 22+π×(r 2+r 1)×5+π×r 1×CD =π×52+π×(2+5)×5+π×2×2 =(60+4)π. V =V 台-V 锥=π(+r 1r 2+)AE -πDE =π(+2×5+)4-π×2=π.【考点】圆台,圆锥的表面积和体积.3.如图,在长方体ABCD—A1B1C1D1中,AB=2,BB1=BC=1,E为D1C1的中点,连结ED,EC,EB和DB.(1)求证:ED⊥平面EBC;(2)求三棱锥E-DBC的体积.【答案】(1)见解析;(2)【解析】(1)易得△DD1E为等腰直角三角形DE⊥EC,BC⊥平面 BC⊥DE,所以DE⊥平面EBC平面DEB⊥平面EBC.(2)需要做辅助线,取CD中点M,连接EM∥,DCB(这个证明很关键),然后根据公式.试题解析:(1)在长方体ABCD-A1B1C1D1中,AB=2,BB1=BC=1,E为D1C1的中点.∴△DD1E为等腰直角三角形,∠D1ED=45°.同理∠C1EC=45°.∴,即DE⊥EC.在长方体ABCD-中,BC⊥平面,又DE平面,∴BC⊥DE.又,∴DE⊥平面EBC.又∴平面DEB⊥平面EBC.(2)取CD中点M,连接EM,E为D1C1的中点,∥,且,又DCB.【考点】线面垂直,三棱锥的体积.4.设甲、乙两个圆柱的底面积分别为,体积分别为,若它们的侧面积相等,且,则的值是.【答案】【解析】设甲、乙两个圆柱的底面半径为,母线长,由于侧面积相等,,,,.【考点】圆柱的体积公式应用.5.如果两个球的体积之比为8:27,那么两个球的表面积之比为()A.8:27B.2:3C.4:9D.2:9【答案】C【解析】由题意,故选C【考点】球的体积和表面积6.棱长为4的正方体的八个顶点都在同一个球面上,则此球的表面积为_____________.【答案】48【解析】正方体的外接球的球心为正方体的中心,球的直径为正方体的对角线,所以球的表面积为【考点】正方体的外接球7.如图是从上下底面处在水平状态下的棱长为的正方体中分离出来的.有如下结论:①在图中的度数和它表示的角的真实度数都是;②;③与所成的角是;④若,则用图示中这样一个装置盛水,最多能盛的水.其中正确的结论是(请填上你所有认为正确结论的序号).【答案】①④【解析】①∵在正视图的等腰直角中,在图中的度数和它表示的角的真实度数都是,故①正确;②补全正方体如图所示:连接.∵,∴是正三角形,故.而==,故②错;③连接、,∵,∴是正三角形,所以与所成的角是,故③错;④用图示中这样一个装置来盛水,那么盛最多体积的水时应是三棱锥的体积.又===,故④正确,故填①④.【考点】1、正方体的性质;2、异面直线所成角;3、三棱锥的体积.8.已知一个正三棱锥的三条侧棱两两垂直且相等,底面边长为,则该三棱锥的外接球的表面积是()A.B.C.D.【答案】A【解析】设该正三棱锥为,依题意两两垂直且,所以,且该正三棱锥的外接球与以为邻边的正方体的外接球是相同的,正方体的边长为,体对角线长为,故球的半径为,所以球的表面积为,故选A.【考点】1.三棱锥的外接球;2.球的表面积公式.9.如图,已知直三棱柱中,,,,D为BC的中点.(1)求证:∥面;(2)求三棱锥的体积.【答案】(1)略(2)【解析】(1)连接交于点O,连接OD,在中可根据中位线证得∥,再根据线面平行的性质定理可证得∥面。
高三数学空间几何体的三视图与直观图试题答案及解析
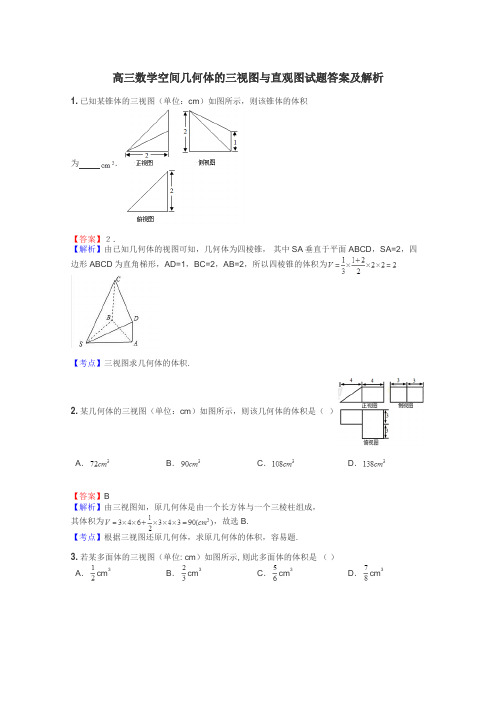
高三数学空间几何体的三视图与直观图试题答案及解析1.已知某锥体的三视图(单位:cm)如图所示,则该锥体的体积为.【答案】2.【解析】由已知几何体的视图可知,几何体为四棱锥,其中SA垂直于平面ABCD,SA=2,四边形ABCD为直角梯形,AD=1,BC=2,AB=2,所以四棱锥的体积为【考点】三视图求几何体的体积.2.某几何体的三视图(单位:cm)如图所示,则该几何体的体积是()A.B.C.D.【答案】B【解析】由三视图知,原几何体是由一个长方体与一个三棱柱组成,其体积为,故选B.【考点】根据三视图还原几何体,求原几何体的体积,容易题.3.若某多面体的三视图(单位: cm)如图所示, 则此多面体的体积是()A.cm3B.cm3C.cm3D.cm3【答案】C【解析】由三视图可得,该几何体相当于一个正方体切去一个三个侧棱长为1的三棱锥.所以该几何体的体积为.故选C.【考点】1.三视图.2.空间想象力.3.几何体的体积.4. (2014·孝感模拟)一个几何体的三视图如图所示,其中俯视图与侧视图均为半径是2的圆,则这个几何体的表面积是( )A.16πB.14πC.12πD.8π【答案】A【解析】由三视图可知,该几何体是球挖去半球.其中两个半圆的面积为π×22=4π.个球的表面积为×4π×22=12π,所以这个几何体的表面积是12π+4π=16π.5.如图,某几何体的三视图都是等腰直角三角形,则几何体的体积是()A.8B.7C.9D.6【答案】C【解析】由三视图可知,几何体是底面为等腰直角三角形,有一侧棱与底面垂直(垂足在非直角处)的三棱锥,其底面面积为×6×3=9,三棱锥的高为3,所以三棱锥的体积=×9×3=9.6.已知某几何体的三视图(如图),正视图和侧视图均为两个相等的等边三角形,府视图为正方形,则几何体的体积为()A.B.4C.9D.9【答案】C【解析】由三视图可知,几何体由两个同底之正四棱锥组成所以其体积为V=2××32×3×=9 7.一空间几何体的三视图如图所示,该几何体的体积为12π+,则正视图中x的值为( )A.5B.4C.3D.2【答案】C【解析】三视图,由正四棱锥和圆柱组成,故选C.8.如图,一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积为()A.1B.2C.3D.4【答案】B【解析】由题意,棱锥的高为,底面面积为,∴.【考点】三视图,体积.9.某几何体的三视图如题(6)所示,其侧视图是一个边长为1的等边三角形,俯视图是两个正三角形拼成的菱形,则这个几何体的体积为()A.1B.C.D.【答案】C【解析】这是由两个三棱锥拼成的几何体,其体积为.选C.【考点】三视图及几何体的体积.10.―个几何体的三视图如图所示(单位:),则该几何体的体积为.【答案】18+9【解析】由三视图可知,此几何体为两个相切的球上方放了一个长方体组成的组合体,所以其体积为:V=3×6×1+2××=18+911.一个空间几何体的三视图如图所示,该几何体的表面积为__________.【答案】152【解析】几何体为一个三棱柱,底面为一个等腰三角形,底边长为6,底边上高为4,腰长为5.棱柱的高为8.因此表面积为【考点】三视图12.某三棱锥的三视图如图所示,则这个三棱锥的体积为;表面积为.【答案】;.【解析】由三视图知几何体如下图,为一个三棱锥,且三棱锥的一个侧面与底面垂直,底面三角形的一条边长为,该边上的高为,∴几何体的体积.它的表面积为.【考点】由三视图求面积、体积.13.已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是_______.【答案】【解析】由题意可得该几何体是一个三棱锥,体积.【考点】1.三视图的知识.2.立几中的线面关系.3.三棱锥的体积公式.14.一个空间几何体的三视图如图所示,其正视图、侧视图、俯视图均为等腰直角三角形,且直角边长都为1,则这个几何体的体积是【答案】【解析】由三视图,可知该几何体是三棱锥,并且侧棱,,,则该三棱锥的高是,底面三角形是直角三角形,所以这个几何体的体积==.【考点】由三视图求几何体的体积.15.一个几何体的三视图如图所示,则该机合体的体积为( )A.B.C.D.【答案】B【解析】分析可得该几何体是底面为菱形的四棱锥,则高底面面积,所以.故选B【考点】三视图四棱锥体积16.一个几何体的三视图如图所示,则该几何体的体积是【答案】【解析】通过三视图的观察可得,该几何体是一个四棱柱,底面是一个直角梯形,其上下底分别为2,3,梯形的高为2.四棱柱的高为2.所以几何体的体积为.【考点】1.三视图的知识.2.几何体的体积.3.空间想象力.17.某长方体被一个平面所截,得到的几何体的三视图如图所示,则这个几何体的体积为()A.4B.4C.6D.8【答案】D【解析】割补可得其体积为2×2×2=8.18.某几何体的三视图如图所示,则该几何体的体积是________.【答案】16π-16【解析】由三视图知,该几何体是由一个底面半径为2,高为4的圆柱内挖去一个底面边长为2,高为4的正四棱柱后剩下的部分,∴V=(π×22-22)×4=16π-16.19.已知正方体ABCD-A1B1C1D1,M为棱A1B1的中点,N为棱A1D1的中点.如图是该正方体被M,N,A所确定的平面和N,D,C1所确定的平面截去两个角后所得的几何体,则这个几何体的正视图为().【答案】B【解析】对于选项A,由于只是截去了两个角,此切割不可能使得正视图成为梯形.故A不对;对于B,正视图是正方形符合题意,线段AM的影子是一个实线段,相对面上的线段DC1的投影是正方形的对角线,由于从正面看不到,故应作成虚线,故选项B正确;对于C,正视图是正方形,符合题意,有两条实线存在于正面不符合实物图的结构,故不对;对于D,正视图是正方形,符合题意,其中的两条实线符合俯视图的特征,故D不对.20.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示,则该棱柱的体积为()A.B.C.D.6【答案】B【解析】由三视图知该直三棱柱高为4,底面正三角形的高为3,所以正三角形边长为6,所以V=×36×4=36.故选B.【考点】1.三视图;2.柱体体积计算.21.某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为的扇形,则该几何体的体积为()A.B.C.D.【答案】D【解析】由题意知道,该几何体体积是圆柱体积的,即.【考点】1、三视图;2、几何体体积.22.右图是一个几何体的三视图,其中正视图和侧视图都是一个两底长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是( )A.B.C.D.【答案】B【解析】由三视图可得该几何体是一个圆台,其两底直径分别为2和4,母线长为4,所以该几何体的侧面积是,选B..【考点】三视图,圆台的侧面积.23.如图是一个组合几何体的三视图,则该几何体的体积是 .A.B.C.D.【答案】A【解析】由三视图还原可知该几何体是一个组合体,下面是一个半径为4,高为8的圆柱,,上面是一个三棱柱,故所求体积为.【考点】三视图,圆柱、三棱柱的体积公式.24.已知一个几何体的三视图如图所示,则该几何体的体积为___________【答案】【解析】该几何体为圆柱中挖去半个球而得的组合体,其体积为.【考点】三视图.25.一个几何体的三视图如图所示(单位长度:),俯视图中圆与四边形相切,且该几何体的体积为,则该几何体的高为 .【答案】【解析】由如图所示的几何体的三视图知:这个几何体是一个半径为的球和一个直四棱柱的结合体,且这个直四棱柱的底面是对角线分别为和的棱形,这个直四棱柱的高为,∴这个几何体的体积:V=,解得h=.【考点】1.三视图;2.几何体的面积和体积26.一个几何体的三视图如图所示,则该几何体的直观图可以是()【答案】D【解析】通过三视图的俯视图可知,该几何体是由两个旋转体组成,故选D.【考点】1.三视图的应用.27.如图为一个几何体的三视图正视图和侧视图均为矩形,俯视图中曲线部分为半圆,尺寸如图所示,则该几何体的表面积为()A.B.C.D.【答案】D【解析】由三视图可知,这是一个由半个圆柱和一个三棱柱构成的组合体,这个组合体仍为一个柱体。
高考数学空间几何体练习题及答案解析

高考数学空间几何体练习题一、选择题1.如图,设地球半径为,点、在赤道上,为地心,点在北纬60°的纬线(为其圆心)上,且点、、、共面,若=90°,则异面直线与所成角的余弦值为A.B.C.D.2.已知球的半径为2,相互垂直的两个平面分别截球面得两个圆.若两圆的公共弦长为2,则两圆的圆心距等于()A.1 B.C.D.23.若三棱柱的一个侧面是边长为2的正方形,另外两个侧面都是有一个内角为的菱形,则该棱柱的体积等于( )(A)(B)(C)(D)4.如图,动点在正方体的对角线上.过点作垂直于平面的直线,与正方体表面相交于.设,,则函数的图象大致是()5. 设分别是中所对边的边长,则直线与的位置关系是()A.平行B.垂直C.重合D.相交但不垂直6. 异面直线a,b成80o角,点P是a,b外的一个定点,若过P点有且仅有2条直线与a,b所成的角相等且等于θ,则θ属于集合( )A.{θ|0o<θ<40o} B.{θ|40o<θ<50o} C.{θ|40o<θ<90o} D.{θ|50o<θ<90o}7.在二面角的两个面内,分别有直线a,b,它们与棱l都不垂直,则()A .当该二面角是直二面角时,可能a//b ,也可能a ⊥bB .当该二面角是直二面角时,可能a//b ,但不可能a ⊥bC .当该二面角不是直二面角时,可能a//b ,但不可能a ⊥bD .当该二面角不是直二面角时,不可能a//b ,也不可能a ⊥b8. 在正方体ABCD -A1B1C1D1中,E 、F 分别为A1D1、B1C1的中点,则在面BCC1B1内到BC 的距离是到EF 的距离的2倍的点的轨迹是( )A .一条线段B .椭圆的一部分C .抛物线的一部分D .双曲线的一部分.9.已知直线,平面,且,给出四个命题:①若,则; ②若,则;③若,则; ④若,则其中正确命题的个数是 A 、4 B 、3 C 、2 D 、110. 长方体一个顶点上三条棱的长分别是6、8、10,且它的八个顶点都在同一个球面上,这个球的表面积是( ) A.B.C.D.11. 如图,在正方体中,M 、N 分别为棱和中点,则异面直线CM 与所成角的正弦值为( )A. B. C. D.12. 在直三棱柱A1B1C1-ABC 中,∠BAC =,AB =AC =AA1=1.已知G 与E 分别为A1B1和CC1的中点,D 与F 分别为线段AC 和AB 上的动点(不包括端点).若GD ⊥EF ,则线段DF 的长度的取值范围为 ( )A .[ ,1)B .[,2)C .[1,)D .[,)13. 已知正四棱锥P —ABCD 的棱长都等于a ,侧棱PB 、PD 的中点分别为M 、N ,则截面AMN 与底面ABCD 所成二面角的大小为A.B.C.D.14.下面命题正确的是A.已知直线,点,直线,则与异面B.已知直线,直线,则C.已知平面,直线,直线,则D.若直线与所成的角相等,则15. 已知平面平面,直线,直线,点,点,记点之间的距离为,点到直线的距离为,直线和的距离为,则()A.B.C.D.16.设为互不重合的平面,l,m,n为互不重合的直线,给出下列四个命题:①若则∥;②若∥∥,则∥;③若∥则∥④若∥则m∥n.其中真命题的个数是()(A)1 (B)2 (C)3 (D)417.已知直线、,平面、,且,给出下列四个命题,其中正确命题的个数为(1)若,则(2)若,则(3)若,则(4)若,则(A) (B) (C)(D)18. 已知是不同的两个平面,直线,直线,命题;命题没有公共点,则的()A.充分不必要的条件 B.必要不充分条件C.充要条件D.既不充分又不必要19. 已知直线和平面m,直线直线b的一个必要不充分的条件是()(A)且(B)且(C)且(D)与m所成角相等20.(给出下列两个命题:甲:异面直线m,n分别在平面α、β内,且n∥α,且m∥β,则α∥β.乙:两平面互相垂直,分别在这两个平面内且互相垂直的两条直线,一定分别与另一平面垂直.正确的判断是A.甲、乙均假B.甲、乙均真C.甲真乙假D.甲假乙真21.设l,m,n是空间三条互相不重合的直线,α,β是空间两个不重合的平面,则下列结论中①当m ,且n 时,“n∥m”是“n∥α”的充要条件②当m 时,“m⊥β”是“αβ”的充要条件③当n⊥α时,“n⊥β”是“α∥β”成立的充要条件④当m 且n是l在α内的射影时,“m⊥n”是“l⊥m”的充要条件正确的个数有( )(A)1个(B)2个(C)3个(D)4个22.设为互不相同的平面,为不重合的三条直线,则的一个充分不必要条件是( ).A. B.C. D.23.在正方体中,分别为和的中点,则与平面所成的角为( ).A. B. C. D.24.如图,在正方体ABCD-A1B1C1D1中,P是侧面BB1C1C内一动点,若P到直线BC 与直线C1D1的距离相等,则动点P的轨迹所在的曲线是()A.直线B.圆C.双曲线 D.抛物线25. 从正方体的八个顶点中任取四个点,在能构成的一对异面直线中,其所成的角的度数不可能是A.B.C.D.26. 已知是直线,是平面,给出下列命题:①若内有两相交直线;②③;④⑤其中正确的命题序号是A.①③⑤B.②④C.①⑤D.①④27. 已知直线m ,n 和平面,则m//n 的必要非充分条件是()A.m//且n//B.m且nC.m//且D.m ,n与成等角28. 在正四面体P---ABC中,D、E、F,分别是AB、BC、CA的中点,下面四个结论不成立的是A.BC∥平面PDF B.DF垂直平面PAEC.平面PDE垂直于平面ABC D.平面PDF垂直平面PAE29.设表示平面,l为直线,l不在平行内,有下列三个事实①②③,以任意两个作为条件,另一个作为结论可构造三个命题,其中正确命题的个数是()A.1 B.2C.3 D.030.设m、n是不同的直线,α、β、γ是不同的平面,有以下四个命题:①;②;③;④其中真命题的序号是()A.①④B.②③C.①③D.②④二、填空题31.斜三棱柱ABC- A1B1C1中,二面角C-A1A-B为120°,侧棱AA1于另外两条棱的距离分别为7cm、8cm,AA1=12cm,则斜三棱柱的侧面积为______ .32.在三棱锥的四个面中,最多有___ 个面为直角三角形.33.在矩形ABCD中,4,3,AB BC==若沿AC将矩形折成一个直二面角B AC D--,则四面体ABCD的外接球的体积为4O___________________。
(完整版)空间几何体练习题含答案
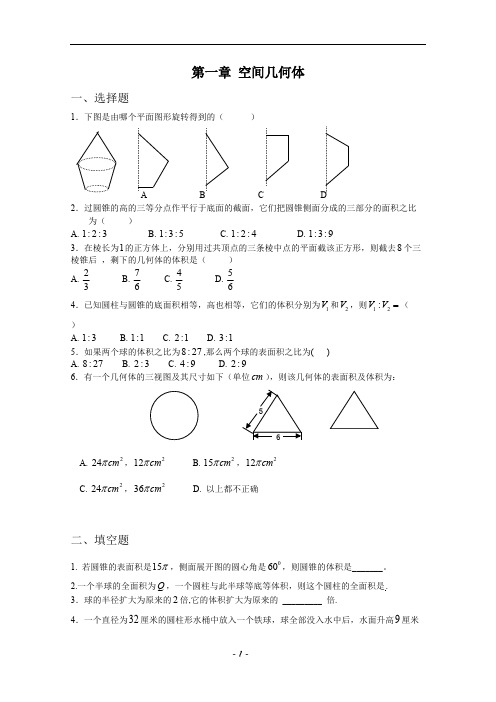
第一章空间几何体一、选择题1.下图是由哪个平面图形旋转得到的()A B C D2.过圆锥的高的三等分点作平行于底面的截面,它们把圆锥侧面分成的三部分的面积之比为()A. B. C. D.1:2:31:3:51:2:41:3:93.在棱长为的正方体上,分别用过共顶点的三条棱中点的平面截该正方形,则截去个三18棱锥后,剩下的几何体的体积是()A. B. C. D.237645564.已知圆柱与圆锥的底面积相等,高也相等,它们的体积分别为和,则(1V2V12:V V=)A. B. C. D.1:31:12:13:15.如果两个球的体积之比为,那么两个球的表面积之比为( )8:27A. B. C. D.8:272:34:92:96.有一个几何体的三视图及其尺寸如下(单位),则该几何体的表面积及体积为:cmA. ,B. ,224cmπ212cmπ215cmπ212cmπC. ,D. 以上都不正确224cmπ236cmπ二、填空题1. 若圆锥的表面积是,侧面展开图的圆心角是,则圆锥的体积是_______。
15π0602.一个半球的全面积为,一个圆柱与此半球等底等体积,则这个圆柱的全面积是.Q3.球的半径扩大为原来的倍,它的体积扩大为原来的_________ 倍.24.一个直径为厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高厘米329则此球的半径为_________厘米.5.已知棱台的上下底面面积分别为,高为,则该棱台的体积为___________。
4,163三、解答题1. (如图)在底半径为,母线长为的圆柱,求圆柱的表面积242.如图,在四边形中,,,,,ABCD 090DAB ∠=0135ADC ∠=5AB =CD =,求四边形绕旋转一周所成几何体的表面积及体积.2AD =ABCD AD参考答案一、选择题1.A 几何体是圆台上加了个圆锥,分别由直角梯形和直角三角形旋转而得2.B 从此圆锥可以看出三个圆锥,123123::1:2:3,::1:2:3,r r r l l l == 12312132::1:4:9,:():()1:3:5S S S S S S S S =--=3.D 111115818322226V V -=-⨯⨯⨯⨯⨯=正方体三棱锥4.D 121:():()3:13V V Sh Sh ==5.C 121212:8:27,:2:3,:4:9V V r r S S ===6.A 此几何体是个圆锥,23,5,4,33524r l h S πππ====⨯+⨯⨯=表面 2134123V ππ=⨯⨯=二、填空题1. 设圆锥的底面半径为,母线为,则,得,r l 123r l ππ=6l r =,得,圆锥的高226715S r r r r ππππ=+⋅==r =h =21115337V r h ππ==⨯=2. 109Q 22223,S R R R Q R πππ=+===全 32222221010,,2233339V R R h h R S R R R R Q πππππ==⋅==+⋅==3. 821212,8r r V V ==4. 12234,123V Sh r h R R ππ=====5. 28'11()(416)32833V S S h =++=⨯+⨯= 三、解答题1.解:圆锥的高,h ==1r =22(2S SS πππ=+=+=侧面表面底面 2.解:S S S S=++表面圆台底面圆台侧面圆锥侧面25(25)2πππ=⨯+⨯+⨯⨯⨯1)π=+ V V V=-圆台圆锥222112211()331483r r r r h r h πππ=++-=。
高一数学空间几何体试题答案及解析

高一数学空间几何体试题答案及解析1.如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=8,BC=6,AB=2,E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使得平面ABEF平面EFDC.(Ⅰ)当,是否在折叠后的AD上存在一点,且,使得CP∥平面ABEF?若存在,求出的值;若不存在,说明理由;(Ⅱ)设BE=x,问当x为何值时,三棱锥A CDF的体积有最大值?并求出这个最大值.【答案】(1)存在点,;(2)当时,三棱锥的最大值.【解析】(1)与立体几何有关的探索问题:第一步:假设符合条件的结论存在;第二步:从假设出发,利用空间中点、线、面的位置关系求解;第三步,确定符合要求的结论存在或不存在;第四步:给出明确结果;第五步:反思回顾,查看关键点;(2)证明线面平行常用方法:一是利用线面平行的判定定理,二是利用面面平行的性质定理,三是利用面面平行的性质;四是利用线面平行的定义,一般用反证法;(3)在求所列函数的最值时,若用基本不等式时,等号取不到时,可利用函数的单调性求解;(4)基本不等式具有将“和式”转化为“积式”和将“积式”转化为“和式”的放缩功能,常常用于比较数的大小或证明不等式,解决问题的关键是分析不等式两边的结构特点,选择好利用基本不等式的切入点.试题解析:解:(Ⅰ)假设存在使得满足条件CP∥平面ABEF在平面内过点作交于,在平面内作直线交于点,连结 3分∵∴ 4分∵5分又∴平面∥平面 6分又∵∴,故点就是所求的点 7分又∵∴ 8分(Ⅱ)因为平面ABEF平面EFDC,平面ABEF平面EFDC=EF,又AF EF,所以AF⊥平面EFDC 10分由已知BE=x,所以AF=x(),则FD=8x.∴ 12分故当且仅当,即=4时,等号成立所以,当=4时,有最大值,最大值为 14分解法二:故所以,当=4时,有最大值,最大值为 14分【考点】(1)探究性问题;(2)求体积的最大值.2.下图中的几何体是由哪个平面图形旋转得到的()【答案】A【解析】几何体的上半部分是一个圆锥,下半部分是一个圆台,故选A【考点】简单旋转体的概念3.一个正方体的顶点都在球面上,它的棱长为,则球的表面积是()A.B.C.D.【答案】B【解析】因为一个正方体的棱长为为2,则该正方体的对角线长为.又因为该正方体的顶点都在球面上,所以球的直径就是正方体的对角线,即球的半径.又因为球的表面积.故选B.【考点】1.球的内接正方体.2.球的表面积公式.3.长方体的对称性.4.若圆锥的表面积,侧面展开图的圆心角为,则该圆锥的体积为______.【答案】【解析】设该圆锥的底面圆的半径为,母线长为,因为侧面展开图的圆心角为,所以,因为圆锥的表面积,所以,所以该圆锥的体积为【考点】本小题主要考查圆锥的侧面积和表面积的关系以及圆锥的体积计算.点评:解决本题的关键是正确运用圆锥中相应的计算公式、圆锥的侧面展开图的关系等求出,进而求出圆锥的高,然后利用圆锥的体积公式计算体积.5.某高速公路收费站入口处的安全标识墩如图1所示。
高三数学空间几何体试题答案及解析

高三数学空间几何体试题答案及解析1.(3分)(2011•重庆)高为的四棱锥S﹣ABCD的底面是边长为1的正方形,点S,A,B,C,D均在半径为1的同一球面上,则底面ABCD的中心与顶点S之间的距离为()A.B.C.1D.【答案】C【解析】由题意可知ABCD所在的圆是小圆,对角线长为,四棱锥的高为,而球心到小圆圆心的距离为,则推出顶点S在球心距的垂直分的平面上,而顶点S到球心的距离为1,即可求出底面ABCD的中心与顶点S之间的距离.解:由题意可知ABCD所在的圆是小圆,对角线长为,四棱锥的高为,点S,A,B,C,D均在半径为1的同一球面上,球心到小圆圆心的距离为,顶点S在球心距的垂直分的平面上,而顶点S到球心O的距离为1,所以底面ABCD的中心O'与顶点S之间的距离为1故选C点评:本题是基础题,考查球的内接多面体的知识,考查逻辑推理能力,计算能力,转化与划归的思想.2.(2013•天津)已知下列三个命题:①若一个球的半径缩小到原来的,则其体积缩小到原来的;②若两组数据的平均数相等,则它们的标准差也相等;③直线x+y+1=0与圆相切.其中真命题的序号是()A.①②③B.①②C.①③D.②③【答案】C【解析】①由球的体积公式V=可知,若一个球的半径缩小到原来的,则其体积缩小到原来的;故①正确;②若两组数据的平均数相等,则它们的标准差不一定相等,如2,2,2和1,2,3;这两组数据的平均数相等,它们的标准差不相等,故②错;③圆的圆心到直线x+y+1=0的距离d==半径r,故直线x+y+1=0与圆相切,③正确.故选C.3.如果,正方体的底面与正四面体的底面在同一平面α上,且AB//CD,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为m,n,那么m+n=()A .8B .9C .10D .11【答案】A【解析】因为过EF 做垂直于CD (AB )的平面垂直平分CD ,所以该平面与过AB 中点并与AB 垂直的平面平行,平面和正方体的4个侧面相交,由于EF 和正方体的侧棱不平行,所以它与正方体的六个面所在的平面相交的平面个数为4.同理与CE 相交的平面有4个,共8个,选A.【考点】该题主要考查空间点、线、面的位置关系,考查空间直线与平面的平行与相交,考查空间想象能力和逻辑思维能力.4. 如图,已知四棱锥,底面是等腰梯形,且∥,是中点,平面,,是中点.(1)证明:平面平面;(2)求点到平面的距离.【答案】(1)详见解析;(2)【解析】(1)根据中位线可得∥,从而可证得∥平面。
高一数学空间几何体的三视图与直观图试题答案及解析

高一数学空间几何体的三视图与直观图试题答案及解析1.已知一个几何体的三视图如图所示.(Ⅰ)求此几何体的表面积;(Ⅱ)在如图的正视图中,如果点为所在线段中点,点为顶点,求在几何体侧面上从点到点的最短路径的长.【答案】(1);(2)【解析】(1)以三视图为载体考查几何体的表面积,关键是能够对给出的三视图进行恰当的分析,从三视图中发现几何体中各元素的位置关系和数量关系;(2)多面体的表面积是各个面的面积之和;组合体的表面积应注意重合部分的处理;(3)圆锥、圆柱、圆台的侧面是曲面,计算侧面积或长度时需要将这个曲面展为平面图形计算,而表面积是侧面积与底面圆的面积之和. 试题解析:(Ⅰ)由三视图知:此几何体是一个圆锥加一个圆柱,其表面积是圆锥的侧面积、圆柱的侧面积和圆柱的一个底面积之和.所以. 6分(Ⅱ)沿点到点所在母线剪开圆柱侧面,如图:则,所以从点到点在侧面上的最短路径的长为. 12分【考点】空间几何体的表面积.2.如果一个水平放置的图形的斜二测直观图是一个底面为,腰和上底均为的等腰梯形,那么原平面图形的面积是_______-【答案】【解析】如图,根据斜二测画法,可得原平面图形是直角梯形,在直观图中,分别过顶点作底面的高,由于是等腰梯形,可得底面边长为,所以在平面图形中,可知DC=2,所以S= ( AD+BC)·DC=.【考点】直观图和平面图的关系.3.下列命题中正确的是()A.空间三点可以确定一个平面B.三角形一定是平面图形C.若A、B、C、D既在平面α内,又在平面β内,则平面α和平面β重合D.四条边都相等的四边形是平面图形【答案】B【解析】不在同一直线的三点确定一个平面,故A错,B对;共线的四点可以构成无数个平面,故C错;正四面体的四个边都相等,但它不是平面图形,故D错.故选B.【考点】平面的基本性质.4.将棱长为2的正方体切割后得一几何体,其三视图如图所示,则该几何体的体积为___________.【答案】.【解析】由三视图可知,该几何体为正方体先切割得到的三棱柱后切割一三棱锥,如图所示,则其体积为.【考点】空间几何体的体积.5.某一几何体的三视图如图所示.按照给出的尺寸(单位:cm),(1)请写出该几何体是由哪些简单几何体组合而成的;(2)求出这个几何体的体积.【答案】(1) 正方体和直三棱柱;(2)10cm3.【解析】(1)画出已知三视图的直观图,就很容易获得此几何体是由哪些简单几何体组合而成的;(1)既然几何体是由简单几何体组合而成的,那就只需先求得各个简单几何体的体积,然后相加即得所求几何体的体积.试题解析:(1)如图是题中所给几何体的直观图,所以这个几何体可看成是由正方体及直三棱柱的组合体.(2)由,,可得.所求几何体的体积:【考点】1.三视图;2.直观图;3.体积公式.6.某向何体的三视图如图所示,则该几何体的体积为()A.B.C.D.【答案】A【解析】由三视图可知,该几何体是一个长方体和一个半圆柱组成的几何体,所以体积为。
高三数学空间几何体的三视图与直观图试题答案及解析
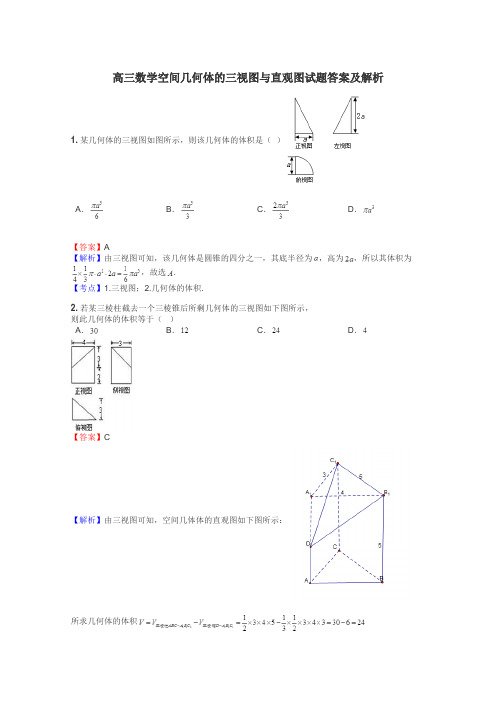
高三数学空间几何体的三视图与直观图试题答案及解析1.某几何体的三视图如图所示,则该几何体的体积是()A.B.C.D.【答案】A【解析】由三视图可知,该几何体是圆锥的四分之一,其底半径为,高为,所以其体积为,故选.【考点】1.三视图;2.几何体的体积.2.若某三棱柱截去一个三棱锥后所剩几何体的三视图如下图所示,则此几何体的体积等于()A.B.C.D.【答案】C【解析】由三视图可知,空间几体体的直观图如下图所示:所求几何体的体积故选C.【考点】1、三视图;2、空间几何体的体积.3.如图,一个几何体的三视图(正视图、侧视图和俯视图)为两个等腰直角三角形和一个边长为1的正方形,则其外接球的表面积为A.πB.2πC.3πD.4π【答案】C【解析】原几何体为有一条侧棱垂直于底面的四棱锥,且底面是边长为1的正方形,垂直于底面的侧棱长也为1,因此,该几何体可以补形为一个棱长为1的正方体,其外接球就是这个正方体的外接球,直径为正方体的对角线长,即2R=,故R=故外接球表面积为:4πR2=3π.【考点】三视图,几何体的外接球及其表面积4.如图所示,一个三棱锥的三视图是三个直角三角形(单位: cm),则该三棱锥的外接球的表面积为________cm2.【答案】29π【解析】从三棱锥的三视图可知,三棱锥有两侧面与底面垂直,把三棱锥补成长,宽,高分别为4,2,3的长方体,设外接球的半径为R,由42+22+32=4R2得,S=4πR2=29π(cm2).球5.某个长方体被一个平面所截,得到的几何体的三视图如图所示,则这个几何体的体积为()A.4B.2C.D.8【答案】D【解析】由三视图可知,该几何体如图所示,其底面为正方形,正方形的边长为2.HD=3,BF =1,将相同的两个几何体放在一起,构成一个高为4的长方体,所以该几何体的体积为×2×2×4=8.6.在一个几何体的三视图中,正视图和俯视图如图所示,则相应的侧视图可以为()【答案】D【解析】由题目所给的几何体的正视图和俯视图,可知该几何体为半圆锥和三棱锥的组合体,如图所示,可知左视图为等腰三角形,且轮廓线为实线,故选D.7.一个几何体的三视图如图所示,已知这个几何体的体积为,= .【答案】【解析】由三视图知,原几何体是一个四棱锥,底面是面积为的矩形,高为,所以,解得.【考点】三视图,空间几何体的体积.8.如图,水平放置的正三棱柱的主视图是一边长为2的正方形,则该三棱柱的左视图的面积为.【答案】【解析】左视图为一个矩形,长宽分别为,因此面积为.【考点】三视图9.若一个正三棱柱的正视图如图所示,其顶点都在一个球面上,则该球的表面积为() A.B.C.D.【答案】B【解析】依题意得,该正三棱柱的底面正三角形的边长为2,侧棱长为1.设该正三棱柱的外接球半径为R,易知该正三棱柱的底面正三角形的外接圆半径是2sin 60°×=,所以R2=+=,则该球的表面积为4πR2=.10.图中的网格是边长为1的小正方形,在其上用粗线画出了某多面体的三视图,则该多面体的体积为________.【答案】16【解析】从三视图可知,这是一个四棱锥,.【考点】三视图.11.如图所示,一个空间几何体的正视图和左视图都是边长为的正方形,俯视图是一个直径为的圆,那么这个几何体的体积为 ( )A.B.C.D.【答案】B【解析】几何体是圆柱,.【考点】三视图,圆柱的体积.12.一个几何体的三视图如图所示,其中正视图是一个正三角形,则该几何体的体积为( )A.1B.C.D.【答案】B【解析】由三视图可知,此几何体为三棱锥,如图,其中正视图为,是边长为2的正三角形,,且,底面为等腰直角三角形,,所以体积为,故选B.13.已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能等于()A.1B.C.D.【答案】C【解析】由题意知,正视图的最大面积为对角面的面积,最小面积为,而,故选C.【考点】三视图.14.已知某几何体的三视图如右图所示,其中俯视图是圆,且该几何体的体积为;直径为2的球的体积为.则()A.B.C.D.【答案】C【解析】由题意,该几何体是一个圆柱挖去一个圆锥得到的几何体,,,∴.选B.【考点】三视图,体积.15.三棱锥S-ABC及其三视图中的正视图和侧视图如图所示,则棱SB的长为()A.B.C.D.【答案】B【解析】过B作BD⊥AC于点D,则BD=2,CD=2,所以BC=,因为SC⊥平面ABC,所以SC⊥BC,所以SB=,故选B.【考点】三视图、直线与平面垂直的性质.16.一个几何体的三视图如图,则该几何体的体积为()A.B.C.D.【答案】A【解析】由三视图可知,该几何体是由一个半圆柱和一个三棱锥拼接而成,且半圆柱的底面是半径为的半圆,高为,其底面积为,故其体积为,三棱锥的底面是一个直角三角形,三棱锥的高也为,其底面积为,故其体积为,所以该几何体的体积为,故选A.【考点】1.三视图;2.组合体的体积17.右图为某几何体的三视图,则该几何体的体积为 .【答案】【解析】所求几何体为一个底面半径为1,高为1的圆柱与半径为1的四分之一的球的组合体,所以体积为【考点】三视图18.一个空间几何体的三视图如图所示,该几何体的体积为______.【答案】96【解析】几何体为一个三棱柱,底面为一个等腰三角形,底边长为6,底边上高为4,棱柱的高为8.因此所求体积为【考点】三视图19.把边长为1的正方形ABCD沿对角线BD折起,形成三棱锥C-ABD,它的主视图与俯视图如右上图所示,则二面角 C-AB-D的正切值为.【答案】【解析】如图所示,做BD,AB的中点分别为点E,F.则有CE面ABD,由于EF为等腰直角三角形ABD的中位线,故EF AB,则为二面角 C-AB-D的代表角,所以,故填.【考点】二面角三视图20.已知水平放置的△ABC的直观图△A′B′C′(斜二测画法)是边长为a的正三角形,则原△ABC 的面积为()A.a2B.a2C.a2D.a2【答案】D【解析】斜二测画法中原图面积与直观图面积之比为1∶,则易知S= ( a)2,∴S=a2.21.一个空间几何体的三视图如图所示,则该几何体的体积为()A.πcm3B.3πcm3C.πcm3D.πcm3【答案】D【解析】由三视图可知,此几何体为底面半径为1cm、高为3cm的圆柱上部去掉一个半径为1cm的半球,所以其体积为V=3π-π=π(cm 3).22. 右图为一简单组合体,其底面ABCD 为正方形,PD ⊥平面ABCD ,EC ∥PD ,且PD =AD =2EC =2.(1)请画出该几何体的三视图; (2)求四棱锥B-CEPD 的体积.【答案】(1)见解析 (2)2【解析】解:(1)该组合体的三视图如图所示.(2)∵PD ⊥平面ABCD , PD ⊂平面PDCE ,∴平面PDCE ⊥平面ABCD. ∵四边形ABCD 为正方形,∴BC ⊥CD ,且BC =DC =AD =2. 又∵平面PDCE∩平面ABCD =CD , BC ⊂平面ABCD. ∴BC ⊥平面PDCE.∵PD ⊥平面ABCD ,DC ⊂平面ABCD , ∴PD ⊥DC.又∵EC ∥PD ,PD =2,EC =1,∴四边形PDCE 为一个直角梯形,其面积: S 梯形PDCE = (PD +EC)·DC =×3×2=3, ∴四棱锥B-CEPD 的体积V B-CEPD =S 梯形PDCE ·BC =×3×2=2.23. 某几何体的三视图如图所示,则该几何体的体积为( ).A .16+8πB .8+8πC .16+16πD .8+16π【答案】A【解析】将三视图还原成直观图为:上面是一个正四棱柱,下面是半个圆柱体.所以V=2×2×4+×22×π×4=16+8π.24.某几何体的三视图如图所示,则其体积为________.【答案】【解析】由三视图还原几何体为半个圆锥,高为2,底面半圆的半径r=1.∴体积V=×(π×12×2)=.25.如图所示为一个几何体的直观图、三视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形).(1)求四棱锥P-ABCD的体积;(2)若G为BC上的动点,求证:AE⊥PG.【答案】(1)(2)见解析【解析】(1)由几何体的三视图可知,底面ABCD是边长为4的正方形,PA⊥平面ABCD,PA∥EB,且PA=4 ,BE=2 ,AB=4.∴VP-ABCD =PA·S四边形ABCD=×4 ×4×4=.(2)∵=,∠EBA=∠BAP=90°,∴△EBA∽△BAP,∴∠BEA=∠PBA.∴∠BEA+∠BAE=∠PBA+∠BAE=90°,∴PB⊥AE又∵BC⊥平面APEB,∴BC⊥AE.∵BC∩PB=B,∴AE⊥平面PBC.∵PG⊂平面PBC,∴AE⊥PG.26.如图所示,网格上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为________.【答案】9【解析】由题意知,此几何体是三棱锥,其高h=3,相应底面面积为S=×6×3=9,∴V=Sh=×9×3=9.27.某几何体的三视图如图所示,主视图和侧视图为全等的直角梯形,俯视图为直角三角形.则该几何体的表面积为( )A. B. C. D【答案】B【解析】此几何体直观图如图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考点33 空间几何体的结构及其三视图和直观图、空间几何体的表面积与体积一、选择题1.(2012·江西高考文科·T7)若一个几何体的三视图如图所示,则此几何体的体积为()A.112 B.5 C.4 D. 92【解题指南】由三视图想像出几何体的直观图,由直观图求得体积。
【解析】选D.由三视图可判断该几何体为直六棱柱,其底面积为4,高为1,所以体积为4.2.(2012·新课标全国高考文科·T7)与(2012·新课标全国高考理科·T7)相同如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为()A.6 B.9 C.12 D.18 【解题指南】由三视图想像出几何体的直观图,由直观图求得体积。
【解析】选B.由题意知,此几何体是三棱锥,其高h=3,相应底面面积为111=63=9,==93=9233S V Sh ⨯⨯∴⨯⨯.3.(2012·新课标全国高考理科·T11)已知三棱锥S-ABC 的所有顶点都在球O 的球面上,△ABC 是边长为1的正三角形,SC 为球O 的直径,且SC=2,则此棱锥的体积为( )A【解题指南】思路一:取AB 的中点为D 将棱锥分割为两部分,利用B CDS A CDS V V V --=+求体积;思路二:设点O 到面ABC 的距离为d,利用123ABC V S d ∆=⨯求体积;思路三:利用排除法求解.【解析】选A 方法一:SC 是球O 的直径,90CAS CBS ∴∠=∠=︒ 1BA BC AC ===,2SC =,AS BS ∴==,取AB 的中点为D ,显然AB CD ⊥,AB CS ⊥,AB ∴⊥平面CDS在CDS ∆中,CD,DS =,2SC =,利用余弦定理可得cos CDS ∠=故sin CDS ∠=12CDS S ∆∴== 13B CDS A CDS CDS V V V S BD --∆∴=+=⨯⨯+1111333CDS CDS S AD S BA ∆∆⨯=⨯== 方法二:ABC ∆的外接圆的半径r =,点O 到面ABC 的距离d ==SC 为球O 的直径⇒点S 到面ABC 的距离为2d =此棱锥的体积为11233ABC V S d ∆=⨯==.方法三:123ABC V S R ∆<⨯=排除,,B C D . 4.(2012·新课标全国高考文科·T8)平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为( )(A )6π (B )43π (C )46π (D )63π【解题指南】利用球心到截面的距离、截面圆的半径、球的半径之间满足勾股关系求得球的半径,然后利用公式求得球的体积。
【解析】选 B 设球O 的半径为R ,则R ==,故343V R π==球.5.(2012·陕西高考文科·T8)将正方形(如图1所示)截去两个三棱锥,得到图2所示的几何体,则该几何体的左视图为 ( )【解题指南】结合原正方体,确定两个关键点1B ,1D 和两条重要线段1DD 和1B C 的投影.【解析】选B. 图2所示的几何体的左视图由点A ,D ,1B ,1D 确定外形为正方形,判断的关键是两条对角线1AD 和1B C 是一实一虚,其中要把1DD 和1B C 区别开来,故选B.6.(2012·浙江高考文科·T3)已知某三棱锥的三视图(单位:cm )如图所示,则该三棱锥的体积是( )A.1cm 3B.2cm 3C.3cm 3D.6cm 3【解题指南】由三视图可知,几何体底面是两直角边分别是1和2的直角三角形,高为3的棱锥.【解析】选A.三棱锥的体积为: 11123132⨯⨯⨯⨯=(cm 3).7.(2012·北京高考文科·T7)与(2012·北京高考理科·T7)相同 某三棱锥的三视图如图所示,该三棱锥的表面积是( )(A )28+B )30+C )56+(D )60+侧(左)视图俯视图【解题指南】由三视图还原直观图,再求表面积.【解析】选B 直观图如图所示,底面是边长AC=5,BC=4的直角三角形,且过顶点P 向底面作垂线PH ,垂足在AC 上,AH=2,HB=3,PH=4.145102ABC S ∆=⨯⨯=,154102PAC S ∆=⨯⨯=.因为PH ABC ⊥面,所以PH BC ⊥.又因为,BC AB PH AC H ⊥=,所以BC PAC ⊥面.所以BC PC ⊥.所以145102PBC S ∆=⨯⨯=.在PAB ∆中,PA PB AB ===,取PA 中点E ,连结BE ,则6BE =,所以162PAB S ∆=⨯=因此三棱锥的表面积为10101030+++=+8.(2012·湖南高考理科·T3)某几何体的正视图和侧视图均如图1所示,则该几何体的俯视图不可能是( )PB A CH【解题指南】从俯视图观察可知,正视图和测试图不同的是D,正视图应有虚线.【解析】选D. 由“正视图俯视图等长,侧视图俯视图等宽”,知本命题正视图与侧视图相同,可知选D.9.(2012·湖南高考文科·T4)某几何体的正视图和侧视图均如图1所示,则该几何体的俯视图不可能是( )【解题指南】找出正视图和侧视图不相同的俯视图。
【解析】选C. “正视图俯视图等长,侧视图俯视图等宽”,本题正视图与侧视图相同,可知选C.10.(2012·福建高考文科·T4)与(2012·福建高考理科·T4)相同一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是()A.球B.三棱锥C.正方体D.圆柱【解题指南】通过了解基本空间几何体的各个视图分别是什么就能直接解题.【解析】选D. 圆柱的三视图,分别矩形,矩形,圆,不可能三个视图都一样,而球的三视图可以都是圆,三棱锥的三视图可以都是三角形,正方体的三视图可以都是正方形.11.(2012·广东高考理科·T6)某几何体的三视图如图所示,它的体积为A.12π B.45π C.57π D.81π【解题指南】根据三视图准确判断出此几何体的形状,是解决本题的关键。
本题显然是一个由同底的圆柱和圆锥组成的组合体。
【解析】选C. 此几何体是一个组合体,上方为一个圆锥,下方为一个同底的圆柱,所以其体积为2213534573Vπππ=⨯⨯+⨯⨯⨯=.12.(2012·广东高考文科·T7)某几何的三视图如图所示,它的体积为A.72πB.48πC.30πD.24π【解题指南】根据三视图准确判断出此几何体的形状,是解决本题的关键。
显然本题是一个由一个半球和倒立的圆锥组成的组合体。
【解析】选C. 由三视图可知一个由一个半球和倒立的圆锥组成的组合体。
2311434330323V πππ=⨯⨯+⨯⨯=.13.(2012·湖北高考理科·T4)已知某几何体的三视图如图所示,则该几何体的体积为( ) A. 83π B.3π C. 103πD.6π【解题指南】本题考查三视图与组合体的体积求法,解答本题的关键是正确的想象出直观图,再补体代入体积公式求解.【解析】选 B. 解答本题可采取补上一个与它完全相同的几何体,21163.2v ππ∴=⨯⨯=二、填空题14.(2012·湖北高考文科·T15)已知某几何体的三视图如图所示,则该几何体的体积为【解题指南】本题考查三视图与组合体的体积求法,解答本题的关键是正确地想象出直观图,再代入体积公式求解.【解析】由本题的三视图可知,该几何体是由三个圆柱组合而成,其中左右两个圆柱等体积.V=π×22×1×2+π×12×4=12π.【答案】12π.15.(2012·江苏高考·T7)在长方体1111ABCD A B C D -中,13,2AB AD cm AA cm ===,则四棱锥11A BB D D -的体积为 3cm .【解题指南】关键是求出四棱锥的高,即A 到面11BB D D 的距离.再接利用公式进行求解.【解析】由题意知,四边形ABCD 为正方形,连接AC,交BD 于O ,则AC⊥BD.由面面垂直的性质定理,可证AO ⊥面11BB D D 。
四棱锥底面11BB D D的面积为2=,从而1111163-=⨯⨯=A BB D D BB D D V OA S .【答案】6.16.(2012·浙江高考理科·T11)已知某三棱锥的三视图(单位:cm )如图所示,则该三棱锥的体积等于________3cm.【解题指南】由三视图可知几何体是一条侧棱与底面垂直的棱锥,而底面为直角三角形,易由锥体的体积公式可求得.【解析】三棱锥的体积为: 1132132⨯⨯⨯=.【答案】1.17.(2012·天津高考理科·T10)一个几何体的三视图如图所示(单位:m ),则该几何体的体积为__________3m .31363223侧视图俯视图正视图【解题指南】由三视图正确判断出组合体的图形是关键.【解析】组合体的上座是一个长、宽、高分别为6、3、、1的长方体,下面是两个个底面半径为1的相切的球体,所以所求的体积是:2432+=2+631=18+932V V V ππ=⨯⨯⨯⨯球长方体(). 【答案】.18.(2012·天津高考文科·T10)一个几何体的三视图如图所示(单位:m ),则该几何体的体积为__________3m .【解题指南】由三视图正确判断出组合体的图形是关键.【解析】组合体的底座是一个长、宽、高分别为4、3、2的长方体,上面是个平躺着的高为4的四棱台,其两个底面的面积相等/32S S ==,所以所求的体积是:=6+24=30.【答案】30.19. (2012·山东高考理科·T14)如图,正方体1111ABCD A B C D -的棱长为1,,E F 分别为线段11,AA B C 上的点,则三棱锥1D EDF -的体积为____________.【解题指南】本题考查利用换顶点法来求三棱锥的体积,只需知道C B 1上的任意一点到面1DED 的距离相等.【解析】1DED ∆的面积为正方形面积的一半,三棱锥的高即为正方体的棱长,所以612131311111=⨯⨯⨯=⋅==∆--AB AD DD h S V V DED DED F EDF D . 【答案】61.20.((2012·山东高考文科·T13)如图,正方体1111ABCD A B C D -的棱长为1,E 为线段1B C 上的一点,则三棱锥1A DED -的体积为_____.【解题指南】本题考查利用换顶点法来求三棱锥的体积,只需知道C B 1上的任意一点到面1DAD 的距离相等.【解析】以△1ADD 为底面,则易知三棱锥的高为1,故111111326V =⋅⋅⋅⋅=. 【答案】61. 21.(2012·安徽高考理科·T12)某几何体的三视图如图所示,该几何体的表面积是【解题指南】根据“长对正、宽相等、高平齐”的原则作出几何体的直观图.【解析】该几何体是底面是直角梯形,高为4的直四棱柱几何体的表面积是12(25)4(2544922S =⨯⨯+⨯+++⨯=.【答案】92.22.(2012·安徽高考文科·T12)某几何体的三视图如图所示,则该几何体的体积等于_____ .【解题指南】根据“长对正、宽相等、高平齐”的原则作出几何体的直观图.【解析】该几何体是底面是直角梯形,高为4的直四棱柱,几何体的的体积是1(25)44562V =⨯+⨯⨯=.【答案】56.23.(2012·辽宁高考理科·T13)一个几何体的三视图如图所示,则该几何体的表面积为______________.【解题指南】读懂三视图,它是长方体(挖去一个底面直径为2cm 的圆柱) ,分别求表面积,注意减去圆柱的两个底面积.【解析】一个长方体的长宽高分别为4,3,1,表面积为43231241238⨯⨯+⨯⨯+⨯⨯=;圆柱的底面圆直径2,母线长1,侧面积为2112ππ⨯⨯=;圆柱的两个底面积2212ππ⨯⨯=故该几何体的表面积为382238ππ+-=.【答案】38.24. (2012·辽宁高考文科·T13)一个几何体的三视图如图所示,则该几何体的体积为_______________.【解题指南】读懂三视图,它是圆柱和长方体的组合,分别求体积即可.【解析】该组合体上边是一个圆柱,底面圆直径2,母线长1;体积2111V sh ππ==⨯⨯=下面是一个长方体;长宽高分别为4,3,1,体积243112V =⨯⨯=.故组合体体积1212V V π+=+. 【答案】12π+.25.(2012·辽宁高考文科·T16)已知点P ,A ,B ,C ,D 是球O 表面上的点,PA ⊥平面ABCD ,四边形ABCD 是边长为正方形.若,则△OAB 的面积为______________.【解题指南】注意到条件中的垂直关系,将点P,A,B,C,D 看作长方体的顶点来考虑就容易多了.【解析】由题意,PA ⊥平面ABCD ,则点P,A,BC,D,可以视为球O 的内接长方体的顶点,球O 位于该长方体的对角线的交点处,那么三角形OAB 的面积为长方体对角面的四分之一126=4AB PA PB OABD ==∴=∴∆⨯,面积.【答案】.26.(2012·新课标全国高考文科·T19)如图,在三棱柱ABC -A 1B 1C 1中,侧棱垂直底面,∠ACB=90°,AC=BC=12AA 1,D 是棱AA 1的中点. (I)证明:平面BDC 1⊥平面BDC ;(Ⅱ)平面BDC 1分此棱柱为两部分,求这两部分体积的比.B 1 DC 1A 1【解题指南】(1)证两个平面垂直,可转化为在其中一个平面内找到一条直线与另一个平面垂直,要证平面BDC 1⊥平面BDC ,可证1DC ⊥平面BCD ;(2)平面BDC 1分棱柱下面部分1B ADC C -为四棱锥,可直接求体积,上面部分可用间接法求得体积,从而确定两部分体积之比.【解析】(I)由题设可知11,,BC CC BC AC CC AC C ⊥⊥=,所以BC ⊥平面11ACC A .又1DC ⊂平面11ACC A ,所以1DC BC ⊥.由题设知1145A DC ADC ∠=∠=︒,所以190CDC ∠=︒,即1DC DC ⊥.又,DC BC C =所以1DC ⊥平面BDC .又1DC ⊂平面1BDC ,故平面1BDC ⊥平面.BDC (II)设棱锥1B DACC -的体积为1V ,1AC =.由题意得1112111322V +=⨯⨯⨯= 又三棱柱111ABC A B C -的体积=1V ,所以()11-:=1:1V V V .故平面1BDC 分此棱柱所得两部分体积的比为1:1.27.(2012·江西高考文科·T19)如图,在梯形ABCD 中,AB ∥CD ,E ,F 是线段AB 上的两点,且DE ⊥AB ,CF ⊥AB ,AB=12,AD=5,,DE=4.现将△ADE ,△CFB 分别沿DE ,CF 折起,使A ,B 两点重合与点G ,得到多面体CDEFG.(1) 求证:平面DEG ⊥平面CFG ;(2) 求多面体CDEFG 的体积.【解题指南】(1)证两个平面垂直,可转化为在其中一个平面内找到一条直线与另一个平面垂直,要证DEG ⊥平面CFG ,可证EG CFG ⊥面;(2)多面体CDEFG 为四棱锥,由DEG ⊥平面CFG 得到四棱锥的高,利用体积公式求体积.【解析】(1)由已知可得AE=3,BF=4,则折叠完后EG=3,GF=4,又因为EF=5,所以可得EG GF ⊥又因为CF EGF ⊥底面,可得CF EG ⊥,即EG CFG ⊥面所以平面DEG ⊥平面CFG.(2)过点G 作GO 垂直于EF,GO 即为四棱锥G-EFCD 的高,所以所求体积为13S 长方形DEFC ·GO=13×4×5×125=16.。
