高三数学空间几何体试题答案及解析
专题14 空间几何体的结构、面积与体积(练)【解析版】

第一篇热点、难点突破篇专题14空间几何体的结构、面积与体积(练)【对点演练】一、单选题1.(2022秋·北京·高三统考阶段练习)已知圆柱的上、下底面的中心分别为1O,2O,过直O O的平面截该圆柱所得的截面是面积为12的正方形,则该圆柱的体积为()线12A.B.12πC.D.则该圆台的体积为()A.36πB.40πC.42πD.45πOO的长度===,1O为ABC的外接圆的圆心,球O的表面积为64π,则1AB BC AC为()B.2C.D.3A【答案】C【分析】由已知求得球O的半径4r=,即可求R=,根据正弦定理求出ABC外接圆半径2出结果.O的半径为r,球O的半径为R.【详解】设圆1依题意得ABC 为等边三角形,则由正弦定理得O 的表面积为如图,根据球的截面性质得2d OA ==的扇形,则该圆锥的侧面积为( ) A .π B .3π2C D .点作球O 的截面,则最小截面的面积为( ) A .3π B .4πC .5πD .6π子,其形状可以看成一个正四面体.广东流行粽子里放蛋黄,现需要在四角状粽子内部放入一个蛋黄,蛋黄的形状近似地看成球,当这个蛋黄的表面积是9π时,则该正四面体的高的最小值为()A.4B.6C.8D.10实物图,石碾子主要由碾盘、碾滚(圆柱形)和碾架组成.碾盘中心设竖轴(碾柱),连碾架,架中装碾滚,以人推或畜拉的方式,通过碾滚在碾盘上的滚动达到碾轧加工粮食作物的目的.若推动拉杆绕碾盘转动2周,碾滚的外边缘恰好滚动了5圈,碾滚与碾柱间的距离忽略不计,则该圆柱形碾滚的高与其底面圆的直径之比约为()A.3:2B.5:4C.5:3D.4:3一卷中称轴截面为等腰直角三角形的圆锥为直角圆锥.若一个直角圆锥的侧面积为,则该圆锥的体积为( )A .B .C .D .9π中,地球静止同步卫星的轨道位于地球赤道所在平面,轨道高度为h (轨道高度是指卫星到地球表面的距离).将地球看作是一个球心为O ,半径r 为的球,其上点A 的纬度是指OA 与赤道平面所成角的度数.地球表面上能直接观测到一颗地球静止同步轨道卫星点的纬度最大值为α,记卫星信号覆盖地球表面的表面积为22(1cos )S r πα=-(单位:2km ),若458h r =,则S 占地球表面积的百分比约为( ) A .26% B .34% C .42% D .50%【答案】C【分析】设C 表示卫星,过CO 作截面,截地球得大圆O ,过C 作圆O 的切线,CA CB ,线段CO 交圆O 于E ,得AOC α∠=,在直角三角形中求出cos α后,可计算两者面积比.【详解】设C 表示卫星,过CO 作截面,截地球得大圆O ,过C 作圆O 的切线,CA CB ,线段CO 交圆O 于E ,如图,则AOC α∠=,r OE =,CE h =,OA CA ⊥,二、填空题10.(2022秋·江苏徐州·高三期末)已知圆柱的高为8,该圆柱内能容纳半径最大的球的表面积为36π,则圆柱的体积为______.【答案】72π【分析】先分析半径最大的球不可能为圆柱的内切球,所以此球是与圆柱侧面与下底面相切的球,就能求出圆柱底面半径,然后根据圆柱的体积公式可得.【详解】圆柱内能容纳半径最大的球的表面积为36π,设此球半径为r,则24π36π3r r=⇒=如果圆柱有内切球,又因为圆柱的高为8,所以内切球半径为43>,说明这个圆柱内能容纳半径最大的球,与圆柱侧面和下底面相切,与上底面相离,易得圆柱底面半径为3,圆柱的体积为2π3872π⋅⨯=故答案为:72π【冲刺提升】一、单选题1.(2022秋·广东东莞·高三统考期末)已知一个装满水的圆台形容器的上底半径为6,下底半径为1,高为,若将一个铁球放入该容器中,使得铁球完全没入水中,则可放入的铁球的体积的最大值为()A.B.C D.108π【答案】B【分析】作出体积最大时的剖面图,分析出此时圆与上底,两腰相切,建立合适直角坐标系,()53,05<<t=-533)32332=模拟预测)某工厂要生产容积为为侧面成本的2倍,为使成本最小,则圆柱的高与底面半径之比应为()A.1B.1C.2D.4 2圆柱上下底的总面积为3.(2022·浙江·模拟预测)如图,正方体1111的棱长为1,,E F 分别为棱BC ,11的中点,则三棱锥1B AEF -的体积为( )A .524B .316C .29D .181AB ES =因为正方体ABCD A B C D -的棱长为1, 所以111(,1,0),(0,1,1),(1,22AE AB AF =-==-的法向量为(,,)n x y z =112n AE x n AB y z ⎧⋅=-⎪⎨⎪⋅=+⎩所以(2,1,1)n =-,F 平面1AB E 的距离为2AF n n-+⋅=又因为1AB =,121122AB EAB S⎫==⋅⎪⎭所以三棱锥故选:AF ,G ,H 分别是SA ,SB ,BC ,AC 的中点,则四边形EFGH 面积的取值范围是( ) A .()0,∞+ B .⎫∞⎪⎪⎝⎭ C .⎫+∞⎪⎪⎝⎭D .1,2⎛⎫+∞ ⎪⎝⎭【答案】B【分析】画出图形,求出,EF HG ,说明EFHG 是矩形,结合图形,说明S 点在ABC 平面时,面积最小,求出即可得到范围 【详解】如图所示:由正三棱锥S ABC -的底面边长是2,因为E 、F 、G 、H 分别是SA 、SB 、BC 、AC 的中点,设ABC 的中心为SC OA >=所以EFGH 所以四边形且4BC =,6BD =,面ABC 与面BCD 夹角正弦值为1,则空间四边形ABCD 外接球与内切球的表面积之比为( )A B C D 【答案】C【分析】根据空间四边形ABCD 的线面关系可得DB ⊥平面ABC ,则空间四边形ABCD 可以内接于圆柱中,根据圆柱的外接球半径求得空间四边形ABCD 的外接球半径R ,又根据内切球的几何性质用等体积法可求得空间四边形ABCD 的内切球半径r ,即可得空间四边形ABCD 外接球与内切球的表面积之比.【详解】解:面ABC 与面BCD 夹角正弦值为1,∴面ABC ⊥面BCD ,又面ABC ⋂面BCD BC =,DB BC DB ⊥⊂面BCD ,DB ∴⊥平面ABC ,则空间四边形ABCD 可以内接于圆柱12O O 中,如下图所示:点在上底面圆周上,ABC三个顶点在下底面圆周上,则圆柱O O的外接球即空间四边连接OA,则球心为为正ABC4sin6032BC=︒1111333ABC ABD ADC BCDS r S r S r S r⋅+⋅+⋅+⋅,,所以()22142132832ADCS=⨯⨯-=,44612ABC ABD ADC BCDS S S S⨯⨯⨯=+++⨯外接球与内切球的表面积之比为6.(2022秋·湖南长沙·高三长郡中学校考阶段练习)三棱锥A BCD -中,AB BC AD CD BD AC ======,则三棱锥A BCD -的外接球的表面积为( )A .20πB .28πC .32πD .36π23AB AD ==且E 为BD 中点,AE BD ∴⊥,AE AB ∴=又AE CE =120, 过BCD △的外心作平面同理过ABD △l l O ''=,易知连接O E ',O 为BCD △又在OO E '中,603=,∴得27O C O O ''=,即外接球半径7=,故外接球表面积28π=.故选:B7.(2022秋·天津河东·高三统考期末)一个球与一个正三棱柱(底面为等边三角形,侧棱与底面垂直)的两个底面和三个侧面都相切,若棱柱的体积为)A.16πB.4πC.8πD.32π8.(2022秋·黑龙江牡丹江·高三牡丹江一中校考期末)如图截角四面体是一种半正八面体,可由四面体经过适当的截角,即截去四面体的四个顶点所产生的多面体.如图,将棱长为3的正四面体沿棱的三等分点作平行于底面的截面得到所有棱长均为1的截角四面体.则该截角四面体的表面积是______.正六边形每个内角均为2π111A B C 中,点P 在棱1BB 上,且1PA PC ⊥,当1APC 的面积取最小值时,三棱锥-P ABC 的外接球的表面积为______.【答案】28π时,1APC 面积取得最小值,补形后三棱锥的外接球,求出外接球半径和表面积【详解】由勾股定理得:AB =,则16PA =(7x y ++1APC S =2169y +,即2x =其中长方体的外接球的直径为,平面PAB ⊥平面PCD ,则P ABCD -体积的最大值为__________.PO ⊥平面ABCD ,PE CD⊥CD平面POE∴⊥,CD OE底面ABCD是边长为∴⊥,CD BCOE⊂平面ABCD OE BC∴,同理可得:OF∥O E F三点共线故,,∥,且有EF BC设平面PAB⋂平面∥AB CD AB,∴∥∥l AB⊥PE CD平面PAB∴⊥平面PEPF⊂平面∴⊥PE PF不妨设PE22∴+x y且2OP=-即2y m11.(2023·广西梧州·统考一模)边长为1的正方形ABCD 中,点M ,N 分别是DC ,BC 的中点,现将ABN ,ADM △分别沿AN ,AM 折起,使得B ,D 两点重合于点P ,连接PC ,得到四棱锥P AMCN -.(1)证明:平面APN ⊥平面PMN ;(2)求四棱锥P AMCN -的体积. ,所以PMN 为直角三角形,即PMN S=111111222AMN ABN ADM CMN ABCD S S S S S =---=-⨯⨯⨯-⨯正方形设点P 到平面AMN 的距离为h ,由A PMN P V V --=1133PMN AMN S PA S h ⋅=⋅△△,即13188h ⨯=,得h =)AMN MCN S S h +=AMCN 的体积为全国·高三对口高考)如题图,是圆锥底面的圆心,ABC 是底面的内接正三角形.P 为DO 上一点,90APC ∠=︒.(1)求证:PC ⊥平面PAB ;(2)若DO =.求三棱锥-P ABC 的体积. 因为ABC 是底面的内接正三角形,CO AB ⊥,PO OC ⋂AB ⊥平面PC ⊂平面AB PC ⊥,PA AB A =,⊥平面PAB(2)解:设圆锥的母线为l,底面半径为r,则圆锥的侧面积为ππ,即,=603所以,在等腰直角三角形APC。
高三数学空间几何体的三视图与直观图试题答案及解析
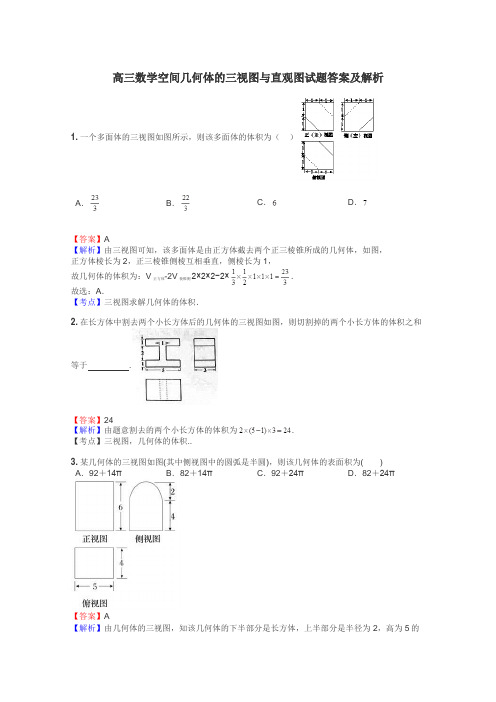
高三数学空间几何体的三视图与直观图试题答案及解析1.一个多面体的三视图如图所示,则该多面体的体积为()A.B.C.D.【答案】A【解析】由三视图可知,该多面体是由正方体截去两个正三棱锥所成的几何体,如图,正方体棱长为2,正三棱锥侧棱互相垂直,侧棱长为1,故几何体的体积为:V正方体-2V棱锥侧2×2×2−2×.故选:A.【考点】三视图求解几何体的体积.2.在长方体中割去两个小长方体后的几何体的三视图如图,则切割掉的两个小长方体的体积之和等于.【答案】24【解析】由题意割去的两个小长方体的体积为.【考点】三视图,几何体的体积..3.某几何体的三视图如图(其中侧视图中的圆弧是半圆),则该几何体的表面积为()A.92+14πB.82+14πC.92+24πD.82+24π【答案】A【解析】由几何体的三视图,知该几何体的下半部分是长方体,上半部分是半径为2,高为5的圆柱的一半.长方体中EH=4,HG=4,GK=5,所以长方体的表面积为(去掉一个上底面)2(4×4+4×5)+4×5=92.半圆柱的两个底面积为π×22=4π,半圆柱的侧面积为π×2×5=10π,所以整个组合体的表面积为92+4π+10π=92+14π,选A.4.在一个几何体的三视图中,正视图和俯视图如图所示,则相应的侧视图可以为()【答案】D【解析】由题目所给的几何体的正视图和俯视图,可知该几何体为半圆锥和三棱锥的组合体,如图所示,可知左视图为等腰三角形,且轮廓线为实线,故选D.5.一个正方体截去两个角后所得几何体的正视图、侧视图如图所示,则其俯视图为()【答案】C【解析】依题意可知该几何体的直观图如图所示,故其俯视图应为C.6.某几何体的三视图如图所示,则该几何体的体积为A.12B.18C.24D.30【答案】C【解析】由三视图可知该几何体是一个底面为直角三角形的直三棱柱的一部分,其直观图如上图所示,其中,侧面是矩形,其余两个侧面是直角梯形,由于,平面平面,所以平面,所以几何体的体积为:故选C.【考点】1、空间几何体的三视图;2、空间几何体的体积.7.一块石材表示的几何体的三视图如图2所示,将石材切削、打磨、加工成球,则能得到的最大球的半径等于()A.1B.2C.3D.4【答案】B【解析】由图可得该几何体为三棱柱,因为正视图,侧视图,俯视图的内切圆半径最小的是正视图(直角三角形)所对应的内切圆,所以最大球的半径为正视图直角三角形内切圆的半径,则,故选B.【考点】三视图内切圆球三棱柱8. [2013·四川高考]一个几何体的三视图如图所示,则该几何体可以是()A.棱柱B.棱台C.圆柱D.圆台【答案】D【解析】由正视图和侧视图可知,该几何体不可能是圆柱,排除选项C;又由俯视图可知,该几何体不可能是棱柱或棱台,排除选项A、B.故选D.9.[2013·宁波质检]如图,水平放置的三棱柱的侧棱长和底边长均为2,且侧棱AA1⊥平面A1B1C1,正视图是正方形,俯视图是正三角形,该三棱柱的侧视图面积为()A.2B.C.2D.4【答案】A【解析】由题意可知,该三棱柱的侧视图应为矩形,如图所示.在该矩形中,MM1=CC1=2,CM=C1M1=·AB=.所以侧视图的面积为S=2.10.某几何体的三视图如图所示,则该几何体的体积的最大值为 .【答案】【解析】该几何体是类似墙角的三棱锥,假设一条直角的棱长为x,则三条直角棱长分别为.所以体积为.当且仅当时取等号.【考点】1.三视图.2.函数最值问题.3.空间想象能力.11.(2012•广东)某几何体的三视图如图所示,它的体积为()A.12πB.45πC.57πD.81π【答案】C【解析】由三视图可知,此组合体上部是一个母线长为5,底面圆半径是3的圆锥,下部是一个高为5,底面半径是3的圆柱故它的体积是5×π×32+π×32×=57π故选C12. (2014·咸宁模拟)某几何体的三视图如图所示(其中侧视图中的圆弧是半圆),则该几何体的表面积为( )A.92+14πB.82+14πC.92+24πD.82+24π【答案】A【解析】由几何体的三视图知该几何体的下半部分是长方体,上半部分是半径为2,高为5的圆柱的一半.所以长方体的表面积为(去掉一个上底面)2(4×4+4×5)+4×5=92.半圆柱的两个底面积为π×22=4π,半圆柱的侧面积为π×2×5=10π,所以整个组合体的表面积为92+4π+10π=92+14π. 13.在一个几何体的三视图中,正视图和俯视图如图所示,则相应的侧视图可以为【答案】D【解析】条件对应的几何体是由底面棱长为r的正四棱锥沿底面对角线截出的部分与底面为半径为r的圆锥沿对称轴截出的部分构成的。
高三数学空间几何体的三视图与直观图试题答案及解析
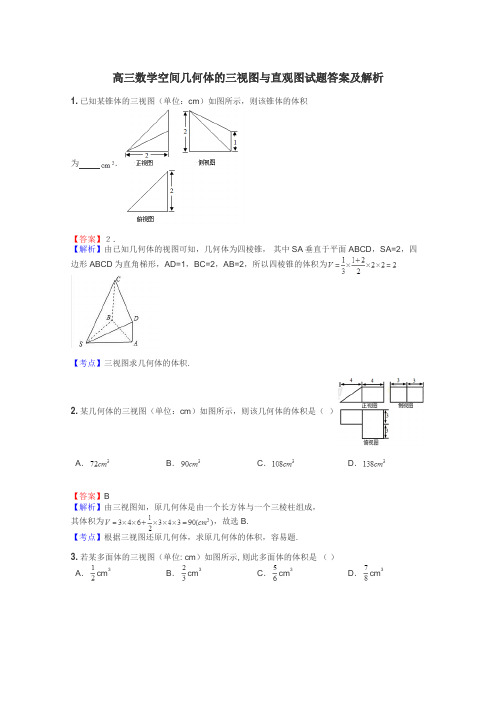
高三数学空间几何体的三视图与直观图试题答案及解析1.已知某锥体的三视图(单位:cm)如图所示,则该锥体的体积为.【答案】2.【解析】由已知几何体的视图可知,几何体为四棱锥,其中SA垂直于平面ABCD,SA=2,四边形ABCD为直角梯形,AD=1,BC=2,AB=2,所以四棱锥的体积为【考点】三视图求几何体的体积.2.某几何体的三视图(单位:cm)如图所示,则该几何体的体积是()A.B.C.D.【答案】B【解析】由三视图知,原几何体是由一个长方体与一个三棱柱组成,其体积为,故选B.【考点】根据三视图还原几何体,求原几何体的体积,容易题.3.若某多面体的三视图(单位: cm)如图所示, 则此多面体的体积是()A.cm3B.cm3C.cm3D.cm3【答案】C【解析】由三视图可得,该几何体相当于一个正方体切去一个三个侧棱长为1的三棱锥.所以该几何体的体积为.故选C.【考点】1.三视图.2.空间想象力.3.几何体的体积.4. (2014·孝感模拟)一个几何体的三视图如图所示,其中俯视图与侧视图均为半径是2的圆,则这个几何体的表面积是( )A.16πB.14πC.12πD.8π【答案】A【解析】由三视图可知,该几何体是球挖去半球.其中两个半圆的面积为π×22=4π.个球的表面积为×4π×22=12π,所以这个几何体的表面积是12π+4π=16π.5.如图,某几何体的三视图都是等腰直角三角形,则几何体的体积是()A.8B.7C.9D.6【答案】C【解析】由三视图可知,几何体是底面为等腰直角三角形,有一侧棱与底面垂直(垂足在非直角处)的三棱锥,其底面面积为×6×3=9,三棱锥的高为3,所以三棱锥的体积=×9×3=9.6.已知某几何体的三视图(如图),正视图和侧视图均为两个相等的等边三角形,府视图为正方形,则几何体的体积为()A.B.4C.9D.9【答案】C【解析】由三视图可知,几何体由两个同底之正四棱锥组成所以其体积为V=2××32×3×=9 7.一空间几何体的三视图如图所示,该几何体的体积为12π+,则正视图中x的值为( )A.5B.4C.3D.2【答案】C【解析】三视图,由正四棱锥和圆柱组成,故选C.8.如图,一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积为()A.1B.2C.3D.4【答案】B【解析】由题意,棱锥的高为,底面面积为,∴.【考点】三视图,体积.9.某几何体的三视图如题(6)所示,其侧视图是一个边长为1的等边三角形,俯视图是两个正三角形拼成的菱形,则这个几何体的体积为()A.1B.C.D.【答案】C【解析】这是由两个三棱锥拼成的几何体,其体积为.选C.【考点】三视图及几何体的体积.10.―个几何体的三视图如图所示(单位:),则该几何体的体积为.【答案】18+9【解析】由三视图可知,此几何体为两个相切的球上方放了一个长方体组成的组合体,所以其体积为:V=3×6×1+2××=18+911.一个空间几何体的三视图如图所示,该几何体的表面积为__________.【答案】152【解析】几何体为一个三棱柱,底面为一个等腰三角形,底边长为6,底边上高为4,腰长为5.棱柱的高为8.因此表面积为【考点】三视图12.某三棱锥的三视图如图所示,则这个三棱锥的体积为;表面积为.【答案】;.【解析】由三视图知几何体如下图,为一个三棱锥,且三棱锥的一个侧面与底面垂直,底面三角形的一条边长为,该边上的高为,∴几何体的体积.它的表面积为.【考点】由三视图求面积、体积.13.已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是_______.【答案】【解析】由题意可得该几何体是一个三棱锥,体积.【考点】1.三视图的知识.2.立几中的线面关系.3.三棱锥的体积公式.14.一个空间几何体的三视图如图所示,其正视图、侧视图、俯视图均为等腰直角三角形,且直角边长都为1,则这个几何体的体积是【答案】【解析】由三视图,可知该几何体是三棱锥,并且侧棱,,,则该三棱锥的高是,底面三角形是直角三角形,所以这个几何体的体积==.【考点】由三视图求几何体的体积.15.一个几何体的三视图如图所示,则该机合体的体积为( )A.B.C.D.【答案】B【解析】分析可得该几何体是底面为菱形的四棱锥,则高底面面积,所以.故选B【考点】三视图四棱锥体积16.一个几何体的三视图如图所示,则该几何体的体积是【答案】【解析】通过三视图的观察可得,该几何体是一个四棱柱,底面是一个直角梯形,其上下底分别为2,3,梯形的高为2.四棱柱的高为2.所以几何体的体积为.【考点】1.三视图的知识.2.几何体的体积.3.空间想象力.17.某长方体被一个平面所截,得到的几何体的三视图如图所示,则这个几何体的体积为()A.4B.4C.6D.8【答案】D【解析】割补可得其体积为2×2×2=8.18.某几何体的三视图如图所示,则该几何体的体积是________.【答案】16π-16【解析】由三视图知,该几何体是由一个底面半径为2,高为4的圆柱内挖去一个底面边长为2,高为4的正四棱柱后剩下的部分,∴V=(π×22-22)×4=16π-16.19.已知正方体ABCD-A1B1C1D1,M为棱A1B1的中点,N为棱A1D1的中点.如图是该正方体被M,N,A所确定的平面和N,D,C1所确定的平面截去两个角后所得的几何体,则这个几何体的正视图为().【答案】B【解析】对于选项A,由于只是截去了两个角,此切割不可能使得正视图成为梯形.故A不对;对于B,正视图是正方形符合题意,线段AM的影子是一个实线段,相对面上的线段DC1的投影是正方形的对角线,由于从正面看不到,故应作成虚线,故选项B正确;对于C,正视图是正方形,符合题意,有两条实线存在于正面不符合实物图的结构,故不对;对于D,正视图是正方形,符合题意,其中的两条实线符合俯视图的特征,故D不对.20.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示,则该棱柱的体积为()A.B.C.D.6【答案】B【解析】由三视图知该直三棱柱高为4,底面正三角形的高为3,所以正三角形边长为6,所以V=×36×4=36.故选B.【考点】1.三视图;2.柱体体积计算.21.某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为的扇形,则该几何体的体积为()A.B.C.D.【答案】D【解析】由题意知道,该几何体体积是圆柱体积的,即.【考点】1、三视图;2、几何体体积.22.右图是一个几何体的三视图,其中正视图和侧视图都是一个两底长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是( )A.B.C.D.【答案】B【解析】由三视图可得该几何体是一个圆台,其两底直径分别为2和4,母线长为4,所以该几何体的侧面积是,选B..【考点】三视图,圆台的侧面积.23.如图是一个组合几何体的三视图,则该几何体的体积是 .A.B.C.D.【答案】A【解析】由三视图还原可知该几何体是一个组合体,下面是一个半径为4,高为8的圆柱,,上面是一个三棱柱,故所求体积为.【考点】三视图,圆柱、三棱柱的体积公式.24.已知一个几何体的三视图如图所示,则该几何体的体积为___________【答案】【解析】该几何体为圆柱中挖去半个球而得的组合体,其体积为.【考点】三视图.25.一个几何体的三视图如图所示(单位长度:),俯视图中圆与四边形相切,且该几何体的体积为,则该几何体的高为 .【答案】【解析】由如图所示的几何体的三视图知:这个几何体是一个半径为的球和一个直四棱柱的结合体,且这个直四棱柱的底面是对角线分别为和的棱形,这个直四棱柱的高为,∴这个几何体的体积:V=,解得h=.【考点】1.三视图;2.几何体的面积和体积26.一个几何体的三视图如图所示,则该几何体的直观图可以是()【答案】D【解析】通过三视图的俯视图可知,该几何体是由两个旋转体组成,故选D.【考点】1.三视图的应用.27.如图为一个几何体的三视图正视图和侧视图均为矩形,俯视图中曲线部分为半圆,尺寸如图所示,则该几何体的表面积为()A.B.C.D.【答案】D【解析】由三视图可知,这是一个由半个圆柱和一个三棱柱构成的组合体,这个组合体仍为一个柱体。
高三高考数学复习练习82空间几何体的表面积与体积

821.一个球的表面积是16π,那么这个球的体积为( )A.163π B.323π C .16π D .24π【解析】 设球的半径为R ,因为表面积是16π,所以4πR 2=16π,解得R =2,所以体积为43πR 3=32π3. 【答案】 B2.某几何体的三视图如图所示,则其表面积为( )A .πB .2πC .3πD .4π【解析】 由三视图可知,该几何体为半径为r =1的半球体,表面积为底面圆面积加上半球面的面积,所以S =πr 2+12×4πr 2=π×12+12×4π×12=3π.故选C. 【答案】 C3.在梯形ABCD 中,∠ABC =π2,AD ∥BC ,BC =2AD =2AB =2.将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )A.2π3B.4π3C.5π3 D .2π【解析】 过点C 作CE 垂直AD 所在直线于点E ,梯形ABCD 绕AD 所在直线旋转一周而形成的旋转体是由以线段AB 的长为底面圆半径,线段BC 为母线的圆柱挖去以线段CE 的长为底面圆半径,ED 为高的圆锥,如图所示,该几何体的体积为V =V圆柱-V 圆锥=π·AB 2·BC -13·π·CE 2·DE =π×12×2-13π×12×1=5π3,故选C. 【答案】 C4.一个四面体的三视图如图所示,则该四面体的表面积是( )A .1+ 3B .2+ 3C .1+2 2D .2 2 【解析】 由空间几何体的三视图可得该空间几何体的直观图,如图所示,∴该四面体的表面积为S 表=2×12×2×1+2×34×(2)2=2+3,故选B. 【答案】 B5.(2018·太原一模)某几何体的三视图如图所示,则该几何体的表面积为( )A .6π+1B.(24+2)π4+1C.(23+2)π4+12D.(23+2)π4+1 【解析】 由几何体的三视图知,该几何体为一个组合体,其中下部是底面直径为2,高为2的圆柱,上部是底面直径为2,高为1的圆锥的四分之一,所以该几何体的表面积为4π+π+3π4+2π4+1=(23+2)π4+1,故选D. 【答案】 D6.甲几何体(上)与乙几何体(下)的组合体的三视图如图所示,甲、乙几何体的体积分别为V 1,V 2,则V 1∶V 2等于( )A .1∶4B .1∶3C .2∶3D .1∶π【解析】 由三视图知,甲几何体是半径为1的球,乙几何体是底面半径为2,高为3的圆锥,所以球的体积V 1=43π,V 2=13π×22×3=4π,所以V 1∶V 2=1∶3.故选B. 【答案】 B7.(2017·全国Ⅲ卷)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A .πB.3π4C.π2D.π4【解析】 设圆柱的底面半径为r ,球的半径为R ,且R =1,由圆柱两个底面的圆周在同一个球的球面上可知,r ,R 及圆柱的高的一半构成直角三角形.∴r = 12-⎝⎛⎭⎫122=32.∴圆柱的体积为V =πr 2h =34π×1=3π4. 故选B.【答案】 B8.(2017·襄阳调研)如图是一个空间几何体的三视图,则该几何体的表面积为________.【解析】 由三视图可知,该几何体是一个正四棱柱挖掉一个半球所得的几何体,其中半球的底面就是正四棱柱上底面的内切圆,正四棱柱的底面边长为4,高为2,半球所在球的半径为2.所以该几何体的表面由正四棱柱的表面与半球的表面积之和减去半球的底面构成,故其表面积为(4×4×2+2×4×4)+12×(4π×22)-π×22=64+4π. 【答案】 64+4π9.(2018·乌鲁木齐二诊)已知四面体ABCD 满足AB =CD =6,AC =AD =BC =BD =2,则四面体ABCD 的外接球的表面积是________.【解析】 (图略)在四面体ABCD 中,取线段CD 的中点为E ,连接AE ,BE .∵AC =AD =BC =BD =2,∴AE ⊥CD ,BE ⊥C D.在Rt △AED 中,CD =6,∴AE =102.同理BE =102.取AB 的中点为F ,连接EF .由AE =BE ,得EF ⊥A B.在Rt △EF A 中,∵AF =12AB =62,AE =102,∴EF =1.取EF 的中点为O ,连接OA ,则OF =12.在Rt △OF A 中,OA =72.∵OA =OB =OC =OD ,∴该四面体的外接球的半径是72,∴外接球的表面积是7π. 【答案】 7π10.(2018·贵州适应性考试)已知球O 的表面积是36π,A ,B 是球面上的两点,∠AOB =60°,C 是球面上的动点,则四面体OABC 体积V 的最大值为________.【解析】 设球的半径为R ,由4πR 2=36π,得R =3.显然在四面体OABC 中,△OAB 的面积为定值,S △OAB =12×R ×32R =34R 2=934.要使三棱锥的体积最大,只需球上的点到平面OAB 的距离最大,显然,到平面OAB 距离的最大值为球的半径,所以四面体OABC 的体积的最大值V =13×934×R =934. 【答案】 93411.(2016·全国丙卷)如图,四棱锥P -ABCD 中,P A ⊥底面ABCD ,AD ∥BC ,AB =AD =AC =3,P A =BC =4,M 为线段AD 上一点,AM =2MD ,N 为PC 的中点.(1)证明:MN ∥平面P AB ;(2)求四面体N -BCM 的体积.【解析】 (1)证明 由已知得AM =23AD =2. 如图,取BP 的中点T ,连接AT ,TN ,由N 为PC 中点知TN ∥BC ,TN =12BC =2. 又AD ∥BC ,故TN 綊AM ,所以四边形AMNT 为平行四边形,于是MN ∥AT .因为AT ⊂平面P AB ,MN ⊄平面P AB ,所以MN ∥平面P AB .(2)因为P A ⊥平面ABCD ,N 为PC 的中点,所以N 到平面ABCD 的距离为12P A. 取BC 的中点E ,连接AE .由AB =AC =3得AE ⊥BC ,AE =AB 2-BE 2= 5.由AM ∥BC 得M 到BC 的距离为5,故S △BCM =12×4×5=2 5. 所以四面体N -BCM 的体积V N -BCM =13×S △BCM ×P A 2=453. 12.如图所示,在空间几何体ADE -BCF 中,四边形ABCD 是梯形,四边形CDEF 是矩形,且平面ABCD ⊥平面CDEF ,AD ⊥DC ,AB =AD =DE =2,EF =4,M 是线段AE 上的动点.(1)试确定点M 的位置,使AC ∥平面MDF ,并说明理由;(2)在(1)的条件下,平面MDF 将几何体ADE -BCF 分成两部分,求空间几何体M -DEF 与空间几何体ADM -BCF 的体积之比.【解析】(1)当M 是线段AE 的中点时,AC ∥平面MDF .理由如下:连接CE 交DF 于点N ,连接MN .因为M ,N 分别是AE ,CE 的中点,所以MN ∥AC .又因为MN ⊂平面MDF ,AC ⊄平面MDF ,所以AC ∥平面MDF .(2)将几何体ADE -BCF 补成三棱柱ADE -B ′CF ,如图所示,三棱柱ADE -B ′CF 的体积为V =S △ADE ·CD =12×2×2×4=8,则几何体ADE -BCF 的体积V ADE BCF =V ADE B ′CF -V F BB ′C=8-13×⎝⎛⎭⎫12×2×2×2=203. 因为三棱锥M -DEF 的体积V M DEF =13×⎝⎛⎭⎫12×2×4×1=43, 所以V ADM BCF =203-43=163, 所以两几何体的体积之比为43∶163=1∶4.。
高三数学空间几何体试题答案及解析

高三数学空间几何体试题答案及解析1.(3分)(2011•重庆)高为的四棱锥S﹣ABCD的底面是边长为1的正方形,点S,A,B,C,D均在半径为1的同一球面上,则底面ABCD的中心与顶点S之间的距离为()A.B.C.1D.【答案】C【解析】由题意可知ABCD所在的圆是小圆,对角线长为,四棱锥的高为,而球心到小圆圆心的距离为,则推出顶点S在球心距的垂直分的平面上,而顶点S到球心的距离为1,即可求出底面ABCD的中心与顶点S之间的距离.解:由题意可知ABCD所在的圆是小圆,对角线长为,四棱锥的高为,点S,A,B,C,D均在半径为1的同一球面上,球心到小圆圆心的距离为,顶点S在球心距的垂直分的平面上,而顶点S到球心O的距离为1,所以底面ABCD的中心O'与顶点S之间的距离为1故选C点评:本题是基础题,考查球的内接多面体的知识,考查逻辑推理能力,计算能力,转化与划归的思想.2.(2013•天津)已知下列三个命题:①若一个球的半径缩小到原来的,则其体积缩小到原来的;②若两组数据的平均数相等,则它们的标准差也相等;③直线x+y+1=0与圆相切.其中真命题的序号是()A.①②③B.①②C.①③D.②③【答案】C【解析】①由球的体积公式V=可知,若一个球的半径缩小到原来的,则其体积缩小到原来的;故①正确;②若两组数据的平均数相等,则它们的标准差不一定相等,如2,2,2和1,2,3;这两组数据的平均数相等,它们的标准差不相等,故②错;③圆的圆心到直线x+y+1=0的距离d==半径r,故直线x+y+1=0与圆相切,③正确.故选C.3.如果,正方体的底面与正四面体的底面在同一平面α上,且AB//CD,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为m,n,那么m+n=()A .8B .9C .10D .11【答案】A【解析】因为过EF 做垂直于CD (AB )的平面垂直平分CD ,所以该平面与过AB 中点并与AB 垂直的平面平行,平面和正方体的4个侧面相交,由于EF 和正方体的侧棱不平行,所以它与正方体的六个面所在的平面相交的平面个数为4.同理与CE 相交的平面有4个,共8个,选A.【考点】该题主要考查空间点、线、面的位置关系,考查空间直线与平面的平行与相交,考查空间想象能力和逻辑思维能力.4. 如图,已知四棱锥,底面是等腰梯形,且∥,是中点,平面,,是中点.(1)证明:平面平面;(2)求点到平面的距离.【答案】(1)详见解析;(2)【解析】(1)根据中位线可得∥,从而可证得∥平面。
高三数学空间几何体的三视图与直观图试题
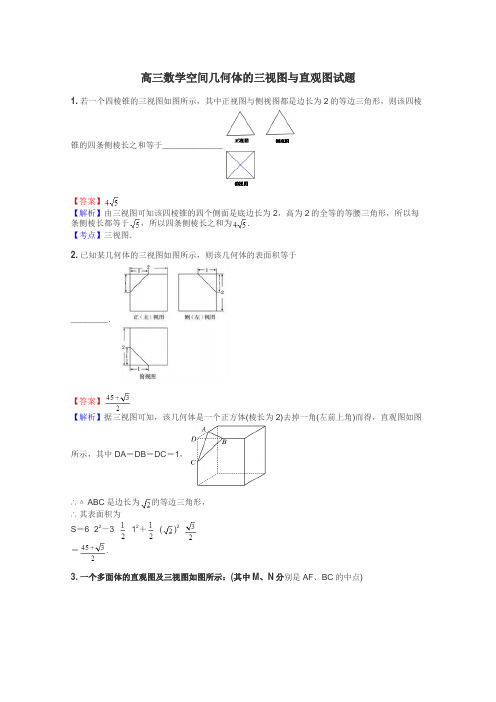
高三数学空间几何体的三视图与直观图试题1.若一个四棱锥的三视图如图所示,其中正视图与侧视图都是边长为2的等边三角形,则该四棱锥的四条侧棱长之和等于_____________【答案】【解析】由三视图可知该四棱锥的四个侧面是底边长为2,高为2的全等的等腰三角形,所以每条侧棱长都等于,所以四条侧棱长之和为.【考点】三视图.2.已知某几何体的三视图如图所示,则该几何体的表面积等于________.【答案】【解析】据三视图可知,该几何体是一个正方体(棱长为2)去掉一角(左前上角)而得,直观图如图所示,其中DA=DB=DC=1,∴△ABC是边长为的等边三角形,∴其表面积为S=6×22-3××12+×()2×=.3.一个多面体的直观图及三视图如图所示:(其中M、N分别是AF、BC的中点)(1)求证:MN∥平面CDEF;(2)求多面体A-CDEF的体积.【答案】(1)见解析(2)【解析】解:由三视图可知,AB=BC=BF=2,DE=CF=2,∠CBF=.(1)证明:取BF的中点G,连接MG、NG,由M、N分别为AF、BC的中点可得,NG∥CF,MG∥EF,∴平面MNG∥平面CDEF,又MN⊂平面MNG,∴MN∥平面CDEF.(2)取DE的中点H.∵AD=AE,∴AH⊥DE,在直三棱柱ADE-BCF中,平面ADE⊥平面CDEF,平面ADE∩平面CDEF=DE.∴AH⊥平面CDEF.∴多面体A-CDEF是以AH为高,以矩形CDEF为底面的棱锥,在△ADE中,AH=.S矩形=DE·EF=4,CDEF∴棱锥A-CDEF的体积为V=·S·AH=×4×=.矩形CDEF4.一个几何体的主视图和俯视图如图所示,主视图是边长为的正三角形,俯视图是边长为的正六边形,则该几何体左视图的面积是【答案】【解析】左视图的面积为.【考点】三视图.5.一空间几何体的三视图如图所示,该几何体的体积为12π+,则正视图中x的值为( )A.5B.4C.3D.2【答案】C【解析】三视图,由正四棱锥和圆柱组成,故选C.6.三棱柱的直观图和三视图如下图所示,其侧视图为正三角形(单位cm)⑴当x=4时,求几何体的侧面积和体积⑵当x取何值时,直线AB1与平面BB1C1C和平面A1B1C1所成角大小相等。
高三数学空间几何体的三视图与直观图试题答案及解析
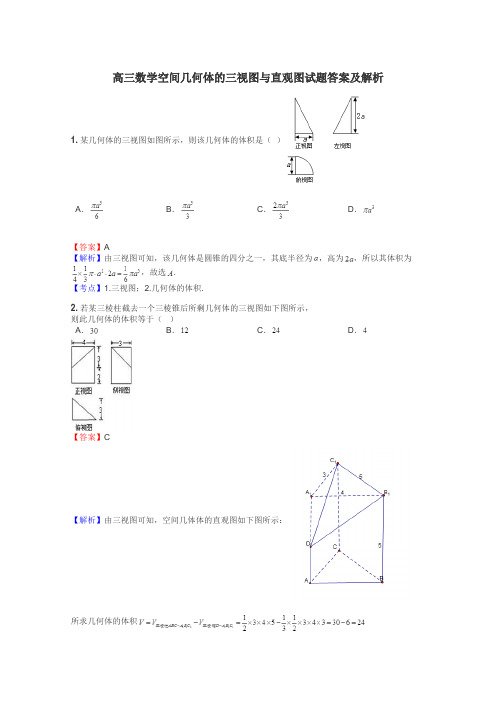
高三数学空间几何体的三视图与直观图试题答案及解析1.某几何体的三视图如图所示,则该几何体的体积是()A.B.C.D.【答案】A【解析】由三视图可知,该几何体是圆锥的四分之一,其底半径为,高为,所以其体积为,故选.【考点】1.三视图;2.几何体的体积.2.若某三棱柱截去一个三棱锥后所剩几何体的三视图如下图所示,则此几何体的体积等于()A.B.C.D.【答案】C【解析】由三视图可知,空间几体体的直观图如下图所示:所求几何体的体积故选C.【考点】1、三视图;2、空间几何体的体积.3.如图,一个几何体的三视图(正视图、侧视图和俯视图)为两个等腰直角三角形和一个边长为1的正方形,则其外接球的表面积为A.πB.2πC.3πD.4π【答案】C【解析】原几何体为有一条侧棱垂直于底面的四棱锥,且底面是边长为1的正方形,垂直于底面的侧棱长也为1,因此,该几何体可以补形为一个棱长为1的正方体,其外接球就是这个正方体的外接球,直径为正方体的对角线长,即2R=,故R=故外接球表面积为:4πR2=3π.【考点】三视图,几何体的外接球及其表面积4.如图所示,一个三棱锥的三视图是三个直角三角形(单位: cm),则该三棱锥的外接球的表面积为________cm2.【答案】29π【解析】从三棱锥的三视图可知,三棱锥有两侧面与底面垂直,把三棱锥补成长,宽,高分别为4,2,3的长方体,设外接球的半径为R,由42+22+32=4R2得,S=4πR2=29π(cm2).球5.某个长方体被一个平面所截,得到的几何体的三视图如图所示,则这个几何体的体积为()A.4B.2C.D.8【答案】D【解析】由三视图可知,该几何体如图所示,其底面为正方形,正方形的边长为2.HD=3,BF =1,将相同的两个几何体放在一起,构成一个高为4的长方体,所以该几何体的体积为×2×2×4=8.6.在一个几何体的三视图中,正视图和俯视图如图所示,则相应的侧视图可以为()【答案】D【解析】由题目所给的几何体的正视图和俯视图,可知该几何体为半圆锥和三棱锥的组合体,如图所示,可知左视图为等腰三角形,且轮廓线为实线,故选D.7.一个几何体的三视图如图所示,已知这个几何体的体积为,= .【答案】【解析】由三视图知,原几何体是一个四棱锥,底面是面积为的矩形,高为,所以,解得.【考点】三视图,空间几何体的体积.8.如图,水平放置的正三棱柱的主视图是一边长为2的正方形,则该三棱柱的左视图的面积为.【答案】【解析】左视图为一个矩形,长宽分别为,因此面积为.【考点】三视图9.若一个正三棱柱的正视图如图所示,其顶点都在一个球面上,则该球的表面积为() A.B.C.D.【答案】B【解析】依题意得,该正三棱柱的底面正三角形的边长为2,侧棱长为1.设该正三棱柱的外接球半径为R,易知该正三棱柱的底面正三角形的外接圆半径是2sin 60°×=,所以R2=+=,则该球的表面积为4πR2=.10.图中的网格是边长为1的小正方形,在其上用粗线画出了某多面体的三视图,则该多面体的体积为________.【答案】16【解析】从三视图可知,这是一个四棱锥,.【考点】三视图.11.如图所示,一个空间几何体的正视图和左视图都是边长为的正方形,俯视图是一个直径为的圆,那么这个几何体的体积为 ( )A.B.C.D.【答案】B【解析】几何体是圆柱,.【考点】三视图,圆柱的体积.12.一个几何体的三视图如图所示,其中正视图是一个正三角形,则该几何体的体积为( )A.1B.C.D.【答案】B【解析】由三视图可知,此几何体为三棱锥,如图,其中正视图为,是边长为2的正三角形,,且,底面为等腰直角三角形,,所以体积为,故选B.13.已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能等于()A.1B.C.D.【答案】C【解析】由题意知,正视图的最大面积为对角面的面积,最小面积为,而,故选C.【考点】三视图.14.已知某几何体的三视图如右图所示,其中俯视图是圆,且该几何体的体积为;直径为2的球的体积为.则()A.B.C.D.【答案】C【解析】由题意,该几何体是一个圆柱挖去一个圆锥得到的几何体,,,∴.选B.【考点】三视图,体积.15.三棱锥S-ABC及其三视图中的正视图和侧视图如图所示,则棱SB的长为()A.B.C.D.【答案】B【解析】过B作BD⊥AC于点D,则BD=2,CD=2,所以BC=,因为SC⊥平面ABC,所以SC⊥BC,所以SB=,故选B.【考点】三视图、直线与平面垂直的性质.16.一个几何体的三视图如图,则该几何体的体积为()A.B.C.D.【答案】A【解析】由三视图可知,该几何体是由一个半圆柱和一个三棱锥拼接而成,且半圆柱的底面是半径为的半圆,高为,其底面积为,故其体积为,三棱锥的底面是一个直角三角形,三棱锥的高也为,其底面积为,故其体积为,所以该几何体的体积为,故选A.【考点】1.三视图;2.组合体的体积17.右图为某几何体的三视图,则该几何体的体积为 .【答案】【解析】所求几何体为一个底面半径为1,高为1的圆柱与半径为1的四分之一的球的组合体,所以体积为【考点】三视图18.一个空间几何体的三视图如图所示,该几何体的体积为______.【答案】96【解析】几何体为一个三棱柱,底面为一个等腰三角形,底边长为6,底边上高为4,棱柱的高为8.因此所求体积为【考点】三视图19.把边长为1的正方形ABCD沿对角线BD折起,形成三棱锥C-ABD,它的主视图与俯视图如右上图所示,则二面角 C-AB-D的正切值为.【答案】【解析】如图所示,做BD,AB的中点分别为点E,F.则有CE面ABD,由于EF为等腰直角三角形ABD的中位线,故EF AB,则为二面角 C-AB-D的代表角,所以,故填.【考点】二面角三视图20.已知水平放置的△ABC的直观图△A′B′C′(斜二测画法)是边长为a的正三角形,则原△ABC 的面积为()A.a2B.a2C.a2D.a2【答案】D【解析】斜二测画法中原图面积与直观图面积之比为1∶,则易知S= ( a)2,∴S=a2.21.一个空间几何体的三视图如图所示,则该几何体的体积为()A.πcm3B.3πcm3C.πcm3D.πcm3【答案】D【解析】由三视图可知,此几何体为底面半径为1cm、高为3cm的圆柱上部去掉一个半径为1cm的半球,所以其体积为V=3π-π=π(cm 3).22. 右图为一简单组合体,其底面ABCD 为正方形,PD ⊥平面ABCD ,EC ∥PD ,且PD =AD =2EC =2.(1)请画出该几何体的三视图; (2)求四棱锥B-CEPD 的体积.【答案】(1)见解析 (2)2【解析】解:(1)该组合体的三视图如图所示.(2)∵PD ⊥平面ABCD , PD ⊂平面PDCE ,∴平面PDCE ⊥平面ABCD. ∵四边形ABCD 为正方形,∴BC ⊥CD ,且BC =DC =AD =2. 又∵平面PDCE∩平面ABCD =CD , BC ⊂平面ABCD. ∴BC ⊥平面PDCE.∵PD ⊥平面ABCD ,DC ⊂平面ABCD , ∴PD ⊥DC.又∵EC ∥PD ,PD =2,EC =1,∴四边形PDCE 为一个直角梯形,其面积: S 梯形PDCE = (PD +EC)·DC =×3×2=3, ∴四棱锥B-CEPD 的体积V B-CEPD =S 梯形PDCE ·BC =×3×2=2.23. 某几何体的三视图如图所示,则该几何体的体积为( ).A .16+8πB .8+8πC .16+16πD .8+16π【答案】A【解析】将三视图还原成直观图为:上面是一个正四棱柱,下面是半个圆柱体.所以V=2×2×4+×22×π×4=16+8π.24.某几何体的三视图如图所示,则其体积为________.【答案】【解析】由三视图还原几何体为半个圆锥,高为2,底面半圆的半径r=1.∴体积V=×(π×12×2)=.25.如图所示为一个几何体的直观图、三视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形).(1)求四棱锥P-ABCD的体积;(2)若G为BC上的动点,求证:AE⊥PG.【答案】(1)(2)见解析【解析】(1)由几何体的三视图可知,底面ABCD是边长为4的正方形,PA⊥平面ABCD,PA∥EB,且PA=4 ,BE=2 ,AB=4.∴VP-ABCD =PA·S四边形ABCD=×4 ×4×4=.(2)∵=,∠EBA=∠BAP=90°,∴△EBA∽△BAP,∴∠BEA=∠PBA.∴∠BEA+∠BAE=∠PBA+∠BAE=90°,∴PB⊥AE又∵BC⊥平面APEB,∴BC⊥AE.∵BC∩PB=B,∴AE⊥平面PBC.∵PG⊂平面PBC,∴AE⊥PG.26.如图所示,网格上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为________.【答案】9【解析】由题意知,此几何体是三棱锥,其高h=3,相应底面面积为S=×6×3=9,∴V=Sh=×9×3=9.27.某几何体的三视图如图所示,主视图和侧视图为全等的直角梯形,俯视图为直角三角形.则该几何体的表面积为( )A. B. C. D【答案】B【解析】此几何体直观图如图所示。
高三数学立体几何试题答案及解析

高三数学立体几何试题答案及解析1.已知三棱锥的三视图,则该三棱锥的体积是()A.B.C.D.【答案】B【解析】如图所示,,点P在侧面ABC的射影为O,.∴该三棱锥的体积.故选:B.【考点】由三视图求面积、体积.2.(本小题满分12分)直三棱柱中,,,分别是、的中点,,为棱上的点.(1)证明:;(2)是否存在一点,使得平面与平面所成锐二面角的余弦值为?若存在,说明点的位置,若不存在,说明理由.【答案】(1)证明见解析;(2)存在,点为中点.【解析】(1)先证明AB⊥AC,然后以A为原点建立空间直角坐标系A-xyz,则能写出各点坐标,由共线可得D(λ,0,1),所以,即DF⊥AE;(2)通过计算,面DEF的法向量为可写成,=(3,1+2λ,2(1-λ)),又面ABC的法向量=(0,0,1),令,解出λ的值即可.试题解析:(1)证明:,又,面又面以为原点建立如图所示的空间直角坐标系则,,,,设,且,即:(2)假设存在,设面的法向量为,则即:令由题可知面的法向量平面与平面所成锐二面角的余弦值为即:或(舍)当点为中点时,满足要求.【考点】1、二面角的平面角及求法;2、直线与平面垂直的性质.【方法点晴】本题考查空间中直线与直线的位置关系、空间向量及其应用,建立空间直角坐标系是解决问题的关键,属中档题.解题时一定要注意二面角的平面角是锐角还是钝角,否则很容易出现错误.3.已知正四棱锥中,,那么当该棱锥的体积最大时,它的高为()A.B.C.D.【答案】C【解析】设正四棱锥的高为,则,则,,所以四棱锥的体积,,由得,所以体积函数在区间上单调递增,在区间上单调递减,所以当时,体积有最大值,故选C.【考点】1.多面体体积;2.导数与函数最值.【方法点睛】本题主要考查本题主要考查立体几何中的最值问题,多面体体积公式、导数与函数等知识,属中档题.解决此类问题的两大核心思路:一是将立体问题转化为平面问题,结合平面几何的相关知识求解;二是建立目标函数的数学思想,选择合理的变量,利用导数、基本不等式或配方法求其最值.4.设三棱锥的三条侧棱两两互相垂直,且长度分别为,则其外接球的表面积为()A.B.C.D.【答案】B【解析】由题意可知其外接球的直径,所以外接球的表面积为.【考点】球的表面积公式.5.某几何体的三视图如图所示,则该几何体的体积为.【答案】【解析】该几何体为一个四棱锥,高为,底面为矩形,长宽分别为,因此体积为【考点】三视图6.已知是两条不同的直线,是三个不同的平面,则下列命题中正确的是()A.若B.若C.若D.若【答案】C【解析】垂直于同一平面的两个平面可能平行,也可能相交,所以A选项不正确;两个平面内存在两条平行的直线时,两平面可能相交,也可能平行,所以B选项不正确;,又,,所以C选项正确;若,则或,所以D不正确.故D正确.【考点】1线面位置关系;2面面位置关系.【易错点晴】本题主要考查的是空间点、线、面的位置关系,属于容易题.解题时一定要抓住题目中的重要字眼“真命题”,否则很容易出现错误.解决空间点、线、面的位置关系这类试题时一定要万分小心,除了作理论方面的推导论证外,利用特殊图形进行检验,也可作必要的合情推理.7.已知直线平面,直线平面,给出下列命题,其中正确的是()①;②;③;④A.②④B.②③④C.①③D.①②③【答案】C【解析】对①,因为直线平面,∥,则,又直线,所以,①对;对②,与的关系是:平行、相交或异面,②错;对③,因为直线平面,∥,所以,又由面面垂直的判定定理得,③对;对④,与可以平行或相交,④错,所以选C.本题可借助于长方体去判定.【考点】1.空间直线、平面的位置关系.【易错点晴】本题主要考查的是空间点、线、面的位置关系,属于中档题.解决空间点、线、面的位置关系这类试题时一定要万分小心,除了作理论方面的推导论证外,利用特殊图形或长方体作为载体进行检验,也可作必要的合情推理.8.利用一个球体毛坯切削后得到一个四棱锥P—ABCD,其中底面四边形ABCD是边长为1的正方形,,且,则球体毛坯体积的最小值应为()A.B.C.D.【答案】D【解析】若使得球体毛坯体积最小,则四棱锥各顶点应都在球上,由题意,将四棱锥补成一个长方体,则转化为求长方体外接球体积,长方体体对角线为外接球直径,体对角线长为,所以球的半径为,体积为.【考点】多面体的外接球.9.(2007•山东)下列几何体各自的三视图中,有且仅有两个视图相同的是()A.①②B.①③C.①④D.②④【答案】D【解析】利用三视图的作图法则,对选项判断,A的三视图相同,圆锥,四棱锥的两个三视图相同,棱台都不相同,推出选项即可.解:正方体的三视图都相同,而三棱台的三视图各不相同,圆锥和正四棱锥的,正视图和侧视图相同,所以,正确答案为D.故选D【考点】简单空间图形的三视图.10.如图是某几何体的三视图,其中正视图为正方形,俯视图是腰长为的等腰直角三角形,则该几何体的体积为_________________;表面积为________________.【答案】体积为;表面积为【解析】由题意可知三视图复原的几何体如图为四棱锥,是正方体的一部分,正方体的棱长为2;所以几何体的体积是正方体体积的一半减去,所求几何体的体积为;表面积为【考点】三视图,几何体的体积,表面积11.已知某几何体的三视图如图,其中正视图中半圆的半径为1,则该几何体的体积为()A.B.C.D.【答案】A【解析】根据该几何体的三视图可知几何体的形状是一个长为,宽为,高为的长方体挖去一个直径为高为的圆柱,该几何体的体积为,选A.【考点】1、三视图;2、组合体的体积.12.如图是一建筑物的三视图(单位:米),现需将其外壁用油漆刷一遍,若每平方米用漆千克,则共需油漆的总量为()A.千克B.千克C.千克D.千克【答案】B【解析】由三视图可知可间房由底部长宽高分别为的长方体与底面半径.母线长分别为圆锥体组合而成,所以其可刷漆的表面积为,则需要漆的总量为千克,故正确选项为B.【考点】空间几何体的表面积.13.若=(2,﹣1,0),=(3,﹣4,7),且(λ+)⊥,则λ的值是()A.0B.1C.﹣2D.2【答案】C【解析】利用(λ+)⊥⇔即可得出.解:∵=λ(2,﹣1,0)+(3,﹣4,7)=(3+2λ,﹣4﹣λ,7),(λ+)⊥,∴,∴2(3+2λ)﹣(﹣4﹣λ)+0=0,解得λ=﹣2.故选C.【考点】向量的数量积判断向量的共线与垂直.14.如图,在四棱锥P﹣ABCD中,AD∥BC,AB⊥AD,AB⊥PA,BC=2AB=2AD=4BE,平面PAB⊥平面ABCD,(Ⅰ)求证:平面PED⊥平面PAC;(Ⅱ)若直线PE与平面PAC所成的角的正弦值为,求二面角A﹣PC﹣D的平面角的余弦值.【答案】(Ⅰ)证明见解析(Ⅱ)【解析】(I)由面面垂直的性质定理证出PA⊥平面ABCD,从而得到AB、AD、AP两两垂直,因此以AB、AD、AP为x轴、y轴、z轴,建立坐标系o﹣xyz,得A、D、E、C、P的坐标,进而得到、、的坐标.由数量积的坐标运算公式算出且,从而证出DE⊥AC且DE⊥AP,结合线面垂直判定定理证出ED⊥平面PAC,从而得到平面PED⊥平面PAC;(II)由(Ⅰ)得平面PAC的一个法向量是,算出、夹角的余弦,即可得到直线PE与平面PAC所成的角θ的正弦值,由此建立关于θ的方程并解之即可得到λ=2.利用垂直向量数量积为零的方法,建立方程组算出=(1,﹣1,﹣1)是平面平面PCD的一个法向量,结合平面PAC的法向量,算出、的夹角余弦,再结合图形加以观察即可得到二面角A ﹣PC﹣D的平面角的余弦值.解:(Ⅰ)∵平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,AB⊥PA∴PA⊥平面ABCD结合AB⊥AD,可得分别以AB、AD、AP为x轴、y轴、z轴,建立空间直角坐标系o﹣xyz,如图所示可得A(0,0,0)D(0,2,0),E(2,1,0),C(2,4,0),P(0,0,λ)(λ>0)∴,,得,,∴DE⊥AC且DE⊥AP,∵AC、AP是平面PAC内的相交直线,∴ED⊥平面PAC.∵ED⊂平面PED∴平面PED⊥平面PAC(Ⅱ)由(Ⅰ)得平面PAC的一个法向量是,设直线PE与平面PAC所成的角为θ,则,解之得λ=±2∵λ>0,∴λ=2,可得P的坐标为(0,0,2)设平面PCD的一个法向量为=(x0,y,z),,由,,得到,令x0=1,可得y=z=﹣1,得=(1,﹣1,﹣1)∴cos<,由图形可得二面角A﹣PC﹣D的平面角是锐角,∴二面角A﹣PC﹣D的平面角的余弦值为.【考点】用空间向量求平面间的夹角;平面与平面垂直的判定;二面角的平面角及求法.15.已知正三棱锥的底面边长为,侧棱长为,则正三棱锥的体积为.【答案】【解析】∵正三棱锥的底面边长为,∴底面正三角形的高为,可得底面中心到三角形顶点的距离为,∵正三棱锥侧棱长为,∴正三棱锥的高,所以三棱锥的体积.所以答案应填:.【考点】棱柱、棱锥、棱台的体积.16.在等腰梯形中,,,,是的中点,将梯形绕旋转,得到(如图).(I)求证:;(II)求二面角的余弦值.【答案】(1)证明见解析;(2).【解析】(I)由题意容易证明四边形是平行四边形,.又为等腰梯形,,四边形是菱形,可证得,根据面面垂直的性质定理可证得平面,从而证得;(II)易证平面,以为坐标原点,建立空间直角坐标系,分别求出平面的法向量和平面的法向量,根据向量的夹角公式求得二面角的余弦值.试题解析:(I)证明:,是的中点,.又,四边形是平行四边形,.又为等腰梯形,,,四边形是菱形,,,即.平面平面,平面平面,平面.又平面,.(II)解:平面,同理平面.如图建立空间直角坐标系,设,则,,,,则,.设平面的法向量为,.设平面的法向量为,,设二面角的平面角为,,二面角的余弦值为.【考点】空间中垂直关系的证明及空间向量的应用.17.如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的正(主)视图与侧(左)视图的面积的比为.【答案】【解析】因为三棱锥的主视图与左视图都是三角形, 正视图和侧视图三角形的底边长都是正方体的棱长,高都是到底面的距离(都是正方体的棱长),所以,三棱锥的主视图与左视图的面积相等,即比值为,故答案为.【考点】1、几何体的三视图;2、三角形面积公式.18.如图,某几何体的正视图(主视图)是平行四边形,侧视图(左视图)和俯视图都是矩形,则几何体的体积为()A.B.C.D.【答案】B【解析】如图所示,该几何体是一个底面为平行四边形,高为的棱柱,体积为,故选B.【考点】几何体的体积.19.如图,矩形O′A′B′C′是水平放置的一个平面图形的直观图,其中O′A′=6,O′C′=2,则原图形OABC的面积为________.【答案】【解析】因为矩形是水平放置的一个平面图形的直观图,所以根据画直观图的基本原理知原图形是底边长为的平行四边形,其高是,因此面积是,故答案为.【考点】1、画直观图的基本原理;2、平行四边形的面积公式.20.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为()A.B.C.D.【答案】D【解析】由三视图知几何体是由正方体截取两个角得到,如图所示,故体积为.【考点】三视图.21.如图所示,四棱锥的底面是梯形,且,平面,是中点,.(Ⅰ)求证:平面;(Ⅱ)若,,求直线与平面所成角的大小.【答案】(I)证明见解析;(II).【解析】(I)取的中点,连结,证得,从而证得平面,根据平行四边形的性质,得,即可证明平面;(II)分别以的方向为轴的正方向,建立空间直角坐标系,求解出平面和向量,即可利用向量所成的角,得到直线与平面所成角的大小.试题解析:(Ⅰ)证明:取的中点,连结,如图所示.因为,所以.因为平面,平面,所以.又因为,所以平面.因为点是中点,所以,且.又因为,且,所以,且,所以四边形为平行四边形,所以,所以平面.(Ⅱ)解:设点O,G分别为AD,BC的中点,连结,则,因为平面,平面,所以,所以.因为,由(Ⅰ)知,又因为,所以,所以所以为正三角形,所以,因为平面,平面,所以.又因为,所以平面.故两两垂直,可以点O为原点,分别以的方向为轴的正方向,建立空间直角坐标系,如图所示.,,,所以,,,设平面的法向量,则所以取,则,设与平面所成的角为,则,因为,所以,所以与平面所成角的大小为.【考点】直线与平面垂直的判定与证明;直线与平面所成角的求解.22.如图,在三棱台中,平面平面,,BE=EF=FC=1,BC=2,AC=3.(Ⅰ)求证:BF⊥平面ACFD;(Ⅱ)求二面角B-AD-F的平面角的余弦值.【答案】(Ⅰ)证明见解析;(Ⅱ).【解析】(Ⅰ)先证,再证,进而可证平面;(Ⅱ)方法一:先找二面角的平面角,再在中计算,即可得二面角的平面角的余弦值;方法二:先建立空间直角坐标系,再计算平面和平面的法向量,进而可得二面角的平面角的余弦值.试题解析:(Ⅰ)延长,,相交于一点,如图所示.因为平面平面,且,所以平面,因此.又因为,,,所以为等边三角形,且为的中点,则.所以平面.(Ⅱ)方法一:过点作于Q,连结.因为平面,所以,则平面,所以.所以是二面角的平面角.在中,,,得.在中,,,得.所以二面角的平面角的余弦值为.方法二:如图,延长,,相交于一点,则为等边三角形.取的中点,则,又平面平面,所以,平面.以点为原点,分别以射线,的方向为,的正方向,建立空间直角坐标系.由题意得,,,,,.因此,,,.设平面的法向量为,平面的法向量为.由,得,取;由,得,取.于是,.所以,二面角的平面角的余弦值为.【考点】线面垂直,二面角.【方法点睛】解题时一定要注意二面角的平面角是锐角还是钝角,否则很容易出现错误.证明线面垂直的关键是证明线线垂直,证明线线垂直常用的方法是直角三角形、等腰三角形的“三线合一”和菱形、正方形的对角线.23.直线a、b是异面直线,α、β是平面,若a⊂α,b⊂β,α∩β=c,则下列说法正确的是()A.c至少与a、b中的一条相交B.c至多与a、b中的一条相交C.c与a、b都相交D.c与a、b都不相交【答案】A【解析】利用空间中线线、线面、面面间的位置关系判断求解.解:由直线a、b是异面直线,α、β是平面,若a⊂α,b⊂β,α∩β=c,知:对于B,c可以与a、b都相交,交点为不同点即可,故B不正确;对于C,a∥c,b∩c=A,满足题意,故C不正确;对于D,c与a、b都不相交,则c与a、b都平行,所以a,b平行,与异面矛盾,故D不正确;对于A,由B,C、D的分析,可知A正确故选:A.24.已知某几何体的三视图如图所示,则该几何体的体积等于()A.B.160C.D.【答案】A【解析】由三视图知该几何体是由一个直三棱柱和一个四棱锥组合的组合体,其中直三棱柱的底面为左视图,高为,故体积.四棱锥的底面为边长为的正方形,高为,所以体积,所以该几何体的体积为.故选A.【考点】1、几何体的三视图;2、几何体的体积.【方法点睛】本题主要考查三视图及空间几何体的体积,属于中档题.空间几何体体积问题的常见类型及解题策略:(1)求简单几何体的体积时若所给的几何体为柱体椎体或台体,则可直接利用公式求解;(2)求组合体的体积时若所给定的几何体是组合体,不能直接利用公式求解,则常用转换法、分割法、补形法等进行求解. (3)求以三视图为背景的几何体的体积时应先根据三视图得到几何体的直观图,然后根据条件求解.25.中国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器——商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其体积为12.6(立方寸),则图中的x为()A.1.2B.1.6C.1.8D.2.4【答案】B【解析】由题意得,即,解得,故选B.【考点】几何体的三视图及体积.26.某几何体的三视图如图所示(单位:cm),则该几何体的体积等于()cm3A.4+B.4+C.6+D.6+【答案】D【解析】由三视图还原原几何体如图,是一个半圆柱与一个直三棱柱的组合体,半圆柱的底面半径为,高为;直三棱柱底面是等腰直角三角形(直角边为),高为.∴.故本题选D.【考点】空间几何体的三视图.27.在正方体中,是的中点,则异面直线与所成角的余弦值等于_______,若正方体边长为1,则四面体的体积为_________.【答案】;【解析】异面直线与所成角为,,.【考点】立体几何中异面直线所成角的余弦值的求法以及三棱锥的体积的求法.28.如图,在四棱锥中,底面,,,,,点为棱的中点.(1)证明:;(2)若为棱上一点,满足,求二面角的余弦值.【答案】(1)证明见解析;(2).【解析】(1)以点为原点建立空间直角坐标系(如图),求得,,可得,即可证结论;(2)先根据确定的位置,在求出平面的一个法向量,可证平面一个的法向量为,利用空间向量夹角余弦公式即可得结论.试题解析:(1)证明:依题意,以点为原点建立空间直角坐标系(如图),可得,,,.由为棱的中点,得.向量,,故.所以.(2)向量,,,.由点在棱上,设,.故.由,得,因此,,解得.即.设为平面的法向量,则,即.不妨令,可得为平面的一个法向量.取平面的法向量,则.易知,二面角是锐角,所以其余弦值为.【考点】1、空间直线垂直的判定;2、空间向量夹角余弦公式.29.如图,在三棱锥中,底面,且,点是的中点, 交于点.(1)求证:平面;(2)当时, 求三棱锥的体积.【答案】(1)详见解析(2)【解析】(1)证明线面垂直,一般利用线面垂直判定定理,即从线线垂直出发给予证明,而线线垂直的证明与寻找,往往从两个方面,一是利用线面垂直性质定理转化为线线垂直,另一是结合平几条件,如本题利用等腰三角形底边中线性质得(2)求三棱锥体积,关键在于确定高,即线面垂直.由(1)得平面,因此,这样只需在对应三角形中求出对应边即可.试题解析:(1)底面,面,又因为是的中点, 面由已知平面.(2)平面,平面,而,又又平面而.【考点】线面垂直判定与性质定理,三棱锥体积【思想点睛】垂直、平行关系证明中应用转化与化归思想的常见类型.(1)证明线面、面面平行,需转化为证明线线平行.(2)证明线面垂直,需转化为证明线线垂直.(3)证明线线垂直,需转化为证明线面垂直.30.过球表面上一点引三条长度相等的弦,且两两夹角都为60°,若球半径为,求弦的长度___________.【答案】【解析】依题意可知,这是一个正四面体的外接球. 若一个正四面体边长为,其外接球半径公式为:,即.【考点】球的内接几何体.【思路点晴】对棱相等的三棱锥,设三对棱长分别为,如下图所示三棱锥,请同学们推导其外接球半径公式,特别地,若一个正四面体边长为,其外接球半径公式为:.设几何体底面外接圆半径为,常见的图形有正三角形,直角三角形,矩形,它们的外心可用其几何性质求;而其它不规则图形的外心,可利用正弦定理来求.2.若长方体长宽高分别为则其体对角线长为;长方体的外接球球心是其体对角线中点.找几何体外接球球心的一般方法:过几何体各个面的外心分别做这个面的垂线,交点即为球心.31.某几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.【答案】D【解析】由题意得,根据给定的三视图可知,原几何体表示,左侧是一个底面半径为,高为半个圆锥,几何体的右侧是一个底面为底边为,高为的等腰三角形三棱锥,其中三棱锥的高为,所以几何体的体积为,故选D.【考点】几何体的三视图及体积的计算.32.已知直线与平面平行,是直线上的一定点,平面内的动点满足:与直线成.那么点轨迹是()A.两直线B.椭圆C.双曲线D.抛物线【答案】C【解析】题意画图如下,是直线上的定点,有一平面与直线平行,平面内的动点满足的连线与成角,因为空间中过与成角的直线组成两个相对顶点的圆锥,即为平行于圆锥轴的平面,点可理解为是截面与圆锥侧面的交点,所以点的轨迹为双曲线,故选C.【考点】1、空间点、线、面的位置关系;2、圆锥曲线的定义.33.三棱锥内接于球,,当三棱锥的三个侧面积和最大时,球的体积为.【答案】【解析】由于三角形的面积公式,当时取得最大值,所以当两两垂直时,侧面积和取得最大值.此时,由于三棱锥三条侧棱两两垂直,所以可以补形为正方体,三棱锥的外接球即正方体的外接球,其直径等于正方体的体对角线即,故求的体积为.【考点】几何体的外接球.【思路点晴】设几何体底面外接圆半径为,常见的图形有正三角形,直角三角形,矩形,它们的外心可用其几何性质求;而其它不规则图形的外心,可利用正弦定理来求.若长方体长宽高分别为则其体对角线长为;长方体的外接球球心是其体对角线中点.找几何体外接球球心的一般方法:过几何体各个面的外心分别做这个面的垂线,交点即为球心.三棱锥三条侧棱两两垂直,且棱长分别为,则其外接球半径公式为: .34.如图,在直三棱柱中,,过的中点作平面的垂线,交平面于,则与平面所成角的正切值为()A.B.C.D.【答案】C【解析】连接,则,由直三棱柱得,因此,因此为的中点,过作于,则为与平面所成角, ,选C.【考点】线面角35.如图,在四棱锥中,底面,底面是直角梯形,(1)在上确定一点,使得平面,并求的值;(2)在(1)条件下,求平面与平面所成锐二面角的余弦值.【答案】(1)(2)【解析】(1)由线面平行的性质定理,可得线线平行,再根据平行得相似,即得比例关系:取。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三数学空间几何体试题答案及解析1.有一正方体,六个面上分别写有数字1、2、3、4、5、6,有3个人从不同的角度观察,结果如图所示.若记3的对面的数字为,4的对面的数字为,则 ( )A.3B.7C.8D.11【答案】C【解析】从图中可看出,与4相邻的是1、6、3、5,故与4相对的是2;与3相邻的是1、2、4、5,故与3相对的是6,所以.【考点】空间几何体.2.有一正方体,六个面上分别写有数字1、2、3、4、5、6,有3个人从不同的角度观察,结果如图所示.若记3的对面的数字为,4的对面的数字为,则 ( )A.3B.7C.8D.11【答案】C【解析】从图中可看出,与4相邻的是1、6、3、5,故与4相对的是2;与3相邻的是1、2、4、5,故与3相对的是6,所以.【考点】空间几何体.3.已知矩形的周长为36,矩形绕它的一条边旋转形成一个圆柱,则旋转形成的圆柱的侧面积的最大值为.【答案】81【解析】假设矩形的一边为(),则另一边为.以x长的变为轴旋转成的圆柱的侧面积为.所以当时,.【考点】1.旋转体的知识.2.函数的最值问题.4.已知四面体的外接球的球心在上,且平面,,若四面体的体积为,则该球的表面积为()A.B.C.D.【答案】D【解析】如下图所示,由于四面体的外接球的球心在上,则为其外接球的一条直径,因此,设球的半径为,在中,,由勾股定理得,,由于为球上一点,则,且平面,所以,,所以球的表面积为,故选D.【考点】1.勾股定理;2.三角形的面积;3.三棱锥的体积;4.球的表面积5.如图所示,在正方体ABCD A1B1C1D1中,M,N分别是BC1,CD1的中点,则下列判断错误的是()A.MN与CC1垂直B.MN与AC垂直C.MN与BD平行D.MN与A1B1平行【答案】D【解析】由于C1D1与A1B1平行,MN与C1D1是异面直线,所以MN与A1B1是异面直线,故选项D错误.6.如图,正方形BCDE的边长为a,已知AB=BC,将直角△ABE沿BE边折起,A点在平面BCDE 上的射影为D点,则对翻折后的几何体有如下描述:(1)AB与DE所成角的正切值是.(2)三棱锥B-ACE的体积是a3.(3)AB∥CD.(4)平面EAB⊥平面ADE.其中正确的叙述有(写出所有正确结论的编号).【答案】(1)(2)(4)【解析】翻折后得到的直观图如图所示.AB与DE所成的角也就是AB与BC所成的角,即为∠ABC.因为AD⊥平面BCDE,所以平面ADC⊥平面BCDE. 又因为四边形BCDE为正方形,所以BC⊥CD.可得BC⊥平面ACD.所以BC⊥AC.因为BC=a,AB=BC=a,则AC== a.在Rt△ABC中,tan∠ABC==.故(1)正确;由AD==a,可得VB-ACE =VA-BCE=×a2·a=,故(2)正确;因为AB与CD异面,故(3)错;因为AD⊥平面BCDE,所以平面ADE⊥平面BCDE.又BE⊥ED,所以BE⊥平面ADE,故平面EAB⊥平面ADE,故(4)正确.7.如图所示的几何体ABCDFE中,△ABC,△DFE都是等边三角形,且所在平面平行,四边形BCED为正方形,且所在平面垂直于平面ABC.(Ⅰ)证明:平面ADE∥平面BCF;(Ⅱ)求二面角D-AE-F的正切值.【答案】(Ⅰ)利用线线平行,则面面平行证明,即可得证;(Ⅱ).【解析】(Ⅰ)先证明四边形为平行四边形得,又,所以平面平面;(Ⅱ)建立空间直角坐标系,先求出平面的一个法向量,再求出平面的一个法向量,然后利用公式即可求出余弦值为,进而求出正切值.试题解析:(Ⅰ)取的中点,的中点,连接.则,又平面平面,所以平面,同理平面,所以又易得,所以四边形为平行四边形,所以,又,所以平面平面. (6分)(Ⅱ)建立如图所示的空间直角坐标系,设,则,,,,,.设平面的一个法向量是,则,令,得. (9分)设平面的一个法向量是,则令,得.所以,易知二面角为锐二面角,故其余弦值为,所以二面角的正切值为. (12分)【考点】1.平面与平面垂直的判定方法;2.二面角的求法.8.已知某四棱锥的三视图,如图。
则此四棱锥的体积为()A.3B.4C.5D.6【答案】B【解析】如图,四棱锥..故选B.【考点】四棱锥的体积点评:主要是考查了四棱锥的体积的计算,属于基础题。
9.直三棱柱中,,规定主视方向为垂直于平面的方向,则可求得三棱柱左视图的面积为;【答案】【解析】根据题意,由于直三棱柱中,,规定主视方向为垂直于平面的方向,则可求得三棱柱左视图的面积为高为1,底面的长为,故可知面积为。
【考点】三视图点评:主要是考查了三视图的基本运用,来求解其面积,属于基础题。
10.下图是一个几何体的正(主)视图和侧(左)视图,其俯视图是面积为的矩形.则该几何体的表面积是()A.B.C.8D.16【答案】A【解析】根据题意,由于三视图可知该几何体是三棱柱,且底面是等腰直角三角形,腰长为2,而俯视图是面积为的矩形.高为h,,故可知表面积为S==,故答案为A.【考点】三视图点评:主要是考查了三视图在亚牛几何体表面积中的运用,属于中档题。
11.一只蚂蚁从正方体的顶点处出发,经正方体的表面,按最短路线爬行到达顶点位置,则下列图形中可以表示正方体及蚂蚁最短爬行路线的正视图是A.①②B.①③C.②④D.③④【答案】C【解析】根据题意,由于蚂蚁从正方体的顶点处出发,经正方体的表面,按最短路线爬行到达顶点位置,那么可知最短的距离即为相邻两个平面的展开图的面对角线的长度,那么展开平面和平面平面得到最短路线,那么正视图对应的为②④,故选C.【考点】侧面展开图点评:主要是考查了空间几何体的侧面展开图的运用,属于基础题。
12.已知三棱锥的三视图如图所示.(Ⅰ)求证:是直角三角形;求三棱锥是全面积;(Ⅲ)当点在线段上何处时,与平面所成的角为.【答案】1)根据视图中所给的数据特证可以证明BC⊥面PAB,由线面垂直的性质证出BC⊥PB,由此证得三角形为直角三角形,(2)(3)当为线段的中点时,与平面所成的角为【解析】解析:(Ⅰ)由三视图可得:由俯视图知,故是以为直角顶点的直角三角形. 4分(Ⅱ)且,,且由(Ⅰ)知是直角三角形,故其面积为故三棱锥的全面积为 8分(Ⅲ)在面内过做的垂线,以为原点,所在直线分别为轴、轴、轴建立空间直角坐标系,如图所示则设为面的一个法向量,则取设,,,故当为线段的中点时,与平面所成的角为……13分【考点】由三视图求几何体的面积、体积点评:本题考点是由三视图求几何体的面积、体积,考查对三视图的理解与应用,主要考查三视图与实物图之间的关系,用三视图中的数据还原出实物图的数据,再根据相关的公式求表面积与体积,本题求的是四棱锥的体积,其公式为 ×底面积×高.三视图的投影规则是:“主视、俯视长对正;主视、左视高平齐,左视、俯视宽相等”,三视图是新课标的新增内容,在以后的高考中有加强的可能.用向量法求线面角是空间向量的一个重要运用,其步骤是:一、建立坐标系,表示出相应量的坐标,二、求出直线的方向向量以及面的法向量,三、利用公式表示线面角或者面面角的三角函数值求角.用向量解决几何问题是新课标的新增内容,这几年高考中此工具是一个常考常新的类型.13.已知四面体的所有棱长都相等,它的俯视图如下图所示,是一个边长为的正方形;则四面体外接球的表面积为()A.B.C.D.【答案】A【解析】根据题意,根据题意,画出图形,结合题目所给数据,求出正视图的三边的长,可求其面积.解:这个正四面体的位置是AC放在桌面上, BD平行桌面,它的正视图是和几何体如图,则正视图 BD=,DO=BO=∴其外接球的半径为故其球的表面积公式为,故答案为,选A.【考点】球的表面积和三视图点评:主要是考查了三视图的运用,以及球的表面积公式的运用,属于基础题。
14.已知正三棱锥的侧面均为等腰直角三角形,侧面的面积为,则它的外接球体积为【答案】【解析】如图,三棱锥P-ABC为正三棱锥,则它的外接球的直径为正方体的对角线PD,求得,,则正三棱锥的体积为D【考点】几何体的体积点评:如果一个三棱锥三个侧面两两互相垂直,且三条棱长分别为,则其外接球的直径为。
15.已知四棱锥的底面是菱形.,为的中点.(1)求证:∥平面;(2)求证:平面平面.【答案】证明如下【解析】(1)证明:设AC BD=O,因为,分别为,的中点,所以∥.因为平面平面所以∥平面.(2)证明:连结因为,所以.在菱形中,因为所以平面因为平面所以平面平面.【考点】直线与平面平行的判定定理;平面与平面垂直的判定定理点评:在立体几何中,常考的定理是:直线与平面垂直的判定定理、直线与平面平行的判定定理。
16.已知一个三棱锥的三视图如图所示,其中俯视图是等腰直角三角形,则该三棱锥的的体积为____________.【答案】【解析】该几何体为三棱锥,底面为等腰三角形,底边长为,高为,三棱锥高为2,所以,该三棱锥的的体积为。
【考点】三视图,几何体的体积。
点评:简单题,三视图问题已成为高考必考知识内容,一般难度不大。
关键是明确三视图画法规则,掌握常见几何体的几何特征。
三视图中虚线,是被遮住的棱。
17.如图,已知正方体的棱长为1,动点P在此正方体的表面上运动,且,记点P的轨迹的长度为,则函数的图像可能是()【答案】B【解析】P的轨迹为以A为球心,PA为半径的球面与正方体的交线。
所以在时,轨迹长度直线增加,而时,轨迹长度由减小到增加,之后逐渐减小,故选B。
【考点】本题主要考查正方体、球的几何特征,轨迹的概念。
点评:中档题,解题的关键是认识到P的轨迹为以A为球心,PA为半径的球面与正方体的交线。
定性分析“交线”的长度变化规律。
18.已知正四面体的俯视图如图所示,其中四边形ABCD是边长为2的正方形,则这个正四面体的体积为.【答案】【解析】由于题目中给定了正四面体的俯视图是一个正方形,边长为2,且有一个虚线和一条实线投在底面上,因此可知该几何体,正四面体的一条棱在平面内,另一条相对棱与平面平行,又正方形ABCD的边长为2 cm∴正四面体的棱长为ABCD对角线长,那么其体积则利用三棱锥的体积公式知道为,故答案为【考点】本试题考查了三视图的运用。
点评:解决该试题的关键是通过三视图的特点来分析得到原几何体的特点,结合四面体的体积公式来求解得到结论,属于中档题。
19.(12分)直三棱柱中,点M、N分别为线段的中点,平面侧面(1)求证:MN//平面 (2)证明:BC平面【答案】(1)只需证;(2)只需证。
【解析】(1)连在中,M、N分别为线段的中点平面故MN//平面(2) 为直三棱柱,方法一:取面上一点P作.又平面面且交线为AB同理BC平面方法二:过C作同理与CT重合为CB BC平面方法三:在面ABC内,作,在面同理BC平面【考点】面面垂直的性质定理;线面平行的判定定理;线面垂直的判定定理;直棱柱的结构特征。
