1-5章答案
C语言1-5章复习题及参考答案

一.选择题1、若a为int类型,且其值为3,则执行完表达式a+=a-=a*a后,a的值是()。
A .-3 B.9 C.-12 D.62、若有定义:int a=8, b=5, c; 执行语句 c=a/b+0.4; 后,c的值为()。
A .1.4 B.1 C.2.0 D.23、有如下程序:void main(){int i,sum;for(i=1;i<=3;sum++)sum+=i;printf("%d\n",sum);}该程序的执行结果是()。
A .6 B.3 C.死循环 D.04、下列关于表达式的描述中,错误的是()。
A . 常量和变量都是表达式。
B. 运算符类型对应表达式的类型。
C. 每一个表达式都有自己的值。
D. 表达式必须以分号结尾。
5、C语言中,合法的长整型常数是()。
A . '\t' B.” A” C.65 D.a6、若已定义 x 和 y为double 类型,则表达式 x=1;y=(x+3)/2 的值是()。
A .1 B.2 C.2.00000 D.2.500007、表达式:10!=9的值是()。
A . true B. 非零值 C.0 D.18、以下程序的输出结果是()。
#include<stdio.h>void main(){printf("%d\n", NULL);}A . 不确定的 B.0 C.-1 D.19、请选出合法的C语言赋值语句。
()A . a=b=58 B.i++; C. a=58,b=58 D. k=int(a+b);10、假设 int b=2; 表达式(b>>2)/(b>>1)的值是()。
A .0 B.2 C.4 D.811、关于语句printf(“hello world\n”);,下列描述中错误的是()。
A . printf()是格式化输出函数,用于输出信息。
B. printf()括号中的内容为函数的参数。
模拟电子技术题库参考答案(1-5章) - 副本

(2) A um
( Rc // Rc )
rbe
30(5 // 15) 75 1
-3-
模拟电子技术试题汇编参考答案
(3)
Ri Rb1 // Rb 2 // rbe rbe 1k R0 Rc 5k
(4) C e 断开, Re 有电流串联负反馈,( Aum 下降), Ri 增加, R0 不变;
(1) 画出直流通路和微变等效电路 (6 分)。 (2)设 U BEQ 0.7V ,求静态工作点
I CQ 、 U CEQ (4 分)
(3)求 Ri 、 Ro 、 Au
.
Uo Ui
.
.
,设 =30,
rbb' =19 4 (6 分)
(4) I CEO 、U CES 忽略不计,估算最大 不失真输出电压峰值 U om
rbe
100 (3 // 3) 50 3
Ri 5 // 15 // 3k 1.66k R0 RC 3k
(3) Aus
. . Ri 1.66 Au (50) 31.2 R s Ri 1 1.66
-4-
模拟电子技术试题汇编参考答案
3、如下图, C1 ~ C4 足够大,
Ri R1 // R3 // rbe rbe rbb ' (1 ) 26 26 194 (1 30) 1K 1 I EQ
(3) R R 10 K 0 4
U ( R4 // R L ) 30(10 // 10) 150 Au 0 1 u rbe
B;A (8)C (9)A (10)B(11)C(12) C
(1)A(2)B;A;C(3)B;C;C (4) C,B (5)C(6) A(7) ① B ② C ③B15、C
C语言1-5章复习题和参考答案.doc

1、若a为int类型,且其值为3,则执行完表达式a+=a-=a*a后,a的值是()。
A .-3 B.9 C.-12 D.62、若有定义:int a=8, b=5, c;执行语句c=a/b+0.4;后,c的值为()。
A .1.4 B.l C.2.0 D.23、有如下程序:void main(){int i,sum;for(i=l;i<=3;sum++)sum+=i;printf("%d\n",sum);}该程序的执行结果是()。
A .6 B.3 C.死循坏D.O4、下列关于表达式的描述屮,错误的是()0A.常量和变量都是表达式。
B.运算符类型对应表达式的类型。
C.每一个表达式都有自己的值。
D.表达式必须以分号结尾。
5、C语言中,合法的长整型常数是()。
A.'\t'B."A"C.65D.a6、若已定义x和y为double类型,则表达式x=l;y= (x+3) /2的值是()。
A.lB.2C.2.00000D.2.500007、表达式:10!二9的值是()oA.trueB.非零值C.OD.l8、以下程序的输出结果是()。
#include<stdio.h>void main(){printf("%d\n", NULL);}A.不确定的B.OC.-lD.l9、请选出合法的C语言赋值语句。
()A . a=b=58 B.i++; C. a=58,b=58 D. k=int(a+b);10^假设int b=2;表达式(b»2)/(b»l)的值是()。
A .0 B.2 C.4 D.811>关于语句printf("hello world\rT);,下列描述中错误的是()。
A . printf()是格式化输出函数,用于输出信息。
B.printf()括号屮的内容为函数的参数。
C.printf()括号中的内容会全部输出到控制台上。
复变函数1到5章测试题及答案

复变函数1到5章测试题及答案(总20页)--本页仅作预览文档封面,使用时请删除本页--- 2 -第一章 复数与复变函数(答案)一、 选择题1.当iiz -+=11时,5075100z z z ++的值等于(B ) (A )i (B )i - (C )1 (D )1-2.设复数z 满足arg(2)3z π+=,5arg(2)6z π-=,那么=z (A )(A )i 31+- (B )i +-3 (C )i 2321+-(D )i 2123+-3.复数)2(tan πθπθ<<-=i z 的三角表示式是(D )(A ))]2sin()2[cos(sec θπθπθ+++i (B ))]23sin()23[cos(sec θπθπθ+++i(C ))]23sin()23[cos(sec θπθπθ+++-i (D ))]2sin()2[cos(sec θπθπθ+++-i4.若z 为非零复数,则22z z -与z z 2的关系是(C ) (A )z z z z 222≥- (B )z z z z 222=- (C )z z z z 222≤- (D )不能比较大小5.设y x ,为实数,yi x z yi x z +-=++=11,1121且有1221=+z z ,则动点),(y x 的轨迹是(B )(A )圆 (B )椭圆 (C )双曲线 (D )抛物线- 3 -6.一个向量顺时针旋转3π,对应的复数为i 31-,则原向量对应的复数是(A )(A )2 (B )i 31+ (C )i -3 (D )i +3 7.使得22z z =成立的复数z 是(D )(A )不存在的 (B )唯一的 (C )纯虚数 (D )实数8.设z 为复数,则方程i z z +=+2的解是(B ) (A )i +-43 (B )i +43 (C )i -43 (D )i --439.满足不等式2≤+-iz iz 的所有点z 构成的集合是(D ) (A )有界区域 (B )无界区域 (C )有界闭区域 (D )无界闭区域10.方程232=-+i z 所代表的曲线是(C )(A )中心为i 32-,半径为2的圆周 (B )中心为i 32+-,半径为2的圆周(C )中心为i 32+-,半径为2的圆周 (D )中心为i 32-,半径为2的圆周11.下列方程所表示的曲线中,不是圆周的为(B ) (A )221=+-z z (B )433=--+z z- 4 -(C ))1(11<=--a azaz (D ))0(0>=-+++c c a a z a z a z z 12.设,5,32,1)(21i z i z z z f -=+=-=,则12()f z z -=(C ) (A )i 44-- (B )i 44+ (C )i 44- (D )i 44+- 13.000Im()Im()limz z z z z z →--(D )(A )等于i (B )等于i - (C )等于0 (D )不存在 14.函数),(),()(y x iv y x u z f +=在点000iy x z +=处连续的充要条件是(C ) (A )),(y x u 在),(00y x 处连续 (B )),(y x v 在),(00y x 处连续 (C )),(y x u 和),(y x v 在),(00y x 处连续(D )),(),(y x v y x u +在),(00y x 处连续15.设C z ∈且1=z ,则函数zz z z f 1)(2+-=的最小值为(A )(A )3- (B )2- (C )1- (D )1二、填空题1.设)2)(3()3)(2)(1(i i i i i z ++--+=,则=z2.设)2)(32(i i z +--=,则=z arg 8arctan -π 3.设43)arg(,5π=-=i z z ,则=z i 21+- 4.复数22)3sin 3(cos )5sin 5(cos θθθθi i -+的指数表示式为 ie θ16- 5 -5.以方程i z 1576-=的根的对应点为顶点的多边形的面积为6.不等式522<++-z z522=++-z (或1)23()25(2222=+y x ) 的内部 7.方程1)1(212=----zi iz 所表示曲线的直角坐标方程为 122=+y x8.方程i z i z +-=-+221所表示的曲线是连接点 12i -+ 和 2i - 的线段的垂直平分线9.对于映射zi =ω,圆周1)1(22=-+y x 的像曲线为()2211u v -+= 10.=+++→)21(lim 421z z iz 12i -+三、若复数z 满足03)21()21(=+++-+z i z i z z ,试求2+z 的取值范围. (]25,25[+-(或25225+≤+≤-z )) 四、设0≥a ,在复数集C 中解方程a z z =+22. (当10≤≤a 时解为i a )11(-±±或)11(-+±a 当+∞≤≤a 1时解为)11(-+±a ) 五、设复数i z ±≠,试证21zz+是实数的充要条件为1=z 或Im()0z =. 六、对于映射)1(21zz +=ω,求出圆周4=z 的像.- 6 -(像的参数方程为π≤θ≤⎪⎩⎪⎨⎧θ=θ=20sin 215cos 217v u .表示w 平面上的椭圆1)215()217(2222=+v u ) 七、设iy x z +=,试讨论下列函数的连续性:1.⎪⎩⎪⎨⎧=≠+=0,00,2)(22z z y x xyz f2.⎪⎩⎪⎨⎧=≠+=0,00,)(223z z y x y x z f .(1.)(z f 在复平面除去原点外连续,在原点处不连续; 2.)(z f 在复平面处处连续)第二章 解析函数(答案)一、选择题:1.函数23)(z z f =在点0=z 处是( B )(A )解析的 (B )可导的(C )不可导的 (D )既不解析也不可导 2.函数)(z f 在点z 可导是)(z f 在点z 解析的( B )(A )充分不必要条件 (B )必要不充分条件(C )充分必要条件 (D )既非充分条件也非必要条件 3.下列命题中,正确的是( D )(A )设y x ,为实数,则1)cos(≤+iy x- 7 -(B )若0z 是函数)(z f 的奇点,则)(z f 在点0z 不可导(C )若v u ,在区域D 内满足柯西-黎曼方程,则iv u z f +=)(在D 内解析 (D )若)(z f 在区域D 内解析,则)(z if 在D 内也解析 4.下列函数中,为解析函数的是( C )(A )xyi y x 222-- (B )xyi x +2 (C ))2()1(222x x y i y x +-+- (D )33iy x + 5.函数)Im()(2z z z f =在0z =处的导数( A )(A )等于0 (B )等于1 (C )等于1- (D )不存在 6.若函数)(2)(2222x axy y i y xy x z f -++-+=在复平面内处处解析,那么实常 数=a ( C )(A )0 (B )1 (C )2 (D )2- 7.如果)(z f '在单位圆1<z 内处处为零,且1)0(-=f ,那么在1<z 内≡)(z f ( C )(A )0 (B )1 (C )1- (D )任意常数8.设函数)(z f 在区域D 内有定义,则下列命题中,正确的是( C )(A )若)(z f 在D 内是一常数,则)(z f 在D 内是一常数 (B )若))(Re(z f 在D 内是一常数,则)(z f 在D 内是一常数 (C )若)(z f 与)(z f 在D 内解析,则)(z f 在D 内是一常数- 8 -(D )若)(arg z f 在D 内是一常数,则)(z f 在D 内是一常数 9.设22)(iy x z f +=,则=+')1(i f ( A )(A )2 (B )i 2 (C )i +1 (D )i 22+ 10.i i 的主值为( D )(A )0 (B )1 (C )2πe (D )2e π-11.z e 在复平面上( A )(A )无可导点 (B )有可导点,但不解析 (C )有可导点,且在可导点集上解析 (D )处处解析 12.设z z f sin )(=,则下列命题中,不正确的是( C )(A ))(z f 在复平面上处处解析 (B ))(z f 以π2为周期(C )2)(iziz e e z f --= (D ))(z f 是无界的13.设α为任意实数,则α1( D )(A )无定义 (B )等于1(C )是复数,其实部等于1 (D )是复数,其模等于114.下列数中,为实数的是( B )(A )3)1(i - (B )i cos (C )i ln (D )i e 23π-15.设α是复数,则( C )(A )αz 在复平面上处处解析 (B )αz 的模为αz- 9 -(C )αz 一般是多值函数 (D )αz 的辐角为z 的辐角的α倍 二、填空题1.设i f f +='=1)0(,1)0(,则=-→zz f z 1)(limi +1 2.设iv u z f +=)(在区域D 内是解析的,如果v u +是实常数,那么)(z f 在D 内是 常数 3.导函数x v i x u z f ∂∂+∂∂=')(在区域D 内解析的充要条件为 xv x u ∂∂∂∂,可微且满足222222,xvy x u y x v x u ∂∂-=∂∂∂∂∂∂=∂∂ 4.设2233)(y ix y x z f ++=,则=+-')2323(i f i 827427- 5.若解析函数iv u z f +=)(的实部22y x u -=,那么=)(z f ic xyi y x ++-222或ic z +2c 为实常数6.函数)Re()Im()(z z z z f -=仅在点=z i 处可导 7.设z i z z f )1(51)(5+-=,则方程0)(='z f 的所有根为 3,2,1,0),424sin 424(cos 28=π+π+π+πk k i k8.复数i i 的模为),2,1,0(2 ±±=π-k e k9.=-)}43Im{ln(i 34arctan -- 10 -10.方程01=--z e 的全部解为),2,1,0(2 ±±=πk i k三、试证下列函数在z 平面上解析,并分别求出其导数 1.;sinh sin cosh cos )(y x i y x z f -= (;sin )(z z f -=')2.);sin cos ()sin cos ()(y ix y y ie y y y x e z f x x ++-=(.)1()(z e z z f +=') 四、已知22y x v u -=-,试确定解析函数iv u z f +=)(. (c i z i z f )1(21)(2++-=.c 为任意实常数)第三章 复变函数的积分(答案)一、选择题:1.设c 为从原点沿x y =2至i +1的弧段,则=+⎰cdz iy x )(2( D )(A )i 6561- (B )i 6561+- (C )i 6561-- (D )i 6561+2.设c 为不经过点1与1-的正向简单闭曲线,则dz z z zc⎰+-2)1)(1(为( D)(A )2i π (B )2iπ- (C )0 (D )(A)(B)(C)都有可能 3.设1:1=z c 为负向,3:2=z c 正向,则=⎰+=dz z zc c c 212sin ( B ) (A ) i π2- (B )0 (C )i π2 (D )i π44.设c 为正向圆周2=z ,则=-⎰dz z zc2)1(cos ( C)(A )1sin - (B )1sin (C )1sin 2i π- (D )1sin 2i π5.设c 为正向圆周21=z ,则=--⎰dz z z z c23)1(21cos( B) (A ))1sin 1cos 3(2-i π (B )0 (C )1cos 6i π (D )1sin 2i π-6.设ξξξξd ze zf ⎰=-=4)(,其中4≠z ,则=')i f π(( A ) (A )i π2- (B )1- (C )i π2 (D )1 7.设)(z f 在单连通域B 内处处解析且不为零,c 为B 内任何一条简单闭曲线,则积分dz z f z f z f z f c ⎰+'+'')()()(2)( ( C )(A )于i π2 (B )等于i π2- (C )等于0 (D )不能确定 8.设c 是从0到i 21π+的直线段,则积分=⎰cz dz ze ( A )(A )21eπ-(B) 21eπ-- (C)i e21π+(D) i e21π-9.设c 为正向圆周0222=-+x y x ,则=-⎰dz z z c1)4sin(2π( A )(A )i π22(B )i π2 (C )0 (D )i π22-10.设c 为正向圆周i a i z ≠=-,1,则=-⎰cdz i a zz 2)(cos ( C) (A )ie π2 (B )eiπ2 (C )0 (D )i i cos 11.设)(z f 在区域D 内解析,c 为D 内任一条正向简单闭曲线,它的内部全属于D .如果)(z f 在c 上的值为2,那么对c 内任一点0z ,)(0z f ( C )(A )等于0 (B )等于1 (C )等于2 (D )不能确定12.下列命题中,不正确的是( D ) (A )积分⎰=--ra z dz a z 1的值与半径)0(>r r 的大小无关 (B )2)(22≤+⎰cdz iy x ,其中c 为连接i -到i 的线段(C )若在区域D 内有)()(z g z f =',则在D 内)(z g '存在且解析 (D )若)(z f 在10<<z 内解析,且沿任何圆周)10(:<<=r r z c 的积分等于零,则)(z f 在0=z 处解析13.设c 为任意实常数,那么由调和函数22y x u -=确定的解析函数iv u z f +=)(是 ( D)(A)c iz +2 (B ) ic iz +2 (C )c z +2 (D )ic z +2 14.下列命题中,正确的是(C)(A )设21,v v 在区域D 内均为u 的共轭调和函数,则必有21v v =(B )解析函数的实部是虚部的共轭调和函数 (C )若iv u z f +=)(在区域D 内解析,则xu∂∂为D 内的调和函数 (D )以调和函数为实部与虚部的函数是解析函数15.设),(y x v 在区域D 内为),(y x u 的共轭调和函数,则下列函数中为D 内解析函数的是( B )(A )),(),(y x iu y x v + (B )),(),(y x iu y x v - (C )),(),(y x iv y x u - (D )xv i x u ∂∂-∂∂二、填空题1.设c 为沿原点0=z 到点i z +=1的直线段,则=⎰cdz z 2 22.设c 为正向圆周14=-z ,则=-+-⎰c dz z z z 22)4(23 i π103.设⎰=-=2)2sin()(ξξξξπd z z f ,其中2≠z ,则=')3(f 0 4.设c 为正向圆周3=z ,则=+⎰cdz zzz i π6 5.设c 为负向圆周4=z ,则=-⎰c z dz i z e 5)(π 12iπ 6.解析函数在圆心处的值等于它在圆周上的 平均值7.设)(z f 在单连通域B 内连续,且对于B 内任何一条简单闭曲线c 都有0)(=⎰cdz z f ,那么)(z f 在B 内 解析8.调和函数xy y x =),(ϕ的共轭调和函数为 C x y +-)(21229.若函数23),(axy x y x u +=为某一解析函数的虚部,则常数=a -3 10.设),(y x u 的共轭调和函数为),(y x v ,那么),(y x v 的共轭调和函数为),(y x u -三、计算积分 1.⎰=+-R z dz z z z)2)(1(62,其中1,0≠>R R 且2≠R ; (当10<<R 时,0; 当21<<R 时,i π8; 当+∞<<R 2时,0) 2.⎰=++22422z z z dz.(0) 四、求积分⎰=1z zdz z e ,从而证明πθθπθ=⎰0cos )cos(sin d e .(i π2)五、若)(22y x u u +=,试求解析函数iv u z f +=)(. (321ln 2)(ic c z c z f ++=(321,,c c c 为任意实常数))第四章 级 数(答案)一、选择题:1.设),2,1(4)1( =++-=n n nia n n ,则n n a ∞→lim ( C )(A )等于0 (B )等于1 (C )等于i (D )不存在 2.下列级数中,条件收敛的级数为( C )(A )∑∞=+1)231(n n i (B )∑∞=+1!)43(n nn i (C ) ∑∞=1n n n i (D )∑∞=++-11)1(n n n i3.下列级数中,绝对收敛的级数为(D )(B ) ∑∞=+1)1(1n n i n (B )∑∞=+-1]2)1([n n n in(C)∑∞=2ln n n n i (D )∑∞=-12)1(n nnn i 4.若幂级数∑∞=0n n n z c 在i z 21+=处收敛,那么该级数在2=z 处的敛散性为( A )(A )绝对收敛 (B )条件收敛 (C )发散 (D )不能确定 5.设幂级数∑∑∞=-∞=01,n n n n nn znc z c 和∑∞=++011n n n z n c 的收敛半径分别为321,,R R R ,则321,,R R R 之间的关系是( D )(A )321R R R << (B )321R R R >> (C )321R R R <= (D )321R R R == 6.设10<<q ,则幂级数∑∞=02n n n z q 的收敛半径=R ( D )(A )q (B )q1(C )0 (D )∞+ 7.幂级数∑∞=1)2(2sinn n z n n π的收敛半径=R ( B ) (A ) 1 (B )2 (C )2 (D )∞+8.幂级数∑∞=++-011)1(n n n z n 在1<z 内的和函数为( A )(A ))1ln(z + (B ))1ln(z - (D )z +11ln(D) z-11ln 9.设函数z e z cos 的泰勒展开式为∑∞=0n nn z c ,那么幂级数∑∞=0n n n z c 的收敛半径=R ( C )(A )∞+ (B )1 (C )2π(D )π 10.级数+++++22111z z z z的收敛域是( B ) (A )1<z (B )10<<z (C )+∞<<z 1 (D )不存在的 11.函数21z在1-=z 处的泰勒展开式为( D)(A ))11()1()1(11<++-∑∞=-z z n n n n (B ))11()1()1(111<++-∑∞=--z z n n n n(C ))11()1(11<++-∑∞=-z z n n n (D ))11()1(11<++∑∞=-z z n n n12.函数z sin ,在2π=z 处的泰勒展开式为( B )(A ))2()2()!12()1(012+∞<--+-∑∞=+ππz z n n n n(B ))2()2()!2()1(02+∞<---∑∞=ππz z n n nn(C ))2()2()!12()1(0121+∞<--+-∑∞=++ππz z n n n n(D ))2()2()!2()1(021+∞<---∑∞=+ππz z n n nn13.设)(z f 在圆环域201:R z z R H <-<内的洛朗展开式为∑∞-∞=-n n nz z c)(0,c 为H 内绕0z 的任一条正向简单闭曲线,那么=-⎰c dz z z z f 2)()(( B )(A)12-ic π (B )12ic π (C )22ic π (D ))(20z f i 'π14.若⎩⎨⎧--==-+=,2,1,4,2,1,0,)1(3n n c nn n n ,则双边幂级数∑∞-∞=n n n z c 的收敛域为( A ) (A )3141<<z (B )43<<z(C )+∞<<z 41 (D )+∞<<z 3115.设函数)4)(1(1)(++=z z z z f 在以原点为中心的圆环内的洛朗展开式有m 个,那么=m ( C )(A )1 (B )2 (C )3 (D )4 二、填空题1.若幂级数∑∞=+0)(n n n i z c 在i z =处发散,那么该级数在2=z 处的收敛性为 发散2.设幂级数∑∞=0n nn z c 与∑∞=0)][Re(n n n z c 的收敛半径分别为1R 和2R ,那么1R 与2R 之间的关系是 12R R ≥ .3.幂级数∑∞=+012)2(n n n z i 的收敛半径=R22 4.设)(z f 在区域D 内解析,0z 为内的一点,d 为0z 到D 的边界上各点的最短距离,那么当d z z <-0时,∑∞=-=00)()(n n n z z c z f 成立,其中=n c ),2,1,0()(!10)( =n z f n n 或()0,2,1,0()()(21010d r n dz z z z f ir z z n <<=-π⎰=-+ ). 5.函数z arctan 在0=z 处的泰勒展开式为 )1(12)1(012<+-∑∞=+z z n n n n .6.设幂级数∑∞=0n nn z c 的收敛半径为R ,那么幂级数∑∞=-0)12(n n n n z c 的收敛半径为2R. 7.双边幂级数∑∑∞=∞=--+--112)21()1()2(1)1(n n n nnz z 的收敛域为 211<-<z . 8.函数zze e 1+在+∞<<z 0内洛朗展开式为 nn nn z n z n ∑∑∞=∞=+00!11!1 . 9.设函数z cot 在原点的去心邻域R z <<0内的洛朗展开式为∑∞-∞=n n nz c,那么该洛朗级数收敛域的外半径=R π .10.函数)(1i z z -在+∞<-<i z 1内的洛朗展开式为 ∑∞=+--02)()1(n n nn i z i 三、若函数211z z --在0=z 处的泰勒展开式为∑∞=0n nn z a ,则称{}n a 为菲波那契(Fibonacci)数列,试确定n a 满足的递推关系式,并明确给出n a 的表达式. ()2(,12110≥+===--n a a a a a n n n ,),2,1,0(})251()251{(5111 =--+=++n a n n n ) 四、求幂级数∑∞=12n nz n 的和函数,并计算∑∞=122n n n 之值.(3)1()1()(z z z z f -+=,6)五、将函数)1()2ln(--z z z 在110<-<z 内展开成洛朗级数.(n n nk k z k n z z z z z z )1()1)1(()2ln(111)1()2ln(001-+--=-⋅⋅-=--∑∑∞==+)第五章 留 数(答案)一、选择题: 1.函数32cot -πz z在2=-i z 内的奇点个数为 ( D ) (A )1 (B )2 (C )3 (D )4 2.设函数)(z f 与)(z g 分别以a z =为本性奇点与m 级极点,则a z =为函数)()(z g z f的( B )(A )可去奇点 (B )本性奇点 (C )m 级极点 (D )小于m 级的极点 3.设0=z 为函数zz ex sin 142-的m 级极点,那么=m ( C ) (A )5 (B )4 (C)3 (D )2 4.1=z 是函数11sin)1(--z z 的( D ) (A)可去奇点 (B )一级极点 (C ) 一级零点 (D )本性奇点5.∞=z 是函数2323z z z ++的( B ) (A)可去奇点 (B )一级极点(C ) 二级极点 (D )本性奇点6.设∑∞==0)(n n n z a z f 在R z <内解析,k 为正整数,那么=]0,)([Re k zz f s ( C ) (A )k a (B )k a k ! (C )1-k a (D )1)!1(--k a k7.设a z =为解析函数)(z f 的m 级零点,那么='],)()([Re a z f z f s ( A ) (A)m (B )m - (C ) 1-m (D ))1(--m8.在下列函数中,0]0),([Re =z f s 的是( D )(A ) 21)(ze zf z -= (B )z z z z f 1sin )(-= (C )z z z z f cos sin )(+= (D) ze zf z 111)(--= 9.下列命题中,正确的是( C )(A ) 设)()()(0z z z z f m ϕ--=,)(z ϕ在0z 点解析,m 为自然数,则0z 为)(z f 的m 级极点.(B ) 如果无穷远点∞是函数)(z f 的可去奇点,那么0]),([Re =∞z f s(C ) 若0=z 为偶函数)(z f 的一个孤立奇点,则0]0),([Re =z f s(D ) 若0)(=⎰cdz z f ,则)(z f 在c 内无奇点10. =∞],2cos [Re 3zi z s ( A ) (A )32- (B )32 (C )i 32 (D )i 32- 11.=-],[Re 12i ez s i z ( B) (A )i +-61 (B )i +-65 (C )i +61 (D )i +65 12.下列命题中,不正确的是( D)(A )若)(0∞≠z 是)(z f 的可去奇点或解析点,则0]),([Re 0=z z f s(B )若)(z P 与)(z Q 在0z 解析,0z 为)(z Q 的一级零点,则)()(],)()([Re 000z Q z P z z Q z P s '= (C )若0z 为)(z f 的m 级极点,m n ≥为自然数,则)]()[(lim !1]),([Re 1000z f z z dzd n z z f s n n nx x +→-= (D )如果无穷远点∞为)(z f 的一级极点,则0=z 为)1(zf 的一级极点,并且)1(lim ]),([Re 0zzf z f s z →=∞ 13.设1>n 为正整数,则=-⎰=211z ndz z ( A ) (A)0 (B )i π2 (C )n i π2 (D )i n π214.积分=-⎰=231091z dz z z ( B ) (A )0 (B )i π2 (C )10 (D )5i π 15.积分=⎰=121sin z dz z z ( C ) (A )0 (B )61-(C )3i π- (D )i π- 二、填空题 1.设0=z 为函数33sin z z -的m 级零点,那么=m 9 .2.函数z z f 1cos 1)(=在其孤立奇点),2,1,0(21 ±±=+=k k z k ππ处的留数=]),([Re k z z f s 2)2()1(π+π-k k. 3.设函数}1exp{)(22zz z f +=,则=]0),([Re z f s 0 4.设a z =为函数)(z f 的m 级极点,那么='],)()([Re a z f z f s m - . 5.设212)(zz z f +=,则=∞]),([Re z f s -2 . 6.设5cos 1)(z z z f -=,则=]0),([Re z f s 241- . 7.积分=⎰=113z z dz e z 12i π .8.积分=⎰=1sin 1z dz z i π2 . 三、计算积分⎰=--412)1(sin z z dz z e z z .(i π-316) 四、设a 为)(z f 的孤立奇点,m 为正整数,试证a 为)(z f 的m 级极点的充要条件是b z f a z m az =-→)()(lim ,其中0≠b 为有限数. 五、设a 为)(z f 的孤立奇点,试证:若)(z f 是奇函数,则]),([Re ]),([Re a z f s a z f s -=;若)(z f 是偶函数,则]),([Re ]),([Re a z f s a z f s --=.。
计算机控制技术课后题答案整理版(1到5章基本都有了)

第一章1、计算机控制系统是由哪几部分组成的?画出方框图并说明各部分的作用。
答:计算机控制系统由工业控制机、过程输入输出设备和生产过程三部分组成;框图P3。
1)工业控制机主要用于工业过程测量、控制、数据采集、DCS操作员站等方面。
2)PIO设备是计算机与生产过程之间的信息传递通道,在两者之间起到纽带和桥梁的作用。
3)生产过程就是整个系统工作的各种对象和各个环节之间的工作连接。
2、计算机控制系统中的实时性、在线方式与离线方式的含义是什么?为什么在计算机控制系统中要考虑实时性?(1)实时性是指工业控制计算机系统应该具有的能够在限定时间内对外来事件做出反应的特性;在线方式是生产过程和计算机直接相连,并受计算机控制的方式;离线方式是生产过程不和计算机相连,并不受计算机控制,而是靠人进行联系并作相应操作的方式。
(2)实时性一般要求计算机具有多任务处理能力,以便将测控任务分解成若干并行执行的多个任务,加快程序执行速度;在一定的周期时间对所有事件进行巡查扫描的同时,可以随时响应事件的中断请求。
3.计算机控制系统有哪几种典型形式?各有什么主要特点?(1)操作指导控制系统(OIS)优点:结构简单、控制灵活和安全。
缺点:由人工控制,速度受到限制,不能控制对象。
(2)直接数字控制系统(DDC) (属于计算机闭环控制系统)优点:实时性好、可靠性高和适应性强。
(3)监督控制系统(SCC)优点:生产过程始终处于最有工况。
(4)集散控制系统优点:分散控制、集中操作、分级管理、分而自治和综合协调。
(5)现场总线控制系统优点:与DOS相比降低了成本,提高了可靠性。
(6)PLC+上位系统优点:通过预先编制控制程序实现顺序控制,用PLC代替电器逻辑,提高了控制是现代灵活性、功能及可靠性。
附加:计算机控制系统的发展趋势是什么?大规模及超大规模集成电路的发展,提高了计算机的可靠性和性能价格比,从而使计算机控制系统的应用也越来越广泛。
为更好地适应生产力的发展,扩大生产规模,以满足对计算机控制系统提出的越来越高的要求,目前计算机控制系统的发展趋势有以下几个方面。
有机化学章节习题参考答案(1-5)
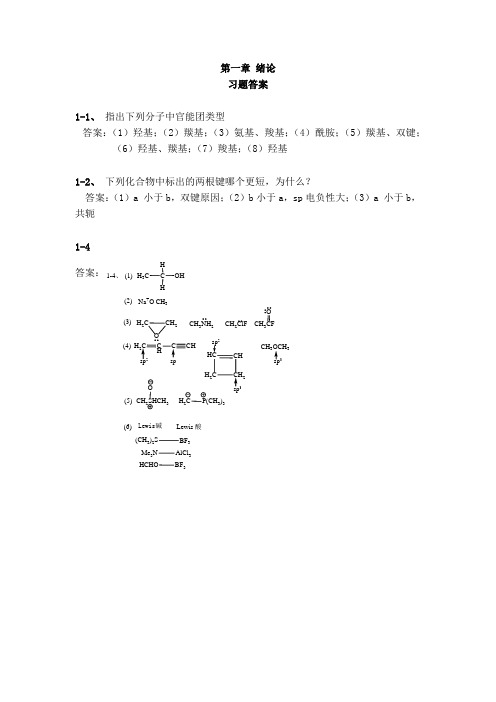
第一章 绪论 习题答案1-1、 指出下列分子中官能团类型答案:(1)羟基;(2)羰基;(3)氨基、羧基;(4)酰胺;(5)羰基、双键;(6)羟基、羰基;(7)羧基;(8)羟基1-2、 下列化合物中标出的两根键哪个更短,为什么?答案:(1)a 小于b ,双键原因;(2)b 小于a ,sp 电负性大;(3)a 小于b ,共轭 1-4 答案:(1)C HHH 3COH(2)Na +O -CH 3(3)H 2C CH 2O(4)CH 3NH 2CH 2ClF3HHC CH H 2CCH2sp 23CH 333(5)CH 2SHCH 3OH 2CP(CH 3)3(6)Lewis 酸Lewis 碱(CH 3)2S BF 3Me 3N AlCl 3HCHOBF 31-4、第2章 烷烃和环烷烃习题及答案2-1 用中文系统命名法命名或写出结构式。
答案: (1)2,6,6-三甲基-3-乙基辛烷 (2)2,6,7-三甲基壬烷(3)1-甲基-1-氯环己烷 (4) 顺-1,2-二溴环己烷 (5(6)(7)CCCC CH 3CH 3CH 3CH 3H 3H 3(8) (CH 3)2CHCH 2CH 2CH 32-2 用不同符号标出下列化合物中伯、仲、叔、季碳原子,并给以命名。
答案: (1) CH 3CH CH 2C C CH 3CH 3CH 2CH 3CH 3CH 3CH 2CH 31o 1o 1o1o1o1oo 2o2o 21o o 3o4o 43,3,4,4,6-五甲基辛烷 (2) CH3CH(CH 3)CH 2C(CH 3)2CH(CH 3)CH 2CH31o1o1o1o1oo2o2o 3o 3o 42,4,4,5-四甲基庚烷2-3 指出下列四个化合物的命名中不正确的地方并给以重新命名。
答案: (1)主链选错。
应为:2,4,6-三甲基-6-乙基辛烷 (2)主链、碳原子编号错。
应为:2-甲基-3乙基己烷 (3)碳原子编号错。
算法与数据结构C语言习题参考答案1-5章

绪论1.将下列复杂度由小到大重新排序:A.2n B.n! C.n5D.10 000 E.n*log2 (n)【答】10 000< n*log2(n)< n5< 2n < n!2.将下列复杂度由小到大重新排序:A.n*log2(n) B.n + n2 + n3C.24D.n0.5【答】24< n0.5< n*log2 (n) < n + n2 + n33.用大“O”表示法描述下列复杂度:A.5n5/2 + n2/5 B.6*log2(n) + 9nC.3n4+ n* log2(n) D.5n2 + n3/2【答】A:O (n5/2) B:O (n) C:O (n4) D:O (n2)4.按照增长率从低到高的顺序排列以下表达式:4n2 , log3n, 3n , 20n , 2000 , log2n , n2/3。
又n!应排在第几位?【答】按照增长率从低到高依次为:2000, log3n, log2n , n2/3 , 20n , 4n2 , 3n。
n!的增长率比它们中的每一个都要大,应排在最后一位。
5. 计算下列程序片断的时间代价:int i=1;while(i<=n){printf(“i=%d\n”,i);i=i+1;}【答】循环控制变量i从1增加到n,循环体执行n次,第一句i的初始化执行次数为1,第二句执行n次,循环体中第一句printf执行n次,第二句i从1循环到n,共执行n次。
所以该程序段总的时间代价为:T(n) = 1 + n + 2n = 3n+ 1 = O(n)6. 计算下列程序片断的时间代价:int i=1;while(i<=n){int j=1;while(j<=n){int k=1;while(k<=n){printf(“i=%d,j=%d,k=%d\n”,I,j,k);k=k+1;}j=j+1;}i=i+1;}【答】循环控制变量i从1增加到n,最外层循环体执行n次,循环控制变量j从1增加到n,中间层循环体执行n次,循环控制变量k从1增加到n,最内层循环体执行n次,所以该程序段总的时间代价为:T(n) = 1 + n + n{1 + n + n[1 + n + 2n +1] +1 +1}+ 1= 3n3 + 3n2 +4n +2= O(n3)2. 线性表1.试写一个插入算法int insertPost_seq(palist, p, x ),在palist所指顺序表中,下标为p的元素之后,插入一个值为x的元素,返回插入成功与否的标志。
习题答案1-5

无机化学习题参考答案(1-5章)第一章习题:1.B(CH 3)3和BCl 3相比,哪一个的Lewis 酸性强,为什么?BCl 3酸性强。
因为CH 3推电子,使B 的缺电子性质减弱,而Cl 吸电子,主要与CH 3相反。
2.题目本身有问题。
3. 无水AlCl 3可作为傅氏烷基化反应的催化剂, 而吸水后则失效, 原因何在?AlCl 3作催化剂是利用其Lewis 酸性(配位不饱和),而吸水后配位饱和,失去Lewis 酸性和催化能力。
,4. p.29, 1.4 (其中的UO 2F 6该为UOF 4)(1)H 2O 22C(2)S 2O 32-3v C(3)N 2O(N -N -O 方式)v C ∞(4)Hg 2Cl 2h D ∞ (5)H 2C=C=CH 2 2d D (6)UOF 4C 4v (7)BF 4-d T(8)SClF 54v C(9)反-Pt(NH 3)2Cl 22h D(10)PtCl 3(C 2H 4)-2v C第二章习题:2.1 解:顺磁性和反磁性可参看p.38的2.3图, 四面体为高自旋, 平面四方形为低自旋.Ni 2+ d 8组态 Pt 2+ d 8组态 第四周期(分裂能小) 第六周期(分裂能大)P Ni ClPClClPtCl P Ptrans cis 四面体构型 平面四方形构型(两种构型) 只有一种结构 (P 代表PPh 3) 2.2 解(1)MA 2B 4 (2)MA 3B 3M A ABB M A BA BM A BAB M A AA Btrans cis fac(面式) mer(经式) D 4h C 2v C 3v C 2v μ=0 μ≠0 μ≠0 μ≠0μfac >μmer2.3 Co(en)2Cl 2+D 2hC 2 光活异构体 C 2Co(en)2(NH 3)Cl 2+33Htrans cis Co(en)(NH 3)2Cl 2+3Cl 333NH NH 33trans(1) trans(2)cis 注意: 光活异构体的数量, 多! 2.4 Co(en)33+ Ru(bipy)32+ 手性分子D 3 D 3 PtCl(dien)+ dien HNCH 2CH 2CH 2NH 2NH 2CH 2基本上为平面分子, 无手性2.5 (1) 分别用BaCl2溶液滴入,有白色沉液出现的为[Co(NH3)5Br]SO4,或分别加入AgNO3溶液,产生浅黄色沉淀的为[Co(NH3)5SO4]Br。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章1.试说明数据与信息的区别和联系。
数据是人们用于记录事物情况的物理符号。
信息是数据中所包含的意义。
数据与信息既有区别,又有联系。
数据是表示信息的,但并非任何数据都能表示信息,信息只是加工处理后的数据,是数据所表达的内容。
另一方面信息不随表示它的数据形式而改变,它是反映客观现实世界的知识,而数据则具有任意性,用不同的数据形式可以表示同样的信息,信息只是加工处理后的数据,是数据所表达的内容。
2.什么是数据库、数据库管理系统和数据库系统?数据库是在数据库管理系统的集中控制之下,按一定的组织方式存储起来的、相互关联的数据集合。
数据库管理系统(Database Management System,DBMS)是对数据进行统一的控制和管理,从而可以有效地减少数据冗余,实现数据共享,解决数据独立性问题,并提供统一的安全性、完整性和并发控制功能的系统软件。
数据库系统是把有关计算机硬件、软件、数据和人员组合起来为用户提供信息服务的系统。
3.简述数据库的三级模式结构。
为了有效地组织、管理数据,提高数据库的逻辑独立性和物理独立性,人们为数据库设计了一个严谨的体系结构,数据库领域公认的标准结构是三级模式结构,它包括外模式、模式和内模式。
模式又称概念模式或逻辑模式,对应于概念级。
它是由数据库设计者综合所有用户的数据,按照统一的观点构造的全局逻辑结构,是对数据库中全部数据的逻辑结构和特征的总体描述,是所有用户的公共数据视图(全局视图)。
外模式又称子模式,对应于用户级。
它是某个或某几个用户所看到的数据库的数据视图,是与某一应用有关的数据的逻辑表示。
内模式又称存储模式,对应于物理级。
它是数据库中全体数据的内部表示或底层描述。
4.数据库系统的特点是什么?特点是数据共享,减少数据冗余,具有较高的数据独立性,增强了数据安全性和完整性保护。
5.实体之间的联系有哪几种?分别举例说明。
(1)一对一联系(1∶1) 例如,一所学校只有一个校长,一个校长只在一所学校任职,校长与学校之间的联系是一对一的联系。
(2)一对多联系(1∶n) 例如,一所学校有许多学生,但一个学生只能就读于一所学校,所以学校和学生之间的联系是一对多的联系。
(3)多对多联系(m∶n) 例如,一个读者可以借阅多种图书,任何一种图书可以为多个读者借阅,所以读者和图书之间的联系是多对多的联系。
6. 数据库有哪几种常用的数据模型?Visual FoxPro属于哪一类?在数据库系统中,常用的数据模型有层次模型、网状模型和关系模型3种。
Visual FoxPro 是一种基于关系模型的关系数据库管理系统。
7.以某种应用目的为背景,试设计一个数据库。
我们以图书馆借书应用为例设计一个最简单的数据库,主要是包括以下几个关系学生关系,图书关系,借书关系,每个关系对应与数据库里面的一个表。
那么学生表应该包括(学号,姓名,专业,年龄等属性),图书表应该包括(图书号,图书名,作者名,出版社等属性),这两个表是通过借书关系来实现多对多的联系的,那么借书表主要包括(学号,图书号等)。
8.关系数据库管理系统的3种基本关系运算是什么?关系运算主要有选择、投影和联接3种。
9. 试述外部关键字的概念和作用。
外部关键字是否允许为空值,为什么?如果关系中某个属性或属性组合并非关键字,但却是另一个关系的主关键字,则称此属性或属性组合为本关系的外部关键字。
关系之间的联系是通过外部关键字实现的。
如果该外部关键字不是该关系的主关键字那么根据参照完整性规则,该外部关键字可以是空值,否则如果该外部关键字也是该关系的主关键字则根据参照完整性规则不能是空值。
10. 数据库系统的体系结构有哪几种?常见的数据库开发工具有哪些?数据库系统的体系结构大体上分为4种模式:单用户模式、主从式多用户模式、客户机/ 服务器模式(Client/Server,C/S)和Web浏览器/服务器模式(Browser/Server,B/S)。
目前,一些专有数据库厂商都提供了数据库编程工具,如Sybase的Power++、Oracle的Developer 2000等,但比较流行的还是Delphi、Visual Basic、PowerBuilder等通用语言,这几个开发工具各有所长、各具优势。
第二章1.如何启动与退出Visual FoxPro?Visual FoxPro 6.0的启动与Windows环境下其他软件一样,有3种常见方法:(1) 在Windows桌面上单击“开始”按钮,选择“程序”选项,单击“Microsoft Visu al Studio 6.0”组中的“Microsoft Visual FoxPro 6.0”选项。
(2) 运行Visual FoxPro 6.0系统的启动程序vfp6.exe。
通过“我的电脑”或“资源管理器”去查找这个程序,然后双击它。
或单击“开始”按钮,选择“运行”选项,在弹出的“运行对话框”中输入Visual FoxPro 6.0启动程序的文件名,单击“确定”按钮。
(3) 在Windows桌面上建立Visual FoxPro 6.0系统的快捷方式图标,只要在桌面上双击该图标即可启动Visual FoxPro。
退出Visual FoxPro有5种常用的方法:(1) 在Visual FoxPro“文件”菜单项下,选择“退出”菜单项;(2) 在Visual FoxPro命令窗口输入QUIT命令并回车;(3) 单击Visual FoxPro主窗口右上角的“关闭”按钮;(4) 单击Visual FoxPro主窗口左上角的控制菜单图标,从弹出的菜单中选择“关闭”,或者双击控制菜单图标;(5) 同时按Alt和F4键。
2.简述Visual FoxPro用户界面的组成与特点。
Visual FoxPro的用户界面由Visual FoxPro系统菜单、工具栏、命令窗口和状态栏等构成。
Visual FoxPro用户界面的最大的特点就是界面简单且灵活。
3.Visual FoxPro有几种操作方式?各有何特点?Visual FoxPro有三种操作方式,菜单操作方式,命令操作方式,程序工作方式。
菜单操作的优点是直观易懂,击键简单(主要是鼠标单击和双击),对于不熟悉Visual FoxPro 命令、又没有或不想花时间去学习它的最终用户十分适合。
命令操作方式相对而言速度更加快并且效率高。
Visual FoxPro除了提供菜单操作方式、命令操作方式外,还提供程序工作方式。
程序由命令或语句组成。
通过运行程序,为用户提供更简洁的界面,达到操作的目的。
4.对话框的作用是什么?它通常包括哪些控制对象?对话框实际上是一个特殊的窗口,它可以用来要求用户输入某些信息或做出某些选择,在Visual FoxPro 6.0中,对话框通常由文本框、列表框、单选按钮、复选框、命令按钮等部件组成。
5.简述Visual FoxPro的可视化设计工具。
Visual FoxPro 6.0提供了多种可视化设计工具,使用它的各种向导(Wizard)、设计器(Designer)和生成器(Builder)可以更简便、快速、灵活地进行应用程序开发。
1. Visual FoxPro向导Visual FoxPro系统为用户提供许多功能强大的向导。
用户通过系统提供的向导设计器,不用编程就可以创建良好的应用程序界面并完成许多对数据库的操作。
2. Visual FoxPro设计器Visual FoxPro系统提供的设计器,为用户提供了一个友好的操作界面。
利用各种设计器使得创建表、数据库、表单、查询以及报表等操作变得轻而易举。
3. Visual FoxPro生成器Visual FoxPro系统提供的生成器,可以简化创建和修改用户界面程序的设计过程,提高软件开发的质量。
6. 完成下列操作:(1)隐藏与激活“命令窗口”;可以通过工具栏上的命令窗口图标来选择隐藏与激活“命令窗口”。
(2)求表达式(3-5.1)*3.14159/14的值;在命令窗口输入(3-5.1)*3.14159/14,然后回车执行得到结果-0.471239(3)设置默认目录;可以在工具菜单的选项对话框里面的文件位置选项卡里设置默认目录。
(4) 创建名为“我的工具栏”的工具栏;在操作过程中,用户可以随时创建一个适合于自己工作需要的新工具栏。
创建名为“我的工具栏”的操作步骤如下:(1) 单击“显示”菜单项,选择“工具栏”选项,在“工具栏”对话框下单击“新建”按钮,出现如图2.5所示的“新工具栏”对话框。
(2) 输入新工具栏名称,输入“我的工具栏”,并单击“确定”按钮,出现如图2.6所示的“定制工具栏”对话框,与此同时,在屏幕窗口上也出现了“我的工具栏”工具栏。
(3) 在“定制工具栏”对话框的最左边是“分类”列表框,选择该列表框中的任何一类,其右侧便显示该类的所有按钮。
(4) 用户可根据需要选择分类中的某一类,并在该分类中选择按钮,当选中了某一个按钮后,用鼠标器将其拖动到“我的工具栏”工具栏下即可。
(5) 查询LIST命令的帮助信息。
首先是通过在命令窗口执行help命令来打开帮助窗口,然后选择“搜索”项,在组合框中输入“LIST”,再自己查找相关标题即可。
第三章1.简述Visual FoxPro的数据类型。
Visual FoxPro中的数据类型包括以下几种:1. 字符型,2. 数值型,3. 货币型,4. 日期型,5. 日期时间型,6. 逻辑型,7. 备注型,8. 通用型,9. 二进制字符型和二进制备注型。
2.字段变量与内存变量有何区别?字段变量就是表中的字段名,它是表中最基本的数据单元。
字段变量是一种多值变量,一个表有多少条记录,那么该表的每一字段就有多少个值,当用某一字段名作变量时,它的值就是表记录指针所指的那条记录对应字段的值。
内存变量独立于表,是一种临时工作单元,它是一种单值变量。
可以用内存变量名直接访问内存变量。
3. 下列数据哪些是变量?哪些是常量?是什么类型的常量?″姓名″,.F.,98/07/21,教授,1E2,[5585211],T其中 T和教授是变量其它是常量,″姓名″和[5585211]是字符常量,.F.是逻辑常量,98/07/21是数值型常量。
4. 求下列表达式的值。
(1) LEN(DTOC(DATE())) :8(2) STUFF(″现代教育中心″,5,0,LEFT(″技术中心″,4)):“现代技术教育中心”(3) VARTYPE(08/23/03):N(4) SPACE(5)-SPACE(5):’’空字符串(5) ″PRO″$″FoxPro″ AND ″100″>″90″:.F.5. 针对学生表,写出下列条件:(1) 入学成绩高于600分的学生:入学成绩>=600(2) 年龄大于18岁但小于25岁的学生:YEAR(DATE())-YEAR(出生日期)<=25 and YEAR(DATE())-YEAR(出生日期)>=18(3) 少数民族的男生:性别=’男’ and 少数民族否(4) 在1985年1月1日至1983年12月31日之间出生的学生:出生日期>={^1983-12-31} and 出生日期<={^1985-01-01}(5) 入学成绩在580分以上的汉族女生:入学成绩>=600 and 少数民族否 and 性别=’女’6. 写出下列表达式。
