实验一 曲柄滑块机构的运动规律
《机构运动方案创新设计实验指导书-学生用-cxc》

《机构运动方案创新设计实验指导书-学生用-cxc》一、实验目的1.培养学生机构型综合的设计能力、创新能力和实践动手能力;2.培养学生综合应用所知识对机构的结构和运动性能加以评价的分析能力。
二、实验原理任何机构都是将基本组依次连接到机架和原动件上而构成的。
三、实验内容1.多功能移动式残病人浴缸翻转机构⑴上身部缸体翻转机构要求上身部缸体从水平位置向上翻转至70度,即翻转角为0-70度.可采用的机构:摆动导杆机构,导杆与上身部缸体固装在-起,带动缸体翻转。
由直线电机带动主动杆摆动。
双摇杆机构,上身部缸体作为从动摇杆,在主动摇杆驱动下作0-70度摆动.主动杆由直线电机带动摆动。
其它机构⑵腿部缸体翻转机构要求腿部缸体从垂直位置向上翻转至水平位置,利用死点保持腿部缸体在水平位置,借助凸轮机构破坏死点,使腿部缸体在重力作用下复位。
可采用机构:双摇杆机构,腿部缸体作为主动摇杆;其它机构2.牛头创床机构要求刨刀(安装在滑枕上)作直线往复运动。
可采用的机构:①转动导杆机构和曲柄滑块机构组合,由电机驱动主动件转动。
②摆动导杆机构和滑块机构组合,由电机驱动主动件转动。
③其它机构3.翻转机要求翻转模板装在连杆上,模板翻转180度。
①四杆机构,电机驱动。
②其它机构4.飞机起落架要求起落架上轮子从水平位置向下翻转至垂直位置,利用死点使起落架轮子保持在垂直位置。
可采用的机构:①四杆机构,电机驱动。
②其它机构5.插床机构要求插刀作垂直上下往复直线运动,向下时(工作行程)较慢,向上运动(空程)时速度较快。
可采用的机构:①双曲柄机构与曲构滑块机构组合,电机驱动。
②其它机构6.冲压成型机压头作垂直上下直线运动,以较小功率带动主动件运动时,滑块能产生巨大的冲压力。
可采用的机构:①六杆增力机构,电机驱动.②其它机构7.其他自选机构四、实验方法本搭接实验是在具有六根立柱的机架上完成的。
配有旋转电动机和直线电动机,以输出直线运动和旋转运动;配有齿轮、凸轮、带轮、槽轮等零件,通过搭接可完成直线、旋转、往复、间歇等运动传递;配有连杆、滑块座及连接零件,可搭接成各种执行机构。
实验20-机构运动参数测定实验

本测试系统测试结果不但可以由曲线形式输出,还可以直接打印出个点数值,克服了以往测试方法所在的须对记录曲线进行人工标定和数据处理,从而带来较大幅值和相位误差等问题。
一、实验目的
1.通过实验了解位移、速度、加速度、位移、角速度、角加速度测定方法。
2.通过实验初步了解“MEC—B机械动态参数测定试仪”即光电脉冲编码器、同步脉冲发生器(或称角度传感器)的基本原理,并掌握它们的使用方法。
3.通过实验曲线和理论曲线的比较,分析产生差异的原因,增加对速度、角速度、特别是加速度、角加速度的感性认识。
MEC—B机械动态参数测试仪由于采用微机及相应的外围设备,因此在数据处理的灵活性和结果显示、记录、打印的便利、清晰、直观等方面明显优于非微机化的同类仪器。另外,操作命令采用代码和专用键相结合,操作灵活方便,实验准备工作非常简单,并且在学生进行实验时稍作讲解学生即可使用。
3、光电脉冲编码器
1、灯泡2、聚光镜3、光电盘4、光拦板5、主轴
图20-6数字电路框图
图10-7输出波形
四、实验步骤
1.滑块位移、速度、加速度测量
(1)将PP—40四色绘图仪接入测试仪后板插座,打开CRT电源开关,启动面板电源开关,数码管显示“P”,适当调整CRT亮度与对比度。若环境温度超过30°C应打开风扇开关。
(2)调整同步脉冲发生器与分度盘位置,使分度盘插入同步脉冲发生器探头的槽内。拨动带轮使分度盘转动,探头上的绿色指示灯每转2°(即一个光栅)闪烁一次,而红灯每转一圈闪烁一次。9即分度盘上同步长光栅进入探头槽内红灯不亮,其余位置都亮)
曲柄(导杆)滑块机构设计分析正文.

目录1 引言1.1 选题的依据及意义·························································································(1)1.2 国内外研究概况及发展趋势··········································································(2)1.3 论文主要工作·······························································································(3)2 曲柄(导杆)滑块机构简介····································································(4)3 曲柄(导杆)滑块机构的运动学分析3.1 曲柄导杆滑块机构的运动分析······································································(5)3.1.1 机构装配的条件····················································································(6)3.1.2 建立数学模型·························································································(6)3.1.3 计算机辅助分析及其程序设计······························································(9)3. 2曲柄滑块机构的运动分析3.2.1 机构装配的条件·····················································································(25)3.2.2 建立数学模型·······················································································(25)3.2.3 计算机辅助分析及其程序设计·····························································(27)4 曲柄(导杆)滑块机构实验台装置设计4. 1 实验台结构·································································································(40)4.2 实验台硬件操作说明···················································································(41)4.3 用SolidWorks 2006实现实验台的立体图形················································(42)总结·········································································································(46)参考文献·········································································································(47)致谢·········································································································(48)1 引言1.1 选题的依据及意义1.曲柄(导杆)滑块机构定义曲柄滑块机构是铰链四杆机构的演化形式,由若干刚性构件用低副(回转副、移动副)联接而成的一种机构。
曲柄滑块机构设计

中国矿业大学成人高等教育本科毕业设计(论文)任务书学院(函授站)专业班级学生姓名任务下达日期:年月日任务完成日期:年月日毕业设计(论文)题目:曲柄滑块机构设计主要内容和要求:1、曲柄滑块的设计(1)曲柄滑块的组成(2)曲柄滑块的运动规律(3)曲柄滑块机构的的特性分析(4)计算滑块的运动范围(5)画出曲柄滑块的轮廓图(6)设计、绘制草图(7)各部件的连接设计2、机构的加工(1)机架的加工工艺分析(2)机架的加工程序3、零件图4、装配图5、参考资料院长(函授站站长)签字:指导教师签字:机械工程(函授)毕业设计指导书一、毕业设计的目的1、通过设计使学生综合运用有关课程的知识,巩固、深化、扩展有关机械设计方面的知识,树立正确的设计思想。
2、培养学生分析和解决工程实际问题的能力,使学生掌握简单机械的一般设计方法和步骤。
3、提高学生的有关设计能力,如计算能力、绘图能力等,使学生熟悉设计资料的使用,掌握经验估算等机械设计的基本技能。
4、掌握NC典型零件的加工方法二、设计内容:设计一对心曲柄滑块机构,曲柄滑块机构的结构图如下:图1 曲柄滑块机构三、原始数据A=400、B=120、C=240四、设计要求:1、采用无纸化绘制出曲柄滑块机构的总装图和零件图,零件图数量不得少于五张。
2、编写二到三个典型零件的加工工艺和CNC加工程序。
3、编写设计任务书一套。
五、设计内容和步骤本次设计分为三个阶段,计划在三个月内完成,各阶段的设计内容和步骤如下:第一阶段:1、设计准备工作(1)熟悉任务书,明确设计的内容和要求;(2)熟悉设计指导书,有关资料、图纸等。
2、总体设计(1)初步确定各部件结构、尺寸;(2)绘制各部件草图;第二阶段:3、零件图的绘制4、装配图的绘制第三阶段:5、编制数控加工程序6、总结写出设计总结,包括课题完成情况,以及个人收获体会。
8、答辩(1)作好答辩准备(概述自己设计的思路和过程,设计的特点);(2)参加答辩(包括个人陈述和答辩组老师提问)。
曲柄滑块工作机构课程设计

摘要曲柄压力机广泛应用于冲裁,弯曲,校正,模具冲压等工作。
本次设计的为开式固定台式中型,公称压力为1600KN曲柄压力机。
本设计主要进行该曲柄压力机曲柄滑块工作机构的设计。
在设计中,首先根据该压力机要保证的主要技术参数——公称压力、滑块行程等,初步估算曲柄,连杆,滑块,导轨相关尺寸,然后分别对其进行校核,修正,最终确定各零部件尺寸;进行装模高度调节装置设计,并最终完成该曲柄滑块工作机构设计。
关键字:公称压力;曲轴;连杆;导轨;调节装置目录第一章曲柄压力机的工作原理及主要参数 (1)1.1压力机技术参数 (1)1.2 曲柄压力机的工作原理. (1)1.3曲柄压力机工作的特点 (2)1.4 曲柄形式 (2)1.4.1、曲轴驱动的曲柄滑块机构 (3)1.4.2、偏心轴驱动的曲柄滑块机构 (4)1.4.3、曲拐驱动的曲柄滑块机构 (4)1.5.4、偏心齿轮驱动的曲柄滑块机构 (4)1.4.5各种结构的区别及最终确定设计设计思路 (6)第二章曲柄滑块机构的构成及相关分析 (6)2.1压力机曲柄滑块机构的构成 (6)2.2曲柄压力机滑块机构的运动规律分析。
(7)2.2.1滑块的位移和曲柄转角之间的关系 (7)2.2.2滑块的速度和曲柄转角的关系 (8)2.3曲柄压力机滑块机构的受力分析 (9)2.3.1忽略摩擦情况下滑块机构主要构件的力学分析 (9)2.3.2考虑摩擦情况下滑块机构主要构件的力学分析 (10)第三章装模高度调节装置总体设计 (13)3.1装模高度调节设计及电动机的选定 (13)3.1.1 装模高度调节装置构成及工做原理 (13)3.1.2调节装置电动机选定............................ 错误!未定义书签。
第四章齿轮传动......................................... 错误!未定义书签。
4.1 齿轮传动的介绍...................................... 错误!未定义书签。
QTD-III型 曲柄滑块、导杆、凸轮组合实验指导书

实验一、机构运动参数的测试和分析实验一、实验目的1.掌握机构运动的周期性变化规律,并学会机构运动参数如位移、速度和加速度等的测试原理和方法;2. 学会运用多通道通用实验仪器、传感器等先进实验技术手段开展实验研究的方法;3. 利用计算机对平面机构动态参数进行采集、处理,作出实测的动态参数曲线,并通过计算机对该平面机构的运动进行数值仿真,作出相应的动态参数曲线,从而实现理论与实际的紧密结合。
二、实验内容1.测试曲柄导杆机构、曲柄滑块机构、凸轮机构等机构的构件转角、移动位移等运动参数;2.比较实测参数曲线与理论仿真曲线的差异。
三、实验仪器QTD-III型曲柄、导杆、凸轮组合实验台该组合实验装置,只需拆装少量零部件,即可分别构成四种典型的传动系统。
他们分别是曲柄滑块机构、曲柄导杆机构、平底直动从动杆凸轮机构和滚子直动从动杆凸轮机构。
具体结构示意图如下图所示。
(a)曲柄滑块机构(b)曲柄导杆机构(c)平底直动从动件凸轮机构(d)滚子直动从动件凸轮机构1、同步脉冲发生器2、涡轮减速器3、曲柄4、连杆5、电机6、滑块7、齿轮8、光电编码器9、导块10、导杆11、凸轮12、平底直动从动件13、回复弹簧14、滚子直动从动件15、光栅盘四、实验原理本实验仪由单片机最小系统组成。
外扩 16 位计数器,接有 3 位 LED 数码显示器可实时显示机构运动时曲柄轴的转速,同时可与 P C 机进行异步串行通讯。
在实验机构动态运动过程中,滑块的往复移动通过光电脉冲编码器转换输出具有一定频率(频率与滑块往复速度成正比),0-5伏电平的两路脉冲,接入微处理器外扩的计数器计数,通过微处理器进行初步处理运算并送入 P C 机进行处理,P C 机通过软件系统在CRT上可显示出相应的数据和运动曲线图。
机构中还有两路信号送入单片机最小系统,那就是角度传感器(同步脉冲发生器)送出的两路脉冲信号。
其中一路是光栅盘每20。
一个角度脉冲,用于定角度采样,获取机构运动线图;另一路是零位脉冲,用于标定采样数据时的零点位置。
曲柄滑块机构的运动分析及应用

机械原理课程机构设计实验报告题目:曲柄滑块机构的运动分析及应用小组成员与学号:泽陆(11071182)柯宇 (11071177)熊宇飞(11071174)保开 (11071183)班级: 1107172013年6月10日摘要 (3)曲柄滑块机构简介 (4)曲柄滑块机构定义 (4)曲柄滑块机构的特性及应用 (4)曲柄滑块机构的分类 (8)偏心轮机构简介 (9)曲柄滑块的动力学特性 (10)曲柄滑块的运动学特性 (11)曲柄滑块机构运行中的振动与平衡 (14)参考文献 (15)组员分工 (15)摘要本文着重介绍了曲柄滑块机构的结构,分类,用途,并进行了曲柄滑块机构的动力学和运动学分析,曲柄滑块机构的运动学特性分析,得出了机构压力表达式,曲柄滑块机构的运动特性分析,得出了滑块的位移、速度和加速度的运动表达式。
最后,对曲柄滑块机构运动中振动、平衡稳定性等进行了总结。
关键字:曲柄滑块动力与运动分析振动与平稳性ABSTRACTThe paper describes the composition of planar linkage, focusing on the structure, classification, use of a slider-crank mechanism and making the dynamic and kinematic analysis, kinematics characteristics of the crank slider mechanism analysis for a slider-crank mechanism, on one hand , we obtain the drive pressure of the slider-crank mechanism ,on the other hand,we obtain the expression of displacement, velocity and acceleration of movement. Finally, the movement of the vibration and balance stability of the crank slider mechanism are summarized.曲柄滑块机构简介曲柄滑块机构定义曲柄滑块机构是铰链四杆机构的演化形式,由若干刚性构件用低副(回转副、移动副)联接而成的一种机构。
机械设计基础课后习题答案
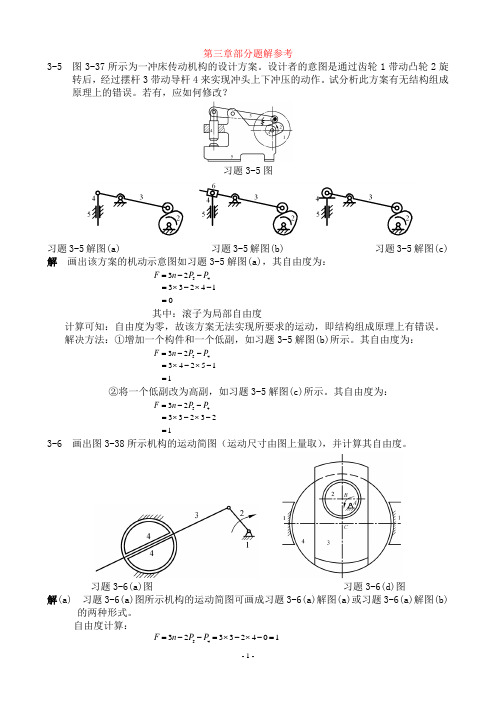
第三章部分题解参考3-5 图3-37所示为一冲床传动机构的设计方案。
设计者的意图是通过齿轮1带动凸轮2旋转后,经过摆杆3带动导杆4来实现冲头上下冲压的动作。
试分析此方案有无结构组成原理上的错误。
若有,应如何修改?习题3-5图习题3-5解图(a) 习题3-5解图(b) 习题3-5解图(c) 解 画出该方案的机动示意图如习题3-5解图(a),其自由度为:14233 2345=-⨯-⨯=--=P P n F 其中:滚子为局部自由度计算可知:自由度为零,故该方案无法实现所要求的运动,即结构组成原理上有错误。
解决方法:①增加一个构件和一个低副,如习题3-5解图(b)所示。
其自由度为:115243 2345=-⨯-⨯=--=P P n F ②将一个低副改为高副,如习题3-5解图(c)所示。
其自由度为:123233 2345=-⨯-⨯=--=P P n F 3-6 画出图3-38所示机构的运动简图(运动尺寸由图上量取),并计算其自由度。
习题3-6(a)图 习题3-6(d)图解(a) 习题3-6(a)图所示机构的运动简图可画成习题3-6(a)解图(a)或习题3-6(a)解图(b)的两种形式。
自由度计算:1042332345=-⨯-⨯=--=P P n F习题3-6(a)解图(a)习题3-6(a)解图(b)解(d) 习题3-6(d)图所示机构的运动简图可画成习题3-6(d)解图(a)或习题3-6(d)解图(b)的两种形式。
自由度计算:1042332345=-⨯-⨯=--=P P n F习题3-6(d)解图(a) 习题3-6(d)解图(b)3-7 计算图3-39所示机构的自由度,并说明各机构应有的原动件数目。
解(a) 10102732345=-⨯-⨯=--=P P n FA 、B 、C 、D 为复合铰链原动件数目应为1说明:该机构为精确直线机构。
当满足BE =BC =CD =DE ,AB =AD ,AF =CF 条件时,E 点轨迹是精确直线,其轨迹垂直于机架连心线AF解(b) 1072532345=-⨯-⨯=--=P P n FB 为复合铰链,移动副E 、F 中有一个是虚约束 原动件数目应为1说明:该机构为飞剪机构,即在物体的运动过程中将其剪切。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上海应用技术学院数学实验报告题目:曲柄滑块机构的运动规律姓名:**院系:理学院数学与应用数学系学号: **********指导老师:***2015年3月30日目录一、实验目的 (3)二、实际问题 (3)三、数学模型 (3)四、数值积分方法 (4)五、实验任务 (6)任务一 (6)任务二 (7)任务三 (9)任务四................................................................. 错误!未定义书签。
一、 实验目的本实验主要涉及微积分中对函数特性的研究。
通过实验复习函数求导法, Taylor 公式和其他有关知识。
着重介绍运用建立近视似模型并进行数值计算来研究讨论函数的方法。
二、 实际问题曲柄滑块机构是一种常用的机械结构,它将曲柄的转动转化为滑块在直线上的往复运动,是气压机、冲床、活塞式水泵等机械的主机构。
右图为其示意图。
记曲柄OQ 的长为r ,连杆QP 的长为l , 当曲柄绕固定点O 以角速度w 旋转时, 由连杆带动滑块P 在水平槽内做往复直线运动。
假设初始时刻曲柄的端点Q 位于水平线段OP 上, 曲柄从初始位置起转动的角度为θ,而连杆QP 与OP 的锐夹角为β(称为摆角) 。
在机械设计中要研究滑块的运动规律和摆角的变化规律, 确切的说,要研究滑块的位移,速度和加速度关于θ的函数关系,摆角β及其角速度和角加速度关于θ的函数关系, 进而(1)求出滑块的行程s (即滑块往复运动时左、右极限位置间的距离);(2)求出滑块的最大和最小加速度(绝对值), 以了解滑块在水平方向上的作用力;(3)求出β的最大和最小角加速度(绝对值), 以了解连杆的转动惯量对滑块的影响;在求解上述问题时,我们假定:100(),3300(),240(/min)r mm l r mm ω====转 符号说明:r -曲柄OQ 的长; l -连杆PQ 的长度; β-摆角(连杆PQ 与OP 的锐夹角); ω-角速度; P -滑块; x -滑块的位移; a -滑块的加速度。
三、 数学模型取O 点为坐标原点,OP 方向为x 轴正方向,P 在x 轴上的坐标为x ,那么可用x 表示滑块的位移。
利用三角关系,立即得到θθ222sin cos r l r x -+= (1.1)由于t ωθ= ,故有θωθθd dx dt d d dx dt dx == (1.2) 而θθθθθ2222sin cos sin sin r l r r d dx ---= (1.3) 于是滑块的速度⎪⎪⎭⎫⎝⎛-+-=θθω222sin cos 1sin r l r r v (1.4) 进而,可以得到滑块的加速度为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-++-===232224222)sin ()sin )2cos((cos θθθθωθωr l r l r r d dv dt dv a (1.5) 同样,基于关系式θβsin sin r l = (1.6)我们有摆角的表达式⎪⎭⎫ ⎝⎛=θβsin arcsin l r(1.7)式(1.6)对t 求导, θωθθββcos cos cos r dtd r dt d l == 可得βθωβcos cos l r dt d = (1.8) 由此再得⎪⎪⎪⎪⎭⎫ ⎝⎛--=βββθβθωωβ222cos sin cos cos sin dt d l r dt d (1.9) 利用(1.6),不难由上两式导出θθωβ222sin cos r l r dt d -= (1.10)和2322222222)sin ()(sin θθωβr l r l r dt d ---= (1.11) 至此,我们得到了滑块位移x 和连杆摆角β运动规律中有关变量依赖θ的表达式。
四、 数值积分方法将位移的表达式(1.1)改写为21222)sin 1(cos θθlr l r x -+=一般而言,22lr 是远比1小的数,于是利用1,1)1(<++=+εαεεα (1.12)得到滑块位移的近似模型为θθ221sin 2cos lr l r x -+= (1.13)从而有相应的近似速度⎪⎭⎫⎝⎛--=⎪⎪⎭⎫ ⎝⎛--===)2sin(2sin )2sin(2sin 2111θθωθθωθθl r r l r r dt d d dx dt dx v (1.14)和近似加速度⎪⎭⎫⎝⎛+-==)2cos(cos 211θθωl r r dt dv a (1.15) 这里的速度1v 和加速度1a 是直接对近似位移模型1x 求导得来的,而不是对v 和a的精确表达式(1.4)和(1.5)的近似。
当然我们也可以直接从滑块速度的解析式(1.4)进行近似。
仍利用公式(1.12)有⎪⎪⎭⎫ ⎝⎛+≈⎪⎪⎭⎫ ⎝⎛-=--θθθ22221222222sin 211sin 11sin 1l r l l r l r l 把上式代入(1.4),就得到滑块速度的近似模型⎪⎪⎭⎫⎝⎛++-=⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛++-=32322224)2sin(sin 2)2sin(sin sin 21cos 1sin l r l r r l r l r r v θθθθωθθθω (1.16) 从(1.16)出发,又可得近似加速度⎥⎦⎤⎢⎣⎡+++-=3223224)2cos(sin 2)2((sin )2cos(cos l r l r r a θθθθθω (1.17) 对摆角β可以利用幂级数展开的Maclaurin 公式1,6arcsin 3<++=εεεε (1.18)得到摆角的近似模型。
粗略一些,可以取θβsin 1lr= (1.19)(当lr 较小时可用此式)。
而必要时可以取θθβ3332sin 6sin lr l r += (1.20)相应的近似角速度为θωβcos 1lrdt d = (1.21) 或⎪⎪⎭⎫ ⎝⎛+=θθθωβcos sin 2cos 2332l r l r dt d (1.22) 近似角加速度为θωβsin 2212l r dtd -= (1.23) 或⎥⎦⎤⎢⎣⎡-+-=)cos )(2sin (sin 2sin 3332222θθθθωβl r l r dt d (1.24)五、 实验任务任务一试用摆角的角加速度的三种表达式, 即式(1.11)、(1.23)和(1.24),取步长为12π,r ,l ,ω的值如前,计算当[0,]θπ∈变化时角加速度的值,并列表加以比较。
实验程序:function m1_2(t)r=100;l=300;w=240/60*2*pi;a0=-r*w^2*sin(t)*(l^2-r^2)./(l^2-r^2*sin(t).^2).^(3/2) a1=-w^2*r*sin(t)/la2=-w^2*(r*sin(t)/l+r^3*(sin(t).^3-sin(2*t).*cos(t))/(2*l^3))>> m1_1([0:pi/12:pi])从结果中可以看出误差的大小,取决于近似表达式的精度,在利用泰勒公式求近似模型时,如果展开的精度越高,则误差就越小,在数据表中也可以看出,dtd 22β取得精度比dtd 12β高,所以结果与真实值相差的更小。
任务二利用(1.12)式,对角摆角的角速度(1.10)式和角速度(1.11)式进行简化,将结果与(1.21)~(1.24)式进行比较,并与上题的计算结果相比较。
解析: 由式 1,1)1(<++=+εαεεα (1.12)θθωβ222sin cos r l r dtd -= (1.10)可以化简为 ⎪⎪⎭⎫ ⎝⎛+=θθθωβsin )2sin(4cos 223l r l r dt d )10.1(' 23222222232)sin ()(sin θθωβr l r l r dt d ---= (1.11) 可以化简为⎪⎪⎭⎫ ⎝⎛+--=θθωβ322322222sin 23sin )(l r l r l r dt d )11.1(' 将化简结果与(1.21)~(1.24)式进行比较,可以发现有类似的项。
实验程序:function m2_1(t)r=100;l=300;w=240/60*2*pi;b0=r*w*cos(t)./sqrt(l^2-r^2*sin(t).^2) b1=w*r*cos(t)/lb2=w*(r*cos(t)/l+r^3*sin(t).^2.*cos(t)/(2*l^3)) b3=r*w/l*(cos(t)+r^2*sin(2*t).*sin(t)/(4*l^2))a0=-r*w^2*sin(t)*(l^2-r^2)./(l^2-r^2*sin(t).^2).^(3/2) a1=-w^2*r*sin(t)/la2=-w^2*(r*sin(t)/l+r^3*(sin(t).^3-sin(2*t).*cos(t))/(2*l^3))a3=-r*w^2*(l^2-r^2)/l^3*(sin(t)+3*r^2*sin(t).^3/(2*l^2)) >> m2_1([0:pi/12:pi])运行结果如下:从上表中可看出dt d 2β与dt d 3β最接近真值dtd β,dt d 32β最接近真值dt d 3β。
由此看来,方案三最优。
任务三给定一机构如右图所示。
设连杆QP 长度l=300mm ,曲柄OQ 的长为r=100mm ,距离e=20mm ,曲柄的角速度w=240转/min 。
对θ在一个周期(即]2,0[π)中计算滑块的位移、行程、速度、加速度和摆角及其最值。
解析:这个机构的特点是:滑块的运动轨迹仍然在原来的平面上,且与轴线Ox 平行,但运动轨迹与Ox 有距离e (称为偏心距)。
这样进程时间将与退程时间不同。
由于P 点始终在直线e y =上,所以我们只需要考虑滑块在x 方向上的位移,不需要再考虑在y 轴上的位移。
取O 点为坐标原点,沿x 轴向右方向为正,P 在x 轴上的坐标为x,用x 表示滑块的位移,利用三角关系有:22)sin (cos e r l r x --+=θθ (2.1)由于t ωθ=,故有θωθθd dx dt d d dx dt dx == (2.2)θd dx求导程序: >> syms r l e t>> x=r*cos(t)+sqrt(l^2-(r*sin(t)-e).^2); >> diff(x,t)得 22)sin ()sin (cos sin θθθθθr e l r e r r d dx ---+-=即22)sin ()sin (cos sin e r l e r r r d dx -----=θθθθθ (2.3)于是滑块的速度 22)sin ()sin (cos sin e r l e r r r v -----=θθθωθω (2.4)从而,得到滑块的加速度为⎪⎪⎭⎫ ⎝⎛---+--+--===3222222222))sin (()sin (cos ))sin ()(sin 2cos (cos e r l e r r e r l re r r d dv dt dv a θθθθθθθωθω(2.5)由关系式θβsin sin r e l =+ (2.6)得摆角的表达式为)sin arcsin(ler -=θβ (2.7) 滑块的行程:68744200.502199)()(2222min max =----+=-=e r l e r l x x s实验程序: (1)滑块的位移: function m3_1(t) r=100; l=300; e=20;x=r*cos(t)+sqrt(l^2-(r*sin(t)-e).^2) >>m3_1([0:pi/12:2*pi])(2)滑块的速度: function m3_2(t) r=100; l=300;w=240/60*2*pi; e=20;v=-w*r*sin(t)-(w*r*cos(t).*(r*sin(t)-e))/sqrt(l^2-(r*sin(t)-e).^2) >>m3_2([0:pi/12:2*pi])(3)滑块的加速度: function m3_3(t) r=100; l=300;w=240/60*2*pi; e=20;a=w^2*(-r*cos(t)-((r^2*cos(2*t)+r*e*sin(t)).*(l^2-(r*sin(t)-e).^2)+r^2*cos(t).^2.*(r*sin(t)-e).^2)./(l^2-(r*sin(t)-e).^2).^(3/2)) >> m3_3([0:pi/12:2*pi])(4)摆角及其最值: function m3_4(t) r=100; l=300;w=240/60*2*pi; e=20;b=asin((r*sin(t)-e)/l) >> m3_4([0:pi/12:2*pi])运行结果如下:由上表可看出,摆角β,在π处取得最小值0.0667;在π23处取得最大值0.4115。
