《图形的位似》综合练习1

合集下载

图形的位似--巩固练习

图形的位似--巩固练习【巩固练习】一. 选择题1.下面给出了相似的一些命题：（1）菱形都相似；（2）等腰直角三角形都相似；（3）正方形都相似；（4）矩形都相似；（5）正六边形都相似；其中正确的有（）.A．2个 B．3个 C．4个 D．5个2.下列说法错误的是（）.A.位似图形一定是相似图形.B.相似图形不一定是位似图形.C.位似图形上任意一对对应点到位似中心的距离之比等于相似比.D.位似图形中每组对应点所在的直线必相互平行.3.下列说法正确的是（） .A.分别在ABC的边AB、AC的反向延长线上取点D、E，使DE∥BC，则ADE是ABC放大后的图形.B.两位似图形的面积之比等于相似比.C.位似多边形中对应对角线之比等于相似比.D.位似图形的周长之比等于相似比的平方.4.（2015•营口）如图，△ABE和△CDE是以点E为位似中心的位似图形，已知点A（3，4），点C （2，2），点D（3，1），则点D的对应点B的坐标是（）A．（4，2）B．（4，1）C．（5，2）D．（5，1）5. 下列命题：①两个正方形是位似图形；②两个等边三角形是位似图形；③两个同心圆是位似图形；④平行于三角形一边的直线截这个三角形的两边，所得的三角形与原三角形是位似图形.其中正确的有( ).二.填空题8. 如果两个位似图形的对应线段长分别为3cm和5cm，且较小图形周长为30cm，则较大图形周长为__________.9.已知ABC，以点A为位似中心，作出ADE，使ADE是ABC放大2倍的图形，则这样的图形可以作出______个，它们之间的关系是__________.'''''，已知OA=10cm，OA′10．如图，以点O为位似中心，将五边形ABCDE放大后得到五边形A B C D E'''''的周长的比值是__________．=20cm，则五边形ABCDE的周长与五边形A B C D E11. △ABC中，D、E分别在AB、AC上，DE∥BC，△ADE是△ABC缩小后的图形.若DE把△ABC的面积分成相等的两部分，则AD：AB=________.12. 把一矩形纸片对折，如果对折后的矩形与原矩形相似，则原矩形纸片的长与宽之比为____________________.13.（2015•钦州）如图，以O为位似中心，将边长为256的正方形OABC依次作位似变换，经第一次变化后得正方形OA1B1C1，其边长OA1缩小为OA的，经第二次变化后得正方形OA2B2C2，其边长OA2缩小为OA1的，经第，三次变化后得正方形OA3B3C3，其边长OA3缩小为OA2的，…，依次规律，经第n次变化后，所得正方形OA n B n C n的边长为正方形OABC边长的倒数，则n= ．14. 如图，△ABC中，AB=AC=4，∠BAC=36°，∠ABC的平分线与AC边的交点D为边AC的黄金分割点（AD＞DC），则BC=______________.三．综合题15.如图，D、E分别AB、AC上的点.　(1)如果DE∥BC，那么△ADE和△ABC是位似图形吗？为什么？　(2)如果△ADE和△ABC是位似图形，那么DE∥BC吗？为什么？16.（2014秋•海陵区校级月考）如图，F在BD上，BC、AD相交于点E，且AB∥CD∥EF，（1）图中有哪几对位似三角形，选其中一对加以证明；（2）若AB=2，CD=3，求EF的长．17. 如图1，矩形ODEF的一边落在矩形ABCO的一边上，并且矩形ODEF∽矩形ABCO，其相似比为1：（1）求矩形ODEF的面积；（2）将图1中的矩形ODEF绕点O逆时针旋转一周，连接EC、EA，△ACE的面积是否存在最大值或最小值？若存在，求出最大值或最小值；若不存在，请说明理由．【答案与解析】一、选择题1．【答案】B【解析】（1）菱形的角不一定对应相等，故错误；（2）（3）（5）符合相似的定义，故正确；（4）对应边的比不一定相等．故错误．故正确的是：（2）（3）（5）．故选B．2．【答案】D.3．【答案】C.4．【答案】C.【解析】设点B 的坐标为（x ，y ），∵△ABE 和△CDE 是以点E 为位似中心的位似图形，∴=，=，解得x=5，y=2，所以，点B 的坐标为（5，2）．故选C ．5．【答案】B【解析】由位似图形的概念可知③和④对，故选B.6．【答案】D.【解析】∵AC＞BC ，∴AC 是较长的线段，AB AC AC≈0.618AB．故选D ．7.【答案】B.二、填空题8.【答案】50cm.9.【答案】2个；全等.10.【答案】1：2．【解析】∵五边形ABCDE 与五边形A′B′C′D′E′位似，OA=10cm ，OA′=20cm， ∴五边形ABCDE∽五边形A′B′C′D′E′，且相似比为：OA ：OA′=10：20=1：2， ∴五边形ABCDE 的周长与五边形A′B′C′D′E′的周长的比为：OA ：OA′=1：2．故答案为：1：2．11.【答案】 .【解析】由BC∥DE 可得△ADE∽△ABC，所以，故.13. 【答案】16.【解析】由图形的变化规律可得×256=，解得n=16．14. 【解析】∵AB=AC，∠A=36°，∴∠ABC=∠C=72°，又BD 平分∠ABC，∴∠ABD=∠CBD=36°，∴∠BDC=72°，∴BC=BD=AD，∵D 点是AC 的黄金分割点，三．解答题15.【答案与解析】(1)△ADE 和 △ABC 是位似图形.理由是： DE∥BC，所以∠ADE=∠B， ∠AED=∠C.所以△ADE∽△ABC，所以. 又因为点A 是△ADE 和 △ABC 的公共点，点D 和点B 是对应点，点E 和点C是对应点，直线BD 与CE 交于点A ，所以△ADE 和 △ABC 是位似图形. (2)DE∥BC.理由是：因为△ADE 和△ABC 是位似图形，所以△ADE∽△ABC 所以∠ADE=∠B 所以DE∥BC.16.【答案与解析】解：（1）△DFE与△DBA，△BFE与△BDC，△AEB与△DEC都是位似图形，理由：∵AB∥CD∥EF，∴△DFE∽△DBA，△BFE∽△BDC，△AEB∽△DEC，且对应边都交于一点，∴△DFE与△DBA，△BFE与△BDC，△AEB与△DEC都是位似图形；（2）∵△BFE∽△BDC，△AEB∽△DEC，AB=2，CD=3，∴==，∴==，解得：EF=．。

图形的位似作图练习

图形的位似作图练习姓名： ___________________1如图，方格纸中的每个小方格都是边长为 1个单位长度的正方形，△ ABC 的顶点都在格点上，建立平面直角坐标系.（1）点A 的坐标为 ____________ ，点C 的坐标为 ______________ .（2）将厶ABC 向左平移7个单位，请画出平移后的△ A i B i C i .若M ABC 内的一点，其坐标为（a, b ），则平移后点M 的对应点M i 的坐标为 ________________ .（3）以原点0为位似中心，将厶ABC 缩小，使变换后得到的△ A 2B 2C 2与厶ABC 对应边的比为1: 2.请在网格内画出 △ A 2B 2C 2，并写出点A 2的坐标： ______________ .2、如图1,正方形ABC 刖正方形OEFG 中，点A 和点F 的坐标分别为（3，2），（ - 1，-1），则两个正方形的位似中心的坐标是 _______________________ 。

3、如图，△ ABC 三个顶点的坐标分别为 A （2，7），B （6，8）， C （8，2），请你分别完成下面的作图并标出所有顶点的坐标。

（不要求写出作法）（1）以0为位似中心，在第三象限内作出△ ABC ,使厶ABC 与厶ABC 的位似比为1 : 2; （ 2）以0为旋转中心，将△ ABC 沿顺时针方向旋转90°得到 △ A 2B2Q 。

4、如图，平面I 直角坐标系* xOy 中，点A 、B 的坐标分别为（3，0）、（2, B ■ 19 P ! * ■!< l _ ip res ” - ■ i ■ ■ - i ■ i -虑 ”' 一 rn ■仃-ICTW - -■■■■■■m-的位似图形,且O 的坐标为（-1,o ）,则点B 的坐标为-3）, △ ABO 是 △- ABO ■关于的 IT ifi n■ ■ T n^iirnay5、如图，在平面直角坐标系中，已知△ ABC三个顶点的坐标分别为A (- 1, 2), B (- 3, 4) C (-2, 6) (1)画出△ ABC绕点A顺时针旋转90°后得到的△ A1B1C1(2)以原点0为位似中心，画出将△ A1B1C1三条边放大为原来的2倍后的△ A2B2C2.。

九年级数学上学期第三章《图形的相似》综合测试题(含答案)

九年级数学上学期第三章《图形的相似》综合测试题（含答案）一、选择题(本大题共8小题,每小题4分,共32分) 1.已知5a=6b (a ≠0),则下列变形正确的是 ( )A .b 6=5aB .b 5=6a C .ab =56D .a -b b=152.如图1,已知AB ∥CD ∥EF ,BD ∶DF=1∶2,那么下列结论中正确的是 ( )图1A .AC ∶AE=1∶3B .CE ∶EA=1∶3C .CD ∶EF=1∶2 D .AB ∶EF=1∶2 3.C 是线段AB 的黄金分割点,且AB=6cm,则BC 的长为 ( ) A .(3√5-3)cm B .(9-3√5)cmC .(3√5-3)cm 或(9-3√5)cmD .(9-3√5)cm 或(6√5-6)cm4.如图2,在四边形ABCD 中,AD ∥BC ,对角线AC ,BD 相交于点O ,AD=1,BC=4,则△AOD 与△BOC 的面积之比为( )A.12 B.14 C.18D.116图2 图35.如图3,已知△ABC 与△BDE 都是等边三角形,点D 在边AC 上(不与点A ,C 重合),DE 与AB 相交于点F ,那么与△BFD 相似的三角形是 ( )A .△BFEB .△BDCC .△BDAD .△AFD6.已知△ABC 与△A 1B 1C 1是关于原点为中心的位似图形,且点A 的坐标为(2,1),△ABC 与△A 1B 1C 1的位似比为12,则点A 的对应点A 1的坐标是 ( )A .(4,2)B .(-4,-2)C .(4,2)或(-4,-2)D .(6,3)7.如图4,在△ABC 中,点D 在BC 边上,连接AD ,点G 在线段AD 上,GE ∥BD ,且交AB 于点E ,GF∥AC,且交CD于点F,则下列结论一定正确的是()A.ABAE =AGADB.DFCF=DGADC.FGAC=EGBDD.AEBE=CFDF图4 图58.如图5,在△ABC中,中线BE,CD相交于点O,连接DE,有下列结论:①DEBC =12;②S△DOES△COB=12;③AD AB =OEOB;④S△DOES△ADE=13.其中正确的有()A.1个B.2个C.3个D.4个二、填空题(本大题共6小题,每小题4分,共24分)9.若△ABC∽△DEF,相似比为3∶2,则对应周长的比值是.10.在比例尺为1∶40000的地图上,某条道路的长为7cm,则该道路的实际长度是_______km.11.若a,b,c,d是成比例线段,其中a=2cm,b=6cm,c=5cm,则线段d= cm.12.如图6,在△ABC中,MN∥BC分别交AB,AC于点M,N.若AM=1,MB=2,BC=3,则MN的长为.图613.在△ABC中,AB=6,AC=5,点D在边AB上,且AD=2,点E在边AC上,当AE= 时,以A,D,E为顶点的三角形与△ABC相似.14.如图7,铁路道口的栏杆短臂长1m,长臂长16m.当短臂端点下降0.5m时,长臂端点升高m.(杆的宽度忽略不计)图7三、解答题(本大题共5小题,共44分)15.(6分)如图8所示,AD,BE分别是钝角三角形ABC的边BC,AC上的高.求证:ADBE =AC BC.图816.(6分)如图9,平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE=12CD.(1)求证:△ABF∽△CEB;(2)若△DEF的面积为2,求平行四边形ABCD的面积.图917.(6分)如图10,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB'C'D',使它与四边形ABCD位似,且位似比为2.(1)在图中画出四边形AB'C'D';(2)试说明△AC'D'是等腰直角三角形.图1018.(12分)为测量操场上旗杆的高度,设计的测量方案如图11所示,标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛距地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,E,C,A三点共线,求旗杆AB的高度.图1119.(14分)如图12,∠ABD=∠BCD=90°,DB平分∠ADC,过点B作BM∥CD交AD于点M,连接CM 交DB于点N.(1)求证:BD2=AD·CD;(2)若CD=6,AD=8,求MN的长.图12参考答案1.D [解析] 选项A,b 6=5a ⇒ab=30,故此选项错误;选项B,b 5=6a ⇒ab=30,故此选项错误;选项C,ab =56⇒6a=5b ,故此选项错误;选项D,a -b b=15⇒5(a-b )=b ,即5a=6b ,故此选项正确.故选D .2.A [解析]∵AB ∥CD ∥EF ,BD ∶DF=1∶2,∴AC ∶AE=1∶3,故A 选项正确;CE ∶EA=2∶3,故B 选项错误;CD ∶EF 的值无法确定,故C 选项错误;AB ∶EF 的值无法确定,故D 选项错误.故选A .3.C [解析]∵C 是线段AB 的黄金分割点,且AB=6cm,∴BC=√5-12AB=(3√5-3)cm 或BC=3−√52AB=(9-3√5)cm .故选C .4.D [解析] 在四边形ABCD 中,AD ∥BC ,所以△AOD ∽△COB.又由AD=1,BC=4,根据相似三角形的面积比等于相似比的平方,即可求得△AOD 与△BOC 的面积之比.5.C [解析]∵△ABC 与△BDE 都是等边三角形,∴∠A=∠BDF=60°.又∵∠ABD=∠DBF ,∴△BFD ∽△BDA ,∴与△BFD 相似的三角形是△BDA.6.A [解析]∵△ABC 与△A 1B 1C 1是关于原点为中心的位似图形,A (2,1),△ABC 与△A 1B 1C 1的位似比为12,∴点A 的对应点A 1的坐标是(2×2,1×2),即(4,2). 7.D8.C [解析] 由BE ,CD 均为△ABC 的中线可知,DE 为△ABC 的中位线,所以DE=12BC ,DE ∥BC ,所以DE BC =12,故①正确;由DE ∥BC 可得△DOE ∽△COB ,所以S △DOE S △COB=DE BC2=14,故②错误;由DE ∥BC 可得△ADE ∽△ABC ,△DOE ∽△COB ,所以AD AB =DE BC ,DE BC =OEOB ,所以AD AB =OEOB ,故③正确; 因为DE ∥BC ,所以△ADE ∽△ABC ,所以S △ADE S △ABC=DE BC2=14,设△DOE 的高为h ,DE=a ,则BC=2a ,△BOC 的高为2h ,所以△ABC 的高为6h ,所以△ADE 的高为3h ,所以S △DOES△ADE =12a ℎ12·a ·3ℎ=13,故④正确.故选C .9.3∶2 [解析] 根据相似三角形的周长比等于相似比求解.10.2.8 [解析] 设这条道路的实际长度为x cm,则140000=7x ,解得x=280000,280000cm =2.8km .11.15 [解析]∵a ,b ,c ,d 是成比例线段,∴a b=c d.∵a=2cm,b=6cm,c=5cm,∴26=5d,解得d=15(cm).12.1 [解析]∵MN ∥BC ,∴△AMN ∽△ABC ,∴AM AB =MNBC ,即11+2=MN 3,∴MN=1.13.125或53 [解析] 当AE AD =ABAC 时,∵∠A=∠A ,∴△AED ∽△ABC ,此时AE=AB ·AD AC=6×25=125;当AD AE =ABAC 时,∵∠A=∠A ,∴△ADE ∽△ABC ,此时AE=AC ·AD AB =5×26=53.故答案为125或53. 14.815.证明:∵AD ,BE 是钝角三角形ABC 的高,∴∠ADC=∠BEC=90°.又∵∠DCA=∠BCE ,∴△DAC ∽△EBC , ∴AD BE =ACBC .16.解:(1)证明:∵四边形ABCD 是平行四边形,∴∠A=∠C ,AB ∥CD ,∴∠ABF=∠CEB ,∴△ABF ∽△CEB.(2)∵四边形ABCD 是平行四边形,∴AD ∥BC ,AB ∥CD ,AB=CD , ∴△DEF ∽△CEB ,△DEF ∽△ABF. ∵DE=12CD ,∴EC=3DE ,AB=2DE ,∴S △DEFS△CEB=DE EC2=19,S △DEF S △ABF=DE AB2=14.∵S △DEF =2,∴S △CEB =18,S △ABF =8, ∴S 四边形BCDF =S △CEB -S △DEF =16,∴S 平行四边形ABCD =S 四边形BCDF +S △ABF =16+8=24.17.解:(1)如图,四边形AB'C'D'即为所求作图形.(2)根据网格的特点,利用勾股定理可以求出AD'=C'D'=2√10,AC'=4√5.利用勾股定理的逆定理可以得出∠AD'C'=90°, 故△AC'D'是等腰直角三角形.18.解:如图,过点E 作EH ⊥AB 于点H ,交CD 于点G ,则EF=DG=BH=1.6m,GH=BD=15m,EG=DF=2m,∴CG=CD-DG=3-1.6=1.4(m). ∵CG ∥AH , ∴△ECG ∽△EAH , ∴CG AH =EGEH ,即1.4AH =22+15,解得AH=11.9(m),∴AB=AH+BH=11.9+1.6=13.5(m).答:旗杆AB 的高度为13.5m . 19.解:(1)证明:∵DB 平分∠ADC ,∴∠ADB=∠BDC.又∵∠ABD=∠BCD=90°, ∴△ABD∽△BCD,∴ADBD =BD CD,∴BD2=AD·CD.(2)∵BM∥CD,∴∠MBD=∠BDC, ∴∠ADB=∠MBD,∴BM=MD.∵∠ABD=90°,∴∠MAB+∠ADB=90°,∠MBA+∠MBD=90°,∴∠MAB=∠MBA,∴BM=AM,∴AM=BM=MD=4.∵BD2=AD·CD,且CD=6,AD=8, ∴BD2=48,∴BC2=BD2-CD2=12,∴MC2=BM2+BC2=28,∴MC=2√7.∵BM∥CD,∴△MNB∽△CND,∴BMCD =MNCN=23,∴MN=4√75.。

第四章图形的相似课时练习题及答案 4.8 图形的位似第1课时位似图形及其画法

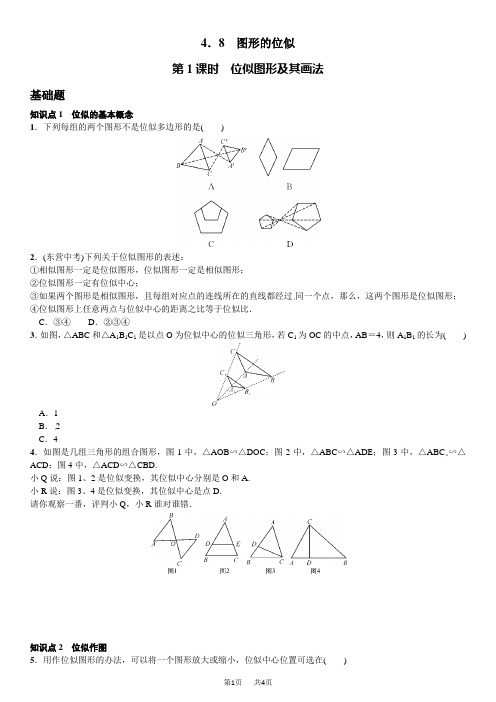
4．8图形的位似第1课时位似图形及其画法基础题知识点1位似的基本概念1．下列每组的两个图形不是位似多边形的是()2．(东营中考)下列关于位似图形的表述：①相似图形一定是位似图形，位似图形一定是相似图形；②位似图形一定有位似中心；③如果两个图形是相似图形，且每组对应点的连线所在的直线都经过同一个点，那么，这两个图形是位似图形；④位似图形上任意两点与位似中心的距离之比等于位似比．C．③④D．②③④3．如图，△ABC和△A1B1C1是以点O为位似中心的位似三角形，若C1为OC的中点，AB＝4，则A1B1的长为()A．1B．2C．44．如图是几组三角形的组合图形，图1中，△AOB∽△DOC；图2中，△ABC∽△ADE；图3中，△ABC∽△ACD；图4中，△ACD∽△CBD.小Q说：图1、2是位似变换，其位似中心分别是O和A.小R说：图3、4是位似变换，其位似中心是点D.请你观察一番，评判小Q，小R谁对谁错．知识点2位似作图5．用作位似图形的办法，可以将一个图形放大或缩小，位似中心位置可选在()A．原图形的外部B．原图形的内部C．原图形的边上D．任意位置6．如图所示是△ABC位似图形的几种画法，其中正确的个数是()A．1个B．2个C．3个D．4个7．如图，已知四边形ABCD和点O，请以O为位似中心，作出四边形ABCD的位似图形，把四边形ABCD放大为原来的2倍．中档题8．(玉林中考)△ABC与△A′B′C′是位似图形，且△ABC与△A′B′C′的相似比是1∶2，已知△ABC的面积是3，则△A′B′C′的面积是()A．3 B．6C．9 D．129．如图，已知△EFH和△M NK是位似图形，那么其位似中心是点________．10．如图，△ABC与△A′B′C′是位似图形，且相似比是1∶2，若AB＝2 cm，则A′B′＝________cm，请在图中画出位似中心O.11．如图，四边形ABCD和四边形A′B′C′D′位似，相似比k1＝2，四边形A′B′C′D′和四边形A″B″C″D″位似，相似比k2＝1.四边形A″B″C″D″和四边形ABCD是位似图形吗？相似比是多少？12．在放映电影时，我们需要把胶片上的图片放大到银幕上，以便人们欣赏．如图，点P为放映机的光源，△ABC 是胶片上面的画面，△A′B′C′为银幕上看到的画面．若胶片上图片的规格是2.5 cm×2.5 cm，放映的银幕规格是2 m×2 m，光源P与胶片的距离是20 cm，则银幕应距离光源P多远时，放映的图像正好布满整个银幕？综合题13．如图，△ABC 与△A′B′C′是位似图形，点A 、B 、A′、B′、O 共线，点O 为位似中心． (1)AC 与A′C ′平行吗？为什么？(2)若AB ＝2A′B′，OC ′＝5，求CC′的长．1．B 2.A 3.B 4.根据位似图形的定义得出：小Q 对，1，2都可以看成位似变换，位似中心分别为O 、A ，3、4虽然都存在相似三角形，但对应顶点的连线不相交于一点，而且对应边也不平行，所以3、4不是位似变换． 5.D 6.D 7.连接OA ，OB ，OC ，OD ，延长OA 到A′使OA′＝2OA ，延长OB 到B′使OB′＝2OB ，延长OC 到C′使OC′＝2OC ，延长OD 到D′使OD′＝2OD ，顺次连接A′、B′、C′、D′，则四边形A′B ′C′D′就是所求作的四边形． 8.D 9.B 10.4 如图，点O 即为所求． 11.∵四边形ABCD 和四边形A′B′C′D′位似，∴四边形ABCD ∽四边形A′B′C′D ′.∵四边形A′B′C′D′和四边形A″B″C″D″位似，∴四边形A′B′C′D′∽四边形A″B″C″D″.∴四边形A″B″C″D″∽四边形ABCD.∵对应顶点的连线过同一点，∴四边形A ″B″C″D″和四边形ABCD 是位似图形．∵四边形ABC D 和四边形A′B′C′D′位似，相似比k 1＝2，四边形A ′B ′C ′D ′和四边形A″B″C″D″位似，相似比k 2＝1，∴四边形A″B″C″D″和四边形ABCD 的相似比为12. 12.图中△A′B′C′是△ABC 的位似图形．设银幕距离光源P 为x m 时，放映的图像正好布满整个银幕．则相似比为x 0.2＝20.025.解得时，放映的图像正好布满整个银幕． 13.(1)AC ∥A′C′.理由如下：∵△ABC 与△A′B′C′是位似图形，∴△ABC ∽△A ′B ′C ′.∴∠A ＝∠C′A′B′.∴AC ∥A′C′.(2)∵△ABC ∽△A′B′C′，∴AB A′B′＝AC A′C′.∵AB ＝2A′B′，∴AC A′C′＝21.又∵△ABC 与△A′B′C′是位似图形，∴OC OC′＝AC A′C′＝21.∵OC ′＝5，∴OC ＝10.∴CC′＝OC －OC′＝10－5＝5.不用注册，！。

九年级数学上册4.8图形的位似第1课时位似图形及其性质同步练习

8 第1课时位似图形及其性质知识点 1 位似图形的认识1．下列各选项的两个图形中，不是位似图形的是( )图4－8－1图4－8－22．图4－8－2中的两个四边形是位似图形，它们的位似中心是( )A．点M B．点NC．点O D．点P知识点 2 画位似图形3．如图4－8－3所示是△ABC的位似图形的几种画法，其中正确的有( )图4－8－3A．1个B．2个C．3个D．4个4．教材例1变式题如图4－8－4，已知四边形ABCD，以点O为位似中心画四边形A′B′C′D′，使四边形A′B′C′D′与四边形ABCD位似，且相似比为1∶2.图4－8－4图4－8－55．2017·贵阳期末如图4－8－5，已知△ABC，任取一点O，连接AO，BO，CO，并取它们的中点D，E，F，得△DEF，则下列说法中正确的个数是( )①△ABC与△DEF是位似图形；②△ABC与△DEF是相似图形；③△ABC与△DEF的周长比为1∶2；④△ABC与△DEF的面积比为4∶1.A．1 B．2 C．3 D．46．如图4－8－6，△ACB与△AED是位似图形．(1)BC与DE平行吗？请说明理由；(2)如果AB＝3，AD＝4，AE＝3.5，试求△ACB与△AED的相似比及AC的长．图4－8－67．如图4－8－7，在矩形ABCD中，对角线AC，BD相交于点O.过点O作OE⊥BC于点E，连接DE交OC于点F，过点F作FG⊥BC于点G，则△ABC与△FGC是位似图形吗？若是，请说出位似中心，并求出相似比；若不是，请说明理由．图4－8－71．C [解析] 对应顶点的连线相交于一点的两个相似多边形叫位似图形．根据位似图形的概念，选项A ，B ，D 中的两个图形都是位似图形．选项C 中的两个图形不符合位似图形的概念，对应顶点不能相交于一点，故不是位似图形．故选C.2．D3．D [解析] 由位似图形的画法可得：4个图形都是△ABC 的位似图形．故选D.4．解：答案不唯一，如图，画法如下： (1)过点O 分别作射线OA ，OB ，OC ，OD ；(2)分别在射线OA ，OB ，OC ，OD 上取点A ′，B ′，C ′，D ′，使得OA ′OA ＝OB ′OB ＝OC ′OC＝OD ′OD ＝12； (3)顺次连接A ′B ′，B ′C ′，C ′D ′，D ′A ′，得到所要画的四边形A ′B ′C ′D ′. 5．C [解析] 根据位似的性质得出： ①△ABC 与△DEF 是位似图形， ②△ABC 与△DEF 是相似图形．∵将△ABC 的三边缩小为原来的12得△DEF ，∴△ABC 与△DEF 的周长比为2∶1，故③错误，根据面积比等于相似比的平方，得△ABC 与△DEF 的面积比为4∶1，故④正确．故选C.6．解：(1)BC ∥DE .理由：∵△ACB 与△AED 是位似图形，∴△ACB ∽△AED ， ∴∠B ＝∠D ，∴BC ∥DE . (2)∵△ACB ∽△AED ，∴AC AE ＝AB AD ＝34， ∴AC ＝3×3.54＝218，△ACB 与△AED 的相似比为34.7．解：△ABC 与△FGC 是位似图形，位似中心是点C . ∵在矩形ABCD 中，AD ∥BC ， ∴∠FAD ＝∠FCE ，∠FDA ＝∠FEC ， ∴△AFD ∽△CFE ，∴AF CF ＝AD CE. ∵∠ABC ＝90°，OE ⊥BC ， ∴OE ∥AB .∵OA ＝OC ，∴CE ＝12BC ，∴AD CE ＝BC CE ＝2，∴AF CF＝2，∴AC CF＝3，即△ABC 与△FGC 的相似比为3∶1.第2课时相似三角形周长和面积的性质知识点 1 有关周长的计算1．已知△ABC ∽△A 1B 1C 1，且AB ＝4，A 1B 1＝6，则△ABC 的周长和△A 1B 1C 1的周长之比是( )A ．9∶4B ．4∶9C ．2∶3D ．3∶2图4－7－102．如图4－7－10，在▱ABCD中，E是AD边上的中点，连接BE，并延长BE交CD的延长线于点F，则△EDF与△BCF的周长之比是( )A．1∶2 B．1∶3 C．1∶4 D．1∶53．2016·贵阳期末如果△ABC∽△DEF，其相似比为3∶1，且△ABC的周长为27，那么△DEF的周长为( )A．9 B．18 C．27 D．814．如图4－7－11，在▱ABCD中，AB＝6，AD＝9，∠BAD的平分线交BC于点E，交DC 的延长线于点F，BG⊥AE于点G，BG＝4 2，求△FCE的周长．图4－7－11知识点 2 有关面积的计算5．2017·重庆已知△ABC∽△DEF，且相似比为1∶2，则△ABC与△DEF的面积比为( ) A．1∶4 B．4∶1 C．1∶2 D．2∶1图4－7－126．2017·永州如图4－7－12，在△ABC中，D是AB边上的一点，若∠ACD＝∠B，AD＝1，AC＝2，△ADC的面积为1，则△BCD的面积为( )A．1 B．2 C．3 D．47．教材例2变式题如图4－7－13，把△ABC沿AB边平移到△A′B′C′的位置，它们重叠部分(即图中阴影部分)的面积是△ABC面积的14，若AB＝2，则△ABC平移的距离是________．4－7－134－7－148．如图4－7－14，在△ABC中，点D，E分别在AB，AC上，∠AED＝∠B，若AE＝2，△ADE的面积为4，四边形BCED的面积为5，则AB的长为________．9．如图4－7－15所示，在▱ABCD中，AE∶EB＝1∶2.(1)求△AEF与△CDF的周长的比；(2)若S△AEF＝6 cm2，求S△CDF.图4－7－1510．若两个相似三角形的面积之比为1∶4，则它们的周长之比为( )A．1∶2 B．1∶4 C．1∶5 D．1∶1611．如图4－7－16，DE是△ABC的中位线，延长DE至点F，使EF＝DE，连接CF，则S ∶S四边形BCED的值为( )△CEFA．1∶3 B．2∶3 C．1∶4 D．2∶54－7－164－7－1712．2017·贵阳期末(教材综合与实践——制作视力表的应用)我们在制作视力表时发现，每个“E”形图的长和宽相等(即每个“E”形图近似于正方形)，如图4－7－17，小明在制作视力表时，测得l1＝14 cm，l2＝7 cm，他选择了一张面积为4 cm2的正方形卡纸，刚好可以剪得第②个小“E”形图．那么下面四张正方形卡纸中，能够刚好剪得第①个大“E”形图的是( )A．面积为8 cm2的卡纸B．面积为16 cm2的卡纸C．面积为32 cm2的卡纸D．面积为64 cm2的卡纸13．如图4－7－18，在△ABC中，BC>AC，点D在BC上，且DC＝AC，∠ACB的平分线CF交AD于点F，E是AB的中点，连接EF.(1)求证：EF∥BC；(2)若四边形BDFE的面积为6，求△ABD的面积．图4－7－1814．如图4－7－19所示，M是△ABC内一点，过点M分别作三条直线平行于△ABC的各边，所形成的三个小三角形△1，△2，△3(图中阴影部分)的面积分别是4，9和49，求△ABC 的面积．图4－7－1915．某社区拟筹资金2000元，计划在一块上、下底长分别是10 m、20 m的梯形空地上种植花草．如图4－7－20，他们想在△AMD和△CMB地带种植单价为10元/m2的太阳花，当△AMD地带种满花后，已经花了500元，请你预算一下，若继续在△CMB地带种植同样的太阳花，资金是否够用，并说明理由．图4－7－2016．如图4－7－21，在△ABC中，AB＝5，BC＝3，CA＝4，PQ∥AB，点P在CA上(与点A，C不重合)，点Q在BC上．(1)当△PQC的面积与四边形PABQ的面积相等时，求CP的长．(2)当△PQC的周长与四边形PABQ的周长相等时，求CP的长．(3)试问：在AB上是否存在一点M，使得△PQM为等腰直角三角形？若存在，请求出PQ 的长；若不存在，请简要说明理由．图4－7－211．C 2.A3．A [解析] ∵△ABC ∽△DEF ，其相似比为3∶1，∴△ABC 的周长△DEF 的周长＝31，∴△DEF 的周长＝13×27＝9.故选A.4．解：∵四边形ABCD 是平行四边形， ∴AB ∥CD ，AD ∥BC ，∴∠BAE ＝∠F ，∠EAD ＝∠AEB . ∵AE 平分∠BAD ， ∴∠BAE ＝∠EAD ， ∴∠BAE ＝∠AEB ， ∴BE ＝AB ＝6， ∴CE ＝BC －BE ＝3.∵∠AEB ＝∠FEC ，∠BAE ＝∠F ， ∴△ABE ∽△FCE ， ∴△ABE 的周长△FCE 的周长＝BECE＝2.∵BG ⊥AE ，∴AE ＝2AG ＝2 AB 2－BG 2＝4， ∴△ABE 的周长＝AB ＋BE ＋AE ＝16， ∴△FCE 的周长＝12×△ABE 的周长＝8.5．A6．C [解析] ∵∠ACD ＝∠B ，∠A ＝∠A ， ∴△ACD ∽△ABC ，∴S △ACD S △ABC ＝(AD AC )2＝14.∵S △ACD ＝1，∴S △ABC ＝4，∴S △BCD ＝S △ABC －S △ACD ＝3.7．1 [解析] 如图，∵把△ABC 沿AB 边平移到△A ′B ′C ′的位置，∴AC ∥A ′C ′，∴△ABC ∽△A ′BD .∵S △ABC ∶S △A ′BD ＝4，∴AB ∶A ′B ＝2.∵AB ＝2，∴A ′B ＝1，∴AA ′＝2－1＝1. 8．3 [解析] ∵∠AED ＝∠B ，∠A 是公共角， ∴△ADE ∽△ACB ，∴S △ADE S △ACB ＝(AE AB)2. ∵△ADE 的面积为4，四边形BCED 的面积为5，∴△ABC 的面积为9. ∵AE ＝2，∴49＝(2AB )2，解得AB ＝3.9．解：(1)∵四边形ABCD 是平行四边形， ∴AB ＝CD ，AB ∥CD ，∴∠AEF ＝∠CDF ，∠FAE ＝∠FCD ， ∴△AEF ∽△CDF . ∵AE ∶EB ＝1∶2， ∴AE ∶AB ＝AE ∶CD ＝1∶3，∴△AEF 与△CDF 的周长的比为1∶3. (2)由(1)知，△AEF ∽△CDF ，相似比为1∶3， ∴它们的面积比为1∶9. ∵S △AEF ＝6 cm 2， ∴S △CDF ＝54 cm 2. 10．A 11.A12．B [解析] ∵每个“E ”形图近似于正方形，∴P 2D 2∥P 1D 1，∴∠PP 2D 2＝∠PP 1D 1，∠P 2D 2P ＝∠P 1D 1P ， ∴△PP 2D 2∽△PP 1D 1. ∵l 1＝14 cm ，l 2＝7 cm ， ∴P 2D 2∶P 1D 1＝1∶2.∵第②个小“E ”形图是面积为4 cm 2的正方形卡纸， ∴第①个大“E ”形图的面积＝4×4＝16(cm 2)．故选B.13．解：(1)证明：∵DC ＝AC ，CF 是∠ACB 的平分线，∴CF 是△ACD 的中线， ∴F 是AD 的中点．又∵E 是AB 的中点， ∴EF ∥BD ，即EF ∥BC . (2)由(1)知，EF ∥BD ， ∴△AEF ∽△ABD ，∴S △AEF S △ABD ＝⎝ ⎛⎭⎪⎫AE AB 2. 又∵AE ＝12AB ，S △AEF ＝S △ABD －S 四边形BDFE ＝S △ABD －6， ∴S △ABD －6S △ABD ＝⎝ ⎛⎭⎪⎫122，∴S △ABD ＝8.14．解：根据题意，容易得到△1∽△2∽△3∽△ABC .因为△1、△2、△3的面积分别是4，9和49，所以它们之间的相似比为2∶3∶7，即BC 边被分成的三段从左到右的比为2∶7∶3，则△1与△ABC 的相似比为2∶12＝1∶6，所以它们的面积比为1∶36，求得△ABC 的面积是144.15．解：不够用．理由如下：在梯形ABCD 中，∵AD ∥BC ， ∴△AMD ∽△CMB ， ∴S △AMD S △CMB ＝(AD BC)2. ∵AD ＝10 m ，BC ＝20 m ， ∴S △AMD S △CMB ＝(1020)2＝14. ∵S △AMD ＝500÷10＝50(m 2)． ∴S △CMB ＝50×4＝200(m 2)．还需要资金200×10＝2000(元)，而剩余资金为2000－500＝1500(元)<2000元， ∴资金不够用．16．解：(1)∵PQ ∥AB ，∴△PQC ∽△ABC . ∵S △PQC ＝S 四边形PABQ ， ∴S △PQC ∶S △ABC ＝1∶2， ∴CP CA ＝12＝22， ∴CP ＝22·CA ＝2 2. (2)∵△PQC ∽△ABC ， ∴CP CA ＝CQ CB ＝PQ AB ，即CP 4＝CQ3，∴CQ ＝34CP .同理：PQ ＝54CP ，∴C △PQC ＝CP ＋PQ ＋CQ ＝CP ＋54CP ＋34CP ＝3CP ，C 四边形PABQ＝PA ＋AB ＋BQ ＋PQ ＝4－CP ＋AB ＋3－CQ ＋PQ ＝4－CP ＋5＋3－34CP ＋54CP ＝12－12CP .由C △PQC ＝C 四边形PABQ ，得3CP ＝12－12CP ，∴72CP ＝12，∴CP ＝247.(3)存在．∵CA ＝4，AB ＝5，BC ＝3， ∴△ABC 中AB 边上的高为125.①如图(a)所示，当∠MPQ ＝90°且PM ＝PQ 时，∵△CPQ ∽△CAB ，∴PQ AB ＝△CPQ 中PQ 上的高△CAB 中AB 上的高， ∴PQ 5＝125－PQ 125，∴PQ ＝6037； ②当∠PQM ＝90°时与①相同；③如图(b)所示，当∠PMQ ＝90°且PM ＝MQ 时，过点M 作ME ⊥PQ ，则ME ＝12PQ ，∴△CPQ 中PQ 上的高为125－ME ＝125－12PQ .∵PQ AB ＝△CPQ 中PQ 上的高△CAB 中AB 上的高，∴PQ 5＝125－12PQ 125，∴PQ ＝12049. 综上可知，存在点M ，使得△PQM 为等腰直角三角形，此时PQ 的长为6037或12049.。

4.8+图形的位似+同步练习+2024-2025学年北师大版九年级数学上册

4.8 图形的位似课时1 图形的位似基础过关题型1 位似多边形的有关概念1、关于对位似图形的表述中：①相似图形一定是位似图形，位似图形一定是相似图形；②位似图形一定有位似中心；③利用位似变换只能放大图形，不能缩小图形；④如果两个图形是相似图形，且每组对应点的连线所在的直线都经过同一个点，那么，这两个图形是位似图形；⑤位似图形上任意两点与位似中心的距离之比等于位似比。

正确的个数为( )A.2个B.3个C.4个D.5个2、下列3组图形中是位似图形的有( )A.0个B.1个C.2个D.3个3、下列四边形ABCD和四边形EFGD是位似图形,它们的位似中心是( )A.点EB.点FC.点GD.点D题型2 位似多边形的性质及应用4、如图,△ABC和△A1B1C1是以点O为位似中心的位似三角形,若C1为OC的中点,AB=4,则A1B1的长为（）A.1B.2C.4D.85、如图，以点O为位似中心，将△ABC 放大后得到△DEF，已知△ABC 与△DEF 的面积比为1:9，则OC：CF的值为（）A.1：2B.1：3C.1：8D.1：96、已知△ABC与△DEF是关于点P的位似图形，它们的对应点到P点的距离分别为3cm和4cm，则△ABC与△DEF的面积比为（）A.3:4B.3:7C. 9:16D.9:49题型3 位似变换作图7、如图，在6×8网格图中，每个小正方形边长均为1，点O和△ABC的顶点均为小正方形的顶点。

（1）在图中△ABC的内部做△A′B′C′，使△A′B′C′和△ABC位似，且位似中心为点O，位似比为1:2；（2）连接（1）中的AA′，则线段AA′的长度是.8、如图，△DEF是△ABC经过位似变换得到的，位似中心是点O，请确定点O的位置，如果OC=3.6cm，OF=2.4cm，求它们的相似比。

课时2 平面直角坐标系中的位似变换题型1 平面直角坐标系中位似变换的相关计算1、如图，已知线段AB两端点的坐标分别为A（1，2），B（3，1），以点O为位似中心，相似比为3，将AB在第一象限内放大，点A的对应点C的坐标为（）A.（3，6）B.（9，3）C.（-3，-6）D.（6，3）2、如图,已知△ABC三个顶点的坐标分别为(1,2),(−2,3),(−1,0),把它们的横坐标和纵坐标都扩大到原来的2倍,得到点A′,B′,C′.下列说法正确的是（）A.△A′B′C′与△ABC是位似图形,位似中心是点(1,0)B.△A′B′C′与△ABC是位似图形,位似中心是点(0,0)C.△A′B′C′与△ABC是相似图形，但不是位似图形D.△A′B′C′与△ABC不是相似图形3、如图，在平面直角坐标系中,有一条鱼,它有六个顶点,则( )A.将各点横坐标乘以2，纵坐标不变，得到的鱼与原来的鱼位似B.将各点纵坐标乘以2，横坐标不变，得到的鱼与原来的鱼位似C.将各点横，纵坐标都乘以2，得到的鱼与原来的鱼位似，得到的鱼与原来的鱼位似D.将各点横坐标乘以2,纵坐标乘以124、如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(−1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍。

1.4 图形的位似综合练习

初三数学图形的位似综合练习
一、复习回顾
位似图形：
如果多边形有一个顶点在，有一条边在上，那么将这个多边形的顶点坐标分别扩大（或缩小）相同的倍数，所得到的图形与原图形是，是它们的位似中心.
二、综合练习
1.如图，是格点三角形（顶点是网格线的交点），点O是格点．
以点O为位似中心，作的位似图形，使新图形与原图形的相似比为；
若的面积是，则中所作的位似图形的面积为________．
2.如图，与是位似图形，在网格上建立平面直角坐标系，使得点A
的坐标为
．
（1）在图上标出与的位似中心P，并写出点P的坐标为________；
（2）以点A为位似中心，在网格图中作，使和位似，且位似比为，并写出点的坐标为________．
3.如图，已知，，是直角坐标系平面上三点．
以原点O 为位似中心，将缩小为原来的一半，得到，请在所给的平面直角坐标系中作出满足条件的．
写出的坐标．
4.如图，在对依次进行旋转、位似、平移变换后得到．
在图中分别画出前两次变换（旋转、位似）后得到的图形；
设是边上任一点，依次写出这几次变换后点P对应点的坐标．5.如图，正方形网格中，的顶点及点O在格点上．
画出与关于点O 对称的；
画出一个以点O 为位似中心的，使得与的相似比为2．
6.如图，在边长为1的正方形网格中，有一格点，已知A、B、C 三点的坐标分别是
、
、．
请在网格图形中画出平面直角坐标系；
以原点O 为位似中心，将放大2倍，画出放大后的；。

图形的位似(1)

（2）等边三角形ABC与等边三角形A′B′C′.
判断下面的正方形是不是位似图形？
2、画出下列位似图形的位似中心 o o o
概念与性质
2. 位似图形的性质
性质：位似图形上任意一对对应点到位似中心的距离之比等于相似比.
2.如图，以点O为位似中心，将五边形ABCDE 放大后得到五边形A′B′C′D′E′，已知 OA=10cm，OA′=20cm，则 AB:A′B′= ，五边形ABCDE的周长与五边形A′B′C′D′E′的周长的比值是

如果∆OAB和 ∆OCD是位似图形，那么 AB∥CD吗？为什么？ C
A
解:AB∥CD.理由是： ∆OAB和 ∆OCD是位似图形，
∆OAB∽ ∆OCD ∠B＝∠C
O
B
D
AB∥CD.
图形的位似
(1)
概念与性质
1．位似图形的概念
如果两个图形不仅相似，而且每
组对应点所在的直线都经过同一点,对应边互相平行(重合),那么
这样的两个图形叫做位似图形,这个点叫做位似中心.
辨一辨
1. 判断下列各对图形是不是位似图形.
（1）正五边形ABCDE与正五边形A′B′C′D′E′；
把图1中的四边形ABCD缩小到原来的一半．作法一：如图2 ，在四边形ABCD外任取一点O；
作法二：如图3，在四边形ABCD外任取一点O；
作法三：如图4，在四边形ABCD内任取一点O；
课堂小结

位似图形的概念：如果两个图形不仅形状相同,而且每组对应顶点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比. 位似图形的性质： 1.位似图形上的任意一对对应点到位似中心的距离之比等于位似比

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

《图形的位似》综合练习1
一、选择题
1．如图，AD 是△ABC 的中线，AE =EF =FC ，则下列关系式： ①
12AG AD =②13GE BE =③3
4
BG BE =，其中正确的是（）．
A ．①②
B ．①③
C ．②③
D ．①②③
2．如图，是由正三角形A 经过一些变换得到的，其中的变换不包含（）．
A ．平移
B ．旋转
C ．位似变换
D ．轴对称 3．下列关于位似图形的表述：
（1）相似图形一定是位似图形，位似图形一定是相似图形；（2）位似图形一定有位似中心；
（3）如果两个图形是相似图形，且每组对应点的连线所在的直线都经过同一个点，那么这两个图形是位似图形；
（4）位似图形上任意两点与位似中心的距离之比等于相似比．其中正确命题的序号是（）．
A ．（2）（3）
B ．（1）（2）
C ．（3）（4）
D ．（2）（3）（4） 4．利用位似变换把多边形ABCDEF 放大到原来的2倍，则下列结论正确的是（）． A ．新图形与原图形的对应边之比是2 B ．新图形与原图形的对应角之比是2 C ．新图形与原图形的面积之比是2 D ．新图形与原图形的边数之比是2
5．如图，已知点E （4-，2），点F （1-，1-），以点O 为位似中心，相似比为1︰2，把△EFO 缩小，则点E 的对应点的坐标是（）．
D
C
F
E G
A
B
A
A．（2-，1）B．（2，1-）或（2-，1-）
C．（2，1-）D．（2-，1）或（2，1-）
6．如图，线段AB的两个端点坐标分别为A（1，1），B（2，1），以原点O为位似中心，将线段AB放大后得到线段CD．若CD=2，则端点C的坐标为（）．A．（2，2）B．（2，4）C．（3，2）D．（4，2）
7．如图所示，点E，F，G，H分别是OA，OB，OC，OD的中点．若四边形EFGH的面积是3，则四边形ABCD的面积是（）．
A．6B．9C．12D．18
8．如图，将△AOB以点O为位似中心，扩大到△COD，各点的坐标分别为A（1，2），B（3，0），D（6，0），则点C的坐标为（）．
A ．（2，3）
B ．（2，4）
C ．（3，3）
D ．（3，4）二、填空题
9．如图所示，工人师傅为了在废旧的三角形铁片上截取一个面积最大的正方形铁片，先用正方形横板在△ABC 内画一个正方形，然后过正方形在三角形内的一个顶点画射线交边AC 于点G ，再作GF ⊥BC ，垂足为F ，GD ∥BC 交AB 于点D ，DE ⊥BC ，垂足为E ，则四边形DEFG 就是面积最大的正方形．这里用到了两个正方形位似的问题，它们的位似中心是________．
10．如图所示，△ABC 是△DEF 经过位似变换得到的，相似比为2︰3．若AD =4 cm ，AB =5 cm ，则OA =________，DE =________．
11．如图所示，火焰的光线穿过小孔O ，在竖直的屏幕上形成倒立的实像，像的高度BD =2 cm ，OA =60 cm ，OB =15 cm ，则火焰的高度为________．
12．如图，五边形ABCDE 与五边形A ′B ′C ′D ′E ′是位似图形，且相似比为
1
2
．若五边形ABCDE 的面积为17 cm 2，周长为20 cm ，那么五边形A ′B ′C ′D ′E ′的面积为________，周长为________．
G
F E D C
B A
O F
E D C B
A
13．如图，作△ABC 的位似图形，如果选取点A 为位似中心，△ABC 的位似图形与△ABC 的相似比为1︰2，作图过程是：延长CA 到C ′，使C′A =________，延长BA 到B ′，使B′A =________，连接________，则________与△ABC 是位似图形．
三、解答题
14．已知平面直角坐标系中，△ABC 的三个顶点的坐标分别为A （2，2），B （1，1-），C （3，0）．画出以点O 为位似中心，放大△ABC 到原来2倍的△A B C '''．
15．在平面直角坐标系中，正方形ABCD 各顶点的坐标分别为A （1，1），B （－1，1），C （－1，－1），D （1，－1），以坐标原点为位似中心，将正方形ABCD 放大，使放大后的正方形A′B′C′D′的边长是原正方形ABCD 的边长的3倍．
（1）写出A′B′C′D′的坐标；
（2）直线AC 与直线B′D′垂直吗？说明理由．
16．在平面直角坐标系中，有两点A （3，6），B （6，6），以原点O 为位似中心，相似比为0.5，把线段AB 缩小，位似变换后，求A ，B 的对应点的坐标．
参考答案
1．B ． 2．C ． 3．A ． 4．A ． 5．D ． 6．A ． 7．C ． 8．B ． 9．点B ．
10．8 cm ，7.5 cm ． 11．8 cm ． 12．
217
cm 4
，10 cm ．
C
B
A
13．1
2
CA；
1
2
BA；C'，B'；△AB C''．
14．解：
15．解：（1）A′（3，3），B′（－3，3），C′（－3，－3），D′（3，－3）或A′（－3，－3），B′（3，－3），C′（3，3），D′（－3，3）．
（2）AC⊥B′D′，理由如下：∵AC⊥BD，而B，B′，D′，D四点共线．∴AC⊥B′D′．16．解：（1.5，3）（3，3）或（－1.5，－3）（－3，－3）．。