轴心受力构件
轴心受力构件

④在设有夹钳吊车或刚性料耙吊车的厂房中,支撑(表中第2项除外)的长细比不宜超过300。
⑤受拉构件在永久荷载与风荷载组合作用下受压时,其长细比不宜超过250。
⑥跨度等于或大于60m的桁架,其受拉弦杆和腹杆的长细比不宜超过300(承受静力荷载)或250(承受动力荷载)。
§6-3轴心受压构件的整体稳定
6.3.1轴心受压构件的整体失稳现象
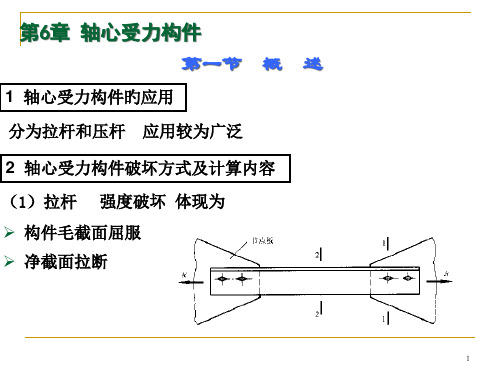
图6.2.2净截面面积的计算
对于高强度螺栓摩擦型连接的构件,可以认为连接传力所依靠的摩擦力均匀分布于螺孔四周,故在孔前接触面已传递一半的力(图6.2.3)。因此,最外列螺栓处危险截面的净截面强度应按下式计算:
(6.2.3)
式中 ;
—连接一侧的高强度螺栓总数;
—计算截面(最外列螺栓处)上的高强度螺栓数目;
1.弹性弯曲屈曲
图6.3.2为两端铰接的理想等截面构件,当轴心压力N达到临界值时,处于屈曲的微弯状态。在弹性微弯状态下,由内外力矩平衡条件,可建立平衡微分方程,求解后可得到著名的欧拉临界力(Eulercriticalforce)公式为:
对无孔洞等削弱的轴心受力构件,以全截面平均应力达到屈服强度为强度极限状态,
应按下式进行毛截面强度计算:
(6.2.1)
式中 —构件的轴心力设计值;
—钢材抗拉强度设计值或抗压强度设计值;
轴心受力构件
18
第6章 轴心受力构件 第三节 轴心受压构件旳受力性能
2 承载力极限状态旳计算内容 (1)截面强度破坏
(2)构件整体失稳(屈曲)
(3)板件局部失稳(屈曲) 限制受压板件旳宽厚比
19
第6章 轴心受力构件 第三节 轴心受压构件旳受力性能
3 稳定问题旳某些概念 (1)应力刚化效应 拉力提升构件旳弯曲刚度 压力降低 (2)只要构件旳截面中存在受压区域,就可能存在稳定问题 (3)强度问题是应力问题,针正确是构件最单薄旳截面,加大截面 积即可提升构件旳强度,计算以净截面为准 (4)稳定问题是刚度(变形)问题,针正确是构件整体,减小变形 (提升刚度)旳措施都能够提升构件旳稳定性,计算以毛截面为准
➢ 根据截面残余应力旳峰值大小和分布,弯曲屈曲旳方向,将截面 分为a、b、c三类,相应地得到a、b、c三条柱子曲线
44
第6章 轴心受力构件 第七节 规范中实腹式轴压构件弯曲屈曲时整体稳定计算
➢ a类截面临界应力最高,残余应力对临界应力起有利作用或影响 很小,只涉及两种截面: ✓ 绕强(x)轴屈曲时旳热轧工字钢和热轧中翼缘、窄翼缘H型钢 ✓ 热轧无缝钢管
(1)发生弯扭屈曲旳条件 ✓ 截面形式:单轴对称截面 ✓ 失稳方向:绕对称轴失稳。绕非对称轴失稳必然是弯曲失稳 ✓ 原因:形心和剪心不重叠,弯曲时截面绕剪心转动
51
第6章 轴心受力构件 第八节 实腹式轴压构件弯扭屈曲时整体稳定计算
(2)单角钢截面、双角钢组合截面弯扭屈曲旳规范计算措施 ➢ 用换算长细比 (考虑扭转效应)替代弯曲屈曲时旳长细比 查得稳定系数 ,再按下列公式验算杆件旳稳定
42
第6章 轴心受力构件 第七节 规范中实腹式轴压构件弯曲屈曲时整体稳定计算
轴心受力构件

还使得构件极限承载力显著降低,同时初弯曲和自重产生的 挠度也将对构件的整体稳定带来不利影响。
(2)扭转屈曲——失稳时除杆件的支撑端外,各截面均绕纵轴扭转,是某 些双轴对称截面可能发生的失稳形式。 (3)弯扭屈曲——单轴对称截面绕对称轴屈曲时,杆件发生弯曲变形的同 时必然伴随着扭转。
5.2 实腹式轴压柱的整体稳定
2.理想轴心压杆的弹性屈曲概念 N
稳 定 平 衡F 状 态
对两端铰支的理想细长压杆, 当压力N较小时,杆件只有轴心压 缩变形,杆轴保持平直。如有干扰 使之微弯,干扰撤去后,杆件就恢 复原来的直线状态,这表示直线状 态的平衡是稳定的。
可认为连接传力所依靠的摩擦力均匀分布于螺孔四周,故在孔前接触面 已传递一半的力,因此最外列螺栓处危险截面的净截面强度应按下式计算:
N
N f
An,1
其中:An,1 b n1 d0 t
N’
N
N
N
1
Байду номын сангаас
0.5n1 n
n1 计算截面上的螺栓数;
n 连接一侧的螺栓总数。
轴心受力构件对刚度提出限值要求的原因
第5章 轴心受压构件
Axially compressive member
5.1 概述
轴心受力构件是指承受通过截面形心轴线的轴向力作用的构件。
N
N
轴心受力构件广泛应用于各种钢结构之中,如 网架与桁架的杆件、钢塔的主体结构构件、双跨 轻钢厂房的铰接中柱、带支撑体系的钢平台柱等。
轴心受力构件

轴心受力构件是指受到力沿着其中心轴线方向作用的构件,包括拉杆、柱子、管道等等。
在机械工程中,充当着至关重要的角色,它们能够在不同的应用场景中承受压力、弯曲和剪切等力量,从而使得机械设备得以正常运转。
让我们深入探讨的运用和作用。
一、的类型及应用常常分为拉压杆和管子。
拉杆用于承受拉伸力,管子用于承受高压液力或燃气力。
在机械设计中,这些构件通常被用于桥梁、塔楼、建筑物和车辆等结构的建造中。
同时,也被广泛应用在航空、航天和船舶设计中,纤维材料的应用更是增强了的使用范围。
二、的受力分析的设计需要考虑很多因素,如承受的荷载大小、材料的强度和刚度、构件的长度和支承方式等。
在实际使用过程中,还需要考虑力的传导和使构件具备符合要求的变形能力等因素。
在受力分析中,的力学特性是重要的。
如果设计不当,构件可能会承受破坏性变形,从而导致严重事故的发生。
例如,当长度超过一定比例时,由于柔性构件的配重达到了高峰值,会导致塔架的共振而倒塌。
三、的设计方法的设计需要考虑构件的应用领域、材料的种类和强度、以及构件长度及支承方式等因素。
设计师需要根据具体的要求进行选择和修改,并根据设计结果进行适当的测试和验证。
其中,材料的选择是重要的一环。
常见的材料有钢、铝和钛合金,选择合适的材料可以提高构件的强度和硬度,从而承受更大的压力。
在设计过程中,还需要使用工具进行力学分析,如荷载分析、变形分析和应力分析等。
对于复杂的结构,还可以通过CAD或其他软件进行模拟和分析。
最终的结果需要根据实际的实验测试结果进行优化,以确保能够达到设计要求。
四、的优化和改进的优化和改进是一个长期的研究领域。
近年来,各国的专家学者已经提出了许多新的方法和技术,如新材料的应用、优化的结构设计和精确的力学分析方法等。
这些技术的不断进步和应用,使得的质量和使用效果都得到了极大的提高。
总之,是机械工程中不可或缺的部分。
在未来,随着科技的进步,的研究将逐步深化,并得到更广泛的应用。
轴心受力构件

4
k
I
2z
2y
2z
2
4 1 a02
/ i02
2y2z
1/
2
通常Nyz恒比Ny和Nw小,因此a0/i0越大, Nyz越小,但可能大
于N
,因此对称截面的承载力决定于
Ex
N
Ex
和Nyz中的较小者。
第四章 轴心受力构件
§4.3.2 初始缺陷对轴心压杆的整体稳定承载力影响
前面介绍的是理想压杆的临界力,实际构件与理想状态有 很大的差别,构件总有初弯曲、初偏心、残余应力存在。理 想的轴心压杆是不存在的。其中初弯曲、初偏心及残余应力 的影响为不利影响,而边界条件的影响往往是有利的(悬臂 杆除外)。
4.3.1 理想轴心压杆的临界力
轴心受力构件由于截面形式不同,可能有三种不同的屈 曲形式而丧失稳定。
弯曲屈曲 对称平面内失稳
扭转屈曲 十字截面
弯扭屈曲 非对称平面内失稳
4.3 轴心压杆的整体稳定
第四章 轴心受力构件
4.3.1 理想轴心压杆的临界力
4.3 轴心压杆的整体稳定
第四章 轴心受力构件
4.3.1 理想轴心压杆的临界力
β为与截面形状有关的系数。
d2y dx2
N EI
y
N
GA
d2y dx2
y(1 N ) N y 0
GA EI
k
2
N E I (1
N
)
GA
y k 2 y 0
代入边界条件x=0和x=l时,y=0,满足上式的最小k值
k2
N E I (1
N
)
2
l2
第四章-轴心受力构件

2
300
200
有重 级工 作制 吊车 旳
厂房
250
-
受压构件旳允许长细比
项次
构件名称
允许长 细比
柱、桁架和天窗架中旳杆件
1 柱旳缀条、吊车梁或吊车桁架 150 下列旳柱间支撑
支撑(吊车梁或吊车桁架下列
旳柱间支撑除外)
2
200
用以降低受压构件长细比旳杆
件
第二节 轴心受压构件旳整体稳定
3、理想构件旳弹性弯曲失稳
根据右图列平衡方程
d2y EI dx2 Ny 0
解平衡方程:得
欧拉临界力只合用
N cr
π2 EI l02
π2 E λ2
A
于材料为弹性时旳 情况,应力一旦超 出材料旳百分比极
σ cr
N cr A
π2 E λ2
限,则欧拉公式不 再合用。
4、理想构件旳弹塑性弯曲失稳
构件失稳时假如截面应力超出弹性
ix( y)
Ix( y) A
实腹式轴心受压构件旳稳定性应按下式计算:
N ≤f
A
A为杆件毛截面面积
式中 为整体稳定系数,实质是临界应力与屈
服点旳比值。柱旳临界应力与截面形状、力作用方
向等有关,
— 轴心受压构件的整体稳定系数
根据构件截面分类取由λx,λy,λyz
fy 决定的
235
max
(1)规范现对t 40mm旳轴压构件作了专门要求。同步补充了d 类
r
2Er 2
5、实际构件旳整体稳定 实际构件与理想构件间存在着初始缺陷,缺陷主要有:
初始弯曲、残余应力、初始偏心。 ⑴、初始弯曲旳影响
1.一经加载产生 挠度,先慢后快
钢结构轴心受力构件

钢结构轴心受力构件在钢结构的世界里,轴心受力构件是其中一类至关重要的组成部分。
它们在建筑结构、桥梁工程以及各类工业设施中都扮演着不可或缺的角色。
那么,什么是钢结构轴心受力构件呢?简单来说,就是在承受外力作用时,构件的截面形心与外力的作用线重合,从而使构件沿着其轴线方向承受拉力或压力的钢结构部件。
钢结构轴心受力构件主要包括轴心受拉构件和轴心受压构件两种类型。
先来说说轴心受拉构件。
这类构件在实际应用中非常常见,比如钢结构中的吊车梁、屋架中的下弦杆等。
当构件受到拉力作用时,其内部的应力分布相对均匀,主要承受拉应力。
在设计轴心受拉构件时,我们需要重点考虑的是材料的抗拉强度。
因为一旦拉力超过了材料的抗拉极限,构件就会发生破坏。
为了保证轴心受拉构件的可靠性和安全性,我们在选材上要格外谨慎。
一般会选择高强度的钢材,以充分发挥其抗拉性能。
同时,在连接节点的设计上也不能马虎,要确保连接牢固,避免出现松动或断裂的情况。
接下来谈谈轴心受压构件。
轴心受压构件在钢结构中也有着广泛的应用,例如柱子、桁架中的受压弦杆等。
与轴心受拉构件不同,轴心受压构件的受力情况要复杂得多。
当受到压力作用时,构件可能会发生整体失稳或者局部失稳的现象。
整体失稳是指整个构件突然发生弯曲变形,失去承载能力。
而局部失稳则是指构件的某个局部区域出现了屈曲现象。
为了防止这些失稳情况的发生,我们在设计轴心受压构件时,需要考虑很多因素。
首先,要合理选择构件的截面形状和尺寸。
常见的截面形状有圆形、方形、矩形等。
对于较大的压力,通常会选择回转半径较大的截面形状,以提高构件的稳定性。
其次,要控制构件的长细比。
长细比是指构件的计算长度与截面回转半径的比值。
长细比越大,构件越容易失稳。
因此,在设计时要通过合理的布置和支撑,减小构件的计算长度,从而降低长细比。
此外,还需要考虑材料的抗压强度和屈服强度。
在实际工程中,为了提高轴心受压构件的稳定性,常常会采用一些加强措施,比如设置纵向加劲肋、横向加劲肋等。
钢结构设计原理4轴心受力构件

轧制普通工字钢,腹板较薄,热轧后首先冷却;翼缘在
冷却收缩过程中受到腹板的约束,因此翼缘中产生纵向
残余拉应力,而腹板中部受到压缩作用产生纵向压应力
。轧制H型钢,由于翼缘较宽,其端部先冷却,因此具
有残余压应力,其值为=0.3
f
左右,残余应力在翼缘宽
y
度上的分布,常假设为抛物线或取为直线。翼缘是轧制
边或剪切边的焊接工字形截面,其残余应力分布情况与
Ncrx
2EIx 2
x
I ex Ix
2EIx 2
x
2t(kb)h2 / 4 2tbh2 / 4
2EIx 2
x
k
N cry
2EI y 2
y
I ey Iy
2EI y 2
y
2t(kb)3 /12 2tb3 /12
2EI y 2
y
k3
由于k<l.0,故知残余应力对弱轴的影响比对强轴的影 响要大得多 。
N f
An
采用高强度螺栓摩擦型连接的构件,验算净截面强度时 应考虑一部分剪力已由孔前接触面传递,验算最外列螺 栓处危险截面的强度时,应按下式计算
N' f
An
N ' N (1 0.5 n1 ) n
摩擦型连接的拉杆,除验算净截面强度外,还应验算毛 截面强度
N f
A
4.2.2轴心受力构件的刚度计算 为满足正常使用要求,构件应具有一定的刚度,保证构 件不会在运输和安装过程中产生弯曲或过大的变形,以 及使用期间因自重产生明显下挠,还有在动力荷载作用 下发生较大的振动。
GIt
1 i02
2E 2z
A
z
I
/ l2
Ai02 GIt
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
轴心受力构件设计轴心受拉构件时需进行强度和刚度的验算,设计轴心受压构件时需进行强度、整体稳定、局部稳定和刚度的验算。
一、轴心受力构件的强度和刚度1.轴心受力构件的强度计算轴心受力构件的强度是以截面的平均应力达到钢材的屈服点为承载力极限状态f A N n ≤=σ (1) 式中 N ——构件的轴心拉力或压力设计值;n A ——构件的净截面面积;f ——钢材的抗拉强度设计值。
采用高强度螺栓摩擦型连接的构件,验算最外列螺栓处危险截面的强度时,按下式计算:f A N n≤='σ (2) 'N =)5.01(1n n N - (3)式中 n ——连接一侧的高强度螺栓总数;1n ——计算截面(最外列螺栓处)上的高强度螺栓数;0.5——孔前传力系数。
采用高强度螺栓摩擦型连接的拉杆,除按式(2)验算净截面强度外,还应按下式验算毛截面强度f A N ≤=σ (4)2.轴心受力构件的刚度计算轴心受力构件的刚度是以限制其长细比保证][λλ≤ (5) 式中 λ——构件的最大长细比;[λ]——构件的容许长细比。
二、 轴心受压构件的整体稳定1.理想轴心受压构件的屈曲形式理想轴心受压构件可能以三种屈曲形式丧失稳定:①弯曲屈曲 双轴对称截面构件最常见的屈曲形式。
②扭转屈曲 长度较小的十字形截面构件可能发生的扭转屈曲。
③弯扭屈曲 单轴对称截面杆件绕对称轴屈曲时发生弯扭屈曲。
2.理想轴心受压构件的弯曲屈曲临界力若只考虑弯曲变形,临界力公式即为著名的欧拉临界力公式,表达式为N E =22l EI π=22λπEA (6) 3.初始缺陷对轴心受压构件承载力的影响实际工程中的构件不可避免地存在初弯曲、荷载初偏心和残余应力等初始缺陷,这些缺陷会降低轴心受压构件的稳定承载力。
1)残余应力的影响当轴心受压构件截面的平均应力p f >σ时,杆件截面内将出现部分塑性区和部分弹性区。
由于截面塑性区应力不可能再增加,能够产生抵抗力矩的只是截面的弹性区,此时的临界力和临界应力应为:N cr =22l EI e π=22lEI π·I I e (7) cr σ=22λπE ·I I e (8) 式中 I e ——弹性区的截面惯性矩(或有效惯性矩);I ——全截面的惯性矩。
2)初弯曲的影响具有初弯曲的轴心受压构件的承载力具有如下特点:①具有初弯曲的压杆,压力一开始作用,杆件就产生挠曲,并随着荷载的增大而增加,开始挠度增加慢,随后迅速增长,当压力N 接近欧拉临界力时,中点挠度趋于无限大。
②压杆的初挠度值愈大,相同压力N 情况下,杆的挠度愈大。
③初弯曲即使很小,轴心受压构件的承载力总是低于欧拉临界力。
3) 初偏心的影响具有初偏心的轴心受压构件的承载力特点与具有初弯曲压杆的承载力特点相同。
可以认为初偏心影响与初弯曲影响类似。
由于初偏心与初弯曲的影响类似,各国在制订设计标准时,通常只考虑其中一个缺陷来模拟两个缺陷的影响。
4.实际轴心受压构件的极限承载力和多柱子曲线以压杆跨中截面边缘屈服时的承载力作为最大承载力,称为边缘屈服准则。
实际上压力还可增加,只是压力超过边缘屈服准则的最大承载力后,构件进入弹塑性阶段,随着截面塑性区的不断扩展,变形值增加得更快,直至压杆不能维持稳定平衡,这才是具有初弯曲压杆真正的极限承载力,以此为准则计算压杆稳定,称为“最大强度准则”。
通常考虑影响最大的残余应力和初弯曲两种缺陷的影响。
压杆失稳时临界应力cr σ与长细比λ之间的关系曲线称为柱子曲线。
规范所采用的轴心受压柱子曲线是按最大强度准则确定的。
规范在理论分析的基础上,结合工程实际,将柱子曲线归纳为四类。
一般的截面情况属于b 类。
轧制圆管以及轧制普通工字钢绕x 轴失稳时其残余应力影响较小,故属a 类。
曲线d 主要用于厚板截面。
5. 轴心受压构件的整体稳定计算轴心受压构件所受应力不应大于整体稳定的临界应力,考虑抗力分项系数R γ,为:f f f A N Ry y cr R cr ϕγσγσσ=⋅=≤= (9) 规范对轴心受压构件的整体稳定计算采用下列形式:f AN ≤ϕ (10) 式中 ϕ—轴心受压构件的整体稳定系数,y crf σϕ=。
整体稳定系数ϕ值应根据构件的截面分类和构件的长细比查得。
构件长细比λ应按照下列规定确定:(1) 截面为双轴对称或极对称的构件⎭⎬⎫==y y y x x x i l i l //00λλ (11) 式中 x l 0、y l 0——构件对主轴x 和y 的计算长度;x i 、y i ——构件截面对主轴x 和y 的回转半径。
对双轴对称十字形截面构件,x λ或y λ取值不得小于5.07b /t(其中b /t 为悬伸板件宽厚比)(2) 截面为单轴对称的构件单轴对称截面,绕对称轴失稳时为弯扭屈曲。
在相同情况下,弯扭失稳比弯曲失稳的临界应力要低。
因此,单轴对称截面绕对称轴(设为y 轴)的稳定应取计及扭转效应的下列换算长细比yz λ代替y λ:[]2/122202022222)/1(4)()(21z y z y z y yz i e λλλλλλλ--+++= (12))/7.25//(2202ωωλl I I A i t z += (13)单角钢截面和双角钢组合T 形截面绕对称轴的换算长细比可采用简化方法确定。
无任何对称轴且又非极对称的截面(单面连接的不等边单角钢除外)不宜用作轴心受压构件。
对单面连接的单角钢轴心受压构件,考虑折减系数后,可不考虑弯扭效应。
当槽形截面用于格构式构件的分肢,计算分肢绕对称轴(y 轴)的稳定性时,不必考虑扭转效应,直接y λ用查出y ϕ值。
四、轴心受压构件的局部稳定一般组成轴心受力构件的板件的厚度与板的宽度相比都较小,如果这些板件过薄,则在压力作用下,板件将离开平面位置而发生凸曲现象,这种现象称为板件丧失局部稳定。
1. 工字形和H 形截面轴心受压构件的局部稳定一般通过限制组成截面的板件宽(高)厚比来保证轴心受压构件的局部稳定。
(1) 工字形和H 形截面的受压翼缘受压翼缘板悬伸部分的宽厚比b /t 限值:yf t b 235)1.010(λ+≤ (14)式中,λ为构件两方向长细比的较大值。
当λ<30时,取λ=30;当λ>100时,取λ=l00。
(2) 工字形和H 形截面的腹板腹板高厚比w t h /0限值:yw f t h 235)5.025(0λ+≤ (15)当工字形截面的腹板高厚比w t h /0不满足式(15)的要求时,除了加厚腹板外,还可采用有效截面的概念进行计算。
计算时腹板截面面积仅考虑两侧宽度各为y w f t /23520 的部分,如图1所示,但计算构件的稳定系数ϕ时仍可用全截面。
当腹板高厚比不满足要求时,亦可在腹板中部设置纵向加劲肋,用纵向加劲肋加强后的腹板仍按式(1)计算,但0h 应取翼缘与纵向加劲肋之间的距离,如图2所示。
图1 腹板有效截面 图2 腹板纵向加劲肋五、实腹式轴心受压构件的截面设计实腹式轴心受压构件一般采用双轴对称截面,以避免弯扭失稳。
常用截面形式有型钢截面和组合截面两种形式。
实腹式轴心受压构件进行截面选择时应主要考虑以下原则:面积的分布应尽量开展,以增加截面的惯性矩和回转半径,提高柱的整体稳定承载力和刚度;两个主轴方向尽量等稳定性,即y x ϕϕ=,以达到经济的效果;便于与其他构件进行连接;尽可能构造简单,制造省工,取材方便。
1.实腹式轴心受压构件的截面设计首先应根据轴心压力的设计值、计算长度选定合适的截面形式,再初步确定截面尺寸,然后进行强度、整体稳定、局部稳定、刚度等的验算。
具体步骤如下:(1)假定柱的长细比λ,求出需要的截面面积A 。
一般假定λ=50~100,当压力大而计算长度小时取较小值,反之取较大值。
根据λ、截面分类可查得稳定系数ϕ,则需要的截面面积为:f N A ϕ= (16)(2)求两个主轴所需要的回转半径λλyy xx l i l i 00;== (17)(3)由已知截面面积A 、两个主轴的回转半径y x i i ,优先选用轧制型钢。
当现有型钢规格不满足所需截面尺寸时,可以采用组合截面,这时需先初步定出截面的轮廓尺寸,一般是根据回转半径确定所需截面的高度h 和宽度b 。
21;ααy xi b i h ≈≈ (18)1α、2α为系数,表示h 、b 和回转半径y x i i ,之间的近似数值关系,常用截面可由表格查得。
例如由三块钢板组成的工字形截面1α=0.43,2α=0.24。
(4)由所需要的A 、h 、b 等,再考虑构造要求、局部稳定以及钢材规格等,确定截面的初选尺寸。
(5)构件强度、稳定和刚度验算。
局部稳定:对于热轧型钢截面,由于其板件的宽厚比较小,一般能满足要求,可不验算。
对于组合截面,则应对板件的宽厚比进行验算。
2.实腹式轴心受压构件的构造要求当实腹式轴心受压构件的腹板高厚比80/0>w t h 时,应设置横向加劲肋。
横向加劲肋的间距不得大于3h 0,其截面尺寸要求为双侧加劲肋的外伸宽度b s 应不小于)4030/(0+h mm ,厚度t s 应大于外伸宽度的l/15。
实腹式轴心受压构件的纵向焊缝(翼缘与腹板的连接焊缝)受力很小,不必计算,可按构造要求确定焊缝尺寸。
六、格构式轴心受压构件的设计格构式轴心受压构件一般采用两个肢件组成,肢件间用缀条或缀板连成整体。
格构柱两肢间距离的确定以两个主轴的等稳定性为准则。
在柱的横截面上穿过肢件腹板的轴称为实轴,穿过两肢之间缀材面的轴称为虚轴。
缀条一般用单根角钢做成,而缀板通常用钢板做成。
1.双肢格构式轴心受压构件绕虚轴的换算长细比格构式轴心受压构件绕实轴的稳定计算与实腹式轴心受压构件相同,但绕虚轴的整体稳定临界力比长细比相同的实腹式轴心受压构件低。
格构式轴心受压构件,当绕虚轴失稳时,采用换算长细比来考虑缀材剪切变形对格构式轴心受压构件绕虚轴的稳定承载力的影响。
(1)缀条式格构式构件双肢缀条式格构构件的换算长细比为:12027A A x x +=λλ (19) 式中 x λ——整个构件对虚轴的长细比;A ——整个构件的毛截面面积;A 1——一个节间内两侧斜缀条毛面积之和。
需要注意的是,式(19)的适用范围为斜缀条与柱轴线间的夹角在400~700之间。
(2) 缀板式格构式构件双肢缀板的换算长细比采用:2120λλλ+=x x (20) 式中 1λ——分肢的长细比;2.格构式轴心受压构件的缀材设计(1) 格构式轴心受压构件的横向剪力格构式构件绕虚轴失稳发生弯曲时,缀材要承受横向剪力的作用。
最大剪力的计算式:23585yf Af V = (21)在设计中,将剪力V 沿柱长度方向取为定值。
(2)缀条的设计图3 缀条计算简图缀条可视为以分肢为弦杆的平行弦桁架的腹杆,内力与桁架腹杆的计算方法相同。
