火车转弯问题分析
17火车拐弯问题

火车转弯问题考点规律分析(1)弯道的特点:在实际的火车转弯处,外轨高于内轨,若火车转弯所需的向心力完全由重力和支持力的合力提供,如图所示,即mg tanθ=m v20R,则v0=gR tanθ,其中R为弯道半径,θ为轨道平面与水平面间的夹角,v0为转弯处的规定速度。
(2)速度与轨道压力的关系①当火车行驶速度v等于规定速度v0时,所需向心力仅由重力和弹力的合力提供,此时火车对内外轨无挤压作用。
②当火车行驶速度v>v0时,火车对外轨有挤压作用。
③当火车行驶速度v<v0时,火车对内轨有挤压作用。
(3)注意事项①合外力的方向:因为火车转弯的圆周平面是水平面,不是斜面,所以火车的向心力即合外力应沿水平面指向圆心,而不是沿轨道斜面向下。
②规定速度的唯一性:火车轨道转弯处的规定速率一旦确定则是唯一的,火车只有按规定的速率转弯,内外轨才不受火车的挤压作用。
速率过大时,由重力、支持力及外轨对轮缘的挤压力的合力提供向心力;速率过小时,由重力、支持力及内轨对轮缘的挤压力的合力提供向心力。
典型例题例有一列质量为100 t的火车,以72 km/h的速率匀速通过一个内外轨一样高的弯道,轨道半径为400 m。
(g取10 m/s2)(1)试计算铁轨受到的侧压力大小;(2)若要使火车以此速率通过弯道,且使铁轨受到的侧压力为零,我们可以适当倾斜路基,试计算路基倾斜角度θ的正切值。
[规范解答](1)m=100 t=1×105 kg,v=72 km/h=20 m/s,外轨对轮缘的侧压力提供火车转弯所需要的向心力,所以有:F N =m v 2r =105×202400 N =1×105 N 。
由牛顿第三定律可知铁轨受到的侧压力大小为1×105 N 。
(2)火车过弯道,重力和铁轨对火车的支持力的合力正好提供向心力,如图所示,则mg tan θ=m v 2r ,由此可得tan θ=v 2rg =0.1。
图解法分析火车转弯中的侧向压力和正压力
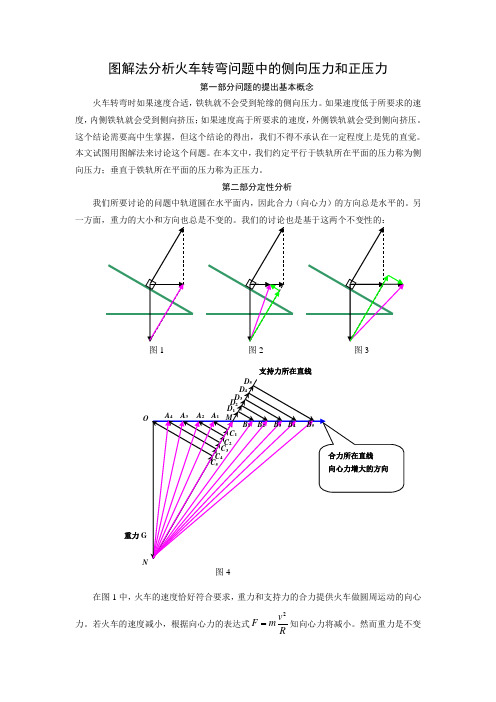
图解法分析火车转弯问题中的侧向压力和正压力第一部分问题的提出基本概念火车转弯时如果速度合适,铁轨就不会受到轮缘的侧向压力。
如果速度低于所要求的速度,内侧铁轨就会受到侧向挤压;如果速度高于所要求的速度,外侧铁轨就会受到侧向挤压。
这个结论需要高中生掌握,但这个结论的得出,我们不得不承认在一定程度上是凭的直觉。
本文试图用图解法来讨论这个问题。
在本文中,我们约定平行于铁轨所在平面的压力称为侧向压力;垂直于铁轨所在平面的压力称为正压力。
第二部分定性分析我们所要讨论的问题中轨道圆在水平面内,因此合力(向心力)的方向总是水平的。
另一方面,重力的大小和方向也总是不变的。
我们的讨论也是基于这两个不变性的:在图1中,火车的速度恰好符合要求,重力和支持力的合力提供火车做圆周运动的向心力。
若火车的速度减小,根据向心力的表达式Rv m F 2知向心力将减小。
然而重力是不变支持力所在直线重力图1 图2图3图4的,因此其他力的合力将变成图2中粉红色的有向线段所表示的力。
我们进一步分析这个力的分力:一是轨道对火车的垂直于轨道所在平面的力(正压力);一是轨道对火车的平行于轨道所在平面的力(侧向压力)。
我们把这个粉红色的线段所表示的力分解到它的两个分力所在的方向,就得到了表示侧向压力的线段和正压力的线段(图2中鲜绿色线段)。
从图中可以看出,这时火车将受到一个沿轨道平面向上的侧向压力,并且它将随着速度的减小而增大(图4)。
另一方面,表示垂直于斜面的支持力(正压力)的线段比原来短了,表明支持力减小了,并且我们会看到,随着速度的减小,支持力将逐渐减小。
当火车的速度增大时(大于所要求的数值),用同样的方法(图3)可以得到:火车将受到一个沿轨道所在平面向下的侧向压力,并且随着速度的增大而增大(图4)。
另一方面,支持力将大于原来的支持力(图3),并且随着速度的增大而增大(图4)。
第三部分定量计算侧向压力的计算:首先我们先看速度较小时的情景,如图2所示,设轨道所在平面的倾角为θ,火车驶过转弯处没有侧向压力时的速度为0v 。
《火车转弯问题》课件

列车重量:列车重量越 大,速度限制越低
列车类型:不同类型的 列车,速度限制不同
轨道条件:轨道条件越 好,速度限制越高
火车转弯时的速度调整方法
减速:在进入弯道前减速,以降低离心力 加速:在弯道中加速,以增加向心力 调整转向架:调整转向架的角度,以适应弯道的曲率 调整轨道:调整轨道的曲率,以适应火车的速度和转向架的角度
摩擦力的方向与 车轮的旋转方向 相反,可以防止 车轮打滑
摩擦力的大小可 以通过调整车轮 与轨道之间的接 触压力和摩擦系 数来控制,以保 持火车的稳定行 驶
火车转弯时的速 度控制
火车转弯时的速度限制
转弯半径:转弯半径越 大,速度限制越低
轨道倾斜度:倾斜度越 大,速度限制越低
弯道长度:弯道长度越 长,速度限制越低
紧急制动系统与安全防护装置
紧急制动系统:在紧急情况下,可以快速、有效地停车,防止事故发生
安全防护装置:包括防滑器、防撞器等,可以防止火车在转弯时发生侧滑、碰撞 等事故
信号系统:包括信号灯、信号机等,可以及时提醒司机注意前方路况,确保安全 行驶
监控系统:可以实时监控火车运行情况,及时发现并处理异常情况,确保行车安 全
火车转弯的几何原理
火车转弯时,外轨与内轨的高度差称为 轨距
轨距的大小决定了火车转弯时的速度
轨距越大,火车转弯时的速度越快
轨距越小,火车转弯时的速度越慢
轨距的大小还与火车的轴距有关,轴距 越大,轨距越大
轨距的大小还与火车的转向向心力来源于车轮与铁轨之间的摩擦力 摩擦力产生于车轮与铁轨之间的接触点,方向与火车前进方向垂直 摩擦力的大小与火车的速度、车轮与铁轨之间的压力以及车轮与铁轨之间的摩擦系数有关 向心力的大小与火车转弯半径、速度以及车轮与铁轨之间的摩擦系数有关
火车转弯实例讲解

火车转弯实例讲解
火车转弯是火车行驶中的一种重要操作,它可以让火车在铁路道路上安全、稳定地转弯。
火车转弯的过程中,需要考虑很多因素,如列车速度、车辆质量、轨道曲率、路基和轨道的状态等等。
下面我们来看几个火车转弯的实例。
第一个实例是一辆火车在高速行驶时进入曲线轨道。
当火车进入曲线轨道时,它会受到向心力的作用,这会让它想往轨道内侧倾斜。
为了防止火车侧翻,车辆的车厢一般会倾斜到轨道外侧,以保持火车的平衡。
此外,火车还需要减速以控制侧向力,以及调整轨距和轮距,使车轮能够更好地贴合轨道。
第二个实例是一列货车在滑行时发生失控。
在这种情况下,火车司机必须迅速做出反应,以避免车辆脱轨。
他们必须减速、减少向心力,并调整车轮以使车辆在轨道上保持稳定。
第三个实例是一列火车在通过急弯时发生抖动。
如果火车在急弯中速度过快,它会出现抖动的问题。
此时,火车司机必须减速,并调整车轮以使车辆保持平衡。
如果车辆抖动得太厉害,司机可能需要紧急制动以避免车辆失控。
这些实例展示了火车转弯时需要考虑的许多因素。
一个好的火车司机必须能够快速做出反应,并通过适当的调整控制火车的运动。
在火车行驶中,安全始终是最重要的考虑因素。
- 1 -。
火车转弯

即“提供过度”,也就是“提供”大于“需要”。
2 m v (3)若 F 合<mrω2 或 F 合< r , 则外力不足以将物体拉回到原
轨道上,而做离心运动,即“需要”大于“提供”或“提供不足”。 (4)若 F 合=0,则物体沿圆周的切线方向做直线运动。
3.如图2-3-10所示,光滑的水平面上,小球
m在拉力F作用下做匀速圆周运动,若小球
[例1] 有一列重为1 00 t的火车,以72 km/h的速率
匀速通过一个内外轨一样高的弯道,轨道半径为400 m。 (g取10 m/s2) (1)试计算铁轨受到的侧压力; (2)若要使火车以此速率通过弯道,且使铁轨受到的
侧压力为零,我们可以适当倾斜路基,试计算路基倾斜
角度θ的正切值。
[思路点拨]
细线一端拴一个小球,另一端固 定,设法使小球在水平面内做圆 周运动,如图所示,细线与竖直 方向夹角为θ,线长为l,小球质 量为m,重力加速度为 g 求 1,小球的向心力大小。 2,小球受到给的拉力大小。 3,小球运动半径大小。 4,小球运动的线速度大小。 5,小球运动的角速度大小。 6,小球运动的周期。
线方向匀速飞出,A正确。若F突然变小不足以提供所需 向心力,小球将做逐渐远离圆心的离心运动,B、D错误。 若F突然变大,超过了所需向心力,小球将做逐渐靠近 圆心的运动,C错误。 答案:A
向右转
N
G
F
(2)向心力的来源:
如果转弯处内外轨一样高,外侧车轮的轮缘挤压外轨,
使外轨发生形变,外轨对轮缘的弹力提供火车转弯的向心力。
向右转 外轨对轮缘的弹力F就是使 火车转弯的向心力
N
G
F
(2)向心力的来源:
如果转弯处内外轨一样高,外侧车轮的轮缘挤压外轨,
曲线运动中“火车转弯”“绳杆模型”“双星多星”-问题分析【范本模板】

曲线运动中“火车转弯”“绳杆模型”“双星/多星”问题分析知识点1.生活中的圆周运动火车转弯问题:1.(多选)(2017·宜宾模拟)在设计水平面内的火车轨道的转弯处时,要设计为外轨高、内轨低的结构,即路基形成一外高、内低的斜坡(如图所示),内、外两铁轨间的高度差在设计上应考虑到铁轨转弯的半径和火车的行驶速度大小。
若某转弯处设计为当火车以速率v通过时,内、外两侧铁轨所受轮缘对它们的压力均恰好为零.车轮与铁轨间的摩擦可忽略不计,则下列说法中正确的是()A.当火车以速率v通过此弯路时,火车所受各力的合力沿路基向下方向B。
当火车以速率v通过此弯路时,火车所受重力与铁轨对其支持力的合力提供向心力C.当火车行驶的速率大于v时,外侧铁轨对车轮的轮缘施加压力D.当火车行驶的速率小于v时,外侧铁轨对车轮的轮缘施加压力【解析】选B、C2.(多选)公路急转弯处通常是交通事故多发地带。
如图,某公路急转弯处是一圆弧,当汽车行驶的速率为v0时,汽车恰好没有向公路内外两侧滑动的趋势。
则在该弯道处()A.路面外侧高内侧低B。
车速只要低于v0,车辆便会向内侧滑动C.车速虽然高于v0,但只要不超出某一最高限度,车辆便不会向外侧滑动D。
当路面结冰时,与未结冰时相比,v0的值变小【解析】选A、C3.(2017·安庆模拟)如图所示,倒置的光滑圆锥面内侧,有两个小玻璃球A、B沿锥面在水平面做匀速圆周运动,则下列关系式正确的是()A.它们的线速度大小v A〈v BB.它们的角速度ωA=ωBC.它们的向心加速度大小a A=a BD.它们的向心力大小F A=F B【解析】选C2.竖直平面的圆周运动1.“绳模型”如右图所示,小球在竖直平面内做圆周运动过最高点情况。
(注意:绳对小球只能产生拉力)(1)小球能过最高点的临界条件:绳子和轨道对小球刚好没有力的作用mg =2vmRv临界=Rg(2)小球能过最高点条件:v≥Rg(当v〉Rg时,绳对球产生拉力,轨道对球产生压力)(3)不能过最高点条件:v〈Rg(实际上球还没有到最高点时,就脱离了轨道)2.“杆模型”,小球在竖直平面内做圆周运动过最高点情况(注意:轻杆和细线不同,轻杆对小球既能产生拉力,又能产生推力。
火车转弯

火车转弯
1.如内外轨一样高,火车转弯所需向心力完全由外轨对
外侧车轮的轮缘的弹力来提供,易损坏铁轨和车轮,
甚至造成火车脱轨.
2.若外内轨有一高度差h:
①如火车按规定的转弯速度转弯v=v0,火车转弯所需
的向心力完全由重力和支持力的合力提供,火车安
全顺利转弯.
②如火车转弯速度大于规定转弯速度v>v0,火车转弯
所需的向心力由重力和支持力的合力提供(不够),
其余由外轨对外侧车轮的轮缘的弹力来补充.
③如火车转弯速度小于规定转弯速度v<v0,火车转弯
所需的向心力由重力和支持力的合力提供(过了
头),其余由内轨对内侧车轮的轮缘的弹力来抵消.
变速圆周运动
1.加速圆周运动受到的合外力方向与速度方向成锐
角.
①切向力F t产生切向加速度a t增大速度;
②法向力(向心力)F n产生法向(向心)加速度a n,
改变速度方向.
2.减速圆周运动受到的合外力方向与速度方向成钝
角.
①切向力F t产生切向加速度a t减少速度;
③法向力(向心力)F n产生法向(向心)加速度a n,
改变速度方向.
离心运动
1.F供=F需,F供=mrω2时,物体做匀速圆周运动.
2.突然F供=0,物体沿切线做离心运动.
3.突然F供<F需,F供<mrω2,物体沿曲线做离心运动.
4.突然F供>F需,F供>mrω2,物体沿曲线做近心运动.。
匀速圆周运动实例分析-火车转弯分析

在平直轨道上匀速行驶的火车,火车受到 几个力的作用?这几个力的关系如何? 火车转弯时,情况会有何不同? 需要提供向心力
1、火车在平直的轨道上匀速行驶时,所 受的合力等于零。
2、火车转弯时,火车做曲线运动,所受的 合外力不等于零,合外力又叫向心力,方 向指向圆心。 外轨对轮缘的弹 力就是使火车转 弯的向心力
2、当火车行驶速率 轨道对轮缘有侧压力
3、当火车行驶速率 轨道对轮缘有侧压力
sin tan
h
L
h F 综合有 , L Mg 2 又因为F M R
ghR L
实际中,铁轨修好以后h、R、L确定,g又 为定值,所以火车转弯时的车速为一定值。 1、当火车行驶速率 外轨道对轮缘都没有压力
ghR 时,F=F向,内 L ghR 时,F〈F向,外 L ghR L 时,F〉F向,内
圆心0
为了使铁轨不容易损坏,在转弯处使外轨略高于 内轨,受力图如下,重力和支持力的合力提供了 向心力;这样,外轨就不受轮缘的挤压了。
同理:汽车转弯做圆周运动时,也需要 向心力,是由地面给的摩擦力提供向心 力的,所以汽车在转弯的地方,路面也 是外高内低,靠合力提供向心力。
那么什么情况下可以完全使铁轨和轨缘间的 挤压消失呢? F h
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
L mg
α
θ
练习1:
火车转弯做圆周运动,如果外轨和内轨一样高,火车能 匀速通过弯道做圆周运动,下列说法中正确的是( )A
A.火车通过弯道向心力的来源是外轨的水平弹力,所以外 轨容易磨损 B.火车通过弯道向心力的来源是内轨的水平弹力,所以内 轨容易磨损 C.火车通过弯道向心力的来源是火车的重力,所以内外轨 道均不磨损 D.以上三种说法都是错误的
§5.7 生活中的圆周运动
-----------火车转弯问题分析
复习:
1、向心力的公式? 2、物体做匀速圆周运动的条件是什么?
F合=F向
3、向心力是否像重力、弹力、摩擦力一样 是一种新的性质力吗?
引入:
问题1:水平道路上,自行车转弯时,身体为
什么向内倾斜?
FN
mg
问题2:高速公路等规定转弯路段,为什么修成
滑的漏斗壁在某一水平面内做匀速圆周运动。
已知条件: m=0.5Kg,圆周半
FN
径r=0.3m, α=370,求小球运动
的线速v=?(g=10m/s2)
α
G
α
练习2:拓展----类圆锥摆
把一个小球放在漏斗中,晃动漏斗,可以使小球沿光
滑的漏斗壁在某一水平面内做匀速圆周运动。
已知条件: m=0.5Kg,圆周半
V限
gRh L
5、当V>V限 时外轨对外轮缘有弹力 当V<V限 时内轨对内轮缘有弹力
知识回顾 Knowledge Review
祝您成功!
速度为v=30m/s,火车轨距L =1.4m,要使火车通过弯道时
仅受重力与轨道的支持力,外轨道应该垫的高度h=?
(较小时tan ≈sin g=10m/s2)
FN
解:
F=mg tan =
m
V2
r
当θ很小时:tan ≈sin = h
L
F
V限
gRh L
h
lv2 rg
=0.14m
h
火车实际受力情景:
FN
V= gR tanα
Fn
mg α
当α很小时:tanα ≈ sinα
h
L
α
α
V gRh LV限 源自gRh L限定的安 全速度
只受重力和支持力 两侧均不受挤压 安全
全体讨论:
问题14:如果火车转弯时V>V限,会有什么后果?
FN
Fn
mg α
h
L
α
α
V限
gRh L
火车弯道车速过大发生侧翻事故
FN
径r=0.3m, α=370,求小球运动
的线速v=?(g=10m/s2)
α
解:小球受力如图:
mg/ tan α=
m
V2
r
G
α
带入数据,得:
V=2m/s
此位置的限定速度!
小结:
1、火车铁轨、车轮结构特点
2、铁轨弯道处------外高内低
3、火车合力与向心力关系:
mg
tan
=
m
V2
r
4、转弯时要以规定速度行驶
全体讨论:
问题15:如果火车转弯时V< V限,会有什么后果?
FN
V限
gRh L
h
Fn
mg α
L
α
α
总结:
1、当V>V限时 外轨对外轮 缘有弹力
离心趋势
外轨受 压磨损
2、当V<V限时
内轨对内轮 缘有弹力
近心趋势
规定路段,限定速度!!
V限
-g-R-h--对司机的要求
L
内轨受 压磨损
例题:火车以半径r=900m转弯,火车质量为m=8×105kg ,
FN
F合=F向
α
mg
问题8:那么如何用做图法,画出火车的合力? (请同学们一起画出草图)
FN
α
mg
问题9:通过图解,如何用相关的物理量来表示F合?
FN
α
α
mg
F合= FN sinα
或
F合= mg tanα
问题10:在这里,向心力用哪一个表达式? 请同学们自己列出火车转弯的向心力方程。
mg tanα=
练习2:拓展----类圆锥摆
把一个小球放在漏斗中,晃动漏斗,可以使小球沿光 滑的漏斗壁在某一水平面内做匀速圆周运动。
已知条件: m=0.5Kg,圆周半 径r=0.3m, α=370,求小球运动 的线速v=?(g=10m/s2)
α
练习2:拓展----类圆锥摆
把一个小球放在漏斗中,晃动漏斗,可以使小球沿光
内低外高呢?
视频1
问题3:火车转弯时,如何实现与汽车和自行车
相同的效果呢?
视频2
详细分析火车转弯问题:
问题4:假设火车匀速率转弯,它的轨道平面在什 么位置? 圆心在哪里?半径如何确定?(请同学 们一起画出草图)
外高
水平面
α 内低
问题5:火车受那些力?现在能求出合力吗?
FN
α
mg
问题6:火车的向心力指向哪里? 问题7:火车的合力与向心力有怎样的关系?
V2 m
R
V= Rg tanα
FN
α
α
mg
mg tanα= m V2
R
V= Rg tanα
问题11:根据日常观察,火车的车轮和轨道与汽车、 自行车有什么不同? 火车车轮的结构特点:
视频3
转弯时,路基水平的情况:
FN
G
F
火车速度与受力的关系:
FN
α α
V2
mg tanα= m R
mg
V= Rg tanα
