分类回归树
logit模型和分类回归树(cart)模型

logit模型和分类回归树(cart)模型
Logit模型和分类回归树(CART)模型都是重要的预测模型,但在应用和
性质上有显著的区别。
Logit模型,也被称为“评定模型”或“分类评定模型”,是离散选择法模
型之一,也是应用最广的模型。
它属于多重变量分析范畴,是社会学、生物统计学、临床、数量心理学、计量经济学、市场营销等统计实证分析的常用方法。
在社会科学中,应用最多的是 Logistic 回归分析。
根据因变量取值
类别不同,Logistic 回归分析又可以分为二元 Logistic 回归分析和多元Logistic 回归分析。
CART,全称为分类回归树,是几乎所有复杂决策树算法的基础。
CART 是
一棵二叉树,既能是分类树,也能是回归树,由目标任务决定。
当CART 是分类树时,采用 GINI 值作为结点分裂的依据;当CART 是回归树时,采用MSE(均方误差)作为结点分裂的依据。
综上所述,Logit模型和CART模型在应用和性质上都有显著的区别。
Logit 模型主要用于离散选择分析,而CART模型主要用于决策树的生成。
如需了解更多关于这两种模型的信息,建议咨询统计学专家或查阅统计学相关书籍。
CART(分类回归树)原理和实现

CART(分类回归树)原理和实现前⾯我们了解了决策树和adaboost的决策树墩的原理和实现,在adaboost我们看到,⽤简单的决策树墩的效果也很不错,但是对于更多特征的样本来说,可能需要很多数量的决策树墩或许我们可以考虑使⽤更加⾼级的弱分类器,下⾯我们看下CART(Classification And Regression Tree)的原理和实现吧CART也是决策树的⼀种,不过是满⼆叉树,CART可以是强分类器,就跟决策树⼀样,但是我们可以指定CART的深度,使之成为⽐较弱的分类器CART⽣成的过程和决策树类似,也是采⽤递归划分的,不过也存在很多的不同之处数据集:第⼀列为样本名称,最后⼀列为类别,中间为特征human constant hair true false false false true false mammalpython cold_blood scale false true false false false true reptilesalmon cold_blood scale false true false true false false fishwhale constant hair true false false true false false mammalfrog cold_blood none false true false sometime true true amphibiouslizard cold_blood scale false true false false true false reptilebat constant hair true false true false true false mammalcat constant skin true false false false true false mammalshark cold_blood scale true false false true false false fishturtle cold_blood scale false true false sometime true false reptilepig constant bristle true false false false true true mammaleel cold_blood scale false true false true false false fishsalamander cold_blood none false true false sometime true true amphibious特征名称如下["temperature","cover","viviparity","egg","fly","water","leg","hibernate"]1:数据集划分评分CART使⽤gini系数来衡量数据集的划分效果⽽不是⾹农熵(借⽤下⾯的⼀张图)def calGini(dataSet):numEntries = len(dataSet)labelCounts={}for featVec in dataSet:currentLabel = featVec[-1]if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0labelCounts[currentLabel] += 1gini=1for label in labelCounts.keys():prop=float(labelCounts[label])/numEntriesgini -=prop*propreturn gini2:数据集划分决策树是遍历每⼀个特征的特征值,每个特征值得到⼀个划分,然后计算每个特征的信息增益从⽽找到最优的特征;CART每⼀个分⽀都是⼆分的,当特征值⼤于两个的时候,需要考虑特征值的组合得到两个“超级特征值”作为CART的分⽀;当然我们也可以偷懒,每次只取多个特征值的⼀个,挑出最优的⼀个和剩下的分别作为⼀个分⽀,但⽆疑这得到的cart不是最优的# 传⼊的是⼀个特征值的列表,返回特征值⼆分的结果def featuresplit(features):count = len(features)#特征值的个数if count < 2:print"please check sample's features,only one feature value"return -1# 由于需要返回⼆分结果,所以每个分⽀⾄少需要⼀个特征值,所以要从所有的特征组合中选取1个以上的组合# itertools的combinations 函数可以返回⼀个列表选多少个元素的组合结果,例如combinations(list,2)返回的列表元素选2个的组合# 我们需要选择1-(count-1)的组合featureIndex = range(count)featureIndex.pop(0)combinationsList = []resList=[]# 遍历所有的组合for i in featureIndex:temp_combination = list(combinations(features, len(features[0:i])))combinationsList.extend(temp_combination)combiLen = len(combinationsList)# 每次组合的顺序都是⼀致的,并且也是对称的,所以我们取⾸尾组合集合# zip函数提供了两个列表对应位置组合的功能resList = zip(combinationsList[0:combiLen/2], combinationsList[combiLen-1:combiLen/2-1:-1])return resList得到特征的划分结果之后,我们使⽤⼆分后的特征值划分数据集def splitDataSet(dataSet, axis, values):retDataSet = []for featVec in dataSet:for value in values:if featVec[axis] == value:reducedFeatVec = featVec[:axis] #剔除样本集reducedFeatVec.extend(featVec[axis+1:])retDataSet.append(reducedFeatVec)return retDataSet遍历每个特征的每个⼆分特征值,得到最好的特征以及⼆分特征值# 返回最好的特征以及⼆分特征值def chooseBestFeatureToSplit(dataSet):numFeatures = len(dataSet[0]) - 1 #bestGiniGain = 1.0; bestFeature = -1;bestBinarySplit=()for i in range(numFeatures): #遍历特征featList = [example[i] for example in dataSet]#得到特征列uniqueVals = list(set(featList)) #从特征列获取该特征的特征值的set集合# 三个特征值的⼆分结果:# [(('young',), ('old', 'middle')), (('old',), ('young', 'middle')), (('middle',), ('young', 'old'))]for split in featuresplit(uniqueVals):GiniGain = 0.0if len(split)==1:continue(left,right)=split# 对于每⼀个可能的⼆分结果计算gini增益# 左增益left_subDataSet = splitDataSet(dataSet, i, left)left_prob = len(left_subDataSet)/float(len(dataSet))GiniGain += left_prob * calGini(left_subDataSet)# 右增益right_subDataSet = splitDataSet(dataSet, i, right)right_prob = len(right_subDataSet)/float(len(dataSet))GiniGain += right_prob * calGini(right_subDataSet)if (GiniGain <= bestGiniGain): #⽐较是否是最好的结果bestGiniGain = GiniGain #记录最好的结果和最好的特征bestFeature = ibestBinarySplit=(left,right)return bestFeature,bestBinarySplit所有特征⽤完时多数表决程序def majorityCnt(classList):classCount={}for vote in classList:if vote not in classCount.keys(): classCount[vote] = 0classCount[vote] += 1sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)return sortedClassCount[0][0]现在来⽣成cart吧def createTree(dataSet,labels):classList = [example[-1] for example in dataSet]# print dataSetif classList.count(classList[0]) == len(classList):return classList[0]#所有的类别都⼀样,就不⽤再划分了if len(dataSet) == 1: #如果没有继续可以划分的特征,就多数表决决定分⽀的类别# print "here"return majorityCnt(classList)bestFeat,bestBinarySplit = chooseBestFeatureToSplit(dataSet)# print bestFeat,bestBinarySplit,labelsbestFeatLabel = labels[bestFeat]if bestFeat==-1:return majorityCnt(classList)myTree = {bestFeatLabel:{}}featValues = [example[bestFeat] for example in dataSet]uniqueVals = list(set(featValues))for value in bestBinarySplit:subLabels = labels[:] # #拷贝防⽌其他地⽅修改if len(value)<2:del(subLabels[bestFeat])myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels)return myTree看下效果,左边是cart,右边是决策树,(根节点⽤cover和temperature是⼀样的,为了对⽐决策树,此时我选了cover),第三个图是temperature作为根节点的cart上⾯的代码是不考虑特征继续使⽤的,也就是每个特征只使⽤⼀次;但是我们发现有些有些分⽀⾥⾯特征值个数多余两个的,其实我们应该让这些特征继续参与下⼀次的划分可以发现,temperature作为根节点的cart没有变化,⽽cover作为根节点的cart深度变浅了,并且cover特征出现了两次(或者说效果变好了)下⾯是有变化的代码特征值多余两个的分⽀保留特征值def splitDataSet(dataSet, axis, values):retDataSet = []if len(values) < 2:for featVec in dataSet:if featVec[axis] == values[0]:#如果特征值只有⼀个,不抽取当选特征reducedFeatVec = featVec[:axis]reducedFeatVec.extend(featVec[axis+1:])retDataSet.append(reducedFeatVec)else:for featVec in dataSet:for value in values:if featVec[axis] == value:#如果特征值多于⼀个,选取当前特征retDataSet.append(featVec)return retDataSetcreateTree函数for循环判断是否需要移除当前最优特征for value in bestBinarySplit:if len(value)<2:del(labels[bestFeat])subLabels = labels[:] #拷贝防⽌其他地⽅修改myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels)这样我们就⽣成了⼀个cart,但是这个数据集没有出现明显的过拟合的情景,我们换⼀下数据集看看sunny hot high FALSE nosunny hot high TRUE noovercast hot high FALSE yesrainy mild high FALSE yesrainy cool normal FALSE yesrainy cool normal TRUE noovercast cool normal TRUE yessunny mild high FALSE nosunny cool normal FALSE yesrainy mild normal FALSE yessunny mild normal TRUE yesovercast mild high TRUE yesovercast hot normal FALSE yesrainy mild high TRUE no特征名称:"Outlook" , "Temperature" , "Humidity" , "Wind"⽣成的cart⽐价合理,这是因为数据⽐较合理,我们添加⼀条脏数据看看cart会变成怎么样(右图),可以看到cart为了拟合我新加的这条脏数据,树深度增加1,叶⼦节点增加3,不过另⼀⽅⾯也是因为样本数少的原因,⼀个噪声样本就产⽣了如此⼤的印象overcast mild normal FALSE no下⼀篇博客我们继续讨论cart连续值的⽣成以及剪枝的实验。
分类与回归树

• 一个节点产生左右孩子后,递归地对左右孩子进 行划分即可产生分类回归树。当节点包含的数据 记录都属于同一个类别时就可以终止分裂了。 • 当分类回归树划分得太细时,会对噪声数据产生 过拟合作用。因此我们要通过剪枝来解决。剪枝 又分为前剪枝和后剪枝:前剪枝是指在构造树的 过程中就知道哪些节点可以剪掉,于是干脆不对 这些节点进行分裂,在分类回归树中可以使用的 后剪枝方法有多种,比如:代价复杂性剪枝、最 小误差剪枝、悲观误差剪枝等等。
• 分类与回归树: • 分类回归树(CART,Classification And Regression Tree)属于一种决策树,分类回 归树是一棵二叉树,且每个非叶子节点都 有两个孩子,所以对于第一棵子树其叶子 节点数比非叶子节点数多1。
• 上例是属性有8个,每个 属性又有多少离散的值可 取。在决策树的每一个节 点上我们可以按任一个属 性的任一个值进行划分。 比如最开始我们按: 1)表面覆盖为毛发和非毛发 2)表面覆盖为鳞片和非鳞片 3)体温为恒温和非恒温 等等产生当前节点的左右两个孩子。按哪种划分最好呢?有 3个标准可以用来衡量划分的好坏:GINI指数、双化指数、 有序双化指数。下面我们只讲GINI指数。
• 总体内包含的类别越杂乱,GINI指数就越大(跟熵的概念很相似)。 比如体温为恒温时包含哺乳类5个、鸟类2个,则: • 体温为非恒温时包含爬行类3个、鱼类3个、两栖类2个,则 • 所以如果按照“体温为恒温和非恒温”进行划分的话,我们得到GINI 的增益(类比信息增益):划分。
决策树之CART算法(回归树分类树)

决策树之CART算法(回归树分类树)
**CART算法(Classification and Regression Trees)**是一种运
用在分类和回归问题中的决策树学习算法,它的本质是一种机器学习算法,主要用于对数据进行分类和回归。
它由美国统计学家 Breiman等人在
1984年提出。
CART算法可以将复杂的数据集简单地划分成多个部分,其本质是一
种贪心算法,可以让学习者从实例中学习决策树,用于解决复杂的分类或
回归问题。
该算法通过构建最优二叉树来实现特征选择,从而使得分类的
准确性最大化。
###CART算法的原理
CART算法是一种有监督学习的算法,可以将训练数据或其他更复杂
的信息表示为一棵二叉树。
通过采用不断划分训练集的方式,将数据集划
分成越来越小的子集,使数据更容易分类。
基本原理如下:
1.首先从根结点开始,从训练集中选择一个最优特征,使用该特征将
训练集分割成不同的子集。
2.递归地从每个子结点出发,按照CART算法,每次选择最优特征将
其分割成不同的子结点。
3.当到达叶子结点时,从所有的叶子结点中选出一个最优的结点,比
如分类误差最小的结点,作为最终的结果。
###CART算法的执行流程
CART算法的执行流程如下:
1.首先,从训练集中获取每个特征的可能取值。
cart算法题目

cart算法题目Cart算法,也称为分类和回归树(Classification and Regression Tree),是一种常用的决策树学习方法。
下面是一些关于Cart算法的题目,用于练习和检验自己对Cart算法的理解:1. 基本概念•解释什么是决策树,并给出其优缺点。
◦解释什么是Cart算法,它在哪些场景中应用?2. 构建决策树•使用Cart算法,给出如何根据数据集构建决策树的步骤。
◦当在某个节点上划分不成功时,如何处理?3. 特征选择•解释如何使用Gini指数或基尼不纯度进行特征选择。
◦解释如何使用信息增益或增益率进行特征选择。
4. 剪枝•为什么要对决策树进行剪枝?◦给出决策树剪枝的几种常见方法。
5. 应用场景•Cart算法可以用于分类问题,还可以用于回归问题。
给出一些应用场景。
6. 与其他算法比较•与其他分类算法(如K近邻、支持向量机、朴素贝叶斯)相比,Cart算法的优点和缺点是什么?7. 实战问题•给出一个数据集,使用Cart算法构建决策树,并解释结果。
◦对于一个分类问题,如何使用Cart算法进行预测?8. 优缺点•列出Cart算法的优缺点,并给出改进的方法。
9. 过拟合与欠拟合•Cart算法也可能遇到过拟合和欠拟合问题,解释这两种问题并给出解决方法。
10. 其他注意事项•在使用Cart算法时,还需要注意哪些问题?例如参数选择、特征选择等。
这些题目涵盖了Cart算法的基本概念、构建、应用和一些注意事项。
通过回答这些问题,可以帮助你深入理解Cart算法,并为实际应用打下基础。
分类与回归树 决策树
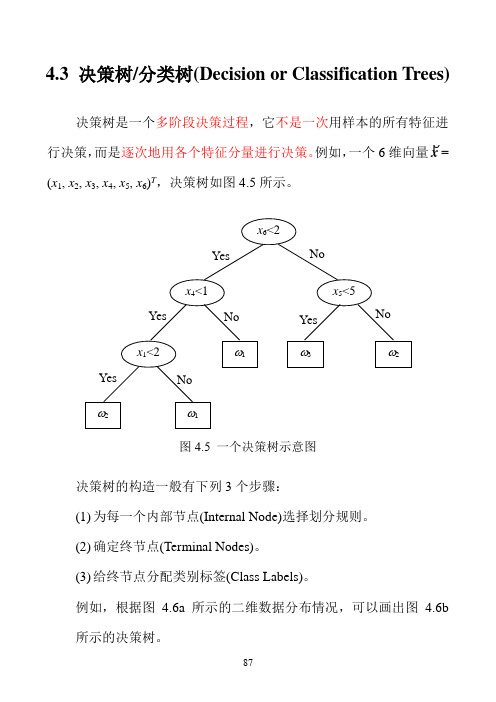
4.3 决策树/分类树(Decision or Classification Trees)
决策树是一个多阶段决策过程,它不是一次用样本的所有特征进
行决策,而是逐次地用各个特征分量进行决策。
例如,一个6维向量x
=
(x 1, x 2, x 3, x 4, x 5, x 6)T ,决策树如图4.5所示。
决策树的构造一般有下列3个步骤:
(1) 为每一个内部节点(Internal Node)选择划分规则。
(2) 确定终节点(Terminal Nodes)。
(3) 给终节点分配类别标签(Class Labels)。
例如,根据图 4.6a 所示的二维数据分布情况,可以画出图 4.6b 所示的决策树。
x 6<2
x 5<5
x 4<1 x 1<2
ω1 ω2
ω1
ω3 ω2 Yes No
Yes Yes
Yes No
No
No
图4.5 一个决策树示意图
我们可以利用决策树的原理来解决多类别问题,例如,用一个线性分类器(例如Fisher 分类器)解决多类别问题。
图4.6a 一个二维空间样本分布示例
图4.6b 对应的决策树
x k >b 2
x k <b 1
x i <a 2 x k >b 3 ω8
ω9 ω6
ω4
Yes No
Yes Yes
Yes
No
No No x i >a 1
ω10
ω1 Yes
No。
分类和回归树算法

分类和回归树算法分类和回归树(CART)是一种常用的决策树算法,用于解决分类和回归问题。
它可以根据给定的特征将数据集划分为不同的区域,并在每个区域内预测目标变量的取值。
在本文中,我将详细介绍CART算法的原理、构建过程和优缺点。
一、CART算法原理CART算法是一种基于特征划分的贪心算法,它通过递归地划分数据集来构建决策树。
算法的核心思想是选择一个最优特征和最优切分点,使得划分后的子集尽可能纯净。
具体来说,CART算法构建决策树的过程如下:1.选择最优特征和最优切分点:遍历所有特征和所有可能的切分点,计算每个切分点的基尼指数(用于分类)或均方差(用于回归),选择使得切分后子集纯度最大或方差最小的特征和切分点。
2.划分数据集:将数据集根据选定特征和切分点划分为两个子集,一个子集包含特征值小于等于切分点的样本,另一个子集包含特征值大于切分点的样本。
3.递归构建子树:对于每个子集,重复上述步骤,直到满足停止条件。
停止条件可以是:达到最大深度、子集中样本数量小于一些阈值、子集中样本类别完全相同等。
4.构建决策树:重复上述步骤,不断构建子树,将所有子树连接起来形成一棵完整的决策树。
5.剪枝:在构建完整的决策树后,通过剪枝来减小过拟合。
剪枝是通过判断在进行划分后树的整体性能是否有所提升,如果没有提升,则将该子树转化为叶节点。
二、CART算法构建过程下面以分类问题为例,详细描述CART算法的构建过程。
1. 输入:训练集D = {(x1, y1), (x2, y2), ..., (xn, yn)},特征集A = {a1, a2, ..., am}。
2.输出:决策树T。
3.若D中所有样本都属于同一类别C,则将T设为单节点树,并标记为C类,返回T。
4.若A为空集,即无法再选择特征进行划分,则将T设为单节点树,并将D中样本数量最多的类别标记为C类,返回T。
5. 选择最优特征a*和最优切分点v*:遍历特征集A中的每个特征ai和每个可能的切分点vi,计算切分后子集的基尼指数或均方差,选择使得基尼指数或均方差最小的特征和切分点a*和v*。
CART分类与回归树方法介绍

1.软件下载与安装
1.软件下载与安装
该软件可从官方网站下载并安装。下载安装过程十分简单,只需根据提示完 成即可。
2.界面介绍
2.界面介绍
该软件采用图形用户界面(GUI),界面简洁明了,操作方便易用。主界面包 括菜单栏、工具栏、数据区和结果区等部分。
3.数据导入与清洗
3.数据导入与清洗
(1)点击菜单栏中的“文件”->“打开”,选择实验数据文件导入。支持多 种文件格式,如CSV、Excel等。
谢谢观看
CART分类
3、递归分割:将生成的两个子节点分别递归执行步骤1和2,直到满足停止条 件,生成最终的决策树。
CART分类
4、决策规则生成:根据生成的决策树,生成相应的决策规则,用于对新数据 进行分类。
回归树方法
回归树方法
回归树方法是CART方法的一种变种,主要用于预测连续型目标变量。回归树 通过构建决策树,实现对目标变量的预测。回归树方法的具体步骤如下:
5.结果输出与保存
5.结果输出与保存
(1)结果展示:在结果区展示拟合的回归模型参数、相关系数等结果。 (2)保存结果:点击“文件”->“保存”,将计算结果保存到本地电脑或云 端存储设备。
三、案例分析
三、案例分析
为了更好地说明毒力回归计算方法的应用和软件使用的效果,我们结合一个 实际案例进行阐述。某研究团队在研究某种生物毒素对水生生物的毒害作用时, 通过实验观测获得了毒素浓度与水生生物死亡率的数据。利用毒力回归计算软件, 我们对该数据进行毒力回归计算,并建立相应的回归模型。
案例分析
1、数据预处理:首先对用户购买行为的数据进行清洗和处理,包括去除异常 值、填补缺失值等。
案例分析
2、特征提取:然后对数据进行分析,选择出与购买行为相关的特征,如年龄、 性别、购买频率、购买金额等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.1.1. 分类回归树分类回归树(Classification and regression trees,CART)是决策树的一种,它是基于吉尼(Gini)指标(并且是最简化的吉尼指标)的方法。
在OpenCV 下函数icvCreateCARTStageClassifier 实现层强分类器的构建,而它又调用了icvCreateCARTHaarClassifier 、icvInitCARTHaarClassifier 、icvEvalCARTHaarClassifier 实现了弱检测器的分类回归树的初始化、构建、赋值。
以下是简化了的算法描述:其中C 代表当前样本集,当前候选属性集用T 表示。
(1)新建一个根节点root(2)为root 分配类别(有人脸还是没有)(3)如果T 都属于同一类别(都是正样本或者反样本)或者C 中只剩下一个样本则返回root 为叶节点,为其分配属性。
(4)对任何一个T 中属性执行该属性上的划分,计算此划分的分类不纯度 (吉尼不纯度)(5)root 的测试属性是T 中最小GINI 系数的属性(6)划分C 得到C1 C2子集(7)对于节点C1重复(1)-(6)(8)对于节点C2重复(1)-(6)至于CART 的修剪、评估等算法就不给出了。
CART 的修剪的算法是分类错误算法。
如果想深入了解CART 树,则阅读上节给出的参考书目。
1.1.2. 弱分类器方法弱分类器的种类很多,但OpenCV 使用的是效果最好的决策树分类器。
关于分类器的介绍在第一章已经讨论过了,如果要有更深入理解可以看一些数据挖掘的图书后,再看看OpenCV 下的cvhaartraining.cpp 文件。
这里特别提下弱分类器的阈值的寻找方法。
阈值寻找算法定义在icvFindStumpThreshold_##suffix 函数里面,它是通过一个宏被定义的。
至于为什么通过这种方式定义,可以参考文献。
[i]函数icvFindStumpThreshold_##suffix输入参数介绍:wk 是第k 个样本的权重,yk 是第k 个样本是正样本还是反样本,如果是正样本则为+1,反样本则为-1,lerror 、rerror 是要求的最低误差,lerror=rerror=3.402823466e+38F(超大的数值),left 、right 是输出的误差。
threshold 是阈值,found 为是否找到阈值,初始是0。
For i=1:num(对每个排序后的样本)(1)∑==i k k wwl 1,∑+==num i k k w wr 1 (2)k i k k y wwyl *1∑== , k numi k k y w wyr *1∑+==(3)curleft=wyl/wl , curright=wyr/wr(4)如果curlerror+currerror<lerror+rerror则lerror=curlerrorrerror=curerrorthreshold 等于当前样本和前一个样本权重的均值left=curleftright=currightfound=1End返回found的值虽然lerror、rerror初始都是很大的值,但保证了程序一开始就可以进入(4),使它们改为当前的误差值(默认一定会找到阈值),不断循环下,它们就可以取得最小的误差值。
1.1.3.DAB的权重调整算法在OpenCV下函数icvBoostNextWeakClassifierDAB用于DAB的样本权重调整。
它实现了以最佳弱分类器进行一次样本权重的调整,并返回这次调整后的错误分类百分比。
流程如下:(1)初始化err=sumw=0;y向量是实际正反样本,f向量是样本在弱分类器下结果,都是1为真,-1为假。
w向量是样本的权重。
(2)调整部分(a)计算误检率。
对应了图中errm=Ew[1(y!=fm(x))]for i=0 to N-1如果y(i)不等于f(i)(表示未被正确分类),则err=err+w(i);如果相等,err不变;累加样本权重放到sumw中end;err=err/sumw;//计算了错误的比例,0<err<1/2err= - log(err/(1 - err));(b)更新权重for i=0 to N-1如果y(i)不等于f(i),则w(i)=w(i)*exp(err);否则w(i)不变累加新的权重放在sumw中end(c)归一化权重for i=0 to N-1w(i)=w(i)/sumw;end(3)返回err的值1.1.4.GAB的权重调整算法OpenCV下使用icvBoostNextWeakClassifierGAB函数调整GAB方法的权重,这个函数返回的alpha值恒为1,这点可以从输出分类器的算法(错误!未找到引用源。
节)中看到,它c项的。
是没有m(1)初始化sumw=0;(2)调整部分(a)更新权重for i=0 to N-1w(i)=w(i)*exp(-y(i)*f(i));//注意这里的f(i)数值不是-1和+1了。
累加权重放入sumw中end(b)权重归一for i=0 to N-1w(i)=w(i)/sumw;end(3)返回1.01.2. OpenCV下训练代码框架解读前几节使用了OpenCV进行了训练,而前几章人脸检测算法讲解比较分散,现在给出一个整体的算法流程,以弄清楚刚才的训练过程是怎么进行的。
首先要介绍下training_data的结构是CvHaarTrainingData,它是整个程序中最重要的数据。
先令N=posnum + negnum,即正反样本数量typedef struct CvHaarTrainingData{CvSize winsize; /* 图像大小*/int maxnum; /* 样本最大数量*/CvMat sum; /* 竖直积分图像,每个积分图像占据一行,N * (W+1)×(H+1)*/CvMat tilted; /* 旋转45度的积分图像,每个积分图像占据一行,N* (W+1)×(H+1) */CvMat normfactor; /* 一维向量, 1 * N*/CvMat cls; /* 所属类一维向量, 1 *N。
1表示有物体,0表示背景*/CvMat weights; /* 权重一维向量, 1 *N*/CvMat* valcache; /* 特征值*/CvMat* idxcache; /* 特征值标号*/} CvHaarTrainigData;函数cvCreateTreeCascadeClassifier的主体流程:(1)icvLoadTreeCascadeClassifier、icvFindDeepestLeaves、icvPrintTreeCascade读入已经训练好的数据,如果是第一次则不运行。
(2)icvCreateIntHaarFeatures//负责创建所有的Haar特征,并保存。
(3)icvCreateHaarTrainingData//给sum、tilted、normfactor、cls、weight分配内存空间(4)icvInitBackgroundReaders//初始化反样本图片的读入(具体实现又调用icvCreateBackgroundData、icvCreateBackgroundReader)(5)进入总循环//构造多层强分类器(A)再进入次循环循环//构造一层强分类器(a)icvSetLeafNode//从root找到路径到leaf(b)icvGetHaarTrainingDataFromVec//从.vec文件读入训练数据,经过计算得到的数据放到training_data下的sum、tilted、normfactor中(c)icvGetHaarTrainingDataFromBG//读入背景图片数据(d)判断是否达到required_leaf_fa_rate和nstages的要求,达到则程序结束。
否则继续(e)icvSetNumSamples//设置training_data中的行列都为总样本个数(f)根据equalweights初始化正反样本权重.如果它是真,则都设为1/num,否则posweight=1/2/poscount;negweight=1/2/negcount;(g)icvSetWeightsAndClasses//根据刚才的数据对training_data结构中的向量指针weights,cls分别赋值。
真样本在前反样本在后。
(h)icvPrecalculate//计算numprecalculated个haar特征(具体又通过icvGetTrainingDataCallback计算),保存到training_data->valcache下(i)icvCreateTreeCascadeNode//初始化,分配空间(j)icvCreateCARTStageClassifier//建立一层强分类器(k)icvNumSplits//返回这次强分类器一共使用的特征数量(l)开始聚类(clustering)操作,调用cvKMeans2函数等,这里最大不超过3类。
从2个类别开始进行聚类,每次聚类重新读入数据构造层CART树,找到最佳的类别数。
(B)次循环结束(6)开始寻找哪些节点应该被分裂,找到后添加新的节点。
并依次保存已经建好的节点,直到这棵树完全被存储。
(7)满足误差率或者层数则结束总循环,否则跳到(5)。
对照上面的步骤就可以很好的解释刚才训练过程。
需要注意的是,每一层训练时,正反样本数据都要重新载入,这个原因谈到过,是因为内存不够。
所以它每次处理后失去了原始的样本数据。
至于为什么最后程序无法停止,目前没有人给出解释。
1.3.对xml文件的解读在OpenCV进行长时间的训练后,我们能够得到一个.xml文件,这种文件是专门用于存储数据的,并且是跨平台的。
我们只是研究物体检测产生的.xml文件,只对它的结果进行解读,如果想深入了解.xml的编程可以参考相关书籍。
下面列出haarcascade_frontalface_alt2.xml文件中的一些内容:(/**/中文字是注释)<size>20 20</size>/*这行告诉我们这个分类器是使用20*20的图像训练出来的,因此他可以检测任何大于20*20的人脸图像。
*/<!-- stage 0-->/*代表第0层强分类器*/-<trees><!-- tree 0-->/*代表此层分类器下第0棵二叉树*/<!-- root node-->/*根节点*/-<feature>-<rects>/*矩形*/<_>2 7 16 4 -1.</_>/*前面四个数据表示矩形左上角坐标和矩形的长、宽,最后一个表示比重*/<_>2 9 16 2 2.</_>/*这个矩形比重是正的,可以画图发现是Haar_y2特征*/</rects><tilted>0</tilted>/*这个标志是不是旋转的特征,0表示不是*/</feature><threshold>4.3272329494357109e-003</threshold>/*表示这棵树的阈值*/<left_val>0.0383819006383419</left_val>/*小于阈值去左树枝*/<right_node>1</right_node>/*大于等于阈值取右树枝,这个节点有分裂了,继续往下找*/之后就可以找到这个节点,结构和刚才分析的是一样的。
