预测控制MATLAB仿真与设计
【学习】第7章模型预测控制系统的计算机辅助设计MATLAB控制系统设计与仿真教学

s1,1,i
Si
s2,1,i
sny ,1,i
s1,2,i sny ,2,i
s1,n ,i
(7.3)
sny ,n ,i
其中, sl,m,i 是第m个输入到第l个输出的第i个阶跃 响应。 MPC工具箱将按照下面的格式存储阶跃响应模
型:
S1
S2
Sn
n o u t(1) 0
0
p la n t
n
y(k) si(ki)sn(kn1) (7.1)
i1
上述阶跃响应模型也可以用于稳定且具有积分性质 的过程。 对于一个积分过程, 我们可以假设系统在n步 以后的响应信号的斜率保持常数, 也就是说:
s n s n 1 s n 1 s n s n 2 s n 1 (7.2)
对于具有nv个输入和ny个输出的多输入多输出 (MIMO)系统, 我们可以得到一系列阶跃响应的系数 矩阵
图 7.1 系统的阶跃响应曲线
我们也可以首先生成系统的状态空间模型, 然后使 用tf2ss函数和ss2step生成阶跃响应模型:
num = [0 0 0 num]; den = [den 0 0]; [phi, gam, c, d] = tf2ss(num, den); % 转换成状态空间形式 plant = ss2step(phi, gam, c, d, tfinal, delt1, delt2, nout); % 计算阶跃响应
归(plsr)计算得到。 下面的程序(mpctutid)演示了
具体的计算步骤:
% 载入系统输入和输出数据, 这些数据由下面的传 递函数和随机白噪声产生
% 从输入1到输出1的传递函数: g11=5.72exp(-14s)/ (60s+1)
基于MatlabGUI的预测控制仿真平台设计

2.2 仿真算法中的几个问题
作为仿真平台,对于算法应该具有可扩展性,并且提供
良好的接口,以便其他算法动态加载。本平台主要针对预测
控制的典型算法,如 DMC,GPC,MAC 的预测控制算法进
行设计,并且对于其他复杂的预测控制算法(如非线性 MPC
算法,鲁棒 MPC 算法等)提供预留接口。下面就离散化仿
as + b s2 + cs + d
也作类似变换。如果
yi,j
是由这两
个环节的不同阶次合成,则每个环节都对应于这样一类递推
关系,所得到的输出再合成为 yi,j,而第 i 个输出 yi 是由各个 输入 ui 所得到的 yi,j 线性叠加而成,这样就可以精确的计算 出仿真输出,如图 2 所示。
图 2 离散仿真计算仿真输出
引 言1
1 仿真平台总体设计
预测控制(Predictive Control)是由 Richalet 等人[1,2]于 1978 年首次提出的。近三十年来,预测控制被广泛应用于 工业领域,特别是针对复杂的控制对象和多样化的控制要 求,具有很好的控制效果。对于预测控制的理论和方法研究, 也始终是控制的热点领域之一。
Abstract:Dealing with the multi-variable predictive control system, from the point of view on avoiding Matlab simulation errors, a new method was proposed, in which the predictive model was decentralized and analyzed accurately. It helps to prove some related conclusions of predictive control. At the same time, Graphic User Interface (GUI) of Matlab was used to design a simulation platform of predictive control, which provides good interaction and extensibility. At last, some simulation examples were given to show the effectiveness of the platform. Key words:predictive control; GUI; simulation platform; extensibility
预测控制MATLAB仿真与设计

动态矩阵控制算法实验报告院系:电子信学院姓名:***学号:*********专业:控制理论与控制工程导师:***MATLAB环境下动态矩阵控制实验一、实验目的:对于带有纯滞后、大惯性的研究对象,通过动态控制矩阵的MATLAB的直接处理与仿真实验,具有较强的鲁棒性和良好的跟踪性。
输入已知的控制模型,通过对参数的选择,来取的良好的控制效果。
二、实验原理:动态矩阵控制算法是一种基于被控对象非参数数学模型的控制算法,它是一种基于被控对象阶跃响应的预测控制算法,以对象的阶跃响应离散系统为模型,避免了系统的辨识,采用多步预估技术,解决时延问题,并按照预估输出与给定值偏差最小的二次性能指标实施控制,它适用于渐进稳定的线性对象,系统动态特性中存在非最小相位特性或纯滞后都不影响算法的直接使用。
三、实验环境:计算机 MATLAB2016b四、实验步骤:影响控制效果的主要参数有:1)采样周期T与模型长度N在DMC中采样周期T与模型长度N的选择需要满足香农定理和被控对象的类型及其动态特性的要求,通常需要NT后的阶跃响应输出值接近稳定值。
2)预测时域长度PP对系统的快速性和稳定性具有重要影响。
为使滚动优化有意义,应使P 包含对象的主要动态部分,P越小,快速性提高,稳定性变差;反之,P越大,系统实时性降低,系统响应过于缓慢。
3)控制时域长度MM控制未来控制量的改变数目,及优化变量的个数,在P确定的情况下,M越小,越难保证输出在各采样点紧密跟踪期望输出值,系统响应速度缓慢,可获得较好的鲁棒性,M越大,控制机动性越强,改善系统的动态性能,但是稳定性会变差。
五、实例仿真(一)算法实现设GP(s)=e-80s/(60s+1),采用DMC后的动态特性如图1所示,采样周期T=20s,优化时域P=10,M=2,建模时域N=20。
MATLAB程序1:g=poly2tfd(1,[60 1],0,80);%通用传函转换为MPC模型delt=20; %采样周期nt=1; %输出稳定性向量tfinal=1000; %截断时间model=tfd2step(tfinal,delt,nt,g);%传函转换为阶跃响应模型plant=model;%进行模型预测控制器设计p=10;m=2;ywt=[];uwt=1;%设置输入约束和参考轨迹等控制器参数kmpc=mpccon(plant,ywt,uwt,m,p);%模型预测控制器增益矩阵计算tend=1000;r=1;%仿真时间[y,u,yrn]=mpcsim(plant,model,kmpc,tend,r);%模型预测控制仿真t=0:20:1000;%定义自变量t的取值数组plot(t,y)xlabel(‘图一DMC控制动态响应曲线(time/s)’);ylabel(‘响应曲线’);结果如下:Percent error in the last step response coefficientof output yi for input uj is :2.2e-05%Time remaining 1000/1000Time remaining 800/1000Time remaining 600/1000Time remaining 400/1000Time remaining 200/1000Time remaining 0/1000Simulation time is 0.003 seconds.结论:采用DMC后系统调整时间减小,响应的快速性好,无超调。
基于MATLAB控制系统的仿真与应用毕业设计论文

基于MATLAB控制系统的仿真与应用毕业设计论文目录一、内容概括 (2)1. 研究背景和意义 (3)2. 国内外研究现状 (4)3. 研究目的和内容 (5)二、MATLAB控制系统仿真基础 (7)三、控制系统建模 (8)1. 控制系统模型概述 (10)2. MATLAB建模方法 (11)3. 系统模型的验证与校正 (12)四、控制系统性能分析 (14)1. 稳定性分析 (14)2. 响应性能分析 (16)3. 误差性能分析 (17)五、基于MATLAB控制系统的设计与应用实例分析 (19)1. 控制系统设计要求与方案选择 (20)2. 基于MATLAB的控制系统设计流程 (22)3. 实例一 (23)4. 实例二 (25)六、优化算法在控制系统中的应用及MATLAB实现 (26)1. 优化算法概述及其在控制系统中的应用价值 (28)2. 优化算法介绍及MATLAB实现方法 (29)3. 基于MATLAB的优化算法在控制系统中的实践应用案例及分析对比研究31一、内容概括本论文旨在探讨基于MATLAB控制系统的仿真与应用,通过对控制系统进行深入的理论分析和实际应用研究,提出一种有效的控制系统设计方案,并通过实验验证其正确性和有效性。
本文对控制系统的基本理论进行了详细的阐述,包括控制系统的定义、分类、性能指标以及设计方法。
我们以一个具体的控制系统为例,对其进行分析和设计。
在这个过程中,我们运用MATLAB软件作为主要的仿真工具,对控制系统的稳定性、动态响应、鲁棒性等方面进行了全面的仿真分析。
在完成理论分析和实际设计之后,我们进一步研究了基于MATLAB 的控制系统仿真方法。
通过对仿真模型的建立、仿真参数的选择以及仿真结果的分析,我们提出了一种高效的仿真策略。
我们将所设计的控制系统应用于实际场景中,通过实验数据验证了所提出方案的有效性和可行性。
本论文通过理论与实践相结合的方法,深入探讨了基于MATLAB 控制系统的仿真与应用。
DMC算法MATLAB编程及仿真
一、前言工业生产的过程是复杂的,建立起来的模型也是不完善的。
即使是理论非常复杂的现代控制理论,其效果也往往不尽人意,甚至在一些方面还不及传统的PID控制。
20世纪70年代,人们除了加强对生产过程的建模、系统辨识、自适应控制等方面的研究外,开始打破传统的控制思想,试图面向工业开发出一种对各种模型要求低、在线计算方便、控制综合效果好的新型算法。
在这样的背景下,预测控制的一种,也就是动态矩阵控制(DMC)首先在法国的工业控制中得到应用。
因此预测控制不是某种统一理论的产物,而是在工业实践中逐渐发展起来的。
预测控制中比较常见的三种算法是模型算法控制(MAC),动态矩阵控制(DMC)以及广义预测控制。
本篇所采用的是动态矩阵控制,其采用增量算法,因此在消除稳态余差方面非常有效。
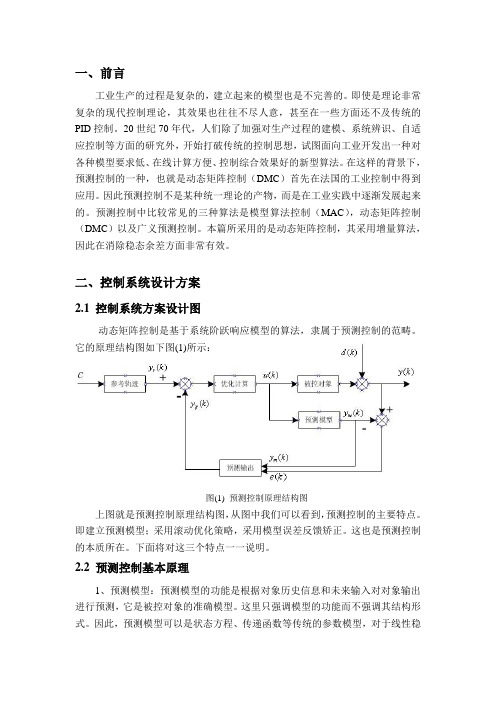
二、控制系统设计方案2.1 控制系统方案设计图动态矩阵控制是基于系统阶跃响应模型的算法,隶属于预测控制的范畴。
它的原理结构图如下图(1)所示:图(1) 预测控制原理结构图上图就是预测控制原理结构图,从图中我们可以看到,预测控制的主要特点。
即建立预测模型;采用滚动优化策略,采用模型误差反馈矫正。
这也是预测控制的本质所在。
下面将对这三个特点一一说明。
2.2 预测控制基本原理1、预测模型:预测模型的功能是根据对象历史信息和未来输入对对象输出进行预测,它是被控对象的准确模型。
这里只强调模型的功能而不强调其结构形式。
因此,预测模型可以是状态方程、传递函数等传统的参数模型,对于线性稳定对象,阶跃响应、脉冲响应这类非参数模型也可以作为预测模型使用。
预测模型具有展示系统未来动态行为的功能,这样,就可以利用预测模型来预测未来时刻被控对象的输出变化及被控变量与其给定值的偏差,作为控制作用的依据,使之适应动态系统所具有的因果性的特点,得到比常规控制更好的控制效果。
2、滚动优化:预测控制是一种优化控制算法,它是通过某一性能指标的最优来确定未来的控制作用。
这一性能指标涉及到系统未来的行为。
模型预测控制及其MATLAB实现

a u (k j i) a
i
p 1
p
u ( k j p )
( j 1,2, , n)
i
p
( j 1,2, , n)
p 1 i 1 a1 y y ˆ ( k 2) a 2 ˆ ( k n) a n y u (k ) y 0 (k 1) u (k 1) y (k 2) a1 0 a n 1 a1 u (k n 1) y 0 (k n)
ˆ ( k 1) e( k 1) y ( k 1) y
并用此误差加权后修正对未来其它时刻的预测 ~ ˆ he(k 1) Yp Y 即 (7-14) p ~ ~ ~ y ( k p )]T 为t=(k+1)T时刻经误差 式中 Y [ y (k 1), y (k 2), , ~ h [h1 , h2 , , h p ]T 校正后所预测的t=(k+1)T时刻的系统输出; h1 1 。 为误差校正矢量,
2015/11/11
第三篇 模型预测控制 及其MATLAB实现
1
第7章 预测控制理论
7.1 7.2 7.3
动态矩阵控制理论 广义预测控制理论 预测控制理论分析
模型预测控制(Model Predictive Control:MPC) 是20世纪80年代初开始发展起来的一类新型计算机控 制算法。该算法直接产生于工业过程控制的实际应用, 并在与工业应用的紧密结合中不断完善和成熟。模型 预测控制算法由于采用了多步预测、滚动优化和反馈 校正等控制策略,因而具有控制效果好、鲁棒性强、 对模型精确性要求不高的优点。
MATLAB预测控制仿真发布系统设计

文章编 号: I 7 10 )
G = ( ) ,输 入 控 制 参 数 P 5 = 0, M= , y = 1 , 1 wt [ l 本 文 主 要 应 用 { 种 典 型 预 测 控 制 算 法 , 即 动 态 矩 阵 控 制 u t[ w =] ,得 到 图22 .。 f DMC 、模 型算 法 控 制 ( C及 状 态 空 间模 型 预测 控 制 ,对 单 输 入 ) MA ) 单 输 出线 性 系 统 仿 真 分 析 对 比 。首 先 在 MAT AB 境 中开 发 模 型 L 环 算法控 I(  ̄ MAC的 通 用 工 具 箱 ,其 次 ,调 用 动态 矩 阵 控 制 ( ] i ) DMC ) 和 状 态 空 问模 型预 测 控 制 现 用 的控 制 工 具 箱 ,利 用Acie I t X4 v ] 技 术 ,基 于VB 软 件 实 现 了预 测 控 制算 法 在 Pw ro t 的发 布 ,通 A o eP i 中 n 过该发布系统 ,仿真发 布了典型预测控制算法 的控 制效果 ,展示 了各 预测 算 法 的特 点 。
G(
为例仿真发布该算法特点 。 选 取 合 适 的 参 数 ,P 5 ,M= , y t[] l t[,即可 得 到 =0 I w =1,l =】 W 比较好 的控制效果 ,其通过该发布系统发布效果如图2 所示 。 . 3
图 21 阶 系统 加 干 扰发 布 .二 由 图 21 知 ,MAC 法 对 于 阶 跃 干 扰 具 有 较 强 的 抗 干 扰 .可 算 性 ,能 够快 速 消 除 干扰 到达 设 定 值 ,并趋 于稳 定 。 22动 态矩 阵控 制f . DMC 仿 真 发布 ) DMC 法 可 以 直 接 利 用 MA AB自带 的 模 型 预 测 控 制 箱 即 算 TL 图 23 阶 系统 仿 真 发 布 .二 可。 由 图23 知 ,此 时 的 控 制参 数 为最 优 参 数 ,响 应 快 速 ,不 存 .可 以高阶系统的仿真发布为例 在稳态余差 ,体现 了比较好的鲁棒性。 在 发 布 系 统 的 界 面 上 输 入 合 适 的参 数 ,对 于 二 阶 系 统 :
控制系统Matlab计算与仿真

14
二、控制系统Matlab仿真基础
1.控制系统在Matlab中的描述
(②3)方环框节图并模联型化化简简 多个环节相并联的连接形式也是控制系统最基本的组
成结构形式之一。
G1(s) +
R(s)
C(s)
Matlab中用函数命令parallel()来G2实(s)现并联+ 化简。其调用格式为:
26
二、 控制系统Matlab仿真基础
3.系统频频域域分分析析法是控制系统研究中应用频率特性来分析系统 性能:稳定性、快速性和稳态精度的方法。此法不必直接求 解系统的微分方程,而是间接地运用系统开环频率特性曲线 分析闭环系统的响应。
Matlab中提供了相应绘制频率特性曲线的命令函数。 (1) nyquist曲线图 调用格式为: Nyquist(sys) 得到连续系统的极坐标图。 Dnyquist(num,den,Ts) Dnyquist(a,b,c,d,Ts) 得到关于离散系统的极坐标图。
Zero/pole/gain:
2 (s+3) -----------------s (s+1) (s+2)
11
二、控制系统Matlab仿真基础
例3 已知某控制系统的传递函数为
G(s)s2
1
,
3s2
求Matlab描述的传递函数模型及零极点增益模型。
解:num=[0 0 1];
den=[1 3 2];
1993年推出了其windows平台下的微机版,现在比较 新的版本是r2012a版
3
一、Matlab简介
2. Matlab语言特点
Matlab以复数矩阵为最基本的运算单元,既可以对它整 体地进行处理,也可以对它的某个或某些元素进行单独 地处理。在Matlab中,数据的存储/输入/输出都是以矩 阵为基础的,矩阵和其它变量不需要预先定义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
动态矩阵控制算法实验报告院系:电子信学院姓名:***学号:*********专业:控制理论与控制工程导师:***MATLAB环境下动态矩阵控制实验一、实验目的:对于带有纯滞后、大惯性的研究对象,通过动态控制矩阵的MATLAB的直接处理与仿真实验,具有较强的鲁棒性和良好的跟踪性。
输入已知的控制模型,通过对参数的选择,来取的良好的控制效果。
二、实验原理:动态矩阵控制算法是一种基于被控对象非参数数学模型的控制算法,它是一种基于被控对象阶跃响应的预测控制算法,以对象的阶跃响应离散系统为模型,避免了系统的辨识,采用多步预估技术,解决时延问题,并按照预估输出与给定值偏差最小的二次性能指标实施控制,它适用于渐进稳定的线性对象,系统动态特性中存在非最小相位特性或纯滞后都不影响算法的直接使用。
三、实验环境:计算机MATLAB2016b四、实验步骤:影响控制效果的主要参数有:1)采样周期T与模型长度N在DMC中采样周期T与模型长度N的选择需要满足香农定理和被控对象的类型及其动态特性的要求,通常需要NT后的阶跃响应输出值接近稳定值。
2)预测时域长度PP对系统的快速性和稳定性具有重要影响。
为使滚动优化有意义,应使P包含对象的主要动态部分,P越小,快速性提高,稳定性变差;反之,P越大,系统实时性降低,系统响应过于缓慢。
3)控制时域长度MM控制未来控制量的改变数目,及优化变量的个数,在P确定的情况下,M 越小,越难保证输出在各采样点紧密跟踪期望输出值,系统响应速度缓慢,可获得较好的鲁棒性,M越大,控制机动性越强,改善系统的动态性能,但是稳定性会变差。
五、实例仿真(一)算法实现设GP(s)=e-80s/(60s+1),采用DMC后的动态特性如图1所示,采样周期T=20s,优化时域P=10,M=2,建模时域N=20。
MATLAB程序1:g=poly2tfd(1,[60 1],0,80);%通用传函转换为MPC模型delt=20; %采样周期nt=1; %输出稳定性向量tfinal=1000; %截断时间model=tfd2step(tfinal,delt,nt,g);%传函转换为阶跃响应模型plant=model;%进行模型预测控制器设计p=10;m=2;ywt=[];uwt=1;%设置输入约束和参考轨迹等控制器参数kmpc=mpccon(plant,ywt,uwt,m,p);%模型预测控制器增益矩阵计算tend=1000;r=1;%仿真时间[y,u,yrn]=mpcsim(plant,model,kmpc,tend,r);%模型预测控制仿真t=0:20:1000;%定义自变量t的取值数组plot(t,y)xlabel(‘图一DMC控制动态响应曲线(time/s)’);ylabel(‘响应曲线’);结果如下:Percent error in the last step response coefficientof output yi for input uj is :2.2e-05%Time remaining 1000/1000Time remaining 800/1000Time remaining 600/1000Time remaining 400/1000Time remaining 200/1000Time remaining 0/1000Simulation time is 0.003 seconds.结论:采用DMC后系统调整时间减小,响应的快速性好,无超调。
二、P和M对系统性能的影响1、P对系统性能的影响P表示我们对K时刻起未来多少步的输出逼近期望值感兴趣,T=20,p=6,10,20时的响应曲线。
Matlab程序2:g=poly2tfd(1,[60 1],0,80);%通用传函转换为MPC模型delt=20; %采样周期nt=1; %输出稳定性向量tfinal=1000; %截断时间model=tfd2step(tfinal,delt,nt,g);%传函转换为阶跃响应模型plant=model;%进行模型预测控制器设计p1=6;p2=10;p3=20;%优化时域m=2;%控制时域ywt=[];uwt=1;%设置输入约束和参考轨迹等控制器参数kmpc1=mpccon(plant,ywt,uwt,m,p1);%模型预测控制器增益矩阵计算kmpc2=mpccon(plant,ywt,uwt,m,p2);kmpc3=mpccon(plant,ywt,uwt,m,p3);tend=1000;r=1;%仿真时间[y1,u,yrn]=mpcsim(plant,model,kmpc1,tend,r);%模型预测控制仿真[y2,u,yrn]=mpcsim(plant,model,kmpc2,tend,r);[y3,u,yrn]=mpcsim(plant,model,kmpc3,tend,r);t=0:20:1000;%定义自变量t的取值数组plot(t,y1,t,y2,t,y3)legend('1-p=6,2-p=10,3-p=20');xlabel('图二p不同对系统性能的影响(time/s)');ylabel(‘响应曲线’);结果l:Percent error in the last step response coefficientof output yi for input uj is :2.2e-05%Time remaining 1000/1000Time remaining 800/1000Time remaining 600/1000Time remaining 400/1000Time remaining 200/1000Time remaining 0/1000Simulation time is 0.003 seconds.Time remaining 1000/1000Time remaining 800/1000Time remaining 600/1000Time remaining 400/1000Time remaining 200/1000Time remaining 0/1000Simulation time is 0.003 seconds.Time remaining 1000/1000Time remaining 800/1000Time remaining 600/1000Time remaining 400/1000Time remaining 200/1000Time remaining 0/1000Simulation time is 0.002 seconds.>>结论:p越大,系统的快速性变差,系统稳定性增强,减小p,系统快速性变好,系统稳定性变差。
2.M对系统的影响T=20,P=20 N=20 m=4、2、1 时的控制规律MATLAB程序3:g=poly2tfd(1,[60 1],0,80);%通用传函转换为MPC模型delt=20; %采样周期nt=1; %输出稳定性向量tfinal=1000; %截断时间model=tfd2step(tfinal,delt,nt,g);%传函转换为阶跃响应模型plant=model;%进行模型预测控制器设计p=20;m1=4;m2=2;m3=1;ywt=[];uwt=1;%设置输入约束和参考轨迹等控制器参数kmpc1=mpccon(plant,ywt,uwt,m,p1);%模型预测控制器增益矩阵计算kmpc2=mpccon(plant,ywt,uwt,m,p2);kmpc3=mpccon(plant,ywt,uwt,m,p3);tend=1000;r=1;%仿真时间[y1,u,yrn]=mpcsim(plant,model,kmpc1,tend,r);%模型预测控制仿真[y2,u,yrn]=mpcsim(plant,model,kmpc2,tend,r);[y3,u,yrn]=mpcsim(plant,model,kmpc3,tend,r);t=0:20:1000;%定义自变量t的取值数组plot(t,y1,t,y2,t,y3)legend('1-m=4,2-m=2,3-m=1');xlabel('图二p不同对系统性能的影响(time/s)');ylabel(‘响应曲线’);结果;Percent error in the last step response coefficientof output yi for input uj is :2.2e-05%Time remaining 1000/1000Time remaining 800/1000Time remaining 600/1000Time remaining 400/1000Time remaining 200/1000Time remaining 0/1000 Simulation time is 0.003 seconds. Time remaining 1000/1000 Time remaining 800/1000 Time remaining 600/1000 Time remaining 400/1000 Time remaining 200/1000 Time remaining 0/1000 Simulation time is 0.003 seconds. Time remaining 1000/1000 Time remaining 800/1000 Time remaining 600/1000 Time remaining 400/1000 Time remaining 200/1000 Time remaining 0/1000 Simulation time is 0.002 seconds. >>三模型失配时的响应曲线模型失配时GM(s)GP(s),当GM(s)=2e-50s/(40s+1)时的响应曲线,为图4所示Matlab程序4:g1=poly2tfd(1,[60 1],0,80);%通用传函转换为MPC模型g2=poly2tfd(2,[40 1],0,50);delt=20; %采样周期nt=1; %输出稳定性向量tfinal=1000; %截断时间model1=tfd2step(tfinal,delt,nt,g1);%传函转换为阶跃响应模型model2=tfd2step(tfinal,delt,nt,g2);plant1=model1;%进行模型预测控制器设计plant2=model2;p=10;m=2;ywt=[];uwt=1;%设置输入约束和参考轨迹等控制器参数kmpc1=mpccon(plant1,ywt,uwt,m,p);%模型预测控制器增益矩阵计算kmpc2=mpccon(plant2,ywt,uwt,m,p);tend=1000;r=1;%仿真时间[y1,u,yrn]=mpcsim(plant1,model1,kmpc1,tend,r);%模型预测控制仿真[y2,u,yrn]=mpcsim(plant2,model2,kmpc2,tend,r);t=0:20:1000;%定义自变量t的取值数组plot(t,y1,t,y2,)legend('1-模型未失配,2-模型未失配');xlabel('图四模型失配响应曲线(time/s)');ylabel(‘响应曲线’);结果分析:Percent error in the last step response coefficientof output yi for input uj is :2.2e-05%Percent error in the last step response coefficient of output yi for input uj is :4.8e-09%Time remaining 1000/1000Time remaining 800/1000Time remaining 600/1000Time remaining 400/1000Time remaining 200/1000Time remaining 0/1000Simulation time is 0.004 seconds.Time remaining 1000/1000Time remaining 800/1000Time remaining 600/1000Time remaining 400/1000Time remaining 200/1000Time remaining 0/1000Simulation time is 0.002 seconds.。
