平行四边形的存在性问题解题策略
也谈平面直角坐标系中平行四边形存在性问题的解题方法

也谈平面直角坐标系中平行四边形存在性问题的解
题方法
平面向量是在二维平面内既有方向又有大小的量,物理学中也称作矢量,与之相对的是只有大小、没有方向的数量。
平面向量用a,b,c上面加一个小箭头表示,也可以用表示向量的有向线段的起点和终点字母表示。
笔者初三,莫挑刺。
存在性问题,一般在函数中有所体现,通常表现为,在任意直角坐标系中的函数内,存在某四点可以使其能构成一个矩形,菱形,正方形。
并对四点其中某些点有所限制,常驻于压轴题内,所以看起来其对部分初中生及其不友好,今天,平面向量将会解决这个问题。
对于向量,我们不再进行赘述,直接上例子
四川成都龙泉驿区期中
A(1,3) B(3,1) k=3
在这里,不妨设M(t,0) N(c, \frac{3}{c} ) 当以AB ,MN为两短边时。
\bar{AB}= (-2,2)因为在平行四边形中,向量AB能与向量MN完全重合,所以\bar{MN}= \bar{AB} (不规范的写法<?)
所以-2=t-c ,-\frac{3}{c} =2 所以c= -\frac{3}{2} t= -\frac{7}{2}
N点坐标呼之欲出,用向量可以简单方便的算出,且省去了多数计算,避免了计算失误(<?如果你的计算不如小学生的话。
)(此处仅算出了一种情况)
1
在此基础上,我们可以对矩形及正方形进行分析,易发现,仅需再次进行对斜率的讨论即可。
证毕!
2。
二次函数背景下的平行四边形存在性问题解题策略

133美眉 2022.09下教研与美育教学研究二次函数背景下的平行四边形存在性问题解题策略杨 柳(遵义市第一初级中学,贵州 遵义 563000)二次函数背景下的存在性问题一直都是中考数学里高频率题型。
这类试题的综合性较强,对分析问题和解决问题的能力要求较高,是中考数学中的重点和难点问题。
平行四边形存在性问题是典型题型,也是讨论特殊平行四边形的存在性问题的基础。
它将分类讨论思想、数形结合思想、方程思想,以及平行四边形的性质和判定方法相结合,需要综合分析后解决问题。
利用平行四边形的判定方法进行判断,此类问题的解题方法有两种:一是几何法,二是代数法。
一、平行四边形存在性问题之几何法:根据题目背景找到图形的特点,确定等量关系求解(一)解题步骤:1.分类;2.画图;3.找到等量关系求解。
(二)分类:三定一动、两定两动A、两定两动B、两定两动C。
(三)解题分析:1.三定一动类问题:【类型分析】三个定点的坐标是确定的;一个动点的坐标不确定。
【解题策略】①命名分类;②分类画出图形;③利用平移法求出动点的坐标。
【例题解析】如图,抛物线,经过点A (﹣3,0)、B (1,0)、C(0,3)。
在抛物线所在的平面内,是否存在点D,使得以A、B、C、D 为顶点的四边形为平行四边形,求出点D 的坐标。
解:由题意可得:A(﹣3,0)、B(1,0)、C(0,3)①平行四边形ADBC,如图1;摘 要:二次函数背景下的平行四边形存在性问题是中考数学中综合性较强的考题,本文针对这类问题解题策略从几何法和代数法两个方面进行了介绍,通过类型分析、解题策略、例题详解等几个方面,帮助学生解决难点问题。
关键词:二次函数;平行四边形;存在性134教研与美育美眉 2022.09下教学研究点C(0,3)——点B(1,0),点A(﹣3,0)——点D (-2,-3)②平行四边形ABDC,如图2:点A(﹣3,0)——点B(1,0),点C(0,3)——点D(4,3)③平行四边形ABCD,如图3;点B(1,0)——点A(﹣3,0),点C(0,3)——点D(-4,3)综上所述,点D(-2,-3)、(4,3)、(-4,3)时,以A、B、C、D为顶点的四边形为平行四边形。
平行四边形存在性问题
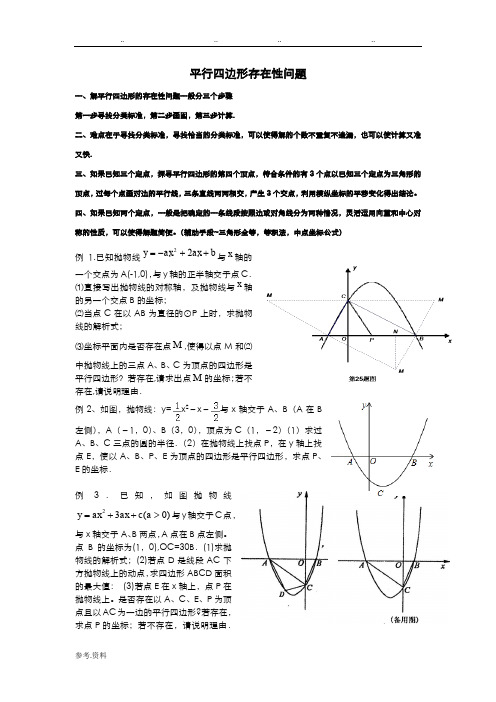
平行四边形存在性问题一、解平行四边形的存在性问题一般分三个步骤 第一步寻找分类标准,第二步画图,第三步计算.二、难点在于寻找分类标准,寻找恰当的分类标准,可以使得解的个数不重复不遗漏,也可以使计算又准又快.三、如果已知三个定点,探寻平行四边形的第四个顶点,符合条件的有3个点以已知三个定点为三角形的顶点,过每个点画对边的平行线,三条直线两两相交,产生3个交点,利用横纵坐标的平移变化得出结论。
四、如果已知两个定点,一般是把确定的一条线段按照边或对角线分为两种情况,灵活运用向量和中心对称的性质,可以使得解题简便。
(辅助手段~三角形全等,等积法,中点坐标公式)例1.已知抛物线b ax ax y ++-=22与x 轴的一个交点为A(-1,0),与y 轴的正半轴交于点C .⑴直接写出抛物线的对称轴,及抛物线与x 轴的另一个交点B 的坐标;⑵当点C 在以AB 为直径的⊙P 上时,求抛物线的解析式;⑶坐标平面内是否存在点M ,使得以点M 和⑵中抛物线上的三点A 、B 、C 为顶点的四边形是平行四边形?若存在,请求出点M 的坐标;若不存在,请说明理由.例2、如图,抛物线:y=x 2﹣x ﹣与x 轴交于A 、B (A 在B左侧),A (﹣1,0)、B (3,0),顶点为C (1,﹣2)(1)求过A 、B 、C 三点的圆的半径.(2)在抛物线上找点P ,在y 轴上找点E ,使以A 、B 、P 、E 为顶点的四边形是平行四边形,求点P 、E 的坐标.例3.已知,如图抛物线23(0)y ax ax c a =++>与y 轴交于C 点,与x 轴交于A 、B 两点,A 点在B 点左侧。
点B 的坐标为(1,0),OC=30B .(1)求抛物线的解析式;(2)若点D 是线段AC 下方抛物线上的动点,求四边形ABCD 面积的最大值: (3)若点E 在x 轴上,点P 在抛物线上。
是否存在以A 、C 、E 、P 为顶点且以AC 为一边的平行四边形?若存在,求点P 的坐标;若不存在,请说明理由.例4.已知抛物线:x x y 22121+-= (1)求抛物线1y 的顶点坐标.(2)将抛物线1y 向右平移2个单位,再向上平移1个单位,得到抛物线2y ,求抛物线2y 的解析式.(3)如下图,抛物线2y 的顶点为P ,x 轴上有一动点M ,在1y 、2y 这两条抛物线上是否存在点N ,使O (原点)、P 、M 、N 四点构成以OP 为一边的平行四边形,若存在,求出N 点的坐标;若不存在,请说明理由.例5.如图,抛物线223y x x =--与x 轴交A 、B 两点(A点在B 点左侧),直线l 与抛物线交于A 、C 两点,其中C 点的横坐标为2.(1)求A 、B 两点的坐标及直线AC 的函数表达式;(2)P 是线段AC 上的一个动点,过P 点作y 轴的平行线交抛物线于E 点,求线段PE 长度的最大值; (3)点G 抛物线上的动点,在x 轴上是否存在点F ,使A 、C 、F 、G 这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F 点坐标;如果不存在,请说明理由.练习1、已知抛物线 c bx ax y ++=2经过A (-3,0),B(1,0),C(0,3)三点.(1)求抛物线的解析式;(2)P 为抛物线的顶点,M 为坐标平面内的点,若以A,C,P,M 为顶点的四边形为平行四边形,求点M 的坐标.2、在平面直角坐标系中,已知抛物线经过A )0,4(-,B )4,0(-,C )0,2(三点.(1)求抛物线的解析式;(2)若点M 为第三象限内抛物线上一动点,点M 的横坐标为m ,△AMB 的面积为S .求S 关于m 的函数关系式,并求出S 的最大值. (3)若点P 是抛物线上的动点,点Q 是直线x y -=上的动点,判断有几个位置能够使得点P 、Q 、B 、O 为顶点的四边形为平行四边形,直接写出相应的点Q 的坐标.2的⊙C与x轴3、如图,在平面直角坐标系中,半径为5交于点A(-1,0),B(3,0)两点,且点C在x轴的上方.(1)求圆心C的坐标;(2)已知一个二次函数的图象经过点A,B,C,求这个二次函数的解析式;(3)设点P在y轴上,点M在(2)的二次函数图象上,如果以点P,M,A,B为顶点的四边形是平行四边形,请你直接写出点M的坐标.4、已知二次函数图象的顶点坐标为M(1,0),直线y=x+m与该二次函数的图象交于A,B两点,其中A点的坐标为(3,4),B点在y轴上.(1)求m的值及这个二次函数的解析式;(2)在x轴上找一点Q,使△QAB的周长最小,并求出此时Q点坐标;(3)若P(a,0)是x轴上的一个动点,过P作x轴的垂线分别与直线AB和二次函数的图象交于D、E两点.①设线段DE的长为h,当0<a<3时,求h与a之间的函数关系式;②若直线AB与抛物线的对称轴交点为N,问是否存在一点P,使以M、N、D、E为顶点的四边形是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由.5.如图,已知抛物线y=-x2-2x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,顶点为P.若以A、C、P、M为顶点的四边形是平行四边形,求点M的坐标.6、如图1,在平面直角坐标系中,抛物线y=ax2+bx-3a经过A(-1,0)、B(0,3)两点,与x轴交于另一点C,顶点为D.(1)求该抛物线的解析式及点C、D的坐标;(2)经过点B、D两点的直线与x轴交于点E,若点F是抛物线上一点,以A、B、E、F 为顶点的四边形是平行四边形,求点F的坐标;(3)如图2,P(2,3)是抛物线上的点,Q是直线AP上方的抛物线上一动点,求△APQ 的最大面积和此时Q点的坐标.7、已知平面直角坐标系xOy (如图),一次函数334y x =+的图像与y 轴交于点A ,点M在正比例函数32y x =的图像上,且MO =MA .二次函数y =x 2+bx +c 的图像经过点A 、M . (1)求线段AM 的长; (2)求这个二次函数的解析式;(3)如果点B 在y 轴上,且位于点A 下方,点C 在上述二次函数的图像上,点D 在一次函数334y x =+的图像上,且四边形ABCD 是菱形,求点C 的坐标.8.如图,在平面直角坐标系xOy 中,△ABC 的A 、B 两个顶点在x 轴上,顶点C 在y 轴的负半轴上.已知|OA |∶|OB |=1∶5,|OB |=|OC |,△ABC 的面积S △ABC =15,抛物线y =ax 2+bx +c (a ≠0)经过A 、B 、C 三点. (1)求此抛物线的函数表达式;(2)设E 是y 轴右侧抛物线上异于点B 的一个动点,过点E 作x 轴的平行线交抛物线于另一点F ,过点F 作FG 垂直于x 轴于点G ,再过点E 作EH 垂直于x 轴于点H ,得到矩形EFGH .则在点E 的运动过程中,当矩形EFGH 为正方形时,求出该正方形的边长;(3)在抛物线上是否存在异于B 、C 的点M ,使△MBC 中BC 边上的高为求出点M 的坐标;若不存在,请说明理由.9、将抛物线c1:2y =x 轴翻折,得到抛物线c 2,如图所示.现将抛物线c 1向左平移m 个单位长度,平移后得到新抛物线的顶点为M ,与x 轴的交点从左到右依次为A 、B ;将抛物线c 2向右也平移m 个单位长度,平移后得到新抛物线的顶点为N ,与x 轴的交点从左到右依次为D 、E .在平移过程中,是否存在以点A 、N 、E 、M 为顶点的四边形是矩形的情形?若存在,请求出此时m 的值;若不存在,请说明理由.。
(完整版)压轴题解题策略:平行四边形的存在性问题

中考数学压轴题解题策略平行四边形的存在性问题解题策略2015年9月13日星期日专题攻略解平行四边形的存在性问题一般分三步:第一步寻找分类标准,第二步画图,第三步计算.难点在于寻找分类标准,分类标准寻找的恰当,可以使解的个数不重复不遗漏,也可以使计算又好又快.如果已知三个定点,探寻平行四边形的第四个顶点,符合条件的有3个点:以已知三个定点为三角形的顶点,过每个点画对边的平行线,三条直线两两相交,产生3个交点.如果已知两个定点,一般是把确定的一条线段按照边或对角线分为两种情况.根据平行四边形的对边平行且相等,灵活运用坐标平移,可以使得计算过程简便.根据平行四边形的中心对称的性质,灵活运用坐标对称,可以使得解题简便.例题解析例❶如图1-1,在平面直角坐标系中,已知抛物线y=-x2-2x+3与x轴交于A、B两点(A在B的左侧),与y轴交于点C,顶点为P,如果以点P、A、C、D为顶点的四边形是平行四边形,求点D的坐标.图1-1【解析】P、A、C三点是确定的,过△P AC的三个顶点分别画对边的平行线,三条直线两两相交,产生3个符合条件的点D(如图1-2).由y=-x2-2x+3=-(x+1)2+4,得A(-3,0),C(0, 3),P(-1, 4).由于A(-3,0)33右,上D1(2, 7).右,上C(0, 3),所以P(-1, 4)33由于C(0, 3)33下,左D2(-4, 1).下,左A(-3,0),所以P(-1, 4)33由于P(-1, 4)11右,下C(0, 3),所以A(-3,0)11右,下D3(-2, -1).我们看到,用坐标平移的方法,远比用解析式构造方程组求交点方便多了.图1-2例❷如图2-1,在平面直角坐标系中,已知抛物线y=-x2+2x+3与x轴交于A、B两点,点M在这条抛物线上,点P在y轴上,如果以点P、M、A、B为顶点的四边形是平行四边形,求点M的坐标.图2-1【解析】在P、M、A、B四个点中,A、B是确定的,以AB为分类标准.由y=-x2+2x+3=-(x+1)(x-3),得A(-1,0),B(3,0).①如图2-2,当AB是平行四边形的对角线时,PM与AB互相平分,因此点M与点P 关于AB的中点(1,0)对称,所以点M的横坐标为2.此时M(2,3).②如图2-3,图2-4,当AB是平行四边形的边时,PM//AB,PM=AB=4.所以点M的横坐标为4或-4.所以M (4,-5)或(-4,-21).我们看到,因为点P的横坐标是确定的,在解图2-2时,根据对称性先确定了点M的横坐标;在解图2-3和图2-4时,根据平移先确定了点M的横坐标.图2-2 图2-3 图2-4 例❸如图3-1,在平面直角坐标系中,直线y=-x+4与x轴交于点A,与y轴交于点B,点C在直线AB上,在平面直角坐标系中求一点D,使得以O、A、C、D为顶点的四边形是菱形.图3-1【解析】由y =-x +4,得A (4, 0),直线AB 与坐标轴的夹角为45°.在O 、A 、C 、D 四个点中,O 、A 是确定的,以线段OA 为分类标准.如图3-2,如果OA 是菱形的对角线,那么点C 在OA 的垂直平分线上,点C (2,2)关于OA 的对称点D 的坐标为(2,-2).如果OA 是菱形的边,那么又存在两种情况:如图3-3,以O 为圆心,OA 为半径的圆与直线AB 的交点恰好为点B (0, 4),那么正方形AOCD 的顶点D 的坐标为(4, 4).如图3-4,以A 为圆心,AO 为半径的圆与直线AB 有两个交点C (422,22)-和C ′(422,22)+-,点C 和C ′向左平移4个单位得到点D (22,22)-和D ′(22,22)-.图3-2 图3-3 图3-4例❹ 如图4-1,已知抛物线241633y x x =+与x 轴的负半轴交于点C ,点E 的坐标为(0,-3),点N 在抛物线的对称轴上,点M 在抛物线上,是否存在这样的点M 、N ,使得以M 、N 、C 、E为顶点的四边形是平行四边形?若存在,请求出点M 的坐标;若不存在,请说明理由.图4-1【解析】C (-4,0)、E (0,-3)两点是确定的,点N 的横坐标-2也是确定的.以CE 为分类标准,分两种情况讨论平行四边形:①如图4-2,当CE 为平行四边形的边时,由于C 、E 两点间的水平距离为4,所以M 、N 两点间的水平距离也为4,因此点M 的横坐标为-6或2.将x =-6和x =2分别代入抛物线的解析式,得M (-6,16)或(2, 16).②如图4-3,当CE 为平行四边形的对角线时,M 为抛物线的顶点,所以M 16(2,)3--.图4-2 图4-3例❺如图1,在平面直角坐标系中,抛物线y=ax2-2ax-3a(a<0)与x轴交于A、B 两点(点A在点B的左侧),点D是第四象限内抛物线上的一点,直线AD与y轴负半轴交于点C,且CD=4AC.设P是抛物线的对称轴上的一点,点Q在抛物线上,以点A、D、P、Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由.图5-1【解析】由y=ax2-2ax-3a=a(x+1)(x-3),得A(-1, 0).由CD=4AC,得x D=4.所以D(4, 5a).已知A(-1, 0)、D(4, 5a),x P=1,以AD为分类标准,分两种情况讨论:①如图5-2,如果AD为矩形的边,我们根据AD//QP,AD=QP来两次平移坐标.由于A、D两点间的水平距离为5,所以点Q的横坐标为-4.所以Q(-4,21a).由于A、D两点间的竖直距离为-5a,所以点P的纵坐标为26a.所以P(1, 26a).根据矩形的对角线相等,得AP2=QD2.所以22+(26a)2=82+(16a)2.整理,得7a2=1.所以77a=-.此时P267(1)7-,.②如图5-3,如果AD为矩形的对角线,我们根据AP//QD,AP=QD来两次平移坐标.由于A、P两点间的水平距离为2,所以点Q的横坐标为2.所以Q(2,-3a).由于Q、D两点间的竖直距离为-8a,所以点P的纵坐标为8a.所以P(1, 8a).再根据AD2=PQ2,得52+(5a)2=12+(11a)2.整理,得4a2=1.所以12a=-.此时P(14)-,.我们从图形中可以看到,像“勾股图”那样构造矩形的外接矩形,使得外接矩形的边与坐标轴平行,那么线段的等量关系就可以转化为坐标间的关系.上面我们根据“对角线相等的平行四边形是矩形”列方程,还可以根据定义“有一个角是直角的平行四边形叫矩形”来列方程.如图5-2,如果∠ADP =90°,那么MA ND MD NP =;如图5-3,如果∠QAP =90°,那么GQ KA GA KP=.图5-2 图5-3例❻ 如图6-1,将抛物线c 1:233y x =-+沿x 轴翻折,得到抛物线c 2.现将抛物线c 1向左平移m 个单位长度,平移后得到新抛物线的顶点为M ,与x 轴的交点从左到右依次为A 、B ;将抛物线c 2向右也平移m 个单位长度,平移后得到新抛物线的顶点为N ,与x 轴的交点从左到右依次为D 、E .在平移过程中,是否存在以点A 、N 、E 、M 为顶点的四边形是矩形的情形?若存在,请求出此时m 的值;若不存在,请说明理由.图6-1【解析】没有人能精确画好抛物线,又怎么平移抛物线呢?我们去伪存真,将A 、B 、D 、E 、M 、N 六个点及它们的坐标在图中都标注出来(如图6-2),如果您看到了△MAB 和△NED 是边长为2的等边三角形,那么平移就简单了.如图6-3,在两个等边三角形平移的过程中,AM 与EN 保持平行且相等,所以四边形ANEM 保持平行四边形的形状,点O 为对称中心.【解法一】如果∠ANE =90°,根据30°角所对的直角边等于斜边的一半,可得AE =2EN =4.而AE =AO +OE =2AO ,所以AO =2.已知AB =2,此时B 、O 重合(如图6-4),所以m =BO =1.【解法二】如果对角线MN =AE ,那么OM =OA ,此时△MAO 是等边三角形.所以等边三角形MAB 与△MAO 重合.因此B 、O 重合,m =BO =1.【解法三】在平移的过程中,(1,0)A m --、(1,0)B m -,M (3)m -,根据OA 2=OM 2列方程(1+m )2=m 2+3.解得m =1.图6-2 图6-3 图6-4 例❼如图7-1,菱形ABCD的边长为4,∠B=60°,E、H分别是AB、CD的中点,E、G分别在AD、BC上,且AE=CG.(1)求证四边形EFGH是平行四边形;(2)当四边形EFGH是矩形时,求AE的长;(3)当四边形EFGH是菱形时,求AE的长.图7-1 【解析】(1)证明三角形全等得EF=GH和FG=HE大家最熟练了.(2)平行四边形EFGH的对角线FH=4是确定的,当EG=FH=4时,四边形EFGH 是矩形.以FH为直径画圆,你看看,这个圆与AD有几个交点,在哪里?如图7-2.如图7-3,当E为AD的中点时,四边形ABGE和四边形DCGE都是平行四边形.如图7-4,当E与A重合时,△ABG与△DCE都是等边三角形.(3)如果平行四边形EFGH的对角线EG与FH互相垂直,那么四边形EFGH是菱形.过FH的中点O画FH的垂线,EG就产生了.在Rt△AOE中,∠OAE=60°,AO=2,此时AE=1.又一次说明了如果会画图,答案就在图形中.图7-2 图7-3 图7-4 图7-5例❽如图8-1,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A(4, 0)、B(0, 3),点C的坐标为(0, m),过点C作CE⊥AB于点E,点D为x轴正半轴的一动点,且满足OD =2OC,连结DE,以DE、DA为边作平行四边形DEF A.(1)如果平行四边形DEF A为矩形,求m的值;(2)如果平行四边形DEF A为菱形,请直接写出m的值.图8-1【解析】这道题目我们着重讲解怎样画示意图.我们注意到,点A和直线AB(直线l)是确定的.如图8-2,先画x轴,点A和直线l.在直线l上取点E,以AE为对角线画矩形DEF A.如图8-3,过点E画直线l的垂线.画∠MDN,使得DN=2MN,MN⊥DN,产生点C.如图8-4,过点C画y轴,产生点O和点B.图8-2 图8-3 图8-4 您是否考虑到,画∠MDN时,还存在DM在x轴下方的情况?如图8-5.同样的,我们可以画如图8-6,如图8-7的两个菱形.图8-5 图8-6 图8-7。
平行四边形的存在性问题

平行四边形存在性问题【知识概括】确定平行四边形:对于A 、B 、C 三点固定,若存在点D 使得四边形ABCD 是平行四边形,则点D 只有一种情况,如图①;若存在点D 使得以A 、B 、C 、D 为顶点的四边形是平行四边形,则点D 有三种情况,如图②。
图 ① 图 ②【方法思路分析】一、必须明确以下情况:①、四边形ABCD 是平行四边形,AC 、BD 一定是对角线,即明确字母顺序,那么对角线就确定了;②、以A 、B 、C 、D 四个点为顶点的四边形是平行四边形,对角线不确定,则需要分类讨论。
二、有关解析法的知识:①两点之间的距离公式:若A ) ,(11y x ,B ) ,(22y x ,则|AB|=特别地,若AB ∥x 轴,则||AB = ,若AB ∥y 轴,则||AB = ②中点坐标公式:若A ) ,(11y x ,B ) ,(22y x ,则A 、B 的中点M 为 ③①ABCD①,设四个顶点坐标分别是) (A A y x A ,,) (B B y x B ,,) (C C y x C ,,) (D D y x D ,,则满足:【方法运用】一、三定一动,探究平行四边形存在性1、已知)3 ,1(A ,)4 ,6(B ,)6 ,4(C ,在坐标系内确定点D 使得以A 、B 、C 、D 四个点为顶点的四边形是平行四边形。
二、两定两动,探究平行四边形存在性2、已知)1 ,1(A 、)2 ,3(B ,点C 在x 轴上,点D 在y 轴上,且以A 、B 、C 、D 四个点为顶点的四边形是平行四边形,求D C 、的坐标。
【解题步骤要点总结】先由题目条件探索三点的坐标(若只有两个定点,可设一个动点的坐标). 再画出以三点为顶点的平行四边形,根据性质写出第四个顶点的坐标.最后根据题目的要求(动点在什么曲线上),判断平行四边形的存在性.三、拓展延伸已知A 为(0,3),B 为(4,2),点C 在x 轴上,D 是平面直角坐标系内一点,(1)若以A 、B 、C 、D 四点为顶点的四边形是矩形,求点D 的坐标。
利用平面向量解决平行四边形存在性问题

技法点拨题意;③当m ≥1时(如图6),只需f (1)<0,即-1-1<0恒成立,所以m ≥1;综上可知,m >-12。
图4图5图6解法二:将两个变量分离,由已知范围求未知范围。
由t ∈[0,1],1-t 2+2mt -2m -2<0,将t 与m 分开,得-t 2-1<2m (1-t ),当t =1时,上式显然成立;当t ∈[0,1),t -1∈[-1,0),从而2m >t 2+1t -1,令g (t )=t 2+1t -1,则只需2m >g (t )max ,对于g (t )max 用两种方法求得。
方法1:对勾函数的思路。
g (t )=t 2+1t -1=(t -1)2+2(t -1)+2t -1=(t -1)+2t -1+2,由对勾函数k (x )=x +2x可知,其在[-2,0)单调递减。
所以g (t )在t -1=-1取最大值为-1,所以2m >-1,即m >-12;方法2:函数求导。
g (t )=t 2+1t -1,g ′(t )=t 2-2t -1(t -1)2,在t ∈[0,1]时,t 2-2t -1<0,即g ′(t )<0,所以g (t )在t ∈[0,1]时单调递减,g (t )max =g (0)=-1,所以2m >-1,即m >-12;解法三:将已知不等式分离成两个函数,通过数形结合,找到参数范围。
由t ∈[0,1],1-t 2+2mt -2m -2<0,得到2m (t -1)<t 2+1,分离出两个函数,令p (t )=2m (t -1),q (t )=t 2+1,画出两个函数在t ∈[0,1]的图象。
如下图。
图7图8图9图7很明显满足题意,此时q (t )函数图象恒在p (t )图象上方,临界值是直线过(0,1)(如图8),此时直线斜率为-1,即2m =-1,m =-12,所以综合知-12<m ≤0;当直线斜率大于0后,如图9所示,也是显然成立,所以m >0成立;综合可知-12<m 。
巧解二次函数中平行四边形存在性问题

图 2 图 3 图1 巧解二次函数中平行四边形存在性问题以二次函数为载体的平行四边形存在性问题是近年来中考的热点,其图形复杂,知识覆盖面广,综合性较强,对学生分析问题和解决问题的能力要求高.对这类题,常规解法是先画出平行四边形,再依据“平行四边形的一组对边平行且相等”或“平行四边形的对角线互相平分”来解决.由于先要画出草图,若考虑不周,很容易漏解.为此,借助探究平行四边形顶点坐标公式来解决这一类题.1 两个结论,解题的切入点数学课标,现行初中数学教材中没有线段的中点坐标公式,也没有平行四边形的顶点坐标公式,我们可帮助学生来探究,这可作为解题的切入点。
1.1 线段中点坐标公式平面直角坐标系中,点A 坐标为(x 1,y 1),点B 坐标为(x 2,y 2),则线段AB 的中点坐标为(221x x +,221y y +). 证明 : 如图1,设AB 中点P 的坐标为(x P ,y P ).由x P -x 1=x 2-x P ,得x P =221x x +,同理y P =221y y +,所以线段AB 的中点坐标为(221x x +,221y y +).1.2 平行四边形顶点坐标公式 □ABCD 的顶点坐标分别为A (x A ,y A )、B (x B ,y B )、C (x C ,y C )、D (x D ,y D ),则:x A +x C =x B +x D ;y A +y C =y B +y D .证明: 如图2,连接AC 、BD ,相交于点E .∵点E 为AC 的中点,∴E 点坐标为(2C A x x +,2C A y y +). 又∵点E 为BD 的中点, ∴E 点坐标为(2D B x x +,2D B y y +). ∴x A +x C =x B +x D ;y A +y C =y B +y D .即平行四边形对角线两端点的横坐标、纵坐标之和分别相等.2 一个基本事实,解题的预备知识如图3,已知不在同一直线上的三点A 、B 、C ,在平面内另找一个点D ,使以A 、B 、C 、D 为顶点的四边形是平行四边形.答案有三种:以AB 为对角线的□ACBD 1,以AC 为对角线的□ABCD 2,以BC 为对角线的□ABD 3C .3 两类存在性问题解题策略例析与反思3.1 三个定点、一个动点,探究平行四边形的存在性问题图4例1 已知抛物线y=x 2-2x+a (a <0)与y 轴相交于点A ,顶点为M .直线y=21x-a 分别与x 轴、y 轴相交于B 、C 两点,并且与直线AM 相交于点N .(1)填空:试用含a 的代数式分别表示点M 与N 的坐标,则M ( ), N ( );(2)如图4,将△NAC 沿y 轴翻折,若点N 的对应点N ′恰好落在抛物线上,AN ′与x 轴交于点D ,连接CD ,求a 的值和四边形ADCN 的面积;(3)在抛物线y=x 2-2x+a (a <0)上是否存在一点P ,使得以P 、A 、C 、N 为顶点的四边形是平行四边形?若存在,求出点P 的坐标;若不存在,试说明理由.解:(1)M (1,a-1),N (a 34,-a 31);(2)a=-49;S 四边形ADCN =16189; (3)由已知条件易得A (0,a )、C (0,-a )、N (a 34,-a 31).设P (m ,m 2-2m +a ). ①当以AC 为对角线时,由平行四边形顶点坐标公式(解题时熟练推导出),得:⎪⎪⎩⎪⎪⎨⎧+-+-=-+=+a m m a a a m a 23134002,∴⎪⎪⎩⎪⎪⎨⎧-==81525a m . ∴P 1(25,-85); ②当以AN 为对角线时,得:⎪⎪⎩⎪⎪⎨⎧+-+-=-+=+a m m a a a m a 23103402,∴⎪⎪⎩⎪⎪⎨⎧==81525a m (不合题意,舍去). ③当以CN 为对角线时,得:⎪⎪⎩⎪⎪⎨⎧+-+=--+=+a m m a a a m a 23103402,∴⎪⎪⎩⎪⎪⎨⎧-=-=8321a m . ∴P 2(-21,87). ∴在抛物线上存在点P 1(25,-85)和P 2(-21,87),使得以P 、A 、C 、N 为顶点的四边形是平行四边形.反思:已知三个定点的坐标,可设出抛物线上第四个顶点的坐标,运用平行四边形顶点坐标公式列方程(组)求解.这种题型由于三个定点构成的三条线段中哪条为对角线不清楚,往往要以这三条线段分别为对角线分类,分三种情况讨论.图53.2 两个定点、两个动点,探究平行四边形存在性问题例2 如图5,在平面直角坐标系中,抛物线A (-1,0),B (3,0),C (0,-1)三点.(1)求该抛物线的表达式;(2)点Q 在y 轴上,点P 在抛物线上,要使以点Q 、P 、A 、B 为顶点的四边形是平行四边形,求所有满足条件点P 的坐标.解 :(1)易求抛物线的表达式为y=132312--x x ; (2)由题意知点Q 在y 轴上,设点Q 坐标为(0,t );点P 在抛物线上,设点P 坐标为(m ,132312--m m ). 尽管点Q 在y 轴上,也是个动点,但可理解成一个定点,这样就转化为三定一动了. ①当以AQ 为对角线时,由四个顶点的横坐标公式得:-1+0=3+m ,∴m=-4,∴P 1(-4,7);②当以BQ 为对角线时,得:-1+m=3+0,∴m=4,∴P 2(4,35); ③当以AB 为对角线时,得:-1+3=m+0,∴m=2,∴P 3(2,-1).综上,满足条件的点P 为P 1(-4,7)、P 2(4,35)、P 3(2,-1). 反思:这种题型往往特殊,一个动点在抛物线上,另一个动点在x 轴(y 轴)或对称轴或某一定直线上.设出抛物线上的动点坐标,另一个动点若在x 轴上,纵坐标为0,则用平行四边形顶点纵坐标公式;若在y 轴上,横坐标为0,则用平行四边形顶点横坐标公式.该动点哪个坐标已知就用与该坐标有关的公式.本例中点Q 的纵坐标t 没有用上,可以不设.另外,把在定直线上的动点看成一个定点,这样就转化为三定一动了,分别以三个定点构成的三条线段为对角线分类,分三种情况讨论.图 6例3 如图6,在平面直角坐标系中,已知抛物线经过A (-4,0),B (0,-4),C (2,0)三点.(1)求抛物线的解析式;(2)若点M 为第三象限内抛物线上一动点,点M 的横坐标为m ,△AMB 的面积为S .求S 关于m 的函数关系式,并求出S 的最大值;(3)若点P 是抛物线上的动点,点Q 是直线y =-x 上的动点,判断有几个位置能使以点P 、Q 、B 、O 为顶点的四边形为平行四边形,直接写出相应的点Q 的坐标.解:(1)易求抛物线的解析式为y=21x 2+x-4; (2)s=-m 2-4m (-4<m <0);s 最大=4(过程略);(3)尽管是直接写出点Q 的坐标,这里也写出过程.由题意知O (0,0)、B (0,-4). 由于点Q 是直线y=-x 上的动点,设Q (s ,-s ),把Q 看做定点;设P (m ,21m 2+m -4). ①当以OQ 为对角线时,⎪⎩⎪⎨⎧-++-=-+=+42140002m m s m s ∴s=-252±.∴Q 1(-2+52,2-52),Q 2(-2-52,2+52);②当以BQ 为对角线时,⎪⎩⎪⎨⎧--=-+++=+s m m s m 44210002 ∴s 1=-4,s 2=0(舍).∴Q 3(-4,4);③当以OB 为对角线时,⎪⎩⎪⎨⎧-++-=-+=+42140002m m s m s ∴s 1=4,s 2=0(舍).∴Q 4(4,-4).综上,满足条件的点Q 为Q 1(-2+52,2-52)、Q 2(-2-52,2+52)、Q 3(-4,4)、Q 4(4,-4).反思:该题中的点Q 是直线y =-x 上的动点,设动点Q 的坐标为(s ,-s ),把Q 看做定点,就可根据平行四边形顶点坐标公式列方程组了.4 问题总结这种题型,关键是合理有序分类:无论是三定一动,还是两定两动,统统把抛物线上的动点作为第四个动点,其余三个作为定点,分别以这三个定点构成的三条线段为对角线分类,分三种情况讨论,然后运用平行四边形顶点坐标公式转化为方程(组).这种解法,不必画出平行四边形草图,只要合理分类,有序组合,从对角线入手不会漏解,条理清楚,而且适用范围广.其本质是用代数的方法解决几何问题,体现的是分类讨论思想、数形结合的思想.。
平行四边形存在性问题的解题策略

平行四边形存在性问题的解题策略
平行四边形存在性问题是一个常见的几何问题,即给定4条线段,判断它们是否可以构成一个平行四边形。
虽然这个问题看起来很简单,但是解决起来却并不容易。
解决平行四边形存在性问题的第一步是要判断这四条线段是否为平行线段。
根据对称性,可以把这四条线段分成两组,分别是AB和CD,那么AB两条线段是否平行,与CD两条线段是否平行,就可以用一般平行线段的性质来判断,即两条平行线段之间的角度是180°。
若AB和CD两组线段都是平行线段,则说明这四条线段可能构成平行四边形,接下来就要判断对角线的关系。
可以用向量的性质来判断,即对角线的夹角是90°,判断时要将AB和CD两组线段的终点向量相加,若其夹角为90°,则说明这四条线段可以构成平行四边形。
另外,若AB两条线段不是平行线段,则这四条线段一定不能构成平行四边形。
因为平行四边形的4条边都是平行线段,而AB两条线段不是平行线段,则说明这四条线段不可能构成平行四边形。
总之,解决平行四边形存在性问题的关键是要判断四条线段之间的关系,即AB两条线段是否平行,以及AB两条线段的终点向量之和的夹角是否为90°。
只有当这两个条件都满足时,这四条线段才能构成平行四边形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平行四边形的存在性问题解题策略专题攻略解平行四边形的存在性问题一般分三步:第一步寻找分类标准,第二步画图,第三步计算.难点在于寻找分类标准,分类标准寻找的恰当,可以使解的个数不重复不遗漏,也可以使计算又好又快.如果已知三个定点,探寻平行四边形的第四个顶点,符合条件的有3个点:以已知三个定点为三角形的顶点,过每个点画对边的平行线,三条直线两两相交,产生3个交点.如果已知两个定点,一般是把确定的一条线段按照边或对角线分为两种情况.根据平行四边形的对边平行且相等,灵活运用坐标平移,可以使得计算过程简便.根据平行四边形的中心对称的性质,灵活运用坐标对称,可以使得解题简便.例题解析例❶如图1-1,在平面直角坐标系中,已知抛物线y=-x2-2x+3与x轴交于A、B两点(A在B的左侧),与y轴交于点C,顶点为P,如果以点P、A、C、D为顶点的四边形是平行四边形,求点D的坐标.图1-1 【解析】P、A、C三点是确定的,过△P AC的三个顶点分别画对边的平行线,三条直线两两相交,产生3个符合条件的点D(如图1-2).由y=-x2-2x+3=-(x+1)2+4,得A(-3,0),C(0, 3),P(-1, 4).由于A(-3,0)33右,上C(0, 3),所以P(-1, 4)33右,上D1(2, 7).由于C(0, 3)33下,左D2(-4, 1).下,左A(-3,0),所以P(-1, 4)33由于P(-1, 4)11右,下D3(-2, -1).右,下C(0, 3),所以A(-3,0)11我们看到,用坐标平移的方法,远比用解析式构造方程组求交点方便多了.图1-2例❷如图2-1,在平面直角坐标系中,已知抛物线y=-x2+2x+3与x轴交于A、B两点,点M在这条抛物线上,点P在y轴上,如果以点P、M、A、B为顶点的四边形是平行四边形,求点M的坐标.图2-1【解析】在P、M、A、B四个点中,A、B是确定的,以AB为分类标准.由y=-x2+2x+3=-(x+1)(x-3),得A(-1,0),B(3,0).①如图2-2,当AB是平行四边形的对角线时,PM与AB互相平分,因此点M与点P 关于AB的中点(1,0)对称,所以点M的横坐标为2.此时M(2,3).②如图2-3,图2-4,当AB是平行四边形的边时,PM//AB,PM=AB=4.所以点M的横坐标为4或-4.所以M (4,-5)或(-4,-21).我们看到,因为点P的横坐标是确定的,在解图2-2时,根据对称性先确定了点M的横坐标;在解图2-3和图2-4时,根据平移先确定了点M的横坐标.图2-2 图2-3 图2-4 例❸如图3-1,在平面直角坐标系中,直线y=-x+4与x轴交于点A,与y轴交于点B,点C在直线AB上,在平面直角坐标系中求一点D,使得以O、A、C、D为顶点的四边形是菱形.图3-1【解析】由y=-x+4,得A(4, 0),直线AB与坐标轴的夹角为45°.在O、A、C、D四个点中,O、A是确定的,以线段OA为分类标准.如图3-2,如果OA是菱形的对角线,那么点C在OA的垂直平分线上,点C(2,2)关于OA的对称点D的坐标为(2,-2).如果OA是菱形的边,那么又存在两种情况:如图3-3,以O为圆心,OA为半径的圆与直线AB的交点恰好为点B(0, 4),那么正方形AOCD的顶点D的坐标为(4, 4).如图3-4,以A 为圆心,AO 为半径的圆与直线AB 有两个交点C (4-和C ′(4+-,点C 和C ′向左平移4个单位得到点D (-和D ′-.图3-2 图3-3 图3-4例❹ 如图4-1,已知抛物线241633y x x =+与x 轴的负半轴交于点C ,点E 的坐标为(0,-3),点N 在抛物线的对称轴上,点M 在抛物线上,是否存在这样的点M 、N ,使得以M 、N 、C 、E为顶点的四边形是平行四边形?若存在,请求出点M 的坐标;若不存在,请说明理由.图4-1【解析】C (-4,0)、E (0,-3)两点是确定的,点N 的横坐标-2也是确定的.以CE 为分类标准,分两种情况讨论平行四边形:①如图4-2,当CE 为平行四边形的边时,由于C 、E 两点间的水平距离为4,所以M 、N 两点间的水平距离也为4,因此点M 的横坐标为-6或2.将x =-6和x =2分别代入抛物线的解析式,得M (-6,16)或(2, 16).②如图4-3,当CE 为平行四边形的对角线时,M 为抛物线的顶点,所以M 16(2,)3--.图4-2 图4-3例❺如图1,在平面直角坐标系中,抛物线y =ax 2-2ax -3a (a <0)与x 轴交于A 、B 两点(点A 在点B 的左侧),点D 是第四象限内抛物线上的一点,直线AD 与y 轴负半轴交于点C ,且CD =4AC .设P 是抛物线的对称轴上的一点,点Q 在抛物线上,以点A 、D 、P 、Q 为顶点的四边形能否成为矩形?若能,求出点P 的坐标;若不能,请说明理由.图5-1【解析】由y=ax2-2ax-3a=a(x+1)(x-3),得A(-1, 0).由CD=4AC,得x D=4.所以D(4, 5a).已知A(-1, 0)、D(4, 5a),x P=1,以AD为分类标准,分两种情况讨论:①如图5-2,如果AD为矩形的边,我们根据AD//QP,AD=QP来两次平移坐标.由于A、D两点间的水平距离为5,所以点Q的横坐标为-4.所以Q(-4,21a).由于A、D两点间的竖直距离为-5a,所以点P的纵坐标为26a.所以P(1, 26a).根据矩形的对角线相等,得AP2=QD2.所以22+(26a)2=82+(16a)2.整理,得7a2=1.所以a=P(1.②如图5-3,如果AD为矩形的对角线,我们根据AP//QD,AP=QD来两次平移坐标.由于A、P两点间的水平距离为2,所以点Q的横坐标为2.所以Q(2,-3a).由于Q、D两点间的竖直距离为-8a,所以点P的纵坐标为8a.所以P(1, 8a).再根据AD2=PQ2,得52+(5a)2=12+(11a)2.整理,得4a2=1.所以12a=-.此时P(14)-,.我们从图形中可以看到,像“勾股图”那样构造矩形的外接矩形,使得外接矩形的边与坐标轴平行,那么线段的等量关系就可以转化为坐标间的关系.上面我们根据“对角线相等的平行四边形是矩形”列方程,还可以根据定义“有一个角是直角的平行四边形叫矩形”来列方程.如图5-2,如果∠ADP=90°,那么MA NDMD NP=;如图5-3,如果∠QAP=90°,那么GQ KAGA KP=.图5-2 图5-3例❻如图6-1,将抛物线c1:2y=x轴翻折,得到抛物线c2.现将抛物线c 1向左平移m 个单位长度,平移后得到新抛物线的顶点为M ,与x 轴的交点从左到右依次为A 、B ;将抛物线c 2向右也平移m 个单位长度,平移后得到新抛物线的顶点为N ,与x 轴的交点从左到右依次为D 、E .在平移过程中,是否存在以点A 、N 、E 、M 为顶点的四边形是矩形的情形?若存在,请求出此时m 的值;若不存在,请说明理由.图6-1【解析】没有人能精确画好抛物线,又怎么平移抛物线呢?我们去伪存真,将A 、B 、D 、E 、M 、N 六个点及它们的坐标在图中都标注出来(如图6-2),如果您看到了△MAB 和△NED 是边长为2的等边三角形,那么平移就简单了.如图6-3,在两个等边三角形平移的过程中,AM 与EN 保持平行且相等,所以四边形ANEM 保持平行四边形的形状,点O 为对称中心.【解法一】如果∠ANE =90°,根据30°角所对的直角边等于斜边的一半,可得AE =2EN =4.而AE =AO +OE =2AO ,所以AO =2.已知AB =2,此时B 、O 重合(如图6-4),所以m =BO =1.【解法二】如果对角线MN =AE ,那么OM =OA ,此时△MAO 是等边三角形.所以等边三角形MAB 与△MAO 重合.因此B 、O 重合,m =BO =1.【解法三】在平移的过程中,(1,0)A m --、(1,0)B m -,M (m -,根据OA 2=OM 2列方程(1+m )2=m 2+3.解得m =1.图6-2 图6-3 图6-4例❼ 如图7-1,菱形ABCD 的边长为4,∠B =60°,E 、H 分别是AB 、CD 的中点,E 、G 分别在AD 、BC 上,且AE =CG .(1)求证四边形EFGH 是平行四边形;(2)当四边形EFGH 是矩形时,求AE 的长;(3)当四边形EFGH 是菱形时,求AE 的长.图7-1【解析】(1)证明三角形全等得EF =GH 和FG =HE 大家最熟练了.(2)平行四边形EFGH 的对角线FH =4是确定的,当EG =FH =4时,四边形EFGH 是矩形.以FH 为直径画圆,你看看,这个圆与AD 有几个交点,在哪里?如图7-2.如图7-3,当E为AD的中点时,四边形ABGE和四边形DCGE都是平行四边形.如图7-4,当E与A重合时,△ABG与△DCE都是等边三角形.(3)如果平行四边形EFGH的对角线EG与FH互相垂直,那么四边形EFGH是菱形.过FH的中点O画FH的垂线,EG就产生了.在Rt△AOE中,∠OAE=60°,AO=2,此时AE=1.又一次说明了如果会画图,答案就在图形中.图7-2 图7-3 图7-4 图7-5例❽如图8-1,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A(4, 0)、B(0, 3),点C的坐标为(0, m),过点C作CE⊥AB于点E,点D为x轴正半轴的一动点,且满足OD =2OC,连结DE,以DE、DA为边作平行四边形DEF A.(1)如果平行四边形DEF A为矩形,求m的值;(2)如果平行四边形DEF A为菱形,请直接写出m的值.图8-1【解析】这道题目我们着重讲解怎样画示意图.我们注意到,点A和直线AB(直线l)是确定的.如图8-2,先画x轴,点A和直线l.在直线l上取点E,以AE为对角线画矩形DEF A.如图8-3,过点E画直线l的垂线.画∠MDN,使得DN=2MN,MN⊥DN,产生点C.如图8-4,过点C画y轴,产生点O和点B.图8-2 图8-3 图8-4 您是否考虑到,画∠MDN时,还存在DM在x轴下方的情况?如图8-5.同样的,我们可以画如图8-6,如图8-7的两个菱形.图8-5 图8-6 图8-7。
