数值传热学陶文铨课后答案第三章
传热学第三章答案(精品资料).doc

【最新整理,下载后即可编辑】第三章思考题1. 试说明集中参数法的物理概念及数学处理的特点答:当内外热阻之比趋于零时,影响换热的主要环节是在边界上的换热能力。
而内部由于热阻很小而温度趋于均匀,以至于不需要关心温度在空间的分布,温度只是时间的函数,数学描述上由偏微分方程转化为常微分方程、大大降低了求解难度。
2. 在用热电偶测定气流的非稳态温度场时,怎么才能改善热电偶的温度响应特性?答:要改善热电偶的温度响应特性,即最大限度降低热电偶的时间常数hA cvc ρτ=,形状上要降低体面比,要选择热容小的材料,要强化热电偶表面的对流换热。
3. 试说明”无限大平板”物理概念,并举出一二个可以按无限大平板处理的非稳态导热问题答;所谓“无限大”平板,是指其长宽尺度远大于其厚度,从边缘交换的热量可以忽略不计,当平板两侧换热均匀时,热量只垂直于板面方向流动。
如薄板两侧均匀加热或冷却、炉墙或冷库的保温层导热等情况可以按无限大平板处理。
4.什么叫非稳态导热的正规状态或充分发展阶段?这一阶段在物理过程及数学处理上都有些什么特点?答:非稳态导热过程进行到一定程度,初始温度分布的影响就会消失,虽然各点温度仍随时间变化,但过余温度的比值已与时间无关,只是几何位置(δ/x)和边界条件(Bi数)的函数,亦即无量纲温度分布不变,这一阶段称为正规状况阶段或充分发展阶段。
这一阶段的数学处理十分便利,温度分布计算只需取无穷级数的首项进行计算。
5.有人认为,当非稳态导热过程经历时间很长时,采用图3-7记算所得的结果是错误的.理由是:这个图表明,物体中各点的过余温度的比值与几何位置及Bi有关,而与时间无关.但当时间趋于无限大时,物体中各点的温度应趋近流体温度,所以两者是有矛盾的。
你是否同意这种看法,说明你的理由。
答:我不同意这种看法,因为随着时间的推移,虽然物体中各点过余温度的比值不变但各点温度的绝对值在无限接近。
这与物体中各点温度趋近流体温度的事实并不矛盾。
数值传热学(陶文铨)第二章习题答案

p1 p2
(1)
p 2 p x2 x 2 x i 2 x i 2 2!
p 2 p x2 p3 p2 x 2 x i 2 x i 2 2!
(2) 式(2)-(1)得
p p1 p 3 x i 2 2 x
2-11.解:对于均分网格用泰勒级数展开法,用 2 点分别表示 1,3,4 处热流量得
(i+1,n)= (i,n)+
(1)
x
( x)
i ,n
2 x 2
i ,n
(( x) )2 2!
(i-1,n)= (i,n)+
(2) 式(1)-(2)得:
x
( x)
i ,n
2 x 2
i ,n
(( x) )2 2!
(i+1,n)- (i-1,n)=
即
krp k krp k 2k rpTp ( )Te ( )T r s r r r 2 r 2 w p
化简后得
2krp
r
Tp
kre kr S Te w Tw rp r r r 2
计算结果与控制容积积分法一致。 2-9.解:对于均分网格用泰勒级数展开法分别表示 1 和 3 点处的压力值
(1) 对 T 随 r 由 Tw 变到 Te 的过程进行积分
(2) 可化为
rk
dT dr
e
w
S 2 r 2 w
e
(3) 取 T 随 r 呈分段线性的变化,则(3)式中
Tw
Tp Tw 2 Tp Te 2
(4)
Te
(5)
dT Te Tp r dr e
(6)
传热学第三章答案

第三章思考题1. 试说明集中参数法的物理概念及数学处理的特点答:当内外热阻之比趋于零时,影响换热的主要环节是在边界上的换热能力。
而内部由于热阻很小而温度趋于均匀,以至于不需要关心温度在空间的分布,温度只是时间的函数, 数学描述上由偏微分方程转化为常微分方程、大大降低了求解难度。
2. 在用热电偶测定气流的非稳态温度场时,怎么才能改善热电偶的温度响应特性?答:要改善热电偶的温度响应特性,即最大限度降低热电偶的时间常数hA cvc ρτ=,形状上要降低体面比,要选择热容小的材料,要强化热电偶表面的对流换热。
3. 试说明”无限大平板”物理概念,并举出一二个可以按无限大平板处理的非稳态导热问题 答;所谓“无限大”平板,是指其长宽尺度远大于其厚度,从边缘交换的热量可以忽略 不计,当平板两侧换热均匀时,热量只垂直于板面方向流动。
如薄板两侧均匀加热或冷却、 炉墙或冷库的保温层导热等情况可以按无限大平板处理。
4. 什么叫非稳态导热的正规状态或充分发展阶段?这一阶段在物理过程及数学处理上都有些什么特点?答:非稳态导热过程进行到一定程度,初始温度分布的影响就会消失,虽然各点温度仍 随时间变化,但过余温度的比值已与时间无关,只是几何位置(δ/x )和边界条件(Bi 数) 的函数,亦即无量纲温度分布不变,这一阶段称为正规状况阶段或充分发展阶段。
这一阶段的数学处理十分便利,温度分布计算只需取无穷级数的首项进行计算。
5. 有人认为,当非稳态导热过程经历时间很长时,采用图3-7记算所得的结果是错误的.理由是: 这个图表明,物体中各点的过余温度的比值与几何位置及Bi 有关,而与时间无关.但当时间趋于无限大时,物体中各点的温度应趋近流体温度,所以两者是有矛盾的。
你是否同意这种看法,说明你的理由。
答:我不同意这种看法,因为随着时间的推移,虽然物体中各点过余温度的比值不变 但各点温度的绝对值在无限接近。
这与物体中各点温度趋近流体温度的事实并不矛盾。
2020年传热学第四版课后思考题答案(杨世铭-陶文铨)]
![2020年传热学第四版课后思考题答案(杨世铭-陶文铨)]](https://img.taocdn.com/s3/m/337c6d7859eef8c75fbfb381.png)
作者:非成败作品编号:92032155GZ5702241547853215475102时间:2020.12.13第一章思考题1. 试用简练的语言说明导热、对流换热及辐射换热三种热传递方式之间的联系和区别。
答:导热和对流的区别在于:物体内部依靠微观粒子的热运动而产生的热量传递现象,称为导热;对流则是流体各部分之间发生宏观相对位移及冷热流体的相互掺混。
联系是:在发生对流换热的同时必然伴生有导热。
导热、对流这两种热量传递方式,只有在物质存在的条件下才能实现,而辐射可以在真空中传播,辐射换热时不仅有能量的转移还伴有能量形式的转换。
2. 以热流密度表示的傅立叶定律、牛顿冷却公式及斯忒藩-玻耳兹曼定律是应当熟记的传热学公式。
试写出这三个公式并说明其中每一个符号及其意义。
答:① 傅立叶定律:dx dt q λ-=,其中,q -热流密度;λ-导热系数;dx dt -沿x 方向的温度变化率,“-”表示热量传递的方向是沿着温度降低的方向。
② 牛顿冷却公式:)(f w t t h q -=,其中,q -热流密度;h -表面传热系数;w t -固体表面温度;f t -流体的温度。
③ 斯忒藩-玻耳兹曼定律:4T q σ=,其中,q -热流密度;σ-斯忒藩-玻耳兹曼常数;T-辐射物体的热力学温度。
3. 导热系数、表面传热系数及传热系数的单位各是什么?哪些是物性参数,哪些与过程有关?答:① 导热系数的单位是:W/(m.K);② 表面传热系数的单位是:W/(m 2.K);③ 传热系数的单位是:W/(m 2.K)。
这三个参数中,只有导热系数是物性参数,其它均与过程有关。
4. 当热量从壁面一侧的流体穿过壁面传给另一侧的流体时,冷、热流体之间的换热量可以通过其中任何一个环节来计算(过程是稳态的),但本章中又引入了传热方程式,并说它是“换热器热工计算的基本公式”。
试分析引入传热方程式的工程实用意义。
答:因为在许多工业换热设备中,进行热量交换的冷、热流体也常处于固体壁面的两侧,是工程技术中经常遇到的一种典型热量传递过程。
《传热学》课后习题答案-第三章

第三章思考题1. 试说明集总参数法的物理概念及数学处理的特点答:当内外热阻之比趋于零时,影响换热的主要环节是在边界上的换热能力。
而内部由于热阻很小而温度趋于均匀,以至于不需要关心温度在空间的分布,温度只是时间的函数, 数学描述上由偏微分方程转化为常微分方程、大大降低了求解难度。
2. 在用热电偶测定气流的非稳态温度场时,怎么才能改善热电偶的温度响应特性?答:要改善热电偶的温度响应特性,即最大限度降低热电偶的时间常数,形状上要降低体面比,要选择热容小的材料,要强化热电偶表面的对流换热。
3. 试说明”无限大平板”物理概念,并举出一二个可以按无限大平板处理的非稳态导热问题 答;所谓“无限大”平板,是指其长宽尺度远大于其厚度,从边缘交换的热量可以忽略 不计,当平板两侧换热均匀时,热量只垂直于板面方向流动。
如薄板两侧均匀加热或冷却、 炉墙或冷库的保温层导热等情况可以按无限大平板处理。
4. 什么叫非稳态导热的正规状态或充分发展阶段?这一阶段在物理过程及数学处理上都有些什么特点?答:非稳态导热过程进行到一定程度,初始温度分布的影响就会消失,虽然各点温度仍 随时间变化,但过余温度的比值已与时间无关,只是几何位置()和边界条件(Bi 数) 的函数,亦即无量纲温度分布不变,这一阶段称为正规状况阶段或充分发展阶段。
这一阶段的数学处理十分便利,温度分布计算只需取无穷级数的首项进行计算。
5. 有人认为,当非稳态导热过程经历时间很长时,采用图3-7记算所得的结果是错误的.理由是: 这个图表明,物体中各点的过余温度的比值与几何位置及Bi 有关,而与时间无关.但当时间趋于无限大时,物体中各点的温度应趋近流体温度,所以两者是有矛盾的。
你是否同意这种看法,说明你的理由。
答:我不同意这种看法,因为随着时间的推移,虽然物体中各点过余温度的比值不变 但各点温度的绝对值在无限接近。
这与物体中各点温度趋近流体温度的事实并不矛盾。
6. 试说明Bi 数的物理意义。
数值传热学陶文铨第三章

3-7证明对流项的背风差分总使扰动逆流而传递。
证明:Taylor 展开法中逆风差分的构造法:1,i i i x x φφφ+-∂=∂∆ u>0 1,i i i x xφφφ--∂=∂∆ u<0 下面以u>0的情形来分析.对于节点i+1,在n 时层产生在节点i 的扰动对i+1的影响由下式确定: 11112n n n n i i i i u t x φφφφ+++++--=-∆∆ (1n i φ+=0,2n i φ+=0)由此得 11n i φ++=0而i-1处则有 1111n n n n i i i i u t x φφφφ+-----=-∆∆ (1n i φ-=0)得 11n i u t x φε+-∆⎛⎫= ⎪∆⎝⎭因此可知对流项的背风差分总使扰动逆流而传递。
3-10一阶导数的而二阶差分格式称为二阶迎风格式(在来流方向区节点构成差分格式)。
试分析其迁移性。
解:经查表2-1可知在来流方向区节点的一阶导数二阶迎风格式为:n n n i i-1i-2i n 34=x 2x φφφφ-+∂∂∆, u>0 下面以u>0的情形来分析.对于节点i+1,在n 时层产生在节点i 的扰动对i+1的影响由下式确定: n+1n n n n i+1i+1i+1i i-1n+1i+134=-u t 2x 2u t =x φφφφφφε--+∆∆∆⎛⎫ ⎪∆⎝⎭ (n i+1φ=0,n i-1φ=0) 得 n+1i+12u t =x φε∆⎛⎫ ⎪∆⎝⎭而i-1处则有 n n n n+1n i-1i-2i-3i-1i-134=-u t2x φφφφφ-+-∆∆ (n i-1φ=0,n i-2φ=0,n i-3φ=0) 因此得n+1i-1φ=0因此可知一阶导数的二阶迎风格式(在来流方向区节点构成差分格式)具有迁移性。
扰动只向后传动!!!。
数值传热学陶文铨主编第二版习题答案
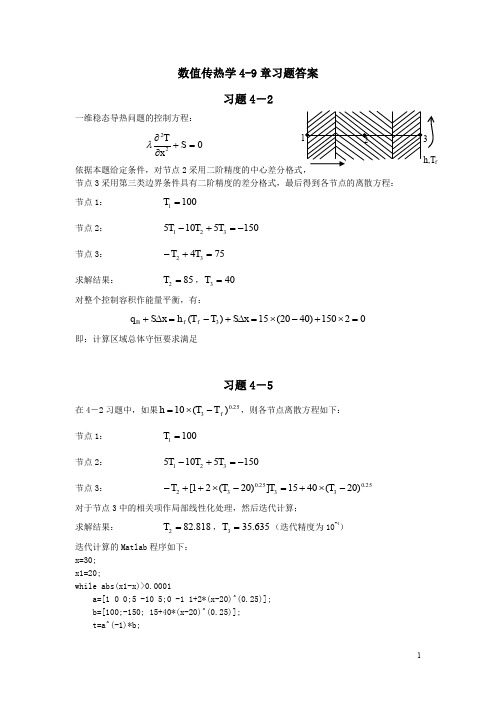
依据本题给定条件,对节点 2 采用二阶精度的中心差分格式, 节点 3 采用第三类边界条件具有二阶精度的差分格式,最后得到各节点的离散方程: 节点 1: 节点 2: 节点 3: 求解结果:
T1 100
5T1 10T2 5T3 150 T2 4T3 75
T2 85 , T3 40
习题 4-12 的 Matlab 程序
%代数方程形式 AiTi=CiTi+1+BiTi-1+Di mdim=10;%计算的节点数 x=linspace(1,3,mdim);%生成 A、C、B、T 数据的基数; A=cos(x);%TDMA 的主对角元素 B=sin(x);%TDMA 的下对角线元素 C=cos(x)+exp(x); %TDMA 的上对角线元素 T=exp(x).*cos(x); %温度数据 %由 A、B、C 构成 TDMA coematrix=eye(mdim,mdim); for n=1:mdim coematrix(n,n)=A(1,n); if n>=2 coematrix(n,n-1)=-1*B(1,n); end if n<mdim coematrix(n,n+1)=-1*C(1,n); end end %计算 D 矢量 D=(coematrix*T')'; %由已知的 A、B、C、D 用 TDMA 方法求解 T %消元 P(1,1)=C(1,1)/A(1,1); Q(1,1)=D(1,1)/A(1,1); for n=2:mdim P(1,n)=C(1,n)/(A(1,n)-B(1,n)*P(1,n-1)); Q(1,n)=(D(1,n)+B(1,n)*Q(1,n-1))/(A(1,n)-B(1,n)*P(1,n-1)); end %回迭 Tcal(1,mdim)=Q(1,mdim); for n=(mdim-1):-1:1 Tcal(1,n)=P(1,n)*Tcal(1,n+1)+Q(1,n); end Tcom=[T;Tcal]; %绘图比较给定 T 值和计算 T 值 plot(Tcal,'r*') hold on plot(T)
数值传热学习题答案(汇总版)
2-4-9
= rP rS
式(2-4-9)也可以写成 a PTP = a E TE + aW TW + b 的形式。而且两种结果是一致的。
2—6:
n n TE −TW dT P , n = 解:将 , dx 2x n n TE −2TPn + TW d 2T P , n = , dx2 x 2
dk = f (x ) 代入原方程,得: dx
令
2-4-4
rk rk a E = , aW = , a P = a E + aW , b x w x e
= SrP r ,
式(2-4-4)可以写成 a PTP = a E TE + aW TW + b 的形式。 2. 再用 Taylor 展开法导出 k
2 2 uE + uP u = , 2 2 e
2 2 uW + uP u = 2 2 w
t u ut N − uP y = (y ) , n n
t
t ut u p − uS y = (y ) 。 s s
t
(y ) n = (y ) s = y
n n n n TE −TW TE −2TPn + TW k + f (x ) +S=0 整理得: 2x x 2
4kT P= 2k + xf ( x)T E+2k − xf ( x)T W +2x 2 S
− 2k 时, a E 会成为负值, x 2k 当 f(x)> 时, aW 会成为负值。 x
rk dr = rk r r dr dr dr
w
e
1 d
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数值传热学陶文铨课后答案第三章
A.陶文铨,
B.周伟俊D.黄仁龙,黄国生,周伟俊,周国生,周大白。
在计算流体力学中,流场是一个基本问题。
计算流体力学中常用到的主要方法是()。
一、对于固体,流场和速度的分布问题的计算是通过计算流体的物理量来进行的。
在计算流体力学中,流场和速度的分布问题的计算是通过计算流体的物理量来进行的。
A.质量流场 F:计算流体力学中流场和速度分布问题方法,其目的是用物理量来表示(质量)。
D.速度分布方程 F:计算流体力学中非稳态速度分布方程。
二、对于固体流动,常用的方法有流线理论法、流体压力分析法、边界层理论法、粒子质量守恒定律法、自由流动技术法、流动力学理论以及流体力学仿真技术。
解析:本题考查的是流线理论中的流场理论。
固体流动方向上分为轴流和向后流场。
在轴流流动中,固体的扩散与温度成正比;向后流一般不流动。
三、流体粘性为固液相物之间的粘滞系数,且在固态中较为稳定,因此研究固液相物之间结合力和粘滞系数问题的方法通常称为粘性流场方法。
【参考答案】 C解析:流体粘性指流体相物之间形成的粘性,根据粘性对固液相物有粘滞力或阻力,流体粘性小于固体流体之间粘滞力或阻力时固体粘滞力>固体之间粘性;流体粘性大于固体之间粘性时固体粘滞力>固体之间粘性。
固液相混是指固液相混在一起。
流体特性参数是用于定量计算和评价流体性能的重要参数。
流体特性参数如流速、温度、压力、密度、粘度等。
A选项; D选项
四、流体流动分为粘性流动和非粘性流动。
A.粘性流动是指流体在流动过程中具有一定的粘性而非粘性,其流动过程主要分为四个阶段:
B.非粘性流动是指流体在流动过程中不具有任何粘性,其流场主要分为湍流、不稳定、流动速度等多种形式。
C.湍流是指流体在湍流状态下不能充分发挥其流动能力,其流场主要分为两种形式:湍流和不稳定。
D.不稳定是指流体在流动过程中没有任何不稳定状态,其流场主要分为两种形式:一种是无规则流动(在流动过程中无规则流动),另一种是不规则流动时无规则流动)。
A.无规则流动是指流动方向不定,无法保证任何流动状态。
此时如果流体进入无规则流动区域而不能保持适当高度或产生不稳定状态,则该区域为不稳定区域。
