圆曲线坐标计算(坐标正算法)
坐标正反算

一、坐标正算与坐标反算 1、坐标正算 已知 点的坐标、 边的方位角、 两点间的水平距离,计算待 定点 的坐标,称为坐标正算。
如图 6-6 所示,点的坐标可由下式计 算:式中 、 为两导线点坐标之差,称为坐标增量,即:【例题 6-1】已知点 A 坐标, =1000 、 =1000 、方位角 =35°17'36.5", 两点水平距离 =200.416 ,计算 点的坐标?35o17'36.5"=1163.580 35o17'36.5"=1115.793 2、坐标反算 已知 两点的坐标,计算 两点的水平距离与坐标方位角, 称为坐标反算。
如图 6-6 可知,由下式计算水平距离与坐标方位角。
(6-3) (6-4) 式中反正切函数的值域是-90°~+90°,而坐标方位角为 0°~ 360°,因此坐标方位角的值,可根据 、 的正负号所在象限,将反 正切角值换算为坐标方位角。
【例题 6-2】 =3712232.528 、 =523620.436 、 =3712227.860 、 =523611.598 ,计算坐标方位角计算坐标方位角、水平距离 。
=62°09'29.4"+180°=242°09'29.4"注意:一直线有两个方向,存在两个方位角,式中:、的计算是过 A 点坐标纵轴至直线 的坐标方位角,若所求坐标方位角为,则应是 A 点坐标减 点坐标。
坐标正算与反算,可以利用普通科学电子计算器的极坐标和直角坐标相互转换功能计算,普通科学电子计算器的类型比较多,操作方法不相同,下面介绍一种方法。
【例题 6-3】坐标反算,已知 =2365.16 、 =1181.77 、=1771.03 、 =1719.24 ,试计算坐标方位角 、水平距离 。
键入 1771.03-2365.16 按等号键[=]等于纵坐标增量,按储存键[ ],键入 1719.24-1181.77 按等号键[=]等于横坐标增量,按[ ]键输入,按[ ]显示横坐标增量,按[ ]键输入,按第二功能键[2ndF],再按[ ]键,屏显为距离,再按[ ]键,屏显为方位角。
坐标正算的公式是什么

坐标正算的公式是什么在地图制图和定位导航系统中,坐标正算是一种重要的计算方法,用于计算出给定地理位置的坐标值。
坐标正算通常基于已知的参考点或者经纬度等信息,计算出目标点的坐标。
本文将介绍坐标正算的公式和计算过程。
坐标正算的基本原理坐标正算基于几何学和数学原理,通过一些特定的计算公式,将地理位置的描述转换为具体的坐标值。
在进行坐标正算之前,需要明确一些基本信息,例如已知参考点的坐标、目标点与参考点的距离和方位角等。
计算目标点坐标的步骤下面是一个常见的坐标正算的步骤:1.确定参考点坐标:首先需要确定至少一个已知坐标的参考点,可以是已知的地理位置或者其他参考点的坐标。
2.测量目标点与参考点之间的距离和方位角:使用合适的测量方法,测量目标点与参考点之间的水平距离和方位角。
这些信息可以由仪器测量,也可以通过其他方法估算得出。
3.计算目标点的坐标:根据已知的参考点坐标、目标点与参考点的距离和方位角,应用特定的计算公式进行坐标计算。
不同的计算方法可能有不同的公式,但基本原理是一致的。
常用的坐标正算公式在不同的坐标系统和进行坐标正算的方法中,可能会使用不同的公式和算法。
以下是一些常见的坐标正算的公式:•平面坐标正算公式:对于平面坐标系统,常见的方法是使用平面直角坐标系或UTM坐标系统。
在这种情况下,可以使用已知参考点的坐标、目标点与参考点的距离和方位角来计算目标点的坐标。
具体的公式可以根据不同的坐标系统而有所不同。
•大地坐标正算公式:对于大地坐标系统,常用的方法是使用经纬度来表示坐标。
在这种情况下,可以通过已知参考点的经纬度以及目标点与参考点的距离和方位角,应用大地测量学中的公式计算目标点的经纬度。
•三角形法:坐标正算中常用的计算方法是三角形法。
通过已知点的坐标和目标点与已知点之间的距离和方位角,可以构建一个三角形模型,然后使用三角函数和三角关系来计算目标点的坐标。
这种方法在平面坐标和大地坐标系统中都可以使用。
公路圆曲线中、边桩坐标及放样计算 (全新版)
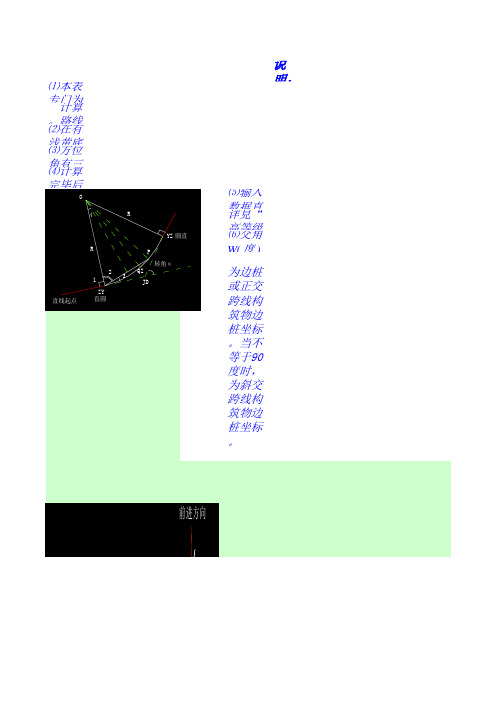
明:
⑴本表专门为圆曲线中、边桩坐标及放样计算而设计,只需输入转点的里程桩号、坐标及 计算。路线右转时R、转角输入正值,当路线左转时,R、转角输入负值。
⑵在有浅黄底色的单元格内输入数据,其它颜色的单元格为计算结果显示区,不能输入数
⑶方位角有三种值均可使用,第一种有正角,第二种为度、分、秒,秒的计算有误差,约
显示区,不能输入数据。
秒的计算有误差,约为0.2秒。
并删除不用数据等才可打印,可缩小比例。
用先删除后输入方法。
用说明”。
断面线与路线的夹角,见下图。当等于 90 度时,
。当不等于90度时,为斜交跨线构筑物边桩坐标。
为07年3月前,就可以不要注册了。
为边桩或正交跨线构筑物边桩坐标。当不等于90度时,
前进方向
P1(XP1,YP1) T W 公路中线 P0(XP0,YP0) T P2(XP2,YP2)Z 桥涵轴线 高速公路跨线建筑物轴线平面图
用时系统时间改为07年3月前,就可
的里程桩号、坐标及转角,圆曲线半径R,直线起点的坐标、桩打印前需进行值与数据格式复制并删除不用数据等才
O 4 R YZ 圆直 R P 转角α 2 1 直线起点 ZY 直圆 3 QZ JD
⑸输入数据直接覆盖原有数据,不用先删除后输入方法 详見“高等级公路测量计算程序使用说明”。
⑹交角 W( 度 ) 系指前进方向左侧横断面线与路线的夹
坐标正反算定义及公式

坐标正反算定义及公式坐标正算和反算是地图投影中的重要概念,用于将地球表面上的经纬度坐标转换为平面坐标(正算),或将平面坐标转换为经纬度坐标(反算)。
这种转换是为了方便地图上的测量和计算。
坐标正算是指根据地球表面上的经纬度坐标,计算出对应的平面坐标。
在这个过程中,需要考虑地球的形状、椭球体模型以及地图投影方法等因素。
不同的投影方法会导致不同的坐标正算公式,下面简单介绍两种常用的投影方法及其公式。
1.经纬度-平面直角坐标投影(简称平面直角投影)平面直角投影是将地球表面上的经纬度坐标转换为平面直角坐标的一种常用方法。
在平面直角投影中,地球被近似为一个大椭球体,通过将经纬度坐标映射到一个平面上完成转换。
公式如下:X = N * (L - L0) * cosφ0Y=N*(φ-φ0)其中,X和Y为平面直角坐标,L和φ分别为经纬度坐标,L0和φ0分别为中央经线和标准纬线,N为椭球的半径。
2.地心正投影(简称球面正投影或者高斯正算)地心正投影是一种在地心球面上进行的坐标正算方法,适用于小范围的地图投影。
在地心正投影中,将地球看作一个球体,并通过一个中央经线来进行投影。
公式如下:X = A * (L - L0) * cosφY=A*(φ-φ0)其中,X和Y为平面直角坐标,L和φ分别为经纬度坐标,L0和φ0分别为中央经线和标准纬线,A为一个与椭球参数相关的常数。
坐标反算是指根据平面坐标计算出对应的经纬度坐标。
在坐标反算中,需要将平面坐标反映射回地球表面,恢复为经纬度坐标。
与坐标正算类似,不同的投影方法会导致不同的坐标反算公式,下面介绍两种常用的投影方法及其公式。
1.平面直角坐标-经纬度投影(平面直角反算)平面直角反算是将平面直角坐标转换为地球表面上的经纬度坐标的一种方法。
利用与坐标正算相反的操作,将平面直角坐标通过逆转换还原为经纬度坐标。
公式如下:φ=φ0+Y/NL = L0 + X / (N * cosφ0)其中,φ和L分别为经纬度坐标,φ0和L0分别为标准纬线和中央经线,X和Y为平面直角坐标,N为椭球的半径。
圆曲线坐标计算(坐标正算法)

2、计算方法 根据交点里程和圆曲线要素计算主点里程。
公路习惯推算方法:
曲线测设是指每隔一定距离测设一个曲线点以在地面上标志曲线平面位置。
现阶段曲线测设主要采用全站仪或GPS进行,而这两种方法所需测设资料是曲线点的坐标,故实施测设前必须计算曲线点的坐标。
四、单圆曲线测设资料计算
1、基本要求 中桩间距:即相邻两曲线点间的距离,一般为 20 米,地形复杂时为 10 米。施工时可按规范或标书要求进行。 桩号:即曲线点的里程,必须是中桩间距的整倍数。 例如:ZY点里程为18+197.36,中桩间距为20m,则第一点里程为________________________________。 第二点里程为______________________________。 依此类推。
18+200
18+220
2、曲线点坐标计算
已知条件:起点、终点及各交点的坐标。
JD1
起点
终点
ZY2
YZ2
ZY1
YZ1
QZ2
JD2
S1-2
T1
T2
X
Y
O
QZ2
1)计算ZY、YZ点坐标
JD1
起点
终点
ZY2
YZ2
ZY1
YZ1
QZ2
JD2
S1-2
T1
T2
X
Y
O
QZ2
通用公式:
JD1
起点
终点
ZY2
YZ2
ZY1
YZ1
QZ2
JD2
S1-2
T1
T2
X
Y
O
QZ2
ZY- i
ZY- JD
坐标正反算

【例题6-3】坐标反算,已知 =2365.16 、 =1181.77 、 =1771.03 、 =1719.24 ,试计算坐标方位角 、水平距离 。
键入1771.03-2365.16按等号键[=]等于纵坐标增量,按储存键[ ],
【例题6-2】 =3712232.528 、 =523620.436 、 =3712227.860 、 =523611.598 ,计算坐标方位角计算坐标方位角 、水平距离 。
=62°09'29.4"+180°=242°09'29.4"
注意:一直线有两个方向,存在两个方位角,式中: 、 的计算是过A点坐标纵轴至直线 的坐标方位角,若所求坐标方位角为 ,则应是A点坐标减 点坐标。
8、系统误差影响观测值的准确度,偶然误差影响观测值的精密度。…………………………()
9、经纬仪整平的目的是使视线水平。……………………………………………………………()
10、用一般方法测设水平角时,应采用盘左盘右取中的方法。………………………………()
11、高程测量时,测区位于半径为10km的范围内时,可以用水平面代替水准面。…………()
4、视准轴是目镜光心与物镜光心的连线。………………………………………………………()
5、方位角的取值范围为0°~±180°。………………………………………………………()
6、象限角的取值范围为0°~±90°。………………………………………………………()
7、双盘位观测某个方向的竖直角可以消除竖盘指标差的影响°。……………………………()
32、测绘地形图时,碎部点的高程注记在点的右侧、字头应。
带有缓和曲线的圆曲线逐桩坐标计算例题

带有缓和曲线的圆曲线逐桩坐标计算
例题:某山岭区二级公路,已知交点的坐标分别为JD1(40961.914,91066.103 )、JD2 (40433.528,91250.097 )、JD3(40547.416,91810.392),JD2里程为
K2+200.000, R=150m缓和曲线长度为40m,计算带有缓和曲线的圆曲线的逐桩坐标。
(《工程测量》第202页36题)
解:(1)转角、缓和曲线角、曲线常数、曲线要素、主点里程、主点坐标计算
方法一:偏角法(坐标正算)
(2)第一缓和段坐标计算-0=7 3822 5 = 160 48 03
X Y
(4)第二缓和段坐标计算.0 = 7 38 22
方法二:切线支距法(坐标系转换)
(2)第一缓和段坐标计算
:-12 =160 48 03
X j =X Z H+ xcosot12+ y si n%2X=X ZH+ xs in a12 - yco^t12(本题为左转曲线)
(3) 圆曲线段坐标计算
0=73822 p = 0.444m q = 19.988m
12 =160 48 03 ZH( 40576.543 , 91200.296)
X i = X ZH xcos:12 ysin:12 Y =Y ZH xsin:12一ycos:12
:12=78 30 37
X i =X HZ—xcosc(23 +ysin o(23 Y =Y HZ— xsin53 _yco^t23 (本题为左转曲线)。
第四讲2、圆曲线

24 图12-
Байду номын сангаас
• 1、要增加曲线测设例题 • 2、极坐标法用例题介绍 • 3、曲线测设技巧和方法
2 1
δ 3 = 3 ⋅ δ1
L
δ n = n ⋅ δ1
•
由于《测规》规定,圆曲线的中桩里程宜为20 m的整倍数,而通常在ZY、QZ、YZ附近的曲 线点与主点间的曲线长不足20 m,则称其所对应的弦为分弦。分弦所对应的偏角可按式(11 -8)来计算。
(二)圆曲线详细测设举例
• • • • •
圆曲线详细测设前,曲线主点ZY、QZ、YZ己测设好,因此通常以ZY为测站,分别测设ZY~ QZ和YZ~QZ曲线段,并闭合于QZ作检核。 以上例资料为依据,举例说明测设的步骤与方法。 1.以ZY为测站 (1)偏角计算 已知ZY里程为DK53+621.56,QZ为DK 53+864.70,R = 500 m,曲线ZY QZ为顺时针转 (图12-20)。偏角资料计算见表12-12。由于偏角值与度盘读数增加方向一致,故称“正 拨”。
左 右
• •
•
R——圆曲线的半径。 α 、R为计算曲线要素的必要资料,是已 知值。α 可由外业直接测出,亦可由纸上 定线求得;R为设计时采用的数据。 圆曲线要素的计算公式,由图12-18得: • α
切线长 曲线长 外矢距 T=R ⋅ tan π L = R ⋅α ⋅ • o 180 α E0 = R ⋅ sec − R 2 2
(12-7) 图12-18
•
α 式中计算L时, 以度为单位。
(三)圆曲线主点里程计算
• •
•
主点里程计算是根据计算出的曲线要素,由一已知点里程来推算,一般沿里程增加的方向由 ZY QZ Y2进行推算。 如上例己知ZY点的里程为DK53+621.56,则各主点里程计算如下: • ZY DK53+621.56 • +L/2 243.14 • QZ DK53+864.70 • +L/2 243.14 • YZ DK 54+107.84 若已知交点JD的里程,则需计算出ZY或YZ的里程,由此推算其它主点的里程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1)
2
q 2T L
三三、、主主点点里里程程计计算算
• 1、基本知识 里程:由线路起点算起,沿线路中线到该
中线桩的距离。 表示方法:DK26+284.56。 • “+”号前为公里数,即26km,“+”后为米
数,即284.56m。 • CK —— 表示初测导线的里程。 • DK —— 表示定测中线的里程。
单圆曲线是一段具有一定半径的圆弧。 单圆曲线最简单的一种连接两相邻直线的形式
。 单圆曲线主要是用于铁路专用线和低等级公路
。
一、圆曲线主点
• 圆曲线主点有三个 点,按线路前进方 向冠名。
• 直圆点(ZY)、曲 中点(QZ)、圆直 点(YZ)是确定圆 曲线位置的主要控 制点,称为主点。
• 交点(JD)也是一 个很重要的点。
X YZ1 X JD1 T1 cos αJD1JD2 YYZ1 YJD1 T1 sin αJD1JD2
Y
X ZY2 X JD2 T2 cos αJD1JD2 YZY2 YJD2 T2 sin αJD1JD2 X YZ2 X JD2 T2 cos αJD2 JD3 YYZ2 YJD2 T2 sin αJD2 JD3
• 通用公式:
X ZYi X JDi Ti cos αi1,i YZYi YJDi Ti sin αi1,i
X YZi X JDi Ti cos αi,i1 YYZi YJDi Ti sin αi,i1
X
起点
ZY1 QZ2 YZ1
JD1
O
JD2
QZ2
ZY2
YZ2
终点
Y
• 2)计算曲线点坐标 • ① 计算坐标方位角 • i 点为曲线上任意一点
• 1、基本要求 中桩间距:即相邻两曲线点间的距离,一般为 20 米,地形复杂时为 10 米。施工时可按规范 或标书要求进行。 桩号:即曲线点的里程,必须是中桩间距的整 倍数。
• 例如:ZY点里程为18+197.36,中桩间距为 20m,则第一点里程为18+200 ____________________1_8__+_2_2_0______。
二、圆曲线要素计算
• 1、圆曲线要素 • R —— 半径 • —— 转向角 • T —— 切线长 • L —— 曲线长 • Eo —— 外矢距 • q —— 切曲差
R、、T、L、Eo、q 称为 圆曲线要素。
• 2、计算公式
• 为测量得到,R 为设计值
。
T
R
tg
2
L R
180
Eo
R
(
1
cos
xi xZY C cos αZY i
yi yZY C sin αZY i
五、圆曲线测设
• 1、全站仪坐标放样 • 将曲线点及控制点坐标数据数据输入全站仪,在控制点上
安置仪器,以相邻控制点为后视点,测设曲线点。 • 2、检核 • 在其它控制点Βιβλιοθήκη 安置仪器,定向后实测各曲线点的坐标,
并与计算值比较,若差值在允许范围内,则测设成果合格 ,否则说明测设错误,应查找原因予以纠正。 • 由于用全站仪极坐标法进行中桩测设时,实际的点位误差 主要是测设时的测量误差,误差一般很小,完全能够达到 精度要求,可不做调整。
。li 为 i 点与ZY点里程之差。
i
li R
180 π
δi
i
2
90 li πR
ZY-
i
ZY-
JD
ZYi ZYJD i 当曲线左转时用“-”,右转时用“+”。
• ② 计算弦长
C 2 Rsin
③ 计算曲线点坐标
此时的已知数据为:
ZY- i
ZY(xZY,yZY)、ZY-
i、C。
根据坐标正算原理:
• 2、计算方法 • 根据交点里程和圆曲线要素计算主点里程。
• 公路习惯推算方法 :
四、单圆曲线测设资料计算
• 曲线测设是指每隔一定距离测设一个曲线 点以在地面上标志曲线平面位置。
• 现阶段曲线测设主要采用全站仪或GPS进行 ,而这两种方法所需测设资料是曲线点的 坐标,故实施测设前必须计算曲线点的坐 标。
• 第二点里程为
2、曲线点坐标计算
X
起点
ZY1
QZ2 YZ1
JD2
QZ2
ZY2
YZ2
终点
JD1
Y
O
• 已知条件:起点、终点及各交点的坐标。
• 1)计算ZY、YZ点坐标
X
起点
ZY1 QZ2 YZ1
JD2
QZ2
ZY2
YZ2
终点
JD1
O
X ZY1 X JD1 T1 cos α起JD1 YZY1 YJD1 T1 sin α起JD1
