第7章 管道的屈曲分析
管道的屈曲分析
• 压扁处容易在疲劳载荷下产生裂纹。
压扁分析的Wierzbicki(维兹比基)模式
• 忽略了环向弯曲和轴向拉伸的塑性相互作用; • 忽略了弹塑性变形的相互作用; • 忽略了应变硬化; • 假定冲击载荷作用于垂直于管道的平面内。
塑性铰
压扁处的位移
临界载荷
直线管道的挠曲微分方程式
Ay P 2By Cy 0
各系数分别为
A EI
B
Ku D1
1
D
C
K 0 D1
2
D
K0
2Ku
EI —管道的弯曲刚度; Ku —土壤对管道的轴向抗力系数; K0 —土壤的压缩抗力系数;
逆解法:假设管道失稳时的弯曲形状为
y f x
y f sin x
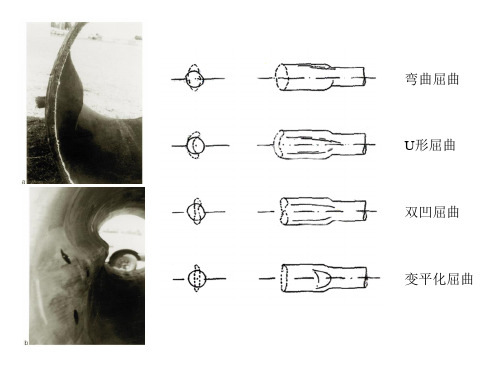
弯曲屈曲 U形屈曲 双凹屈曲 变平化屈曲
屈曲分析的内容
轴向屈曲 地下埋设管道
屈 曲
上浮屈曲
局部屈曲
地下埋设管道 海底埋设管道
机械作用 外压
屈曲传播
4-1 地下管道的轴向稳定性
• 在嵌固段,管道所受到的最大轴向力为:
P pD ET A
2t
• 管道轴向稳定性的验算条件
P nPcr
n——安全系数,可取n=0.6~0.75。
0.39D
soh02tg0.7
0.7Ch0
cos0.7
式中: γso——管顶填土的容重,N/m3; φ——土壤内摩擦角; C——土壤粘着力。
当向上弯曲管道的轴向稳定性得不到保证时,可采 用增加埋深、设置固定墩或锚固等方法。
4-2 海底管线的上浮屈曲
• 海底(或地震液化土)覆盖土层的刚性较小,管 子容易因屈曲而产生向上拱的弯曲变形,称为上 浮屈曲。
材料力学管道分析知识点总结

材料力学管道分析知识点总结材料力学是工程力学的一个重要分支,研究材料在外力作用下的力学行为。
管道作为一种常见的工程结构,在各个领域都有广泛应用,了解材料力学管道分析的知识点,对于工程设计和施工具有重要意义。
本文将对材料力学管道分析的知识点进行总结,旨在帮助读者更好地理解和应用该领域的知识。
1. 弹性力学基本概念弹性力学是研究材料在小应变作用下的力学行为的分支。
在材料力学管道分析中,弹性力学的基本概念是必须要了解的。
弹性体的本构方程、应力-应变关系、应变能密度以及泊松比等概念是分析管道弹性行为的基础。
2. 管道的应力分析管道在使用过程中会承受外部载荷的作用,因此对管道的应力分析是非常重要的。
在材料力学管道分析中,应力的分布和大小对于设计管道的强度和稳定性具有重要意义。
应力分析会涉及到静力学平衡、材料的弹性性质以及管道的几何尺寸等因素。
3. 管道的变形分析管道在受到外部载荷作用下,会发生弯曲、拉伸和压缩等变形。
变形分析是了解管道结构受力情况以及变形形式和程度的手段。
在变形分析中,考虑到材料的弹性性质、几何尺寸的变化以及边界条件的影响。
4. 管道的稳定性分析管道的稳定性是指管道在受力作用下不产生破坏或失稳的能力。
稳定性分析是确保管道在使用过程中具有足够的强度和刚度以防止破坏的重要手段。
管道稳定性分析会考虑到材料的弹性性质、几何尺寸的变化、外界环境的影响以及边界条件等因素。
5. 管道的疲劳分析管道在长期使用过程中,会受到交变载荷的作用,从而引发疲劳破坏。
疲劳分析是为了评估管道在反复载荷下的寿命和安全性。
在疲劳分析中,需要考虑到材料的疲劳性能、载荷的频率和幅值、应力范围和设计寿命等因素。
6. 管道的裂纹扩展分析管道的裂纹扩展分析是为了评估管道在裂纹存在的情况下的寿命和安全性。
裂纹扩展分析需要考虑到材料的断裂韧性、裂纹形态和尺寸、应力场分布以及环境因素等因素。
7. 管道的振动分析管道在某些情况下会受到振动的激励,从而引发共振或者疲劳破坏。
屈曲分析常用方法

屈曲分析常用方法
介绍了用于屈曲分析的常用方法
处理屈曲问题可以用的几种计算方式
关键字特点
线性屈曲分析*buckle用于估计最大临界载荷和屈曲模态,无法查看屈曲后状态。
可用作引入缺陷的之前的计算分析步,需要加载荷;屈曲特征值与载荷相乘就是屈曲载荷。
主要用于缺陷不敏感结构。
非线性屈曲分析*static, riks用于计算最大临界载荷和屈曲以后的后屈曲响应,可以查看后屈曲状态,用弧长量代替时间量。
载荷比例因子与载荷相乘就是屈曲载荷。
可以用于缺陷敏感结构,如果结构存在接触,容易出现收敛问题。
通用静力分析*static用于计算结构刚度不变或结构刚度增大的结构,如果结构出现屈曲或者垮塌,很容易出现不收敛问题,无法计算后屈曲状态。
通用静力分析+阻尼稳定*static, stabilize在静力分析步中加阻尼,有助于收敛,计算的结束点可以比通用静力分析要后一些,但要注意阻尼不能加得过大。
隐式动力分析*Dynamic将屈曲问题作为隐式动力问题来处理,适合接触脱开的问题,但是假如结构接触对较多,很容易出现收敛问题。
这种分析类型使用的是隐式积分方法。
显式动力分析*dynamic, explicit将屈曲问题作为显式动力问题来处理,适合接触脱开的问题,能够适应复杂的模型,复杂的接触对,收敛效果较好。
但是计算量较大,计算时间较长,计算完以后需要评估计算结果是否可靠。
这种分析类型使用的是显式积分方法。
屈曲分析实例解析

屈曲分析屈曲分析- 分析内容屈曲分析主要用于研究结构在特定载荷下的稳定性以及确定结构失稳的临界载荷,屈曲分析包括:线性屈曲和非线性屈曲分析。
线弹性失稳分析又称特征值屈曲分析;线性屈曲分析可以考虑固定的预载荷,也可使用惯性释放;非线性屈曲分析包括几何非线性失稳分析,弹塑性失稳分析,非线性后屈曲(Snap-through)分析。
欧拉屈曲buckling结构丧失稳定性称作(结构)屈曲或欧拉屈曲。
L.Euler从一端固支另一端自由的受压理想柱出发.给出了压杆的临界载荷。
所谓理想柱,是指起初完全平直而且承受中心压力的受压杆。
设此柱是完全弹性的,且应力不超过比例极限,若轴向外载荷P小于它的临界值,此杆将保持直的状态而只承受轴向压缩。
如果一个扰动(如—横向力)作用于杆,使其有一小的挠曲,在这一扰动除去后。
挠度就消失,杆又恢复到平衡状态,此时杆的直的形式的弹性平衡是稳定的。
若轴向外载荷P大于它的临界值,柱的直的平衡状态变为不稳定,即任意扰动产生的挠曲在扰动除去后不仅不消失,而且还将继续扩大,直至达到远离直立状态的新的平衡位置为止,或者弯折。
此时,称此压杆失稳或屈曲(欧拉屈曲)。
屈曲分析- 分析分类线性屈曲:是以小位移小应变的线弹性理论为基础的,分析中不考虑结构在受载变形过程中结构构形的变化,也就是在外力施加的各个阶段,总是在结构初始构形上建立平衡方程。
当载荷达到某一临界值时,结构构形将突然跳到另一个随遇的平衡状态,称之为屈曲。
临界点之前称为前屈曲,临界点之后称为后屈曲。
侧扭屈曲:梁的截面一般都作成窄而高的形式,对截面两主轴惯性矩相差很大。
如梁跨度中部无侧向支承或侧向支承距离较大,在最大刚度主平面内承受横向荷载或弯矩作用时,荷裁达一定数值,梁截面可能产生侧向位移和扭转,导致丧失承载能力,这种现象叫做梁的侧向弯扭屈曲,简称侧扭屈曲。
理想轴向受压直杆的弹性弯曲屈曲:即假定压杆屈曲时不发生扭转,只是沿主轴弯曲。
但是对开口薄壁截面构件,在压力作用下有可能在扭转变形或弯扭变形的情况下丧失稳定,这种现象称为扭转屈曲或弯扭屈曲。
管道的屈曲分析

可以求得
EI
4
K0 D 1
2
D
Pcr
2
Ku D 1
1 D
EIK0
D
1
2 D
• 失稳时,轴向位移与横向位移相比只是一个二 阶小数,可忽略不计。
4 EI
K0D Pcr 2 EIK0D
适用于直线管道(或曲率半 径1000D的弯曲管道)。
土壤的压缩抗力系数K0
弯曲屈曲 U形屈曲 双凹屈曲 变平化屈曲
屈曲分析的内容
轴向屈曲 地下埋设管道
屈 曲
上浮屈曲
局部屈曲
地下埋设管道 海底埋设管道
机械作用 外压
屈曲传播
4-1 地下管道的轴向稳定性
• 在嵌固段,管道所受到的最大轴向力为:
P pD ET A
2t
• 管道轴向稳定性的验算条件
P nPcr
n——安全系数,可取n=0.6~0.75。
• 压扁深度大于管道直径8%时,影响管道的爆破 强度;
• 压扁处容易在疲劳载荷下产生裂纹。
压扁分析的Wierzbicki(维兹比基)模式
• 忽略了环向弯曲和轴向拉伸的塑性相互作用; • 忽略了弹塑性变形的相互作用; • 忽略了应变硬化; • 假定冲击载荷作用于垂直于管道的平面内。
塑性铰
压扁处的位移
2 210 103 (1 0.32 )
6
3
273
4.90MPa
4-5 海底管道的屈曲传播
• 局部屈曲 • 屈曲传播 • 止屈措施
1、局部屈曲
• 对管子局部屈曲可定义为:管子截面扁平化或翘 曲折皱超过规定的限度。
• 实际管子存在残余的椭圆度,而且还可能产生显 著的塑性变形。因此,管道的失稳的临界外压是 材料屈服极限的函数。
钻井用连续管的屈曲分析

钻井用连续管的屈曲分析张辛1, 徐兴平1, 王龙庭2,王雷1(1.中国石油大学(华东)机电学院,山东东营,207061;2. 胜利油田高原石油装备有限责任公司研发中心)摘要:连续管弯曲可能会出现在任何井段。
但是,在不同的井段开始形成弯曲的临界压缩载荷不同。
本文在总结国内外学者研究的基础上,以垂直井段为例,对已有公式的适用条件进行了探讨。
采用能量守恒原理,对垂直井段的连续管进行临界屈曲载荷分析,得到连续管的临界屈曲载荷。
利用拉格朗日乘子方法分别对管柱处于不同屈曲形式下进行管柱与套管壁的接触载荷计算。
并对管柱的屈曲行为进行了ABAQUS计算机模拟分析。
关键词:连续管屈曲分析计算模型计算机模拟Buckling Analysis of Drilling Coiled TubingZhang Xin1, Xu Xingping1, Wang Longting2, Wang Lei1(1. College of Mechanical and Electronic Engineering, China University of Petroleum, Dongying, Shandong, 257061, China; 2. Shengli Oilfield Highland Petroleum Equipment Co., Ltd. R&Dcenter)Abstract:The bend of coiled tubing may appear in any hole section. However, the critical compressive load is different in different interval when the bend is generated. On the base of the research of domestic and foreign scholars, applicable conditions to the existed formulas are researched in this paper with the example of vertical interval. Using energy method, equations are derived to predict the axial compression force required to produce buckling in vertical wells. Utilizing the Lagrange multiplier method, the unit lateral contact force corresponding to straight, sinusoidal, and helical configurations between CT and casing are obtained in vertical, inclined, and curved wells, respectively. The buckling of CT is also discussed on the basis of ABAQUS computer simulations.Keywords: Coiled tubing Buckling analysis Computation model Computer simulation前言在连续管下入过程中,由于管柱本身重力的影响和管柱与井壁摩擦的影响,使得管柱在受压时由初始的近似直线状态变为曲线状态,这就是管柱的屈曲。
埋设悬跨海底管道的屈曲分析

第23卷第2期 V ol.23 No.2 工 程 力 学 2006年 2 月 Feb. 2006 ENGINEERING MECHANICS173———————————————收稿日期:2004-03-26;修改日期:2004-05-27作者简介:*邢静忠(1966),男,甘肃人,教授,博士,从事海洋石油工程力学研究(E-mail: hsingjzh@); 柳春图(1935),男,江苏人,研究员,博士生导师,从事固体力学、断裂和疲劳研究; 徐永君(1964),男,河北人,博士,从事工程力学研究。
文章编号:1000-4750(2006)02-0173-04埋设悬跨海底管道的屈曲分析*邢静忠1,2,柳春图1,徐永君1(1. 中国科学院力学研究所, 北京 100080; 2. 兰州理工大学理学院, 兰州 730050)摘 要:考虑海床刚度,研究了埋设悬跨海底管道在热膨胀引起的轴向压力下的屈曲问题。
传统方法是将悬跨管道简化为两端简支或者两端固支梁来处理。
基于欧拉-伯努利梁理论,考虑线弹性海床刚度和轴向压力,建立并求解了埋设段管道和悬跨段管道在自重作用下的四阶常微分方程,获得了两段管道的静挠度和内力的解析公式。
通过对静挠度的特性分析,给出了埋设管道段和悬跨管道段的稳定性判断准则。
关键词:屈曲;海底管道;悬跨;弹性地基;热膨胀 中图分类号:O343 文献标识码:ABUCKLING ANALYSIS OF BURIED SPANNING SUBMARINE PIPELINE*XING Jing-zhong 1,2 , LIU Chun-tu 1 , XU Yong-jun 1(1. Institute of Mechanics, Chinese Academy of Sciences, Beijing 100080, China; 2. School of Science, Lanzhou University of Science, Lanzhou 730050, China)Abstract: This paper presents a buckling analysis of buried spanning submarine pipelines under axial compressive force caused by thermal expansion, in which the seabed stiffness is taken into account. Traditional methods treat each span segment as a simply-supported beam or clamped-clamped beam in practice. A new approach is developed based on Euler-Bernoulli beam theory, taking into account the linear elastic stiffness of seabed and temperature-driving axial force. A fourth order ordinary differential equation governing buried segment in elastic seabed and spanning segment under self-weight and axial compressive force is established and solved. The static deflection and internal force function of both segments are obtained in closed form. Stability criteria of buried segment and spanning segment are established through analyzing the characteristics of static deflection.Key words: buckling; submarine pipeline; spanning; elastic foundation; thermal expansion由于海床不平整,或者海流淘蚀,海底管道经常出现悬跨(Spanning)情况。
海底长输油气管道的隆起屈曲分析

海底长输油气管道的隆起屈曲分析余志兵;孙国民;王辉;高嵩【摘要】该文基于Palmer等研究学者提出的半经验解析公式,探讨了海床几何初始缺陷、温降及土壤特性等因素对分析结果的敏感性.结合工程计算所需的前提假设,通过使用自编程序对一工程实例进行分析,结果表明该方法的计算量小、直观性强,对工程设计具有一定的指导意义.【期刊名称】《中国海洋平台》【年(卷),期】2015(030)002【总页数】6页(P64-69)【关键词】长输海底管道;高温高压;初始几何缺陷;隆起屈曲【作者】余志兵;孙国民;王辉;高嵩【作者单位】海洋石油工程股份有限公司,天津300452;海洋石油工程股份有限公司,天津300452;海洋石油工程股份有限公司,天津300452;海洋石油工程股份有限公司,天津300452【正文语种】中文【中图分类】P756随着海上油气资源不断地开发与利用,高温高压海底管道的工程应用逐渐增多,同时海底管道在温度与压力下的变形问题也逐渐显现出来。
对于埋设在海床以下的管道,受管沟不平整度及海床土壤约束的影响,管线无法自由变形,应力不断累积,当应力值超过上覆盖土体抗力时,管线将发生竖直方向的弯曲大变形,最终发生失效而破坏[1,2]。
通常可以采取一些工程附加措施以避免海底管道发生隆起屈曲,例如加大管道埋设深度,增加管道配重厚度,提高铺设后的残余张力及改变管道结构形式等[3,4],特殊情况下还可以采取降低工艺输送要求的方式,达到减小管道轴向压力的目的。
而对于高温高压长输埋设海底管道,为抑制其隆起屈曲变形,考虑到工程经济性,一般会选取增大管道埋设深度或增加上覆盖土厚度等方式。
但在工程设计阶段,若过于保守地考虑一些基础参数,同样会导致较高的工程施工费用。
因此,在开展长输海底管线的隆起屈曲分析时,应着重考虑环境因素变化的影响。
该文基于Palmer等学者提出的隆起屈曲分析中经典的孤立点支撑模型及半经验解析公式[5],假设了一些必需的工程分析前提条件,结合工程实例,分析了管道路由的土壤特性、输送介质温度变化及海床沟槽位置的几何初始缺陷等因素对抑制管线发生隆起屈曲所需的最小上覆盖土厚度的影响,数值计算得出的结果可以用于指导工程实践。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
1
管道的屈曲分析
• 屈曲也称为失稳,是指结构丧失了保持其原有平 衡形状的能力。 • 由于管道的薄壁、细长的结构特性,在其受力和 变形条件稍有恶化时,容易产生屈曲破坏。 • 与陆上管道相比,海底管道可能更容易发生屈曲 破坏。 • 管道产生屈曲的原因,通常有外压作用下的弹性 失稳、机械作用或管道本身缺陷造成的局部屈曲、 弯曲屈曲和象“压杆”一样的纵向屈曲等。
P ≤ nPcr
n——安全系数,可取n=0.6~0.75。
5
临界载荷
直线管道的挠曲微分方程式
Ay′′′′ + (P − 2 B ) y′′ + Cy = 0 各系数分别为
A = EI B = K u D 1 + C = K 0 D 1 + 1 βD 2 βD
• 几种常见的屈服形式有:轴向屈曲、上浮屈曲、压扁、 外压下的屈曲、屈曲传播等; • 陆上管道的屈曲验算的安全系数取0.60~0.75; • 在陆地管道的屈曲分析中需要考虑土壤刚度的影响; 按考虑管道的弯曲曲率和不考虑管道的弯曲曲率两种 情形考虑。 • 海底管道的上浮屈曲中存在安全温升; • 管道有临界外压; • 在外压下,局部屈曲管道会发生屈曲传播,分别存在 屈曲起始压力和屈曲传播压力,屈曲起始压力大于屈 曲传播压力; • 三种形式的止屈器。
α
300 p e α = 1+ D / t p cr
Mcr和pcr分别是管道单独受弯曲和外压时的临界值。
24
2、屈曲传播
• 管道的局部屈曲可以传播,传播的速度异常迅速, 屈曲传播的长度有几百米至上千米。 • 屈曲起始压力和屈曲传播压力。
pi > p p
pe > pi
2
弯曲屈曲
U形屈曲
双凹屈曲
变平化屈曲
3
屈曲分析的内容
轴向屈曲
地下埋设管道
屈 曲
上浮屈曲
地下埋设管道 海底埋设管道
局部屈曲
机械作用 外压 屈曲传播
4
7.1 地下管道的轴向稳定性
• 在嵌固段,管道所受到的最大轴向力为:
pD P = −ν + αE∆T A 2t
• 管道轴向稳定性的验算条件
两式须联立求Pcr。
[
]
1 2
14
安全温升
150温 120 90 60 30 0 0
T( ℃
f=0.01 f=0.05 f=0.1 f=0.2 f=0.4 f=0.6
20
40
60
80
不同摩擦系数
T( ℃)
100 L(m)
150 120 90 60 30 0 0 10
w=1200N/m w=2400N/m w=3600N/m w=4800N/m w=6000N/m
10
qcr—土壤抗管道作向上的横向位移时临界支承力,N/m。
土壤的临界支承力
0.7Ch0 qcr = γ so D(h0 − 0.39 D ) + γ so h0 tg (0.7ϕ ) + cos(0.7ϕ )
2
式中: γso——管顶填土的容重,N/m3; φ——土壤内摩擦角; C——土壤粘着力。 当向上弯曲管道的轴向稳定性得不到保证时,可采 用增加埋深、设置固定墩或锚固等方法。
E
q k 2 L2 k 2 x2 coskx y = 2 − + +1− k P cos kL 8 2 2
13
临界载荷与长度
EI Pcr = 80.73 2 L
qL 2 5 P0 − P cr = 1.598 EAfqL − 0.25( fEI ) EI
26
3、止屈器
为了防止屈曲和屈曲的传播,可以采取两种措施: –加大全线管壁厚度:可行,但不经济 –管道局部加厚,或采用止屈器,使屈曲传播只 限于两止屈器之间。
27
止屈器的形式
a)活动式(套 筒式)屈曲限 制器; b)厚壁管筒式 (或整体式) 屈曲限制器; c)焊接固定式 屈曲限制器。
28
本章小结
20
例: Ф273×6钢管能承受的极限外压
2E t C= 2 (1 − υ ) D 式中:C — 极限外压; D — 外径;
t — 壁厚;
3
ν —泊松比(0.3);
E — 弹性模量(210GPa )。
计算结果:
2 × 210 × 10 6 C= = 4.90 MPa 2 (1 − 0.3 ) 273
3 3
21
7.5
海底管道的屈曲传播
• 局部屈曲 • 屈曲传播 • 止屈措施
22
1、局部屈曲
• 对管子局部屈曲可定义为:管子截面扁平化或翘 曲折皱超过规定的限度。 • 实际管子存在残余的椭圆度,而且还可能产生显 著的塑性变形。因此,管道的失稳的临界外压是 材料屈服极限的函数。
t p cr = 2σ D
中等密度的土壤
9
向上弯曲管线时 式中:
Pcr = 0.375qρ 0
ρ0—计算曲率半径,m;
q=q0+qcr,N/m; q—管道向上位移时的土壤极限阻力, q =q1+q2 ,N/m; q0—管道所受的向下压力,
0
q1—管子本身和管内流体重量,N/m; q2—压重物的重量或锚栓对管道的拉力,N/m; n —土壤的载荷系数,n=0.8~1.2;
29
压扁分析的Wierzbicki(维兹比基)模式
• 忽略了环向弯曲和轴向拉伸的塑性相互作用; • 忽略了弹塑性变形的相互作用; • 忽略了应变硬化; • 假定冲击载荷作用于垂直于管道的平面内。 塑性铰
18
压扁处的位移
3 ud = 32π 2 P
(σ t )
2 3 y
ud — 压扁处的位移
• 失稳时,轴向位移与横向位移相比只是一个二 阶小数,可忽略不计。
EI λ =π4 K0 D Pcr = 2 EIK 0 D
适用于直线管道(或曲率半 径ρ≥1000D的弯曲管道)。
8
土壤的压缩抗力系数K0
土壤性质 密度小的土壤 土壤名称 泥煤土 流 砂 软湿土 新填砂 压实砂 砾 石 湿粘土 K0,kgf/cm3 0.05~0.1 0.1~0.5 0.1~0.5 0.1~0.5 0.5~5.0 0.5~5.0 0.5~5.0
2σ s t 1 p cr = 2σ s 1 − D 3 σ e
2 σe ≤ σs 3
2 σe > σs 3
23
考虑实际管子不可能是理想的圆形,并且受环向和 弯曲应力的联合作用,其临界压力值会大大减小。
M M cr pe + p =1 cr
EI — 管道的弯曲刚度; K u — 土壤对管道的轴向抗力系数; K 0 — 土壤的压缩抗力系数;
β=
K0 2Ku
6
逆解法:假设管道失稳时的弯曲形状为
y
f
x
λ
πx y = f sin λ
λ — 称为管道的失稳波长。
7
可以求得
λ =π
4
EI 2 K 0 D 1 + βD
1 2 2 Ku D 1 + P = cr + EIK 0 D 1 + βD βD
20
30
40
50
60
70
80
90
不同覆盖土层载荷
100 L(m)
15
7.3 压扁
在冲击载荷的作用下,会产生较大的塑性变形, 即被压扁。
16
压扁的影响
• 压扁深度大于管道直径5%时,影响清管球的 通过; • 压扁深度大于管道直径8%时,影响管道的爆 破强度; • 压扁处容易在疲劳载荷下产生裂纹。
17
11
7.2 海底管线的上浮屈曲
• 海底(或地震液化土)覆盖土层的刚性较小,管 子容易因屈曲而产生向上拱的弯曲变形,称为上 浮屈曲。 • 上浮屈曲产生过量的垂直位移和塑性变形,被认 为是一种失效情形。 • 和铁路铁轨中的热胀屈曲相类似。
12
上浮屈曲的形状
y C' A
△L
B B'
C L x
D' D
△L
pe > p p pe < p p
一旦造成屈曲,肯定传播 屈曲发生 屈曲传播 屈曲传播停止
25
pi
pp
管道的屈曲传播压力的确定(试验和理论研究)
Battelle
2t p p = 6σ s= 1.15πσ s D−t
2
传播压力只取决于屈服极限和径厚比。
P — 压扁处的集中力
σ y — 屈服应力
t — 壁厚
19
7.4 管道在外压作用下的稳定性
• 对于外压作用下的管子,稳定性是必须优先考虑 的因素。 • 理想圆管的临界压力:
2E t C= 2 (1 − υ ) D
3
• 当管子承受的外压大于临界值时,管子将不能保 持圆形形状或完全坍塌。 • 考虑实际管子不是理想的圆形,并且受环向和弯 曲应力的联合作用,其临界压力值会大大减小。
