2017选择题专项训练参考答案
2017年盘锦市中考数学试题(含答案和解释)

2017年盘锦市中考数学试题(含答案和解释)一、选择题(下列各题的备选答案中,只有一个是正确的,请将正确答案的序号涂在答题卡上,每小题3分,共30分)1.﹣2的相反数是()A.2B..﹣D.﹣2 【答案】A.【解析】试题分析:﹣2的相反数是2,故选A.考点:相反数.2.以下分别是回收、节水、绿色包装、低碳四个标志,其中是中心对称图形的是()A.B..D.【答案】.考点:中心对称图形.3.下列等式从左到右的变形,属于因式分解的是()A.B..D.【答案】.【解析】试题分析:A.,故A不是因式分解;B.,故B不是因式分解;.,故正确;D.=a(x+1)(x﹣1),故D分解不完全.故选.考点:因式分解的意义.4.如图,下面几何体的俯视图是()A.B..D.【答案】D.【解析】试题分析:从上面可看到第一行有三个正方形,第二行最左边有1个正方形.故选D.考点:简单组合体的三视图..在我市举办的中学生“争做明盘锦人”演讲比赛中,有1名学生进入决赛,他们决赛的成绩各不相同,小明想知道自己能否进入前8名,不仅要了解自己的成绩,还要了解这1名学生成绩的()A.众数B.方差.平均数D.中位数【答案】D.考点:统计量的选择.6.不等式组的解集是()A.﹣1<x≤3B.1≤x<3.﹣1≤x<3D.1<x≤3【答案】.考点:解一元一次不等式组.7.样本数据3,2,4,a,8的平均数是4,则这组数据的众数是()A.2B.3.4D.8【答案】B.【解析】试题分析:a=4×﹣3﹣2﹣4﹣8=3,则这组数据为3,2,4,3,8;众数为3,故选B.考点:众数;算术平均数.8.十一期间,几名同学共同包租一辆中巴车去红海滩游玩,中巴车的租价为480元,出发时又有4名学生参加进,结果每位同学比原少分摊4元车费.设原游玩的同学有x名,则可得方程()A.B..D.【答案】D.【解析】试题分析:由题意得:,故选D.考点:由实际问题抽象出分式方程.9.如图,双曲线(x<0)经过▱AB的对角线交点D,已知边在轴上,且A⊥于点,则▱AB的面积是()A.B..3D.6【答案】.考点:反比例函数系数的几何意义;平行四边形的性质.10.如图,抛物线与x轴交于点A(﹣1,0),顶点坐标(1,n),与轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①ab>0;②3a+b<0;③﹣≤a≤﹣1;④a+b≥a2+b(为任意实数);⑤一元二次方程有两个不相等的实数根,其中正确的有()A.2个B.3个.4个D.个【答案】B.【解析】试题分析:∵抛物线开口向下,∴a<0,∵顶点坐标(1,n),∴对称轴为直线x=1,∴=1,∴b=﹣2a>0,∵与轴的交点在(0,3),(0,4)之间(包含端点),∴3≤≤4,∴ab<0,故①错误;3a+b=3a+(﹣2a)=a<0,故②正确;∵与x轴交于点A(﹣1,0),∴a﹣b+=0,∴a﹣(﹣2a)+=0,∴=﹣3a,∴3≤﹣3a≤4,∴﹣≤a≤﹣1,故③正确;∵顶点坐标为(1,n),∴当x=1时,函数有最大值n,∴a+b+≥a2+b+,∴a+b≥a2+b,故④正确;一元二次方程有两个相等的实数根x1=x2=1,故⑤错误.综上所述,结论正确的是②③④共3个.故选B.考点:抛物线与x轴的交点;根的判别式;二次函数的性质.二、填空题(每小题3分,共24分)11.2016年我国对“一带一路”沿线国家直接投资14亿美元,将14亿用科学记数法表示为.【答案】14×1010.【解析】试题分析:将14亿用科学记数法表示为:14×1010.故答案为:14×1010.考点:科学记数法—表示较大的数.12.若式子有意义,则x的取值范围是.【答案】x>.考点:二次根式有意义的条.13.计算:= .【答案】.【解析】试题分析:原式= ,故答案为:.考点:整式的除法.14.对于▱ABD,从以下五个关系式中任取一个作为条:①AB=B;②∠BAD=90°;③A=BD;④A⊥BD;⑤∠DAB=∠AB,能判定▱ABD是矩形的概率是.【答案】.【解析】试题分析:由题意可知添加②③⑤可以判断平行四边形是矩形,∴能判定▱ABD是矩形的概率是,故答案为:.考点:概率公式;矩形的判定.1.如图,在△AB中,∠B=30°,∠=4°,AD是B边上的高,AB=4,分别以B、为圆心,以BD、D为半径画弧,交边AB、A于点E、F,则图中阴影部分的面积是2.【答案】.考点:扇形面积的计算;勾股定理.16.在平面直角坐标系中,点P的坐标为(0,﹣),以P为圆心的圆与x轴相切,⊙P的弦AB(B点在A点右侧)垂直于轴,且AB=8,反比例函数(≠0)经过点B,则= .【答案】﹣8或﹣32.【解析】试题分析:设线段AB交轴于点,当点在点P的上方时,连接PB,如图,∵⊙P 与x轴相切,且P(0,﹣),∴PB=P=,∵AB=8,∴B=4,在Rt△PB 中,由勾股定理可得P= =3,∴=P﹣P=﹣3=2,∴B点坐标为(4,﹣2),∵反比例函数(≠0)经过点B,∴=4×(﹣2)=﹣8;当点在点P下方时,同理可求得P=3,则=P+P=8,∴B(4,﹣8),∴=4×(﹣8)=﹣32;综上可知的值为﹣8或﹣32,故答案为:﹣8或﹣32.考点:反比例函数图象上点的坐标特征;切线的性质;分类讨论.17.如图,⊙的半径A=3,A的垂直平分线交⊙于B、两点,连接B、,用扇形B围成一个圆锥的侧面,则这个圆锥的高为.【答案】.考点:圆锥的计算;线段垂直平分线的性质.18.如图,点A1(1,1)在直线=x上,过点A1分别作轴、x轴的平行线交直线于点B1,B2,过点B2作轴的平行线交直线=x于点A2,过点A2作x轴的平行线交直线于点B3,…,按照此规律进行下去,则点An的横坐标为.【答案】.考点:一次函数图象上点的坐标特征;规律型:点的坐标;综合题.三、解答题(19小题8分,20小题10分,共18分)19.先化简,再求值:,其中a= .【答案】,1.【解析】试题分析:根据分式的加法和除法可以化简题目中的式子,然后将a 的值代入化简后的式子即可解答本题.试题解析:原式===当a=1+2=3时,原式= =1.考点:分式的化简求值;零指数幂;负整数指数幂.20.如图,码头A、B分别在海岛的北偏东4°和北偏东60°方向上,仓库在海岛的北偏东7°方向上,码头A、B均在仓库的正西方向,码头B和仓库的距离B=0,若将一批物资从仓库用汽车运送到A、B两个码头中的一处,再用货船运送到海岛,若汽车的行驶速度为0/h,货船航行的速度为2/h,问这批物资在哪个码头装船,最早运抵海岛?(两个码头物资装船所用的时间相同,参考数据:≈14,≈17)【答案】这批物资在B码头装船,最早运抵海岛.由题意∠=7°,∠B=60°,∠=4°,∠=90°,∴∠=1°,∠B=30°,=A,∵∠B=∠+∠B,∴∠=∠B=1°,∴B=B=0(),在Rt△B中,= B=2(),B= = (),在Rt△A中,=A=2(),A= ≈3,∴AB=B﹣A≈17(),∴从A码头的时间= =34(小时),从B码头的时间= =3(小时),3<34.答:这批物资在B码头装船,最早运抵海岛.考点:解直角三角形的应用﹣方向角问题;勾股定理的应用.21.如今很多初中生购买饮品饮用,既影响身体健康又给家庭增加不必要的开销,为此数学兴趣小组对本班同学一天饮用饮品的情况进行了调查,大致可分为四种:A:自带白开水;B:瓶装矿泉水;:碳酸饮料;D:非碳酸饮料.根据统计结果绘制如下两个统计图,根据统计图提供的信息,解答下列问题:(1)这个班级有多少名同学?并补全条形统计图.(2)若该班同学没人每天只饮用一种饮品(每种仅限1瓶,价格如下表),则该班同学用于饮品上的人均花费是多少元?(3)若我市约有初中生4万人,估计我市初中生每天用于饮品上的花费是多少元?(4)为了养成良好的生活习惯,班主任决定在自带白开水的名同学(男生2人,女生3人)中随机抽取2名同学做良好习惯监督员,请用列表法或树状图法求出恰好抽到2名女生的概率.【答案】(1)0;(2)26;(3)104000元;(4).【解析】试题分析:(1)由B类型的人数及其百分比求得总人数,在用总人数减去其余各组人数得出类型人数,即可补全条形图;(2)由各类的人数可得其总消费,进而可求出该班同学用于饮品上的人均花费是多少元;(3)用总人数乘以样本中的人均消费数额即可;(4)用列表法或画树状图法列出所有等可能结果,从中确定恰好抽到一名男生和一名女生的结果数,根据概率公式求解可得.试题解析:(1)∵抽查的总人数为:20÷40%=0人,∴类人数=0﹣20﹣﹣1=10人,补全条形统计图如下:(2)该班同学用于饮品上的人均花费=(×0+20×2+3×10+4×1)÷0=26元;(3)我市初中生每天用于饮品上的花费=40000×26=104000元.(4)列表得:或画树状图得:所有等可能的情况数有20种,其中一男一女的有12种,所以P(恰好抽到一男一女)= = .考点:列表法与树状图法;用样本估计总体;扇形统计图;条形统计图;加权平均数.22.如图,在平面直角坐标系中,直线l:与x轴、轴分别交于点,N,高为3的等边三角形AB,边B在x轴上,将此三角形沿着x轴的正方向平移,在平移过程中,得到△A1B11,当点B1与原点重合时,解答下列问题:(1)求出点A1的坐标,并判断点A1是否在直线l上;(2)求出边A11所在直线的解析式;(3)在坐标平面内找一点P,使得以P、A1、1、为顶点的四边形是平行四边形,请直接写出P点坐标.【答案】(1)A1(,3),在直线上;(2);(3)P1(,3),P2(,﹣3),P3(﹣,3).试题解析:(1)如图作A1H⊥x轴于H.在Rt△A1H中,∵A1H=3,∠A1H=60°,∴H=A1H•tan30°= ,∴A1(,3),∵x= 时,=3,∴A1在直线上.(2)∵A1(,3),1(,0),设直线A11的解析式为=x+b,则有:,解得:,∴直线A11的解析式为.(3)∵(4 ,0),A1(,3),1(2 ,0),由图象可知,当以P、A1、1、为顶点的四边形是平行四边形时,P1(,3),P2(,﹣3),P3(﹣,3).考点:一次函数综合题;分类讨论.23.端午节前夕,三位同学到某超市调研一种进价为80元的粽子礼盒的销售情况,请根据小梅提供的信息,解答小慧和小杰提出的问题.(价格取正整数)【答案】小慧:定价为102元;小杰:880元的销售利润不是最多,当定价为110元或111元时,销售利润最多,最多利润为9300元.=﹣10x2+2210x﹣112800,当=880时,﹣10x2+2210x﹣112800=880,整理,得:x2﹣221x+12138=0,解得:x=102或x=119,∵当x=102时,销量为1410﹣1020=390,当x=119时,销量为1410﹣1190=220,∴若要达到880元的利润,且薄利多销,∴此时的定价应为102元;小杰:=﹣10x2+2210x﹣112800= ,∵价格取整数,即x为整数,∴当x=110或x=111时,取得最大值,最大值为9300.答:880元的销售利润不是最多,当定价为110元或111元时,销售利润最多,最多利润为9300元.考点:二次函数的应用;二次函数的最值;最值问题.24.如图,在等腰△AB中,AB=B,以B为直径的⊙与A相交于点D,过点D作DE⊥AB交B延长线于点E,垂足为点F.(1)判断DE与⊙的位置关系,并说明理由;(2)若⊙的半径R=,tan= ,求EF的长.【答案】(1)直线DE是⊙的切线;(2).(2)过D作DH⊥B于H,∵⊙的半径R=,tan= ,∴B=10,设BD=,D=2,∴B= =10,∴=2 ,∴BD=2 ,D=4 ,∴DH= =4,∴H= =3,∵DE⊥D,DH⊥E,∴D2=H•E,∴E= ,∴BE= ,∵DE⊥AB,∴BF∥D,∴△BFE∽△DE,∴,即,∴BF=2,∴EF= = .考点:直线与圆的位置关系;等腰三角形的性质;解直角三角形;探究型.2.如图,在Rt△AB中,∠AB=90°,∠A=30°,点为AB中点,点P 为直线B上的动点(不与点B、点重合),连接、P,将线段P绕点P 顺时针旋转60°,得到线段PQ,连接BQ.(1)如图1,当点P在线段B上时,请直接写出线段BQ与P的数量关系.(2)如图2,当点P在B延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;(3)如图3,当点P在B延长线上时,若∠BP=1°,BP=4,请求出BQ的长.【答案】(1)BQ=P;(2)成立:P=BQ;(3).(3)如图3中,作E⊥P于E,在PE上取一点F,使得FP=F,连接F.设E==a,则E=FP=2a,EF= a,在Rt△PE中,表示出P,根据P+B=4,可得方程,求出a即可解决问题;试题解析:(1)结论:BQ=P.理由:如图1中,作PH∥AB交于H.在Rt△AB中,∵∠AB=90°,∠A=30°,点为AB中点,∴=A=B,∠B=60°,∴△B是等边三角形,∴∠HP=∠B=60°,∠PH=∠B=60°,∴∠HP=∠PH=60°,∴△PH是等边三角形,∴P=PH=H,∴H=PB,∵∠PB=∠PQ+∠QPB=∠B+∠P,∵∠PQ=∠P=60°,∴∠PH=∠QPB,∵P=PQ,∴△PH≌△QPB,∴PH=QB,∴P=BQ.(3)如图3中,作E⊥P于E,在PE上取一点F,使得FP=F,连接F.∵∠P=1°,∠B=∠P+∠P,∴∠P=4°,∴E=E,设E==a,则E=FP=2a,EF= a,在Rt△PE中,P= = = ,∵P+B=4,∴,解得a= ,∴P= ,由(2)可知BQ=P,∴BQ= .考点:几何变换综合题;探究型;变式探究;压轴题.26.如图,直线=﹣2x+4交轴于点A,交抛物线于点B(3,﹣2),抛物线经过点(﹣1,0),交轴于点D,点P是抛物线上的动点,作PE⊥DB交DB所在直线于点E.(1)求抛物线的解析式;(2)当△PDE为等腰直角三角形时,求出PE的长及P点坐标;(3)在(2)的条下,连接PB,将△PBE沿直线AB翻折,直接写出翻折点后E的对称点坐标.【答案】(1);(2)PE=或2,P(2,﹣3)或(,3);(3)E的对称点坐标为(,﹣)或(36,﹣12).【解析】试题分析:(1)把B(3,﹣2),(﹣1,0)代入即可得到结论;(2)由求得D(0,﹣2),根据等腰直角三角形的性质得到DE=PE,列方程即可得到结论;(3)①当P点在直线BD的上方时,如图1,设点E关于直线AB 的对称点为E′,过E′作E′H⊥DE于H,求得直线EE′的解析式为,设E′(,),根据勾股定理即可得到结论;②当P点在直线BD的下方时,如图2,设点E关于直线AB的对称点为E′,过E′作E′H⊥DE 于H,得到直线EE′的解析式为,设E′(,),根据勾股定理即可得到结论.(2)设P(,),在中,当x=0时,=﹣2,∴D(0,﹣2),∵B(3,﹣2),∴BD∥x轴,∵PE⊥BD,∴E(,﹣2),∴DE=,PE= ,或PE= ,∵△PDE为等腰直角三角形,且∠PED=90°,∴DE=PE,∴= ,或= ,解得:=,=2,=0(不合题意,舍去),∴PE=或2,P(2,﹣3)或(,3);②当P点在直线BD的下方时,如图2,设点E关于直线AB的对称点为E′,过E′作E′H⊥DE于H,由(2)知,此时,E(2,﹣2),∴DE=2,∴BE′=BE=1,∵EE′⊥AB,∴设直线EE′的解析式为,∴﹣2= ×2+b,∴b=﹣3,∴直线EE′的解析式为,设E′(,),∴E′H= = ,BH=﹣3,∵E′H2+BH2=BE′2,∴()2+(﹣3)2=1,∴=36,=2(舍去),∴E′(36,﹣12).综上所述,E的对称点坐标为(,﹣)或(36,﹣12).考点:二次函数综合题;动点型;翻折变换(折叠问题);分类讨论;压轴题.。
2017年消费者权益保护法知识竞赛试题及参考答案

2017年消费者权益保护法知识竞赛试题及参考答案一、单项选择题(在A、B、C、D四个选项中只有一个是正确答案,选出正确答案填在括号里)1、消费者为( )消费需要购买,使用商品或接受服务,其权益受《消费者权益保护法》保护。
A 生产B生活C生产和生活D个人答案:B2、经营者提供商品或服务,应向消费者出具购货凭证或服务单据;消费者索要购货凭证或服务单据的,经营者()出具。
A必须B不一定C可以D视具体情况答案:A3、《消法》是()实施的A1993年10月31日B1993年1月1日C1994年10月31日D1994年1月1日答案:D4、《消法》中,消费者的消费客体是()。
A生活消费B商品C服务D商品和服务答案:D5、经营者对行政处罚决定不服的,可以自收到处罚决定书之日起()内向上一级机关申请复议。
A15日B30日C60日D90日答案:C6、经营者对商品或者服务作引人误解的虚假宣传的,处以非法所得()的罚款。
A一倍以上三倍以下B一倍以上五倍以下C一们以上十倍以下D一倍以上三十倍以下答案:B7、经营者提供商品或者服务有欺诈行为的,应当按照消费者的要求增加赔偿其受到的损失,增加赔偿的金额为消费者购买商品的价款或者接受服务的费用的()A一倍B二倍C三倍D五倍答案:A8、对国家规定或者经营者与消费者约定包修、包换、包退的商品,经营者应当负责修理,更换或者退货,保修期内()修理仍不能正常使用的,经营者应当负责更换或者退货。
A一次B二次C三次D四次答案:B9、经营者以邮购方式提供商品,应当按照约定提供。
未按照约定提供的,应当按照消费者的要求履行约定或者()。
A退回货款B承担消费者支付的所有费用C赔礼道歉D依法追究刑事责任答案:A10、依法经()认定为不合格的商品,消费者要求退货的,经营者应当负责退货。
A消费者协会B 法院C行业协会D有关行政部门答案:D11、消费者购买法律禁止购买、使用的商品引起纠纷的()《消法》调整范围。
2017年教师资格证考试《小学教育教学知识与能力》单选题专项训练二(教师版)

【答案】C
【解析】荀子、赫尔巴特、涂尔干都是社会本位论的代表人物。
26、综合实践活动的过程取向决定了其( )特点。 A、生成性 B、开放性 C、实践性 D、自主性
试卷链接:/t/R2K7TJf.html
4/8
云测库,互联网测评考试与人才管理平台
【答案】A
6、教师在教学生掌握科学概念时,一般多采用“变式”,其主要是( )。
试卷链接:/t/R2K7TJf.html
1/8
云测库,互联网测评考试与人才管理平台 A、丰富想象 B、激发兴趣 C、引起注意 D、区分本质特征与非本质特征
【答案】D
【解析】客观事物的本质特征和非本质特征往往是交融在一起的,这给学生学习科学概念增加了难度。使用变式就是为了让学 生区分概念的本质特征与非本质特征。
20、教学过程也称教学步骤或教学程序,即用于指导和规范教师课堂活动的步骤,教学过程不包括( )。 A、导入环节 B、讲授环节 C、巩固环节 D、设计教学重难点
【答案】D
【解析】教学过程的编写要做到各个环节衔接,内容充实,重点突出,详略得当。教学过程包括以下几个部分:导入环节、讲 授环节、巩固练习、归纳小结。
云测库,互联网测评考试与人才管理平台
2017年教师资格证考试《小学教育教学知识与能力》单选题专项训练二
(教师版)
试卷题量:50题 试卷总分:100分 试卷限时:60分钟 测评/引用码:R2K7TJf
一、单项选择题
1、每个学生在所属的班集体中都有一定的权利和义务,都能找到适合于自己的角色与活动。因此,班集体有利于训练学生的
2/8
云测库,互联网测评考试与人才管理平台
【解析】综合实践活动尊重学生的兴趣、爱好,注重发挥学生的自主性。学生自己选择学习的目标、内容、方式及指导教师,
2017版高中化学新课标训练题及参考答案

2017版高中化学新课标训练题及参考答案2017版普通高中课程标准测试题本次测试共分为两部分,总分100分,考试时间50分钟。
一、单项选择题(共15题,每小题2分,计30分。
每小题只有1个选项符合题意)1.以下对于研究新课标后对课程基本理念的描述,哪一个是错误的?A.高中化学课程应满足学生多元发展需求B.化学课程内容应体现基础性和时代性C.教学应重视“素养为本”D.教学评价与学业评价应基于“三维”目标2.以下对于化学学科核心素养的认识,哪一个是错误的?A.是学生通过化学学科研究而逐步形成的必备品格、关键能力与价值观念B.是学生科学素养的重要组成部分C.是学生综合素质的具体体现D.是针对选修化学的学生提出的素养要求3.以下对于化学学科核心素养与课程目标的描述中,哪一个是错误的?A.化学学科核心素养对高中学生发展提出了具体要求,是确立课程目标的依据B.化学学科核心素养包括五个方面C.根据化学学科核心素养,制定了高中化学课程的四个方面的课程目标D.化学学科核心素养的每个方面划分为四个水平层次4.以下对于学业质量的描述中,哪一个是错误的?A.化学学业质量水平分为4级B.每一级水平的描述中均包含化学学科核心素养的五个方面C.每一级水平依据侧重的内容将其划分为五个条目D.学业质量是学生在完成本学科课程研究后的学业成就表现5.以下对于高中化学新课程组成与性质的描述中,哪一个是错误的?A.高中化学课程由必修、选择性必修和选修三部分组成B.必修课程为全修全考课程C.选择性必修课程为选修必考课程D.选修课程为学而不考或学而备考课程6.以下对于高中化学课程结构的描述中,哪一个是不正确的?A.必修课程共有五个主题B.选择性必修课程共有三个模块C.选修课程共有三个系列D.《化学与生活》和《化学与技术》属于校本化学课程7.以下对于必修模块变化的描述中,哪一个是错误的?A.必修的学分没变,仍然是4分B.将化学1、化学2中的6个主题整合为5个主题C.每个主题的内容从“内容要求”、“教学提示”、“学业要求”三个方面呈现D.对学生应完成的化学实验作出了具体要求8.以下对于必修课程主题的描述中,哪一个不属于必修课程?A.常见的无机物及其应用B.物质结构基础与化学反应规律C.简单的有机化合物及其应用D.化学与社会9.对于选修化学的学生来说,以下哪些内容可以不修?A.模块1:化学反应原理B.模块2:物质结构与性质C.系列3:有机化学基础D.系列3:发展中的化学学科10.关于新课标学分设置的描述,正确的是:A。
2017全国卷试题及答案

2017全国卷试题及答案2017年全国卷是中国中学生高考的一场重要考试,本文将为您介绍2017年全国卷的试题内容以及答案。
第一部分:选择题这一部分包含了多个选择题,题目如下:1. 【选择题】在下列选项中,哪一个单词的拼写是正确的?A. RecieveB. ProccessC. AchieveD. Acheive答案:C. Achieve2. 【选择题】在下列选项中,哪一个单词的词性不同于其他三个?A. RevolutionaryB. ConceptualC. AdvantageousD. Appreciation答案:D. Appreciation第二部分:填空题这一部分包含了多个填空题,题目如下:1. 【填空题】根据所给的线索,填写空白处的单词。
The _______ of the new scientific discovery is expected to have a significant impact on the field of medicine.答案:implementation2. 【填空题】请在下列选项中填入合适的单词,使得句子通顺。
The company has decided to _______ its production capacity in order to meet the increasing demand.答案:expand第三部分:阅读理解这一部分包含了多个阅读理解题,题目如下:Passage 1After several months of hard work, the students finally completed their research projects. The next step was to present their findings to their classmates and teachers. Each student was expected to give a ten-minute presentation, followed by a question and answer session. The presentations were scheduled for the following week.1. 【选择题】What is the purpose of the students' presentations?A. To complete their research projects.B. To present their findings.C. To answer questions from classmates.D. To schedule the presentations for the following week.答案:B. To present their findings.Passage 2According to recent studies, the quality of our sleep has a significant impact on our overall health and well-being. Lack of sleep can lead to a range of issues, including decreased cognitive function and increased risk of chronic diseases. It is important to prioritize proper sleep habits in order to maintain good health.2. 【选择题】What can be inferred from the passage?A. Lack of sleep can lead to chronic diseases.B. Proper sleep habits are important for good health.C. Recent studies have shown the impact of sleep on cognitive function.D. Chronic diseases can be prevented through proper sleep habits.答案:B. Proper sleep habits are important for good health.第四部分:写作本部分包含了一篇写作题,题目如下:作文题目:如何保持健康的生活方式?请你根据题目要求,写一篇关于如何保持健康生活方式的短文。
2017年(文科数学)(新课标Ⅱ)试卷真题+参考答案+详细解析
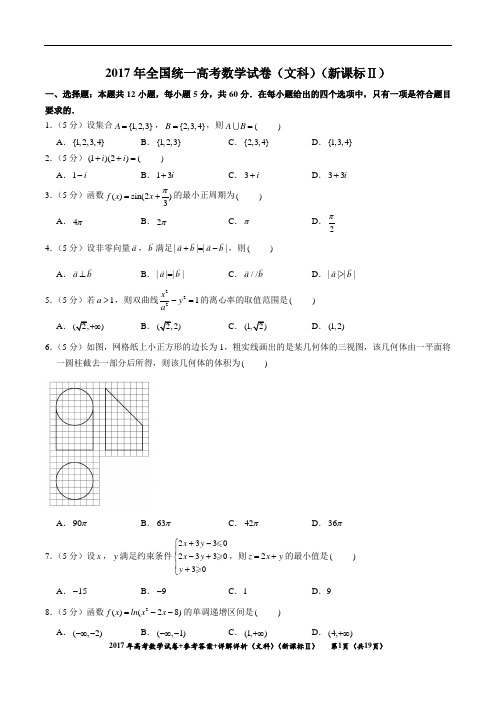
2017年全国统一高考数学试卷(文科)(新课标Ⅱ)一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)设集合{1,2,3}A =,{2,3,4}B =,则(A B = )A .{1,2,3,4}B .{1,2,3}C .{2,3,4}D .{1,3,4}2.(5分)(1)(2)(i i ++= ) A .1i -B .13i +C .3i +D .33i +3.(5分)函数()sin(2)3f x x π=+的最小正周期为( )A .4πB .2πC .πD .2π 4.(5分)设非零向量a ,b 满足||||a b a b +=-,则( ) A .a b ⊥B .||||a b =C .//a bD .||||a b >5.(5分)若1a >,则双曲线2221x y a-=的离心率的取值范围是( )A.)+∞B.C.D .(1,2)6.(5分)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )A .90πB .63πC .42πD .36π7.(5分)设x ,y 满足约束条件2330233030x y x y y +-⎧⎪-+⎨⎪+⎩,则2z x y =+的最小值是( )A .15-B .9-C .1D .98.(5分)函数2()(28)f x ln x x =--的单调递增区间是( ) A .(,2)-∞-B .(,1)-∞-C .(1,)+∞D .(4,)+∞9.(5分)甲、乙、丙、丁四位同学一起去问老师询问成语竞赛的成绩.老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上信息,则( ) A .乙可以知道四人的成绩 B .丁可以知道四人的成绩C .乙、丁可以知道对方的成绩D .乙、丁可以知道自己的成绩10.(5分)执行如图的程序框图,如果输入的1a =-,则输出的(S = )A .2B .3C .4D .511.(5分)从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为( ) A .110B .15C .310D .2512.(5分)过抛物线2:4C y x =的焦点F ,3C 于点(M M 在x 轴上方),l 为C 的准线,点N 在l 上,且MN l ⊥,则M 到直线NF 的距离为( ) A 5B .22C .23D .33二、填空题,本题共4小题,每小题5分,共20分 13.(5分)函数()2cos sin f x x x =+的最大值为 .14.(5分)已知函数()f x 是定义在R 上的奇函数,当(,0)x ∈-∞时,32()2f x x x =+,则(2)f = . 15.(5分)长方体的长、宽、高分别为3,2,1,其顶点都在球O 的球面上,则球O 的表面积为 . 16.(5分)ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,若2cos cos cos b B a C c A =+,则B = .三、解答题:共70分.解答应写出文字说明,证明过程或演算步骤,第17至21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.17.(12分)已知等差数列{}n a 的前n 项和为n S ,等比数列{}n b 的前n 项和为n T ,11a =-,11b =,222a b +=. (1)若335a b +=,求{}n b 的通项公式; (2)若321T =,求3S .18.(12分)如图,四棱锥P ABCD-中,侧面PAD为等边三角形且垂直于底面ABCD,12AB BC AD==,90BAD ABC∠=∠=︒.(1)证明:直线//BC平面PAD;(2)若PCD∆面积为27,求四棱锥P ABCD-的体积.19.(12分)海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg ),其频率分布直方图如下:(1)记A 表示事件“旧养殖法的箱产量低于50kg ”,估计A 的概率;(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:箱产量50kg <箱产量50kg旧养殖法 新养殖法(3)根据箱产量的频率分布直方图,对两种养殖方法的优劣进行比较. 附:2()P K K0.050 0.010 0.001 K3.8416.63510.8282()()()()K a b c d a c b d =++++.20.(12分)设O为坐标原点,动点M在椭圆22:12xC y+=上,过M作x轴的垂线,垂足为N,点P满足2NP NM=.(1)求点P的轨迹方程;(2)设点Q在直线3x=-上,且1OP PQ=.证明:过点P且垂直于OQ的直线l过C的左焦点F.21.(12分)设函数2()(1)x f x x e =-. (1)讨论()f x 的单调性;(2)当0x 时,()1f x ax +,求实数a 的取值范围.(二)选考题:共10分。
2017考研:法律硕士选择专项训练题(二十)
2017考研:法律硕士选择专项训练题(二十)凯程法律硕士培训班选择专项训练题(二十)崔某在北京工作,但家在吉林,1991年春节时要回家探望家人。
邻居胡某听说后请他带1斤长白山的人参回来,说要泡酒做药用。
春节过后,崔某从吉林带回1斤人参,价值1850元,崔某送至胡家,胡某的儿子说因父亲年事已高,春节期间不幸过世。
以前也只有他父亲用人参泡酒做药用,现在他父亲不在了,也就不需要这斤人参,况且他父亲是在他生前委托他代买1斤人参,现在他父亲去世了,代理权也就终止了,所以请崔某将这1斤人参自己留着再做处理。
崔某不得已就去律师事务所去请教律师,问问他可不可以让胡某的儿子收下这1斤人参并支付1850元的价款。
31.崔某实施的代理行为的效力如何?()A.有效B.无效C.效力待定D.可撤销32.崔某与胡某之间的委托代理关系是否终止?()A.终止,因为代理事务已经完成B.终止,因为被代理人已死亡C.不终止,因为代理人不知道被代理人已死亡D.不能确定33.委托代理、法定代理、指定代理终止的共同原因有哪些?()A.代理人死亡B.被代理人死亡C.代理人丧失民事行为能力A.被代理人取得民事行为能力本题涉及代理行为的效力、代理关系的终止等问题。
31.答案:A。
本问涉及代理行为的效力。
依《民通意见》第82条规定,被代理人死亡后,代理人不知道被代理人死亡的,委托代理人实施的代理行为有效。
故本问选项为A。
32.答案:C。
本问涉及被代理人死亡后代理关系的终止问题。
依《民法通则》第69条和《民通意见》第82条规定,被代理人死亡并不必然导致委托代理关系的终止,本题中,代理人不知道被代理人死亡的,其所进行的代理行为仍然有效,代理关系也依然存续。
故本问选项为C。
33.答案:AC。
本问涉及委托代理、法定代理、指定代理终止的共同原因。
依《民法通则》第69、70条规定,可知代理人死亡或丧失民事行为能力为它们终止的共同原因。
故本问选项为AC。
34.甲出海打鱼因遇台风而未归。
2017版高中化学新课标训练题及参考答案
2017版普通高中课程标准测试题总分100分,考试时间50分钟。
一、单项选择题(共15题,每小题2分,计30分。
每小题只有1个选项符合题意)1. 学习新课标后对课程基本理念的以下描述有误的是A. 设罝满足学生多元发展需求的高中化学课程B. 选择能体现基础性和时代性的化学课程内容C. 重视开展“素养为本”的教学D. 倡导基于“三维”目标的教学评价与学业评价2.关于化学学科核心素养的以下认识中有误的是A. 是学生通过化学学科学习而逐步形成的必备品格、关键能力与价值观念B. 是学生科学素养的重要组成部分C. 是学生综合素质的具体体现D. 是针对选考化学的学生提出的素养要求3. 关于化学学科核心素养与课程目标的以下描述中有误的是A. 确立课程目标的依据是化学学科核心素养对高中学生发展的具体要求B. 化学学科核心素养有五个方面C. 根据化学学科核心素养对高中学生提出四个方面的课程目标D. 化学学科核心素养的每个方面划分为四个水平层次4. 关于学业质量的以下描述错误的是A. 化学学业质量水平分为4级B. 每一级水平的描述中均包含化学学科核心素养的5个方面C. 每一级水平依据侧重的内容将其划分为5个条目D. 学业质量是学生在完成本学科课程学习后的学业成就表现5.有关高中化学新课程组成与性质的以下描述有误的是A. 高中化学课程由必修、选择性必修和选修三部分组成B. 必修课程为全修全考课程C. 选择性必修课程为选修必考课程D. 选修课程为学而不考或学而备考课程6.关于高中化学课程结构的描述中不正确的是A. 必修课程共有5个主题B. 选择性必修课程共3个模块C. 选修课程有3个系列D.《化学与生活》和《化学与技术》属于校本化学课程7.关于必修模块变化的以下描述中有误的是A.必修的学分没变,仍然是4分B.由化学1、化学2中的6个主题整合为5个主题C.每个主题的内容从“内容要求”“教学提示”“学业要求”三个方面呈现D.对学生应完成的化学实验作出具体要求8.必修课程是以主题的形式呈现的,其中不属于必修课程的主题是A. 常见的无机物及其应用B. 物质结构基础与化学反应规律C. 简单的有机化合物及其应用D. 化学与社会9. 对选考化学的学生来说,以下内容可以不修习的是模块1:化学反应原理模块2:物质结构与性质模块3:有机化学基础系列3:发展中的化学学科10.关于新课标学分设置的以下描述中有误的是A. 必修课程共4学分B. 选择性必修课程共6学分C. 选修课程每修习完成10学时可获得0.5学分,最高可获得4学分D. 修习完高中化学课程最多可得14学分11.对高中学生修习化学所得学分分布要求合理的是高中毕业不高考:0~4学分高中毕业高考但不选考化学:不少于4分(必修)高中毕业高考且选考化学:不少于10分(必修+选修)高中毕业高考且选考化学:不少于6分(选修性必修+选修)12.高中学生修习化学学科提出以下申请,不合理的是A. 选考政治学科的学生:只修习必修课程B. 选考化学学科的学生:修习全部高中化学课C. 选考地理学科的学生:修习必修课程和选择性必修课程D. 选考历史学科的学生:只修习选修课程13.高中学生自主选择修习化学学科在流程上提出以下申请,不合理的是A. 高中毕业不高考:只选修化学校本课程B. 高中毕业不选考化学学科:必修→选修C. 高中毕业选考化学学科:必修→选择性必修→选修D. 高中毕业选考生物学科:必修→选择性必修→选修14.关于有机化学以下内容对高中毕业生不作整体要求的是,A.知道有机化合物存在同分异构现象,能写出丁烷和戊烷的同分异构体B.能书写乙烯、乙醇、乙酸的主要化学性质相关的化学反应方程式C.能说明常见污染的成因和防治措施的化学原理,能结合具体的污染问题设计简单的防D.能描述和分析烃类衍生物的典型代表物的重要反应,能书写相应的化学反应方程式15.以下要求与新课标要求不一致的是A. 全体学生:了解第三周期元素的递变规律B. 全体学生:准确书写钛元素电子排布式C. 选考化学的学生:能结合实例描述晶体中微粒排列的周期性规律D. 选考化学的学生:能从原子价电子数目和价电子排布的角度解释元素周期表的分区、二、多项选择题(共15题,小题2分,计30分。
国家司法考试卷二多项选择题专项强化真题试卷1(题后含答案及解析)
国家司法考试卷二多项选择题专项强化真题试卷1(题后含答案及解析)1.关于因果关系,下列哪些选项是正确的?(2017年卷二52题)A.甲以杀人故意用铁棒将刘某打昏后,以为刘某已死亡,为隐藏尸体将刘某埋入雪沟,致其被冻死。
甲的前行为与刘某的死亡有因果关系B.乙夜间驾车撞倒李某后逃逸,李某被随后驶过的多辆汽车辗轧,但不能查明是哪辆车造成李某死亡。
乙的行为与李某的死亡有因果关系C.丙将海洛因送给13周岁的王某吸食,造成王某吸毒过量身亡。
丙的行为与王某的死亡有因果关系D.丁以杀害故意开车撞向周某,周某为避免被撞跳入河中,不幸溺亡。
丁的行为与周某的死亡有因果关系正确答案:A,B,C,D解析:本题考查刑法中的因果关系。
A项:这种情形属于事前故意,不影响因果关系的成立。
故A项正确。
B项:根据条件说,没有乙的交通肇事行为就不会导致李某死亡结果的发生,所以乙的行为与李某的死亡结果之间具有因果关系。
故B项正确。
C项:将毒品送给未成年人吸食容易导致严重的危害后果,行为人对此负有刑事上的责任,最终导致了未成年人死亡,行为人的行为和结果之间存在因果关系。
故C项正确。
D项:这种情形属于狭义的因果关系错误,不影响因果关系的成立。
故D项正确。
2.关于自首中的“如实供述”,下列哪些选项是错误的?( )A.甲自动投案后,如实交代自己的杀人行为,但拒绝说明凶器藏匿地点的,不成立自首B.乙犯有故意伤害罪、抢夺罪,自动投案后,仅如实供述抢夺行为,对伤害行为一直主张自己是正当防卫的,仍然可以成立自首C.丙虽未自动投案,但办案机关所掌握线索针对的贪污事实不成立,在此范围外丙交代贪污罪行的,应当成立自首D.丁自动投案并如实供述自己的罪行后又翻供,但在二审判决前又如实供述的,应当认定为自首正确答案:A,D解析:本题考了三个司法解释,一个是最高人民法院《关于处理自首和立功具体应用法律若干问题的解释》(以下本题中简称《解释》),一个是最高人民法院、最高人民检察院《关于办理职务犯罪案件认定自首、立功等量刑情节若干问题的意见》(以下本题中简称《意见》)。
2017年普通高等学校招生全国统一考试(答案)
2017年普通高等学校招生全国统一考试(课标全国卷Ⅲ)一、选择题1.B 因为集合A和集合B有共同元素2,4,所以A∩B={2,4},所以A∩B中元素的个数为2.2.C z=i(-2+i)=-2i+i2=-2i-1=-1-2i,所以复数z在复平面内对应的点为(-1,-2),位于第三象限.故选C.3.A 由题中折线图可知,每年的月接待游客量从8月份开始有下降趋势.故选A.4.A ∵(sin α-cos α)2=1-2sin αcos α=1-sin 2α==,∴sin 2α=-.5.B 由题意,画出可行域(如图中阴影部分所示),易知A(0,3),B(2,0).由图可知,目标函数z=x-y在点A,B处分别取得最小值与最大值,z min=0-3=-3,z max=2-0=2,故z=x-y的取值范围是[-3,2].故选B.6.A ∵f(x)=sin+cos=+cos x+sin x=sin x+cos x=×2sin=sin,∴f(x)的最大值为.故选A.cos=cos=sin =sin,f(x)=sin,=.7.D 当x∈(0,1)时,sin x>0,∴y=1+x+>1+x>1,排除A、C.令f(x)=x+,则f(-x)=-x+=-f(x),∴f(x)=x+是奇函数,∴y=1+x+的图象关于点(0,1)对称,故排除B.故选D.8.D 本题考查程序框图.要求N的最小值,观察选项,发现其中最小的值为2,不妨将2代入检验.当输入的N为2时,第一次循环,S=100,M=-10,t=2;第二次循环,S=90,M=1,t=3,此时退出循环,输出S=90,符合题意,故选D.9.B 设圆柱的底面圆半径为r,由题意可得12+(2r)2=22,解得r=.∴圆柱的体积V=πr2×1=,故选B.10.C ∵A1B1⊥平面BCC1B1,BC1⊂平面BCC1B1,∴A1B1⊥BC1,又BC1⊥B1C,且B1C∩A1B1=B1,∴BC1⊥平面A1B1CD,又A1E⊂平面A1B1CD,∴BC1⊥A1E.故选C.11.A 由题意可得a=,故a2=3b2,又b2=a2-c2,所以a2=3(a2-c2),所以=,所以e==.12.C 由函数f(x)有零点得x2-2x+a(e x-1+e-x+1)=0有解,即(x-1)2-1+a(e x-1+e-x+1)=0有解,令t=x-1,则上式可化为t2-1+a(e t+e-t)=0,即a=.令h(t)=,易得h(t)为偶函数,又由f(x)有唯一零点得函数h(t)的图象与直线y=a有唯一交点,则此交点的横坐标为0,所以a==,故选C.二、填空题13.答案 2解析∵a⊥b,∴a·b=0,又a=(-2,3),b=(3,m),∴-6+3m=0,解得m=2.14.答案 5解析由题意可得=,所以a=5.15.答案75°解析由正弦定理得=,∴sin B=,又∵c>b,∴B=45°,∴A=75°.sin B=后16.答案解析当x≤0时,f(x)+f=x+1+x-+1>1,∴x>-,∴-<x≤0;当0<x≤时,f(x)+f=2x+x-+1>1恒成立;当x>时, f(x)+f=2x+>1恒成立.综上,x的取值范围为.三、解答题17.解析(1)因为a 1+3a2+…+(2n-1)a n=2n,故当n≥2时,a1+3a2+…+(2n-3)a n-1=2(n-1).两式相减得(2n-1)a n=2.所以a n=(n≥2).又由题设可得a1=2,从而{a n}的通项公式为a n=(n∈N*).(2)记的前n项和为S n.由(1)知==-.则S n=-+-+…+-=.18.解析本题考查概率的计算.(1)这种酸奶一天的需求量不超过300瓶,当且仅当最高气温低于25,由表格数据知,最高气温低于25的频率为=0.6,所以这种酸奶一天的需求量不超过300瓶的概率的估计值为0.6.(2)当这种酸奶一天的进货量为450瓶时,若最高气温不低于25,则Y=6×450-4×450=900;若最高气温位于区间[20,25),则Y=6×300+2×(450-300)-4×450=300;若最高气温低于20,则Y=6×200+2×(450-200)-4×450=-100.所以,Y的所有可能值为900,300,-100.Y大于零当且仅当最高气温不低于20,由表格数据知,最高气温不低于20的频率为=0.8,因此Y大于零的概率的估计值为0.8.19.解析(1)取AC的中点O,连接DO,BO.因为AD=CD,所以AC⊥DO.又由于△ABC是正三角形,所以AC⊥BO.从而AC⊥平面DOB,故AC⊥BD.(2)连接EO.由(1)及题设知∠ADC=90°,所以DO=AO.在Rt△AOB中,BO2+AO2=AB2.又AB=BD,所以BO2+DO2=BO2+AO2=AB2=BD2,故∠DOB=90°.由题设知△AEC为直角三角形,所以EO=AC.又△ABC是正三角形,且AB=BD,所以EO=BD.故E为BD的中点,从而E到平面ABC的距离为D到平面ABC的距离的,四面体ABCE的体积为四面体ABCD的体积的,即四面体ABCE与四面体ACDE的体积之比为1∶1.20.解析(1)不能出现AC⊥BC的情况,理由如下:设A(x1,0),B(x2,0),则x1,x2满足x2+mx-2=0,所以x1x2=-2.又C的坐标为(0,1),故AC的斜率与BC的斜率之积为·=-,所以不能出现AC⊥BC的情况.(2)BC的中点坐标为,可得BC的中垂线方程为y-=x2.由(1)可得x1+x2=-m,所以AB的中垂线方程为x=-.联立又+mx2-2=0,可得所以过A,B,C三点的圆的圆心坐标为,半径r=.故圆在y轴上截得的弦长为2=3,即过A,B,C三点的圆在y轴上截得的弦长为定值.21.解析(1)f(x)的定义域为(0,+∞), f '(x)=+2ax+2a+1=.若a≥0,则当x∈(0,+∞)时, f '(x)>0,故f(x)在(0,+∞)单调递增.若a<0,则当x∈时, f '(x)>0;当x∈时, f '(x)<0,故f(x)在单调递增,在单调递减.(2)由(1)知,当a<0时, f(x)在x=-取得最大值,最大值为f=ln-1-. 所以f(x)≤--2等价于ln-1-≤--2,即ln++1≤0.设g(x)=ln x-x+1,则g'(x)=-1.当x∈(0,1)时,g'(x)>0;当x∈(1,+∞)时,g'(x)<0.所以g(x)在(0,1)单调递增,在(1,+∞)单调递减.故当x=1时,g(x)取得最大值,最大值为g(1)=0.所以当x>0时,g(x)≤0.从而当a<0时,ln++1≤0,即f(x)≤--2.22.解析(1)消去参数t得l1的普通方程l1:y=k(x-2);消去参数m得l2的普通方程l2:y=(x+2).设P(x,y),由题设得消去k得x2-y2=4(y≠0).所以C的普通方程为x2-y2=4(y≠0).(2)C的极坐标方程为ρ2(cos2θ-sin2θ)=4(0<θ<2π,θ≠π).联立得cos θ-sin θ=2(cos θ+sin θ).故tan θ=-,从而cos2θ=,sin2θ=,代入ρ2(cos2θ-sin2θ)=4得ρ2=5,所以交点M的极径为.23.解析(1)f(x)=当x<-1时, f(x)≥1无解;当-1≤x≤2时,由f(x)≥1得,2x-1≥1,解得1≤x≤2;当x>2时,由f(x)≥1解得x>2.所以f(x)≥1的解集为{x|x≥1}.(2)由f(x)≥x2-x+m得m≤|x+1|-|x-2|-x2+x.而|x+1|-|x-2|-x2+x≤|x|+1+|x|-2-x2+|x|=-+≤,且当x=时,|x+1|-|x-2|-x2+x=. 故m的取值范围为.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
答 案
C C D C A A C B
2017届选择题专项训练(15)
题 号 答 案
1 2 3 4 5 6 7 8 9 10
D B A C D C C D B B
题 号
答 案 题 号
11 12 13 14 15 16 17 18 19 20
B B A C C A C D C A 21 22 23 24 25 26 27 28
答 案
C B B B C C D D
2017届选择题专项训练(18)
题 号 答 案
1 2 3 4 5 6 7 8 9 10
B A A D C A C B A A
题 号
答 案 题 号
11 12 13 14 15 16 17 18 19 20
C B B D D B D C C A 21 22 23 24 25 26 27 28
21 22 23 24 25 26 27 28
题 号
答 案 题 号
答 案
2017选择题专项训练
参考答案
2017届选择题专项训练(12)
题 号 答 案
1 2 3 4 5 6 7 8 9 10
C B C A A C B B B D
题 号
答 案 题 号
11 12 13 14 15 16 17 18 19 20
A C D C A B B A B B 21 22 23 24 25 26 27 28
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28
题 号
答 案 题 号
答 案
2017届选择题专项训练(18)
题 号 答 案
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
题 号 答 案
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28
题 号
答 案 题 号
答 案
2017届选择题专项训练(18)
题 号 答 案
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
答 案
A B C B B D B C
2017届选择题专项训练(17)
题 号 答 案
1 2 3 4 5 6 7 8 9 10
B A D B D A B C A C
题 号
答 案 题 号
11 12 13 14 15 16 17 18 19 20
D A A D C B C B D C 21 22 23 24 25 26 27 28
21 22 23 24 25 26 27 28
题 号
Hale Waihona Puke 答 案 题 号答 案2017届选择题专项训练(18)
题 号 答 案
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28
题 号
答 案 题 号
答 案
2017届选择题专项训练(18)
答 案
B A B A C B D B
2017届选择题专项训练(18)
题 号 答 案
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28
题 号
答 案 题 号
答 案
2017届选择题专项训练(18)
题 号 答 案
答 案
B C B A B C B A
2017届选择题专项训练(16)
题 号 答 案
1 2 3 4 5 6 7 8 9 10
D C C B C B D C D D
题 号
答 案 题 号
11 12 13 14 15 16 17 18 19 20
A D C A B D A B B C 21 22 23 24 25 26 27 28
