变质量完整力学系统的形式不变性与Lie对称性
合集下载
准坐标下完整力学系统Lie对称性的共形不变性与守恒量

de r i v e d u s i n g t he Eu l e r o pe r a t o r , a n d t h e i r d e t e r mi n i n g e qu a t i o n s a r e t h e n p r e s e n t e d. Mo r e o v e r , t he r e l a t i o n s h i p b e t we e n c o n f o m a r l i n v a r i a n c e a nd t h e t hr e e s y mme t r i e s, No e t h e r s y mme t y, r Li e s y mme t y r
L i e s y mme t y r or f t h e s y s t e r m a r e p r o v i d e d . C o n d i t i o n s t h a t t h e c o n f o r ma l i n v a r i a n c e s h o u l d s a t i s f y a r e
a n d Me i s y mme t y, r a r e d i s c u s s e d . T h e s y s t e m S c o r r e s p o n d i n g c o n s e r v e d q u a n t i t i e s a r e o b t a i n e d, a c —
第3 1卷
第1 期
江
西
科
学
V0 1 . 3l No .1
2 0 1 3年 2 月
CI ENCE J I ANG XI S
Fe b. 2 0l 3
L i e s y mme t y r or f t h e s y s t e r m a r e p r o v i d e d . C o n d i t i o n s t h a t t h e c o n f o r ma l i n v a r i a n c e s h o u l d s a t i s f y a r e
a n d Me i s y mme t y, r a r e d i s c u s s e d . T h e s y s t e m S c o r r e s p o n d i n g c o n s e r v e d q u a n t i t i e s a r e o b t a i n e d, a c —
第3 1卷
第1 期
江
西
科
学
V0 1 . 3l No .1
2 0 1 3年 2 月
CI ENCE J I ANG XI S
Fe b. 2 0l 3
完整力学系统Nielsen方程的Lie对称性-形式不变性

对 称性一 形式 不 变性导 出的 N eh r 恒量和 H ja o te 守 om n守恒量 。
关键词:完整力学 系统;N e l方程;Le对称性一 ile sl i 形式不变性;N e h r守恒量;Hj a o te om n
守恒量
中图分 类 号 :0 1 文 献标 识码 :A 文章 编号 :10-6 1(0 7 40 8.3 36 094 0 20 )0.0 30
不变性 是指这种对称性既是 Le对称性的,又是形 i 式不变性的。 3 .L i e对称性一 形式不变性导致 的 N e h r守 o te 恒量
力 系 的 能 数 《 香 系 学 统 动 函 为 = (+; 统 } l
受到的非广义力为 =曹, 2=香. lO 2 试研究 Le对 i
有类型的对称性以便 了解物质世界 的变化 。N ehr o te 对称性,L e对称性 和形式不变性 “ ( i 也称 M i e 对称 性) 以及相应地三种主要的守恒量.N ehr守恒量“ ot e ’
・
N )Q =
一
( 2 )
般 说 T f,, = ( , 来 . = (q ) f q ,q , )设 q
维普资讯
第 1 第 4期 5卷
2 0 年 8月 0 7
呼伦 贝 尔学 院学报
J u n l fHu u b irCo lg o r a ln e e l e o e
No4 .
V ll o _5
P b i e n Au u t 0 7 u l h d i g s. 0 s 2
H ja 守 恒量 。 om n
= , , ) ( k 1, , 口( =,… n) ( , 口 , 2 q 3 )
力学系统的对称性和守恒量的应用

这里ξ 0,ξs为无限小生成元,而 Noether 守恒量有形式
(2.6)
ξ ξ ξ I N = L
0
+
∂L ∂q s
(
s − qs
)
0
+G
N
=常数
(2.7)
如果由 Noether 等式可找到生成元ξ 0,ξs和规范函数 GN =GN (t,q,q) ,那么便可由
式(2.5)找到守恒量。这类守恒量称为 Noether 守恒量。
英文版上发表。有的文章称形式不变性为 Mei 对称性。形式不变性的优点在
于从力学意义上较易理解。缺点在于由式(2.15),(2.16)找到相应的守恒量
(2.18)较困难。
由 Noether 和 Lie 对称性通过形式不变性可导出守恒量(2.18);由形式
1992 年的工作,他既不用 Lagrange 函数也不用 Hamilton 函数来构造了一类
新守恒量。由他导出的守恒量被人称为 Hojman 型守恒量。
对 Lagrange 系统(2.1),将其展开为
qs= Fs (t, q, q)
Lie 对称性的确定性方程表为
ξs−q s ξ0−2ξ0Fs = X (1)(F s)
E s{X (1) (L)} = 0
11
(2.15)
如果存在规范函数 GF =GF (t,q,q) 满足结构方程
X~
(1)
(L)
dξ dt
0+
X~
(1){X~ (1) (L)}
+
d dt
GF
=
0
(2.16)
其中
ξ ξ ξ q X~ (1) = ∂ + ∂ + ( d − d ) ∂
(2.6)
ξ ξ ξ I N = L
0
+
∂L ∂q s
(
s − qs
)
0
+G
N
=常数
(2.7)
如果由 Noether 等式可找到生成元ξ 0,ξs和规范函数 GN =GN (t,q,q) ,那么便可由
式(2.5)找到守恒量。这类守恒量称为 Noether 守恒量。
英文版上发表。有的文章称形式不变性为 Mei 对称性。形式不变性的优点在
于从力学意义上较易理解。缺点在于由式(2.15),(2.16)找到相应的守恒量
(2.18)较困难。
由 Noether 和 Lie 对称性通过形式不变性可导出守恒量(2.18);由形式
1992 年的工作,他既不用 Lagrange 函数也不用 Hamilton 函数来构造了一类
新守恒量。由他导出的守恒量被人称为 Hojman 型守恒量。
对 Lagrange 系统(2.1),将其展开为
qs= Fs (t, q, q)
Lie 对称性的确定性方程表为
ξs−q s ξ0−2ξ0Fs = X (1)(F s)
E s{X (1) (L)} = 0
11
(2.15)
如果存在规范函数 GF =GF (t,q,q) 满足结构方程
X~
(1)
(L)
dξ dt
0+
X~
(1){X~ (1) (L)}
+
d dt
GF
=
0
(2.16)
其中
ξ ξ ξ q X~ (1) = ∂ + ∂ + ( d − d ) ∂
【国家自然科学基金】_无限小变换_基金支持热词逐年推荐_【万方软件创新助手】_20140801
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
2011年 科研热词 推荐指数 特殊无限小变换 2 特殊守恒量 2 守恒量 2 mei守恒量 2 lagrange系统 2 非完整系统 1 翻译方法 1 绝热不变量 1 离散 1 确定方程 1 相对运动动力学 1 独立变量 1 特殊统一对称性 1 特殊noether-lie对称性 1 无限小变换 1 摄动 1 广义hamilton系统 1 广义birkhoff系统 1 对称性 1 变质量 1 动力学系统 1 三体问题 1 noether对称性 1 nielsen方程 1 mei对称性 1 lie对称性 1 kdv 1 hojman守恒量 1 h6non-heiles方程 1 burgers方程 1 appell方程 1
推荐指数 3 2 2 2 1 1 1 1 1 1 1 1 1 1 1
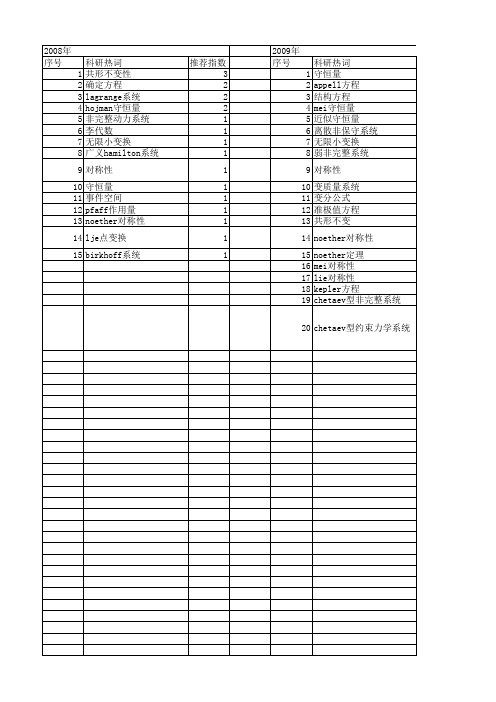
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
科研热词 守恒量 appell方程 结构方程 mei守恒量 近似守恒量 离散非保守系统 无限小变换 弱非完整系统 对称性 变质量系统 变分公式 准极值方程 共形不变 noether对称性 noether定理 mei对称性 lie对称性 kepler方程 chetaev型非完整系统 chetae4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
科研热词 推荐指数 mei对称性 3 noether对称性 2 nielsen方程 2 lie对称性 2 hojman守恒量 2 结构方程 1 约束力学系统 1 积分 1 相对运动动力学系统 1 无限小正则变换 1 无限小变换 1 新的结构方程 1 新的守恒量 1 新守恒量 1 新型守恒量 1 广义tzénoff方程 1 广义birkhoff系统 1 完整系统 1 守恒量 1 nielsen equation, mei symmetry, 1 structural equati mei对称 1 hénon-heiles系统 1 h·non-heiles系统 1 birkhoff系统 1 a型 1 appell方程 1
约束Birkhoff方程的形式不变性与Lie对称性

Ab t a t Rea i n b t e h o m n a i n e a d L e s mme r f c n t a n d Bi h fi n sr c : lt e we n t e f r i v ra c n i y o ty o o sr ie r o a k s s e s i s u id y t m s t d e .Fis ,t e d fn t n n r t r n ft e f r i v r n e a d Li y r t h e i ii sa d c i i so h o m n a i c n e s mme r o e o a ty i h y t m sa e g v n n t e s s e r i e .Ne t h e a i n b t e h m x o n e n r v d ti h wn x ,t e r l t e we n t e i e p u d d a d p o e ,I s s o o s t a h t u t r q a i n a d c n e v d q a t t f t e f r i v ra c n e s mme r f h t t e s r c u e e u t n o s r e u n i o h o m n a in e a d Li y o y ty o c n t an d Bi h fi n s s e a e t es m ef r .F n l o s r i e r o a y t ms h v h a o m k i a l a x mp e i g v n t l s r t h y, n e a l s ie o i u t a e t e l a p ia i n o h e u t p l t ft e r s l. c o Ke wo d : a a y i a y rs n l tc l m e h n c ; c n t a n d ik o f n c a is o s r i e B r h fi me h n c ; f r a c a is o m i v r n e; Ii n ai c a e
变质量单面非Chetaev型非完整系统的Lie对称性和Mei守恒量

摘
要: 究 了变 质量 单 面 非 C eav型非 完 整 系统 的 Le 称 性 和 Me 守 恒 量 。给 出 了 系统 Le对 称 性 的 定 义 ; 研 ht e i对 i i 研
究 了 系 统 Le 称 性 为 M i 称 性 的 充 分 的 Me 守 恒 量 。 最 后举 例说 明 i i
m i , , ) ( , , = ( q 口 l … N) m t 系统 的运动 受有 g个 理想单 面 非 C ea v 非完整 约束 h te 型 () 1
(, 口 >0 £q, ) = , ,) 1 l … g () 2 () 中, 2式 当左 边部 分 函数值 为正 时 , 系统 脱离 约束 ; 当左边 部 分 函数 值等 于零 时 , 系统 处 于约 束 上 。 当系 统 处 于 约束上 时 . 约束 加在 虚位 移 上 的限制 为 设
维普资讯
2 4
苏 州科技 学院 学报 ( 自然科 学版 )
20 0 7血
变质 量单 面非 C eav型非 完整 系统 的 R uh方 程可 表示 为 h te ot
E( ) Q+ A , a 0 ≥0 A 0(= , ;= , , ) £= 。 + A> ,  ̄ , s l … r 1 … g , t 其 中 £为系统 的 L ga g arn e函数 , Q 为非 势广义 力 , 为约 束乘子 , 为广义 反 推力 , 有
变 换 群作用 下 的不 变性 。1 7 9 9年 , uzy将 Le理论 引入 到力学 研究 领域 , 出 了使 力学 系统 的运动 微 分 方 Lt k i 提 程 不 变 的 Le 称性 的概 念 。在一 定 的条 件下 ,i i 对 Le对称 性 能导致 N eh r 恒 量【 】 j n守 恒 量 [ , ote 守 , ma “ Ho 8 广 ' 义 Hja om n守 恒量【' L t y守 恒 量 , 义 L t y 恒 量【 和 Me 守 恒量【1 笔 者进 一 步研 究 变 质 量 1 3 , uz k 广 uz 守 k i 88 I。 ] 单 面 非 C eav型非完 整 系统 的 Le对称 性 和 Me 守 恒量 。 出系统 Le h te i i 给 i 对称 性 的定义 , 研究 系统 Le 称 性 i对 为 Me 对 称性 的充分 必要 条件 , 到 系统 Le i 得 i 对称性 间 接导致 的 Me 守恒 量 。 i
完整系统广义Tzénoff方程的Lie对称性及其Hojman守恒量

0t 0 s
1 ( ) ,
( )
f )
+ 1一 岳 o n
( 1 o )
K 一 [ 丁一( ) o ( m+1T ] 一Q q m=2 3 …) ,,
( 1 )
则T 6 o 方程 的Le z f n i 对称性直接导致 H j a 守恒量 o n m
出这种 守恒量的判据方程。该研 究结果具有一般性 , 为进 一步探 究非 完整 系统 广义T 6or zn f方程的守恒规律奠定 了理论基础 。 [ 关键词] 完整 系统 广义Tzn 方程 Le 6o i对称 Homa j n守恒量
1引 言 .
1 1 年德 国女科 学家 N e e 98 ot r首先发现对称性与守恒 量之间具有 h ̄ I 定 的内在关 系 , 但是 , 当时并没有 引起太 多人 的重视 , 直到 2 世纪 7 0 O 年代 , 分析力 学界才开 始认识到 N e e理论 的科学价 值 , ot r h 其科学 价值 就 在于通过研究 动力学系统 的对 称性可 以寻找 系统的守恒量 , 从此对 称 性与守恒量 的研究得 到蓬勃发 展 , 并取得 了一 系列 重要成果 , 其 中专著 【] 6的研究 范 围最 为全 面 , 括 了 N eh r 包 ote 对称 性 、 i对称 性和 Le Me对称性 以及三 者直 接导出 的守恒量 和相互间接导 出的守恒量 。后 i 来 文献[5 ̄发现 Lga g 系统 的 Me对称性 可直接导 出有别于 Me守 11 arn e i i 恒量的一 种新 的守恒量 。以上这 些成果 大都是 借助 于动力学 系统的 L gag 函数 、 a io 函数和 A p l ar e n H mln t p e 函数来求 系统 的守 恒量 , 实在 l 其 分 析力学 中有 多种运动微分方程 , 中最为简捷 的是 T 6o 方程 , 其 znf 只要 给出系统 的 T6 o 函数 , znf 研究 系统 的运动规律是 比较方 便的 。 目前 , T 6 o 方 程的对称性 与守恒量的研 究也有了一些成果[2, zn f 1 5但这些成果 6] - 都是针对 一般 T 6o 方程 , zn f 还没有涉及到广义 T 6o 方程。 znf 本 文企 图研究 完整约束状态下 广义 T6 o 方程 的 L 对称性及其 znf i e 直接导 出的 H j a 守恒量 , o n m 力求给 出完整 系统广 义T 6 o 方程 Le z f n i对 称性的判据方程及其 守恒量 的表达式 , 最后举例说 明研究结果 的应用 。 2完整 系统 的广义 T  ̄ of . z n f方程 假设 力 学 系统 由 N 个 质 点 组成 , 统 的位 形 由 个 广 义 坐标 系 吼 =1 … , 来确定, , ) 系统广义 T o 函数为 z nf 6
1 ( ) ,
( )
f )
+ 1一 岳 o n
( 1 o )
K 一 [ 丁一( ) o ( m+1T ] 一Q q m=2 3 …) ,,
( 1 )
则T 6 o 方程 的Le z f n i 对称性直接导致 H j a 守恒量 o n m
出这种 守恒量的判据方程。该研 究结果具有一般性 , 为进 一步探 究非 完整 系统 广义T 6or zn f方程的守恒规律奠定 了理论基础 。 [ 关键词] 完整 系统 广义Tzn 方程 Le 6o i对称 Homa j n守恒量
1引 言 .
1 1 年德 国女科 学家 N e e 98 ot r首先发现对称性与守恒 量之间具有 h ̄ I 定 的内在关 系 , 但是 , 当时并没有 引起太 多人 的重视 , 直到 2 世纪 7 0 O 年代 , 分析力 学界才开 始认识到 N e e理论 的科学价 值 , ot r h 其科学 价值 就 在于通过研究 动力学系统 的对 称性可 以寻找 系统的守恒量 , 从此对 称 性与守恒量 的研究得 到蓬勃发 展 , 并取得 了一 系列 重要成果 , 其 中专著 【] 6的研究 范 围最 为全 面 , 括 了 N eh r 包 ote 对称 性 、 i对称 性和 Le Me对称性 以及三 者直 接导出 的守恒量 和相互间接导 出的守恒量 。后 i 来 文献[5 ̄发现 Lga g 系统 的 Me对称性 可直接导 出有别于 Me守 11 arn e i i 恒量的一 种新 的守恒量 。以上这 些成果 大都是 借助 于动力学 系统的 L gag 函数 、 a io 函数和 A p l ar e n H mln t p e 函数来求 系统 的守 恒量 , 实在 l 其 分 析力学 中有 多种运动微分方程 , 中最为简捷 的是 T 6o 方程 , 其 znf 只要 给出系统 的 T6 o 函数 , znf 研究 系统 的运动规律是 比较方 便的 。 目前 , T 6 o 方 程的对称性 与守恒量的研 究也有了一些成果[2, zn f 1 5但这些成果 6] - 都是针对 一般 T 6o 方程 , zn f 还没有涉及到广义 T 6o 方程。 znf 本 文企 图研究 完整约束状态下 广义 T6 o 方程 的 L 对称性及其 znf i e 直接导 出的 H j a 守恒量 , o n m 力求给 出完整 系统广 义T 6 o 方程 Le z f n i对 称性的判据方程及其 守恒量 的表达式 , 最后举例说 明研究结果 的应用 。 2完整 系统 的广义 T  ̄ of . z n f方程 假设 力 学 系统 由 N 个 质 点 组成 , 统 的位 形 由 个 广 义 坐标 系 吼 =1 … , 来确定, , ) 系统广义 T o 函数为 z nf 6
变质量非Четаев型非完整系统在相空间的Lie对称性与守恒量

约 束 ( ) 在 虚 位 移 上 的 条 件 为 1加
( q, 吼 = 0 , 圣)
一
( : 12 … , , . 8 , , g)
,
() 2 B型 非 完 整 约 束 .
,
般 来说 ,
与 a / 无关 , 别 地 当 ,= a / 时 则 约 束 为 a 特 a
( 油 大 学 应 用 物 理 系 , 东 东 营 27 6 ) 石 山 5 0 1
( 张石 生推 荐 )
摘 要 : 在 相 空 间 引 入 无 限 小 群 变 换 , 究 变 质 量 非 q re 研 eas型 非 完 整 系 统 的 “ e对 称 和 守 恒 量 . 利
用 系 统 运 动 微 分 方 程 在 无 限 小 群 变 换 下 的 不 变 性 建 立 Ie 称 的 确 定 方 程 和 限 制 方 程 , 到 Le对 j对 得 i
果 具有更普遍 的意义 .
1 系 统 的 运 动 微 分 方 程
研 究 N 个 质 点 组 成 的力 学 系 统 , t 在 时刻 第 i 个质 点 的 质 量 为 m , t+d 在 时 刻 由质 点 分
离 ( 并 人 )的微 粒 的 质 量 为 d 系 统 的位 形 有 n个 广 义 坐 标 吼( 或 m. s= 12 … , ) 定 , m ,, n 确 设
对 称 性 与 守 恒 量 的 近 代 理 论 包 括 N e e 对 称 性 理 论 和 Le对 称 性 理 论 . 1 7 ot r h i 9 9年 M. u k L t y等 z 人 把 数 学 家 S Le 究 微 分 方 程 不 变性 的 扩 展 群 方 法 引 入 力 学 领 域 加 以研 究 ,提 出 了 使 运 动 .i研 微 分 方 程 不 变 的 Le 称 性 ¨2. 近 年 来 ,对 完 整 系统 和 非 完 整 系 统 在位 形 空 间 的 Le对 称 性 i对 1] . i 与 守 恒 量 的 研 究 取 得 了一 系 列 成 果 [ ] ,文 [ ] 究 了常 质 量 非 q re 6研 eaB型 非 完 整 系 统 在 位 形 空 间 的 Le 称 性 与守 恒 量 ,文 [ ] 究 了变 质 量 完 整 系 统 在 位 形 空 间 的 Le对 称 性 与 守 恒 i对 7研 i 量 . 文 [ ] 究 了 常 质 量 qeaB型 非 完 整 系 统 在 相 空 间 的 Le对 称 性 与 守 恒 量 . 本 文 研 究 变 8研 Te i 质 量 非 q Te 非 完 整 系 统 在 相 空 间 的 Le对 称 性 与 守 恒 量 ,给 出 其 正 则 形 式 的 Le 称 性 e aB型 i i 对 质 . 由于 变 质 量 非 qeaB型 非 完 整 系 统 比 常质 量 qeaB型 非 完 整 系 统 更 一 般 , Te re 因此 本 文 的 结
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
力 学 系统 的守 恒 量 ( 变 量 ) 映 了 物理 的 不 反 本 质 。 11 98年 Nehr 究 Hmio 作 用 量 泛 函 ote研 a ln t 在 时空 无 限小 变换 群作 用 下 的不 变性 时 , 示 了 揭
力学 系 统守 恒 量与 对 称性 之 问 的关 系 , 出 了著 提 名 的 N e e 定 理 ,9 0年 前 后 ,azy PiC ot r h 18 I t 、 r e和 _ k l q
Ab t c : I i a e .h e t n b t e n te fr i v r n e a d L e s mme r o aib e na sh ln mi y t s sz t n t sp p r te rli ew e m a i c n y  ̄ h ao h o n a i ty fv r l 1 o o c s s ms i a s o e s d e , i t t e d f i ol a d c t r n f ef r v r l n es mmer nt es se I ie N x , errl— t i F r 。 e n t t n r e o so t m i a i ea d L y u d s h i i s i i h o n b a i t i /tms aegv n. e t t i e y h _ h a t n i d d c d. e s o a e s u tr q a o d c n e v u n t o t efr v r n ea d L e smmer fv r i e u e W h w t t t cu e e u t n a o s r e q a t yf h m i ai c n y o s h t h r i n d i o n a i t o ai y — a l l 8 h ln mi y tm a e te s me fr . ia y w ie a x mp et lsrt e a p e t n o e rs tt b e na oo o c s s s h v a m F n l , e gv n e a l o i u t e t p l ai f e ue . s e h o l l a h i o h t Ke o s An lt a c a i ,V r l n s c a is F r v r n e Le s mme y y wr d . ayi l c me h n c s ai e l 8 me h ne , o i ai e , y b a a m n a i t r
维普资讯
第2 O卷
第 2期
江
西
科 学
20 0 2年 6月
J AN I GXI SCI CE EN
Vo , 0 No. l2 2 J ,0 2 山l 2 0
文章 编 号 :0 137 (02 0.0 3 4 10 .69 20 )206 . 0
对 称 性 的 定 义 和 判 据 ; 后 导 出形 式 不 变 性 与 Ue 称 性 的 关 系 , 出形 式 不 变性 与 Le 称 性 的 结 构 方 程 和 然 对 指 i 对
ห้องสมุดไป่ตู้
守恒量有相 同的形式 ; 最后 , 出一个说 明性 的例子。 给 关键词 : 分析力 学 ; 变质 量力学 ; 形式 不变性 ; e i L 对称性。
中 图 分 类 号 :O 1 36 文 献 标 识 码 :A
Fo m n a in e a d Li y r I v ra c n e S mm er fEq a i n f ty o u t so o Va i b eM a sHoo o c S se s ra l s ln mi y tm
W AN G h — o g -, EIF n - in S u y n . M e g xa g
( . eatet f pl dM ca i ,B i gIsteo T ho g ,ei 0 8 R 1D pr n o pi ehnc e i t t f e nl yB in 1 0 1 C; m A e s j ni c n u o jg 0 P 2 G agogTcncl oee f t eor s n l tcE g eI gG ag o 165P C . undn ehi lg e Rsu e dEe r ni e n , unz u 03 R ) a C l o Wa r c a ci n i h 5
变 质 量 完 整 力 学 系 统 的形 式 不 变 性 与 Le对 称 性 i
王树 勇 , 梅 凤 翔 一 ,
( . 京理 工大学应用力 学系, 1北 北京 108 2 广 东水利 电力职业技术 学院, 00 1 . 广东 广 州 5 03 ) 165
摘 要 :研 究变质 量完整力 学系统 运动方程的形式不 变' - i对称性 的关 系。首先, 出了形式不 变性和 Le L b Le  ̄ 给 i
已经成为近代数理科学 中一个非常重要和活 跃 的领 域 。 形 式 不 变 是 力学 系 统 运 动方 程 在无 限 小 变
换下 的 一 种 不 变 性 , 种 不 变 性 不 同 于 N e e 这 ot r h
对称 性 和 Le 称性 , 式 不 变性 在一 定 条 件 下 i 对 形
Ei e 曾举 出例 子 说 明 对 称 性 不 一 定 是 Ne e lzr e ot r h
型的【 J从而促使人们从不同的角度去重新认 卜3, 识对称性 , 而提出一系列新 的对称性概念 , 进 其 中研 究使 力 学 系 统 运 动 微 分 方 程 不 变 的 Le对 i 称性 方 法 发 展 迅 速 J 不 变 量 与 对 称 性 的研 究 。
