《工程经济学》计算题
工程经济学计算题.doc

1、现设年名义利率为10%,则分别以年、半年、季、月、周、日计息的年实际利率各是多少?年=10%半年 =(1+2) ^2-1 = %季度 =(1+4) ^4-1=%月=(1+12)^12-1=%周=(1+52)^52-1=%日=(1+360) ^360-1=%2、某人在银行存入一笔 2 万元的款项,为期 5 年,单利计息,年利率为 8%,根据这笔资金,说明其现值、时值、终值及等值的含义,并绘出现金流量图。
现值,是指对未来现金流量以恰当的折现率折现后的价值把资金运动过程中某一时间点上与现值等值的金额称为时值终值又称将来值或本利和,是指现在一定量的资金在将来某个时点上的价值资金等值是指在时间因素的作用下,不同的时间点发生的绝对值不等的资金具有相同的价值。
3、试用内插法求下表的项目的内部收益率。
若基准折现率为15%,问项目能否通过?单位:万元年份净现金流量累计净现金10%的折现累计净现值流量净现值系数1 -200 -2002 -150 -3503 100 -2504 100 -1505 100 -506 100 507 100 1508 100 2509 100 35010 100 450-200*Q-150*Q^2+100*Q^3+100*Q^4+100*Q^5+100*Q^6+100*Q^7+100* Q^8+100*Q^9+100*Q^10=0Q=P===%%>15%能通过4、某项目有 A、B、C三个互斥方案, A 方案的总投资为 1000 万元,预计每年净收益为 280 万元; B 方案的总投资为 1600 万元,预计每年净收益为 310 万元; C 方案的总投资为 2000 万元,预计每年净收益为 500 万无。
寿命期均为10 年,基准折现率为15%。
试确定最优方案。
A:280/+280/^2+ ⋯⋯ +280/^10=1405/1000=B:310/+310/^2+ ⋯⋯ +310/^10=1600=C:500/+500/^2+ ⋯⋯ +500/^10=2000=A最5、有某目的A、B、C 三个互斥方案,各自的金流量如下表所示,基准折率15%,用法确定最方案。
工程经济学综合计算题
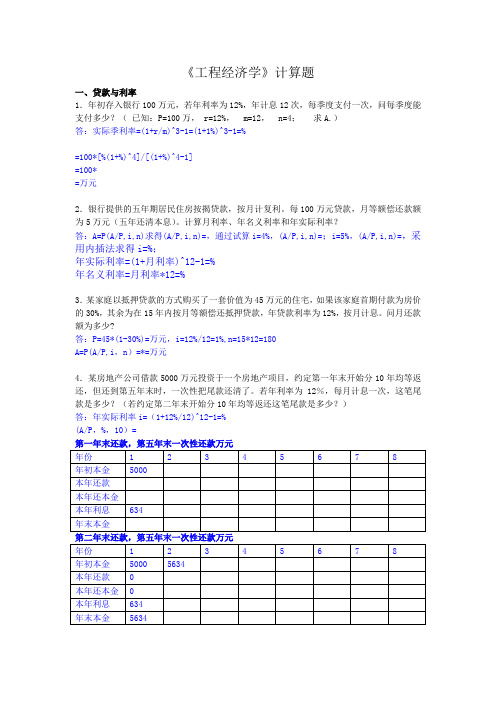
《工程经济学》计算题一、贷款与利率1.年初存入银行100万元,若年利率为12%,年计息12次,每季度支付一次,问每季度能支付多少?(已知:P=100万, r=12%, m=12, n=4;求A.)答:实际季利率=(1+r/m)^3-1=(1+1%)^3-1=%=100*[%(1+%)^4]/[(1+%)^4-1]=100*=万元2.银行提供的五年期居民住房按揭贷款,按月计复利。
每100万元贷款,月等额偿还款额为5万元(五年还清本息)。
计算月利率、年名义利率和年实际利率?答:A=P(A/P,i,n)求得(A/P,i,n)=,通过试算i=4%,(A/P,i,n)=;i=5%,(A/P,i,n)=,采用内插法求得i=%;年实际利率=(1+月利率)^12-1=%年名义利率=月利率*12=%3.某家庭以抵押贷款的方式购买了一套价值为45万元的住宅,如果该家庭首期付款为房价的30%,其余为在15年内按月等额偿还抵押贷款,年贷款利率为12%,按月计息。
问月还款额为多少?答:P=45*(1-30%)=万元,i=12%/12=1%,n=15*12=180A=P(A/P,i,n)=*=万元4.某房地产公司借款5000万元投资于一个房地产项目,约定第一年末开始分10年均等返还,但还到第五年末时,一次性把尾款还清了。
若年利率为12%,每月计息一次,这笔尾款是多少?(若约定第二年末开始分10年均等返还这笔尾款是多少?)答:年实际利率i=(1+12%/12)^12-1=%(A/P,%,10)=1-5.某企业获得800万元贷款,偿还期10年,年利率为10%,试就以下4种还款方式,分别计算还款额及10年还款总额。
⑴每年年末还80万元本金和所欠利息;⑵每年年末只还所欠利息,本金在第10年末一次还清;⑶每年末等额偿还本金和利息;⑷第10年末一次还清本金和利息。
第10年末一次还清本金和利息=800*(1+10%)^10=答案正确,方法可简单1-6.某构件厂欲购买设备,现有四家银行可以提供货款。
工程经济学计算题及答案
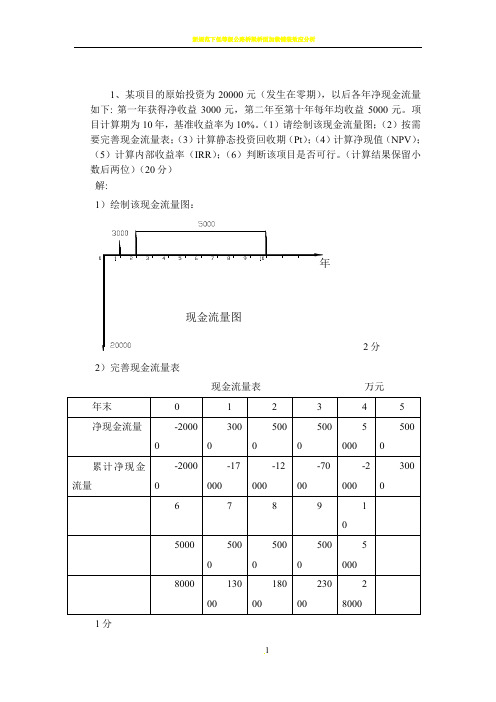
1、某项目的原始投资为20000元(发生在零期),以后各年净现金流量如下: 第一年获得净收益3000元,第二年至第十年每年均收益5000元。
项目计算期为10年,基准收益率为10%。
(1)请绘制该现金流量图;(2)按需要完善现金流量表;(3)计算静态投资回收期(Pt);(4)计算净现值(NPV);(5)计算内部收益率(IRR);(6)判断该项目是否可行。
(计算结果保留小数后两位)(20分)解:1)绘制该现金流量图:2分2)完善现金流量表现金流量表万元1分3)计算静态投资回收期(Pt ) Pt=累计净现金流量出现正值的年份-1+当年净现金流量绝对值上年累计净现金流量的 2分=5-1+年4.450002000=- 1分4)计算净现值(NPV )NPV(10%)=-20000+3000(P/F.10%.1)+5000(P/A.10%.9)(P/F.10%.1) 2分 =-20000+3000×0.9091+5000×5.759×0.9091=8904.83万元 1分 5)计算内部收益率(IRR )设1i =15% 1分 NPV 1(15%)=-20000+3000(P/F.15%.1)+5000(P/A.15%.9)(P/F.15%.1) 1分 =-20000+(3000+5000×4.7716)×0.8696 =3355.72万元 1分 设2i =20% 1分 NPV 2(20%)=-20000+3000(P/F.20%.1)+5000(P/A.20%.9)(P/F.20%.1) 1分 =-20000+(3000+5000×4.0310)×0.8333 =-704.94万元 1分∵IRR=1i +(2i -1i )211NPV NPV NPV +2分∴IRR=15%+(20%-15%)3355.723355.72704.94+=0.1913=19.13%1分6)判断该项目是否可行∵ Pt=4.4年<10年NPV(10%)=8904.83万元>0 IRR=19.13%>10%∴该项目可行 2分2、某建设项目现金流量如下表所示,若基准收益率i c=10%。
《工程经济学》计算题

《工程经济学》计算题●某新建项目,建设期为3年,分年均衡进行贷款,第一年贷款300万元,第二年600万元,第三年400万元,年利率为12%,建设期内利息只计息不支付,计算建设期贷款利息。
答:q1=1/2×300×12%=18(万元)q2=(300+18+1/2×600)×12%=74.16(万元)q3=(300+18+600+74.16+1/2×400)×12%=143.06(万元)所以,建设期贷款利息=18+74.16+143.06=235.22(万元)●某企业技术改造有两个方案可供选择,各方案的有关数据见表,设基准收益率为12%。
问:采用那个方案有利?A、B方案的数据案投资额(万元)年净收益(万元)寿期A 800 360 6B 1200 480 8NPVA=-800-800(P/F,12%,6)-800(P/F,12%,12)-800(P/F,12%,18)+360(P/A,12%,24)NPVB=-1200-1200(P/F,12%,8)-1200(P/F,12%,16)+480(P/A,12%,24)=1856.1(万元)由于NPVA < NPVB,故方案B优于方案A。
●某八层住宅工程,结构为钢筋混凝土框架,材料、机械、人工费总计为216357.83元,建筑面积为2091.73m2,。
各分部工程所占费用如下表,试用ABC分析法选择该住宅工程的研究对象。
分部名称代号费用(元)%基础 A 29113.01 13.46墙体 B 41909.53 19.37框架 C 75149.86 34.73楼地面 D 10446.04 4.83装饰 E 20571.49 9.51门窗 F 33777.31 15.61其他G 5390.59 2.49 总计216357.83 100答:按费用(或其百分比)大小排序:分部名称代号费用(元)% 累计百分比(%)框架 C 75149.86 34.73 34.73墙体 B 41909.53 19.37 54.1门窗 F 33777.31 15.61 69.71基础 A 29113.01 13.46 83.17装饰 E 20571.49 9.51 92.68楼地面 D 10446.04 4.83 97.51其他G 5390.59 2.49 100 总计216357.83 100 —由上表可知:应选框架、墙体、门窗或包含基础作为研究对象。
(完整word版)工程经济学计算题

工程经济学计算题),,/(,),,/(,),i ,/(,),i ,/(,),,/(,),,/(,n i P A P A A P n i A P A P P A n F A F A A F n A F A F F A n i F P F P P F n i P F P F F P ======:求已知:求已知:求已知:求已知:求已知:求已知1. 南桥跨越幅度较大,要建吊桥,其投资为3000万元,建桥购地80万元,年维修费1.5万元,水泥桥面每10年翻修一次5万元;北桥跨越幅度较小,可建木行架桥,预计投资1200万元,年维修费8000元,该桥每三年粉刷一次需一万元,每10年喷砂整修一次,需4.5万元,购地用款1030万元。
若年利率为6%,试比较两方案何者为优? 解:年值法: AC 南=3080×6%+1.5+5(A/F ,6%,10)=187AC 北=2230×6%+0.8+1(A/F ,6%,3)+4.5(A/F ,6%,10)=135 因为AC 南>AC 北,所以北桥的方案为优。
2. 某项目生产某种产品的设计能力为年产量100000件,产品出厂单价为200元,单位产品可变成本为100元,正常生产年份的年固定成本为680万元,试对该项目进行盈亏平衡分析。
解:Q *=Cv P Cf -=1002006800000-=68000B *=P ·Cv P Cf -=200×1002006800000-=13600000E *=QdQ *=68000/100000×100%=68%P *=Q C f +Cv=1000006800000+100=1683. 某工程方案设计生产能力为1.5万t/年,产品销售价格为3000元/t ,销售税金及附加为150元/t ,增值税为70元/t ,年总成本为3600万元,其中固定成本为1500万元。
试求以产量、销售收入、生产能力、生产能力利用率、销售价格和单位产品变动成本表示的盈亏平衡点。
工程经济学计算题

工程经济学计算题),,/(,),,/(,),i ,/(,),i ,/(,),,/(,),,/(,n i P A P A A P n i A P A P P A n F A F A A F n A F A F F A n i F P F P P F n i P F P F F P ======:求已知:求已知:求已知:求已知:求已知:求已知1. 南桥跨越幅度较大,要建吊桥,其投资为3000万元,建桥购地80万元,年维修费1.5万元,水泥桥面每10年翻修一次5万元;北桥跨越幅度较小,可建木行架桥,预计投资1200万元,年维修费8000元,该桥每三年粉刷一次需一万元,每10年喷砂整修一次,需4.5万元,购地用款1030万元。
若年利率为6%,试比较两方案何者为优? 解:年值法: AC 南=3080×6%+1.5+5(A/F ,6%,10)=187AC 北=2230×6%+0.8+1(A/F ,6%,3)+4.5(A/F ,6%,10)=135 因为AC 南>AC 北,所以北桥的方案为优。
2. 某项目生产某种产品的设计能力为年产量100000件,产品出厂单价为200元,单位产品可变成本为100元,正常生产年份的年固定成本为680万元,试对该项目进行盈亏平衡分析。
解:Q *=Cv P Cf -=1002006800000-=68000B *=P ·Cv P Cf -=200×1002006800000-=13600000E *=QdQ *=68000/100000×100%=68%P *=Q C f +Cv=1000006800000+100=1683. 某工程方案设计生产能力为1.5万t/年,产品销售价格为3000元/t ,销售税金及附加为150元/t ,增值税为70元/t ,年总成本为3600万元,其中固定成本为1500万元。
试求以产量、销售收入、生产能力、生产能力利用率、销售价格和单位产品变动成本表示的盈亏平衡点。
工程经济学综合计算题(已做)
《工程经济学》计算题一、贷款与利率1.年初存入银行100万元,若年利率为12%,年计息12次,每季度支付一次,问每季度能支付多少?(已知:P=100万, r=12%, m=12, n=4;求A.)答:实际季利率=(1+r/m)^3-1=(1+1%)^3-1=3.03%=100*[3.03%(1+3.03%)^4]/[(1+3.03%)^4-1]=100*0.2692=26.92万元2.银行提供的五年期居民住房按揭贷款,按月计复利。
每100万元贷款,月等额偿还款额为5万元(五年还清本息)。
计算月利率、年名义利率和年实际利率?答:A=P(A/P,i,n)求得(A/P,i,n)=0.05,通过试算i=4%,(A/P,i,n)=0.044201845;i=5%,(A/P,i,n)=0.052828185,采用内插法求得i=4.67%;年实际利率=(1+月利率)^12-1=72.93%年名义利率=月利率*12=56.04%3.某家庭以抵押贷款的方式购买了一套价值为45万元的住宅,如果该家庭首期付款为房价的30%,其余为在15年内按月等额偿还抵押贷款,年贷款利率为12%,按月计息。
问月还款额为多少?答:P=45*(1-30%)=31.5万元,i=12%/12=1%,n=15*12=180A=P(A/P,i,n)=31.5*0.012=0.378万元4.某房地产公司借款5000万元投资于一个房地产项目,约定第一年末开始分10年均等返还,但还到第五年末时,一次性把尾款还清了。
若年利率为12%,每月计息一次,这笔尾款是多少?(若约定第二年末开始分10年均等返还这笔尾款是多少?)答:年实际利率i=(1+12%/12)^12-1=12.68%(A/P,12.68%,10)=0.1819年份 1 2 3 4 5 6 7 8年初本金5000 4724.5 4414.07 4064.273670.12本年还款909.50 909.50 909.50 909.50 4135.49本年还本金275.5 310.43 349.8 394.15本年利息634 599.07 559.7 515.35 465.37年末本金4724.5 4414.07 4064.273670.12年份 1 2 3 4 5 6 7 8 年初本金5000 5634 5323.54973.74579.61-5.某企业获得800万元贷款,偿还期10年,年利率为10%,试就以下4种还款方式,分别计算还款额及10年还款总额。
工程经济学复习题计算题答案汇总
第2章1.某房地产开发项目建设期为3年,在建设期第一年借款500万元,第2年借款为600万元,第三年借款为400万元,年利率为8%,试计算建设期利息。
1、建设期每年应计利息=(以前年度贷款本息累计+本年度贷款额/2)×利率I1=500/2×8%=20万I2=(500+20+600/2)×8%=65.5万I3=(500+20++600+65.5+400/2)×8%=110.848万 I=20+65.5+110.848=196.448万2.假设某项目建设期3年,各年计划投资额分别为:第一年4000万元,第二年4800万元,第三年3800万元,年平均价格上涨率为5%,则该项目建设期间涨价预备费为多少?PF1=4000×[(1+5%)-1]=200万 PF2=4800×[(1+5%)2-1]=492万 PF3=3800×[(1+5%)3-1]=598.975万PF= PF1 +PF2 +PF3 =200+492=598.975=1290.975万第3章四、计算题1. 某投资者以400万元购入一写字楼物业20年的使用权出租经营,已知该投资者的目标收益率为18%,预计未来20年内的年租金上涨率为5%,问该写字楼第一年的租金收入为多少 时方能满足投资者收益目标的要求?第8年的租金净收入又是多少?(57.58;81万元)解:已知P=400万元,n=20,i=18%,g=5%,先求A1则第8年收益为:∑=-+=nt tt f I PF 1]1)1[(()()()()()12020201111400(1)15%118%118%5%18%57.58n nn g i A i g iA A --+-+=+-+-+=+-=()()7857.5815%81A =⨯+=万元2. 某企业从银行一次性贷款30万元 ,承诺20年每年年末等额偿还,年利率为10%,若还了12次后,该企业打算来年一次性还清,那么,一次性还款为多少万元?(20.67万元)解、已知P=30万元,i =10%,n=20,先求A(1)A= P(A/P,i,n)=30(A/P , 10%, 20)=30×0.1175=3.525 (2)P13 +A = A (P/A,i,n)+A=3.525(P/A , 10%, 7)+A=3.525×4.8684+3.525=20.67(万元)3. 银行为某家庭提供年利率为6%,按月等额偿还的10年期个人住房抵押贷款,若每月的还款额为2000元,则该家庭在第5年最后一个月的还款额中的本金额是多少?(1475.37) 解:4. 某家庭以4000元/平方米的价格,购买了一套建筑面积为120平方米的住宅,银行为其提供了15年期的住房抵押贷款。
工程经济学计算题及答案
⼯程经济学计算题及答案1、某项⽬的原始投资为20000元(发⽣在零期),以后各年净现⾦流量如下: 第⼀年获得净收益3000元,第⼆年⾄第⼗年每年均收益5000元。
项⽬计算期为10年,基准收益率为10%。
(1)请绘制该现⾦流量图;(2)按需要完善现⾦流量表;(3)计算静态投资回收期(Pt );(4)计算净现值(NPV );(5)计算内部收益率(IRR );(6)判断该项⽬是否可⾏。
(计算结果保留⼩数后两位)(20分)解:1)绘制该现⾦流量图:2分2)完善现⾦流量表3)计算静态投资回收期(Pt ) Pt=累计净现⾦流量出现正值的年份-1+当年净现⾦流量绝对值上年累计净现⾦流量的2分=5-1+年4.450002000=- 1分4)计算净现值(NPV )NPV(10%)=-20000+3000(P/F.10%.1)+5000(P/A.10%.9)(P/F.10%.1) 2分 =-20000+3000×0.9091+5000×5.759×0.9091=8904.83万元 1分 5)计算内部收益率(IRR )设1i =15% 1分 NPV 1(15%)=-20000+3000(P/F.15%.1)+5000(P/A.15%.9)(P/F.15%.1) 1分=-20000+(3000+5000×4.7716)×0.8696=3355.72万元 1分设2i =20% 1分 NPV 2(20%)=-20000+3000(P/F.20%.1)+5000(P/A.20%.9)(P/F.20%.1) 1分 =-20000+(3000+5000×4.0310)×0.8333=-704.94万元 1分∵IRR=1i +(2i -1i )211NPVNPVNPV + 2分∴IRR=15%+(20%-15%)3355.723355.72704.94+=0.1913=19.13% 1分6)判断该项⽬是否可⾏∵ Pt=4.4年<10年NPV(10%)=8904.83万元>0 IRR=19.13%>10%∴该项⽬可⾏ 2分2、某建设项⽬现⾦流量如下表所⽰,若基准收益率i c=10%。
工程经济学计算练习题(修正版)含答案解析
第一题某拟建工业项目建设投资3000万元,建设期2年,生产运营期8年。
其他有关资料和基础数据如下:(1)建设投资预计全部形成固定资产,固定资产使用年限为8年,残值率为5%,采用直线法折旧。
(2)建设投资来源为资本金和贷款。
其中贷款本金为1800万元,贷款年利率为6%,按年计息。
贷款在两年内均衡投入。
(3)在生产运营期前4年按照等额还本付息方式偿还贷款。
(4)生产运营期第1年由资本金投入300万元作为生产运营期间的流动资金。
(5)项目生产运营期正常年份营业收入为1500万元,经营成本为680万元,生产运营期第1年营业收入和经营成本均为正常年份的80%,第2年起各年营业收入和营业成本均达到正常年份水平。
(6)项目所得税税率为25%,营业税金及附加税率为6%。
求:1.列式计算项目的年折旧额。
2.列式计算项目生产运营期第1年、第2年应偿还的本息额。
3.列式计算项目生产运营期第1年、第2年的总成本费用。
4.判断项目生产运营期第1年末项目还款资金能否满足约定还款方式要求,并通过列式计算说明理由。
5.列式计算项目正常年份的总投资收益率。
(计算结果均保留两位小数)解答:1.建设期第1年贷款利息=900×6%×1/2=27.00(万元);建设期第2年贷款利息=(1800/2+27.00+1800/2×50%)×6%=82.62(万元);建设期贷款利息合计=27.00+82.62=109.62(万元)。
项目固定资产原值=3000+109.62=3109.62(万元);项目的年折旧额=3109.62×(1-5%)/8=369.27(万元)。
2.运营期第1年年初贷款本息和=1800+27.00+82.62=1909.62(万元);还款期4年中每年等额还本付息额=1909.62×(A/P,6%,4)=551.10(万元)。
运营期第1年应付利息=1909.62×6%=114.58(万元);运营期第1年应还本金=551.10-114.58=436.52(万元)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《工程经济学》计算题●某新建项目,建设期为3年,分年均衡进行贷款,第一年贷款300万元,第二年600万元,第三年400万元,年利率为12%,建设期内利息只计息不支付,计算建设期贷款利息。
答:q1=1/2×300×12%=18(万元)q2=(300+18+1/2×600)×12%=74.16(万元)q3=(300+18+600+74.16+1/2×400)×12%=143.06(万元)所以,建设期贷款利息=18+74.16+143.06=235.22(万元)●某企业技术改造有两个方案可供选择,各方案的有关数据见表,设基准收益率为12%。
问:采用那个方案有利?A、B方案的数据案投资额(万元)年净收益(万元)寿期A 800 360 6B 1200 480 8NPVA=-800-800(P/F,12%,6)-800(P/F,12%,12)-800(P/F,12%,18)+360(P/A,12%,24)NPVB=-1200-1200(P/F,12%,8)-1200(P/F,12%,16)+480(P/A,12%,24)=1856.1(万元)由于NPVA < NPVB,故方案B优于方案A。
●某八层住宅工程,结构为钢筋混凝土框架,材料、机械、人工费总计为216357.83元,建筑面积为2091.73m2,。
各分部工程所占费用如下表,试用ABC分析法选择该住宅工程的研究对象。
分部名称代号费用(元)%基础 A 29113.01 13.46墙体 B 41909.53 19.37框架 C 75149.86 34.73楼地面 D 10446.04 4.83装饰 E 20571.49 9.51门窗 F 33777.31 15.61其他G 5390.59 2.49 总计216357.83 100答:按费用(或其百分比)大小排序:分部名称代号费用(元)% 累计百分比(%)框架 C 75149.86 34.73 34.73墙体 B 41909.53 19.37 54.1门窗 F 33777.31 15.61 69.71基础 A 29113.01 13.46 83.17装饰 E 20571.49 9.51 92.68楼地面 D 10446.04 4.83 97.51其他G 5390.59 2.49 100 总计216357.83 100 —由上表可知:应选框架、墙体、门窗或包含基础作为研究对象。
●假设某项目建设期3年,各年计划投资额分别为:第一年4000万元,第二年4800万元,第三年3800万元,年平均价格上涨率为5%,则该项目建设期间涨价预备费为多少?答:PF1=4000×[(1+5%)-1]=200万PF2=4800×[(1+5%)2-1]=492万PF3=3800×[(1+5%)3-1]=598.975万PF= PF1 +PF2 +PF3 =200+492=598.975=1290.975万●某家庭欲购买一套面积为80m2的经济适用房,单价为3500元/m2,首付款为房价的25%,其余申请公积金和商业组合抵押贷款,已知公积金和商业贷款的利率分别为4.2%和6.6%,期限为15年,公积金贷款的最高限额为10万元。
问该家庭申请组合抵押贷款后的最低月还款额是多少?答:P=3500×80(1-25%)=21万n=15×12=180i1=4.2%/12=0.35% i2=6.6%/12=0.55% P1=10万 P2=11万A1=100000×0.35%×(1+0.35%)180/[(1+0.35%)180-1]=749.75元A2= 110000×0.55%(1+0.55)180/[(1+0.55%)180-1]=964.28元A=A1+A2=1714.03元●何谓现金流量表?现金流量表的纵列、横行各是什么?答:现金流量表是指能够直接、清楚地反映出项目在整个计算期内各年现金流量情况的一种表格,利用它可以进行现金流量分析、计算各项静态和动态评价指标,是评价项目投资方案经济效果的主要依据。
现金流量表的纵列是现金流量的项目,其编排按现金流入、现金流出、净现金流量的顺序进行;现金流量表的横行是年份,按项目计算期的各个阶段来排列。
●某三个互斥的投资方案的期初投资额、每年的净收益如下表所示,假设各方案的寿命均为10年。
(P/A,10%,10)=6.1446表投资方案的期初投资额、每年的净收益投资方案期初投资额(万元)每年的净收益(万元)A 5000 1224B 3000 970C 1000 141求:当资本的利率i=10%时,此时哪个方案最优?答:NPVB-C=-(3000-1000)+(970-141)(P/A,10%,10)=-2000+829×6.1446=3093.87差额净现值大于零,所以投资大的方案好,在B,C两个方案中B优NPVA-B=-(5000-3000)+(1224-970)(P/A,10%,10)=-2000+254×6.1446=-439.3 差额净现值小于零,所以投资小的方案好,在A,B两个方案中B优所以在A,B,C,三个方案中B方案最优●某工程项目拟定了两个方案,若年利率为10%, 试作方案选择。
项目投资(万元)年收入(万元)年经营成本(万元)残值(万元)寿命(年)大修费(万元/次)I方案20 18 2.5 6 4 2(二年一次)II方案10 10 1 4 3答:I方案净现值=-20+(18-2.5)*(P/A,10%,4)-2*(P/F,10%,2)+6*(P/F,10%,4) =-20+15.5*3.1699-2*0.8264+6*0.6830=31.58万元II方案净现值=-10+(10-1)*(P/A,10%,3)+4*(P/F,10%,3)=-10+9*2.4869+4*0.7513=15.39万元选择I方案●今有两个寿命期均是10年的互斥方案:A方案初始投资额为50万元,年净收益为14万;B 方案初始投资额为100万元,年净收益为25万元。
设基准贴现率是15 %,请通过计算回答:(1)两方案的内部收益率是否都大于15 %?(2)根据上述计算哪个方案优选?答:(1)两方案净现值分别为:NPVA = -50 + 14(P/A, 15%, 10) = -50 + 14×5.0188=20.26万元NPVB = -100 + 25(P/A, 15%, 10) = -100 + 25×5.0188 =25.47万元由上计算可知,NPVB > NPVA> 0,故两方案的内部收益率均大于15 %。
(2)由于NPVB > NPVA,故方案B优选。
●某音像公司经济分析人员提出六个可供选择的方案,每个方案的使用期都是10年,且期末均无残值。
各方案的数据见表所示。
请根据下列假设进行决策。
(1)假设各方案互斥,基准收益率为12%;(2)假设各方案独立,且有足够的资本,基准收益率为12%;(3)假设各方案独立,只有90000元的资金,基准收益率为10%。
单位:元方案 A B C D E F投资资本年净现金流量80000110004000080001000020003000071501500025009000014000答:寿命期相同,采用净现值法。
NPVA=-80000+11000(P/A,12%,10) =-80000+11000×5.6502=-17847.8<0NPVB=-40000+8000(P/A,12%,10) =-40000+8000×5.6502=5201.6>0NPVC=-10000+2000(P/A,12%,10) =-10000+2000×5.6502=1300.4>0NPVD=-30000+7150(P/A,12%,10) =-30000+7150×5.6502=10398.93>0NPVE=-15000+2500(P/A,12%,10) =-15000+2500×5.6502=-874.5<0NPVF=-90000+14000(P/A,12%,10) =-90000+14000×5.6502=-10897.2<0 故方案B、C、D可行(1)若各方案互斥,NPVD >NPVB>NPVC,则选择D方案(2)各方案独立,且有足够的资本,则同时选择方案B、C、D(3)假设各方案独立,有90000元的资金限额时(基准收益率为10%):=-80000+11000(P/A,10%,10) =-80000+11000×5.6502=-12409.4<0NPVA=-40000+8000(P/A,10%,10) =-40000+8000×5.6502=9156.8>0NPVB=-10000+2000(P/A,10%,10) =-10000+2000×5.6502=2289.2>0NPVC=-30000+7150(P/A,10%,10) =-30000+7150×5.6502=13933.89>0NPVD=-15000+2500(P/A,10%,10) =-15000+2500×5.6502=361.5>0NPVE=-90000+14000(P/A,10%,10) =-90000+14000×5.6502=-3975.6<0NPVF方案B、C、D、E可行故若各方案独立,只有90000元的资金,则选择方案组合(D+ B+C)●某企业账面反映的长期资金共500万元,其中长期借款100万元,应付长期债券50万元,普通股250万元,保留盈余100万元;其资金成本分别为6.7%、9.17%、11.26%、11%。
该企业的加权平均资金成本为:答:●年初存入银行100万元,若年利率为12%,年计息12次,每季度支付一次,问每季度能支付多少?(已知:P=100万, r=12%, m=12, n=4;求A.)答:实际季利率=(1+r/m)^3-1=(1+1%)^3-1=3.03%=100*[3.03%(1+3.03%)^4]/[(1+3.03%)^4-1]=100*0.2692=26.92万元●某项目建筑工程费5500万元,设备及工器具购置费12000万元,安装工程费3500万元,工程建设其他费用9600万元,建设期各年价格上涨指数均为5%,项目建设期2年,各项费用的第一年和第二年的分年投入比例为4:6,求该项目的涨价预备费。
●某人购买一套10平方米的住房,单价1.5万/平方米,当付50万元后,贷款100万元,贷款利率为5%,贷款期限为15年,采用等额还款抵押贷款的公式计算,每月贷款的金额是多少万元?前三个月还款中每个月的应付利息和应还的本金各是多少万元?若分期还款5年后,则贷款余额还剩下多少万元?(1)100=A*年金现值系数(P/A,5%/12,180) =A*126.455A=7907.95(2)第一个月本金=100万元 / 180 = 5555.56元第一个利息=100万元*(5%/12) = 4166.67元第一月 = 5555.56+4166.67=9722.23元(3)还款5年后总还=5555.56*12*5=333333.6贷款余额=1000000-333333.6=666666.4●.假设某项目建设期3年,各年计划投资额分别为:第一年4000万元,第二年4800万元,第三年3800万元,年平均价格上涨率为5%,则该项目建设期间涨价预备费为多少?答:PF1=4000×[(1+5%)-1]=200万PF2=4800×[(1+5%)2-1]=492万PF3=3800×[(1+5%)3-1]=598.975万PF= PF1 +PF2 +PF3 =200+492=598.975=1290.975万●银行为某家庭提供年利率为6%,按月等额偿还的10年期个人住房抵押贷款,若每月的还款额为2000元,则该家庭在第5年最后一个月的还款额中的本金额是多少?答:●某工程项目需要投资,现在向银行借款为 100万元,年利率为 10%,借款期为 5年,一次还清。
