工程经济学计算题
一级建造师《工程经济》必考计算题
2020年一级建造师《工程经济》必考计算题1.利息的计算单利(利不生利)F=P(1+n*i)复利(利生利) F=P(1+i)^n;【典型例题】某施工企业从银行借款100万元，期限3年，年利率8%,按年计息并于每年末付息，则第3年末企业需偿还的本利和为( )万元。
A.100B.124C.108D.126【答案】C【解析】本题考查的是利息的计算——单利计息。
本题，第3年末企业需偿还的本利和为：100+100×8%=108万元。
【典型例题】某施工企业每年年末存入银行100万元，用于3年后的技术改造，已知银行存款年利率为5%,按年复利计息，则到第3年末可用于技术改造的资金总额为( )。
A.331.01B.330.75C.315.25D.315.00【答案】C【解析】本题考查等值计算。
已知年金A 求终值F, 每年年末存100万为年金A, 第3年末可取出的金额为终值F,F=100×[(1+5%)^3-1]/5%=315.25 万元。
【考点来源】资金时间价值的计算及应用2.有效利率和名义利率有效利率=(1+计息周期利率)^m-1m-所求期限(问题)内的计息次数【典型例题】已知年名义利率为10%,每季度计息1次，复利计息，则年有效利率为()。
A. 10.00%B.10.25%C. 10.38%D.10.47【答案】C【解析】年有效利率= )4-1=10.38%【考点来源】资金时间价值的计算及应用3.总投资收益率的计算式中EBIT——技术方案正常年份的年息税前利润或运营期内年平均息税前利润；TI——技术方案总投资(包括建设投资、建设期贷款利息和全部流动资金)。
【典型例题】某工业项目建设投资额8250万元(不含建设期贷款利息),建设期贷款利息为1200万元，全部流动资金700万元，铺底流动资金为200万元，项目投产期的息税前利润为300万元/年，项目达产期的息税前利润为500万元/年，则该项目的总投资收益率为( )。
工程经济学综合计算题
《工程经济学》计算题一、贷款与利率1．年初存入银行100万元，若年利率为12%，年计息12次，每季度支付一次，问每季度能支付多少？（已知：P=100万， r=12%， m=12， n=4；求A.）答：实际季利率=(1+r/m)^3-1=(1+1%)^3-1=%=100*[%(1+%)^4]/[(1+%)^4-1]=100*=万元2．银行提供的五年期居民住房按揭贷款，按月计复利。
每100万元贷款，月等额偿还款额为5万元（五年还清本息）。
计算月利率、年名义利率和年实际利率？答：A=P(A/P,i,n)求得(A/P,i,n)=，通过试算i=4%，(A/P,i,n)=；i=5%，(A/P,i,n)=，采用内插法求得i=%；年实际利率=(1+月利率)^12-1=%年名义利率=月利率*12=%3．某家庭以抵押贷款的方式购买了一套价值为45万元的住宅，如果该家庭首期付款为房价的30%，其余为在15年内按月等额偿还抵押贷款，年贷款利率为12%，按月计息。
问月还款额为多少?答：P=45*(1-30%)=万元，i=12%/12=1%,n=15*12=180A=P(A/P,i，n）=*=万元4．某房地产公司借款5000万元投资于一个房地产项目，约定第一年末开始分10年均等返还，但还到第五年末时，一次性把尾款还清了。
若年利率为12％，每月计息一次，这笔尾款是多少？（若约定第二年末开始分10年均等返还这笔尾款是多少？）答：年实际利率i=（1+12%/12)^12-1=%(A/P，%，10）=1-5．某企业获得800万元贷款，偿还期10年，年利率为10％，试就以下4种还款方式，分别计算还款额及10年还款总额。
⑴每年年末还80万元本金和所欠利息；⑵每年年末只还所欠利息，本金在第10年末一次还清;⑶每年末等额偿还本金和利息；⑷第10年末一次还清本金和利息。
第10年末一次还清本金和利息=800*（1+10%）^10=答案正确，方法可简单1-6．某构件厂欲购买设备，现有四家银行可以提供货款。
工程经济学计算题及答案
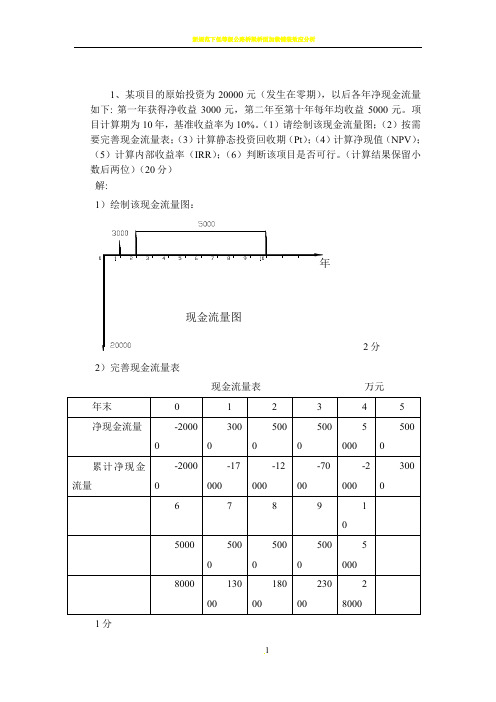
1、某项目的原始投资为20000元（发生在零期），以后各年净现金流量如下: 第一年获得净收益3000元，第二年至第十年每年均收益5000元。
项目计算期为10年，基准收益率为10%。
（1）请绘制该现金流量图；（2）按需要完善现金流量表；（3）计算静态投资回收期（Pt）；（4）计算净现值（NPV）；（5）计算内部收益率（IRR）；（6）判断该项目是否可行。
（计算结果保留小数后两位）（20分）解:1）绘制该现金流量图：2分2）完善现金流量表现金流量表万元1分3）计算静态投资回收期（Pt ） Pt=累计净现金流量出现正值的年份-1+当年净现金流量绝对值上年累计净现金流量的 2分=5-1+年4.450002000=- 1分4）计算净现值（NPV ）NPV(10%)=-20000+3000(P/F.10%.1)+5000(P/A.10%.9)(P/F.10%.1) 2分 =-20000+3000×0.9091+5000×5.759×0.9091=8904.83万元 1分 5）计算内部收益率（IRR ）设1i =15% 1分 NPV 1(15%)=-20000+3000(P/F.15%.1)+5000(P/A.15%.9)(P/F.15%.1) 1分 =-20000+（3000+5000×4.7716）×0.8696 =3355.72万元 1分 设2i =20% 1分 NPV 2(20%)=-20000+3000(P/F.20%.1)+5000(P/A.20%.9)(P/F.20%.1) 1分 =-20000+（3000+5000×4.0310）×0.8333 =-704.94万元 1分∵IRR=1i +(2i -1i )211NPV NPV NPV +2分∴IRR=15%+(20%-15%)3355.723355.72704.94+=0.1913=19.13%1分6）判断该项目是否可行∵ Pt=4.4年＜10年NPV(10%)=8904.83万元＞0 IRR=19.13%＞10%∴该项目可行 2分2、某建设项目现金流量如下表所示，若基准收益率i c=10％。
(完整word版)工程经济学计算题
工程经济学计算题),,/(,),,/(,),i ,/(,),i ,/(,),,/(,),,/(,n i P A P A A P n i A P A P P A n F A F A A F n A F A F F A n i F P F P P F n i P F P F F P ======：求已知：求已知：求已知：求已知：求已知：求已知1. 南桥跨越幅度较大，要建吊桥，其投资为3000万元，建桥购地80万元，年维修费1.5万元，水泥桥面每10年翻修一次5万元；北桥跨越幅度较小，可建木行架桥，预计投资1200万元，年维修费8000元，该桥每三年粉刷一次需一万元，每10年喷砂整修一次，需4.5万元，购地用款1030万元。
若年利率为6％，试比较两方案何者为优？ 解：年值法： AC 南=3080×6％+1.5+5（A/F ，6％，10）=187AC 北=2230×6％+0.8+1（A/F ，6％，3）+4.5（A/F ，6％，10）=135 因为AC 南>AC 北，所以北桥的方案为优。
2. 某项目生产某种产品的设计能力为年产量100000件，产品出厂单价为200元，单位产品可变成本为100元，正常生产年份的年固定成本为680万元，试对该项目进行盈亏平衡分析。
解：Q *=Cv P Cf -=1002006800000-=68000B *=P ·Cv P Cf -=200×1002006800000-=13600000E *=QdQ *=68000/100000×100％=68％P *=Q C f +Cv=1000006800000+100=1683. 某工程方案设计生产能力为1.5万t/年，产品销售价格为3000元/t ，销售税金及附加为150元/t ，增值税为70元/t ，年总成本为3600万元，其中固定成本为1500万元。
试求以产量、销售收入、生产能力、生产能力利用率、销售价格和单位产品变动成本表示的盈亏平衡点。
《工程经济学》计算题
《工程经济学》计算题●某新建项目，建设期为3年，分年均衡进行贷款，第一年贷款300万元，第二年600万元，第三年400万元，年利率为12%，建设期内利息只计息不支付，计算建设期贷款利息。
答：q1＝1/2×300×12％＝18（万元）q2＝（300+18+1/2×600）×12％＝74.16（万元）q3＝（300+18+600+74.16+1/2×400）×12％＝143.06（万元）所以，建设期贷款利息＝18+74.16+143.06＝235.22（万元）●某企业技术改造有两个方案可供选择，各方案的有关数据见表，设基准收益率为12％。
问：采用那个方案有利？A、B方案的数据案投资额（万元）年净收益（万元）寿期A 800 360 6B 1200 480 8NPVA=－800－800(P/F,12%,6)-800(P/F,12%,12)-800(P/F,12%,18)+360(P/A,12%,24)NPVB=－1200－1200(P/F,12%,8)-1200(P/F,12%,16)+480(P/A,12%,24)=1856.1(万元)由于NPVA < NPVB，故方案B优于方案A。
●某八层住宅工程，结构为钢筋混凝土框架，材料、机械、人工费总计为216357.83元，建筑面积为2091.73m2,。
各分部工程所占费用如下表，试用ABC分析法选择该住宅工程的研究对象。
分部名称代号费用（元）%基础 A 29113.01 13.46墙体 B 41909.53 19.37框架 C 75149.86 34.73楼地面 D 10446.04 4.83装饰 E 20571.49 9.51门窗 F 33777.31 15.61其他G 5390.59 2.49总计216357.83 100答：按费用（或其百分比）大小排序：分部名称代号费用（元）% 累计百分比（%）框架 C 75149.86 34.73 34.73墙体 B 41909.53 19.37 54.1门窗 F 33777.31 15.61 69.71基础 A 29113.01 13.46 83.17装饰 E 20571.49 9.51 92.68楼地面 D 10446.04 4.83 97.51其他G 5390.59 2.49 100 总计216357.83 100 —由上表可知：应选框架、墙体、门窗或包含基础作为研究对象。
工程经济学计算题及答案
1、某项目的原始投资为20000元（发生在零期），以后各年净现金流量如下: 第一年获得净收益3000元，第二年至第十年每年均收益5000元。
项目计算期为10年，基准收益率为10%。
（1）请绘制该现金流量图；（2）按需要完善现金流量表；（3）计算静态投资回收期（Pt）；（4）计算净现值（NPV）；（5）计算内部收益率（IRR）；（6）判断该项目是否可行。
（计算结果保留小数后两位）（20分）解:1）绘制该现金流量图：2分2）完善现金流量表现金流量表万元1分3）计算静态投资回收期（Pt）Pt=累计净现金流量出现正值的年份-1+当年净现金流量绝对值上年累计净现金流量的2分=5-1+年4.450002000=- 1分4）计算净现值（NPV ）NPV(10%)=-20000+3000(P/F.10%.1)+5000(P/A.10%.9)(P/F.10%.1) 2分 =-20000+3000×0.9091+5000×5.759×0.9091=8904.83万元 1分 5）计算内部收益率（IRR ）设1i =15% 1分 NPV 1(15%)=-20000+3000(P/F.15%.1)+5000(P/A.15%.9)(P/F.15%.1) 1分 =-20000+（3000+5000×4.7716）×0.8696 =3355.72万元 1分 设2i =20% 1分NPV 2(20%)=-20000+3000(P/F.20%.1)+5000(P/A.20%.9)(P/F.20%.1) 1分 =-20000+（3000+5000×4.0310）×0.8333 =-704.94万元 1分 ∵IRR=1i +(2i -1i )211NPV NPV NPV + 2分∴IRR=15%+(20%-15%)3355.723355.72704.94+=0.1913=19.13% 1分6）判断该项目是否可行 ∵ Pt=4.4年＜10年NPV(10%)=8904.83万元＞0 IRR=19.13%＞10%∴该项目可行 2分2、某建设项目现金流量如下表所示，若基准收益率i c=10％。
工程经济学计算题
1、时间价值及等值计算某人得了5000元，打算在48个月中以等额月末支付分期付款，在归还25次之后，他想第26次以一次支付立即归还余下借款，年利率为24%，每月计息一次，问此人归还的总金额为多少？解：每月利率为i=24%÷12=2%前25次中,每次支付金额为A=P ×(A/P,i，n)=5000×(A/P,2%,48)=5000×0.03264=163.2前 25 次支付的现值为 P1=A×（P/A，i，n）=163.2×（P/A，2%，25）=163.2×19.5235=3186.2（元）前 25 次支付后欠款的现值为 P2=P-P1=5000-3186.2=1813.8前 25 次应偿还的金额为F=P2×(F/P，i,n)=1813.8×1.6734=3035.2总还款金额为=F+25×A=3035.2+25×163.2=7115.22、按揭还款计算某人购买一套10平方米的住房，单价1.5万/平方米，当付50万元后，贷款100万元，贷款利率为5%，贷款期限为15年，采用等额还款抵押贷款的公式计算，每月贷款的金额是多少万元？前三个月还款中每个月的应付利息和应还的本金各是多少万元？若分期还款5年后，则贷款余额还剩下多少万元？（1）100=A*年金现值系数(P/A，5%/12，180) =A*126.455A=7907.95（2）第一个月本金=100万元/ 180 = 5555.56元第一个利息=100万元*(5%/12) = 4166.67元第一月= 5555.56+4166.67=9722.23元（3）还款5年后总还=5555.56*12*5=333333.6贷款余额=1000000-333333.6=666666.43、项目经济评价指标计算（现在、投资回收期、内部收益率）①某项目初始投资为8000万元，第一年末的现金流入为2000万元，第二年末的现金流入为3000万元，第三年、四年末的现金流入均为4000万元，设基准收益率为10%，请计算该项目的静态投资回收期，动态投资回收期，净现值，净年值，净现值率，内部收益率？（一）NPV（净现值）=-8000+2000（P/F，10%，1）+3000（P/F，10%，2）+4000（P/F，10%，3）+4000（P/F，10%，4）=2035.9（二）NAV（净年值）=NPV（A / P，10%，4）=2035.9×0.3154=642.3（元）（三）NPVR（净现值率）=NPV / I P = 2035.9 / 8000 = 0.254 =25.4%＞0（方案可行）（四）内部收益率NPV1（15%）=-8000+2000（P / F，15%，1）+3000（P / F，15%，2）+4000（P / A，15%，2）（P / F，15%，2）=-8000+2000×0.8696+3000×0.7561+4000×1.626×0.7561=925（元）＞0NPV2（20%）= -8000+2000（P / F，20%，1）+3000（P / F，20%，2）+4000（P / A，20%，2）（P / F，20%，2）= -8000+2000×0.8333+3000×0.6944+4000×1.528×0.6944= -6.03＜0由NPV1（15%）=925（元）＞0NPV2（20%）= -6.03＜0及（i2-i1)=20%- 15%=5%（符合《5%）得:IRR= i1+（NPV1/NPV1+|NPV2|）×（i2-i1）=15%+（925/925+|-6.03|）×（20%-15%）= 0.1997 ≈ 0.20 = 20%（五）静态投资回收期Pt=（T-1）+|第（T-1）年的累计净现金流量|/第T年的净现金流量Pt=3-1+|-3000|/4000=2.75动态投资回收期Pd=（T-1）+|第（T-1）年的累计折现值|/第T年净现金流量的折现值Pd= = 4 — 1 +∣— 698∣/ 2732= 3 + 0.26 = 3.26 （年）②某开发公司购买空地一块，拟开发住宅小区，地价800万元一次付清，预计建设期两年，第一年建设投资800万元，第二年建设投资1000万元，住宅建筑总面积15000平方米，预计平均售价3000元/平方米，销售计划为：建设期第一、二年分别预售房屋的10%和5%，销售期第一、二年分别销售40%和35%，销售税、代理费等占销售收入的10%，基准收益率为10%，根据上述材料，要求：（1）绘制该项目的现金流量图；总销售金额=1.5×3000×（1-10%）=4050（万元）第一年净现金=4050×10%-800=-395第二年净现金=4050×5%-1000=-797.5第三年净现金=4050×40%=1620第四年净现金=4050×35%=1417.5（2）计算该项目的静态投资回收期和动态投资回收期；Pt=4-1+|-372.5|/1417.5=3.26Pd=4-1+|-601.03|/968.15=3.62（3）计算该项目的净现值为多少万元？净现值=968.15+1217.11-659.05-359.09-800=367.12（4）该项目是否经济合理，其依据有哪些？净现值=367.12大于0，动态投资回收期为3.62年小于4年，说明内部收益率大于基准收益率为10%。
工程经济学综合计算题(已做)
《工程经济学》计算题一、贷款与利率1．年初存入银行100万元，若年利率为12%，年计息12次，每季度支付一次，问每季度能支付多少？（已知：P=100万， r=12%， m=12， n=4；求A.）答：实际季利率=(1+r/m)^3-1=(1+1%)^3-1=3.03%=100*[3.03%(1+3.03%)^4]/[(1+3.03%)^4-1]=100*0.2692=26.92万元2．银行提供的五年期居民住房按揭贷款，按月计复利。
每100万元贷款，月等额偿还款额为5万元（五年还清本息）。
计算月利率、年名义利率和年实际利率？答：A=P(A/P,i,n)求得(A/P,i,n)=0.05，通过试算i=4%，(A/P,i,n)=0.044201845；i=5%，(A/P,i,n)=0.052828185，采用内插法求得i=4.67%；年实际利率=(1+月利率)^12-1=72.93%年名义利率=月利率*12=56.04%3．某家庭以抵押贷款的方式购买了一套价值为45万元的住宅，如果该家庭首期付款为房价的30%，其余为在15年内按月等额偿还抵押贷款，年贷款利率为12%，按月计息。
问月还款额为多少?答：P=45*(1-30%)=31.5万元，i=12%/12=1%,n=15*12=180A=P(A/P,i，n）=31.5*0.012=0.378万元4．某房地产公司借款5000万元投资于一个房地产项目，约定第一年末开始分10年均等返还，但还到第五年末时，一次性把尾款还清了。
若年利率为12％，每月计息一次，这笔尾款是多少？（若约定第二年末开始分10年均等返还这笔尾款是多少？）答：年实际利率i=（1+12%/12)^12-1=12.68%(A/P，12.68%，10）=0.1819第一年末还款，第五年末一次性还款4135.49万元1-5．某企业获得800万元贷款，偿还期10年，年利率为10％，试就以下4种还款方式，分别计算还款额及10年还款总额。
工程经济学计算题及答案
1、某项目的原始投资为20000元（发生在零期），以后各年净现金流量如下: 第一年获得净收益3000元，第二年至第十年每年均收益5000元。
项目计算期为10年，基准收益率为10%。
（1）请绘制该现金流量图；（2）按需要完善现金流量表；（3）计算静态投资回收期（Pt ）；（4）计算净现值（NPV ）；（5）计算内部收益率（IRR ）；（6）判断该项目是否可行。
（计算结果保留小数后两位）（20分） 解:1）绘制该现金流量图：2分2）完善现金流量表3）计算静态投资回收期（Pt ） Pt=累计净现金流量出现正值的年份-1+当年净现金流量绝对值上年累计净现金流量的 2分=5-1+年4.450002000=- 1分4）计算净现值（NPV ）NPV(10%)=-20000+3000(P/F.10%.1)+5000(P/A.10%.9)(P/F.10%.1) 2分 =-20000+3000×0.9091+5000×5.759×0.9091=8904.83万元 1分 5）计算内部收益率（IRR ）设1i =15% 1分 NPV 1(15%)=-20000+3000(P/F.15%.1)+5000(P/A.15%.9)(P/F.15%.1) 1分=-20000+（3000+5000×4.7716）×0.8696 =3355.72万元 1分 设2i =20% 1分 NPV 2(20%)=-20000+3000(P/F.20%.1)+5000(P/A.20%.9)(P/F.20%.1) 1分 =-20000+（3000+5000×4.0310）×0.8333 =-704.94万元 1分 ∵IRR=1i +(2i -1i )211NPV NPV NPV + 2分∴IRR=15%+(20%-15%)3355.723355.72704.94+=0.1913=19.13% 1分6）判断该项目是否可行 ∵ Pt=4.4年＜10年NPV(10%)=8904.83万元＞0 IRR=19.13%＞10%∴该项目可行 2分2、某建设项目现金流量如下表所示，若基准收益率i c=10％。
工程经济学综合计算题
《工程经济学》计算题一、贷款与利率1．年初存入银行100万元，若年利率为12%，年计息12次，每季度支付一次，问每季度能支付多少（已知：P=100万， r=12%， m=12， n=4；求A.）答：实际季利率=(1+r/m)^3-1=(1+1%)^3-1=%=100*[%(1+%)^4]/[(1+%)^4-1]=100*=万元2．银行提供的五年期居民住房按揭贷款，按月计复利。
每100万元贷款，月等额偿还款额为5万元（五年还清本息）。
计算月利率、年名义利率和年实际利率答：A=P(A/P,i,n)求得(A/P,i,n)=，通过试算i=4%，(A/P,i,n)=；i=5%，(A/P,i,n)=，采用内插法求得i=%；年实际利率=(1+月利率)^12-1=%年名义利率=月利率*12=%3．某家庭以抵押贷款的方式购买了一套价值为45万元的住宅，如果该家庭首期付款为房价的30%，其余为在15年内按月等额偿还抵押贷款，年贷款利率为12%，按月计息。
问月还款额为多少答：P=45*(1-30%)=万元，i=12%/12=1%,n=15*12=180A=P(A/P,i，n）=*=万元4．某房地产公司借款5000万元投资于一个房地产项目，约定第一年末开始分10年均等返还，但还到第五年末时，一次性把尾款还清了。
若年利率为12％，每月计息一次，这笔尾款是多少（若约定第二年末开始分10年均等返还这笔尾款是多少）答：年实际利率i=（1+12%/12)^12-1=%(A/P，%，10）=年份12345678年初本金5000本年还款本年还本金本年利息634年末本金年份12345678年初本金50005634本年还款0本年还本金0本年利息6341-5．某企业获得800万元贷款，偿还期10年，年利率为10％，试就以下4种还款方式，分别计算还款额及10年还款总额。
⑴每年年末还80万元本金和所欠利息；⑵每年年末只还所欠利息，本金在第10年末一次还清;⑶每年末等额偿还本金和利息；⑷第10年末一次还清本金和利息。
工程经济学试题(全)
工程经济学一、计算题1. 某设备资产原值 5000 万元，折旧年限为 10 年，估计净残值率为 5%，试采用年限平均法计算该设备年折旧额。
(5 分)解：2. 某项目第 1 年初投入资金 100 万元，第 2 年初又投入 50 万元，第 3 年末收入 80 万元，第 4 年初支出 10 万元，第 5 年末收入 98 万元。
请绘制出流量图。
(5 分)解：绘图如下：3. 某企业投资 1000 万元进行投资，年利率 7%，5 年后可得本利共多少？F＝1000×(F/P，7%，5)＝1000×(1+7%) 5＝1000×1.4026＝1403 (万元)4. 某公司 5 年后需一次性还一笔 200 万元的借款，存款利率为 10%，从现在起企业每笔等额存入银行多少偿债基金？(5 分)A＝200×(A/F，10%，5)98100 1 2 3 4 5T (年)50单位：万元10080＝200×0.1638 ＝32.75 (万元)5. 某工程初期总投资为 1000 万元，利率为 5%，问在 10 年内需将总投资连本带息收回，每年净收益应为多少？(5 分) A ＝1000×(A/P ，5%，10) ＝1000×0.1295 ＝129.5 (万元)6. 已知某项目投资现金流量表如下所示，求该项目静态投资回收期。
( 10分)年份 12 3 4~10 现金流入/ 万元60 80 100现金流出/ 万元200202020解：7. 某企业为筹集资金，发行面值为 600 万元的 8 年期债券，票面利率为 10%，发行费用为 5%，企业所得税率为 33%；发行 400 万元优先股，筹资费用 率为 4%，股息年利率为 12%，则该企业的加权平均资金成本率为多少？ 解：计算债券和优先股的个别资金成本： 债券成本＝4.429 (年)T ＝5-1+年份 12 3 4 5 现金流入 /万元60 80 100 100 现金流出 /万元 200 20 20 30 30净现金流 量 -200 40 60 70 70 累计净现 金流量-200-160-100-3040优先股成本加权资金成本8. 某方案年设计生产能力 6000 件，每件产品价格为 50 元，每件产品变动成本为 20 元，单件产品销售税金及附加(含增值税)为 10 元，年固定总成本为 64000 元，用产量表示的盈亏平衡点应为多少件？(10 分)解：设盈亏平衡点为 X 件(50-20-10) X=64000X=3200 (件)9. 现有如下两个方案： A 方案初始投资为 5000 万元，从第 2 年起到第 10年每年盈利 2400 万元，每年的设备维护费及租金为 1000 万元； B 方案初始投资 8000 万元，从第 2 年起到第 10 年每年盈利 3100 万元，每年的设备维护费及租金为 1200 万元。
工程经济学计算
1.1、某工程项目第一年初投资2000万元，第二年末投资2500万元，第三年末建成，投资全部是银行贷款,利率为10％，贷款偿还从第四年末开始，每年年末等额偿还，偿还期为10年，试画出现金流量图,并计算偿还期内每年应还银行多少万元？（计算结果保留小数点后两位)解：（1)画现金流量图（2）计算总投资，即第3年末建成时的总投资(3）计算每年应偿还的金额A即每年应偿还银行880.8万元。
1。
2、某企业兴建一工程项目,第一年投资1000万，第二年投资2000万，第三年投资1500万，其中第二年、第三年的投资使用银行贷款，年利率为12%，该项目从第三年起开始获利并偿还贷款，银行贷款分5年等额偿还，问每年应偿还银行多少万元?(计算结果保留小数点后两位)解：A=[2000(F/P,12％，1）+1500](A/P,12%，5）=（2000×1。
12+1500) ×0.27741=1037.51（万元)即每年应偿还银行1037。
51万元。
1。
3、某项目资金流动情况如下图所示,求现值及第四期期末的等值资金。
（i=15％）（单位：万元）现值=－30—30(P/A,15%,3）+[40+70（P/A,15%,4)](P/F,15％,4）=－30-30×2.2832+［40+70×2。
8550]×0.5718=38.65（万元）第四期期末的等值资金=40+70(P/A,15%,4)—30（F/A，15％，4）(F/P,15%,1)=40+70×2.8550—30×4.9930×1。
1500=67.59（万元)1.4、某项目资金流动情况如下图所示，求现值及第四期期末的等值资金.（i=15%)（单位：万元）解：现值=－30—30（P/A，15%,3）+70(P/A，15％，4)(P/F,15%，4)=－30-30×2。
2832+70×2.8550×0。
工程经济学计算题
年度使用总 13200 12300 费用 47 假定某工厂有□条运输道路已经使用多年，需要进行人修理，估计大修理费用为15000元，道路经过大修 理后可以继续使用3年，每年的维修费为2500元。另□方案是把原有道路完全部翻新，估计造价为60000 元，可使用20年，每年维修费用为200元。设该工厂规定的基准贴现率为12%，试比较两个方案。 48 某机械厂欲新建一个车间，有三个可行方案：甲方案总投资1000万元，年经营成本120万元；乙方案总投 资l100万元，年经营成本115万元；丙方案总投资为1400万元，年经营成本105万元。已知行业规定的投 资收益率为20％，问选哪个方案较合理？ 49 企业欲购置某种设备一台，每年可增加收益1000元。若该设备可使用10年，期末残值为零，预期年利率 为10％。问从该企业的角度看，该设备最高可接受的价格是多少元？如该设备售价为7000元，是否应当 购买？ 50 已知两建厂方案：A方案投资为1200万元，年经营成本300万元，年产量为1000台；B方案投资为800万 元，年经营成本为260万元，年产量为800台。若基准投资回收期为6年，何者为优？ 51 有两种可供选择的车床， A车床：投资 10 000元，使用寿命为 5年，残值为 2 000元，使用后年收人为 5 000元，年支出为 2 200元； B车床：投资为 15 000元，使用寿命为 10年，残值为零，使用后年收人 为7 000元，年支出为4 300元。设目标收益率为8％，用净现值法比较两方案的经济效益。 52 为保证某种产品的产量达到计划标准，现有三种基本建设投资方案：方案Ⅰ是改建现有工厂，其一次性 投资为 2545万元，年经营成本 760万元；方案 Ⅱ是建新厂，一次性投资3340万元，年经营成本670万 元，方案Ⅲ是扩建现有工厂，其一次性投资4360万元，年经营成本650万元。若该企业要求的基准投资回 收期为10年，试用差额投资回收期法进行选优。 53 某建设工程有两个可行方案，每个方案均按两期进行建设。第Ⅰ方案：第一期工程初始投资100万元，年 经营费用5万元，服务期10年，期末残值5万元；第二期工程自第5年开始生产，第5年初二期投资30万 元，年经营费用2万元，服务期5年，期末残值为0 。第Ⅱ方案：第一期工程初始投资 80万元，经营费用 6万元，服务期 10年，期末残值 3万元；第二期工程自第4年开始生产，第4年初二期投资40万元，年经 营费用3万元，服务期6年，期末残值为0，设目标收益率为10％，试用现值成本（PC）法选择较优方案。 54 有甲、乙两个投资项目，甲项目投资2000万元，年收人1000万元，年经营成本500万元；乙项目投资3000 万元，年收人1500万元，年经营成本sin万元。若基准投资回收期为6年，试 （1）用差额投资回收期法分析方案的优劣； （2）如果两个方案的寿命期均为4年，试用投资回收期法评价两个方案的可行性。 55 某市为扩大自来水供应需兴建输水管道，其中某一段的设计有两个方案可供选择：或是穿山挖隧洞，或 是绕山铺设管道。如果输水管道是永久性工程，那么这一段应采用隧洞还是管道？假定利率为6％，其他 资料如下表所示。 方案数据表 隧洞 管道 初期投资情 5.5 5 况（百万 元） 维护费用 0 0 （百万元） 使用寿命 永久性的 50 （年） 残值（百万 0 0 元） 56 某汽车发动机的制造工艺过程有3种方案供选择，它们的总投资和年经营成本分别为： 第 Ⅰ方案：总投资 100万元，年经营成本 120万元； 第 Ⅱ方案：总投资 110万元，年经营成本 115万元； 第 Ⅲ方案：总投资 140万元，年经营成本 105万元。 若该工业部门规定的基准投资回收期为5年，试用差额投资回收期法选择最优方案。
工程经济学 计算题汇集
计算题汇集第二章工程经济评价基本要素1.某房地产开发项目建设期为3年，在建设期第一年借款500万元，第二年借款为600万元，第三年借款为400万元，年利率为8%，试计算建设期利息。
2.假设某项目建设期3年，各年计划投资额分别为：第一年4000万元，第二年4800万元，第三年3800万元，年平均价格上涨率为5%，则该项目建设期间涨价预备费为多少？第三章资金时间价值1.某投资者以400万元购入一写字楼物业20年的使用权出租经营，已知该投资者的目标收益率为18%，预计未来20年内的年租金上涨率为5%，问该写字楼第一年的租金收入为多少时方能满足投资者收益目标的要求？第8年的租金净收入又是多少？（81万元）2.某企业从银行一次性贷款30万元，承诺20年每年年末等额偿还，年利率为10%，若还了12次后，该企业打算来年一次性还清，那么，一次性还款为多少万元？（20.67万元）3.银行为某家庭提供年利率为6%，按月等额偿还的10年期个人住房抵押贷款，若每月的还款额为2000元，则该家庭在第5年最后一个月的还款额中的本金额是多少？（1475.37）4.某家庭以4000元/平方米的价格，购买了一套建筑面积为120平方米的住宅，银行为其提供了15年期的住房抵押贷款。
该贷款的年利率为6%，抵押贷款价值比率为70%.如该家庭在按月等额还款5年后，于第6年年初一次提前还了贷款8万元。
问从第6年开始的抵押贷款月还款额是多少？（1947.20）5.某投资者将其商铺出租经营，租期20年，预计第一年的净租金收入为8万元，且每年递增6%，年租金均发生在年末，若折现率为6%，该商铺净租金收入的现值是多少？（150.94）第四章工程经济评价基本方法案例题某公司经济分析人员提出4个可供考虑的方案，假设每个方案均无残值，并有8年寿命。
(1) 若公司有足够的资本，且方案是独立的，i C=10%，应选择哪些方案？(2) 若公司仅有100000元的投资资本，i C=10%，应如何选择？(3) 若方案是互斥的，i C=10%，应如何选择？第六章工程项目经济评价案例题1．某公司拟上一个新项目，预计该项目的生命周期为10年，其中，建设期为2年，生产期为8年。
工程经济学复习重点计算题
1.企业进囗一高新设备，原价为41万元，预计使用5年，预计报废时净残值为20000元，要求采用双倍余额递减法为该设备计提的各年折旧额。
解：年折旧率=（2÷5）×100%=40%接前例，要求采用年数总和法计算各年折旧额。
月折旧额=年折旧额÷12双倍余额递减法和年数总和法相比：（1）计算基数的确定方式不同：双倍余额递减法的逐年减少；年数总和法的每年均相同。
（2）年折旧率的确定方式不同：双倍余额递减法的每年均相同：年数总和法的逐年减少。
2.某新建房地产项目，建设期为三年，在建设期第一年贷款300万元，第二年600万元，第三年400万元，年利率为12%。
请估算计算建设期利息。
在建设期，各年利息计算如下：第一年利息=300/2*12%=18（万元）第二年利息=（300+18+600/2）*12%=74.16（万元）第三年利息=（318+600+74.16+400/2）*12%=143.06（万元）3.存入银行1000元，年利率6%，存期5年，求本利和。
解：1）单利法2）复利法4.例：现设年名义利率r=10%，则年、半年、季、月、日的年有效利率如下表所示。
每年计息周期m 越多，ieff 与r 相差越大；另一方面，名义利率为10%，按季度计息时，按季度利率2.5%计息与按年利率10.38%计息，二者是等价的。
在工程经济分析中，必须换算成有效利率进行评价，否则会得出不正确的结论。
本金1000元，年利率12%年名义利率计息期 年计息次数计息期利率 年有效利率10%年 1 10% 10% 半年 2 5% 10.25% 季 4 2.5% 10.38% 月 12 0.833% 10.46% 日3650.0274%10.51%1300%)651(1000=⨯+=F 23.1338%)61(10005=+=F5.每年计息一次，一年后本利和为每月计息一次，一年后本利和为计算年实际利率6.某人把1000元存入银行，设年利率为 6%，5年后全部提出，共可得多少元？7.某企业计划建造一条生产线，预计5年后 需要资金1000万元，设年利率为10%，问现需要存入银行多少资金？8.某公司对收益率为15%的项目进行投资，希望8年后能得到1000万元，试计算现在需投资多少？327万元9.某房地产推出“还本销售”商品房的办法。
工程经济学计算题及答案
1、某项目建设期2年，第1年投资1000万元，第2年投资1500万元，项目建成后，第3年至第9年末收益为600万元，其中回收固定资产余值500万元，试画出现金流量图。
2、现有A、B两个方案，A方案实施年数为10年，B方案实施年数为5年，基准收益率为10%，其净现金流量如表所示：年份12～56～910A-3008080100B-10050————试用最小公倍数法，比较A、B方案。
（单位：万元）已知：（P/F,10%,1）=0.9091，（P/F,10%,10）=0.3855，（P/F,10%,2）=1.2100，（P/F,10%,6）=0.5645，（P/A,10%,8）= 5.3349，（P/A,10%,4）=3.16993、某项目设计生产能力为年产50万件产品，根据资料分析，估计单位产品价格为100元，单位产品可变成本为80元，固定成本为300万元，试用产量、生产能力利用率、销售额、单位产品价格和单位产品变动成本表示项目的盈亏平衡点。
已知，该产品销售税金及附加的合并税率为5%。
4、某企业购入一项原价为24300元的固定资产，估计净残值为300元，估计耐用年限为4年，试分别用平均年限法、双倍余额递减法、年数总和法计算每年的折旧金额。
5、某新建项目计算期为7年，建设期为1年。
期初投资800万元，项目建成后每年年末收益为260万元，其中第7年年末回收固定资产余值100万元.年利率为10%。
试画出现金流量图，并计算项目在第7年年末的金额。
已知（F/A,10%,7）=9.4872，（F/A,10%,6）=7.7156,(F/P,10%,7)=1.94876、某建设项目有A、B、C三个设计方案，其寿命期均为10年，各方案的初始投资和年净收益见下表，假定年利率为10%。
已知（A/P,10%,10）=0.1627，(P/A,10%,10)=6.1446单位：万元年份01-10A17044B26059C30068若三个方案为互斥方案，试选择最佳方案。
工程经济学
r1=13%∴i1=-1=-1=13.65% r2=12%∴i2= -1=-1=12.68%方案A:PC=1000+500(P/A,10%,3)+600(F/A,10%,3)(P/F,10%,6)-400(P/F,10%,6)=1000+500×2.4869+600×3.31×0.5645-400×0.5645=3138.75万元方案B:PC=800+550(P/A,10%,3)+650(F/A,10%,3)(P/F,10%,6)-3400(P/F,10%,6)=800+550×2.4869+650×3.31×0.5645-300×0.5645=3212.97万元年值法：方案A:AC=3138.75(A/P,10%,6)=3138.75×0.2296=720.66万元方案B:AC=3212.97(A/P,10%,6)=3212.97×0.2296=737.70万元选A方案。
4、某新建项目正常年份的设计生产能力为100万件，年固定成本为580万元，每件产品销售价预计60元，单位产品的可变成本估算额为40元。
问题：（1）对项目进行盈亏平衡分析，计算项目的产量盈亏平衡点。
（2）在市场销售良好情况下，正常生产年份的最大可能盈利额为多少？（3）在市场销售不良情况下，为了促销，产品的市场价格由60元降低10%销售时，若欲每年获年利润60万元的年产量应为多少？∴Q*= ==29(万件)某建设项目有A、B两个方案，其净现金流量情况如表所示，若i c=10%,试对方案进行比选。
B.折旧C.工资D.管理费用错误:【B】12、单因素敏感性分析图中，影响因素直线斜率（），说明该因素越敏感。
A.大于零B.绝对值越大C.小于零D.绝对值越小错误:【B】13、项目的（）计算结果越大，表明其盈利能力越强。
A.投资回收期B.盈亏平衡点C.财务净现值D.借款偿还期错误:【C】14、（）的盈亏平衡产量和（）的单位产品变动成本会导致项目在面临不确定因素时发生亏损的可能性（）。
工程经济学计算题
第一章7、某工程投资100万元，第三年开始投产，需要流动资金300万元，投产后，每年销售收入抵销经营成本后为300万元，第5年追加投资500万元，当年见效且每年销售收入抵销经营成本后为750万元，该项目的经济寿命为10年，残值100万元，绘制该项目的现金流量图？解:9.某工程项目需要投资，现在向银行借款为100万元，年利率为10％，借款期为5年，一次还清。
问第五年年末一次偿还银行的资金是多少？解：（1）画现金流量图（2）计算nF = P1i= P(F/P , i , n) = 100(F/P , 10% , 5) = 100×1.6105 = 161.05(万元)答：5年末一次偿还银行本利和161.05万元。
10.某工厂拟在第5年年末能从银行取出2万元，购置一台设备，若年利率为10％。
那么现在应存入银行多少钱？解：（1）作图（2）计算1P = F = F(P/F , i , n) = 2(P/F , 10% , 5) = 2×0.6209 = 1.2418(万元)1ni答：现在应存入银行的现值为1.2418万元。
11.某项改扩建工程，每年向银行借款为 100万元，3年建成投产，年利率为 10％，问投产 时一次还款多少钱？ 解：（1）作图（2）计算F = A(F/A , i , n)(F/P, i, n) = 1000(F/A , 10% ,3) (F/P,10%,1)= 100×3.310×1.10 =364.1(万元)答：投产时需一次还清本利和 364.1万元。
12.某工厂计划自筹资金于 5年后新建一个生产车间，预计需要投资为 5 000万元，若年利 率为 5％，从现在起每年年末应等额存入银行多少钱才行？ 解：（1）作图（2）计算i 1= F(A/F , i , n) = 5000(A/F , 5% ,5) = 5000×0.181 = 905（万元）A = F1 in答：每年年末应等额存入银行 905万元。
工程经济学计算题
1.投资的估算已知某钢厂年产200万t 钢，投资为15亿元，现要新建一年产量为400万t 的钢铁厂，估算投资为多少？解：应用公式K 2=K 1n Q Q )(12 ，已知K 1=15亿元，Q 1=200万t,Q 2=400万t,取n=0.8。
代入公式K 2=15亿元×8.0)200400(=26.12亿元 2.资金的时间价值在年利率8%的情况下，现在的100元相当于5年后的多少钱？解：100×（F/P ，8%，5）=100×（1+0.08）5=146.9元3.资金的等值计算①整付终值公式 某人现借出100元，年利率为7%，借期5年，若考虑一次收回本利，5年后他将收回多少款额？解：F=P （F/P ，7%，5)=100元×（1+7%）5=140.30元②整付现值公式 已知10年后的一笔款式2594万元，如果年利率为10%，这笔款的现值是多少？解：P=F （1+i ）-n =2594万元×10%)101(1+=2594万元×0.3855=1000万元 ③等额分付终值公式 某场基建5年，每年末向银行贷款1000万元，利率8%，投产时一次偿还，问5年末共应偿还多少？解：F=A ⎥⎦⎤⎢⎣⎡-+i i n 1)1(=1000万元×⎥⎦⎤⎢⎣⎡-+08.01)08.01(5=5866.6万元 ④等额分付现值公式 某工厂15年中每年年末应为设备支付维修费350元，年利率为12%，现应存入多少钱？解：P=A ⎥⎦⎤⎢⎣⎡+-+n n i i i )1(1)1(=350元×⎥⎦⎤⎢⎣⎡+-+1515)12.01(12.01)12.01(=2383.85元 ⑤等额分付偿债基金公式 某厂计划从现在起每年等额自筹资金，在5年后进行扩建，扩建项目预计需要资金150万元，利率10%，每年应等额筹集多少资金？解：A=F 1)1(-+n i i =150万元×1)1.01(1.05-+≈150万元×0.1638=24.57万元⑥等额分付资本回收公式 建一工厂，初期投资1000万元，利率10%，打算投产后5年内收回全部投资，每年要获利多少？解：A=P ⎥⎦⎤⎢⎣⎡-++1)1()1(n n i i i =1000万元×⎥⎦⎤⎢⎣⎡-++1)1.01()1.01(1.055≈1000万元×0.2638=263.8万元4.静态评价方法：包括投资回收期法、投资收益率法、差额投资回收期法及计算费用法。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
工程经济学计算题————————————————————————————————作者：————————————————————————————————日期：2第一章7、某工程投资100万元，第三年开始投产，需要流动资金300万元，投产后，每年销售收入抵销经营成本后为300万元，第5年追加投资500万元，当年见效且每年销售收入抵销经营成本后为750万元，该项目的经济寿命为10年，残值100万元，绘制该项目的现金流量图？解:9.某工程项目需要投资，现在向银行借款为100万元，年利率为10％，借款期为5年，一次还清。
问第五年年末一次偿还银行的资金是多少？解：（1）画现金流量图（2）计算nF = P1i= P(F/P , i , n) = 100(F/P , 10% , 5) = 100×1.6105 = 161.05(万元)答：5年末一次偿还银行本利和161.05万元。
10.某工厂拟在第5年年末能从银行取出2万元，购置一台设备，若年利率为10％。
那么现在应存入银行多少钱？解：（1）作图（2）计算1P = F = F(P/F , i , n) = 2(P/F , 10% , 5) = 2×0.6209 = 1.2418(万元)1ni答：现在应存入银行的现值为1.2418万元。
11.某项改扩建工程，每年向银行借款为 100万元，3年建成投产，年利率为 10％，问投产 时一次还款多少钱？解：（1）作图（2）计算F = A(F/A , i , n)(F/P, i, n) = 1000(F/A , 10% ,3) (F/P,10%,1)= 100×3.310×1.10 = 364.1(万元)答：投产时需一次还清本利和 364.1万元。
12.某工厂计划自筹资金于 5年后新建一个生产车间，预计需要投资为 5 000万元，若年利 率为 5％，从现在起每年年末应等额存入银行多少钱才行？解：（1）作图 （2）计算i 1= F(A/F , i , n) = 5000(A/F , 5% ,5) = 5000×0.181 = 905（万元） A = F 1 i n 答：每年年末应等额存入银行 905万元。
13.某项投资，预计每年受益为 2万元，年利率为 10％时，10年内可以全部收回投资，问 期初的投资是多少钱？解：（1）作图 （2）计算1 i 1 n P = A = A(P/A , i , n) = 2(P/A , 10% ,10) = 2×6.1446 = 12.2892（万元） i 1i n答：期初投资为 12.2892万元。
14.某项工程投资借款为 50万元，年利率为 10％，拟分 5年年末等额偿还，求偿还金额是 多少？解：（1）作图 （2）计算i 1i nA = P = P(A/P , i , n) = 50(A/P , 10% , 5) = 50×0.2638 = 13.19（万元） 1 i n 1 答：偿还金额是 13.19万元。
15、某借款金额 1万元，利率 8%，分 5年于年末等额偿还，问每年的偿付值？若在每年初 偿还，每期偿付值又是多少？解：（1）作图 图 1.年末等额偿还图 2.年初等额偿还（2）计算①A = P(A/P, i, n) = 1(A/P, 8%, 5) = 0.2505万元②P = A +A(P/A, i, n)PA = = 0.2319万元1 (P / A ,8%,4) 答：若年末等额偿还，每年偿还 0.2505万元，若在每年初偿还，每期偿还 0.2594万元。
16、某项目第 1~4年平均投资 50万元，第 4年建成投产，年净收益 40万元，第 5~10年生 产达产后年均净收益 70万元。
第 11~12年生产约有下降，年均净收益 50万元，在年利率 8%时，求终值、现值、第 4年期末的等值资金？解：（1）作图（2）计算P = -50+(-50)(P/A, 8%, 3)+40(P/F, 8%, 4)+70(P/A, 8%, 6)(P/F, 8%,4)+50(P/A, 8%,2)(P/F, 8%, 10) = 129.6142万元F = P(F/P, 8%, 12) = 326.3686万元F = P(F/P, 8%, 4) = 176.2753万元4 第四章1.某建设项目方案表明，该项目在建设的第一年完工，投资为 10 000元，第二年投产并获 净收益为 2 000元，第三年获净收益为 3 000元，第四年至第十年获净收益为 5 000元，试 求该项目的静态投资回收期。
解：（1）作图（2）计算p t CI CO = -10000+2000+3000+5000 =0 t t 1 p = 4t 3.某项目的各年金现金流量如表 4-17所示，收益率在 15％时，试用净现值判断项目的经济 性。
（表 4 -17见书 p95）解：（1）作图（2）计算 n F 1 i t =－40－10 115%1＋8(P/A , 15%, 2)(P/F, 15%, 1)＋ NPV =t n t 013(P/A, 15%, 16)(P/F, 15%, 3)＋33(P/F, 15%, 20)=－40－10×0.8696＋8×1.6257×0.8696＋13×5.9542×0.6575＋33×0.0611= 15.52>0合理4.甲、乙两项目的有关费用支出如表 4-18所示，在收益率为 10％时，试用费用现值法选择 方案。
（表 4 -18见书 p95）解：（1）作图（2）计算 PC = 8001 0.1 ＋320(P/A, 0.1, 9)(1＋0.1) 1 1 甲 = 800×0.9091＋320×5.759×0.9091 = 2402.64 PC = 9001 0.1 ＋300(P/A, 0.1, 9)(1＋0.1) 1 1 乙 = 900×0.9091＋300×5.759×0.9091 = 2388.84PC > PC 乙 甲因此乙方案好5.某方案需要投资为 1 995元，当年见效年收益为 1 500元，年成本支出为 500元，第四年 有 1 000元追加投资，服务期为 5年，在收益率为 10％时，用净现值率法评价方案。
解：（1）作图 （2）计算3 NPV =－1995－1000（1＋0.1）＋（1500－500）（P/A, 0.1, 5）=－1995－753.3＋1000×3.7908 = 1042.5K = 1995＋1000（1＋0.1）= 1995＋753.3 = 2748.3p 1042.5 NPVR = = 0.38 > 10%合理 2748.36.某项目需要投资为2万元，经济寿命为5年，残值为0.4万元，每年收益为1万元，每年支出成本费用为0.44万元，若基准收益率为8％，用效益成本比率法确定方案是否可取？解：（1）作图（2）计算B t1 i= 1（P/A, 8%, 5）＋0.4（P/F, 8%, 5）= 3.9927＋0.4×0.6806 = 4.265 tC t1 i= 2＋0.44×3.9927 = 3.757 t4.265B/C = = 1.13523.757此方案可取，除收回投资外，还可获得相当于投资总成本现值总额0.1352倍的净值。
7.某投资项目，投资额为1万元，在5年中每年的平均收入为0.6万元，每年的费用支出为0.3万元，期末残值为0.2万元，若投资收益率为10％，试用净未来值法评价方案。
解：（1）作图（2）计算NFV =－1（F/P, 0.1, 5）＋0.3（F/A, 0.1, 5）＋0.2=－1.611＋0.3×6.105＋0.2 = 0.4205 > 0因此该方案可行8.某项目投资为700万元，每年的净收益均为200万元，寿命期为5年，基准收益率为10 ％，试用内部收益率判断方案。
解：（1）作图（2）计算设NPV = -700+200(P/A, I , 5) NPV = 0(P/A,I,5) = 3.5查表可知12％与15％可以作为比较值。
i = 12% NPV 1 = -700+200(P/A, I , 5) = 20.96>0i = 15% NPV 2 = -700+200(P/A, I , 5) = -29.56<020.96i 0= 0.12+(0.15-0.12) = 13.2%>i n 可行20.96 29.569.有两个投资方案A和B，其投资分别为1.8万元和 1.6万元，年净收益分别为0.34万元和0.3万元，项目寿命期均为20年，基准收益率为10％，用差额投资收益率比较方案。
解：（1）作图（2）计算A-B: -0.2 0.04 0.04……0.04判断方法如上题：i1= 15% NPV = -0.2+0.04(P/A,15%,20) = 0.05>01i 2 =20% NPV = -0.2+0.04(P/A,20%,20) = -0.005<020.05i’ = 0.15+(0.2-0.15)×= 19.5% > i n则投资大的方案A优0.05 0.00510.某项目总产量为 6 000吨，产品售价为 1 335元/吨，其固定成本为 1 430 640元，单位可变成本为930.65元。
试求盈亏平衡点产量和盈亏平衡点时的生产能力利用率。
（分别用计算法和作图法求解）。
解：（1）作图法①画直角坐标图②在纵坐标轴上找点 B ，C ，S ，F 。
已知：B = 1430640元，F = B 则C = B + VQ = 1430640 + 930.65×6000 = 7014540元S = PQ = 1335×6000 = 8010000元③连接 FB ，FC ，OS 三线。
④找出 FC 与 OS 的交点 G ，其对应的产量为 3500吨，即为所求盈亏平衡点产量（2）计算法B 1430640 BEP = = =3538.123吨 Q P V 1335930.65 BEP Q Q i 3538.123×100%=58.97% ×100%= 6000BEP = i11.生产某种产品有三种工艺方案，采用方案 A ，年固定成本为 800万元，单位变动成本为 10元；采用方案 B ，年固定成本为 500万元，单位变动成本为 20元；采用方案 C ，年固定 成本为 300万元，单位变动成本为 30元。