高斯定理
高斯定理的数学表达式
高斯定理的数学表达式为：∮E·dA = Q/ε0。
该公式表达的是在闭合曲面S上的电场E的通量，与该闭合曲面内的总电荷量Q与真空介电常数ε0的比值相等。
换句话说，电场的总通量等于在闭合曲面S内的总电荷量与真空介电常数之比。
这个定理表明，电场通量的大小与所选取的闭合曲面无关，只与该曲面内的电荷量有关。
因为电场线从正电荷流出，流入负电荷，因此正电荷和负电荷的电场线互相抵消，而只有闭合曲面内的电荷对电场通量产生贡献。
高斯定理在静电场情况下类比于应用在磁场学的安培定律，而二者都被集中在麦克斯韦方程组中。
因为数学上的相似性，高斯定律也可以应用于其它由平方反比律决定的物理量，例如引力或者辐照度。
高斯定理公式
高斯定理公式
高斯定理数学公式是：∮F·dS=∫(▽·F)dV。
高斯定律表明在闭合曲面内的电荷分布与产生的电场之间的关系。
高斯定理（Gauss' law）也称为高斯通量理论（Gauss' flux theorem），或称作散度定理、高斯散度定理、高斯－奥斯特罗格拉德斯基公式、奥氏定理或高－奥公式（通常情况的高斯定理都是指该定理，也有其它同名定理）。
高斯定律在静电场情况下类比于应用在磁场学的安培定律，而二者都被集中在麦克斯韦方程组中。
因为数学上的相似性，高斯定律也可以应用于其它由平方反比律决定的物理量，例如引力或者辐照度。
扩展资料：
高斯定理指出：穿过一封闭曲面的电通量与封闭曲面所包围的电荷量成正比。
换一种说法：电场强度在一封闭曲面上的面积分与封闭曲面所包围的电荷量成正比。
它表示，电场强度对任意封闭曲面的通量只取决于该封闭曲面内电荷的代数和，与曲面内电荷的位置分布情况无关，与封闭曲面外的电荷亦无关。
在真空的情况下，Σq是包围在封闭曲面内的自由电荷的代数和。
当存在介质时，Σq应理解为包围在封闭曲面内的自由电荷和极化电荷的总和。
1.3高斯定理
S，两底面到带电平面距离相同。
E dS E dS E dS E dS 2ES
s
左底
右底
側
圆柱形高斯面内电荷 q S
由高斯定理得
E
S
E
2ES S / 0
E 2 0
σ
33
E 20
0 场强方向指离平面; / 20 / 20
§1.3 高斯定理
/ 2 0 / 2 0
§1.3 高斯定理
ห้องสมุดไป่ตู้
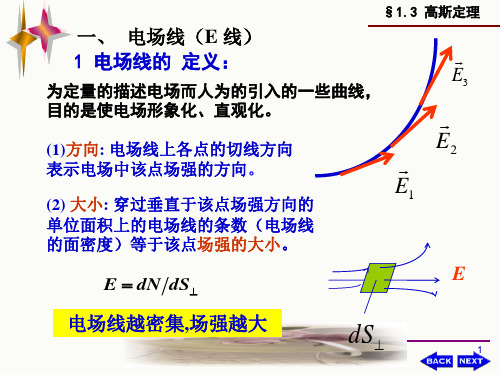
一、 电场线（E 线）
1 电场线的 定义：
为定量的描述电场而人为的引入的一些曲线，
E3
目的是使电场形象化、直观化。
(1)方向: 电场线上各点的切线方向 表示电场中该点场强的方向。
E2
(2) 大小: 穿过垂直于该点场强方向的
E1
单位面积上的电场线的条数（电场线
的面密度）等于该点场强的大小。
E dN dS
E
电场线越密集,场强越大
dS
1
2. 电场线示例
几
+
种
电
荷
分
布
的
+
电
场
线
+
图
§1.3 高斯定理
-
+
-
2
3. 电场线的性质：
§1.3 高斯定理
1）电场线起于正电荷，终止于负电 荷；电荷是电场线的“源”和“尾闾 ”2）电场线不会在无电荷的地方中断；
3）电场线不会在无电荷的地方相交； q
（2）半径为R的均匀带电体密度为ρ
的长圆柱体。
R2
E
2 0 r
r
2 0
(r R) (r R)
高斯定理内容总结
高斯定理内容总结1. 高斯定理的概念高斯定理，也称为“散度定理”或“高斯-奥斯特罗格拉茨基定理”，是一个基本的数学定理，用来描述矢量场在一个闭合曲面上的整体特性。
它是物理中应用广泛的定理之一，可以用来求解电场、磁场和流体力学问题。
2. 高斯定理的表述高斯定理可以表述为：对于一个闭合曲面S，其向外法向量为n，矢量场F，高斯定理给出了矢量场在S上的通量与该矢量场在S包围的体积的关系。
具体表述如下：∮S F·n dS = ∭V ∇·F dV其中，∮代表闭合曲面S上的曲面积分，∭代表闭合曲面S包围的体积积分，F为矢量场，n为曲面S的向外法向量，·表示内积运算，∇表示梯度运算，∇·F表示矢量场的散度。
3. 高斯定理的推导与理解高斯定理可以通过对体积积分进行数学推导得到。
假设有一个闭合曲面S，体积为V，如下图所示：________/ // //_______ /根据高斯定理的表述，我们需要计算矢量场F在曲面S上的通量。
我们将曲面S分成许多小面元，每个小面元上的通量为F·n，其中n为该小面元的法向量。
当我们把曲面S分割为无数个小面元时，可以将曲面S视为由这些小面元组成的连续曲面。
在极限情况下，当每个小面元的面积无限接近于0时，我们可以将曲面S视为无限小的曲面。
此时，我们可以对矢量场F在曲面S上的通量进行积分，得到：∮S F·n dS = lim(S→0) ∑(F·n)dS通过将曲面S分割为无数个小面元，并将每个小面元的通量求和，我们可以得到矢量场F在整个曲面S上的通量。
同时，根据散度的定义，我们知道散度可以表示为矢量场的微分运算。
因此，我们可以将散度运算应用到上述积分中，得到：∮S F·n dS = ∑(∇·F)dV其中，∇·F表示矢量场F的散度，∑表示对整个体积V进行求和。
为了获得正确的结果，我们需要取极限，将小面元的面积趋近于0，体积元的体积趋近于0，从而得到公式的最终形式：∮S F·n dS = ∭V ∇·F dV这就是高斯定理的推导过程。
高斯定理及应用
物理学方法概论
目录 §2.1 高斯定理与运动电荷 §2.2 在无磁场情况下电场旳变换 §2.3 匀速直线运动点电荷旳电场 §2.4 电场对运动电荷旳作用力
物理学方法概论
§2.1 高斯定理与运动电荷 静止点电荷旳电场 运动点电荷旳电场
球对称
轴对称
库仑定律成立
库仑定律不成立！
+
+v
1、横向场强增大到 倍。
v
S系
E
E
v
静电场 E 0
S系
E
0
0
E
2、纵向场强不变
E
物理学方法概论
E
v
S系
S系
E E
物理学方法概论
§2.3 匀速直线运动点电荷旳电场
z
S系
E ?
？
P(x, y, z,t)
r
vt
x
OQv
物理学方法概论
电荷系S' 中 P( x, y, z, t)点电场(静电场)：
S
E
各类点电荷旳电场线 +
物理学方法概论
+
++
2q
q
+++++++
电场线特征
物理学方法概论
1） 始于正电荷,止于负电荷(或来自无 穷远,去向无穷远)，在没有电荷旳地方 电场线不会中断
2） 静电场电场线不闭合
3） 电场线不相交 +
4） 电场线密集处,电场强度较大, 电场线稀疏处电场强度较小。
注意：电场线是为了描述电场分布而引 入旳曲线,不是电荷旳运动轨迹
场点旳变换：
物理学方法概论
高斯定理数学
高斯定理数学高斯定理，又称为高斯-奥斯特罗格雷定理（Gauss-Ostrogradsky theorem），是描述向量场通过曲面的流量密度与该曲面边界上环绕该曲面沿法向量方向的一圈线积分之间的关系的定理，是矢量分析的重要内容之一，也是工程中常用的理论。
$$\oint_S \textbf{F} \cdot \textbf{n} dS = \iiint_V \nabla \cdot \textbf{F} dV$$$\textbf{F}$ 表示某个向量场，$S$ 表示一个逐片光顺的曲面，$V$ 为该曲面所包围的立体。
$\textbf{n}$ 表示曲面上某一点的法向量，$\nabla \cdot \textbf{F}$ 为向量场 $\textbf{F}$ 的散度。
该式中左边表示 $\textbf{F}$ 向外通过曲面 $S$ 的流量密度。
左侧积分的意思是，对于曲面 $S$ 的每一点，对由该点到曲面外侧的垂直方向的投影所围成的小面积$dS$ 进行积分，得到整个曲面通过的总流量密度。
右边表示 $\textbf{F}$ 在立体$V$ 中的散度。
右侧积分的意思是，对于立体 $V$ 中的每一点，计算该点的散度，然后对整个立体进行积分，得到散度在整个立体中的总量。
高斯定理适用于任意的向量场，包括电场、磁场等。
它可以用来推导一些物理方程，并在基础数学领域中起到重要作用。
对于电场，高斯定理可以用来计算电通量，即电场向外通过一个立体的总电量。
对于静电场和恒定电场来说，高斯定理可以推导出库仑定律。
对于磁场，高斯定理可以用来推导出安培环路定理。
高斯定理在物理学和工程学中有非常广泛的应用，是理解和解决问题的重要工具之一。
高斯定理的证明可以通过追踪微小体积元素上的向外流量来完成。
假设该体积元素为$\Delta V$，体积元素表面上带有一小片面积为 $\Delta S$，该片面积的法向量表示为$\textbf{n}$。
向量场 $\textbf{F}$ 在该面积上的流量为 $\textbf{F} \cdot\textbf{n} \Delta S$，如果对所有该体积元素上的面积进行累计，则构成了整个曲面的流量，并得到了高斯定理的左侧积分：$$\oint_S \textbf{F} \cdot \textbf{n} dS$$接下来，可以通过施加散度定理来将该定理转化为该向量场的散度在这个立方体中的积分：证明中还需要使用到一些高等数学的知识，如积分中值定理等，具体证明过程相对复杂。
高斯定理(电磁学)
证明方法
高斯定理的证明通常基于库仑定律、电场线性质和微积分等 基本原理。通过选择适当的闭合曲面和运用微积分中的高斯 公式，可以推导出高斯定理。
推导过程
首先，根据库仑定律，电场线从正电荷发出，终止于负电荷 或无穷远处。然后，通过选取适当的闭合曲面，将电荷包围 在其中，运用高斯公式和高斯定理的推导过程，最终得到高 斯定理的数学表述。
要点一
总结词
高斯定理在其他领域也有广泛的应用，如电场、量子力学 、光学等。
要点二
详细描述
高斯定理在电场中可以用来计算电场的分布和强度，以及 电通量的计算等问题。在量子力学中，高斯定理可以用来 研究波函数的性质和演化。在光学中，高斯定理可以用来 研究光场的分布和强度，以及光通量的计算等问题。
05
高斯定理的扩展和深化
磁场中的应用
总结词
高斯定理在磁场中也有广泛的应用，它可以 帮助我们理解和计算磁场的分布和强度。
详细描述
在磁场中，高斯定理可以用来计算球形区域 内磁场的分布和强度，通过球面上的磁场强 度的积分可以得到球内的磁场。此外，高斯 定理还可以用来研究磁场线的闭合性质，以 及磁通量的计算等问题。
其他领域的应用
引力场中的应用
总结词
高斯定理在引力场中也有重要的应用，它可以帮助我们理解和计算引力场的分布和强度。
详细描述
在引力场中，高斯定理可以用来计算球形区域内物质的质量分布，通过球面上的引力场强度的积分可以得到球内 的质量。此外，高斯定理还可以用来研究引力场的空间分布，通过球面上的引力场强度的分布，可以推导出球内 引力场的分布情况。
高斯定理的应用条件
适用范围
高斯定理适用于任何线性、非自相互作用、电荷连续分布的电场。对于非线性、 自相互作用或离散分布的电荷，高斯定理可能不适用。
高斯定理
λ
∑q
r
∑ q = λh
φ = ∫∫S EdS cosθ =
φ左底 = φ右底 = 0
φ = φ左底 + φ侧 + φ右底
ε0
h
Q E⊥dS , cosθ = 0
§4.高斯定理 / 五、解题方法及应用举例 高斯定理
φ = φ侧 = ∫∫侧 EdS cosθ
侧面上各点的场强 E 大小相等，方向 大小相等， 与法线相同。 与法线相同。
E = E+ − E− = 0
+σ
−σ
E+ E− E+
极板右侧
E = E+ − E− = 0
E+
E−
E−
两极板间
σ σ σ + = E = E+ + E− = 2ε 0 2ε 0 ε 0
§4.高斯定理 / 五、解题方法及应用举例 高斯定理
E
n
r
λ
φ = E ∫∫侧 dS
= E 2πrh =
∑q
ε0
λh = ε0
λ E= 2πε 0r
h
§4.高斯定理 / 五、解题方法及应用举例 高斯定理
例3：无限大带电平面，面电荷密度为 σ， ：无限大带电平面， 求平面附近某点的电场强度。 求平面附近某点的电场强度。 解：作底面积为 S ， 高为 h 的闭合圆柱面， 的闭合圆柱面， σ
S
r
ε0 σS 2ES = ε0 σ E= 2ε 0
§4.高斯定理 / 五、解题方法及应用举例 高斯定理
φ=
∑q
例4：两无限大带电平面（平行板电容 ：两无限大带电平面（ 器），面电荷密度分别为 +σ 和 −σ ， ），面电荷密度分别为 电容器内、外的电场强度。 求：电容器内、外的电场强度。 解：极板左侧
高斯定理
1
4π0
q r3
rdS
e
S de
q
q
dS
S 4π0r 2
4π0r 2
dS q
S
0
Φe 与r 无关q ，也就是说，无论高斯面多大，总 电通量都为 0 ，即通过各球面的电力线总条数相 等。 说明点电荷的电力线可以延伸到无限远处。 9
2. 点电荷在任意封闭曲面内
穿过球面S1和S2的电场线，必定也穿 过闭合曲面S。所以穿过任意闭合曲
e ES cos 或 e E S
S cos
(3) 非均匀电场强度电通量
de E dS
通过任一曲面S 的电通量：
e de EdS
S
S
5
思考题：电场线与电通量的区别
(4) 任意闭合曲面的电通量：
e d e E dS
S
S
一个闭合曲面把整个空间分割成两部分： 内部空间和外部空间
外法线矢量：指向曲面外部空间的法线矢量 内法线矢量：指向曲面内部空间的法线矢量
S2
S
E
面 S的电通量必然为q/ 0 ，即
q S1
Φe
s
Ev dSv
q
0
• 点电荷为-q时，通过任意闭合曲面的电通量
Φe
S
Ev
dSv
q
0
电场线是穿入闭合曲面的。
10
3. 任意闭合曲面S包围多个点电荷q1、q2、…、qn 根据电通量的定义和电场强度的叠加原理，其电通
量可以表示为
Φe
E
S
dS
(E1
其实高斯定理不仅适用于静电场，还可用于变化的电 场，比库仑定律更广泛，是Maxwell方程组之一
16
5-3 高斯定理
q
高斯面
r
4 3 pR 3
可见，球体内场强随 线性增加 线性增加。 可见，球体内场强随r线性增加。 均匀带电球体电场强度曲线如 上图。 上图。
+ q + + + + + + + + + + + + + + + + + +
上页 下页 返回 退出
例2
均匀带电无限大平面的电场. 均匀带电无限大平面的电场. 高斯面:作轴线与平面垂直的圆柱形高斯面， 高斯面:作轴线与平面垂直的圆柱形高斯面， 底面积为S，两底面到带电平面距离相同。 底面积为 ，两底面到带电平面距离相同。
r E=
lr v e 2 r 2pe0R
上页 下页 返回 退出
（2）当r>R 时，
λ E= 2 0r πε
r E=
E λ 2πε0R
∑q = λl
矢量式为： 矢量式为：
r l er 2pe0r
Er 关系曲线
r
均匀带电圆柱面的电场分布
l
−1
∝r
R
0
r
上页 下页 返回 退出
均匀带电球体空腔部分的电场， 例4 均匀带电球体空腔部分的电场，球半径为R， 在球内挖去一个半径为r（ 在球内挖去一个半径为 （r<R）的球体。 ）的球体。 试证：空腔部分的电场为匀强电场，并求出该电场。 试证：空腔部分的电场为匀强电场，并求出该电场。 证明： 用补缺法证明。 证明： 用补缺法证明。 在空腔内任取一点p, 在空腔内任取一点 , 设该点场强为 E E r1 设想用一个半径为r且体电荷密度与大球相 设想用一个半径为 且体电荷密度与大球相 c 同的小球将空腔补上后， 同的小球将空腔补上后，p点场强变为 E 1 u r v o pE r uu
高斯定理
同 学 们 好§8-3 高斯定理德国数学家和物理学家。
长期从事于数学并将数学应用 于物理学、天文学和大地测量 学等领域的研究.著述丰富，成 就甚多。
他一生中共发表323篇 （种）著作，提出404项科学创 见。
在CGS电磁系单位制中磁感应强 高斯（德 ） 度的单位定为高斯，便是为了 （ 1777-1855） 纪念高斯在电磁学上的卓越贡 献。
一.电场强度通量 通过电场中某一给定面的电场线的总条数叫做通 过该面的电通量。
1.匀强电场，规则面积下的电通量Sθ ESΨe = ES⊥SSΨe = ES⊥ = ES cosθ2.非匀强电场或不规则面积下的通量 r v 面积元矢量： dS = dS e n r 面积元范围内 E 视为均匀 微元分析法：以平代曲； 以不变代变。
dSr dSθr ES（1）通过面元的电通量：r r dΨe = EdS⊥ = E (dS cosθ ) = E ⋅ dS（1） 通过面元的电通量：πr r dΨe = EdS⊥ = E(dS cosθ ) = E ⋅ dSθ < θ > θ = π π2 2 2 dΨe > 0 dΨe < 0 dΨe = 0r dSθdSr ESr r （2）通过曲面 S 的电通量 Ψe = ∫s d Ψe = ∫s E ⋅ d S(3) 通过封闭曲面的电通 量r r Ψe = ∫ E ⋅ dSs通过封闭曲面的电通量r r Ψe = ∫ E ⋅ dSsr n规定：封闭曲面外法向为正 穿入的电场线 穿出的电场线r n rEΨe < 0 Ψe > 0r nS二、 高斯定理 高斯定理的导出 库仑定律 高斯 定理电场强度叠加原理 1.点电荷电场中电通量与电荷的关系 （1）曲面为以电荷为中心的球面E=Sq 4 π ε 0rS2r2v dSv v Ψe = ∫ E ⋅ dS = ∫qΨe =q4 πε 0 rdS+ε0(2)曲面为包围电荷的任意封闭曲面dΨe =q 4 πε 0 r2dS cos θq dS＇ = 2 4π ε0 r其中立体角dS＇ = dΩ 2 r q q Ψe = ∫ dΨ = ε 0 4 πε 0v v dS＇ dS+rθv dS＇v dS（3）曲面为不包围电荷的任意封闭曲面r v d Ψ1 = E 1 ⋅ d S 1 > 0v v dΨ2 = E 2 ⋅ dS 2 < 0v E2qv dS 2v dS 1 vE1d Ψ1 + d Ψ 2 = 0 v v ∫ E ⋅ dS = 0S2.点电荷系电场中通量 与电荷的关系v v Ψe = ∫ E ⋅ dS = ∫Sv v v E = E1 + E2 + LS iq1q2v EvdSv v ∑ Ei ⋅ dSsSqi=i (内）∑∫eSv v Ei ⋅ dS +i （外）∑ ∫v Eiv v Ei ⋅ dSQ∴ Ψ =i （外）∑∫Sv ⋅ d S = 01i （内）∑ ∫Sv v E i ⋅dS =ε0i ( 内）∑qi曲面上各点处电场强度：nE E E E r L r r r +++=21(包括S 内、S 外，所有电荷的贡献)只有S 内的电荷对穿过S 的电通量有贡献。
数学高斯定理
数学高斯定理
高斯定理也称为高斯通量理论，或称作散度定理、高斯散度定理、高斯-奥斯特罗格拉德斯基公式、奥氏定理或高-奥公式
在静电学中，表明在闭合曲面内的电荷之和与产生的电场在该闭合曲面上的电通量积分之间的关系，高斯定律表明在闭合曲面内的电荷分布与产生的电场之间的关系。
高斯定律在静电场情况下类比于应用在磁场学的安培定律，而二者都被集中在麦克斯韦方程组中。
因为数学上相似性，高斯定律也可以应用于其它由平方反比律决定的物理量，例如引力或者辐照度。
高斯定理的解释和公式
高斯定理的解释和公式
高斯定理，也称为散度定理，是数学中的一个重要定理。
它描述了一个向量场通过一个封闭曲面的总量。
高斯定理在物理学和工程学的许多领域中都有广泛的应用，如电磁学、流体力学和热传导等。
高斯定理的数学表达形式如下：
对于一个平滑的三维矢量场F=(Fx,Fy,Fz)，定义一个封闭曲面S来围绕一个具有体积V的区域D。
那么，高斯定理可以写作：
∬S F·dS = ∭D ∇·F dV
其中，F·dS表示向量场F在曲面元dS上的点积积分，∇·F表示向量场F的散度，dV表示体积元。
这个定理的物理解释是，对于一个流经封闭曲面的流体量，其发散性（流出和流入区域的总和）等于其在包围该区域的体积中的源和汇的总量。
高斯定理的应用非常广泛。
在电磁学中，它可以用来计算通过一个闭合曲面的电场强度和磁场强度的总量。
在流体力学中，它可以用来计算液体或气体通过一个封闭曲面的流量。
在热传导中，它可以用来计算热量通过一个封闭曲面的扩散量。
总之，高斯定理提供了一个非常强大的工具，用于计算向量场通过封闭曲面的总量。
它在物理和工程学中的应用使得我们能够更好地理解和分析各种自然现象和工程问题。
高斯定理
dE
以 O 为中心，r 为半径的球面 S 上各点彼此等价
E 大小相等
以 O 为中心的球面 S 上各点
E
方向沿径向
确定高斯面
R dq
以半径 r 的同心球 S q
o
dq
面 S为高斯面
r
P
dE ' dE dE'
dE
通过S的电通量： E dS E cos0dS E 4r2
s
s
由高斯定理：
E E1
r
o
1
0
q内
L 0
r
E 2 0 r
讨论：
R
oo
E o
1. 无限长均匀带电柱面的电场分布
对称性分析：视
为无限长均匀带
电直线的集合；
选高斯面；同轴
圆柱面
rr
P
dE
P
dE '
dE
dE '
由高斯定理计算
r R: E0 r R:
Rr
E
2 0r
讨论：
2.求无限长、 均匀带电柱体的电场分布时，高斯面如 何选取？
电场相互抵消： E 0
NP
L o L x
NP
x L : 选如图高斯面
E
S
L o x L xq内源自dVLx
ax Sdx
aS 1 (L2 x2 ) 2
E dS 左 E dS 右 E dS 侧E dS E S
E0
cos 0 穿入
由高斯定理：
1
E dS
高
高
r
斯 面
r
斯 面
l
l
3.当带电直线，柱面，柱体不能视为无限长时，
高斯定理
高斯定理科技名词定义中文名称：高斯定理英文名称：Gauss theorem定义：通过任意闭合曲面的电通量等于该闭合曲面所包围的所有电荷量的代数和与电常数之比。
所属学科：电力（一级学科）；通论（二级学科）本内容由全国科学技术名词审定委员会审定公布目录编辑本段高斯定理1矢量分析的重要定理之一。
穿过一封闭曲面的电通量与封闭曲面所包围的电荷量成正比。
换一种说法：电场强度在一封闭曲面上的面积分与封闭曲面所包围的电荷量成正比由于磁力线总是闭合曲线，因此任何一条进入一个闭合曲面的磁力线必定会从曲面内部出来，否则这条磁力线就不会闭合起来了。
如果对于一个闭合曲面，定义向外为正法线的指向，则进入曲面的磁通量为负，出来的磁通量为正，那么就可以得到通过一个闭合曲面的总磁通量为0。
这个规律类似于电场中的高斯定理，因此也称为高斯定理[1]。
与静电场中的高斯定理相比较，两者有着本质上的区别。
在静电场中，由于自然界中存在着独立的电荷，所以电场线有起点和终点，只要闭合面内有净余的正（或负）电荷，穿过闭合面的电通量就不等于零，即静电场是有源场；而在磁场中，由于自然界中没有单独的磁极存在，N极和S极是不能分离的，磁感线都是无头无尾的闭合线，所以通过任何闭合面的磁通量必等于零。
电场 E （矢量）通过任一闭曲面的通量，即对该曲面的积分等于4π乘以该曲面所包围的总电荷量。
公式表达：∫(E·da) = 4π*S(ρdv)适用条件：任何电场静电场（见电场）的基本方程之一，它给出了电场强度在任意封闭曲面上的面积分和包围在封闭曲面内的总电量之间的关系。
根据库仑定律可以证明电场强度对任意封闭曲面的通量正比于该封闭曲面内电荷的代数和，即公式这就是高斯定理。
它表示，电场强度对任意封闭曲面的通量只取决于该封闭曲面内电荷的代数和，与曲面内电荷的分布情况无关，与封闭曲面外的电荷亦无关。
在真空的情况下,Σq是包围在封闭曲面内的自由电荷的代数和。
当存在介质时,Σq应理解为包围在封闭曲面内的自由电荷和极化电荷的总和。
高斯定理表达式及其物理意义
高斯定理表达式及其物理意义
高斯定理是18世纪德国数学家卡尔高斯提出的一个重要定理，它对于计算物体表面积和空间容积具有极大的意义。
高斯定理的表达式为：
S = 2λπr^2 V =/2πr^2
其中，S表示物体的表面积，V表示物体的容积，λ表示表面张力，r表示物体的半径。
高斯定理的定理推导是以表面张力和表面张力作为基础，表明物体表面积与物体容积之间存在联系。
因为表面张力是以米为单位的，所以用高斯定理可以用来测量物体的表面面积和容积。
物体的表面积指的是物体的外表面的投影面积大小。
物体的表面系数是指物体的表面积与物体体积的比值，用高斯定理可以很容易求出表面系数的大小。
由高斯定理可以推出：
S = 2λπr^2
∴A = S/V = 2λπr^2/ (λ/2πr^2) = 4πr
从上面的结果可以看出，表面系数A与物体的半径r有关。
物体的容积指的是物体内积的大小，用高斯定理可以求出物体的容积：
V =/2πr^2
从上面的结果可以看出，物体的容积与物体的表面张力以及半径有关。
高斯定理的物理意义在于它可以将物体的表面积和容积联系起
来，用高斯定理可以很容易求出物体的表面系数，从而得出物体的表面积和容积。
因此，高斯定理在测量物体表面积和容积以及应用面及润滑学、汽车工程等领域都有重要的意义。
总之，高斯定理表达式是描述物体表面积和容积之间关系的一个重要定理，对于测量物体表面积和容积以及应用于润滑学和汽车工程等领域都有重要的意义。
数学中的高斯定理
数学中的高斯定理高斯定理是数学中的一个非常重要的定理，它是现代微积分理论的基石之一。
该定理最初由德国数学家高斯在18世纪末发现，一直到今天，它依然广泛应用于物理学、工程学、计算机科学等多个领域。
本文将从高斯定理的数学原理、物理应用和现代研究方向三个方面来介绍这一重要的定理。
一、高斯定理的数学原理高斯定理是关于矢量场的定理，它是一种矢量积分定理。
简单来说，该定理描述了在一个体积内的矢量场在该体积表面所引起的通量的关系。
通量是一个常用的物理概念，它可以理解为矢量场流经一个表面所引起的量，通量可以正、负或者为零，具体取决于矢量场和表面的相对方向。
图1展示了一个二维平面内的矢量场和一个封闭曲线，该曲线的起点和终点相同，它将该平面划分成了内部和外部两个区域。
高斯定理告诉我们，曲线内部的通量等于曲线外部的通量，即：$\int_{S}\textbf{F}\cdotd\textbf{S}=\int_{V}\nabla\cdot\textbf{F}\textbf{dV}$ （1）其中，$\textbf{F}$表示一个三维矢量场，$d\textbf{S}$表示曲线的微元面积，$\nabla\cdot\textbf{F}$表示矢量场的散度，$dV$表示一个三维体积元，$S$表示封闭曲线的表面。
公式(1)即为高斯定理的数学形式。
图1 二维平面内的矢量场和封闭曲线从数学角度来看，高斯定理是一个非常重要的结果。
它表明，在矢量场满足一定条件的情况下，我们可以通过计算矢量场的散度来推导出曲面与体积之间的通量关系。
这种关系对于求解物理问题和工程实践非常有用，因此高斯定理在物理学和工程学等领域中得到了广泛的应用。
二、高斯定理的物理应用高斯定理在物理学中的应用非常广泛，其中最为典型的就是电场通量和磁场通量的计算。
在静电场问题中，电场可以看作是一个矢量场，它的导数就是该场的散度。
因此，应用高斯定理可以计算出电场通过一个闭合曲面的通量，具体而言，该通量等于该曲面内部所包含的电荷量除以真空介电常数，即：$\int_{S}\textbf{E}\cdotd\textbf{S}=\frac{Q}{\varepsilon_0}$ （2）其中，$\textbf{E}$表示电场强度，$dS$表示曲面微元面积，$Q$表示曲面内所包含的电荷量，$\varepsilon_0$表示真空介电常数。
高 斯 定 理
1.3 高斯定理
静电场是由电荷所激发的，通过电场空间某一给定闭合 曲面的电通量与激发电场的场源电荷必定有确定的关系。德 国科学家高斯通过缜密运算论证了这个关系，并提出了著名 的高斯定理。该定理给出了通过任何曲面S的电通量φe与闭 合曲面内部所包围的电荷之间的关系。下面就以点电荷为例 来讨论。
（3）利用高斯定理解出场强E。
【例7-4】求点电荷Q的电场强度的分布情况。
S
0
由此可见，通过此球面的电通量等于球面内的电荷量q除以 真空电容率ε0 ，与球面半径无关。
（2）一个正点电荷q，被任意闭合曲 面S′和球面S同时包围，如下图所示。根 据电力线的连续性可知，凡是通过球面S 的电力线都一定通过曲面S′。所以通过闭 合曲面S′的电通量等于通过球面S的电通 量，均为 q/ε0 。
物理学
高斯定理
1.1 电场线
电场线是空间中一系列假想的曲线，主要反映电场的特
征，描述电场中各点场强E的大小和方向。为此，对电场线作
如下规定：
（1）电场线上每一点的切线方向与该点场强E的方向一
致。这样，电场线的方向就反映了场强方向的分布情况。
（2）在任一场点，使通过垂直于场强E的单位面积的电
场线数目（称为电场线密度），正比于该点处场强E的大小。
2．非均匀电场的电通量
在非均匀电场中，为了求出通过任意曲面S的电通量φe， 可以把曲面S分成无限多个面元dS，如下图所示。此时，面元 dS可以近似看成一个平面，并且在面元的范围内电场强度可 以近似看成大小相等、方向相同的匀强电场。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1、电力线 若已知电荷分布，则空间各点的场强原则上都可求出。为了形象化地把客观存在的电场
表示出来，常引入电场线这一辅助工具。 （1）电力线的定义 ·电力线上每一点的切线的方向与相应点场强的方向一致。 ·电力线的数密度与该点的场强的大小成正比。
ΔN = EΔS ⊥
则这样定义的电力线既可以表示场强的方向，又可以表示场强的大小。 所谓电场线的数密度，就是通过垂直于场强方向的单位面积的电场线的条数。这样，凡 是电场线密集的地方，场强就大，电场线稀疏的地方，场强就小。 （2）电力线的性质
斯定理导出库仑定律。库仑定律不但说明电荷间的相互作用力服从平方反比律，而且说明电
荷间的作用力是有心力。因此，在静电范围内，库仑定律比高斯定理包含更多的信息。 四、高斯定理举例
高斯定理也是静电场的基本定理之一，它给出了场与源的联系，但并没有给出场分布与 产生电场的源电荷之间的直接联系。因此在一般情况下，已知电荷分布，并不能直接从高斯 定理求得场强分布。这也是高斯定理没有包括库仑定律全部信息的反映。
（2）高斯面上的电荷问题 高斯面把电荷区分为内外两种，是否存在一种点电荷正好在高斯面上？这是不存在
的，因为只有点电荷和线度要远小于 q 与高斯面间的距离，才能视为点电荷。 （3）高斯定理中的 E 问题 高斯定理中的 E 是全部电荷所产生的 E，而不管这电荷是在曲面内部或在曲面外
部。同一高斯面的 E 可能相同，也可能不同，因为高斯面是任意选取的。 （4）高斯定理表明的只是电通量和电荷的关系 如果在高斯面内部或外部电荷分布发生改变，则空间电场分布将发生变化，高斯面
部，把 qi +1，…， q N 包围在外部，则由叠加原理，总电场 E 对封增长曲面的电通量为
或者
图 1-51 电场对封闭曲面的通量只与曲面所包含的电荷有关 电场对任意封闭曲面的电通量只决定于被包围在封闭曲面内部的电荷，且等于包围在封
闭曲面内电量代数和除以 ε0 ，与封闭曲面外的电荷无关。这一结论就是静电场的高斯
Φ total = Φ Fr + Φ Bk + Φ Lf + Φ Rt + ΦTp + Φ Bt = 0
二、高斯定理 1、数学家和物理学家高斯
图 1-44 数学家和物理学家高斯（1777-1855） 高斯是德国数学家，也是物理雪茄家，他和牛顿、阿基米德，被誉为有史以来的三大数 学家。高斯是近代数学奠基者之一，在历史上影响之大，可以和阿基米德、牛顿、欧拉并列， 有“数学王子”之称。 高斯的数学研究几乎遍及所有领域，在数论、代数学、非欧几何、复变函数和微分几何 等方面都做出了开创性的贡献。由于高斯在数学、天文学、大地测量学和物理学中的杰出研 究成果，他被选为许多科学院和学术团体的成员。“数学之王”的称号是对他一生恰如其分 的赞颂。 2、高斯定理 （1）对任意曲面的电通量 假定电场由一电量为 q 的点电荷产生，dS 是曲面上的任一面元，它的位置由径矢 r 表 示，r 的起点取在点电荷上。电场对 dS 的通量为：
（Gauss）定理。
若包围在 S 面内的电荷具有一定的体分布，电荷体密度为 ρ ，则高斯定理可写成：
式中 V 是 S 所包围的体积。 3、高斯定理的讨论 （1）高斯定理表明是静电场是有源场
高斯定理给出了场和场源的一种联系，这种联系是场强对封闭曲面的通量与场源间 的联系，并非场强本身与源的联系。电荷是静电场的源。
（2）电通量 ·电通量的定义
电通量的正负取决于电力线与曲面的法线方向的夹角θ 。
对电力线不均匀或曲面不规则时，电通量可以由积分计算：
Φ = ∫∫ E cosθdS = ∫∫ E ⋅ dS
s
s
曲面法线方向的规定：
开曲面：凸侧一方的方向的外法线方向为正；
闭曲面：外法线方向为正，内法线方向为负。
图 1-42 曲面的法线方向与电场方向 ·电通量的特点 ◇由电场的叠加原理可推出电通量也满足叠加原理
·电力线起自正电荷或无限远，终止于负电荷或无限远； ·若体系正负电荷一样多，则正电荷发出的电力线全部终止于负电荷； ·两条电力线不会相交； ·静电场中的电力线不会形成闭合曲线。 电力线之所以具有这些基本性质，是由静电场的基本性质和场的单值性决定的。可用 静电场的基本性质方程加以证明。 （3）一些典型电荷分布的电力线 ·点电荷的电力线：
体角为 4π ，曲面不包含电荷时，曲面对电荷所张的立体角为 0。 若电场由一组点电荷 q1 , q2 , q3 L， q N 共同产生，用 E1 , E2 , E3 ,L, E N 分别代表各点
电荷单独产生的电场的场强。设有一任意形状的封闭曲面 S，它把 q1 , q2 , q3 L qi 包围在内
正点电荷的电力线是各个方向均匀地射出 N 根，同一球面相同面积的 ΔS1 、 ΔS 2 有
相同根数的电力线穿过。如图电力线的密度为：
N 4πr 2
2、电通量 （1）电力线的根数
电力线的密度为 E∞ΔN / ΔS ⊥ 取比例系数为 1，则 ΔN = E ⋅ ΔS ⊥ 当 E 与 ΔS 不垂直时， ΔS 的法线与 E 不平行，则有： ΔN = E ⋅ ΔS
但仍满足高斯定理。 变化的磁场产生的涡旋电场，在涡旋场中任取一闭合曲面 S，显然
也满足高斯定理，但涡旋电场不具有径向性和球对称性 认为高斯定理与库仑定律完全等价，或认为从高斯定理出发可以导出库仑定律的看法是
欠妥的，因为高斯定理并没有反映静电场是有心力场这一特性。 实际上，不增添附加条件如点电荷的电场方向沿径向并具有球面对称性等，并不能从高
若点电荷在封闭曲面内部，如图所示，则因封闭曲面对曲面内任意一点张的立体角和
单位园对 q 张的立体角相同，均匀 4π ，故
图 1-46 当 q 在封闭曲面内，曲面对 dS 对 q 张的立体角为 4π
若曲面的形状如图所示，点电荷在曲面的内部，从电荷 q 发出的电力线将在 A 区域穿 过曲面三次，三次穿进穿出对应的面元对 q 点张的立体角值相同，穿出为正，穿入为负，故 净穿出一次。在 B 区域只穿过曲面一次。只要电荷在曲面内部，穿进穿出的次数总是奇数
Φ = ∫∫ E ⋅ dS = ∫∫ ∑ Ei ⋅ dS = ∑ ∫∫ Ei ⋅ dS = ∑ Φi
i
i
◇电通量是标量
·通过闭合曲面的电通量
通过闭合曲面的电通量是通过该闭合曲面电通量的净电力力线数目。如果闭合曲面
内无电荷，则通过闭合曲面的电通量是零。
[例]求在均匀电场通过一矩形闭合曲面的电通量
[解]通过矩形闭合曲面的电通量由通过六个面的电通量之和，根据对称性，有：
对任一闭合曲面，由于规定外法线方向为正，因此， dS1和dS 2对q 张的立体角不仅大小
相等，而且正负相反。因而两面元对 q 张的立体角之和为零。
图 1-49 电荷在曲面的外面，穿进穿出的两曲面对 q 所张的立体角相互抵消 故：
因此封闭曲面总是由一一对应的一组面元构成，每一组面元对点 q 张的立体角都为零，因此， 整个闭合曲面对曲面外任一点张的立体角为零。
次。该曲面 q 点张的立体角与单位园的相同，为 4π 。
图 1-47 点电荷在曲面的内部，穿进穿出的次数总是奇数次 （3）点电荷在曲面外部
若点电荷在封闭曲面外部，如图所示，则任一面元 dS1 对 q 所张的立体角必与另一面 元 dS 2 对 q 张的立体角大小相等。
图 1-48 面元对点电荷所张的立体角
到空腔中心的距离为 a。
[解]将空腔看作是同时填满 + ρ 和 − ρ 的电荷，腔内任一点的电场强度就由一个实心大 球电荷密度为 + ρ 和一个实心小球电荷密度为 − ρ 的叠加而成，如图所示：
得：
图 1-54 球体中的球形空腔的电场
同理可得：
所以，
a 为矢量，方向由 O 指向 O′ 。可见空腔内电场强度是均匀的。
但是在电荷分布具有某种对称性，从而使场分布也具有某种对称性注意这些信息并非来 自高斯定理）时，我们可以直接用高斯定理通过电荷分布找到场的分布。
[例]求均匀带电球面产生的电场。已知球面的半径为 R，电量为 Q。 [解]根据球对称性可以判定，不论在球内还是在球外，场强的方向必定沿球的半径，
图 1-52 均匀带电球面产生的电场 与球心等距离的各点的场强大小应相等。作如图所示的高斯面，当 r ＜R 时，有：
若以 q 所在处为中心、r 为半径作一球面，则 er dS 就是面元 dS 在球面上的投影 dS0 ， dS0 / r 2 为 dS0 对球心所张的立体角 dΩ ，如图所示，
dΩ 正负由 dS 与 r 的交角而定，所以，点电荷的通量为：
积分的值取决于点电荷在封闭曲面内部还是外部。 （2）点电荷在曲面内部
当r ＞R时，作S2的高斯面，有：
由此得到：
[例]求无限大均匀带电平面的电场 [解]根据对称性，可以判定无限大带电平面的电场应指向两侧，离平面等距离处电场强 度相同，作一矩形高斯面，周围四个面无电通量，只有上下两面有电通量。因而可得：
图 1-53 无限大均匀带电平面的电场
[例]求均匀带电球体中所挖出的球形空腔中的电场强度。球体电荷密度为 ρ ，球体球心
上的电场也会发生变化，但只要内部总电荷数不变，高斯定理指出，电场对该封闭曲面的电 通量并无变化。
（5）高斯定理的微分形式
由场论中知识，高斯定理可以写成微分形式：
表明电力线不会在没有电荷的空间产生或消失。 三、高斯定理与库仑定律的关系
1、高斯定理来源于库仑定理ห้องสมุดไป่ตู้高斯定理是静电场的一条重要基本定理，它是从库仑定律导出来的。它主要反映了库
仑定律的平方反比律，即1/ r 2 。如果库仑定律不服从平方反比律，我们就不可能得到高斯
定理。 若：
则：
亦即：
高斯定理不成立。 因此证明高斯定理的正确性是证明库仑定律中平方反比律的一种间接方法，直接用扭秤 证明平方反比律的精度是非常低的，通过高斯定律证明平方反比律可获得非常高的精度。 2、高斯定理比库仑定理更普遍 高斯定理是库仑定律为基础导出的，但其使用范围远远超出静电场。库仑定律决定静电 场具有平方反比律、径向性和球对称性，加上叠加原理可以推广到任意的静电场。 运动点电荷由于在运动方向上的特殊性，破坏了球对称性，匀速运动的点电荷的场为：