云南省香格里拉县第一中学高一数学上学期期中试题
云南省2020年高一上学期数学期中联考试卷(I)卷

云南省2020年高一上学期数学期中联考试卷(I)卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共20分)1. (2分) (2019高一上·银川期中) 已知集合,集合,则()A .B .C .D .2. (2分) (2019高一上·重庆月考) 函数的定义域是()A .B .C .D .3. (2分) (2020高二下·吉林期中) 下列各组函数中,表示同一个函数的是()A . 与B . 与C . 与D . 与4. (2分) (2016高一上·邹平期中) 使函数y=xα的定义域为R且为奇函数的α的值为()A . ﹣1B . 0C .D . 35. (2分)三个数,,的大小关系为()A . <<B . <<C . <<D . <<6. (2分)已知函数,下列结论正确的是()A . 函数为奇函数B .C . 函数的图象关于直线y=x对称D . 函数在R上是增函数7. (2分) (2016高一上·烟台期中) 函数f(x)= + 的定义域为()A . [﹣2,0)∪(0,2]B . (﹣1,0)∪(0,2]C . [﹣2,2]D . (﹣1,2]8. (2分)已知函数满足对任意x1≠x2 ,都有(x1﹣x2)[f(x1)﹣f(x2)]<0成立,则a的取值范围为()A .B . (0,1)C .D . (0,3)9. (2分) (2019高一上·沈阳月考) 已知函数在上的最大值与最小值之和为 ,则的值为()A .B .C .D .10. (2分) (2020高三上·四川月考) 已知,,若存在,,使得,则称函数与互为“ 度零点函数”.若与互为“ 度零点函数”,则实数的取值范围为()A .B .C .D .二、填空题 (共6题;共6分)11. (1分) (2020高一上·三明月考) 已知集合,,则中的元素个数为________.12. (1分) (2020高二下·吉林月考) 若,则 ________.13. (1分) (2019高一上·金台期中) 若二次函数y=kx2-8x+1在区间[4,6]上是增加的,则实数k的取值范围是________.14. (1分) (2016高一上·南京期中) 已知,则f(4)=________.15. (1分) (2016高一上·南京期中) 已知函数,若函数的值域为R,则常数a的取值范围是________16. (1分) (2018高三上·北京月考) 已知函数,若,则的取值范围是________.三、解答题 (共5题;共50分)17. (10分) (2018高一上·北京期中) 已知,,求的值.18. (10分) (2016高一上·黄陵期中) 已知集合A={x|3≤x<7},B={x|2<x<10},求:A∪B,(∁RA)∩B.19. (10分)已知幂函数y=xm2﹣2m﹣3(m∈Z)的图象与x , y轴都无公共点,且,求m的值.20. (10分)(2019·台州模拟) 已知斜率为的直线经过点,且直线交椭圆于,两个不同的点.(I)若,且是的中点,求直线的方程;(Ⅱ)若随着的增大而增大,求实数的取值范围.21. (10分) (2019高一上·永嘉月考) 已知函数.(1)求函数的定义域;(2)判断的奇偶性并加以证明;(3)若在上恒成立,求实数的范围.参考答案一、单选题 (共10题;共20分)答案:1-1、考点:解析:答案:2-1、考点:解析:答案:3-1、考点:解析:答案:4-1、考点:解析:答案:5-1、考点:解析:答案:6-1、考点:解析:答案:7-1、考点:解析:答案:8-1、考点:解析:答案:9-1、考点:解析:答案:10-1、考点:解析:二、填空题 (共6题;共6分)答案:11-1、考点:解析:答案:12-1、考点:解析:答案:13-1、考点:解析:答案:14-1、考点:解析:答案:15-1、考点:解析:答案:16-1、考点:解析:三、解答题 (共5题;共50分)答案:17-1、考点:解析:答案:18-1、考点:解析:答案:19-1、考点:解析:答案:20-1、考点:解析:答案:21-1、答案:21-2、答案:21-3、考点:解析:。
云南省高一上学期数学试期中考试试卷

云南省高一上学期数学试期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)(2017·山东模拟) 已知集合A={x||x|≤2},B={x|x2﹣x﹣2<0},则A∩∁RB=()A . RB . {x|﹣2≤x≤﹣1}C . {x|﹣2≤x≤﹣1或x>2}D . {x|﹣2≤x≤﹣1或x=2}2. (2分) (2020高二下·江西期中) 若函数,则()A . -3B . 1C . -1D . 33. (2分) (2019高一上·集宁月考) 已知函数,则()A . 3B . 5C . 6D . 324. (2分) (2018高一上·中原期中) 函数的图象大致是()A .B .C .D .5. (2分)下列四个函数中,在(0,1)上为增函数的是()A . y=﹣log2xB . y=sinxC .D . y=arccosx6. (2分) (2019高一上·西安期中) 若函数在定义域A上的值域为 ,则区间A 不可能为()A .B .C .D .7. (2分)已知函数设,b=f(log20.3),c=f(ln10),则a, b,c的大小关系是()A . a>c>bB . b>a>cC . c>a>bD . a>b>c8. (2分)(2017·海淀模拟) 下列函数图象不是轴对称图形的是()A .B . y=cosx,x∈[0,2π]C .D . y=lg|x|9. (2分)函数有且仅有一个正实数的零点,则实数m的取值范围是()A .B .C .D .10. (2分)(2020·临沂模拟) 已知,,,则()A .B .C .D .11. (2分)某种细菌在培养过程中,每15分钟分裂一次(由一个分裂成两个),这种细菌由1个繁殖成4096个需经过()A . 12小时B . 4小时C . 3小时D . 2小时12. (2分) (2017高一上·河北月考) 已知点,动点的坐标满足,那么的最小值是()A .B .C .D . 1二、填空题 (共4题;共4分)13. (1分) (2019高一上·武汉月考) 函数的定义域为________.14. (1分)已知幂函数y=f(x)的图象过点(4,),则该幂函数的定义域是________15. (1分) (2020高一上·嘉兴期末) 设函数则的值为________;若 ,则 =________.16. (1分)已知函数f(x)是定义在R上的偶函数,且当x≥0,f(x)=ex﹣ax,若函数在R上有且仅有4个零点,则实数a的取值范围是________.三、解答题 (共6题;共60分)17. (10分) (2017高一上·温州期中) 已知函数f(x)=loga(1+x)﹣loga(1﹣x)(a>0且a≠1),(1)求函数f(x)的定义域;(2)若关于x的方程|f(x)|=2的解集为,求a的值.18. (10分) (2016高一上·崇礼期中) 已知集合A={x|3≤x<7},B={x|2<x<10},C={x|a<x<a+5}.(1)求A∪B,(∁RA)∩B;(2)若C⊆B,求a的取值范围.19. (10分)设a为正实数,记函数f(x)=a﹣﹣的最大值为g(a).(1)设t=+,试把f(x)表示为t的函数m(t);(2)求g(a);(3)问是否存在大于的正实数a满足g(a)=g()?若存在,求出所有满足条件的a值;若不存在,说明理由.20. (10分) (2019高一上·双鸭山期中) 设函数在[0,1]上是减函数,(1)求实数的范围;(2)求 = 的单调递增区间和值域.21. (10分) (2015高二下·九江期中) 已知函数f(x)=|2x﹣1|+|2x+a|,g(x)=x+3.(Ⅰ)当a=﹣2时,求不等式f(x)<g(x)的解集;(Ⅱ)设a>﹣1,且当时,f(x)≤g(x),求a的取值范围.22. (10分)若f(x)是定义在(0,+∞)上的增函数,且=f(x)﹣f(y)(1)求f(1)的值;(2)若f(6)=1,解不等式f(x+3)﹣<2.参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共60分) 17-1、17-2、18-1、18-2、19-1、20-1、20-2、21-1、22-1、。
云南高一高中数学期中考试带答案解析
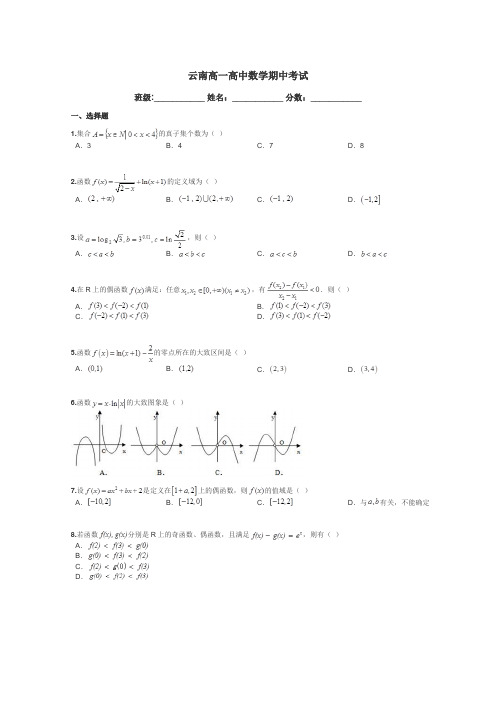
云南高一高中数学期中考试班级:___________ 姓名:___________ 分数:___________一、选择题1.集合的真子集个数为()A.3B.4C.7D.82.函数的定义域为()A.B.C.D.3.设,则()A.B.C.D.4.在R上的偶函数满足:任意,有.则()A.B.C.D.5.函数的零点所在的大致区间是()A.B.C.D.6.函数的大致图象是()7.设是定义在上的偶函数,则的值域是()A.B.C.D.与有关,不能确定8.若函数分别是R上的奇函数、偶函数,且满足,则有()A.B.C.D.9.已知奇函数在时的图象如图所示,则不等式的解集为()A.B.C.D.10.若函数是上的减函数,则实数的取值范围是()A.B.C.D.11.对于集合M、N,定义:且,,设=,,则=()A.(,0]B.[,0)C.D.12.记实数,,…,中的最大数为,最小数为,则()A.B.C.D.二、填空题1.已知幂函数的图象经过(3,27),则=________.2.函数的图像恒过定点,则点的坐标是________.3.函数,满足,则的值为________.4.已知函数,,,实数是函数的一个零点.给出下列四个判断:①;②;③;④.其中可能成立的是________.(填序号)三、解答题1.已知集合,.求:(1);(2);(3).2.计算下列各题:(1);(2).3.铁路运输托运行李,从甲地到乙地,规定每张客票托运费计算方法为:行李质量不超过,按元计算;超过而不超过时,其超过部分按元计算,超过时,其超过部分按元计算.设行李质量为,托运费用为元.(Ⅰ)写出函数的解析式;(Ⅱ)若行李质量为,托运费用为多少?4.已知函数是定义在上的偶函数,当时,.(1)求的函数解析式,并用分段函数的形式给出;(2)作出函数的简图;(3)写出函数的单调区间及最值.5.已知.(1)证明为奇函数;(2)求使>0成立的的集合.6.已知:定义在R上的函数,对于任意实数a, b都满足,且,网当.(Ⅰ)求的值;(Ⅱ)证明在上是增函数;(Ⅲ)求不等式的解集.云南高一高中数学期中考试答案及解析一、选择题1.集合的真子集个数为()A.3B.4C.7D.8【答案】C【解析】,它的真子集分别为,{1},{2},{3},{1,2},{1,3},{2,3}.一般一个集合中含有n个元素,则它的子集的个数为个,真子集去掉它本身之后为.【考点】集合的关系:真子集.2.函数的定义域为()A.B.C.D.【答案】C【解析】要使函数有意义,需满足:,所以.【考点】函数的定义域.3.设,则()A.B.C.D.【解析】先和0比较,得到c最小;再与1比较,得到b最大.故选A.【考点】指数函数、对数函数的单调性的应用,指数式、对数式比较大小.4.在R上的偶函数满足:任意,有.则()A.B.C.D.【答案】A【解析】由得分子分母异号,所以若x的值小,则对应的y大,可得函数在为减函数.则,而函数为偶函数则.故选A.【考点】函数单调性的定义、偶函数的定义.5.函数的零点所在的大致区间是()A.B.C.D.【答案】B【解析】,,由零点存在性定理得选B.【考点】零点存在性定理.6.函数的大致图象是()【答案】D【解析】由选项得图象具有对称性,与函数的奇偶性有关,而,所以函数为奇函数,所以图象关于原点对称,应从C,D中选一个.C与D的一个很大差别是在x趋向于无穷大时,y是趋于无穷大还是无穷小,显然此时应该趋向于无穷大.【考点】函数的图象、函数的性质特别是奇偶性、函数的值域.7.设是定义在上的偶函数,则的值域是()A.B.C.D.与有关,不能确定【答案】A【解析】函数的定义域关于原点对称是函数成为奇偶函数的必要条件,所以1+a=-2,a=-3.【考点】函数的奇偶性.8.若函数分别是R上的奇函数、偶函数,且满足,则有()A.B.C.D.【解析】因为①,所以,又因为是R上的奇函数、偶函数,所以②,①、②相加、相减得:,,所以,,,所以f(3)>f(2)>g(0).【考点】函数的奇偶性、函数的解析式的求法.9.已知奇函数在时的图象如图所示,则不等式的解集为()A.B.C.D.【答案】B【解析】∵xf(x)<0则:当x>0时,f(x)<0,结合函数的图象可得,1<x<2,当x<0时,f(x)>0,根据奇函数的图象关于原点对称可得,-2<x<-1,∴不等式xf(x)<0的解集为(-2,-1)∪(1,2).故答案为:(-2,-1)∪(1,2).【考点】函数的图象.10.若函数是上的减函数,则实数的取值范围是()A.B.C.D.【答案】B【解析】要使此分段函数在上为减函数,需满足两个条件:每一段为减函数,界点处左端图象也应在右端图象上方.所以列出下式:,解此不等式组得.【考点】分段函数的单调性、基本初等函数的单调性.【易错点睛】本题容易出错的地方是学生往往忽视第三个式子,分段函数在R上为单调函数需要从负无穷到正无穷处一直都在单调.【方法点睛】分段函数在其定义域内是增函数必须满足两个条件:①每一段都是增函数;②相邻两段函数中,自变量取值小的一段函数的最大值(或上边界),小于等于自变量取值大的一段函数的最小值(或下边界).分段函数在其定义域内是减函数必须满足两个条件:①每一段都是减函数;②相邻两段函数中,自变量取值小的一段函数的最小值(或下边界),大于等于自变量取值大的一段函数的最大值(或上边界).11.对于集合M、N,定义:且,,设=,,则=()A.(,0]B.[,0)C.D.【答案】D【解析】设,,,,集合,定义,,,,.【考点】集合间交、并、补的运算,函数的定义域、值域的求法,根据新概念解决问题的能力.【易错点晴】本题中易错的地方是已知条件中集合A所能取到的数是函数中y能取到的数,集合B所能取到的数是函数中x能取到的数,实际上是考查了一些常见的基本初函数的定义域、值域问题.另外,注意练习运用新概念解决问题的能力,可以经历读题、转化成所学知识、列出式子、得到答案过程.12.记实数,,…,中的最大数为,最小数为,则()A.B.C.D.【答案】D【解析】在同一平面内作函数在同一平面内作函数的图象,取它们最下端的曲线(如图阴影部分的上沿),这曲线的最高点的纵坐标就是所求,可以看出,它是 y="x+1" 与 y=" -x+6" 的交点,解得,,也即.【考点】一元一次、二次函数在同一坐标系的图象,分段函数最值问题.【方法点晴】本题意在考查在同一直角坐标系中做出不同函数的图象,在难度上要比做单一图象难度高很多.要注意x取同一个值时不同的函数对应的y值得大小.另外,本题的已知条件显得比较繁琐,一定形式上给考生增加了难度,所以对于考生来说一定要放平心态.已知中无非是告诉我们取这几个函数中最小的那个函数,从图象上来说就是取最低的那块图象.这样本题就成了分段函数的问题,最后求分段函数的最大值,从图象上一看就一目了然了.本题用到了数形结合的思想.二、填空题1.已知幂函数的图象经过(3,27),则=________.【答案】8【解析】设幂函数,把点代入,得,解得,,故答案为:.【考点】幂函数.2.函数的图像恒过定点,则点的坐标是________.【答案】(2,1)【解析】,,即时,,点的坐标是,故答案为: .【考点】对数函数性质.3.函数,满足,则的值为________.【答案】2019【解析】设,则,而g(x)显然为奇函数,所以g(3)=-g(-3)=2017,即f(3)-2=2017,因此f(3)=2019.【考点】函数的奇偶性.【方法点晴】本题意在考查函数的奇偶性,但所给函数不符合奇偶性,其部分式子所组成的函数具有奇偶性.做题时要学会仔细观察,善于对函数式子变形,再利用所学知识解决问题的能力.4.已知函数,,,实数是函数的一个零点.给出下列四个判断:①;②;③;④.其中可能成立的是________.(填序号)【答案】①②③【解析】在单调递减,,,,或,是函数的一个零点,即,若,则可得,,若,则可得,.综上可得①可能成立;②可能成立;③可能成立;④不可能成立.故答案为①②③.【考点】函数的单调性.【方法点晴】对于函数的题目中涉及到几个x的取值大小与y的取值大小比较的题目常常函数的单调性,本题中由f(x)的解析式很容易得到其为单调函数,由x的取值大小自然可以利用单调性比较对应y值得大小,本题中涉及到x的四个取值a,b,c,d,四个对应的y值,它们与d的关系衔接的纽带是,考虑到其成立的各种情况即可.三、解答题1.已知集合,.求:(1);(2);(3).【答案】(1);(2);(3).【解析】利用数轴,在数轴上画出全集,集合A,集合B,即可求得.试题解析:(1)(2),(3)【考点】集合的交集、并集、补集运算.2.计算下列各题:(1);(2).【答案】(1)89;(2).【解析】主要涉及到指数式的运算和对数式的运算两个考点.指数式的运算主要是分数指数幂的运算,要学会应用转化的思想,将分数指数幂转化为整数指数幂来算,常用的方法就是将底数化成分数幂中分母次方的形式.对数的运算要掌握住对数运算的运算法则、对数恒等式、对数的换底公式等.试题解析:(1)原式= =(2)原式== .【考点】指数、对数式的运算.【方法点晴】指数和对数的运算是学习指数函数和对数函数的基础,也是高考考试的重点.涉及的常见的题型与解题方法主要有:1、重视指数式与对数式的互化;2.根式运算时,常转化为分数指数幂,再按幂的运算法则运算;3.不同底的对数运算问题,应化为同底对数式进行运算;4.运用指数、对数的运算公式解题时,要注意公式成立的前提;5.指数方程和对数方程按照不同类型的对应方法解决.3.铁路运输托运行李,从甲地到乙地,规定每张客票托运费计算方法为:行李质量不超过,按元计算;超过而不超过时,其超过部分按元计算,超过时,其超过部分按元计算.设行李质量为,托运费用为元.(Ⅰ)写出函数的解析式;(Ⅱ)若行李质量为,托运费用为多少?【答案】(Ⅰ);(Ⅱ)14.6.【解析】第一问根据题中的条件,结合题意,将函数值与自变量之间的关系找出来,注意分类讨论思想的应用,注意分段函数的应用,第二问根据自变量所属的范围,带入相应的解析式,从而求得对应的函数值.试题解析:(Ⅰ)(1)若,则;(2)若,则;(3)若,则.所以,由(1)(2)(3)可知(Ⅱ)因为,所以(元).【考点】函数应用题,分类讨论的思想,分段函数的应用,已知自变量求函数值.4.已知函数是定义在上的偶函数,当时,.(1)求的函数解析式,并用分段函数的形式给出;(2)作出函数的简图;(3)写出函数的单调区间及最值.【答案】(1);(2)见解析;(3)单调增区间为和;单调减区间为和;当或时,有最小值-2.【解析】此题是由函数的一半解析式求另外一半解析式,常常利用函数的奇偶性联系到一块,解题时要注意一开始x所设的范围应该是所求的那段解析式的x的范围,“立场”不要弄错.然后-x即成了已知条件中的范围,代入可得f(-x)的解析式,再利用奇偶性即可得所求范围内的解析式.从形式上讲任然是分段函数问题的考查.分段函数画图及单调性的求解仍然是运用“分段函数分段处理”的思想.试题解析:(1)当时,,是偶函数(如果通过图象直接给对解析式得2分)(2)函数的简图:(3)单调增区间为和单调减区间为和当或时,有最小值-2【考点】函数的解析式、奇偶性、单调性及最值、图象、分段函数.5.已知.(1)证明为奇函数;(2)求使>0成立的的集合.【答案】(1)见解析;(2)时,时.【解析】函数的奇偶性的证明分三步:第一、判断函数的定义域是否关于原点对称;第二、求解f(-x)与f(x)进行比较;第三、下结论.本题第一问就按此三步来处理即可,当然要注意对数的运算法则.第二问对数不等式的求解,一般不同形式的化成相同形式,不是对数的化成对数形式,不同底的化成同底的.然后利用对数函数的单调性解决.试题解析:证:由题得所以函数定义域为所以为奇函数(2)>0由(1)得函数定义域为当时即得当时即得得综上,时,时.【考点】函数的奇偶性,对数的运算及对数函数的性质,分式不等式的求解.6.已知:定义在R上的函数,对于任意实数a, b都满足,且,网当.(Ⅰ)求的值;(Ⅱ)证明在上是增函数;(Ⅲ)求不等式的解集.【答案】(Ⅰ)1;(Ⅱ)见解析;(Ⅲ).【解析】函数对于任意实数a,b都满足式子成立,所以这里a,b可以取任何值,要求f(0)可令a=1,b=0;抽象函数单调性的证明因为没有解析式所以可以采用的只有定义法,难点是怎样定号,需要想方设法利用上已知的条件.第三问常常与解不等式结合到一块,这里需要利用已知恒等式及函数的单调性来解决.试题解析:(Ⅰ)解:令(Ⅱ)证明:当由得设(Ⅲ)解:由(Ⅱ)可得:解得所以原不等式的解集是【考点】抽象函数的求值、单调性,一元二次不等式的求解.【方法点晴】抽象函数是指没有明确给出具体的函数表达式,只是给出一些特殊条件的函数,它是中学数学函数部分的难点.因为抽象,学生难以理解,接受困难.其实,大量的抽象函数都是以中学阶段所学的基本函数为背景抽象而得,解题时,若能从研究抽象函数的“背景”入手,根据题设中抽象函数的性质,通过类比、猜想出它可能为某种基本函数,常可觅得解题思路.常见的题型有:1.定义域问题 2、求值问题3、值域问题 4、解析式问题5、单调性问题6、奇偶性问题7、周期性与对称性问题等类型.求值问题常常采用赋值法,判断单调性常常采用定义法.。
云南省2020版高一上学期数学期中考试试卷(I)卷

云南省 2020 版高一上学期数学期中考试试卷(I)卷姓名:________班级:________成绩:________一、 单选题 (共 8 题;共 8 分)1. (1 分) (2019 高一上·成都月考) 已知全集集合,则()A.B.C.D.2. (1 分) 函数 A . (1,4) B . [1,4) C.的定义域为( )D. 3. (1 分) 集合 M={x∈N|x=5﹣2n,n∈N}的子集个数是( ) A.9 B.8 C.7 D.64. (1 分) (2019 高一上·兴平月考) 下列四个函数中,在上为减函数的是( )第 1 页 共 20 页A.B.C.D.5. (1 分) (2018 高一上·舒兰月考) 若函数 四象限,则一定有( )A.且B.且C.且D.且(,且)的图象经过第二、三、6. (1 分) (2020 高三上·福州期中) 若函数 围是( )A.B. C. D.7. (1 分) (2019 高三上·汉中月考) 设 A. B. C.在 R 上没有零点,则 的取值范 ,则( )第 2 页 共 20 页D.8. (1 分) (2019 高一上·沈阳月考) 奇函数函数的图为( ),,当时,,则A.B. C.D.二、 填空题 (共 8 题;共 8 分)9. (1 分) (2017 高一上·沛县月考) 已知集合 A=[0,8],集合 B=[0,4],则下列对应关系中,不能看作从 A 到 B 的映射的是________.(填写序号)①f:x→y= x②f:x→y= x③f:x→y= x④f:x→y=x10. (1 分) (2016 高一上·黄冈期末) 已知 f(x)=,则 f(f( ) )=________11. (1 分) (2020 高三上·湖北月考) 黎曼函数是一个特殊的函数,由德国著名的数学家波恩哈德·黎曼发第 3 页 共 20 页现提出,在高等数学中有着广泛的应用,其定义为:当(为正整数, 是既约真分数)时,当或上的无理数时,若函数是定义在 上的奇函数,且对任意 都有,当时,,则________.12. (1 分) 设函数 f(x)=2a﹣x﹣2kax(a>0 且 a≠1)在(﹣∞,+∞)上既是奇函数又是减函数,则 g (x)=loga(x﹣k)的图象是________.13. (1 分) 函数 y=的单调递减区间是________.14. (1 分) (2015 高二下·黑龙江期中) 给出下列 5 种说法:①标准差越小,样本数据的波动也越小;②回归分析研究的是两个相关事件的独立性;③在回归分析中,预报变量是由解释变量和随机误差共同确定的;④相关指数 R2 是用来刻画回归效果的,R2 的值越大,说明回归模型的拟合效果越好.⑤对分类变量 X 与 Y 的随机变量 K2 的观测值 k 来说,k 越小,判断“X 与 Y 有关系”的把握越小.其中说法正确的是________(请将正确说法的序号写在横线上).15. (1 分) (2016 高一上·金华期中) 已知 f(x)= =5,则 x=________,则 f[f(1)]=________.如果 f(x)16. (1 分) 已知定义在 R 上的函数 f(x)满足:f(x+1)= (log29)等于________, 当 x∈(0,1]时,f(x)=2x , 则 f三、 解答题 (共 6 题;共 13 分)17. (2 分) (2020 高一上·大庆期末) 若集合 A={x|+1}.}和 B={ x|2m-1≤x≤m(1) 当时,求集合.(2) 当时,求实数 的取值范围.第 4 页 共 20 页18. (2 分) (2016 高三上·闵行期中) 已知函数 f(x)= 方程 f(x)=x 有且仅有一个实数解;(1) 求 a、b 的值;,a,b∈R,a≠0,b≠0,f(1)= ,且(2) 当 x∈( , ]时,不等式(x+1)•f(x)>m(m﹣x)﹣1 恒成立,求实数 m 的范围.19. (2 分) (2020 高一下·郑州期末) 红外线治疗仪的治疗作用是在红外线照射下,组织温度升高,毛细血 管扩张,血流加快,物质代谢增强,组织细胞活力及再生能力提高,对我们身体某些疾病的治疗有着很大的贡献, 某药店兼营某种红外线治疗仪,经过近 5 个月的营销,对销售状况进行相关数据分析,发现月销售量与销售价格有 关,其统计数据如下表:每台红外线治疗仪的销售价格: 元140 150 160 170 180红外线治疗仪的月销售量: 台6455453526参考公式:回归直线方程,,.(1) 根据表中数据求 关于 的线性回归方程;(2) ①每台红外线治疗仪的价格为元时,预测红外线治疗仪的月销售量;(四舍五入为整数)②若该红外线治疗仪的成本为元/台,药店为使每月获得最大的纯收益,利用(1)中结论,问每台该种红外线治疗仪的销售价格应定为多少元?(四舍五入,精确到 元).20. (3 分) (2019 高一下·桦甸期末) 已知,函数,.(1) 若在上单调递增,求正数 b 的最大值;(2) 若函数在内恰有一个零点,求 a 的取值范围.21. (1 分) (2016 高一上·荆门期末) 近几年,由于环境的污染,雾霾越来越严重,某环保公司销售一种 PM2.5第 5 页 共 20 页颗粒物防护口罩深受市民欢迎.已知这种口罩的进价为 40 元,经销过程中测出年销售量 y(万件)与销售单价 x(元) 存在如图所示的一次函数关系,每年销售这种口罩的总开支 z(万元)(不含进价)与年销量 y(万件)存在函数关 系 z=10y+42.5.(I)求 y 关于 x 的函数关系; (II)写出该公司销售这种口罩年获利 W(万元)关于销售单价 x(元)的函数关系式 (年获利=年销售总金额﹣年销售口罩的总进价﹣年总开支金额);当销售单价 x 为何值时,年获利最大?最大 获利是多少? (III)若公司希望该口罩一年的销售获利不低于 57.5 万元,则该公司这种口罩的销售单价应定在什么范围? 在此条件下要使口罩的销售量最大,你认为销售单价应定为多少元?22. (3 分) (2016 高一上·杭州期中) 已知函数 f(x)=a﹣ (1) 判断函数 f(x)的单调性并给出证明;(a∈R)(2) 若函数 f(x)是奇函数,则 f(x)≥ 当 x∈[1,2]时恒成立,求 m 的最大值.第 6 页 共 20 页一、 单选题 (共 8 题;共 8 分)答案:1-1、 考点:参考答案解析: 答案:2-1、 考点: 解析:答案:3-1、 考点: 解析:第 7 页 共 20 页答案:4-1、 考点: 解析:答案:5-1、 考点:第 8 页 共 20 页解析: 答案:6-1、 考点:解析: 答案:7-1、 考点:第 9 页 共 20 页解析: 答案:8-1、 考点: 解析:二、 填空题 (共 8 题;共 8 分)答案:9-1、第 10 页 共 20 页考点:解析:答案:10-1、考点:解析:答案:11-1、考点:解析:答案:12-1、考点:解析:答案:13-1、考点:解析:答案:14-1、考点:解析:答案:15-1、考点:解析:答案:16-1、考点:解析:三、解答题 (共6题;共13分)答案:17-1、答案:17-2、考点:解析:答案:18-1、答案:18-2、考点:解析:答案:19-1、答案:19-2、考点:解析:答案:20-1、答案:20-2、考点:解析:答案:21-1、考点:解析:答案:22-1、答案:22-2、考点:解析:。
云南省2021年高一上学期数学期中考试试卷A卷

云南省2021年高一上学期数学期中考试试卷A卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分) (2019高三上·城关期中) 若集合,,则()A .B .C .D .2. (2分)下列四组函数中,表示相等函数的一组是()A .B .C .D . ,3. (2分) (2019高一上·青冈期中) 已知函数=,则的值是()A . 2B . -1C . 0D . -24. (2分)函数y=2sinπx﹣(﹣2≤x≤4)的所有零点之和为()A . 2B . 4C . 6D . 85. (2分) (2019高三上·洛阳期中) 已知,,,则、、的大小关系是()A .B .C .D .6. (2分) (2018高一上·宝坻月考) 已知函数在上单调递增,则()A .B .C .D .7. (2分) (2017高一上·肇庆期末) 函数y=logax(a>0且a≠1)的图象经过点,函数y=bx (b>0且b≠1)的图象经过点,则下列关系式中正确的是()A . a2>b2B . 2a>2bC .D . (a >b )8. (2分)某部队练习发射炮弹,炮弹的高度h与时间t的函数关系式是h(t)=﹣4.9t2+14.7t+18,则炮弹在发射几秒后最高呢?()A . 1.3秒B . 1.4秒C . 1.5秒D . 1.6秒9. (2分) f()是定义在区间[-c,c]上的奇函数,其图象如图所示:令g()=af()+b,则下列关于函数g()的叙述正确的是()A . 若a<0,则函数g()的图象关于原点对称.B . 若a=-1,-2<b<0,则方程g()=0有大于2的实根.C . 若a≠0,b=2,则方程g()=0有两个实根.D . 若a≥1,b<2,则方程g()=0有三个实根10. (2分) (2019高一上·台州月考) 函数的单调递减区间为()A .B .C .D .11. (2分)函数的单调递增区间是()A .B .C .D .12. (2分)我国的人口普查每十年进行一次,在第五次(2000年11月1日开始)人口普查时我国人口约为13亿,并发现我国人口的年平均增长率约为1%,如果按照这种速度增长,在我国开始第七次(2020年11月1日开始)普查时的人口数约为()亿.A . 13(1+20×1%)B . 13(1+19×1%)C . 13(1+1%)20D . 13(1+1%)19二、填空题 (共4题;共4分)13. (1分) (2019高一上·昌吉期中) 已知函数,则的值是________.14. (1分) (2020高二下·宝坻月考) 函数的定义域为________.15. (1分)(2020·苏州模拟) 己知正实数满足,则的最小值为________.16. (1分)已知增函数f(x)=x3+bx+c,x∈[﹣1,1],且,则f(x)的零点的个数为________三、解答题 (共4题;共32分)17. (10分)计算:(1);(2).18. (10分) (2018高一上·武汉月考) 已知函数 .(I)求,的值;(II)求;(III)若,求 .19. (2分)已知函数f(x)=log3(3+x)+log3(3﹣x).(1)求函数f(x)的定义域和值域;(2)判断函数f(x)的奇偶性,并说明理由.20. (10分) (2015高一上·柳州期末) 设函数f(x)=kax﹣a﹣x(a>0且a≠1)是定义域R上的奇函数.(1)若f(1)>0,试求不等式f(x2+2x)+f(x﹣4)>0的解集;(2)若f(1)= ,且g(x)=a2x+a﹣2x﹣4f(x),求g(x)在[1,+∞)上的最小值.参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共4题;共32分) 17-1、17-2、18-1、19-1、19-2、20-1、20-2、。
云南省2020年高一上学期数学期中考试试卷(I)卷

云南省2020年高一上学期数学期中考试试卷(I)卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分) (2018高二上·会宁月考) 已知集合,,则的真子集的个数为()A . 3B . 4C . 7D . 82. (2分) (2017高二下·淄川期中) 命题“对任意x∈R,都有x2≥0”的否定为()A . 存在x0∈R,使得x02<0B . 对任意x∈R,使得x2<0C . 存在x0∈R,都有D . 不存在x∈R,使得x2<03. (2分) (2015九上·沂水期末) 已知函数在上是单调函数,且满足对任意,都有,则的值是()A . 85B . 82C . 80D . 764. (2分) (2016高一上·邹平期中) 使函数y=xα的定义域为R且为奇函数的α的值为()A . ﹣1C .D . 35. (2分) (2015高一下·凯里开学考) 函数f(x)=2x+3,则f(﹣1)=()A . 2B . 1C .D .6. (2分) (2020高一下·杭州期中) 已知函数的图象过点,令, .记数列的前n项和为,则()A .B .C .D .7. (2分) (2018高一上·太原期中) 已知全集,集合和关系的韦恩图如图所示,则阴影部分所示集合中的元素共有()A . 3个C . 5个D . 无穷多个8. (2分) (2019高一上·温州期中) 下面各组函数中表示同一个函数的是()A . ,B . ,C . ,D . ,9. (2分) (2020高一上·滨州期中) 下列结论正确的是()A . 若,,则B . 若,则C . 若,,则D . 若,,则10. (2分)设则().A . c<b<aB . a<b<cC . c<a<bD . a<c<b11. (2分)已知函数f(x)=log2(x2﹣ax+3a)在[2,+∞)上是增函数,则a的取值范围是()A . (﹣∞,4]B . (﹣∞,2]C . (﹣4,4]D . (﹣4,2]12. (2分)设是连续的偶函数,且当时是单调函数,则满足的所有x之和为()A .B . 3C . -8D . 8二、填空题 (共4题;共4分)13. (1分) (2020高一上·郑州期中) 已知集合,,若,则 ________.14. (1分) (2017高一上·萧山期中) 若函数f(x)= 在(﹣1,+∞)上的值域为________.15. (1分) (2019高三上·苏州月考) 已知,且,则的最小值为________.16. (1分) (2015高三上·泰州期中) 设x∈R,则“|x﹣2|<1”是“x2+x﹣2>0”的________条件.(填充分不必要、必要不充分、充要条件、既不充分也不必要)三、解答题 (共4题;共40分)17. (10分) (2018高一上·浙江期中) 已知函数.(1)判断并证明在上的单调性;(2)若,求的值域.18. (10分) (2019高二下·上海期末) 若集合具有以下性质:(1)且;(2)若,,则,且当时,,则称集合A为“闭集”.(1)试判断集合是否为“闭集”,请说明理由;(2)设集合是“闭集”,求证:若x,,则;(3)若集合是一个“闭集”,试判断命题“若,,则”的真假,并说明理由.19. (10分) (2016高一上·余杭期末) 如图,正方形ABCD的边长为1,P,Q分别为AB,DA上动点,且△APQ 的周长为2,设 AP=x,AQ=y.(1)求x,y之间的函数关系式y=f(x);(2)判断∠PCQ的大小是否为定值?并说明理由;(3)设△PCQ的面积分别为S,求S的最小值.20. (10分)已知二次函数f(x)满足f(x+1)﹣f(x)=2x+3,且f(0)=2.(1)求函数f(x)的解析式;(2)求f(x)在[﹣3,2)上的值域.参考答案一、单选题 (共12题;共24分)答案:1-1、考点:解析:答案:2-1、考点:解析:答案:3-1、考点:解析:考点:解析:答案:5-1、考点:解析:答案:6-1、考点:解析:考点:解析:答案:8-1、考点:解析:答案:9-1、考点:解析:答案:10-1、考点:解析:答案:11-1、考点:解析:答案:12-1、考点:解析:二、填空题 (共4题;共4分)答案:13-1、考点:解析:答案:14-1、考点:解析:答案:15-1、考点:解析:答案:16-1、考点:解析:三、解答题 (共4题;共40分)答案:17-1、答案:17-2、考点:解析:答案:18-1、答案:18-2、答案:18-3、考点:解析:答案:19-1、答案:19-2、答案:19-3、考点:解析:答案:20-1、答案:20-2、考点:解析:。
云南省迪庆州香格里拉中学2023届数学高一上期末综合测试试题含解析
C.5D.6
3.已知 , , 是三个不同的平面, 是一条直线,则下列说法正确的是()
A.若 , , ,则
B.若 , ,则
C.若 , ,则
D.若 , , ,则
4.已知幂函数 的图象过点 ,则 的值为
A. B.
C. D.
5.命题“ , ”的否定为
A. , B. ,
C. , D. ,
6.设m,n为两条不同的直线,,为两个不同的平面,则下列结论正确的是()
12.已知函数 ( , )的部分图象如图所示,则 的值为
13.函数 的最小值为______
14.已知集合 , .若 ,则 ___________.
15.若函数 的定义域为 ,则函数 的定义域为______
三、解答题(本大题共6小题.解答应写出文字说明,证明过程或演算步骤.)
16.已知函数 .
(1)当 时,求函数 在区间 上的值域;
A.18B.17
C.15D.13
9.直线 与数 的图像恰有三个公共点,则实数 的取值范围是
A. B.
C. D.
10.已知函数 ,则 ()
A. B.
C. D.1
二、填空题(本大题共5小题,请把答案填在答题卡中相应题中横线上)
11.函数 的部分图像如图所示, 轴,则 _________, _________
【详解】解:因为 ,
所以
,当且仅当 时,等号成立
故函数 的最小值为 .
故答案为:
14、
【解析】根据给定条件可得 ,由此列式计算作答.
【详解】因集合 , ,且 ,于是得 ,即 ,解得 ,
所以 .
故答案为:
15、
【解析】利用 的定义域,求出 的值域,再求x的取值范围.
云南省高一上学期上学期数学期中试试卷
云南省高一上学期上学期数学期中试试卷姓名:________班级:________成绩:________一、 单选题 (共 12 题;共 24 分)1. (2 分) (2020 高二下·浙江期末) 已知集合 A.,A∩B=( )B.C.D. 2. (2 分) 下列函数中,在其定义域内既是奇函数又是增函数的是( ) A. B. C.D. 3. (2 分) (2019 高二下·宁波期中) 已知集合(),全集,则A.B.C.D.第 1 页 共 19 页4.(2 分)(2016 高一下·南安期中) 设[x]表示不超过 x 的最大整数(如[2]=2,定义,,则当时,函数 的值域是( )A.),对于给定的,B.C.D. 5. (2 分) (2019 高一上·温州期中) 下面各组函数中表示同一个函数的是( )A.,B.,C.,D.,6. (2 分) 函数的定义域为( )A.B.C.D.7. (2 分) (2018 高一上·湖南月考) 若函数( 为常数),则()是定义在 上的奇函数,且当A.第 2 页 共 19 页时,B. C. D.8. (2 分) (2019 高一上·遵义期中) 已知函数 根,则实数 的取值范围为( )A. B. C. D. 9. (2 分) 函数 y=lg(x+1)的图象大致是( ),若方程有三个不同的实数A. B. C.D. 10. (2 分) 定义在 R 上的偶函数 满足:对任意第 3 页 共 19 页,且,都有,则( )A. B. C. D. 11. (2 分) (2017 高一上·吉林月考) 若函数 的取值范围是( ) A. B. C. D.的定义域为,值域为,则12. (2 分) (2019 高三上·攀枝花月考) 已知函数 的取值范围是( )A.B.C.D.二、 填空题 (共 4 题;共 4 分)13. (1 分) (2020 高一上·秭归期中) 已知集合 ________.第 4 页 共 19 页,若,,则,,若,则14. (1 分) 已知函数 f(x)=x2﹣kx﹣8 在区间[2,5]上具有单调性,则实数 k 的取值范围是________ 15. (1 分) 不等式 x2﹣x+1<0 的解集为________. 16. (1 分) (2016 高一上·杭州期中) 奇函数 f(x)满足:①f(x)在(0,+∞)内单调递增;②f(1)=0; 则不等式(x﹣1)f(x)>0 的解集为:________三、 解答题 (共 6 题;共 60 分)17. (10 分) (2019 高一上·上海月考) 已知集合,,求 a 的值.18. (10 分) (2018 高一上·盘锦期中) 如图是一个二次函数 y=f(x)的图象,若(1) 写出这个二次函数的零点 (2) 求这个二次函数的解析式 (3) 当实数 k 在何范围内变化时,函数 g(x)=f(x)-kx 在区间[-2,2]上是单调函数?19. (10 分) (2019 高二上·上饶月考) 已知二次函数且.的两个零点为 和 ,(1) 求函数的解析式;(2) 解关于 x 的不等式.20. (15 分) (2019·吉林模拟) 已知函数.第 5 页 共 19 页(1) 讨论函数的单调性;(2) 设函数 件的 最小的整数值.,当时,对任意的恒成立,求满足条21. (5 分) (2016 高一上·平罗期中) 若函数 y=lg(3﹣4x+x2)的定义域为 M.当 x∈M 时,求 f(x)=2x+2 ﹣3×4x 的最值及相应的 x 的值.22. (10 分) (2019·赤峰模拟) 已知函数,其中 为自然对数的底数.(1) 若,判断函数的单调性,并写出证明过程;(2) 若,求证:对任意,都有第 6 页 共 19 页一、 单选题 (共 12 题;共 24 分)答案:1-1、 考点:参考答案解析: 答案:2-1、 考点: 解析:答案:3-1、 考点:解析:第 7 页 共 19 页答案:4-1、 考点: 解析:答案:5-1、 考点:解析: 答案:6-1、 考点: 解析: 答案:7-1、 考点: 解析:第 8 页 共 19 页答案:8-1、 考点: 解析:答案:9-1、 考点:第 9 页 共 19 页解析: 答案:10-1、 考点: 解析:答案:11-1、 考点: 解析:答案:12-1、 考点: 解析:第 10 页 共 19 页二、填空题 (共4题;共4分)答案:13-1、考点:解析:答案:14-1、考点:解析:答案:15-1、考点:解析:答案:16-1、考点:解析:三、解答题 (共6题;共60分)答案:17-1、考点:解析:答案:18-1、答案:18-2、答案:18-3、考点:解析:答案:19-1、答案:19-2、考点:解析:答案:20-1、答案:20-2、考点:解析:答案:21-1、考点:解析:答案:22-1、考点:解析:。
云南省2021年高一上学期期中数学试卷A卷(考试)
云南省2021年高一上学期期中数学试卷A卷姓名:________ 班级:________ 成绩:________一、填空题 (共14题;共14分)1. (1分) (2019高一上·周口期中) 设集合,集合,则________.2. (1分) (2020高一下·太原期中) 若,则该函数定义域为________3. (1分) (2019高一上·江苏月考) 已知函数的图象如图所示,则 ________.4. (1分) (2019高一上·射洪月考) 给出定义:若 (其中为整数),则叫做离实数最近的整数,记作,即 . 在此基础上给出下列关于函数的四个命题:① 的定义域是,值域是;②点是的图象的对称中心,其中;③函数的最小正周期为;④ 函数在上是增函数.则上述命题中真命题的序号是________.5. (1分) (2019高三上·西藏月考) 函数在定义域上单调递增,则a的取值范围是________6. (1分) (2019高一上·成都月考) 已知函数 (其中、是常数),且,则 ________.7. (1分)设方程2x+x=4的根为x0 ,若x0∈(k﹣,k+ ),则整数k=________.8. (1分) (2019高三上·攀枝花月考) 已知幂函数的图象经过点,则________.9. (1分) (2017高一上·舒兰期末) 函数,则 ________.10. (1分) (2017高一上·安庆期末) 如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则的值等于________.11. (1分) =________.12. (1分) (2020高一下·海淀期中) 设函数是定义在上的偶函数,记,且函数在区间上是增函数,则不等式的解集为________13. (1分) (2015高一下·沈阳开学考) 函数y=lg(3﹣4x+x2)的定义域为M,当x∈M时,则f(x)=2x+2﹣3×4x的最大值为________.14. (1分) (2018高一上·黑龙江期中) 已知函数和同时满足以下两个条件:⑴对于任意实数,都有或;⑵总存在,使成立.则实数的取值范围是 ________.二、解答题 (共6题;共55分)15. (10分) (2016高一上·商州期中) 不用计算器求下列各式的值(1)(2 )﹣(﹣9.6)0﹣(3 ) +(1.5)﹣2(2) lg5+lg2﹣(﹣)﹣2+(﹣1)0+log28.16. (5分)已知全集U=R,集合 A={x|﹣3≤x≤5},B={x|x<2m﹣3}.(1)当m=5时,求A∩B,(∁UA)∪B;(2)当 A⊆B时,求m的取值范围.17. (10分) (2019高一上·泸县月考) 如图是边长为2的正三角形,记位于直线左侧的图形的面积为 .(1)试求函数的解析式;(2)画出函数图象.18. (5分) (2017高一上·武汉期末) 现有一圆心角为,半径为12cm的扇形铁皮(如图).P,Q是弧AB上的动点且劣弧的长为2πcm,过P,Q分别作与OA,OB平行或垂直的线,从扇形上裁剪出多边形OHPRQT,将该多边形面积表示为角α的函数,并求出其最大面积是多少?19. (10分) (2019高一上·南京期中) 已知函数,其中且 .(1)求函数的定义域,并判断函数的奇偶性;(2)解关于的不等式 .20. (15分) (2017高一上·钦州港月考) 已知函数对任意实数恒有,且当时,,又 .(1)判断的奇偶性;(2)求证:是R上的减函数;(3)若对一切实数,不等式恒成立,求实数的取值范围.参考答案一、填空题 (共14题;共14分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、二、解答题 (共6题;共55分)15-1、15-2、16-1、17-1、17-2、18-1、19-1、19-2、20-1、20-2、20-3、。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
云南省香格里拉县一中2018-2019学年期中考试
高一数学
本试卷分第Ⅰ卷和第Ⅱ卷两部分,共150分,考试时间120分钟。
学校:___________姓名:___________班级:___________考号:___________
一、选择题(共12小题,每小题5.0分,共60分)
1.设函数f(x)=x2+2(-2≤x<0),其反函数为f-1(x),则f-1(3)等于( )
A.-1 B. 1 C. 0或1 D. 1或-1
2.函数y=的值域是( )
A. (0,1) B. (0,1] C. (0,+∞) D. [0,+∞)
3.等于( )
A. 25 B. C. 5 D.
4.集合A={x∈N|1≤x<4}的真子集的个数是( )
A. 16 B. 8 C. 7 D. 4
5.的值等于( )
A. 3 B. C. D.
6.已知幂函数y=f(x)的图象过点(,),则log2f(2)的值为( )
A. B.- C. 2 D.-2
7.已知集合P={x|y=},集合Q={y|y=},则P与Q的关系是( )
A.P=Q B.P Q C.P Q D.P∩Q=∅
8.集合A={x||x|≤1,x∈R},B={y|y=x2,x∈R},则A∩B为( )
A. {x|-1≤x≤1} B. {x|x≥0}
C. {x|0≤x≤1} D.∅
9.满足{1}∪A={1,5}的集合A的个数是( )
A. 1 B. 2 C. 3 D. 4
10.已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递增.若实数a满足f(log2a)
+f(log a)≤2f(1),则a的取值范围是( )
A. [1,2] B. C. D. (0,2]
11.已知f(x)=3x,x1,x2∈R,则有( )
A.≤f() B.≥f()
C.=f() D.以上都不是
12.函数f(x)=|x|(-)是( )
A.是奇函数又是减函数 B.是奇函数但不是减函数
C.是减函数但不是奇函数 D.不是奇函数也不是减函数
分卷II
二、填空题(共4小题,每小题5.0分,共20分)
13.若幂函数y=(m2+3m+3)的图象不过原点,且关于原点对称,则m=________.
14.设函数y=x2-2x,x∈[-2,a],若函数的最小值为g(a),则g(a)=________.
15.已知集合A={3,4,m},集合B={3,4},若∁A B={5},则实数m=________.
16.已知下列四个条件,其中能够组成集合的是________.
①数轴上到原点距离大于1的点的全体;
②大于10且小于100的全体素数;
③与1非常接近的实数的全体;
④实数中不是无理数的所有数的全体.
三、解答题(共6小题,共70分)
17.判断下列函数的奇偶性.
(1)f(x)=x-2+x2,x∈(-1,0)∪(0,1];
(2)f(x)=.
18.试用描述法表示下列集合.
(1)方程x2-2=0的所有实数根组成的集合;
(2)由大于10小于20的所有整数组成的集合.
19.设集合A={x|x2+bx+c=x},B={x|(x-1)2+b(x-1)+c=x+1},若A={2},求集合B.
20.求下列函数的定义域:
(1)f(x)=;。
