75中高二数学竞赛训练试卷(4)
陕西省西安市第七十五中高二数学5月月考试题 文 新人教A版

参考公式: 《选修4-4》抛物线)0(22>=p px y 的参数方程为⎩⎨⎧==pt y pt x 222(t 为参数)空间点P 的直角坐标(x, y, z)与柱坐标(ρ,θ, z)之间的变换关系为 ⎪⎩⎪⎨⎧===z z y x θρθρsin cos空间点P 的直角坐标(x, y, z)与球坐标(r, ϕ,θ)之间的变换关系为⎪⎪⎩⎪⎪⎨⎧====++ϕθϕθϕcos sin sin cos sin 2222r z r y r x r z y x一、选择题:本大题共12小题,每小题4分,共48分. 在每小题给出的四个选项中,只有一项是符合题目要求的 1. 已知极坐标,5(-M),3π 下列所给出的不能表示点的坐标的是A .,5( )3π-B .,5()34π C .,5( )32π- D .,5(- )35π-2.已知点,1(P ),3- 则它的极坐标是 A .,2()3π B .,2( )34π C .,2( )3π- D .,2( )34π- 3. 把点M 的直角坐标(-1, 1, 1)化为柱坐标是 A. ,2( ,43π )1 B. ,2( ,34π )1C. ,2(,4π )1 D. ,2(- ,4π )14. 曲线⎪⎩⎪⎨⎧+-=++-=λλλλ11132y x (λ为参数)与y 坐标轴的交点是 A .,0( )52 B .,0( )51 C .,0( )4- D .,0( )95 5.若直线的参数方程为⎩⎨⎧-=+=t y tx 3221 (t 为参数),则直线的斜率为A .32 B .32- C .23 D .23-6. 直线:3x-4y-9=0与圆:⎩⎨⎧==θθsin 2cos 2y x (θ为参数)的位置关系是A. 相切B. 相离C. 相交D.相交且过圆心7.《11年陕西高考题(改编)》 设抛物线的顶点在原点,准线方程为2x =-,则抛物线的的参数方程是A. ⎩⎨⎧-=-=t y t x 442B. ⎩⎨⎧==t y t x 442C. ⎩⎨⎧-=-=t y t x 882 D. ⎩⎨⎧==t y t x 8828. 极坐标方程1cos =θρ和θρcos =所表示的图形分别是A .圆、圆B .直线、直线C .圆、直线D .直线、圆 9.下列在曲线⎩⎨⎧+==θθθcos sin 2sin y x (θ为参数)上的点是A .,43(- )21B .,21( )2- C .,1( )3 D .,2( )3 10. 圆)sin (cos 2θθρ+=的圆心坐标是A .,1()4π B .,21( )4π C .,2( )4π D .,2( )4π11.在极坐标系中与圆4sin ρθ=相切的一条直线的方程为A .cos 2ρθ=B .sin 2ρθ=C .4sin()3πρθ=+D .4sin()3πρθ=- 12. 参数方程⎪⎩⎪⎨⎧+=+=2211t t y t t x (t 为参数)所表示的曲线是 A. 抛物线 B. 一条直线 C. 两条射线 D.两条曲线 二、填空题:本大题共4小题,每小题5分,共20分13. 把点M 的球坐标,8( ,3π )6π化为直角坐标为__________ 14.《12年陕西高考题》 直线2cos 1ρθ=与圆2cos ρθ=相交的弦长为 _______15. 两直线,2012)4sin(=+πθρ 2013)4cos(=-πθρ的位置关系是________16. 设t y x =+(t 为参数), 则双曲线 422=-y x 的参数方程为_________ 三、解答题:本大题共4小题,共32分,解答写出文字说明或演算步骤 17.(本小题满分8分)已知直线l 过点P(1,0),倾斜角为,3π (1) 求直线l 的参数方程 (2) 求直线l 被双曲线122=-y x 截得的弦长 18.(本小题满分8分)已知x 、y 满足圆C 的极坐标方程 θθρsin 4cos 2-= (1) 求圆C 的参数方程 (2) 求x y S 34-=的最大值 19.(本小题满分8分)已知直线1l 的参数方程为⎪⎩⎪⎨⎧+-=+-=t y tx 2223223 (t 是参数), 直线2l 的极坐标方程为06)cos sin 2(=++θθρ(1) 求直线1l 与直线2l 的交点P 的坐标 (2) 若直线l 过点P , 且与圆:C ⎩⎨⎧==θθsin 5cos 5y x (θ为参数)相交于A 、B 两点,,8||=AB 求直线l 的方程20.(本小题满分8分) 12年陕西高考题(改编)已知椭圆:1C ⎩⎨⎧==θθsin cos 2y x (θ为参数), 椭圆2C 以1C 的长轴为短轴, 且与1C 有相同的离心率(1)求椭圆2C 的普通方程(2)设O 为坐标原点,点A ,B 分别在椭圆1C 和2C 上,,2= 求直线AB 的方程. 《用参数方程的知识求解》数学试题参考答案一、选择题(本大题共12题.每小题4分,共48分)1. D2. C3. A4. B5. D6. C7.D8. D9. A 10. A 11. A 12. D二、填空题(本大题共4小题.每小题5分.共20分)13. (6, ,32 4) 14. 3 15. 平行 16. ⎪⎩⎪⎨⎧-=+=)4(21)4(21t t y t t x 三、解答题 (本大题共4小题.共32分) 17.(本小题8分)(1)直线l 的参数方程⎪⎩⎪⎨⎧=+=3sin 3cos 1ππt y t x ⎪⎩⎪⎨⎧=+=∴t y t x 23211 (2)1)23()211(22=-+t t 022=-∴t t 2,021==∴t t )3,2(),0,1(B A ∴ 2||=∴AB18.(本小题满分8分)(1) θθρsin 4cos 2-= 5)2()1(22=++-∴y x 参数方程⎩⎨⎧+-=+=θθsin 52cos 51y x(2) )sin(5511cos 53sin 541134ϕθθθ-+-=-+-=-=∴x y S )53sin 54cos (⎪⎩⎪⎨⎧==ϕϕ1155max -=∴S19.(本小题满分8分)(1) 直线2l 的普通方程为062=++x y直线1l 的参数方程为⎪⎩⎪⎨⎧+-=+-=ty t x 2223223 06)223()23(=++-++-∴t t 0=∴t ⎪⎩⎪⎨⎧-=-=∴233y x )23,3(--∴P (2) 由圆C 的参数方程225cos 255sin x x y y θθ=⎧⇒+=⎨=⎩,设直线l 的参数方程为①3cos ()3sin 2x t t y t αα=-+⎧⎪⎨=-+⎪⎩为参数,①代入圆的方程2225x y += 得2412(2cos sin )550t t αα-+-=,∴△216[9(2cos sin )55]0αα=++>,所以方程有两相异实数根1t 、2t,∴12||||8AB t t =-==, 化简有23cos 4sin cos 0ααα+=,解之cos 0α=或3tan 4α=-, 从而求出直线l 的方程为30x +=或34150x y ++=20.(本小题满分8分)(1)椭圆:1C ⎩⎨⎧==θθsin cos 2y x (θ为参数) 的普通方程为1422=+y x由椭圆2C 以1C 的长轴为短轴,设椭圆2C 的普通方程为14222=+x ay4144222-=-=a a e 162=∴a 椭圆2C 的普通方程为141622=+x y(2) 椭圆,1C 2C 的参数方程为⎩⎨⎧==θθsin cos 2y x , ⎩⎨⎧==ϕϕsin 4cos 2y x)sin 4,cos 2(),sin ,cos 2(ϕϕθθB A ∴,2= )sin ,cos 2(2)sin 4,cos 2(θθϕϕ=∴ ⎩⎨⎧==∴θϕθϕsin sin 4cos 4cos 21)sin 4()2cos (22=+∴ϕϕ 51sin 2=∴ϕ 21tan ±=∴ϕ直线AB 的方程为 x x y ±==ϕϕcos 2sin 4。
2019年湖北省武汉市第七十五中学高二数学文联考试题含解析

2019年湖北省武汉市第七十五中学高二数学文联考试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 命题:“?x∈R,x2+x﹣1>0”的否定为()A.?x∈R,x2+x﹣1<0 B.?x∈R,x2+x﹣1≤0C.?x?R,x2+x﹣1=0 D.?x∈R,x2+x﹣1≤0参考答案:B【考点】命题的否定.【专题】简易逻辑.【分析】根据特称命题的否定是全称命题.即可得到结论.【解答】解:根据特称命题的否定是全称命题.得命题的否定是:?x∈R,x2+x﹣1≤0,故选:B【点评】本题主要考查含有量词的命题的否定,根据特称命题的否定是全称命题.即可得到结论.2. 如果椭圆的弦被点(4,2)平分,则这条弦所在的直线方程是 ( )A. B. C. D.参考答案:D3. 在正方体ABCD﹣A1B1C1D1中,E,F分别为CC1和BB1的中点,则异面直线AE与D1F所成角的余弦值为()A.0 B.C.D.参考答案:D【考点】异面直线及其所成的角.【分析】以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出直线AE与D1F所成角的余弦值.【解答】解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,设正方体ABCD﹣A1B1C1D1中棱长为2,则A(2,0,0),E(0,2,1),D1(0,0,2),F(2,2,1),=(﹣2,2,1),=(2,2,﹣1),设直线AE与D1F所成角为θ,则cosθ=||=.∴直线AE与D1F所成角的余弦值为.故选D.4. 若是等差数列,公差,成等比数列,则公比为()(A)1 (B)2 (C)3(D)4参考答案:C5. 假设有两个变量与的列联表如下表:对于以下数据,对同一样本能说明x与y有关系的可能性最大的一组为()A. ,,,B. ,,,C. ,,,D. ,,,参考答案:B【分析】当ad与bc差距越大,两个变量有关的可能性就越大,检验四个选项中所给的ad与bc的差距,只有第二个选项差距大,得到结果.【详解】解:根据观测值求解的公式可以知道,当ad与bc差距越大,两个变量有关的可能性就越大,检验四个选项中所给的ad与bc的差距:显然中最大. 故答案为B.【点睛】本题考查独立性检验,得出ad与bc差距越大,两个变量有关的可能性就越大是解决问题的关键,属基础题.6. 按如图所示的程序框图,在运行后输出的结果为A.36B.45C.55D.56参考答案:C7. 已知复数z满足(i为虚数单位),其中是z的共轭复数,,则复数z的虚部为()A.±2 B.±2i C.2 D.2i参考答案:A设,的共轭复数是,又,,又,,.8. (x2﹣x+y)5的展开式中,x4y3的系数为()A.8 B.9 C.10 D.12参考答案:C【考点】DB:二项式系数的性质.【分析】由题意,由题意,含y3的为C53(x2﹣x)2y3,而(x2﹣x)2含x4的系数为1,即可得出结论.【解答】解:由题意,含y3的为C53(x2﹣x)2y3,而(x2﹣x)2含x4的系数为1∴x4y3的系数为C53=10.故选:C【点评】本题考查乘法原理的运用,考查学生的计算能力,比较基础.9. 在△ABC中,已知3b=2asin B,且cos B=cos C,角A是锐角,则△ABC的形状是( )A.直角三角形B.等腰三角形C.等腰直角三角形D.等边三角形参考答案:D10. 如果点P在以F为焦点的抛物线x2=2y上,且∠POF=60o(O为原点),那么△POF的面积是().A.B.C.D.参考答案:C略二、填空题:本大题共7小题,每小题4分,共28分11. 在△ABC中,角A,B,C的对边分别是a,b,c,,△ABC的面积为,则△ABC的最大角的正切值是______.参考答案:或-试题分析:由题意得,由余弦定理得:,因此B角最大,考点:正余弦定理【名师点睛】1.正弦定理可以处理①已知两角和任一边,求另一角和其他两条边;②已知两边和其中一边的对角,求另一边和其他两角.余弦定理可以处理①已知三边,求各角;②已知两边和它们的夹角,求第三边和其他两个角.其中已知两边及其一边的对角,既可以用正弦定理求解也可以用余弦定理求解.2.利用正、余弦定理解三角形其关键是运用两个定理实现边角互化,从而达到知三求三的目的.12. 在△ABC中,内角A,B,C所对应的边分别是a,b,c,若c2=(a﹣b)2+6,C=,则△ABC的面积是.参考答案:【考点】余弦定理;正弦定理.【分析】利用余弦定理,结合c2=(a﹣b)2+6,C=,求出ab=6,利用S△ABC=absinC,求出△ABC的面积.【解答】解:由c2=(a﹣b)2+6,可得c2=a2+b2﹣2ab+6,由余弦定理:c2=a2+b2﹣2abcosC=a2+b2﹣ab=a2+b2﹣ab,所以:a2+b2﹣2ab+6=a2+b2﹣ab,所以ab=6;所以S△ABC=absinC=×6×=.故答案为:.13. 在二项式的展开式中,系数最大项的项数为第________项.参考答案:7【分析】利用二项式展开式的通项公式,求得展开式中数最大项的项数.【详解】二项式的展开式的通项公式为,各项的系数为,由于题目要求系数最大项的项数,所以为偶数.故,对应的系数为,根据的单调性可知,或时,最大,故最大的项的系数为,对应为第项.故答案为:【点睛】本小题主要考查二项式展开式的通项公式的运用,属于基础题.14. 若两个球的表面积之比是4∶9,则它们的体积之比是。
2021-2022年高二数学竞赛试卷含答案

13.(本小题满分 20 分)
已知椭圆的中心在坐标原点,左顶点,离心率,为右焦点,过焦点的直线交椭圆于、两点(不
同于点).
(Ⅰ)求椭圆的方程;
(Ⅱ)当时,求直线 PQ 的方程;
(Ⅲ)判断能否成为等边三角形,并说明理由.
13.解:(Ⅰ)设椭圆方程为 (a>b>0) ,
由已知
∴
-----------------------------------------2 分
)(
x0
2
x1
)
x02
x1
( x02
1)2 4
x02
∵,∴ .解得.
∴直线 PQ 方程为,即或. ----------12 分
解法二: 椭圆右焦点.当直线的斜率不存在时,,不合题意.
设直线方程为,
--------------------------------------5 分
由 得 3 4k 2 x2 8k 2x 4k 2 12 0 . ①
.
3.定义两种运算:,,则函数为( )
(A)奇函数 (C)奇函数且为偶函数
(B)偶函数 (D)非奇函数且非偶函数
3.A. f (x) 22 x2 22 x2 22 x2 (x [2, 2]) .
(2 x)2 2 | 2 x | 2
x
4.圆周上按顺时针方向标有 1,2,3,4,5 五个点,一只青蛙按顺时针方向绕圆从一个点跳
∴ 5 x 2 ( y 1) 2 其表示双曲线上一点(x,y)到定点(0,-1)与定直线 x-2y+3=0 之比为常数 e=, m | x2y3| 5
又由 e>1,可得 0<m<5.
7.直线 ax+by-1=0(a,b 不全为 0),与圆 x2+y2=50 有公共点,且公共点的横、纵坐标均为整数,
高二数学竞赛试题及答案

高二数学竞赛试题及答案一、选择题(每题5分,共30分)1. 若函数\( f(x) = 2x^2 - 3x + 5 \),则\( f(-1) \)的值为多少?A. 12B. 10C. 8D. 62. 已知圆的半径为5,圆心在原点,求圆上一点到原点的距离最远是多少?A. 10B. 5C. 15D. 203. 一个等差数列的前三项分别为2,5,8,求这个数列的第20项是多少?A. 47B. 49C. 52D. 554. 一个直角三角形的两条直角边分别为3和4,求斜边的长度?A. 5B. 6C. 7D. 85. 已知\( \sin(\alpha) = \frac{3}{5} \),求\( \cos(\alpha) \)的值(假设\( \alpha \)在第一象限)?A. \( \frac{4}{5} \)B. \( -\frac{4}{5} \)C. \( \frac{3}{5} \)D. \( -\frac{3}{5} \)6. 一个函数\( g(x) \)满足\( g(x) = x^2 + 2x + 3 \),求\( g(-1) \)的值?A. 1B. 3C. 5D. 7二、填空题(每题5分,共20分)7. 已知\( a \)和\( b \)是方程\( x^2 + 5x + 6 = 0 \)的根,求\( a + b \)的值。
______(答案:-5)8. 一个数列的前五项为1, 1, 2, 3, 5,这个数列是斐波那契数列,求第10项的值。
______(答案:55)9. 已知三角形的三边长分别为3, 4, 5,求这个三角形的面积。
______(答案:6)10. 已知\( \tan(\beta) = 2 \),求\( \sin(\beta) \)的值。
______(答案:\( \frac{2\sqrt{5}}{5} \))三、解答题(每题25分,共50分)11. 证明:对于任意实数\( x \),不等式\( e^x \ge x + 1 \)恒成立。
遵义数学竞赛高二试题及答案

遵义数学竞赛高二试题及答案一、选择题(每题5分,共20分)1. 已知函数\( f(x) = x^2 - 4x + 4 \),求\( f(1) \)的值。
A. 1B. -1C. 3D. 52. 若\( a \),\( b \),\( c \)是三角形的三边长,且满足\( a^2 + b^2 = c^2 \),该三角形是:A. 直角三角形B. 等边三角形C. 等腰三角形D. 钝角三角形3. 已知圆的半径为5,圆心到直线的距离为3,则直线与圆的位置关系是:A. 相切B. 相交C. 相离D. 包含4. 若\( \sin(\alpha + \beta) = \sin\alpha \),且\( \alpha \)和\( \beta \)均不为0,求\( \beta \)的值。
A. \( \frac{\pi}{2} \)B. \( -\frac{\pi}{2} \)C.\( \frac{\pi}{4} \) D. \( -\frac{\pi}{4} \)二、填空题(每题4分,共16分)5. 若\( \cos(\theta) = \frac{1}{3} \),求\( \sin(\theta) \)的值(结果保留根号)。
6. 将\( 8^3 \)写成\( 2 \)的幂次形式。
7. 已知等差数列的首项为2,公差为3,求第10项的值。
8. 已知\( \log_{10} 100 = 2 \),求\( \log_{10} 0.01 \)的值。
三、解答题(每题14分,共40分)9. 证明:若\( a \),\( b \),\( c \)是正数,且\( a + b + c =1 \),则\( \frac{1}{a} + \frac{1}{b} + \frac{1}{c} \geq 9 \)。
10. 解不等式:\( |x - 2| + |x + 3| > 4 \)。
11. 已知点A(-1, 2),B(2, -1),C(3, 6),求三角形ABC的面积。
高二数学竞赛试卷
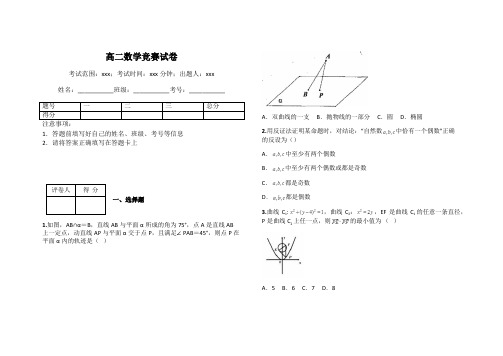
高二数学竞赛试卷考试范围:xxx ;考试时间:xxx 分钟;出题人:xxx 姓名:___________班级:___________考号:___________1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上一、选择题1.如图,AB∩α=B ,直线AB 与平面α所成的角为75°,点A 是直线AB 上一定点,动直线AP 与平面α交于点P ,且满足∠PAB =45°,则点P 在平面α内的轨迹是( )A .双曲线的一支B .抛物线的一部分C .圆 D.椭圆 2.用反证法证明某命题时,对结论:“自然数中恰有一个偶数”正确的反设为()A .中至少有两个偶数B .中至少有两个偶数或都是奇数 C .都是奇数 D .都是偶数3.曲线C 1:,曲线C 2:,EF 是曲线C 1的任意一条直径,P 是曲线C 2上任一点,则·的最小值为 ( )A .5B .6C .7D .84.如果方程表示焦点在轴上的椭圆,则的取值范围是( ) ABC D5.在直四棱柱ABCD —A 1B 1C 1D 1中,底面是有一个角为的菱形,AA 1 = AB ,从顶点中取出三个能构成不同直角三角形的个数有( )个A .48B .40C .24D .166.若椭圆两准线间的距离是焦距的4倍,则该椭圆的离心率为( ) A . B . C . D .7.奇函数上的解析式是的函数解析式是( ) A .B .C .D .8.已知,则( )A .B .C .D .9.椭圆的焦点坐标是( ). A .B .C .D .10.用反证法证明某命题时,对结论:“自然数中恰有一个偶数”正确的反设为( ) A .都是奇数 B .都是偶数 C .中至少有两个偶数D .中至少有两个偶数或都是奇数11.已知(1+x)10=a 0+a 1(1-x)+a 2(1-x)2+…+a 10(1-x)10,则a 8=( ) A .180 B .90 C .-5 D .5 12.命题“若,则”以及它的逆命题、否命题、逆否命题中,假命题的个数为( )A .1B .2C .3D .4 13.若点在平面内,且满足(点为空间任意一点),则抛物线的准线方程是( ) A .B .C .D .14.运行如图所示的程序框图.若输入,则输出的值为( )A .49B .25C .13D .7 15.已知函数,若存在,使得不等式成立,则实数的最小值是( )A .3B .C .2D .16.如图,从点发出的光线,沿平行于抛物线的对称轴方向射向此抛物线上的点,经抛物线反射后,穿过焦点射向抛物线上的点,再经抛物线反射后射向直线上的点,经直线反射后又回到点,则等于( )A .B .C .D .17.已知两圆的圆心距=" 3" ,两圆的半径分别为方程的两根,则两圆的位置关系是( )A .相交B .相离C .相切D .内含18.已知是三条不重合的直线,是三个不重合的平面,给出下列四个命题: ①若②若直线与平面所成的角相等,则//;③存在异面直线,使得//,// ,//,则//;④若,则;其中正确命题的个数是 A .1 B .2 C .3 D .419.设点P 是直线L 外一点,过P 与直线L 成600角的直线有( ) A .一条 B .两条 C .无数条 D .以上都不对20.正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积是 A .9 B .16 C . D .二、填空题21.在极坐标系下,点到直线的距离为 .22.在区间(0,1)中随机地取出两个数,则两数之和小于的概率是__________. 23.中,角的对边分别为,下列四个论断正确的是__________.(把你认为正确论断的序号都写上)①若,则;②若,,,则满足条件的三角形共有两个;③若成等差数列,成等比数列,则为正三角形;④若,,的面积,则.24.某市有一个玉米种植基地.该基地的技术员通过种植实验发现,一种品质优良的玉米种子每粒发芽的概率都为0.95,现在该种植基地播种了10000粒这种玉米种子,对于没有发芽的种子,每粒需再播种1粒,补种的种子数记为,则的数学期望 .25.已知x 和y 满足约束条件则的取值范围为 。
高二下册数学竞赛试题
高二试题一. 填空题:共8道小题,每小题8分,共64分.将每小题的答案填在题后的横线上.1.已知函数2221(),1x x f x x ++=+若3()4f a =,则()f a -=_________. 2.甲、乙、丙三人进行羽毛球比赛,每局两人进行单打比赛,另外一个人当裁判,若干局后比赛结束,经统计,甲共打了7局,且当了3局裁判,乙共打了5局,则丙所打局数为_________.3.若函数()cos 2cos f x x a x =+在区间63ππ(,)是减函数,则a 的取值范围是_________.4.在△ABC 中,D 为边BC 的中点,动点E 在线段AD 上移动时,若BE BA BCλμ=+,则2s λμ=+的最小值是_________. 5.已知某函数的图象'C 与21:1ax a C y x a ++=+-关于直线y x =对称,且图象'C 关于点(3,2)-对称,则实数a 的值为_________.6.函数x x x f -+-=363)(的值域是__________.7.实数,x y 满足223,x y xy ++=则22x y +的取值范围是_________.8.数列{}n a 满足113a =,且对于任意21,,n n n n N a a a +∈*=+则2016111n na =+∑的整数部分是_________.二.解答题:共6道小题,共86分.解答应写出文字说明、证明过程或演算步骤. 9. (本题满分14分)已知2sin 3(sin )sin x f x x=(1)求()f x 解析式及定义域;(2)方程()f x m =有两个不等实根,求m 的取值范围。
10.(本题满分14分)函数()f x 对任意,a b R ∈,都有()()()1f a b f a f b +=+-,且当0x >时,() 1.f x >(1)判断并证明()f x 在R 上的单调性;(2)若(2)2f =,解不等式2(2) 5.f m m -<11.(满分14分)已知a 为实数,函数2()21f x ax x a =-++在区间[1,1]-有零点,求a 的取值范围。
高二数学竞赛试卷
高二数学竞赛试卷考试范围:xxx ;考试时间:xxx 分钟;出题人:xxx 姓名:___________班级:___________考号:___________1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上一、选择题1.已知长方体中,,E 、F 分别为和AD 的中点,则异面直线、EF 所成的角为( ) A . B .C .D .2.曲线在点处的切线方程为( )A .B .C .D .3.设则等于( )A .B .C .D .4.点(2,1)到直线3x ﹣4y+2=0的距离是( ) A . B . C . D .5.已知是实数,则“且”是“”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件6.曲线与坐标周围成的面积( )A . 4B . 2C .3D .7.复数z 满足·(1+2i )=4+3i ,则z 等于 ( ) A .B .C .1+2iD .8.双曲线(a>0,b>0)的离心率是,则的最小值为()A. B.1 C.2 D.9.下列四个命题中,为真命题的是()①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;③垂直于同一直线的两条直线相互平行;④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.A.①和② B.②和③ C.③和④ D.②和④10.如图,,是双曲线的左、右两个焦点,若直线与双曲线交于,两点,且四边形为矩形,则双曲线的离心率为()A. B. C. D.11.设,若,则()A. B. C. D.12.各项均为正数的等比数列的前项和为,若, 则()A. B. C. D.13.不等式的解集是()A.B.C.D.14.篮子里装有2个红球,3个白球和4个黑球.某人从篮子中随机取出两个球,记事件“取出的两个球颜色不同”,事件“取出一个红球,一个白球”,则()A. B. C. D.15.下列说法错误的是( )A.“”是“方程表示双曲线”的充分不必要条件B.命题“若,则”的否命题是:“若,则”C.若命题p:存在,则命题p的否定:对任意D.若命题“非p”与命题“p或q”都是真命题,那么命题q一定是真命题16.等差数列{an }的公差d<0,且a=a,则数列{an}的前n项和Sn取最大值时的项数n是()A.5 B.6 C.5或6 D.6或717.若,则下列不等式成立的是()A. B. C. D.18.已知圆,圆上到直线距离为1的点有()个A.4 B.3 C.2 D.119.已知M={x|x2-2x-3>0}N={x|x2+ax+b≤0},若M∪N=R,M∩N=,,则a+b=()A.—7 B.-1 C.1 D.720.(本小题满分12分)NBA总决赛采用“7场4胜制”,由于NBA有特殊的政策和规则,能进入决赛的球队实力都较强,因此可以认为,两个队在每一场比赛中取胜的概率相等。
2021年陕西省西安市第七十五中学高二数学文下学期期末试卷含解析
2021年陕西省西安市第七十五中学高二数学文下学期期末试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知是偶函数,当时,;若当时,恒成立,则的最小值为()A.1 B. C. D.参考答案:A2. 某射手在一次射击中,射中10环,9环,8环的概率分别是0.20,0.30,0.10,则该射手在一次射击中不够8环的概率为()A.0.90 B.0.30 C.0.60 D.0.40参考答案:D【考点】C5:互斥事件的概率加法公式.【分析】由题意知射手在一次射击中不够8环的对立事件是射手在一次射击中不小于8环,射手在一次射击中不小于8环包括击中8环,9环,10环,这三个事件是互斥的,可以做出在一次射击中不小于8环的概率,从而根据对立事件的概率得到要求的结果.【解答】解:由题意知射手在一次射击中不够8环的对立事件是射手在一次射击中不小于8环,∵射手在一次射击中不小于8环包括击中8环,9环,10环,这三个事件是互斥的,∴射手在一次射击中不小于8环的概率是0.20+0.30+0.10=0.60,∴射手在一次射击中不够8环的概率是1﹣0.60=0.40,故选:D.【点评】本题考查互斥事件和对立事件的概率,是一个基础题,解题的突破口在理解互斥事件的和事件的概率是几个事件的概率的和.3. 函数在区间上有最小值,则实数的取值范围是( )A. B. C. D.参考答案:D略4. 已知实数x,y满足约束条件,目标函数z=x+y,则当z=3时,x2+y2的取值范围是()A.B.C.D.参考答案:C【考点】简单线性规划.【分析】作出不等式组对应的平面区域,利用目标函数的几何意义,即可得到结论【解答】解:作出不等式对应的平面区域,当目标函数z=x+y,则当z=3时,即x+y=3时,作出此时的直线,则x2+y2的几何意义为动点P(x,y)到原点的距离的平方,当直线x+y=3与圆x2+y2=r2相切时,距离最小,即原点到直线x+y=3的距离d=,即最小值为d2=,当直线x+y=3与圆x2+y2=r2相交与点B或C时,距离最大,由,解得x=1,y=2,即B(1,2),由,解得x=2,y=1,即C(2,1)此时r2=x2+y2=22+12=5,故选:C.【点评】本题主要考查线性规划的应用,利用目标函数的几何意义,结合数形结合的数学思想是解决此类问题的基本方法.5. 函数的定义域是()A.(0,+∞)B.(1,+∞)C.(0,1)D.(0,1)∪(1,+∞)参考答案:B【考点】33:函数的定义域及其求法.【分析】由题意可得 2x﹣1>0,且 x>1,由此求得函数的定义域.【解答】解:∵函数,∴2x﹣1>0,且 x>1.解得 x>1,故函数的定义域为 {x|x>1},故选B.6. 若点P(2,-1)为圆(x-1)2+y2=25的弦AB的中点,则直线AB的方程是().A.x-y-3=0 B.2x+y-3=0 C.x+y-1=0 D.2x-y-5=0参考答案:A7. 曲线在处的切线的倾斜角是()A. B. C.D.参考答案:C略8. 直线与椭圆相交于A、B两点,椭圆上的点P使的面积等于12,这样的点P共有()个A.1 B.2 C.3 D.4参考答案:D错因:不会估算。
高二数学竞赛试题
高二数学竞赛试题(考试时间90分钟,满分120分,命题人:黄盛华) 班级________姓名_____________得分________________ 一、选择题(本大题有8小题,每小题5分,共40分)分)1.抛物线y 2=8x 的焦点到准线的距离是的焦点到准线的距离是( ) A .1 B .2 C .4 D .8 2.一个单位有职工800人,其中具有高级职称的160人,具有中级职称的320人,具有初级职称的200人,其余人员120人.人.为了解职工收入情况,决定采用分层抽样的方法,为了解职工收入情况,决定采用分层抽样的方法,为了解职工收入情况,决定采用分层抽样的方法,从中从中抽取容量为40的样本.则从上述各层中依次抽取的人数分别是的样本.则从上述各层中依次抽取的人数分别是 ( ) A .12,24,15,9 B .9,12,12,7 C .8,15,12,5 D .8,16,10,6 3.已知椭圆x 210-m +y 2m -2=1,长轴在y 轴上,若焦距为4,则m 等于等于 ( ) A .4 B .5 C .7 D .8 4.先后抛掷两枚均匀的骰子(骰子是一种正方体玩具,在正方体各面上分别有点数1,2,3,4,5,6),骰子落地后朝上的点数分别为x ,y ,则log 2x y =1的概率为的概率为 ( ) A.16 B.536 C.112 D.125. . 如图给出的是计算如图给出的是计算1+13+15+…+129的值的一个程序框图,则图中执行框中的①处和判断框中的②处应填的语句是行框中的①处和判断框中的②处应填的语句是 ( ) A .n =n +2,i =15? B .n =n +2,i >15? C .n =n +1,i =15? D .n =n +1,i >15? 6.双曲线x 26-y 23=1的渐近线与圆(x -3)2+y 2=r 2(r >0)相切,则r =( )A.3 B .2 C .3 D .67.200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,时速在[50,60)的汽车大约有的汽车大约有 ( ) A .30辆B .40辆C .60辆D .80辆 8.F 1,F 2是椭圆x 22+y 2=1的左右两个焦点,过F 2作倾斜角为π4的弦AB ,则△F 1AB 的面积为的面积为 ( ) A.43B.233 C.433D.423-1 二、填空题(本大题有4小题,每小题5分,共20分)分)9.如图,一不规则区域内,有一边长为1米的正方形,向区域内随机地撒1000颗黄豆,数得落在正方形区域内得落在正方形区域内((含边界含边界))的黄豆数为375颗,以此实验数据为依据可以估计出该不规则图形的面积为据为依据可以估计出该不规则图形的面积为________________________平方米.平方米.平方米.10区.在区间间[-1,2]机上随机取取一个数x ,则|x |≤1率的概率为为________.11. “a >2”是“方程x 2a +1+y 22-a =1表示双曲线”的________条件(填“充分不必要,必要不充分,充要,既不充分也不必要”).12. 若一个椭圆长轴的长度、短轴的长度和焦距成等差数列,则该椭圆的离心率是________. 三 解答题(本大题共5小题,共60分)分) 13. 13. (本小题满分(本小题满分12分)分)随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图:的茎叶图如图:(1)根据茎叶图判断哪个班的平均身高较高;根据茎叶图判断哪个班的平均身高较高;(2)计算甲班的样本方差;计算甲班的样本方差; (3)现从乙班这10名同学中随机抽取两名身高不低于名同学中随机抽取两名身高不低于 173 cm 的同学,求身高为176 cm 的同学被抽中的概率.的同学被抽中的概率.14.(本小题满分12分)分)-3x [3,PA ·PB =y 2-(1)从袋中随机取两个球,求取出的球的编号之和不大于4的概率;的概率;(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求n<m+2的概率.的概率.17. (本小题满分12分)分)设F1,F2分别是椭圆E:x2a2+y2b2=1(a>b>0)的左、右焦点,过F1斜率为1的直线l与E相交于A,B两点,且|AF2|,|AB|,|BF2|成等差数列.成等差数列.(1)求E的离心率;的离心率;(2)设点P(0,-1)满足|P A|=|PB|,求E的方程.的方程.高二数学限时训练(4)一 选择题: 题号 1 2 3 4 5 6 7 8 答案 CDDCBACA40=1,因此,从各层依次抽取的人数为1=1=×1=×1=ö=3=1. +1+1+1是连续奇数的前+1,+1+1++1需要循环= 3. 倾斜角为π的直线为=1| 49+43=4. 【答案】2⇒+=反过来,a +a ==3或3x 1=1x =14=2.-3x -37,[3,=7,[7,|7≤≤7,∴≥3或-3. ,-3][3,+PA·PB=(-x·y=y y=-=2=1. =3. -3=13. =4a=a2-b2. 22=2b2,=()2b2. =2|2[(x1+x2)2-4x1x2]. 4a=4ab22,故=ca=a2-b2a=22. =x1+x22=-a ca2+b2=-23c=c3. 即y0+1x=-32,的方程为x218+y29=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
75中高二数学竞赛训练试卷(4)班级 姓名一、选择题1.设函数,86)(2++=x x x f 如果,15164)(2++=+x x c bx f 那么b c 2-的值等于( )A .3B .7C .-3D .-72.已知P 为四面体S-ABC 的侧面SBC 内的一个动点,且点P 与顶点S 的距离等于点P 到底面ABC 的距离,那么在侧面SBC 内,动点P 的轨迹是某曲线的一部分,则该曲线是( )A .圆或椭圆B .椭圆或双曲线C .双曲线或抛物线D .抛物线或椭圆 3.给定数列{x n },x 1=1,且x n+1=nn x x -+313,则∑=20051n nx=( )A ,1B .-1C .2+3D .-2+34.已知=)(x f ⎪⎩⎪⎨⎧∈-∈+]1,21[),1(2)21,0[,21x x x x ,定义)()()),(()(11x f x f x f f x f n n ==-其中,则等于)51(2007f ( )A .51 B .53 C .54 D .525.在△ABC 中,角A 、B 、C 的对边分别记为a 、b 、c(b ≠1),且A C ,ABsin sin 都是方程logbx=log b (4x-4)的根,则△ABC ( ) A .是等腰三角形,但不是直角三角形 B .是直角三角形,但不是等腰三角形 C .是等腰直角三角形 D .不是等腰三角形,也不是直角三角形 二、填空题6.若log 4(x+2y)+log 4(x-2y)=1,则|x|-|y|的最小值是_________. 7.如果:(1)a, b, c, d 都属于{1, 2, 3, 4} (2)a ≠b, b ≠c, c ≠d, d ≠a (3)a 是a, b, c, d 中的最小数 那么,可以组成的不同的四位数abcd 的个数是________.8.设,)65()32()21(xxxt ++=则关于x 的方程0)3)(2)(1(=---t t t 的所有实数解之和为 9.若对|x|≤1的一切x ,t+1>(t 2-4)x 恒成立,则t 的取值范围是_______________. 10.边长为整数且面积(的数值)等于周长的直角三角形的个数为 。
11.对每一实数对(x, y),函数f(t)满足f(x+y)=f(x)+f(y)+f(xy)+1。
若f(-2)=-2,试求满足f(a)=a 的所有整数a=__________.三、解答题(每小题20分,共60分) 12.已知a, b, c ∈R +,且满足cb a kabc++≥(a+b)2+(a+b+4c)2,求k 的最小值。
13.已知半径为1的定圆⊙P 的圆心P 到定直线l 的距离为2,Q 是l 上一动点,⊙Q 与⊙P 相外切,⊙Q 交l 于M 、N 两点,对于任意直径MN ,平面上恒有一定点A ,使得∠MAN 为定值。
求∠MAN 的度数。
14. 数列{}n a 定义如下:11a =,且当2n ≥时,211,1,n n n a n a n a -+⎧⎪⎪=⎨⎪⎪⎩当为偶数时,当为奇数时.已知3019n a =,求正整数n .高二数学竞赛模拟试卷(4)答案一、选择题1.设函数,86)(2++=x x x f 如果,15164)(2++=+x x c bx f 那么b c 2-的值等于( )A .3B .7C .-3D .-7解:取11521616)2(,2-=+⨯-=--=b c f x 有,而当31862-=-=++x x x 时有,所以32-=-b c ,故选C.2.已知P 为四面体S-ABC 的侧面SBC 内的一个动点,且点P 与顶点S 的距离等于点P 到底面ABC 的距离,那么在侧面SBC 内,动点P 的轨迹是某曲线的一部分,则该曲线是( )A .圆或椭圆B .椭圆或双曲线C .双曲线或抛物线D .抛物线或椭圆 解:把问题转化成动点P 到S 的距离与它到边BC 的距离比值问题,容易的出答案D 3.给定数列{x n },x 1=1,且x n+1=nn x x -+313,则∑=20051n nx=( )A ,1B .-1C .2+3D .-2+3解:x n+1=nn x x 33133-+,令x n =tan αn ,∴x n+1=tan(αn +6π), ∴x n+6=x n , x 1=1,x 2=2+3, x 3=-2-3, x 4=-1, x 5=-2+3, x 6=2-3, x 7=1,……,∴有∑===2005111n nx x。
故选A 。
4.已知=)(x f ⎪⎩⎪⎨⎧∈-∈+]1,21[),1(2)21,0[,21x x x x ,定义)()()),(()(11x f x f x f f x f n n ==-其中,则等于)51(2007f ( )A .51 B .53 C .54 D .52解:计算=======)51(,51)51(,109)51(,52)51(,54)51(,53)51(,107)51(7654321f f f f f f f 107 可知)51(n f 是最小正周期为6的函数。
即得)51()51(6n n f f =+,所以)51()51(32007f f ==54,故选C.5.在△ABC 中,角A 、B 、C 的对边分别记为a 、b 、c(b ≠1),且A C ,ABsin sin 都是方程log b x=log b (4x-4)的根,则△ABC ( ) A .是等腰三角形,但不是直角三角形 B .是直角三角形,但不是等腰三角形C .是等腰直角三角形D .不是等腰三角形,也不是直角三角形解:由logbx=log b (4x-4)得:x 2-4x+4=0,所以x 1=x 2=2,故C=2A ,sinB=2sinA ,因A+B+C=180°,所以3A+B=180°,因此sinB=sin3A ,∴3sinA-4sin 3A=2sinA ,∵sinA(1-4sin 2A)=0,又sinA ≠0,所以sin 2A=41,而sinA>0,∴sinA=21。
因此A=30°,B=90°,C=60°。
故选B 。
二、填空题6.若log 4(x+2y)+log 4(x-2y)=1,则|x|-|y|的最小值是_________.答案:3。
⎩⎨⎧=->⇒⎪⎩⎪⎨⎧=-+>->+44||24)2)(2(020222y x y x y x y x y x y x 由对称性只考虑y ≥0,因为x>0,∴只须求x-y 的最小值,令x-y=u ,代入x 2-4y 2=4,有3y 2-2uy+(4-u)2=0,这个关于y 的二次方程显然有实根,故△=16(u 2-3)≥0。
7.如果:(1)a, b, c, d 都属于{1, 2, 3, 4} (2)a ≠b, b ≠c, c ≠d, d ≠a (3)a 是a, b, c, d 中的最小数 那么,可以组成的不同的四位数abcd 的个数是________. 答案:46个。
abcd 中恰有2个不同数字时,能组成C 24=6个不同的数。
abcd 中恰有3个不同数字时,能组成1212121213C C C C C +=16个不同数。
abcd 中恰有4个不同数字时,能组成A 44=24个不同数,所以符合要求的数共有6+16+24=46个。
8.设,)65()32()21(xxxt ++=则关于x 的方程0)3)(2)(1(=---t t t 的所有实数解之和为答案:4解:令,)65()32()21()x x x x f ++=(变形为,)65()64()63()(x x x x f ++=可以发现函数)(x f 是R 上的减函数。
又因为3)0(,2)1(,1)3(===f f f ,从而关于x 的方程0)3)(2)(1(=---t t t 的解分别为0、1、3,9.若对|x|≤1的一切x ,t+1>(t 2-4)x 恒成立,则t 的取值范围是_______________. 答案:2121,2113+-。
解:①若t 2-4>0,即t<-2或t>2,则由412-+t t >x(|x|≤1)恒成立,得1412>-+t t , t+1>t 2-4, t 2-t-s<0解得22112211+<<-t ,从而2211-<t<-2或2<t<2211+。
②若t 2-4=0,则t=2符合题意。
③若t 2-4<0,即-2<t<2,则由412-+t t <x(|x|≤1)恒成立,得1412-<-+t t ,t+1>-t 2+4; t 2+t-3>0,解得:t<2131--或t>2131+-,从而2131+-<t<2。
综上所述,t 的取值范围是:2113-<t<2121+。
10.边长为整数且面积(的数值)等于周长的直角三角形的个数为 。
解:设直角三角形的三边为a,b,22a b +,则有ab 21=a+b+22a b +,=∴b -a -ab 2122a b +,两边平方并整理有ab-4a-4b+8=0, ∴(a-4)(b-4)=8, a,b 都是正整数,∴a=5时b=12;a=6时b=8,所以满足题意的三角形有2个。
11.对每一实数对(x, y),函数f(t)满足f(x+y)=f(x)+f(y)+f(xy)+1。
若f(-2)=-2,试求满足f(a)=a 的所有整数a=__________.答案:1或-2。
令x=y=0得f(0)=-1;令x=y=-1,由f(-2)=-2得,f(-1)=-2,又令x=1, y=-1可得f(1)=1,再令x=1,得f(y+1)=f(y)+y+2 ①,所以f(y+1)-f(y)=y+2,即y 为正整数时,f(y+1)-f(y)>0,由f(1)=1可知对一切正整数y ,f(y)>0,因此y ∈N *时,f(y+1)=f(y)+y+2>y+1,即对一切大于1的正整数t ,恒有f(t)>t ,由①得f(-3)=-1, f(-4)=1。
下面证明:当整数t ≤-4时,f(t)>0,因t ≤-4,故-(t+2)>0,由①得:f(t)-f(t+1)=-(t+2)>0, 即f(-5)-f(-4)>0,f(-6)-f(-5)>0,……,f(t+1)-f(t+2)>0,f(t)-f(t+1)>0相加得:f(t)-f(-4)>0,因为:t ≤4,故f(t)>t 。
