2016届高考数学100个热点问题之千题百炼(3)第92炼算法——程序框图
高考数学命题热点名师解密专题:程序框图的应用(理)含答案解析

专题38 程序框图的应用一.【学习目标】1.了解算法的含义,了解算法的思想;理解程序框图的三种基本逻辑结构:顺序结构、条件结构、循环结构.2.理解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句的含义.3.初步了解几个典型的算法案例.二.知识要点1.算法通常是指可以用计算机来解决某一类问题的程序或步骤,必须是明确和有序的,而且能够在有限步之内完成.2.程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形.通常程序框图由程序框和流程线组成,一个或几个程序框的组合表示算法中的一个步骤,流程线带方向箭头,按照算法进行的顺序将程序框连接起来.3.三种基本逻辑结构(1)顺序结构是由若干个依次执行的处理步骤组成的,其结构形式为:(2)条件结构是指算法的流程根据给定的条件是否成立而选择执行不同的流向的结构形式,即:(3)循环结构是指从某处开始,按照一定的条件反复执行处理某一步骤的情况.反复执行的处理步骤称为循环体.循环结构又分为当型循环和直到型循环.结构形式为:4.基本算法语句(1)输入、输出语句和赋值语句:输入语句格式:INPUT“提示内容”;变量;输出语句格式:PRINT“提示内容”;表达式;赋值语句格式:变量=表达式.(2)条件语句:①框图:②条件语句格式:IF—THEN格式IF条件THEN语句体END IFIF—THEN—ELSE格式IF条件THEN语句体1ELSE语句体2END IF5.循环语句循环语句的格式①UNTIL语句②WHILE语句DO循环体LOOP UNTIL条件WHILE条件循环体WEND③顺序结构是每个算法结构都含有的,而对于循环结构有重复性,条件结构具有选择性没有重复性,并且循环结构中必定包含一个条件结构,用于确定何时终止循环体.循环结构和条件结构都含有顺序结构.④利用循环结构表示算法,第一要先确定是利用当型循环结构,还是直到型循环结构;第二要选择准确的表示累计的变量;第三要注意在哪一步开始循环,满足什么条件不再执行循环体.6.算法案例(1)辗转相除法与更相减损术①辗转相除法:求两个正整数的最大公约数的方法,用较大的数m除以较小的数n得到余数r,反复操作,直到余数为0为止,即m=nt+r(0≤r<n).因此要用“后测试型”循环语句表示,其程序如下:INPUT m,nDOr=m MOD nm=nn=rLOOP UNTIL r=0PRINT mEND(2)秦九韶算法n次多项式f(x)=a n x n+a n-1x n-1+…+a1x+a0=(a n x n-1+a n-1x n-2+…+a1)x+a0…=(…((a n x+a n-1)x+a n-2)x+…+a1)x+a0得到递推公式v0=a n且v k=v k-1x+a n-k,其中k=1,2,…,n其算法可用循环语句来实现.(3)进位制①将十进制数化为二进制数的算法称为除2取余法;将十进制数化为k进制数的算法称为除k取余法.②将k进制数化为十进制数的算法步骤为:第一步:从左到右依次取k进制数a n a n-1…a1a0(k)各位上的数字乘以k的幂,k的幂从n开始取值,每次递减1,递减到0,即a n·k n,a n-1·k n-1,…,a1·k,a0·k0;第二步:把所有积加起来,就得到十进制数.三.典例分析(一)秦九韶算法与框图例1.秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例.若输入n,x的值分别为5,2,则输出v的值为( )A.64B.68 C.72D.133【答案】B练习1.秦九韶算法是将求次多项式的值转化为求个一次多项式的值。
(完整版)程序框图与算法的高考常见题型及解题策略
算法及程序框图高考常有题型及解题策略算法和程序框图是新课程高考的新增内容,主要以客观形式题出现,不大会出现让考生就一详细问题编写一个算法,并画出程序框图的题目。
主要考察算法思想和算法框图的3 种基本构造:次序构造、选择构造和循环构造,且考察最多的是循环构造,考察还常常以算法和程序框图为载题考察高中其余重要数学知识的理解。
算法和程序框图常有的题型有两种:一种是阅读算法程序框图,写出履行结果;第二种是已知算法程序框图的履行的结果,填写算法框图的空白部份,下边就这两种题型和解决议略做一简单介绍,望能对2012 年参加高考的考生起到一点点作用。
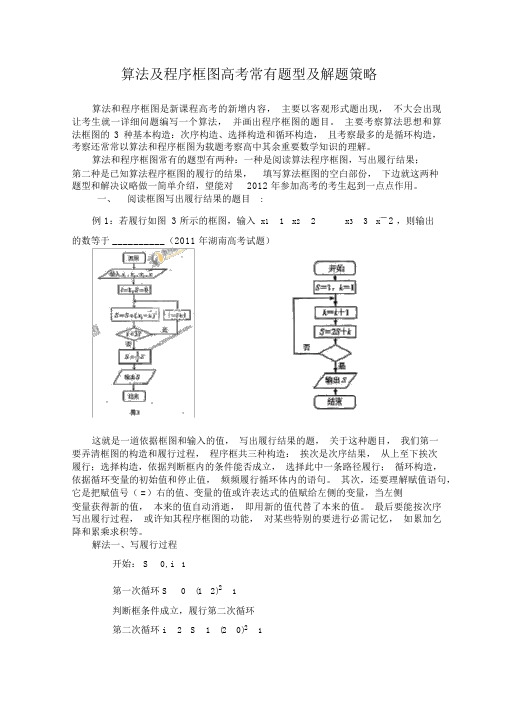
一、阅读框图写出履行结果的题目:例 1:若履行如图 3 所示的框图,输入x1 1 x22x3 3 x 2,则输出的数等于 __________(2011 年湖南高考试题)这就是一道依据框图和输入的值,写出履行结果的题,关于这种题目,我们第一要弄清框图的构造和履行过程,程序框共三种构造:挨次是次序结果,从上至下挨次履行;选择构造,依据判断框内的条件能否成立,选择此中一条路径履行;循环构造,依据循环变量的初始值和停止值,频频履行循环体内的语句。
其次,还要理解赋值语句,它是把赋值号( =)右的值、变量的值或许表达式的值赋给左侧的变量,当左侧变量获得新的值,本来的值自动消逝,即用新的值代替了本来的值。
最后要能按次序写出履行过程,或许知其程序框图的功能,对某些特别的要进行必需记忆,如累加乞降和累乘求积等。
解法一、写履行过程开始: S 0, i1第一次循环 S 0 (1 2)21判断框条件成立,履行第二次循环第二次循环 i 2 S 1 (2 0)21判断框条件成立,履行第三次循环i3 S 1 (3 2)21判断框条件不可立,跳出循环,履行2S32∴ 结果为S31 到 3,循环体的功能是累解法二 本框图中音是一个循环结果,循环变量是从 加乞降,是求 ( x 1 x) 2,( x 2 x)2 ,( x 2 x)2 的和,因此 S=2,最后这个履行框 S1S 获得2 。
专题三:程序框图2013-2016高考数学全国卷(文)

1、(2016全国I 卷10题)执行右面的程序框图,如果输入的0,1,x y ==n =1,则输出,x y 的值满足(A )2y x =(B )3y x =(C )4y x =(D )5y x =【答案】C【解析】试题分析:第一次循环:0,1,2x y n ===, 第二次循环:1,2,32x y n ===, 第三次循环:3,6,32x y n ===,此时满足条件2236x y +≥,循环结束,3,62x y ==,满足4y x =.故选C2、(2015全国I 卷9题)执行右面的程序框图,如果输入的t=0.01,则输出的n=(A )5 (B )6 (C )7 (D )8解析:故答案选C3、(2014全国I 卷9题)执行下图的程序框图,若输入的,,a b k 分别为1,2,3,则输出的M =A .203B .165C .72D .158【答案】:D【解析】:输入1,2,3a b k ===;1n =时:1331,2,222M a b =+===; 2n =时:28382,,3323M a b =+===;3n =时:3315815,,28838M a b =+===; 4n =时:输出158M = . 选D.4、(2013全国I 卷7题)执行右面的程序框图,如果输入的[1,3]t ∈-,则输出的S 属于(A )[3,4]-(B )[5,2]-(C )[4,3]-(D )[2,5]-5、(2016全国II卷9题)中国古代有计算多项式值得秦九韶算法,右图是实现该算法的程序框图.执行该程序框图,若输入的a为2,2,5,则输出的s=(A)7(B)12(C)17(D)34【答案】C【解析】第一次运算,a=2,s=2,n=2,k=1,不满足k>n;⨯+=,k=2,不满足k>n;第二次运算,a=2,s=2226⨯+=,k=3,满足k>n,第三次运算,a=5,s=62517输出s=17,故选C.6、(2015全国II卷8题)右边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的,a b分别为14,18,则输出的a为()A.0B.2C.4D.14【答案】B【解析】试题分析:由题意输出的a 是18,14的最大公约数2,故选B.考点:1. 更相减损术;2.程序框图.7、(2014全国II 卷8题)执行右面的程序框图,如果如果输入的x ,t 均为2,则输出的S=(A )4(B )5(C )6(D )7【答案】 D【解析】.3 7 22 5 2 13 1 ,2,2D KS M t x 故选变量变化情况如下:== 8、(2013全国II 卷7题)执行右面的程序框图,如果输入的4N =,那么输出的S =( )(A )1111234+++ (B )1111232432+++⨯⨯⨯ (C )111112345++++ (D )111112324325432++++⨯⨯⨯⨯⨯⨯ 【答案】B【解析】第一次循环,1,1,2T S k ===;第二次循环,11,1,322T S k ==+=;第三次循环,111,1,423223T S k ==++=⨯⨯,第四次循环,1111,1,5234223234T S k ==+++=⨯⨯⨯⨯⨯,此时满足条件输出1111223234S =+++⨯⨯⨯,选B. 9、(2016全国III 卷8题)执行右面的程序框图,如果输入的a =4,b =6,那么输出的n =(A )3(B )4(C )5(D )6【答案】B。
2016届高考数学100个热点问题之千题百炼(1)第1炼命题形式变化及真假判定

第1炼 命题形式变化及真假判定一、基础知识: (一)命题结构变换1、四类命题间的互化:设原命题为“若p ,则q ”的形式,则 (1)否命题:“若p ⌝,则q ⌝” (2)逆命题:“若q ,则p ” (3)逆否命题:“若q ⌝,则p ⌝”2、p q ∨,p q ∧(1)用“或”字连接的两个命题(或条件),表示两个命题(或条件)中至少有一个成立即可,记为p q ∨(2)用“且”字连接的两个命题(或条件),表示两个命题(或条件)要同时成立,记为p q ∧ 3、命题的否定p ⌝:命题的否定并不是简单地在某个地方加一个“不”字,对于不同形式的命题也有不同的方法(1)一些常用词的“否定”:是→不是 全是→不全是 至少一个→都没有 至多n 个→至少1n +个 小于→大于等于 (2)含有逻辑联结词的否定:逻辑联接词对应改变,同时,p q 均变为,p q ⌝⌝:p 或q →p ⌝且q ⌝ p 且q →p ⌝或q ⌝(3)全称命题与存在性命题的否定全称命题:():,:,()p x M p x p x M p x ∀∈→⌝∃∈⌝ 存在性命题:():,:,()p x M p x p x M p x ∃∈→⌝∀∈⌝ 规律为:两变一不变① 两变:量词对应发生变化(∀⇔∃),条件()p x 要进行否定()p x ⇒⌝ ② 一不变:x 所属的原集合M 的不变化(二)命题真假的判断:判断命题真假需要借助所学过的数学知识,但在一组有关系的命题中,真假性也存在一定的关联。
1、四类命题:原命题与逆否命题真假性相同,同理,逆命题与否命题互为逆否命题,所以真假性也相同。
而原命题与逆命题,原命题与否命题真假没有关联2、p q ∨,p q ∧,如下列真值表所示:简而言之“一真则真” 简而言之“一假则假” 3、p ⌝:与命题p 真假相反。
4、全称命题:真:要证明每一个M 中的元素均可使命题成立 假:只需举出一个反例即可 5、存在性命题:真:只需在M 举出一个使命题成立的元素即可 假:要证明M 中所有的元素均不能使命题成立 二、典型例题例1:命题“若方程20ax bx c -+=的两根均大于0,则0ac >”的逆否命题是( ) A. “若0ac >,则方程20ax bx c -+=的两根均大于0” B. “若方程20ax bx c -+=的两根均不大于0,则0ac ≤” C. “若0ac ≤,则方程20ax bx c -+=的两根均不大于0” D. “若0ac ≤,则方程20ax bx c -+=的两根不全大于0”思路:所谓逆否命题是要将原命题的条件与结论否定后并进行调换,“0ac >”的对立面是“0ac ≤”,“均大于0”的对立面是“不全大于0”(注意不是:都不大于0),再调换顺序即可,D 选项正确 答案:D例2:命题“存在2,20x Z x x m ∈++≤”的否定是( )A . 存在2,20x Z x x m ∈++> B .不存在2,20x Z x x m ∈++>C . 对任意2,20x Z x x m ∈++≤D .对任意2,20x Z x x m ∈++>思路:存在性命题的否定:要将量词变为“任意”,语句对应变化222020x x m x x m ++≤→++>,但x 所在集合不变。
(完整版)高考算法程序框图真题练习及答案详解

高中算法程序框图一 •选择题(共18小题)1 •如图给出了一个算法程序框图,该算法程序框图的功能是( )A .求输出a , b , c 三数的最大数 C .将a , b , c 按从小到大排列3. (2012?三明模拟)如图给出一个算法的程序框图,该程序框图的功能是(A .找出a 、b 、c 三个数中最大的数 C .找出a 、b 、c 三个数中第二大的数 4. 程序框图表示的算法的运行结果是(B .找出a 、b 、c 三个数中最小的数 D .把c 的值赋给a)A .求a , b , c 三数的最大数 C .将a , b , c 按从小到大排列2. 如图给出一个算法的程序框图,该程序框图的功能是(B .求 a , D .将 a , )b ,c 三数的最小数 b , c 按从大到小排列CMB .求输出a , b , c 三数的最小数 D .将a , b , c 按从大到小排列)5•程序框图中所表示的算法是(A . 3B . 7C . 157. (2013?合肥二模)如图所示,程序框图(算法流程图)的输出结果是(B . 6B .求x 的相反数C •求x 的平方根 6. (2014?泉州一模)运行图中所示程序框图所表达的算法,输出的结果是(D .求x 的算术平方根)D .31)A .求x 的绝对值 •帕J&阅读如图所示的程序框图,运行相应的程序,输出的结果为(9•阅读如图所示的程序框图,运行相应的程序,输出的结果是(A . 1B . 2C . 310 . (2014?福建)阅读如图所示的程序框图,运行相应的程序,输出的「我] 启~I/•is/IA . 18B . 20C . 2111. (2014?北京)当m=7, n=3时,执行如图所示的程序框图,输出的S 的值为(D . 40)B . 26S 的值等于(口 w fl 十142 C . 21012.(2013?辽宁)执行如图所示的程序框图,若输入 n=10,则输出的S=()GE®/输A/i /72 5513.(2012?天津)阅读程序框图,运行相应的程序,当输入 x 的值为-25时,输出x 的值为()B . 10C. 3&D . _[H 五55A .14. (2012?福建)阅读如图所示的程序框图,运行相应的程序,输出15 . (2012?广东)执行如图所示的程序框图,若输入 n 的值为6,则输出s 的值为( )A . 105B . 16C . 15D .116 . (2012?辽宁)执行如图所示的程序框图,则输出的 S 的值是( )3^:B . - 10s 值等于( )A.4B .::C .::D . - 12 317. (2011?北京)执行如图所示的程序框图,若输入A . 2B . 318.(2011?北京)执行如图所示的程序框图,输出的 s 值为(20 .有如图程序框图,则该程序框图表示的算法功能是 _一A 的值为2,则输入的P 值为( )A . — 3.填空题(共9小题)21 •如图所示的程序框图,其算法功能是_____________________24 •某算法的程序框图如图所示,则程序输出y的值是________________26. (2014?惠州模拟)如图所示,程序框图(算法流程图)的输出结果为27 •阅读如图所示的程序框图,运行相应的程序,则输出的三•解答题(共1小题)s值等于________________参考答案与试题解析一•选择题(共18小题)1 •如图给出了一个算法程序框图,该算法程序框图的功能是()A .求a, b, c三数的最大数B •求a, b,c三数的最小数C.将a, b, c按从小到大排列 D .将a, b, c按从大到小排列考点:设计程序框图解决实际问题.专题:操作型.分析:逐步分析框图中的各框语句的功能,第一个条件结构是比较a, b的大小,并将a, b中的较小值保存在变量a中,第二个条件结构是比较a, c的大小,并将a, c中的较小值保存在变量a中,故变量a的值最终为a, b, c中的最小值.由此不难推断程序的功能.解答:解:逐步分析框图中的各框语句的功能,第一个条件结构是比较a, b的大小,并将a, b中的较小值保存在变量a中,第二个条件结构是比较a, c的大小,并将a, c中的较小值保存在变量a中,故变量a的值最终为a, b, c中的最小值. 由此程序的功能为求a, b, c三个数的最小数.故答案选B点评:算法是新课程中的新增加的内容,也必然是新高考中的一个热点,应高度重视•要判断程序的功能就要对程序的流程图(伪代码)逐步进行分析,分析出各变量值的变化情况,特别是输出变量值的变化情况,就不难得到正确的答案.2 •如图给出一个算法的程序框图,该程序框图的功能是()c®CiteA •求输出a , b , c 三数的最大数 C •将a , b , c 按从小到大排列B •求输出a , b , c 三数的最小数 D •将a , b , c 按从大到小排列考点:程序框图. 专题:算法和程序框图.分析:根据框图的流程判断,第一个环节的功能是输出的a 是a ,b 之间的最大数,第二个环节功能是输出 a , c之间的最大数,由此可得答案.解答:解:由程序框图知:第一个环节是比较a ,b ,输出的a 是a , b 之间的最大数;第二个环节是比较 a, c ,输出的a 是a , c 之间的最大数. •••算法的功能是输出a , b , c 三数的最大数. 故选:A .点评:本题考查了排序程序框图,根据框图的流程判断算法的功能是关键.3. (2012?三明模拟)如图给出一个算法的程序框图,该程序框图的功能是( )考点: 程序框图• 专题: 阅读型•分析: 再输入了三个实数 a 、b 、c 后,首先对其中的两个数 a 、b 的大小加以判断,二者取小的数,然后再比较取 得的数与c 的大小,再取小的数输出•解答: 解:输入框中输入了三个实数a 、b 、c ,然后首先判断a 与b 的大小,若a >b 成立,则用b 替换a ,若a 哉不进仃替换,这样再用两者之间的小的数和c 比较,右a >c ,用c 替换a ,输出a ,否则,直接输出小的数a 所以程序框图的功能是找出a 、b 、c 三个数中最小的数•故选B •点评: 本题考查了程序框图中的条件结构,条件结构有两个路径,满足条件执行一个路径,不满足条件,执行另A .找出a 、b 、c 三个数中最大的数 C .找出a 、b 、c 三个数中第二大的数B .找出a 、b 、c 三个数中最小的数 D .把c 的值赋给a一个路径,解答本题时,一定要注意 =”的意义,是用后者替换前者.考点:程序框图. 专题:计算题.分析:由判断框可知:只要 s€0,则程序就执行 是”,否则就跳出循环程序,执行否”并输出i .据此可得出答案.解答:解:由判断框可知:只要 s €0,则程序就执行 是”否则就跳出循环程序,执行否”并输出i .当s=1+2+3+4+5=15 V 20,应继续执行 是”贝U s=15+6=21 >20,此时i=6+仁7,要跳出循环,输出 7. 故选C .点评:理解循环结构的工作原理并会计算s 与i 是解决问题的关键.5•程序框图中所表示的算法是( )考点:选择结构. 专题:图表型.分析:写出经过选择结构得到的结果,得到求的 y 的值的形式,即可判断出框图的功能.解答:解:逐步分析框图中的各框语句的功能,fig该程序框图表示算法的功能是求函数 y= '沁的值,即 y=|x|, 故选A .点评:本题考查解决程序框图中的选择结构时,常采用写出前几次选择的结果,找规律.6. (2014?泉州一模)运行图中所示程序框图所表达的算法,输出的结果是( )B .求x 的相反数C •求x 的平方根D •求x 的算术平方根4 •程序框图表示的算法的运行结果是(A .求x 的绝对值考点:循环结构. 专题:图表型.分析:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是利用循环计算 并输出满足条件 S >20的第一个i 值,模拟程序的运行过程,用表格将程序运行过程中变量 况进行分析,不难给出答案.解答:解:程序在运行过程中各变量的值如下表示:s i 是否继续循环 循环前 1 1/第一圈 1 2 是第二圈23是C . 15D . 31考点:程序框图. 专题:算法和程序框图.分析:由算法的程序框图,计算各次循环的结果,满足条件,结束程序. 解答:解:根据算法的程序框图知,第一次循环得 a=2X1+1=3, 第二次循环得 a=2X 3+1=7,第三次循环得a=2X7+1=15,结束循环, 故选C ,点评:本题考查了应用程序框图进行简单的计算问题,是基础题.7. (2013?合肥二模)如图所示,程序框图(算法流程图)的输出结果是(i 值,k 的值的变化情A . 6第三圈 6 4 是故最后输出的i 值为:5,图(或伪代码),从流程图(或伪代码)中即要分析出计算的类型,又要分析出参与计算的数据(如果参与 择恰当的数学模型 ③解模.&阅读如图所示的程序框图,运行相应的程序,输出的结果为( )A . 676考点: 循环结构.专题:图表型.分析: 根据已知中的流程图,我们模拟程序的运行结果,看变量 不满足时执行循环,满足时退出循环,即可得到输出结果.a 的值是否满足判断框的条件,当判断框的条件解答:解:a=1,满足条件a v 15,执行循环, a=2,满足条件a v 15,执行循环, a=5,满足条件a v 15,执行循环, a=26,不满足条件a v 15,退出循环, 执行输出语句,输出 a=26.故选B .点评:本题主要考查的知识点是程序框图,模拟循环的执行过程是解答此类问题常用的办法,属于基础题.9.阅读如图所示的程序框图,运行相应的程序,输出的结果是( )第四圈24 5 否 点评:根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是: :①分析流程运算的数据比较多,也可使用表格对数据进行分析管理) ?②建立数学模型,根据第一步分析的结果,选 B . 26故选B .A . 1B . 2C . 3D . 4考点:程序框图. 专题:图表型.分析:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是利用循环计算 重新为2时变量n 的值,并输出,模拟程序的运行过程,即可得到答案.解答: 解:程序在运行过程中各变量的值如下表示:S n 是否继续循环循环前 2 1/ 第一圈-1 2是 第二圈 丄3是 第三圈 2 4否则输出的结果为4故选D点评:本题考查的知识点是程序框图,在写程序的运行结果时,模拟程序的运行过程是解答此类问题最常用的办法.10. (2014?福建)阅读如图所示的程序框图,运行相应的程序,输出的叠—考点:循环结构.S 的值等于( )A . 18B . 20C . 21D . 40总三刃十L专题:计算题;算法和程序框图.分析:算法的功能是求 S=21+22+・・+2n +1+2+・・+ n 的值,计算满足条件的 S 值,可得答案.解答:解:由程序框图知:算法的功能是求S=21+22+ ..+2n +1+2+ -+n 的值,12123S =2 +2 +1+2=2+4+1+2=9 V 15, S=2 +2 +2 +1+2+3=2+4+8+1+2+3=20 昌5.•••输出 S=20. 故选:B .点评:本题考查了直到型循环结构的程序框图,根据框图的流程判断算法的功能是解题的关键.11. (2014?北京)当m=7, n=3时,执行如图所示的程序框图,输出的 S 的值为( )考点:循环结构.专题:计算题;算法和程序框图.分析:算法的功能是求 S=7>6X ・・・kx 的值,根据条件确定跳出循环的 k 值,计算输出S 的值.解答: 解:由程序框图知:算法的功能是求S=7>6 >•••>的值,当 m=7 , n=3 时,m - n +1=7 - 3+仁5 , •跳出循环的k 值为4, •输出 S=70X5=210 . 故选:C .点评:本题考查了循环结构的程序框图,根据框图的流程判断算法的功能是解答本题的关键.12 . (2013?辽宁)执行如图所示的程序框图,若输入 n=10,则输出的S=( )(幵晞J丄/输心/1i=2------ 1 -------青r-l/ S H .'ISS7工i=i+2B . 42C . 210D . 840Iwn * 少 IA . 7B .」11C . _557255考点:循环结构.专题:计算题;图表型.分析:框图首先给累加变量S和循环变量i分别赋值0和2,在输入n的值为10后,对i的值域n的值大小加以判断,满足i韦, 执行二$十一,i=i+2,不满足则跳出循环,输出S.-1解答:解:输入n的值为10,框图首先给累加变量S和循环变量i分别赋值0和2,判断2<10 成立,执行S二。
(新课标)2016届高考数学5年真题备考题库第十章第1节算法与程序框图理(含解析)

第10章 算法初步、统计、统计案例第1节 算法与程序框图1.(2014新课标全国Ⅰ,5分)执行如图所示程序框图,若输入的a ,b ,k 分别为1,2,3,则输出的M =( )A.203B.165C.72D.158解析:第一次循环:M =32,a =2,b =32,n =2;第二次循环:M =83,a =32,b =83,n =3;第三次循环:M =158,a =83,b =158,n =4.则输出M =158,选D答案:D2.(2014新课标全国Ⅱ,5分)执行如图的程序框图,如果输入的x ,t 均为2,则输出的S =( )A .4B .5C .6D .7解析:在循环体部分的运算为:第一步,M =2,S =5,k =2;第二步,M =2,S =7,k =3.故输出结果为7.答案:D3.(2014安徽,5分) 如图所示,程序框图(算法流程图)的输出结果是( )A .34B .55C .78D .89解析:由题中程序框图(算法流程图)知:x =1,y =1,z =2;x =1,y =2,z =3;x =2,y =3,z =5;x =3,y =5,z =8;x =5,y =8,z =13;x =8,y =13,z =21;x =13,y =21,z =34;x =21,y =34,z =55>50,跳出循环.故输出结果是55.答案:B4.(2014福建,5分) 阅读如图所示的程序框图,运行相应的程序,输出的S 的值等于( )A.18 B.20C.21 D.40解析:S=0,n=1,S=0+21+1=3,n=2,因为3≥15不成立,执行循环:S=3+22+2=9,n=3,因为9≥15不成立,执行循环:S=9+23+3=20,n=4,因为20≥15成立,停止循环,输出S的值等于20,故选B.答案:B5.(2014天津,5分) 阅读如图所示的程序框图,运行相应的程序,输出S的值为( )A.15 B.105C.245 D.945解析:逐次计算的结果是T=3,S=3,i=2;T=5,S=15,i=3;T=7,S=105,i=4,此时输出的结果为S=105.选B.答案:B6.(2014北京,5分) 当m=7,n=3时,执行如图所示的程序框图,输出的S值为( )A.7 B.42C.210 D.840解析:m=7,n=3,k=m=7,S=1,m-n+1=5;第一步:k=7>5,S=1×7=7,k=7-1=6;第二步:k=6>5,S=7×6=42,k=6-1=5;第三步:k=5,S=42×5=210,k=5-1=4;第四步:k=4<5,输出的S=210.故选C.答案:C7.(2014湖南,5分) 执行如图所示的程序框图,如果输入的t∈[-2,2],则输出的S属于( )A.[-6,-2] B.[-5,-1]C.[-4,5] D.[-3,6]解析:由程序框图可知S是分段函数,且S =⎩⎪⎨⎪⎧2t 2-2,t ∈[-2,,t -3,t ∈[0,2],其值域为(-2,6]∪[-3,-1]=[-3,6],故选D.答案:D8.(2014陕西,5分) 根据如图所示的框图,对大于2的整数N ,输出的数列的通项公式是( )A .a n =2nB .a n =2(n -1)C .a n =2nD .a n =2n -1解析:由程序框图可知:a 1=2×1=2,a 2=2×2=4,a 3=2×4=8,a 4=2×8=16,归纳可得:a n =2n,故选C .答案:C9.(2014四川,5分) 执行如图所示的程序框图,如果输入的x ,y ∈R ,那么输出的S 的最大值为( )A .0B .1C .2D .3解析: 当⎩⎪⎨⎪⎧x ≥0,y ≥0,x +y ≤1时,由线性规划的图解法知,目标函数S =2x +y 的最大值为2,否则,S 的值为1.所以输出的S 的最大值为2.答案:C10.(2014重庆,5分) 执行如图所示的程序框图,若输出k 的值为6,则判断框内可填入的条件是( )A .s >12B .s >35C .s >710D .s >45解析:当输出k 的值为6时,s =1×910×89×78=710,结合题中的程序框图知,选C.答案:C11.(2014江西,5分) 阅读如下程序框图,运行相应的程序,则程序运行后输出的结果为( )A .7B .9C .10D .11解析: i =1,S =0,第一次循环:S =0+lg 13=-lg 3>-1;第二次循环:i =3,S =lg 13+lg 35=lg 15=-lg 5>-1;第三次循环:i =5,S =lg 15+lg 57=lg 17=-lg 7>-1;第四次循环:i =7,S =lg 17+lg 79=lg 19=-lg 9>-1;第五次循环:i =9,S =lg 19+lg 911=lg 111=-lg 11<-1.故输出i =9.答案:B12.(2014江苏,5分) 如图是一个算法流程图,则输出的n 的值是________.解析:该流程图共运行5次,各次2n的值分别是2,4,8,16,32,所以输出的n 的值是5. 答案:513.(2014浙江,5分) 若某程序框图如图所示,当输入50时,则该程序运行后输出的结果是________.解析:S =0,i =1;S =1,i =2;S =4,i =3;S =11,i =4;S =26,i =5;S =57,i =6,此时S >n ,所以i =6.答案:614.(2014辽宁,5分) .执行如图所示的程序框图,若输入x =9,则输出y =________.解析:第一次循环:y =5,x =5;第二次循环:y =113,x =113;第三次循环:y=299,此时|y -x |=⎪⎪⎪⎪⎪⎪299-113=49<1,故输出y =299. 答案:29914.(2014湖北,5分) 设a 是一个各位数字都不是0且没有重复数字的三位数,将组成a 的3个数字按从小到大排成的三位数记为I (a ),按从大到小排成的三位数记为D (a )(例如a=815,则I (a )=158,D (a )=851).阅读如图所示的程序框图,运行相应的程序,任意输入一个a ,输出的结果b =________.解析:当a =123时,b =321-123=198≠123; 当a =198时,b =981-189=792≠198; 当a =792时,b =972-279=693≠792; 当a =693时,b =963-369=594≠693; 当a =594时,b =954-459=495≠594;当a =495时,b =954-459=495=a ,终止循环,输出b =495. 答案:49515.(2013新课标全国Ⅰ,5分)执行如图的程序框图,如果输入的t ∈[-1,3],则输出的s 属于( )A .[-3,4]B .[-5,2]C .[-4,3]D .[-2,5]解析:本题主要考查对程序框图的认识、分段函数求值域及数形结合思想.作出分段函数s =⎩⎪⎨⎪⎧3t ,t <1,-t 2+4t ,t ≥1的图像(图略),可知函数s 在[-1,2]上单调递增,在[2,+∞)上单调递减,∴t ∈[-1,3]时,s ∈[-3,4].答案:A16.(2013新课标全国Ⅱ,5分)执行下面的程序框图,如果输入的N =10,那么输出的S =( )A. 1+12+13+…+110B. 1+12!+13!+ (110)C. 1+12+13+…+111D. 1+12!+13!+…+111!解析:本题考查算法、程序框图以及考生的逻辑推理能力,属于基础题.根据程序框图的循环结构,依次T =1,S =0+1=1,k =2;T =12!,S =1+12!,k =3;T =12×3=13!,S=1+12!+13!,k =4;…;T =110!,S =1+12!+13!+…+110!,k =11>10=N ,跳出循环,输出结果.答案:B17.(2013浙江,5分)某程序框图如图所示,若该程序运行后输出的值是95,则( )A .a =4B .a =5C .a =6D .a =7解析:本题考查对程序框图的循环结构的理解,考查简单的数列裂项求和方法,意在考查考生推理的严谨性等.k =1,S =1+1-12=32;k =2,S =1+1-13=53;k =3,S =1+1-14=74;k =4,S =1+1-15=95.输出结果是95,这时k =5>a ,故a =4. 答案:A18.(2013重庆,5分)执行如图所示的程序框图,如果输出s =3,那么判断框内应填入的条件是( )A .k ≤6B .k ≤7C .k ≤8D .k ≤9解析:本题考查算法与框图,意在考查考生知识交汇运用的能力.首次进入循环体,s =1×log 23,k =3;第二次进入循环体,s =lg 3lg 2×lg 4lg 3=2,k =4;依次循环,第六次进入循环体,s =3,k =8,此时终止循环,则判断框内填k ≤7.答案:B19.(2013陕西,5分)根据下列算法语句,当输入x 为60时,输出y 的值为( )输入x ;If x ≤50 Theny =0.5*xElsey =25+0.6*(x -50)End If输出y .A .25B .30C .31D .61解析:本题考查考生对算法语句的理解和分段函数的求值.阅读算法语句易知,本题是一个求解分段函数f (x )=⎩⎪⎨⎪⎧0.5x ,x ≤50,25+x -,x >50的值的算法,∴f (60)=25+0.6×(60-50)=31.答案:C20.(2013山东,4分)执行右面的程序框图,若输入的ε的值为0.25,则输出的n 的值为________.解析:本题考查程序框图,考查考生的运算求解能力以及分析问题、解决问题的能力.逐次计算的结果是F 1=3,F 0=2,n =2;F 1=5,F 0=3,n =3,此时输出, 故输出结果为3.答案:36.(2013湖北,5分)阅读如图所示的程序框图,运行相应的程序,输出的结果i =________.解析:本题考查程序框图,意在考查考生对程序框图中的三种结构的掌握情况.a =10≠4且a 是偶数,则a =102=5,i =2; a =5≠4且a 是奇数,则a =3×5+1=16,i =3; a =16≠4且a 是偶数,则a =162=8,i =4; a =8≠4且a 是偶数,则a =82=4,i =5.所以输出的结果是i =5. 答案:521.(2012新课标全国,5分)如果执行下边的程序框图,输入正整数N (N ≥2)和实数a 1,a 2,…,a N ,输出A ,B ,则( )A .A +B 为a 1,a 2,…,a N 的和 B.A +B2为a 1,a 2,…,a N 的算术平均数C .A 和B 分别是a 1,a 2,…,a N 中最大的数和最小的数D .A 和B 分别是a 1,a 2,…,a N 中最小的数和最大的数解析:结合题中程序框图,由当x >A 时A =x 可知A 应为a 1,a 2,…,a N 中最大的数,由当x<B时B=x可知B应为a1,a2,…,a N中最小的数.答案:C22.(2012天津,5分)阅读下面的程序框图,运行相应的程序,当输入x的值为-25时,输出x的值为( )A.-1 B.1C.3 D.9解析:按照程序框图逐次写出运行结果.由程序框图可知,该程序运行2次后退出循环,退出循环时x=1,所以输出的x的值为3.答案:C23.(2012北京,5分)执行如图所示的程序框图,输出的S值为( )A.2 B.4C.8 D.16解析:框图的功能为计算S=1·20·21·22的值,计算结果为8.答案:C24.(2011新课标全国,5分)执行右面的程序框图,如果输入的N是6,那么输出的p是( )A.120 B.720C.1440 D.5040解析:执行程序输出1×2×3×4×5×6=720.答案:B25.(2011天津,5分)阅读下边的程序框图,运行相应的程序,则输出i的值为( )A.3 B.4C.5 D.6解析:因为该程序框图执行4次后结束,所以输出的i的值等于4.答案:B26.(2011山东,4分)执行下图所示的程序框图,输入l=2,m=3,n=5,则输出的y的值是__________.解析:逐次计算.第一次y=70×2+21×3+15×5=278,执行循环;第二次y=278-105=173;再次循环,y=173-105=68,此时输出,故输出结果是68.答案:6827.(2011江苏,5分)根据如图所示的伪代码,当输入a,b分别为2,3时,最后输出的m的值为____.Read a,bIf a>b Thenm←aElsem←bEnd IfPrint m解析:此题的伪代码的含义:输出两数的较大者,所以m=3.答案:3。
历年高考算法与框图试题.docx
绝密★启用前:O...................... O ......... K .......... O ......... 垛 ............... O........... 参 ...............O •:・:O......... 都...............O...........H.......... O......... 蝶............... O........... M..........O•:・2013-2014学年度???学校9月月考卷试卷副标题题号一二三总分得分注意事项:1. 答题前填写好自己的姓名、班级、考号等信息2. 请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明评卷人得分一、选择题(题型注释)1.阅读右图所示的程序框图,运行相应的程序,输出的结果是A. 2B. 4C. 8D. 16【答案】C【解析】由程序框图可知:当s = —1时,〃 =2;当s =-时,〃=4;当s = 2时,〃 =8, 2 故选C 。
2.如图所示,程序框图(算法流程图)的输出结果是( )A 、3B 、4 c 、5 D 、A 、 -1B 、 1C 、 3D 、 9【答案】C【解析】解:当输入x=-25时,x | >1,执行循环,x= J|-25IT=4; x |=4>1,执行循环,x=JT 折 T=l, Ix|-1,退出循环,输出的结果为x=2Xl+l=3.故选C【考点定位】本题考查流程图,考查学生的分析问题的能力4. 某店一个月的收入和支出总共记录了 N 个数据%, %,。
O N ,其中收入记为正数,支出记为负数。
该店用如下图的程序框图计算月总收入S 和月净盈利V,那么在图中空 白的判断框和处理框中,应分别填入下列四个选项中的X1 2 y12【答案】B 【解析】3.阅读右边的程序框图,运行相应的程序,当输入x 的值为-25时,输出x 的值为※※贸※※灿※※长※※书※※云※※垛※※W※※鄙※※K -※※迎淤※x = 2x+l结束开始C M 3A 、A>0, V=S-TB 、A<0, V=S-TC 、A>0, V=S+TD 、A<0, V=S+T【答案】C【解析】月总收入为S,因此A>0时归入S,判断框内填A>0 支出T 为负数,因此月盈利V=S+T5. 如图的程序框图,如果输入三个实数a, b, c,要求输出这三个数中最大的数,那么在空白的判断框中,应该填入下面四个选项中的()A. c > xB. x> cC. c>bD. b> c【答案】A【解析】变量x 的作用是保留3个数中的最大值,所以第二个条件结构的判断框内语句 为“ c >x ”,满足“是”则交换两个变量的数值后输出x 的值结束程序,满足“否”直 接输出X 的值结束程序。
(完整word)高中数学算法框图习题及详解.doc
专题复习:算法框图高中数学算法框图习题(含答案详解)一、1. (理 )如所示算法程序框运行,入a= tan315 ,°b= sin315 ,°c= cos315 ,° 出果 ()2 2A. 2 B .-2 C.- 1 D .1[答案 ] C[解析 ] a、 b、 c 三数中的最小,又cos315 °>0, sin315 =°-2此程序框是出 2,2tan315 =°- 1<-2,故 C.2.下列程序运行后出果()x= 1;for i = 1 10x= 2]A.1B.23 C. 113 D.以上都不[答案 ] B[解析 ] 每一次循 x 都重新,与原来 x 的无关,故最后出x 的只与最后一次循 i 的有关,∵i =10,∴ x=23.1( 共 6 个 2)的的算法的程序框,中的判断框中填3. (理 )下面是求 12+12+⋯+ 2A . i ≤5? B. i <5? C.i ≥5? D. i>5?[答案 ] A[解析 ] 由于所给计算的表达式中共有 6 个2,故只需 5 次循环即可,由此控制循环次数的变量i 应满足 i≤ 5.故选 A.4. (理 )已知数列 { a n} 中, a1= 1, a n+1= a n+ n,利用如图所示的程序框图计算该数列第10 项,则判断框中应填的语句是( )A . n>10B . n≤ 10 C. n<9 D. n≤ 9[答案 ] D[解析 ] 本题在算法与数列的交汇处命题,考查了对程序框图的理解能力.数列{ a } 是n一个递推数列,因为递推公式为a1 n +1 n 10 9= 1, a = a + n,故 a =a+9,因为循环体为m=m +1, n= n+ 1,当 n= 10 时结束循环,故判断框内应为n≤ 9.5. (理 )下列程序运行后输出结果为()S= 1;n= 1;while S<100S = S* n ;n = n + 3;endnA . 4B .10C . 13D . 16[答案 ]C[解析 ]S = 1<100,进行第一次循环后S = 1, n = 4; S = 1<100再进行第二次循环.循环后 S = 4,n = 7;第三次循环后 S = 28,n = 10;第四次循环后 S = 280,n = 13.因 故不再循环,跳出循环后输出 n = 13. 6. (文 )在如图的程序框图中,若输入 m = 77,n = 33,则输出的 n 的值是( S = 280>100,)A . 3B . 7C . 11D . 33[答案 ] C[解析 ] 这个程序框图执行的过程是:第一次循环: m = 77,n = 33, r =11;第二次循环: m = 33,n = 11, r = 0.因为 r =0,则结束循环,输出n = 11.7.下面的程序框图,若输入 a = 0,则输出的结果为 ( )A . 1022B . 2046C . 1024D . 2048[答案 ] B[解析 ]由程序框图中的循环结构可得到递推公式, a = 2a + 2,且 a = 0,由 ak +1k1k +1a k +1 + 2=2a k + 2 可得, a k +1+ 2= 2(a k + 2),即 = 2 且 a 1+ 2= 2,∴ { a k + 2} 是以 2 为公比, 2a + 2k为首项的等比数列, ∴ a + 2= 2×2 k - 1k,即 ak11= 2k = 2 - 2,从而a = 2 - 2= 2046,故选k11B.[点评 ]本题的关键是弄清输出的a 的值为数列{ a n } 的第几项,k =1 算出的是a 2,k = 2满足条件得a 3,故k =10满足条件计算后得到a 11,k = 11不满足,故输出的是a 11 而不是a 10,有不少人在这里搞不清楚,以为判断条件是k ≤ 10,故最后输出的是 a 10,这是没有完整理解算法的典型表现. 因为对同一个判断条件k ≤10,a =2a + 2 与 k = k + 1 语句的先后顺序不同输出结果也不同, 还与 k 的初值有关等等, 故应统盘考虑, 解决的一个有效途径就是循环几次把握其规律.【解答题】8.为了让学生更多的了解“数学史”知识,其中学高二年级举办了一次“追寻先哲的足迹, 倾听数学的声音”的数学史知识竞赛活动,共有 800 名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100 分 )进行统计.请你根据频率分布表,解答下列问题:序号 (i) 分组 (分数 ) 组中值 (G i) 频数 (人数 ) 频率 (F i)1 [60,70) 65 ①0.122 [70,80) 75 20 ②3 [80,90) 85 ③0.244 [90,100] 95 ④⑤合计50 1(1)填充频率分布表中的空格 (在解答中直接写出对应空格序号的答案);(2)为鼓励更多的学生了解“数学史”知识,成绩不低于85 分的同学能获奖,请估计在参加的 800 名学生中大概有多少同学获奖?(3)在上述统计数据的分析中有一项计算见算法流程图,求输出S 的值.[解析 ] (1)∵样本容量为50,∴①为 6,②为 0.4,③为 12,④为 12,⑤为 0.24.(2)在 [80,90) 之间, 85 分以上约占一半,∴12× 0.24+ 0.24 × 800= 288,即在参加的800 名学生中大概有288 名同学获奖.(3)由流程图知S= G1 F1+ G2F2+ G3F3+G4F 4=65×0.12+ 75× 0.4+ 85× 0.24+ 95× 0.24= 81.。
(完整word版)算法及程序框图练习试题及答案解析
第一章 算法初步1.1算法与程序框图 1。
1.1算法的概念1。
已知直角三角形两直角边长为a ,b ,求斜边长c 的一个算法分下列三步: ①计算22c a b =+a ,b 的值;③输出斜边长c 的值,其中正确的顺序是 【 】 A.①②③ B。
②③① C。
①③② D。
②①③2。
若()f x 在区间[],a b 内单调,且()()0f a f b <,则()f x 在区间[],a b 内 【 】 A.至多有一个根 B.至少有一个根 C 。
恰好有一个根 D 。
不确定3.已知一个学生的语文成绩为89,数学成绩为96,外语成绩为99。
求他的总分和平均成绩的一个算法为:第一步:取A =89 ,B =96 ,C =99; 第二步:____①______; 第三步:_____②_____; 第四步:输出计算的结果。
4。
写出按从小到大的顺序重新排列,,x y z 三个数值的算法.1.1.2 程序框图1.在程序框图中,算法中间要处理数据或计算,可分别写在不同的 【 】 A .处理框内 B .判断框内 C .终端框内 D .输入输出框内2.将两个数a=10,b=18交换,使a=18,b=10,下面语句正确一组是 【 】A. B. C. D 。
a=c=b b=aa=c b=a=c c=b b=a3指出下列语句的错误,并改正:(1)A=B=50(2)x=1,y=2,z=3(3)INPUT “How old are y ou” x(4)INPUT ,x(5)PRINT A+B=;C(6)PRINT Good—b y e!4.2000年我国人口为13亿,如果人口每年的自然增长率为7‰,那么多少年后我国人口将达到15亿?设计一个算法的程序。
5。
儿童乘坐火车时,若身高不超过1。
1 m,则不需买票;若身高超过1。
1 m但不超过1.4 m,则需买半票;若身高超过1。
4 m,则需买全票。
试设计一个买票的算法,并画出相应的程序框图及程序.1.2基本算法语句1.2。
高考数学复习算法与程序框图模拟考点训练题100题WORD版含答案
高考数学复习算法与程序框图模拟考点训练题100题WORD 版含答案一、选择题1.元朝著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒,携着游春走,遇店添一倍,逢友饮一斗,店友经四处,没了壶中酒,借问此壶中,当原多少酒?”用程序框图表达如图所示,即最终输出的x =0,则一开始输入的x 的值为()A .43B .87 C. 1615 D .32312.执行完如图的程序框图后,S 与i 应满足的关系为( )A .32S i =-B .7(2)S i =- C.81S i =- D .9(2)S i =+3. 运行如右程序框图,若输入的1[,3]2t ∈-,则输出s 取值为( )A.[1s ∈-B.1[,8]2s ∈C.[1s ∈D. [0,8]s ∈ 4. 执行如图的程序框图,当输入的n =351时,输出的k =( )A .355B .354C .353D .3525. 已知402cos 2d t x x π=⎰,执行下面的程序框图,如果输入的,2a t b t ==,那么输出的n 的值为()A. 3B. 4C. 5D. 66.执行下面的程序框图,如果输入的N=10,那么输出的S=A.111 12310 +++⋅⋅⋅+B.111 12!3!10! +++⋅⋅⋅+C.111 12311 +++⋅⋅⋅+D .11112!3!11!+++⋅⋅⋅+7. 执行下面的程序框图,若输入S ,a 的值分别为1,2,输出的n 值为4,则m 的取值范围为( )A .37m <≤B .715m <≤ C.1531m <≤ D.3163m <≤8.一个算法的程序框图如下,则其输出结果是( )A 1B .12+C .2D .09.执行如图所示的程序框图,输出的T =( )A.21 B.43 C.53 D.6410.利用我国古代数学名著《九章算法》中的“更相减损术”的思路,设计的程序框图如图所示.执行该程序框图,若输入a,b,i的值分别为6,9,0,则输出的i=A.2 B.3 C.4 D.511.宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而等长.右图是源于其思想的一个程序框图,若输入的a,b分别为5,2,则输出的n=()A.2 B.3 C. 4 D.512.我国南宋时期的数学家秦九韶(约1202—1261)在他的著作《数书九章》中提出了多项式求值的秦九韶算法,如图所示的框图给出了利用秦九韶算法求多项式的一个实例.若输入的6n =,2v =,3x =,则程序框图计算的结果对应的多项式()f x 等于( )A .543221x x x x x +++++B .54321x x x x x +++++ C. 6543221x x x x x x ++++++D .654321x x x x x x ++++++ 13.执行如图所示的程序框图,输出s 的值为( )A .-1008B .-1010C .1009D .100714.我国古代著名的“物不知数”问题:“今有物其数大于八,二二数之剩一,三三数之剩一,五五数之剩二,问物几何? ”即“已知大于八的数,被二除余一,被三除余一,被五除余二,问该数为多少? ”为解决此问题,现有同学设计了如图所示的程序框图,则框图中的“” 处应填入( )A.16aZ-∈ B.110aZ-∈ C.210aZ-∈ D.215aZ-∈15.我们可以用随机模拟的方法估计π的值,如图示程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为786,则由此可估计π的近似值为()A.3.126 B.3.144 C.3.213 D.3.15116.《孙子算经》中有一道题:“今有木不知长短,引绳度之,余绳四尺五寸;屈绳开始度之,不足一尺,木长几何?”译文大致是:“用一根绳子去量一根木条,绳子剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?解决本题的程序框图如图所示,则输出的i=()A .4.5B .5 C. 6 D .6.517.如果下面程序框图运行的结果1320s =,那么判断框中应填入( )A .10?k <B .10?k >C .11?k <D .11?k >18.执行如图所示的程序框图,若输入的001.0=t ,则输出的n =( )A.6 B.5 C.4 D.319.辗转相除法是欧几里德算法的核心思想,如图所示的程序框图所描述的算法就是辗转相除法,若输入8521n=,则输出m的值为( )m=,6105A.148B.37C.333D.020.a=,则输出的S=()执行如图的程序框图,若8A .2B .12C .0D .-1 21.如图,当输出4y =时,输入的x 可以是( )A .2018B .2017C .2016D .201422.如图,给出了一个程序框图,令()y f x =,若()1f a >,则a 的取值范围是( )A .(-∞,2)∪(2,5]B .(-∞,-1)∪(1,+∞)C. (-∞,2)∪(2,+∞) D .(-∞,-1)∪(1,5]23.在如图所示的程序框图中,若输出i 的值是3,则输入x 的取值范围是( )A .(3,+∞)B .(3,7]C .(7,+∞)D .(7,19] 24.已知()201720162018201721f x x x x =++++,下列程序框图设计的是求()0f x 的值,在“ ”中应填的执行语句是( )A .2018n i =-B .2017n i =-C .2018n i =+D .2017n i =+25.执行如图所示的程序框图,则输出的s 的值为( )26.执行下边的程序框图,假如输入两个数是1S =、2k =,那么输出的S =( )A.1+27.我国古代数学名著《九章算术》中的更相减损法的思想与下面的程序框图相似.执行该程序框图,若输入的a ,b 分别为14,18,则输出的a 等于( )A .2B .4C .6D .828.当4n =时,执行如图所示的程序框图,则输出的S 值为( )29.中国古代数学著作《孙子算经》中有这样一道算术题:“今有物不知其数,三三数之余二,五五数之余三,问物几何?”人们把此类题目称为“中国剩余定理”,若正整数n 除以正整数m 后的余数为r ,则记为()mod n r m =,例如()112mod3=.现将该问题设计一个程序框图.执行该程序框图,则输出的n 等于( )A .21B .22C .23D .2430.执行如图所示的程序框图,如果输出的结果为0,那么输入的x 为( )A .19B .-1或1C .1D .-1 31.在如图所示的框图中,若输出S =360,那么判断框中应填入的关于k 的判断条件是A .2?k >B .2?k <C .3?k >D .3?k <32.执行如图的程序框图,若输入的0x =,1y =,1n =,则输出的p 的值为()A .81B .812C .814 D .81833.执行如图所示的程序框图,那么输出的S 值是( )A .12 B .-1 C .2018 D .2 34.某数学爱好者编制了如图的程序框图,其中()mod ,m n 表示m 除以n 的余数,例如()mod 7,31=.若输入m 的值为8,则输出i 的值为( )A .2B .3C .4D .535.执行如图所示的算法,则输出的结果是( )A.2 B.43C.54D.136.执行如图所示的程序框图,为使输出S的值大于110,则输入正整数N的最小值为()A.5 B.4 C.3 D.237.执行如图所示的程序框图,则输出的x=()A .6B .7C .8D .938.如果执行右边的程序框图,输入正整数(2)N N ≥和实数12,,N a a a …,输出A ,B ,则A. A B +为12,,,N a a a …的和B. 2A B +为12,,,N a a a …的算术平均数 C. A 和B 分别是 12,,,N a a a …中最大的数和最小的数D. A 和B 分别是12,,,N a a a …中最小的数和最大的数 39.见右侧程序框图,若输入110011a =,则输出结果是A.51B.49C.47D.4540.执行如图所示的程序框图,若输入的a=2,b=1,则输出的n值为()A.7 B.6 C.5 D.441.一个算法的程序框图如图所示,若该程序输出的结果是34,则判断框中应填入的条件是()A . 5i > B. <5i C. 4i > D. <4i42.阅读右侧程序框图,运行相应程序,则输出i 的值为A .3B .4C .5D .6 43.某程序框图如图所示,则该程序运行后输出的值是( )A.2019B.2018C.2017D.201644.《孙子算经》是中国古代重要的数学著作,书中有一问题:“今有方物一束,外周一匝有三十二枚,问积几何?”“重置二位,左位减八,余加右位,至尽虚减一,即得.”n是8的整数倍时,均可采用此方法求解.如图是解决这类问题的程序框图,若输入n=24,则输出的结果为()A.23 B.47 C.24 D.48 45.执行如图所示的程序框图,输出的s值为A. 1B. 2C. 3D. 446.阅读右边的程序框图,运行相应的程序,输出S的值为A.5B.8C.24D.2947.如图是求112122++的程序框图,图中空白框中应填入A.A=12A+B.A=12A+C.A=112A+D.A=112A+48.运行如图所示的程序框图,设输出的数据构成集合A,从集合A中任取一个元素a,则函数ax y 在(0,+∞)是增函数的概率为( )A .21 B .52 C .32 D .43 49.执行如图所示的程序框图,输出的S 值为A .43 B. 55 C. 61 D. 8150.宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.下图是源于其思想的一个程序框图,若输入的a 、b 分别为5,2,则输出的n = ( )A.2B.3C.4D.551.如图所示的程序框图是为了求出满足2228n n ->的最小偶数n ,那么空白框中的语句及最后输出的n 值分别是( )A. n =n +1和6B. n =n +2和6C. n =n +1和8D. n =n +2和852.阅读如图的程序框图,运行相应的程序,若输入4x =-,1y =,则输出z 的值为A.52B.54C.23D.1253.执行如图所示的程序框图,输出的S和n的值分别是()A.20,5 B.20,4 C.16,5 D.16,4 54.已知程序框图如图,则输出结果是A.919 B. 1021 C. 1819 D. 202155.执行如图的程序框图,如果输入的a ,b ,k 分别为1,2,3,输出的158M =,那么判断框中应填入的条件为( )A . n k <B .n k ≥C .1n k <+D .1n k ≥+56.有一程序框图如图所示,要求运行后输出的值为大于1000的最小数值,则在空白的判断框内可以填入的是A .5i ≥B .6i ≥C .7i ≥D .8i ≥57.执行下面的程序框图,则输出K 的值为( )A.99B.98C.100D.10158.某篮球运动员6场比赛得分如下表:(注:第n场比赛得分为a n)a输出的s的值是A.73B.2 C.53D.4359.执行如图的程序框图,若输出S的值是2,则a的值可以为A.2014 B.2015 C.2016 D.201760.元朝时,著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒,携着游春走,与店添一倍,逢友饮一斗,店友经三处,没了壶中酒,借问此壶中,当原多少酒?”用程序框图表达如图所示,即最终输出的x=0时,问一开始输入的x=()A.34B.78C.1516D.313261.执行右图所示的程序框图,则输出n 的值为( ).A.63B.47C.23D.762.在右图算法框图中,若dx x a ⎰-=30)12(,程序运行的结果S 为二项式5)2(x +的展开式中3x 的系数的9倍,那么判断框中应填入的关于k 的判断条件是( )A .3k <B .3>kC .2<kD .2>k63.运行如图所示的程序框图,若输入的i a (i =1,2,…,10)分别为1.5、2.6、3.7、4.8、7.2、8.6、9.1、5.3、6.9、7.0,则输出的值为( )A.49B.25C.12D.5964.执行如图的程序框图,若输出的S=48,则输入k的值可以为()A.6 B. 10 C. 4 D.865.如图是一个算法流程图,若输入n的值为13,输出S的值是46,则a的取值范围是A.910a ≤<B.910a <≤C.1011a <≤D.89a <≤66.2017年国庆期间,全国接待国内游客7.05亿人次,其中某30个景区日均实际接待人数与最大接待人数比值依次记为()1,2,...,30i a i =,若该比值超过1,则称该景区“爆满”,否则称为“不爆满”,则如图所示的程序框图的功能是( )A.求30个景区的爆满率B.求30个景区的不爆满率C.求30个景区的爆满数D.求30个景区的不爆满数67.执行如图所示的程序框图,则输出的结果为(A) 20 (B) 30 (C) 40 (D) 5068.执行如图所示的程序框图,则输出的结果是A.8 B.16 C.32 D.64 69.如图,若依次输入的x分别为56π、6π,相应输出的y分别为y1、y2,则y1、y2的大小关系是A.y1=y2B.y1>y2 C.y1<y2D.无法确定70.执行如右图所示的程序框图,则输出的s的值是A.7 B.6 C.5 D.371.对于实数a,b,定义一种新运算“⊗”:y a b=⊗,其运算原理如程序框图所示,则⊗+⊗()5324=A.26 B.32 C.40 D.4672.执行如图所示的程序框图,则输出的a=()A .14-B .45C .4D .5 73. 执行如图所示的程序框图,则输出的结果是A.171B.342C.683D.34174.如图所示的程序框图是为了求出满足2228n n ->的最小偶数n ,那么空白框中的语句及最后输出的n 值分别是A. n =n +1和6B. n =n +2和6C. n =n +1和8D. n =n +2和875.已知函数()3212f x ax x =+,在1x =-处取得极大值,记()()1'g x f x =,程序框图如图所示,若输出的结果20142015S >,则判断框中可以填人的关于n 的判断条件是( )A .2014n ≤?B .2015n ≤?C .2014n >?D .2015n >?76.运行如图所示的程序框图,设输出的数据构成集合A ,从集合A 中任取一个元素a ,则函数y =x a 在(0,+∞)上是增函数的概率为( )A.12B.25C.23D.3477.宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.下图是源于其思想的一个程序框图,若输入的a ,b 分别为5,2,则输出的n =A.2 B.3 C.4 D.578.执行如图所示的算法流程图,则输出的结果S的值为()A.2 B.1 C.0 D.-179.执行如图所示的程序框图,如果输入的x的值在区间[-2,-1.5)内,那么输出的y属于()A.[0,0.5) B.(0,0.5] C.(0.5,1] D.[0.5,1)80.如果执行如图的程序框图,那么输出的值是( )A .2010B .-1C .12D .2(第7题图)81.若某程序框图如图所示,则该程序运行后输出的B =A .4B .13C .40D .4182.下面程序框图是为了求出满足321000n n ->的最小偶数n ,那么在◇和两个空白框中,可以分别填入( )A .1000A >和1n n =+B .1000A >和2n n =+C .1000A ≤和1n n =+D .1000A ≤和2n n =+83.如果执行右边框图,,则输出的数S 与输入的N 的关系是( )A. 1(1)22N N +-⋅+B. 122N N +⋅+C. 1(1)22N N +-⋅-D. 122N N +⋅-84.如果执行右边框图,,则输出的数s 与输入的N 的关系是( )A. 1(1)22N N +-⋅+B. 122N N +⋅+ C. 1(1)22N N +-⋅- D. 122N N +⋅-85.已知点()mod N n m ≡表示N 除以m 余n ,例如()71mod6≡,()133mod5≡,则如图所示的程序框图的功能是( )A . 求被5除余1且被7除余3的最小正整数B .求被7除余1且被5除余3的最小正整数C. 求被5除余1且被7除余3的最小正奇数D .求被7除余1且被5除余3的最小正奇数86.执行如图所示的程序框图,若输入5,4,1n A x ===-,则输出的A 的值为( )A. -2B. -1C. 2D. 387.如图所示的程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a ,b 分别为63,36,则输出的a =( )A .3B .6C .9D .1888. 若执行如图所示的程序框图,输入1231,2,3,2x x x x ====,则输出的数等于( )A.13B.23C.1 D.289.执行右图的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为()A.5 B.4 C.3 D.290.执行如图的程序框图,则输出的S值为()A. 1B. 32C.12- D. 091.要计算1111++++232017的结果,如图程序框图中的判断框内可以填()A.n<2017 B.n≤2017C.n>2017 D.n≥201792.执行如图所示的程序框图,若输入x=8,则输出的y值为()A.34- B.12C.52D.3二、填空题93.x ,,则输出值S的取值范围是.下图是一个算法流程图,若输入值[02]94.下图是一个算法流程图,则输出的S的值是_____.95.如图是一个算法的流程图,则输出S的值是.96.如图是一个算法的流程图,则输出的n的值是▲ .97.执行如图所示程序框图,输出的S为.98.更相减损术是出自《九章算术》的一种算法.如图所示的程序框图是根据更相减损术写出的,若输入91,39a b ==,则输出的值为_____.99.右图是一个算法流程图,则输出的k 的值是 .100.执行下图的程序框图,则输出的n = .答案1.C2. B根据题中所给的程序框图,在执行完后, 不难算出输出的的值分别是,将两个量分别对各个选项逐一验证,可以发现,故选B.3. C由程序框图可知,该程序表示分段函数,,当时,解析式化为,,当时,,, 综上所述,的取值范围是,故选C.4.B①351=n ,则351=k ,0=m ,20000≤=m 成立,3521351=+=k ,02352704m =+⨯=;②7042000m =≤成立,3531352=+=k ,70423531410m =+⨯=; ③14102000m =≤成立,3541353=+=k ,141023542118m =+⨯=; ④21182000m =≤不成立,所以输出354=k .故选B . 5. B由题意得.所以输入的.执行如图所示的程序,可得:①,不满足条件,继续运行;②,不满足条件,继续运行;③,满足条件,停止运行,输出4.选B.6.B7.B根据题中所给的程序框图,可以判断出,根据判断框里的条件,就要求,从而求得,故选B.8.B由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量的值,是以为周期的周期函数,故又故选B.9.B执行程序框图,有S=4,n=1,T=3,不满足条件T>2S,S=7,n=2,T=7,不满足条件T >2S,S=10,n=3,T=13,不满足条件T>2S,S=13,n=4,T=21,不满足条件T>2S,S=16,n=5,T=31不满足条件,S=19,n=6,T=43满足条件T>2S,退出循环,输出T的值为43.故选:B.10.B模拟执行程序框图,可得:a=6,b=9,i=0,i=1,不满足a>b,不满足a=b,b=9﹣6=3,i=2,满足a>b,a=6﹣3=3,i=3,满足a=b,输出a的值为3,i的值为3.故选B.11.C12.C13.C执行程序框图:,否;否;否;……,是.输出.故选C.14.A由题意,判断框内应该判断a的值是否同时能被二除余一,被三除余一,即判断是否为整数.故选:A.15.B16.D本题考查数学文化以及程序框图问题,考查运算求解能力.i i=≠=≠i i=≠=≠5,9.58; 5.5,109;3,7.54; 3.5,85;i i=≠=≠4,8.56; 4.5,97;i==.输出 6.5i=≠ 6.5,11116,10.510;i=.17.A18.C第一次循环,;第二次循环,;第三次循环,;第四次循环,,不成立,此时结束循环,所以输出的的值为,故选C.19.B由题意得,,则;,则;,则;,则;,则;,则余数.故选B.20.B若,则:满足循环的条件,;满足循环的条件,;满足循环的条件,;满足循环的条件,;满足循环的条件,;满足循环的条件,;满足循环的条件,;满足循环的条件,,当时,不满足进行循环的条件,此时输出结果,故选B.21.B22.D根据程序框图可知函数解析式为不等式等价于或或,由上述三个不等式组可解得或的取值范围为,故选D.23.B模拟程序的运行,可得:当i=1时,3x-2≤55,解之得x≤19.当i=2时,3(3x﹣2)﹣2≤55,解之得x≤7.当i=3时,3(9x﹣8)﹣2>55,解之得x>3.满足判断框内的条件,退出循环,输出i的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第
2题
第92炼 算法——程序框图
算法与程序框图在高考中常以小题出现,难度不大,主要考察循环结构。
在处理这类问题时关键在于计算的准确。
一、基础知识:读框图时,要抓住“看头,审尾,记过程”这三点
1、看头:观察框图中变量的个数,以及赋予的初始值
2、审尾:强调细致的“审查”循环结束时,变量所取到的最后一个值,这也是易错点
3、记过程:为了保证计算的准确,在读取框图的过程中,可详细记录循环体中每经过一个步骤,变量取值的变化情况,以便于在跳出循环时能快速准确得到输出变量的值
二、典型例题:
例1:执行下图所示的程序框图,若输入2x =,则输出y 的值为 .
思路:通过框图的判断语句可知y 关于x 的函数为:
2321,01,012,1x x y x x x x x -<⎧⎪=+≤<⎨⎪+≥⎩
,所以当2x =时,322212y =+⋅=
答案:12
例2:阅读右边的程序框图,运行相应的程序,则输出i 的值为( )
A .3
B .4
C .5
D .6
思路:循环的流程如下:
① 1,2i a ==
② 2,5i a ==
③ 3,16i a ==
④ 4,65i a ==
循环终止,所以4i =
答案:B
例3:某程序框图如图所示,若输出的57S =,则判断框内为( )
A. 4?k >
B. 5?k >
C. 6?k >
D. 7?k >
思路:循环的流程如下:
① 2,4k S ==
② 3,11k S ==
③ 4,26k S ==
④ 5,57k S ==
所以应该在此时终止,所以填入4?k >
答案:A
例4:执行右面的程序框图,如果输入的N 是6,那么输出的p 是( )
A. 120
B. 720
C. 1440
D. 5040
思路:循环的流程如下:
① 1p =
② 2,2k p ==
③ 3,6k p ==
④ 4,24k p ==
⑤ 5,120k p ==
⑥ 6,720k p ==
答案:B
例5:右图是一个算法的流程图,则输出S 的值是______
思路:循环的流程如下:
① 1123S =+=
② 2
2,327n S ==+=
③ 33,7215n S ==+=
第4题
④ 44,15231n S ==+=
⑤ 55,31263n S ==+=
循环结束,所以63S =
答案:63S =
例6:执行如图所示的程序框图,若输出i 的值为2,则输入x 的最大值是( )
A .5
B .6
C .22
D .33
思路:因为输出的2i =,说明只经过了一次循环。
则第一次判断的
结果为“是”,所以x 的取值要求为132
x ->,第二次循环时,此时x 的值刷新为“12
x -”,在第二次判断为“否”,所以x 的取值要求为112322x ⎛⎫--≤ ⎪⎝⎭,从而132112322x x ⎧->⎪⎪⎨⎛⎫⎪--≤ ⎪⎪⎝⎭
⎩,解得822x <≤,x 的最大值为22
答案:D
例7.执行如图的程序框图,输出的T =( )
A .30
B .25
C .20
D .12
思路:程序执行过程中的变量数值变化如下:
① 5,2,2S n T ===
② 10,4,6S n T ===
③ 15,6,12S n T ===
④ 20,8,20S n T ===
⑤ 25,10,30S n T === 从而T S >,结束循环
所以30T =
答案:A
例8:运行如图所示的程序框图.若输入4x =,则输出y 的值为( )
A .49
B .25
C .13
D .7
思路:程序执行过程中变量数值的变化如下:
① 4,7x y ==
② 7,13x y ==
③ 13,25x y ==,则有8x y ->循环结束
25y ∴=
答案:B
例9:某班有24名男生和26名女生,数据1250,,,a a a 是该班50名学生在一次数学学业水平
模拟考试中的成绩(成绩不为0),如图所示的程序用来
同时统计全班成绩的平均数:A ,男生平均分:M ,
女生平均分:W .为了便于区别性别,输入时,男生
的成绩用正数,女生的成绩用其相反数,那么在图中空
白的判断框和处理框中,应分别填入( )
A .0?,50
M W
T A +>= B .0?,50
M W T A +<= C .0?,50
M W T A -<= D .0?,50M W T A ->=
思路:首先解决判断框,由框图可得,满足判断框条件
则进入男生的成绩统计,不满足条件则进入女生成绩统
计,依题意男生成绩记为正,女生成绩记为负,所以判
断框应填入0?T >对于矩形框,要得出A 的值,即全
班的平均值,所以可将男女生成绩作和并除以人数。
但
因为女生成绩为负数,所以0W <,所以5050
M W M W A +-=
= 答案:D
例10:如果执行如图所示的程序框图,输入正整数()2N N ≥和实数12,,,N a a a ,输出,A B ,则( )
A. A B +为12,,
,N a a a 的和 B. 2A B +为12,,,N a a a 的算术平均数
C. A 和B 分别是12,,,N a a a 中的最小数和最大数
D. A 和B 分别是12,,,N a a a 中的最大数和最小数
表的思路:可先执行几次循环,寻找规律,从而发现,A B 所代
含义:
① 1x a =,1A a =,所以1a A =且1a B =
② 2x a =,若2a A >,则2A a =;若21a A a <=,则2B a =
③ 3x a =,若3a A >,则3A a =;若3a A ≤,则A 不变,并判断3a 与B 的大小,若3a B <,则3B a =,否则,B 不变
经过几次循环后便可发现A 代表的是经过k 次循环后,12,,
,k a a a 的最大值,B 代表的是最小值,从而可得A 和B 分别是12,,
,N a a a 中的最大数和最小数 答案:D。
