定解条件初始条件
偏微分方程的定解条件与解的存在唯一性

偏微分方程的定解条件与解的存在唯一性偏微分方程(Partial Differential Equation, 简称PDE)是数学领域中的重要研究对象,广泛应用于物理学、工程学、金融学等领域。
在求解偏微分方程时,我们需要考虑定解条件,以确保解的存在和唯一性。
本文将探讨偏微分方程的定解条件,并讨论解的存在唯一性。
一、偏微分方程的定解条件在求解偏微分方程之前,我们需要明确的是问题的定解条件。
定解条件是指在区域Ω上关于未知函数u及其偏导数的附加条件。
常见的定解条件包括初始条件和边界条件。
1. 初始条件(Initial Condition)初始条件是在区域Ω的某个子集Ω₀上给定的函数值及其偏导数,常用符号表示为u(x, t₀) = g(x, t₀),其中g(x, t₀)为已知函数,t₀为给定的初始时间。
2. 边界条件(Boundary Condition)边界条件是在区域Ω的边界上给定的函数值及其偏导数,常用符号表示为u(x, t) = f(x, t),其中f(x, t)为已知函数。
在一些情况下,还需要考虑特殊的边界条件,如周期性边界(Periodic Boundary Conditions)和运动边界(Moving Boundary Conditions)等。
二、解的存在唯一性偏微分方程的解的存在唯一性是指在给定的定解条件下,方程是否有解以及解是否唯一。
1. 解的存在性对于某些偏微分方程,我们可以通过适当的数学工具(如变分法、分离变量法、线性化等)证明其存在解。
然而,并非所有的偏微分方程都具备解的存在性,存在着某些无解的情况。
因此,对于求解偏微分方程问题,我们需要首先考虑其解的存在性。
2. 解的唯一性在一些情况下,即使偏微分方程存在解,其解也不一定是唯一的。
对于线性偏微分方程,我们可以通过使用变分法或利用极大模原理来证明解的唯一性。
而非线性偏微分方程的唯一性则比较复杂,通常需要借助于更加深入的分析和数学工具。
定解条件
自由冷却:规定了从杆端流出的热流强度(-kun )与温度差(u xa -)
之间的关系。
即:-kun xa h(u xa - ), h : 热交换系数
即:(u Hun ) xa ,
Hk n
若说杆的两端自由冷却:在x = l端,nˆ即xˆ,(u Hux ) xl 在x = 0端,nˆ即-xˆ,(u Hux ) x0
若h ? k,即:H 0,则u 0 (退化为第一类边界条件) x0 u 0 xl
又如:作纵振动杆,在某一端点x = a既非固定也非自由而是通过弹性联结体 连接到固定物上。
弹性联结:规定杆中弹性力(YSun)等于弹性连接物中的弹性恢复力 (-ku, k为劲度系数)
YSun xa ku xa
即:(u+ YS k
以上边界条件都是线性的(u,ux都为一次的) 其中f 0的边界条件又叫齐次的。除此以外,还有其它类边界条件。
杆的一端挂有重物作纵振动。
对重物有:Mg T Ma Mutt T M (g utt )
杆端受力T ', 对杆端有:YS ux xl T ' Mg M utt xl
T T’ 边界条件中出现了u对x,u对t的偏导数。
x l
u x0 0,ux xl 0
例:细杆导热:qv
ku,
从u高
u低,u
v i
u
v j
u
v k
u
x y z
nˆ(xv)
nˆ(xv)
u u n x
u u x
n x
若杆的某端点x = a有热流f (t)沿该端点外法线方向流出: -kun xa f (t) 若杆的某端点x = a有热流f (t)沿该端点外法线方向流入: -kun xa -f (t) 若端点绝热:un xa 0
D5-2 定解条件

x 0 为原点, 取弦的水平位置为 x 轴,
弦作自由(无外力)横振动,所以泛定方程为齐次波动方程
utt a2uxx 0
(2)确定边界条件 对于弦的固定端,显然有 u(x,t)|x=0=0, ux(x,t)|x=l=0 另一端自由,意味着弦的张力为零.则
2016/9/30
u x x , t x l 0
定义:系统的物理量在边界上具有的情况。
常见的线性边界条件分为三类:
A.第一类(狄利克雷)边界条件 给出未知函数在边界上的函数值。
例2:两端固定的弦振动时的边界条件:
u( x, t )
x 0
0
和
u( x, t )
x l
0
2016/9/30
4
例3:细杆热传导
x0
xl
细杆x=l端的温度处于恒温状态,边界的数理方程
h
· ·
状如图所示,且弦处于静止状态,即有方程
l x
l/2
初始速度 ut ( x, t ) 初始位移 u( x , t )
t 0
t 0
2016/9/30
2h x l 2h ( l x ) l
0
l x [0, ] 2 l x [ , l ] 23
(二)边界条件
ku YSux
x l
弹性力: f ku
则在端点
(u
YS ux ) k
0
u ) n
xl
f ( x0 , y0 , z0 , t )
x
第三类边界条件的基本形式: (u H
边界x0 , y0 , z0
这些是最常见的线性边界条件,还有其它形式。
(三)衔接条件
《流体力学》课件 1.17 定解条件

k
T n
介质 2
(三)、固壁边界处
1. 能量边界条件
Tf Tw
k
T n
f
k T n w
2. 速度边界条件
(1) 切向速度
Vf Vf
Vw Vw
粘性流体 理想流体
(2)法向速度
n
Vf
n
Vw
Fx, y, z,t 0 Fx dx, y dy, z dz,t dt 0
1 R2
1 0
sij2 in j 0
p
1
p2
22
sij2ni
n
j
1 3
skk2
1 R1
1 R2
忽略表面张力
sij2 in j 0
p
2
2
2
sij2
ni
n
j
1 3
skk2
p0
2. 运动学边界条件
n
V1
n
V2
例题:试写出如图所示自由液面 波动的运动学边界条件。
答:设自由面方程为
F内 x 0t 2 y2 a2 0,F外 x2 y2 b2 0
1. 无粘流体在内、外圆柱面上的速度边界条件
F内 x
uf
F内 y
f
F内 z
wf
F内 t
0
F外
x
uf
F外 y
f
F外 z
wf
F外 t
0
x
uf
0
x0 0 u f
内圆柱体边界
y f 0
xu f y f
定解条件
一、初始条件
V
r,t0源自V1r,pr,
t
0
p1 r , r, t 0
微分方程的定解条件与特殊解法

定义:在定解区 间的闭区间端点 上,微分方程的 解必须满足一定 的连续性条件。
类型:对于一阶 微分方程,连续 性条件包括自然 边界条件、周期 边界条件等。
作用:连续性条 件是保证微分方 程解的连续性和 物理意义的重要 条件。
应用:在解决实 际问题时,需要 根据具体问题的 性质和要求,选 择适当的连续性 条件。
PART THREE
定义:欧拉方法是微分方程数值解法的一种,通过离散化微分方程,用差分代替微分,得到离 散化的数值解。
原理:利用已知的初值条件,逐步推算出微分方程的解在各个离散点上的近似值。
步骤:先确定初始值,然后按照一定的步长逐步计算出各个离散点上的近似解。
优缺点:欧拉方法简单易懂,易于实现,但精度较低,稳定性较差。
描述生物系统的动态行为
生理学和病理学中的数学模型
添加标题
添加标题
药物设计和药物动力学
添加标题
添加标题
医学影像和信号处理
汇报人:XX
优点:计算简单、易于编程实现、精度可控等。
PART FOUR
力学:描述物体运动规律,如万有引力定律、牛顿第二定律等。 电磁学:解释电磁场的变化规律,如麦克斯韦方程组等。 热学:研究热量传递规律,如热传导方程等。 波动:描述波动现象,如波动方程等。
航空航天:飞行器设计和优化中的气动动力学方程求解 机械工程:机器人运动轨迹规划和控制算法的微分方程求解 化学工程:化学反应动力学模型和传递过程的动力学方程求解 交通工程:交通流理论和车辆动力学的微分方程求解
注意事项:需要满 足一定的条件才能 使用分离变量法
定义:通过引入新的变量来简化微分方程的形式,从而求解微分方程的方法。 适用范围:适用于形式较为复杂的微分方程,特别是难以直接求解的方程。 常用方法:常见的变量代换法包括三角代换、指数代换等。 实例:通过变量代换法,可以将一些复杂的微分方程转化为容易求解的形式。
7-2定解条件

解:初始位移
初始速度
u
t0
tan
x
tan
l
x
x
l 2
xห้องสมุดไป่ตู้
l 2
u 0 (还没来得及运动) t t0
3. 稳定方程:与时间无关,没有初始条件
二. 边界条件 描述边界上各点在任一时刻的状况.
1. 弦振动边界条件 例如两端固定的弦:
2. 杆振动边界条件 ①两端固定的杆:
u u
x0 xl
0 0
t≥0
数学物理方法
定解条件
丁成祥
§7.2 定解条件
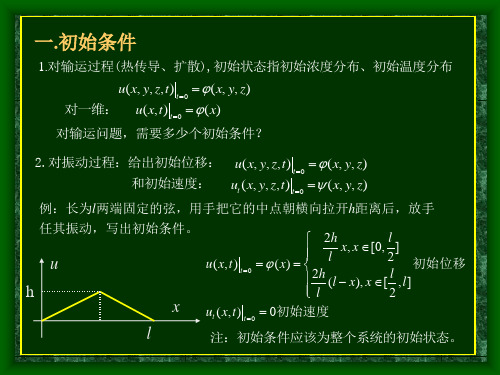
一. 初始条件 给出初始时刻(t=0)介质上任一质点的状况.
1. 对波动方程,要给出初始位移和初始速度
u t0 x, y, z
u t
t0
x, y, z
2. 对于热传导方程,只须给出初始时刻的温度分布
u t0 x, y, z
例. 如右图所示,将弦轻轻拉起,再突然放开,试写出振动方程的初始条件(θ 很小).
H k
u
xl
H k
u0
或
u x
hu
xl
hu0
此为初稿,疏漏之处,敬请指正
数学物理方法
类型 一类 二类
三类
定解条件
丁成祥
总结:三类边界条件
表达式
u (,t)
u f (,t) n
u n
hu
f
(, t )
此为初稿,疏漏之处,敬请指正
“流出”,而非“流入”,或者说“流入为负”. 如果左端绝热,则边界条件为
③边界按“牛顿冷却定律”散热;则
u 0 x x0
k
u n
H[u(,t) u0 ]
初始条件与边界条件

x0
xl
若弦的两端不是固定的,而是按照规律 u1(t), u2(t) 在运动,则其边界条件为
u x0 u1(t ); u xl u2 (t )
热传导问题:当物体与外界接触的表面温度 f(M,t) 已知时,其边界条件为
u f (M,t) S
第二类边界条件:给出 u 沿 S 的外法线方向的
ut a2uxx 0
u |t0 ( x)
( x ,t 0) ( x )
热传导方程的Cauchy问题
utt u |t
0
a 2uxx
(x
)
0
ut |t0 ( x)
( x ,t 0) ( x )
0, 0 0, 0 0, 0
第一类边界条件 第二类边界条件 第三类边界条件
§1.3 定解问题的提法
初始条件和边界条件都称为定解条件。 定解问题是指偏微分方程和相应定解条件的结合体。
偏微分方程和相应初始条件构成的定解问题称为初 值问题或者柯西(Cauchy)问题。
边界条件是给出具体物理现象在边界上所处的物 理情况。根据边界条件数学表达方式的不同,一 般把边界条件分为三类。设 u 是未知函数,S 为边界,则分类如下:
第一类边界条件:直接给出 u 在边界 S 上的值
u S
f1 .
弦振动问题:如果弦的两端是固定的,也就是说 端点无位移,则其边界条件为
u 0; u 0
(x, y,z)
uzz )
0
(u u) f ( x, y, z, t )
n
(x, y,z) ,t 0 (x, y,z)
定解条件和定解问题

定解条件与定解问题含有未知函数得偏导数得方程叫偏微分方程,常微分方程可以瞧成就是特殊得偏微分方程。
方程得分数就是1得称为方程式,个数多于1得叫做方程组。
方程(组)中出现得未知函数得最高阶偏导数得阶数称为方程(组)得阶数。
如果方程(组)中得项关于未知函数及其各阶偏导数得整体来讲就是线性得,就称方程(组)为线性得,否则就称为非线性得。
非线性又分为半线性、拟线性与完全非线性。
一、定解条件给定一个常微分方程,有通解与特解得概念。
通解只要求满足方程,即满足某种物理定律,而不能完全确定一个物理状态。
特解除了要求满足方程还要满足给定得外加(特殊)条件。
对偏微分方程也就是如此,换句话说,只有偏微分方程还不足以确定一个物理量随空间与时间得变化规律,因为在特定情况下这个物理量还与它得初始状态与它在边界受到得约束有关。
描述初始时刻得物理状态与边界得约束情况,在数学上分别称为初始条件(或初值条件)与边界条件(或边值条件),她们统称为定解条件。
初始条件:能够用来说明某一具体物理现象初始状态得条件,即描述物理过程初始状态得数学条件。
边界条件:能够用来说明某一具体物理现象边界上得约束情况得条件,即描述物理过程边界状态得数学条件。
定解条件:初始条件与边界条件得统称。
非稳态问题:定解条件包括初始条件与边界条件。
稳态问题:定解条件为边界条件。
1、弦振动方程 ( )初始条件就是指初始时刻()弦得位移与速度。
若以, 分别表示弦上任意点得初始位移与初始速度,则初始条件为:边界条件就是指弦在两端点得约束情况,一般有三种类型。
(1)第一类边界条件(狄利克雷(Dirichlet)边界条件):已知端点处弦得位移就是,则边界条件为:或当时,表示在该点处弦就是固定得。
(2)第二类边界条件(诺伊曼(Neumann)边界条件):已知端点弦所受得垂直于弦线得外力或,则边界条件为:或当,表示弦在端点处自由滑动。
(3)第三类边界条件(混合边界条件或罗宾(Robin)边界条件:已知端点处弦得位移与所受得垂直于弦线得外力得与:或,其中表示两端支承得弹性系数,当时,表示弦在该端点处被固定在一个弹性支承上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初始速度:
u t
(
x,
t0
)
(
x)
定解条件---边界条件
当求解区域D不是整个空间时,
在区域边界D 上,提出边界条件:
(D)Dirichlet 边界条件:u在边界上的 值是给定的;
(N)Neumann边界条件:u沿法方向导
数
u n
的值给定;
(R)Robin边界条件: 定
u
n
au
的值给
定解条件---自然边界条件
定解条件---初始条件
PDE 一般具有无穷多解,为选出一个满足实际 物理过程的解,需要从物理过程提出定解条件 发展方程的初始条件:给定特定时刻的物理状 态 热传导方程、扩散方程、薛定谔方程(关于时 间t是求一阶导数)
u(x, t0)= (x)
定解条件---初始条件
波动方程:关于时间t求二阶导数
初始位置:u(x, t0)= (x)
定解条件---无穷远处边界条件
有界条件:u有界当x趋向无穷远点 衰减条件 u(x, t) 0,| x |
2
薛定谔方程 归一化条件 | u | dxdydz 1 R3
声波、电磁波的散射 Sommerfeld外辐
射条件
lim r(u u ) 0 r r t
有界性条件:在非奇异情形下,物理量 应该是有界的,特别是在利用极坐标、 柱坐标以及球坐标时,在r=0处有界
周期性条件,在平面极坐标、球坐标等 中,物理量关于经度的角度是以2π为周 期的
定解条件---物理实现
(D)边界条件 弦振动:一维:端点固定(吉他等弦乐器)
高维:边界固定(鼓) 扩散方程:边界可渗透物质,流出边界的
物质立即被冲走 热传导:边界保持给定温度 泊松方程:静电场 边界接地
定ቤተ መጻሕፍቲ ባይዱ条件---物理实现
(N)边界条件 弦振动:端点在竖直方向自由移动,ux=0 或受到给定外力作用 ux=g(x) 扩散方程:边界隔绝 ux=0 热传导方程:绝热 ux=0
定解条件---物理实现
(R)边界条件 弦振动:端点在竖直方向受弹簧弹力作用 扩散方程:边界有扩散, 扩散速率正比于内外浓度差 热传导方程:边界有热交换 交换速率正比于内外温度差
