最新Qh2-8线元法任意路线与匝道曲线坐标正、反算程序
任意匝道坐标正反算程序
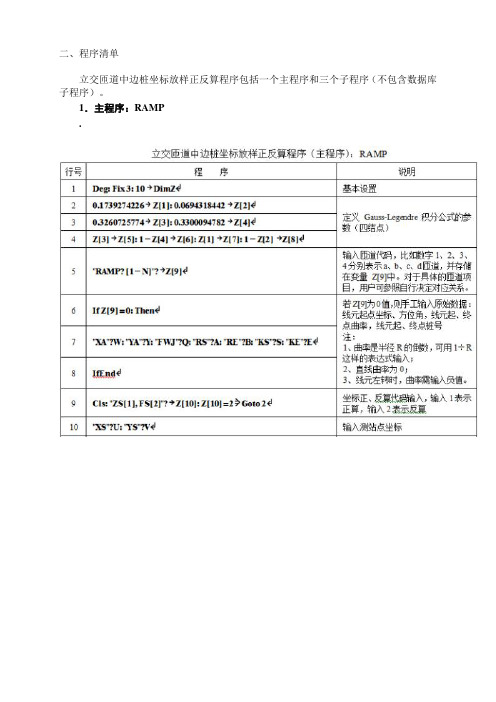
二、程序清单立交匝道中边桩坐标放样正反算程序包括一个主程序和三个子程序(不包含数据库子程序)。
1.主程序:RAMP..2.子程序1:RAMP-ZBJS功能:使用Gauss-Legendre积分公式(四结点)计算匝道坐标。
..3.子程序2:RAMP-XS功能:显示计算结果。
.特别说明:在程序第2行,Locate 4, 3, J后面有一个度的符号(可按“度分秒”的那个按键输入),注意不要漏了。
.4.子程序3:RAMP-DATA功能:调用相关匝道的数据库子程序。
..三、程序变量清单立交匝道中边桩坐标放样正反算程序变量清单见下表。
..四、程序运行流程RAMP程序运行流程示意图如下:...1.互通匝道数据库子程序格式说明每条互通匝道建立一个数据库子程序,子程序名称格式建议为:RAMP-DAT1-1RAMP-DAT1-2RAMP-DAT1-3……本来,笔者为了不建立太多的数据库子程序,曾将尝试将一条互通所有匝道的数据全部写在一个子程序RAMP-DATA1中(参照路线计算ROAD-2程序采用的数据库子程序的办法),后来发现:一是数据太过庞大,查找和修改数据相当麻烦(按上、下键按得手指发酸),二来逻辑判断语句太多,影响计算速度,因此舍弃。
每一段线元写成一行数据,格式如下:2.立交匝道参数辅助计算EXCEL程序的使用说明前面介绍了线元的数据格式,这里小结一下,每条线元需要确定以下数据:(1)线元起点的X/Y坐标;(2)线元起点的切线方位角;(3)线元起、终点的曲率(半径的倒数,左偏为负);(4)线元起、终点的桩号。
以上参数,要数第(3)种参数最难确定,因为在设计图表中没有直接标注,需要根据其它相关参数进行计算确定。
除第(3)种参数外,其它三种参数的确定就比较简单了,因为他们基本可以在匝道的设计图表中直接获取。
3.互通匝道数据库子程序的编写为说明清晰起见,笔者将每条匝道的每个线元都一一进行编号,比如a匝道的第一条线元编为“a-1”,读者可结合立交匝道设计图表进行判读。
线元法线路坐标正反算程序

经苦心钻研,奋战多日,终于编写出了代码短,速度快,精度高,功能全的线路坐标正反算程序,欢迎试用并提出宝贵意见。
功能简介及特点:1、选用高斯-勒让德公式作计算内核,保证精度,模块化设计,便于扩充功能。
2、线元数据可自动从数据库调用,也可手工输入。
3、可管理多条线路,如里程不在线路或线元范围,将警告里程偏大、偏小。
4、边桩计算设计为导线式递推方式,可用于由一个中桩推出结构物所有角点坐标。
5、反算实现了智能化操作,只需输入线路号(或手工输线元资料)、坐标,不需近似里程,即可自动从起点向后开始试算出里程、位置,如对算出里程、位置表示怀疑,还可以让计算器从终点起再向前试算下一个可能的位置(匝道、回头曲线同一坐标可能会有一个以上结果)。
第三次及以后试算才要求输入近似里程。
6、程序代码规范简洁,便于阅读、理解。
完整程序清单:ZFS %正反算主程序B=.1739274226:C=.5-B:Lbl 1:U"0 ZS 1 FS"=0=>Prog "ZS":≠>U=1=>Prog"FS":≠>Goto 1ZS %正算子程序{K}:Prog"ZZ":I=0:{I}:I"L"≠0=>"Prog"WY":≠>Prog"ZB"FS %反算子程序{KVW}:V"XC"W"YC":Lbl 2:Prog "ZZ":I=V-S:J=W-T:Pol(I,J: J=J-F:K=K+Rec(I,J:AbsI<1m=>Prog"WZ":≠>Goto 2ΔM=0:{M}:M"0 NEXT"=0=>U=U+1:Goto 2:≠>U=1ZZ %高斯法中桩子程序(4节点)Prog"XL":M=K-L:O=(P-R)÷2PQR:D=.0694318442:E=.3300094782:F=1:G=1-E:H=1-D:I=5:Lbl 1:C[I]=A+MrC[I](1÷P+OMC[I]:Dsz I:Goto 1:S=X+M(BcosD+CcosE+CcosG+BcosH:T=Y+M(BsinD+CsinE+CsinG+BsinHWY %外移点计算子程序Lbl 1:J=90:{J}:J=F+J"<":F=J:S=S+Rec(I,J:T=T+J: Prog"ZB":I=0:{I}:I"L"≠0=>Goto 1WZ %位置显示子程序"KJ":K:Pause 1:J◢ZB %坐标显示子程序"XY":S:Pause 1:T◢YC %异常处理子程序U=1=>K=L:U=2ΔU=3=>K=M:U=4ΔU=5=>{K}:U=4ΔK<L=>"<<!":Z=1ΔK>M=>">>!":Z=1DL %断链处理子程序"DL":K=L:I>0=>K=L+Q-------------------------以上为程序运算部分,以下为数据库部分-------------------------------XL %线路数据库选择子程序Lbl 1:Z=0:N"0 SD"=0=>Prog"0"△N=1=>Prog"1"△N=2=>Prog"2"△...有几条线路仿上行格式输几行Z=1=>{NLXYOPQRK}:Goto 10 %手工输入子程序L"K0"XYAQ"LS"P"R0"R"RN":M=L+Q:Prog"YC"1 %线路一数据库子程序①Lbl B:L=线路起点里程:M=线路终点里程:Prog"YC":Z=1=>Goto EΔ②Q=线元长:P=起点半径:R=终点半径:K≤L+Q=>X=起点X坐标:Y=起点Y坐标:A=起点方位角:Goto EΔL=L+Q:③......④Q=短链长:K<L+Q=>Prog "DL":Goto BΔL=L+Q:⑤Q=线元长:P=起点半径:R=终点半径:K≤L+Q=>X=起点X坐标:Y=起点Y坐标:A=起点方位角:Goto EΔL=L+Q:⑥......⑦Q=线元长:P=起点半径:R=终点半径:X=起点X坐标:Y=起点Y坐标:A=起点方位角:Lbl E2 %线路二数据库子程序输入要求和线路一相同。
部分Q程序简介

近期卡西欧5800程序新书《fx-5800P公路与铁路施工测量程序》配套的多媒体教学光盘。
1)QH2-7程序,含SUBQ2-71~SUBQ2-77子程序
交点法非对称基本型曲线坐标正、反算程序
可输入测站与后视点坐标,计算极坐标放样参数
2) QH2-8程序,含SUBQ2-81~SUBQ2-87子程序
线元法任意路线与匝道曲线坐标正反、算程序
可输入测站与后视点坐标,计算极坐标放样参数
3) QH2-9程序,含SUBQ2-91~SUBQ2-94子程序
线元法任意路线与匝道曲线直线斜交程序
可输入测站与后视点坐标,计算极坐标放样参数
4) QH2-10程序,含SUBQ2-10子程序
任意个变坡点连续竖曲线高程计算程序
QH2-7/QH2-8/QH2-9程序的反算与斜交功能
理论上用我们最新研发的拟合圆弧直接解算法
使缓和曲线正交与斜交反算时间
由2.5分钟减小到→7秒钟,计算速度提高21倍。
QH2-7/QH2-8/QH2-9程序
大量使用了fx-5800P先进的复数与串列功能
其中,QH2-8/QH2-9程序
最多可以对含150个线元的任意路线或匝道
进行坐标正反、算与斜交计算
计算精度超高,坐标计算误差≤0.5mm
而高速公路或高速铁路一个标段的线元数≤50
可以全面满足公路与铁路工程用户的测算需求。
公路工程坐标正反算原理及5800计算器程序

0年11月14日目录一、坐标正算基本公式...............................................................02 二、坐标反算原理...............................................................04 三、高程数据库录入变换.........................................................05 四、计算器程序...............................................................07 01、ZBZS(坐标正算)...............................................................07 02、ZBFS (坐标反算)...............................................................08 03、GCJF(高程积分)...............................................................09 04、PJFY (坡脚放样)...............................................................10 05、JFCX (积分程序)...............................................................11 06、ZBFY (坐标放样)...............................................................11 07、DT (递推)...............................................................12 08、HP (横坡)...............................................................13 09、LK (路宽)...............................................................14 10、SJK1(平面数据库)......................................................14 11、SJK2(纵面数据库)......................................................14 12、SJK3(左路宽度数据库)......................................................15 13、SJK4(右路宽度数据库)......................................................15 14、SJK5(横坡数据库) (16)15、SJK6(下边坡数据库)......................................................16 16、SJK7(左上边坡数据库)......................................................17 17、SJK8(右上边坡数据库)......................................................18 五、后记 (19)0年11月14日CASIO 5800计算器公路工程测量程序一、正算所涉及的计算公式XR id XαβBd Yd ld βI图表 1在图1中,A 点为回旋曲线起点,B 点为回旋曲线止点,I 点为所求坐标点。
公路曲线及匝道多线路正、反算综合程序四(4.3修改版)

公路曲线及匝道多线路正、反算综合程序(修改版)这里才是真正的坐标计算程序,上面那个ZDY-1是计算各个要素,可以作为校核之用。
⑴有关资料采用复化辛普森公式:X=XA+H / 6(cos aA+4∑cos aK+1/2 +2 ∑cos aK +cos ai)(K=0~n-1)Y=Y A+ H / 6(sin aA+4∑sin aK+1/2 +2 ∑sin aK +sin ai)(K=0~n-1)式中:aA为回旋曲线起点A的切线方位角;aK+1/2为里程DX K+1/2点切线方位角;aK为里程DXK点切线方位角;ai为里程DKi点切线方位角。
对于上式,虽然是由回旋曲线导出的,但该式也适用直线段和圆曲线段。
⑵ZDY-8程序(主程序)Lbl 0 ∶“1.KB=>XY”: “2.XY=>KB”: {J}:J=1=> Goto 1∶≠> GOTO 2∶LbI 1∶{H L O}∶H“KP”L“B”O∶Prog ″A BCD1″∶Prog ″XY9 ″∶Prog ″XY10 ″∶Goto 1∶Lbl 2∶Prog ″XY8 ″∶GOTO 0 EXE⑵支程序①XY8程序(反算程序)Lbl 0 ∶H“KP”∶Prog ″A1″∶Prog ″Z BZS ″∶{LO}∶L”X0”∶O”Y0” ∶U= Z - 90∶P= (O-N)cos U -(L-M) sin U ∶AbsP≥0.001=>H=H+P∶GOTO 0 : ≠>H” KI =” ∶″ZH= ″∶H▲V= (O -N)cos Z - (L -M) sin Z ∶″BJ= ″∶V▲②XY9程序(正算程序)P=(E-D)÷(G-F)∶Q= H-F∶I=PQ ∶R =8∶LbI 3∶R[R]=C+RQ(RI÷8+2D)r÷16∶DSZ R∶Goto 3∶R=C∶M“X Z”=A+Q∑(cosR[2K]+4 cos R[2K+1]+cos R[2K+2],K,0,3)÷24: ″XZ= ″∶M▲N“Y Z”=B+Q∑(sinR[2K]+4 sin R[2K+1]+sin R[2K+2],K,0,3)÷24 : ″YZ= ″∶N▲Z“QI”=360 Fr ac((Z+360) ÷ 360 ) :“Z=”:Z▲③XY10程序(边桩计算程序)U“X B”=M+Lcos(Z+O)∶″X B= ″∶U▲V“Y B”=N+Lsin(Z+ O)∶″Y B= ″∶V▲{TS}∶W=Z+O∶“W=”:W▲E“X1”=U+S cos(W+T)∶″X1= ″∶E▲F“Y1”=V+S sin(W+T)∶″Y1= ″∶F▲为何红色的变量总是变成那个起始的方位角呢?请帮忙修改一下,谢谢!!!!④ABCD程序系列⑴ABCD1程序第一条匝道AC MODE 5 1 ABCD ALPHA 1 EXE 1H≤G =>H≥F=>F“KA”=***∶A“XA”=***∶B“Y A”=***∶C“QA” =***∶D“PA” =***∶G“KB” =***∶E“PB” =***∶ΔΔH≤G =>H>F=>F“KA”=***∶A“XA”=***∶B“Y A”=***∶C“QA” =***∶D“PA” =***∶G“KB” =***∶E“PB” =***∶ΔΔH≤G=>H>F=> F“KA”=***∶A“XA”=***∶B“Y A”=***∶C“QA”=***∶D“PA” =***∶G“KB” =***∶E“PB” =***∶ΔΔ……H≤G=>H>F=>F“KA”=***∶A“XA”=***∶B“Y A”=***∶C“QA” =***∶D“PA”=***∶G“KB” =***∶E“PB” =***∶ΔΔ⑵ABCD 2程序第二条匝道AC MODE 5 1 ABCD ALPHA 2 EXE 1H≤G =>H≥F=>F“KA”=***∶A“XA”=***∶B“Y A”=***∶C“QA” =***∶D“PA” =***∶G“KB” =***∶E“PB” =***∶ΔΔH≤G =>H>F=>F“KA”=***∶A“XA”=***∶B“Y A”=***∶C“QA” =***∶D“PA” =***∶G“KB” =***∶E“PB” =***∶ΔΔH≤G=>H>F=> F“KA”=***∶A“XA”=***∶B“Y A”=***∶C“QA”=***∶D“PA” =***∶G“KB” =***∶E“PB” =***∶ΔΔ……H≤G=>H>F=>F“KA”=***∶A“XA”=***∶B“Y A”=***∶C“QA” =***∶D“PA”=***∶G“KB” =***∶E“PB” =***∶ΔΔ⑶ABCD 3 程序第三条匝道AC MODE 5 1 ABCD ALPHA 3 EXE 1H≤G =>H≥F=>F“KA”=***∶A“XA”=***∶B“Y A”=***∶C“QA” =***∶D“PA” =***∶G“KB” =***∶E“PB” =***∶ΔΔH≤G =>H>F=>F“KA”=***∶A“XA”=***∶B“Y A”=***∶C“QA” =***∶D“PA” =***∶G“KB” =***∶E“PB” =***∶ΔΔH≤G=>H>F=> F“KA”=***∶A“XA”=***∶B“Y A”=***∶C“QA”=***∶D“PA” =***∶G“KB” =***∶E“PB” =***∶ΔΔ……H≤G=>H>F=>F“KA”=***∶A“XA”=***∶B“Y A”=***∶C“QA” =***∶D“PA”=***∶G“KB” =***∶E“PB” =***∶ΔΔ⑷ABCD i 第i条匝道注:式中的“**”便于输入数据时便于识别,避免输错,因此在计算器输入时均可将“**”删去。
线元法计算器兼匝道程序(精编文档).doc

【最新整理,下载后即可编辑】5800 计算程序主程序QXJSLbI 0: “1.SZ=>XY”:“2.XY=>SZ”“3.GC=>SQX”:? Q :Q=1=> Goto1:Q=2=>Goto2:Q=3 => Goto3LbI 1: “CE:X”?G:“CEY:”?H:Prog“XLXY”: LbI A: “K= ” ?S: Prog“KM”:“-B,0,B=”? Z: “σ右交角=”?M:Prog“SUB1”: Fix 4:Cls“X=”: Locate3,1,N◢“Y=”: Locate3,1,E◢Prog“JI”:Goto ALbI 2: “X=”? B: “Y=”? C:B→N: C→E:Prog“SUB2”: “K =”:S◢“-B,0,B=”:Z◢Goto 0LbI 3: 0→B: “H-B”?B:B→Z[9]: LbI D: Prog“XLXY”: “KM”?Z: Prog“KM”:“-B,0,B”?D:Prog“H”Fix 5:“H=”:H-Z[9] →H◢“I=”: I◢Goto D说明:Q: 代表正反算及竖曲线,其中1 为正算,2 为反算;3代表竖曲线;S: 代表里程;Z :代表偏移距离;M :代表偏移角度(以线路前进方向为X 方向,顺时针转为正;N :X 坐标;E :Y 坐标;F :切线方位角;SUB1 正算子程序0.5 (1÷R-1÷P)÷L→D:S-O→XU+∫(cos(A+(X÷P+DX2)×180÷π,0,X)→NV+∫( sin(A+(X÷P+DX2)×180÷π,0,X)→EA+(X÷P+DX2)×180÷π→FN+Zcos(F+M) →N:E+Zsin(F+M) →EReturnSUB2 反算子程序Lbl 1:0→Z :1→Q :Prog“KM”: Prog“SUB1”Pol(N-B+10^(-46), E-C+10^(-46)):Isin(F-90-J) →W:S+W→SIf Abs(W)>0.0001 :Then Goto1Lbl 2: 0→Z :Prog“SUB1”:(C-E) ÷sin(F+90) →Z次程序JIClstatPol(N-G,-E-H):ClsIf J<0:Then J+360→Y:Ease J→Y:Ifend“F J L=”:I◢“F W J=”:Y▲ DMS ◢XLXZ(线路选择)1→I:“XLXZ:Z=1:A=2,B=3,C=4,D=5,E=6,F=7,L=8”?I: I →Z[1]: IF I =0:Then Goto 0:Else Goto 1:IfEndLbI 0 : “F”?A: “QDZH”?O: “X”?U: “Y”?V: “R1”?P: “R2”?R:“L”?L: Goto 1LbI 1SUB0 ( 数据库)Goto1 ↙Lbl 1IF S<157687.528:Then157547.528→o :2884169.2517→U:471475.6573→V:98 °32 ′43.08 ″→A:10^45→P:10000;→R:140→L: Return:IfEnd 说明:S :里程;O 为线元起点里程;U 为线元起点X 坐标;V 为线元起点Y 坐标;A 线元起点切线方位角;P 线元起点半径(左转为负右转为正);R 线元终点半径(左转为负右转为正)高程计算子程序(H)程序名:HP rog “S1”:C-T→F:Z-F→S:C+T→E:G-TI→Q:If T=O:Then Q+S I→H:Goto 0:Else If Z<F:Then Q+SI→H:Goto 0:Else If Z≤E:T hen Q+SI+S2÷2÷R→H:Goto 0:LbI 0:H:If D=0:Then Goto I:Else Prog“I”:H+V→H:Goto ILbI I高程超高计算程序(I)程序名:IIf Z[3]=1:Then Prog “I1”:Goto 1: IfEndLbI 1: If W=1:Then Goto Z:Else Goto X: IfEndLbI Z:If S=0:Then Abs(D)×M→V:Goto 2:Else Abs(D)×((N-M)×(Z-C)÷S+M)→V:Goto 2:IfEnd:LbI X:If S=0:Then Abs(D)×M→V:Goto 2:Else Abs(D)×(((3((Z-C)÷S)2-2((Z-C)÷S)∧(3))×(N-M))+M)→V:Goto 2:IfEndLbI 2:Abs(D)→E:V÷E→I:I(E-K)→V②-1程序名:S1(线路1高程竖曲线要素子程序)If Z[1]=1:Then Goto 1:Else If Z[1]=2:Then Prog“SA”: Else I f Z[1]=3:Then Prog “SB”: Else If Z[1]=4: Then Prog“SC”: Else If Z[1]=5:Then Prog“SD”: Else If Z[1]=6: Then Prog“S E”: Else If Z[1]=7:Then Prog“SF”: Else If Z[1]=8:Then Pro g“SL”:IfEndGoto 1LbI 1If Z≤26157.8:Then -200000→R:157.8→T:26000→C:37.1→G:0.012 22→I:Return:IfEnd程序字母说明:R-竖曲线半径(分正负:凹曲线为正,凸曲线为负);T-竖曲线切线长(标段结尾或开头没有竖曲线的输0);C-竖曲线交点桩号;G-交点桩号高程(未竖曲线调整的);I-竖曲线前纵坡③-1程序名:I1(线路1高程超高参数子程序)If Z[1]=1:Then Goto L:Else If Z[1]=2:Then Prog“IA”: Else I f Z[1]=3:Then Prog “IB”: Else If Z[1]=4: Then Prog“IC”: Else If Z[1]=5:Then Prog“ID”: Else If Z[1]=6: Then Prog“I E”: Else If Z[1]=7:Then Prog“IF”: Else If Z[1]=8:Then Pro g“IL”:IfEnd1.5→K:If D<0:Then Goto L:Else Goto R:IfEnd:LbI LIf Z≤26735.555:Then 1→W: 120→S:26615.555→C:-0.02→M:0.02→N:Goto 0:IfEndLbI RIf Z≤26735.555:Then 1→W:0→S:-0.02→M: Goto 0:IfEndLbI 0字程序中字母表示说明:K-中央分隔带半幅宽(中桩标高至中桩中线距离,无分隔带则为0)本线路中为0;W-超高方式参数(W=1为一般直线方式超高,W=2为三次抛物线方式超高);S-超高渐变段距离(不是渐变段则输入0);C-超高渐变段起点桩号(不是渐变段,无需输入);M-超高段起点横坡,N-超高渐变段终点横坡(不是渐变段,无需输入)H (高程主程序)Fix 3 :Lb1 3: “ K=” ?Z: Prog“SQX”:(P-Q) ÷ Abs(P-Q) →W If Z<(H-T):Then(H-Z) × P →X:Goto 2:IfEndIf Z ≥ (H-T) And Z<H:Then (H-Z) × P+(Z-H+T)2÷ (2WR)→X:Else (H+T-Z)2÷ (2WR)-(Z-H) × Q→X: Goto 2:IfEn dLb1 2: ” GAO CHENG= ” D-X →X ◢Goto 3SQX (竖曲线数据库)Goto 1Lb1 1IfZ≤157893.75:Then25000→R:93.75→T:157800→H:421.977→D:-0. 0045→P:0.003→Q:Return:IfEnd说明:Z代表竖曲线终点里程,R 代表竖曲线半径;T 代表竖曲线切长;D 代表变坡点标高(未改正之前);P 代表前段坡度,上坡为正,下坡为负;Q 代表后段坡度,上坡为正,下坡为负;。
Q2V9程序操作说明

• • • • •
当内存只有Q2V9程序及11个子程序、 清空全部串列文件时,Q2V9程序最多可以计算 430个连续变坡点的高程正算 3) 连续路线或匝道平竖曲线三维坐标正反算 执行程序,显示xy(1)/H(2)/xyH(3)=?时,输3响应
• 计算前,先设置当前串列文件, • 在List 1~List 4串列输入平曲线已知数据 • 在List 12~List 14串列输入竖曲线已知数据 • • • • 坐标正算时,显示加桩中桩三维坐标; 坐标反算时,显示垂点与交点中桩三维坐标; 只能计算边桩点的平面坐标, 不能计算边桩点的设计高程。
• Eile6.CSV文件
• CSFile6.dat,SVFile6.dat坐标文件
• ⑤ 广州东(沙)新(联)高速公路禹山互通立交L匝道 • ——13个线元平曲线已知数据
• 设置File1为当前串列文件 • 输入13个线元平曲线已知数据到List 1~List 10串列
• 设置File1为当前串列文件,执行程序Q2V9
• ① 输入每个线元起点半径Rs,终点半径Re时, • Rs或Re为∞时输0; • 执行程序Q2V9后,程序自动将半径0修改为1E30 • • • • ② 只有当线元为缓和曲线或圆曲线时 需要输入偏转系数,直线线元不需要输入偏转系数 沿路线走向,线元左偏输-1,右偏输1。 ③ List 5的缓曲参数A由程序反求出,无需输入。
• • • • • • • •
4) 平曲线与竖曲线数据的关系 ① 平曲线已知数据预先输入List 1~List 4串列 程序将中间结果——缓曲参数存入List 5串列 平曲线主点数据存入List 6~List 10串列 List 11串列存储控制数据。 ② 竖曲线已知数据预先输入List 12~List 14串列 反求坡度结果存入List 15串列 竖曲线主点数据存入List 16~List 18串列。
高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式【精选】

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x<0时sgn(x)=-1,当x>0时sgn(x)=1,当x=0时sgn(x)=0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Q h2-8线元法任意路线与匝道曲线坐标正、反算程序5800计算器坐标计算程序(线元法任意路线与匝道曲线坐标正、反算程序)程序1:QH2-8"ROUTE Or RAMP QH2-8"◢书中多了个个双引号(这里说的书是产品配备的说明书)Deg:Fix 3:书中Freqon取消"NEW(0),OLD(≠0)DATA="?→CIf C≠0:Then "RECOMP(0),NO(≠)= "?→G书中0取消If G=0:Then Goto T:Else Goto J: IfEnd“CURVE NUM=”?N1→Q:5N+11→DimZ“START a(Deg)=”?→Z[5]For 1→I To N“n=”:I◢“START R(m)=”?→Z[5I-4]Z[5I-4]=0=>1X1030→Z[5I-4]“END R(m)=”?→Z[5I-3]Z[5I-3]= 0=>1X1030→Z[5I-3]“LENGTH(m)=”?→Z[5I-2]If Z[5I-4]<1X1030 Or Z[5I-3] <1X1030Then “DEFLEX L(-1),R(1)=”?→Z[5I-1]:IfEnd 注意-1是减1NEXT“[MODE][1] =>Stop!”◢Lb1 T:0→I:For 1→I To NList X[I]+Rep(Z[5I-2])→List X[I+1]List X[I+1]→ZIf Z[5I-4]=Z[5I-3]And Z[5I-4]= 1X1030Then 0→S:0→T:Z[5I-2]→DProg “SUBQ2-84”:Goto 0:IfEndIf Z[5I-4]=Z[5I-3] And Z[5I-4] <1X1030Then Prog “SUBQ2-83”:Goto 0:IfEnd√根号(Rep(Z[5I-2])÷Abs(Z[5I-4]-1-Z[5I-3]-1))→A Rep(Z[5I-2])+Ai→Z[5I-2]Prog “SUBQ2-82”Lb1 0:T→Z[5I+1]]Rep(U)→List Y[I+1]:Imp(U)→List Freq[I+1] Next“PEG-END(m)=”:List X[N+1] ◢“a-END(DMS)=”DMS◢“X-END(m)=”:List Y[N+1] ◢“Y-END(m)=”:List Freq[N+1] ◢“[MODE][4]=>Stop!”◢Lb1 J:”STA BACKXY,NEW(0),O LD(≠0)=”?→JJ≠0=>Goto 1“STAn,X(m),<0=>NO=“?→S0→Z[5N+6]:S<0=>Goto 1If Frac(S)=0 And S≤N+1Then List Y[S]+List Freq[S]i→Z[5N+6]Else “STA Y(m)=”?→T:S+Ti→Z[5N+6]:IfEndLb1 B:”BACKn,X(m),OLDa(0),<0=>a=”?→UU=0=>Goto 1If U<0:Then “a-BACK(Deg)=”?→Z[5N+8]:Goto 1:IfEnd If S=U And Frac(U)=0Then”STAn=BACKn,REPEAT!”Goto B:IfEndIf Frac(U)=0 AND U≤N+1Then List Y[U]+List Freq[U]i→Z[5N+7]Else”BACK Y(m)=”?→V:U+Vi→Z[5N+7]:IfEndLb1 S:Arg(Z[5N+7]-Z[5N+6])→JJ<0=>J+360→J:J→Z[5N+8]Lb1 1:”PEG→XY(1),XY→PEG(≠1)=”?→QQ≠1=>Goto 2Do:”+PEG(m),<0=>END=”?→ZZ<List X[1] Or Z>List X[N+1]=>BreakFor 1→I To NZ<List X[I] Or Z>List X[I+1]=>Goto NZ-List X[I]→LIf Z[5I-4]=Z[5I-3] And Z[5I-4]= 1X1030Then 0→S:0→T:L→DProg “SUBQ2-84”: Prog “SUBQ2-85”:Break:IfEnd If Z[5I-4]=Z[5I-3] And Z[5I-4]<1X1030Then Prog”SUBQ2-83”Prog “SUBQ2-85”: Break:IfEndProg “SUBQ2-82”: Prog “SUBQ2-85”:BreakLb1 N:NextLpWhile Z>0:Goto ELb1 2:”XJ(m), <0=>END=”?X:X<0=>Goto E“YJ(m)=”?Y“J in NUM,<0=>AUTO=”?→I:I>0=>Goto3Abs(X+Yi-List Y[1]-List Freq[1]i→CList X[1]+C→ZFor 1→S To NZ>List X[S] And Z<List X[S+1]=>Break:Next 9000→C:S→EFor E→I To N(List Y[I]+ListY[I+1])÷2→U(List Freq[I]+List Freq[I+1])÷2→VAbs(X+Yi-U-Vi)→DIf D<C:Then D→C:I→F:IfEndNext:F≥2=>F-1→ILb1 3:If Z[5I-4]=Z[5I-3] And Z[5I-4]=1X1030 Then tan(Z[5I])→T(X+T2List Y[I]-T(List Freq[I]-Y))÷(T2+1)→UU+(Y-(U+X)÷T)i→U:Z[5I]→TU-List Y[I]-List Freq[I]→FArg(F)→H:H<0=>H+360→H1→J:Abs(T-H)>150=>-1→JList X[I]+JAbs(F)→ZIf Z≥List X[I] And Z≤List X[I+1]:Then Goto Z Else I+1>N=>Goto Z:I+1→I:Goto 3:IfEnd:IfEnd If Z[5I-4]=Z[5I-3] And Z[5I-4]<1X1030Then List Y[I]+List Freq[I]i→SZ[5I]+90Z[5I-1]→AZ[5I-4]→R:S+R<A→VX+Yi→U:Arg(U-V)→F:Abs(U-V)→DV+R<F→UAbs(U-S)→C:sin-1(C÷2÷R)→EZ[5I]+2Z[5I-1]E→TList X[I]+∏ER÷90→ZIf Z≥List X[I] And Z≤List X[I+1]:Then Goto ZElse I+1>N=>Goto Z:I+1→I:Goto 3:IfEnd:IfEnd List Y[I+]+List Freq[I]i→UList Y[I+1]+List Freq[I+1]→V(U+V)÷2→FV-U→C:Abs(C)→S:Arg(C)→JJ<0=>J+360→J:J+90Z[5I-1]→GIf Z[5I-4]>Z[5I-3]:Then 2Z[5I-3]→RElse 2Z[5I-4]→R:IfEnd√(R2-S2÷4)→TF+T<G→OSin-1(S÷R÷2)→V:∏VR÷90→J(Rep(Z[5I-2])-J)÷J→PX+Yi-O→V:Arg(V)→JO+R<J→C:Abs(C-U)→SSin-1(S÷R÷2)→V:∏VR÷90→JList X[I]+J(1-P)→ZProg “SUBQ2-82”DoX+Yi-U→C:Abs(C)→SArg(C)→J:J<0=>J+360→JJ-T→J:J<0=>J+360→JIf J>220:Then J-270→J:-1→FElse 90-J→J:1→F:IfEndIf Z[5I-4]>Z[5I-3]Then πJ÷180÷(FZ[5I-1]L÷A2+S-1)→EElse πJ÷180÷(-FZ[5I-1]L÷A2+S-1)→E:IfEndZ+E→ZIf Z>List X[I+1]:Then I+1→I:Goto 3:IfEndProg “SUBQ2-82”Tan(T)(ImP(U)-Y)+ReP(U)-X→CLpWhile Abs(C)>0.001Fix 4:”f(Lp)=”:C◢Fix 3:Lb1 Z:Prog “SUBQ2-85”:Goto 2Lb1 E:”QH2-8=>END”程序2:SUBQ2-81If L<1X10-5:Then 0→U:0→J:Return:IfEndL-L∧(5)÷40÷A∧(4)+L∧(9)÷3456÷A∧(8)-L∧(13)÷599040÷A∧(12)+L∧(17)÷175472640÷A∧(16)→OL∧(3)÷6÷A2-L∧(7)÷336÷A∧(6)+L∧(11)÷42240÷A∧(10)-L∧(15)÷9676800÷A∧(14)+L∧(19)÷3530096640÷A∧(18)→UO+Ui→U:(L2÷(2A2))r→JReturn程序3:SUBQ2-82ImP(Z[5I-2])→AA2÷Z[5I-4]→LProg “SUBQ2-81”:U→V:J→EIf Z[5I-4]>Z[5I-3]:Then Z-List X[I]+L→L Prog “SUBQ2-81”:U-V→OElse A2÷Z[5I-3]→LList X[I+1]-Z+L→LProg “SUBQ2-81”:V-U→O:IfEdnAbs(O)→D:Arg(O)→TAbs(T-E)→S:Abs(J-E)→TProg “SUBQ2-84”Return程序4:SUBQ2-83Z[5I-4]→R:Z-List X[I]→L(L÷2÷R)r→S:2Rsin(s)→D2S→T:Prog”SUBQ2-84”Return程序5:SUBQ2-84Z[5I]+Z[5I-1]S→S:Z[5I]+Z[5I-1]T→TT<0=>T+360→T:T>360=>T-360→TList Y[I]+List Freq[I]i+D<S→UReturn程序6:SUBQ2-85T<0=>T+360→T:T>360=>T-360→TIf Q=1:Then “ai(DMS)=”:T◢“Xi(m)=”:Rep(U)◢“Yi(m)=”:Imp(U)◢Else Z<List X[I] Or Z>List X[I+1]=>”OUT OF The CURVE!”◢Arg(X+Yi-U)→H:H<0=>H+360→HAbs(X+Yi-U)→DIf H>180:Then “J in Left,NUM=”:I◢Else “J in Right,NUM=”:I◢IfEnd“p PEG(m)=”:z◢“ap(DMS)=”◢“Xp(m)=”:Rep(U)◢“YP(m)=”:Imp(U) ◢“J→p DIST(m)=”:D◢IfEndIf Abs(Z[5N+6])>0:Then U→Z[5N+7]:Prog “SUBQ2-87”:IfEndZ≠0=>Porg “SUBQ2-86”Return程序7:SUBQ2-86“ANGLE(0)=>NO,-L+R(Deg)=”?KK=0=>ReturnIf K<0:Then K+180→P:Else K→P:K-180→K:IfEnd “WL(m),0=>NO=”?MIf M>0:Then U+M<(T+K)→V“XL(m)=”:Rep(V) ◢“YL(m)=”:Imp(U) ◢If Abs(Z[5N+6])>0:Then V→Z[5N+7]:Prog “SUBQ2-87”:IfEnd:IfEdn“WR(m),0=>NO=”?WIf W>0:Then U+W<(T+P)→V“XR(m)=”:Rep(V) ◢“YR(m)=”:Imp(V) ◢If Abs(Z[5N+6])>0:Then V→Z[5N+7]:Prog “SUBQ2-87”:IfEndIfEdn:Return程序8:SUBQ2-87Z[5N+7]-Z[5N+6]→O:Arg(O)→JJ<0=>J+360→JJ-Arg(Z[5N+8])→J:J<0=>J+360→J(J+1X10-8)≥360=>J-360→J“HR(DMS)=”◢“HD(m)=”:Abs(O) ◢Return红色“O”表示为字母,仅对单个字母另作标记。
