最新费马点及其在中考中的应用
费马点及其在中考中的应用

章 , 以对 碰撞 过程 “ 可 放大 ” “ 和 强化 ” 处理 , 学生 使
明确质点 组 间的碰撞 由于一对 内力 做功 一般 不为 零, 因此机械 能有损失.
[ 丁三 七. 4 】 几个功 能 问题 的错 解分 析及 原 因
探 究U_ l 中学物理 ,0 8 7 . 20 ()
作 D /A 交 B E / B, C的延长线于点 E .
( ) D点 的坐标 ; 1求
角形.
因此 , + + C PC+ , P . 船 P = ' JP C P+
由此可知 当 C , , , P , C四点共线时 ,A P + C P P +BP = P c+ ,+ C为最小. , PP P 当 C , P共线时 ,. .PP-0 ’. cP曰 P , ’ AB - 。 _ ’ 6 . ~ :
/ APB=1 0 . 2 。
( ) C点关 于直线 D 2作 E的对称点 F 分别连结 ,
D , ,若 过 曰点的直 线 y k+ 将 四边 形 C F F =x b DE
分成周长相等 的两个 四边形 , 试确定此直线 的解析
式;
同理 , P , , 若 , C共线时 , ‘/B P= 0, P 则 ._ P 6 。 ‘
学家 、物理 学家. 费马一生从 未受过 专门的数学教 1 对三 角形 内任 , 育, 数学研 究也 不过是 业余 爱好 . 然而 , 1 在 7世纪 意一 点 P,延 长 的法 国还找 不到哪位数学家可 以与之 匹敌. 他是解 B A至点 c , 使得 析几 何 的发 明者 之一 ; 概率 论 的主要创 始 人 ; 以及 AC = C, A 作 C
教 师 ,0 9 7 . 20( )
费马点问题(含答案)

>费马点的问题定义:数学上称,到三角形3个顶点距离之和最小的点为费马点。
它是这样确定的:1. 如果三角形有一个内角大于或等于120°,这个内角的顶点就是费马点;2. 如果3个内角均小于120°,则在三角形内部对3边张角均为120°的点,是三角形的费马点。
3. 费马点与3个顶点连成的线段是沟通3点的最短路线,容易理解,这个路线是唯一的。
我们称这一结果为最短路线原理。
【性质:费马点有如下主要性质:1.费马点到三角形三个顶点距离之和最小。
2.费马点连接三顶点所成的三夹角皆为120°。
3.费马点为三角形中能量最低点。
)4.三力平衡时三力夹角皆为120°,所以费马点是三力平衡的点。
例1:已知:△ABH是等边三角形。
求证:GA+GB+GH最小证明:∵△ABH是等边三角形。
G是其重心。
^∴∠AGH=∠AGB=∠BGH=120°。
以HB为边向右上方作等边三角形△DBH.以HG为边向右上方作等边三角形△GHP.∵ AH=BH=AB=12.!∴∠AGH=120°, ∠HGP=60°.∴ A、G、P三点一线。
再连PD两点。
∵△ABH、△GHP和△BDH都是等边三角形,∠GHB=30°.!∴∠PHD=30°,.在△HGB和△HPD中∵ HG=HP∠GHB=∠PHD;:HB=HD;∴△HGB≌△HPD;(SAS)∴∠HPD=∠HGB=120°;∵∠HPG=60°.@∴ G、P、D三点一线。
∴ AG=GP=PD,且同在一条直线上。
∵ GA+GH+GB=GA+GP+PD=AD.∴ G点是等边三角形内到三个顶点的距离之和最小的哪一点,费马点。
也就是重心。
,、|例2:已知:△ABC是等腰三角形,G是三角形内一点。
∠AGC=∠AGB=∠BGC=120°。
求证:GA+GB+GC最小证明:将△BGC逆时针旋转60°,连GP,DB.则△HGB≌△HPD;!∴∠CPD=∠CGB=120°,CG=CP,GB=PD, BC=DC,∠GCB=∠PCD.∵∠GCP=60°,∴∠BCD=60°,∴△GCP和△BCD都是等边三角形。
2023年中考数学常见几何模型之最值模型费马点问题

专题12 最值模型-费马点问题最值问题在中考数学常以压轴题的形式考查,费马点问题是由全等三角形中的手拉手模型衍生而来,主要考查转化与化归等的数学思想。
在各类考试中都以中高档题为主,中考说明中曾多处涉及。
本专题就最值模型中的费马点问题进行梳理及对应试题分析,方便掌握。
【模型背景】皮耶·德·费马,17世纪法国数学家,有“业余数学家之王”的美誉,之所以叫业余并非段位不够,而是因为其主职是律师,兼职搞搞数学.费马在解析几何、微积分等领域都有卓越的贡献,除此之外,费马广为人知的是以其名字命名的“费马小定理”、“费马大定理”等.费马点:三角形内的点到三个顶点距离之和最小的点。
【模型解读】结论1:如图,点M为△ABC内任意一点,连接AM、BM、CM,当M与三个顶点连线的夹角为120°时,MA+MB+MC的值最小。
注意:上述结论成立的条件是△ABC的最大的角要小于120º,若最大的角大于或等于120º,此时费马点就是最大角的顶点A。
(这种情况一般不考,通常三角形的最大顶角都小于120°)【模型证明】以AB为一边向外作等边三角形△ABE,将BM绕点B逆时针旋转60°得到BN,连接EN.∵△ABE为等边三角形,∴AB=BE,∠ABE=60°.而∠MBN=60°,∴∠ABM=∠EBN.在△AMB 与△ENB 中,∵AB BEABM EBN BM BN =⎧⎪∠=∠⎨⎪=⎩,∴△AMB ≌△ENB (SAS ). 连接MN .由△AMB ≌△ENB 知,AM =EN .∵∠MBN =60°,BM =BN ,∴△BMN 为等边三角形.∴BM =MN .∴AM +BM +CM =EN +MN +CM .∴当E 、N 、M 、C 四点共线时,AM +BM +CM 的值最小.此时,∠BMC =180°﹣∠NMB =120°;∠AMB =∠ENB =180°﹣∠BNM =120°;∠AMC =360°﹣∠BMC ﹣∠AMB =120°.费马点的作法:如图3,分别以△ABC 的AB 、AC 为一边向外作等边△ABE 和等边△ACF ,连接CE 、BF ,设交点为M ,则点M 即为△ABC 的费马点。
2024成都中考数学二轮复习专题:费马点求最小值
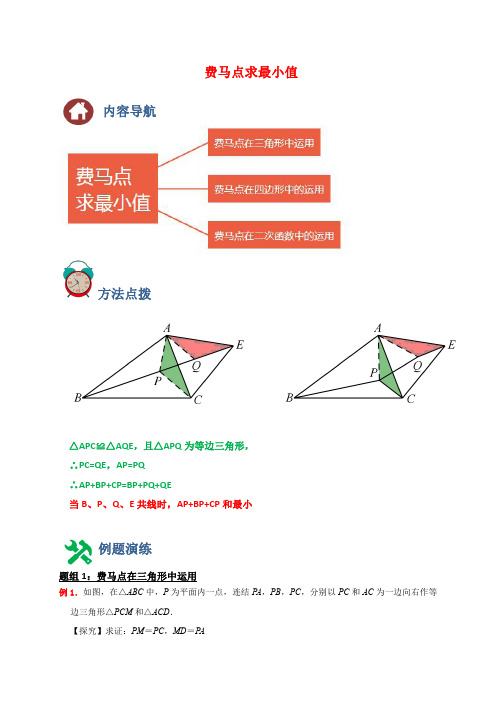
费马点求最小值内容导航方法点拨△APC≌△AQE,且△APQ为等边三角形,∴PC=QE,AP=PQ∴AP+BP+CP=BP+PQ+QE当B、P、Q、E共线时,AP+BP+CP和最小例题演练题组1:费马点在三角形中运用例1.如图,在△ABC中,P为平面内一点,连结PA,PB,PC,分别以PC和AC为一边向右作等边三角形△PCM和△ACD.【探究】求证:PM=PC,MD=PA【应用】若BC=a,AC=b,∠ACB=60°,则PA+PB+PC的最小值是(用a,b表示)【解答】【探究】证明:∵以PC和AC为一边向右作等边三角形△PCM和△ACD,∴PM=PC,AC=CD,PC=CM,∠PCM=∠ACD=60°,∴∠PCA=∠MCD,在△ACP和△DCM中,,∴△ACP≌△DCM(SAS),∴MD=PA;【应用】解:连接BD,如图所示:∵△APC≌△DCM,∴∠ACP=∠DCM,AC=CD=b,∴∠ACP+∠PCB=∠DCM+∠PCB,∴∠DCM+∠PCB=∠ACB=60°,∴∠BCD=∠DCM+∠PCB+∠PCM=60°+60°=120°,作DF⊥BC于F,则∠CFD=90°,在Rt△CDF中,∵∠DCF=180°﹣120°=60°,CD=b,∴∠CDF=30°,∴CF=AC=b,DF=CF=b,∴BF=a+b,∴BD===;当B、P、M、D共线时,PA+PB+PC的值最小,即PA+PB+PC的最小值为:;故答案为:.练1.1问题提出(1)如图①,在△ABC中,BC=2,将△ABC绕点B顺时针旋转60°得到△A′B′C′,则CC′=;问题探究(2)如图②,在△ABC中,AB=BC=3,∠ABC=30°,点P为△ABC内一点,连接PA、PB、PC,求PA+PB+PC的最小值,并说明理由;问题解决(3)如图③,在四边形ABCD中,AD∥BC,AB=6,AD=4,∠ABC=∠BCD=60°.在四边形ABCD内部有一点,满足∠APD=120°,连接BP、CP,点Q为△BPC内的任意一点,是否存在一点P和一点Q,使得PQ+BQ+CQ有最小值?若存在,请求出这个最小值;若不存在,请说明理由.【解答】解:(1)如图①,由旋转的性质可知:△BCC′是等边三角形,∴CC′=BC=2,故答案为2.(2)如图②,将△ABP绕点B逆时针旋转60°得到△BFE,连接PF,EC.由旋转的性质可知:△PBF是等边三角形,∴PB=PF,∵PA=EF,∴PA+PB+PC=PC+PF+EF,∵PC+PF+EF≥EC,∴当P,F在直线EC上时,PA+PB+PC的值最小,易证BC=BE=BA=3,∠CBE=90°,∵EB⊥BC,∴EC=BC=3,∴PA+PB+PC的最小值为3.(3)如图③﹣1中,将△PBQ绕点B逆时针旋转60°得到△EBG,则PQ=EG,△BQG是等边三角形,∴BQ=QG,PQ=EG,∴PQ+BQ+CQ=EG+GQ+QC≥EC,∴EC的值最小时,QP+QB+QC的值最小,如图③﹣2中,延长BA交CD的延长线于J,作△ADJ的外接圆⊙O,将线段BO,BP绕点B逆时针旋转60°得到线段BO′,BE,连接EO′,OB,OP.易证△BEO′≌△BPO(SAS),∴EO′=OP,∵∠APD+∠AJD=180°,∴A,P,D,J四点共圆,∴OP=,∴EO′=,∴点E的运动轨迹是以O′为圆心,为半径的圆,∴当点E在线段CO′上时,EC的值最小,最小值=CO′﹣EO′,连接OO′,延长OO′到R,使得O′R=OO′,连接BR,则∠OBR=90°,作RH⊥CB交CB 的延长线于H,O′T⊥CH于T,OM⊥BC于M.在Rt△OBM中,BM=5,OM=,∴OB==,∴BR=OB=14,由△BHR∽△OMB,∴=,∴RH=5,∵HR∥O′T∥OM,OO′=RO′,∴TM=TH,∴O′T==,∴BT==3,∴CO′==,∴CO′﹣EO′=﹣=.∴QP+QB+QC的最小值为.题组2:费马点在四边形中运用例2.如图,P为正方形ABCD内的动点,若AB=2,则PA+PB+PC的最小值为.【解答】解:将△BPC绕点B顺时针旋转60°,得到△BP'C',∴BP=BP',∠PBP'=60°,△BPC≌△BP'C',∴△BPP'是等边三角形,PC=P'C',∠PBC=∠P'BC',BC=BC'=2,∴BP=PP',∴PA+PB+PC=AP+PP'+P'C',∴当线段AP,PP',P'C'在一条直线上时,PA+PB+PC有最小值,最小值是AC'的长,过点C'作C'E⊥AB交AB的延长线于E,∵∠ABP+∠PBP'+∠P'BC'=60°+∠ABP+∠PBC=150°,∴∠EBC'=30°,∴EC'=1,BE=EC'=,∴AE=2+,∴AC'===+,故答案为:+.练2.1如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD上任意一点,将BM 绕点B逆时针旋转60°得到BN,连接BN、AM、CM.(1)求证:△AMB≌△ENB;(2)若正方形的边长为,正方形内是否存在一点P,使得PA+PB+PC的值最小?若存在,求出它的最小值;若不存在,说明理由.【解答】解:(1)如图1,∵四边形ABCD为正方形,△ABE为等边三角形,∴BE=BA,BA=BC,∠ABE=60°;∵∠MBN=60°,∴BE=BA,∠MBN=∠ABE,∴∠MBA=∠NBE;在△AMB与△ENB中,,∴△AMB≌△ENB(SAS),(2)顺时针旋转△BPC60度,可得△PBE为等边三角形.即得PA+PB+PC=AP+PE+EF要使最小只要AP,PE,EF在一条直线上,即如下图:可得最小PA+PB+PC=AF.BM=BF•cos30°=BC•cos30°=,则AM=+=,∵AB=BF,∠ABF=150°∴∠BAF=15°既得AF==+1.例3.如图,在平面直角坐标系xOy中,点B的坐标为(0,2),点D在x轴的正半轴上,∠ODB=30°,OE为△BOD的中线,过B、E两点的抛物线与x轴相交于A、F两点(A在F的左侧).(1)求抛物线的解析式;(2)等边△OMN的顶点M、N在线段AE上,求AE及AM的长;(3)点P为△ABO内的一个动点,设m=PA+PB+PO,请直接写出m的最小值,以及m取得最小值时,线段AP的长.【解答】解:(1)过E作EG⊥OD于G(1分)∵∠BOD=∠EGD=90°,∠D=∠D,∴△BOD∽△EGD,∵点B(0,2),∠ODB=30°,可得OB=2,;∵E为BD中点,∴∴EG=1,∴∴点E的坐标为(2分)∵抛物线经过B(0,2)、两点,∴,可得;∴抛物线的解析式为;(3分)(2)∵抛物线与x轴相交于A、F,A在F的左侧,∴A点的坐标为∴,∴在△AGE中,∠AGE=90°,(4分)过点O作OK⊥AE于K,可得△AOK∽△AEG∴∴∴∴∵△OMN是等边三角形,∴∠NMO=60°∴;∴,或;(6分)(写出一个给1分)(3)如图;以AB为边做等边三角形AO′B,以OA为边做等边三角形AOB′;易证OE=OB=2,∠OBE=60°,则△OBE是等边三角形;连接OO′、BB′、AE,它们的交点即为m最小时,P点的位置(即费马点);∵OA=OB′,∠B′OB=∠AOE=150°,OB=OE,∴△AOE≌△B′OB;∴∠B′BO=∠AEO;∵∠BOP=∠EOP′,而∠BOE=60°,∴∠POP'=60°,∴△POP′为等边三角形,∴OP=PP′,∴PA+PB+PO=AP+OP′+P′E=AE;=AE=;即m最小如图;作正△OBE的外接圆⊙Q,根据费马点的性质知∠BPO=120°,则∠PBO+∠BOP=60°,而∠EBO=∠EOB=60°;∴∠PBE+∠POE=180°,∠BPO+∠BEO=180°;即B、P、O、E四点共圆;易求得Q(,1),则H(,0);∴AH=;由割线定理得:AP•AE=OA•AH,即:AP=OA•AH÷AE=×÷=.故:m可以取到的最小值为当m取得最小值时,线段AP的长为.(如遇不同解法,请老师根据评分标准酌情给分)练3.1如图,抛物线y=ax2+bx+过点A(1,0),B(5,0),与y轴相交于点C.(1)求抛物线的解析式;(2)定义:平面上的任一点到二次函数图象上与它横坐标相同的点的距离,称为点到二次函数图象的垂直距离.如:点O到二次函数图象的垂直距离是线段OC的长.已知点E为抛物线对称轴上的一点,且在x轴上方,点F为平面内一点,当以A,B,E,F为顶点的四边形是边长为4的菱形时,请求出点F到二次函数图象的垂直距离.(3)在(2)中,当点F到二次函数图象的垂直距离最小时,在以A,B,E,F为顶点的菱形内部是否存在点Q,使得AQ,BQ,FQ之和最小,若存在,请求出最小值;若不存在,请说明理由.【解答】解:(1)∵抛物线y=ax2+bx+过点A(1,0),B(5,0),∴0=a+b+0=25a+5b+∴a=,b=﹣3∴解析式y=x2﹣3x+(2)当y=0,则0=x2﹣3x+∴x1=5,x2=1∴A(1,0),B(5,0)∴对称轴直线x=3,顶点坐标(3,﹣2),AB=4∵抛物线与y轴相交于点C.∴C(0,)如图1①如AB为菱形的边,则EF∥AB,EF=AB=4,且E的横坐标为3∴F的横坐标为7或﹣1∵AE=AB=4,AM=2,EM⊥AB∴EM=2∴F(7,2),或(﹣1,2)∴当x=7,y=×49﹣7×3+=6∴点F到二次函数图象的垂直距离6﹣2②如AB为对角线,如图2∵AEBF是菱形,AF=BF=4∴AB⊥EF,EM=MF=2∴F(3,﹣2)∴点F到二次函数图象的垂直距离﹣2+2(3)当F(3,﹣2)时,点F到二次函数图象的垂直距离最小如图3,以BQ为边作等边三角形BQD,将△BQF绕B逆时针旋转60°到△BDN位置,连接AN,作PN⊥AB于P∵等边三角形BQD∴QD=QB=BD,∵将△BQF绕B逆时针旋转60°到△BDN位置∴NB=BF=4,∠FBN=60°,DN=FQ∵AQ+BQ+FQ=AQ+QD+DN∴当AQ,QD,DN共线时AQ+BQ+FQ的和最短,即最短值为AN的长.∵AF=BF=4=AB,∴∠ABF=60°∴∠NBP=60°且BN=4,∴BP=2,PN=2∴AP=6在Rt△ANP中,AN==4∴AQ+BQ+FQ的和最短值为4.。
中考复习之线段和差最值之费马点问题-附练习题含参考答案
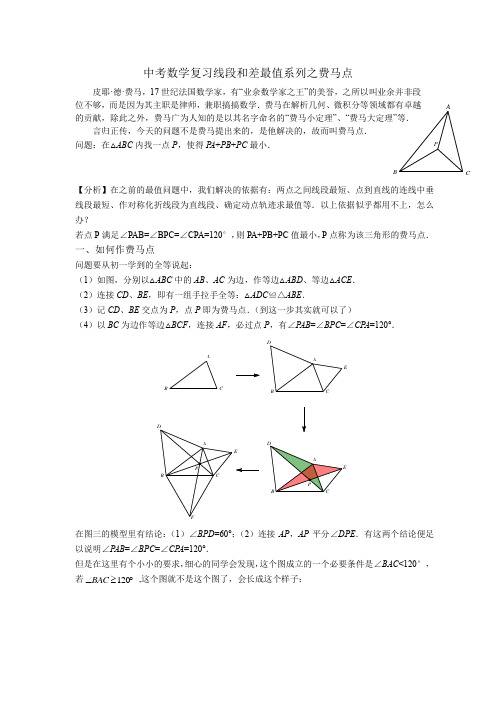
ABCP中考数学复习线段和差最值系列之费马点皮耶·德·费马,17世纪法国数学家,有“业余数学家之王”的美誉,之所以叫业余并非段位不够,而是因为其主职是律师,兼职搞搞数学.费马在解析几何、微积分等领域都有卓越的贡献,除此之外,费马广为人知的是以其名字命名的“费马小定理”、“费马大定理”等.言归正传,今天的问题不是费马提出来的,是他解决的,故而叫费马点. 问题:在△ABC 内找一点P ,使得P A +PB +PC 最小.【分析】在之前的最值问题中,我们解决的依据有:两点之间线段最短、点到直线的连线中垂线段最短、作对称化折线段为直线段、确定动点轨迹求最值等.以上依据似乎都用不上,怎么办?若点P 满足∠PAB=∠BPC=∠CPA=120°,则PA+PB+PC 值最小,P 点称为该三角形的费马点.一、如何作费马点问题要从初一学到的全等说起:(1)如图,分别以△ABC 中的AB 、AC 为边,作等边△ABD 、等边△ACE . (2)连接CD 、BE ,即有一组手拉手全等:△ADC ≌△ABE .(3)记CD 、BE 交点为P ,点P 即为费马点.(到这一步其实就可以了)(4)以BC 为边作等边△BCF ,连接AF ,必过点P ,有∠P AB =∠BPC =∠CP A =120°.在图三的模型里有结论:(1)∠BPD =60°;(2)连接AP ,AP 平分∠DPE .有这两个结论便足以说明∠P AB =∠BPC =∠CP A =120°.但是在这里有个小小的要求,细心的同学会发现,这个图成立的一个必要条件是∠BAC <120°,若120BAC ∠≥︒ ,这个图就不是这个图了,会长成这个样子:EB ACAB CDE此时CD 与BE 交点P 点还是我们的费马点吗?显然这时候就不是了,显然P 点到A 、B 、C 距离之和大于A 点到A 、B 、C 距离之和.所以,是的,你想得没错,此时三角形的费马点就是A 点!当然这种情况不会考的,就不多说了.二、为什么是这个点为什么P 点满足∠P AB =∠BPC =∠CP A =120°,P A +PB +PC 值就会最小呢?归根结底,还是要重组这里3条线段:P A 、PB 、PC 的位置,而重组的方法是构造旋转!在上图3中,如下有△ADC ≌△ABE ,可得:CD =BE .类似的手拉手,在图4中有3组,可得:AF =BE =CD .巧的,它们仨的长度居然一样长!更巧的是,其长度便是我们要求的P A +PB +PC 的最小值,这一点是可以猜想得到的,毕竟最小值这个结果,应该也是个特别的值! 接下来才是真正的证明:考虑到∠APB =120°,∴∠APE =60°,则可以AP 为边,在PE 边取点Q 使得PQ =AP ,则△APQ 是等边三角形.△APQ 、△ACE 均为等边三角形,且共顶点A ,故△APC ≌△AQE ,PC =QE . 以上两步分别转化P A =PQ ,PC =QE ,故P A +PB +PC =PB +PQ +QE =BE .没有对比就没有差别,我们换个P 点位置,如下右图,同样可以构造等边△APQ ,同样有△APC ≌△AQE ,转化P A =PQ ,PC =QE ,显然,P A +PB +PC =PB +PQ +QE >BE .还剩下第3个问题!如果说费马点以前还算是课外的拓展内容,那现在,已经有人把它搬上了中考舞台!【中考再现】问题背景:如图1,将△ABC 绕点A 逆时针旋转60°得到△ADE ,DE 与BC 交于点P ,可推出结论:P A +PC =PE .问题解决:如图2,在△MNG 中,MN =6,∠M =75°,MG=O 是△MNG 内一点,则点O 到△MNG 三个顶点的距离和的最小值是______.【分析】本题的问题背景实际上是提示了解题思路,构造60°的旋转,当然如果已经了解了费马点问题,直接来解决就好了!如图,以MG 为边作等边△MGH ,连接NH ,则NH 的值即为所求的点O 到△MNG 三个顶点的距离和的最小值.(此处不再证明)过点H 作HQ ⊥NM 交NM 延长线于Q 点,根据∠NMG =75°,∠GMH =60°,可得∠HMQ =45°,∴△MHQ 是等腰直角三角形, ∴MQ =HQ =4,∴NH== 练习题1.如图,在△ABC 中,△ACB=90°,AB=AC=1,P 是△ABC 内一点,求P A +PB +PC 的最小值.2. 如图,已知矩形ABCD ,AB =4,BC =6,点M 为矩形内一点,点E 为BC 边上任意一点,则MA +MD +ME 的最小值为______.NG图2图1ABCD EPHGN M464Q HGN MABCDME3.如图,矩形ABCD中,AB=10,BC=15,现在要找两点E、F,则EA+EB+EF+FC+FD的最小值为__________4.如图,等腰Rt∆ABC中,AB=4,P为∆ABC内部一点,则PA+PB+PC的最小值为_______5.如图,∆ABC中,AB=4,,∠ABC=75°,P为∆ABC内的一个动点,连接PA、PB、PC,则PA+PB+PC的最小值为________6.如图,P为正方形ABCD对角线BD上一动点,若AB=2,则PA+PB+PC的最小值为______7.在Rt∆ABC中,∠ACB=90°,AC=1,,点O为Rt∆ABC内一点,连接AO、BO、CO,且∠AOC=∠COB=∠BOA=120°,则OA+OB+OC=_______8.如图,在四边形ABCD中,∠B=60°,AB=BC=3,AD=4,∠BAD=90°,点P是四边形内部一点,则PA+PB+PD的最小值是______9.如图,点P是矩形ABCD对角线BD上的一个动点,已知AB=2,,则PA+PB+PC 的最小值为_______10.如图,菱形ABCD的对角线AC上有一动点P,BC=6,∠ABC=150°,则PA+PB+PD的最小值为__________11.已知,在∆ABC中,∠ACB=30°点P是ABC内一动点,则PA+PB+PC的最小值为__________12.如图,设点P到等边三角形ABC两顶点A、B的距离分别为2则PC的最大值为______13.如图,设点P到正方形ABCD两顶点A、D的距离为2PC的最大值为________14.如图,设点P到正方形ABCD两顶点A、D的距离为2则PO的最大值为_________.15.如图,在Rt∆ABC中,∠BAC=90⁰,AB=AC,点D是BC边上一动点,连接AD,把AD 绕点A逆时针旋转90⁰,得到AE,连接CE、DE,点F是DE的中点,连接CF问题:在点D运动的过程中,在线段AD上存在一点P,使PA+PB+PC的值最小,当PA+PB+PC 取最小值时,AP的长为m,用含有m的式子表示CE的长.参考答案1.7.8.7 9.3 10. 12.2+13.2+1 15.32m +。
旋转中的最值模型(费马点模型)(解析版)—2024-2025学年九年级数学上学期(人教版)
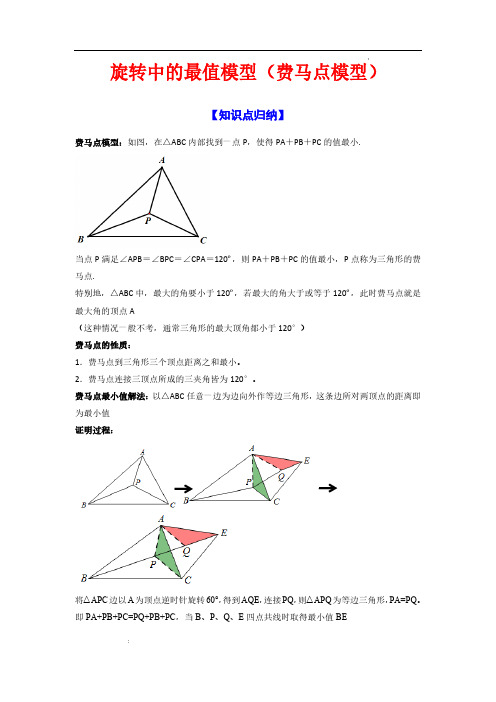
旋转中的最值模型(费马点模型)【知识点归纳】费马点模型:如图,在△ABC内部找到一点P,使得PA+PB+PC的值最小.当点P满足∠APB=∠BPC=∠CPA=120º,则PA+PB+PC的值最小,P点称为三角形的费马点.特别地,△ABC中,最大的角要小于120º,若最大的角大于或等于120º,此时费马点就是最大角的顶点A(这种情况一般不考,通常三角形的最大顶角都小于120°)费马点的性质:1.费马点到三角形三个顶点距离之和最小。
2.费马点连接三顶点所成的三夹角皆为120°。
费马点最小值解法:以△ABC任意一边为边向外作等边三角形,这条边所对两顶点的距离即为最小值证明过程:将△APC边以A为顶点逆时针旋转60°,得到AQE,连接PQ,则△APQ为等边三角形,PA=PQ。
即PA+PB+PC=PQ+PB+PC,当B、P、Q、E四点共线时取得最小值BE【例题精讲】例1.(等边三角形费马点)如图,在ABC V 中,3AB =,2AC =,60BAC Ð=°,P 为ABC V 内一点,则PA PB PC ++的最小值为 .【点睛】本题考查了全等三角形判定与性质,旋转的性质,以及等边三角形的性质和求线段最值的问题,掌握做辅助线是解题的关键.例2.(直角三角形费马点)如图,已知Rt △ABC 中,∠ABC =90°,∠ACB =30°,斜边AC =4,点P 是三角形内的一动点,则PA +PB +PC 的最小值是 .∵∠90,30ABC ACB °°=Ð=,AC 2,AB \=结AD,BE,CE.若AB=DE=BC=10,∠ABC=75°,则AD+BE+CE的最小值为.【点睛】本题考查轴对称求最短距离,熟练掌握轴对称的性质,通过构造平行四边形、旋转例4.(加权费马点)如图,Rt ABC △中,30CAB Ð=°,3BC =,点P 为ABC V 内一点,连接,,PA PB PC ,则PC PB +的最小值为 .++++的最小值为.AP BP PQ QC QD∴AP BP PQ CQ DQ ++++B P P P PQ QQ Q C ¢¢¢¢¢¢=++++,∴当,,,,,B P P Q Q C ¢¢¢¢六点共线时AP BP PQ CQ ++++连接,¢¢BB CC ,∵AB AB ¢=,60B AB ¢Ð=°,∴ABB ¢V 是等边三角形,∴1AB BB ¢¢==,∴B ¢在AB 的垂直平分线上,例6.(培优综合)在ABCD Y 中,45ABC Ð=°,连接AC ,已知AB AC ==E 在线段AC 上,将线段DE 绕点D 顺时针旋转 90° 为线段DF .(1)如图1,线段AC 与线段BD 的交点和点E 重合,连接EF ,求线段EF 的长度;(2)如图2,点G 为DC 延长线上一点,使得GC EC =,连接FG 交AD 于点H ,求证:CD =;(3)如图3,在(2)的条件下,平面内一点P ,当HP CP +最小时,求HPB △的面积.∵45BAC Ð=°,AB AC ==∴45ACB ABC Ð=Ð=°,BAC Ð∴2222BC AB ==´=,∵ABCD Y ,∴45DCG ABC Ð=Ð=°,CD∵90BAC Ð=°,AB CD ∥,∴AC GD ^,90GCA ECD Ð=Ð=°,又∵GC EC =,AC DC =,∴()SAS GCA ECD V V ≌,∴GA ED =,GAC EDC Ð=Ð,∵ED FD =,ED FD ^,∴GA FD =,90AGC GDF Ð+Ð=°-Ð由旋转的性质可得,2BC BC ¢==,∵AD BC ∥,∴90AIB Ð=°,45IAB ABC Ð=Ð=°,∴222122IB IA AB ===´=,在Rt IC H ¢V 中,12IC IB BC ¢¢=+=+22223213C H IC IH ¢¢=+=+=,∵1122BC H S C H BJ BC IH ¢¢¢=⋅=⋅V ,即:在Rt IBH V 中,221BH IB IH =+=在Rt BJH V 中,22JH BH BJ =-=【课后训练】1.如图,在ABC V 中,90,5,BAC AB AC Ð==°=P 为ABC V 内部一点,则点P 到ABC V 三个顶点之和的最小值是 .∴BAP HAE Ð=Ð,AE AP =,AH AB ==∴60HAB EAP Ð=Ð=°,∴AEP △是等边三角形,∴AE AP EP ==,∴AP BP PC EP EH PC ++=++,∴当点H 、E 、P 、C 共线时,AP BP PC ++∵18018060NAC BAH BAC Ð=°-Ð-Ð=°-条动线段MN BC ∥,且MN =,则AN BM CN ++的最小值为 .【点睛】本题考查了平行四边形的判定与性质,旋转变换,的一半,等边三角形的判定与性质,勾股定理,两点之间线段最短等知识,解题的关键是学会利用旋转法添加辅助线,构造全等三角形解决问题..如图,点M 是矩形ABCD 内一点,且,,MA MD MN ,则MA MD MN ++的最小值为 .【答案】7532+根据旋转的性质有:ADD ¢\△为等边三角形,同理AMM ¢V 为等边三角形,AM AM MM ¢==\MA MD MN +\+=\当线段M D ¢¢、MM 在矩形ABCD 中,D 即可知四边形ABEF 是矩形,ADD ¢QV 为等边三角形,\12AF FD AD ===\2D F D A AF ¢¢=-4.如图,P为正方形ABCD内的动点,若AB=2,则PA+PB+PC的最小值为.(1)如图1,已知150AOB Ð=°,120BOC Ð=°,将BOC V 绕点C 按顺时针方向旋转60°得ADC △.①DAO Ð的度数是 ;②用等式表示线段OA ,OB ,之间的数量关系,并证明;(2)设AOB a Ð=,BOC b Ð=.①当a ,b 满足什么关系时,OA OB OC ++有最小值?请在图2中画出符合条件的图形,并说明理由;②若等边ABC V 的边长为1,直接写出OA OB OC ++的最小值.QV ADC BOC \≌△△,OCD ÐCD OC \=,ADC BOC Ð=ÐOCD \△是等边三角形,OC OD CD \==,COD Ð=150AOB Ð=°Q ,120BOC Ð=90AOC \Ð=°,\O C OC ¢\=,O A OA ¢¢=,A C BC ¢=,A O C AOC ¢¢Ð=Ð.(1)如图1, 连接DE BE 、, 若5,3BCE ABE S S ==V V ,求BED S V ;(2)如图2, 若,DM BC DM BM ^=, 延长BE 交DM 于点N , 且NM MC =, 求证:AD DN =-;(3)如图3,若4,90AD AB ABD ==Ð=°,P 为BCD △内一点,请直接写出PD PC PB ++的最小值.∵,DM BC DM BM ^=,∴BDM V 是等腰直角三角形,∴222BD BM DM DM =+=∴BD BF =,∴45F BDM CBD Ð=Ð=Ð=∴90DBF Ð=°,∴2DF BD =,∴4CH BC ==,DCH BCD BCH Ð=Ð+Ð∴PG PC =,∴PD PC PB PD PG GH DH ++=++³即当点D ,P ,G ,H 四点共线时,PD 在Rt DCH △中,22DH CD CH =+=即PD PC PB ++的最小值为27.【点睛】本题主要考查了等边三角形的判定和性质,平行四边形的性质,勾股定理,图形的形ACFG ,点D 恰好在线段GF 上.(1)若AB的长度比BC少4,8V的面积;AC=,求ABC(2)求证:BG DG-;(3)已知点P是ABCV的顶点和边重合,在(1)的条件下,请直V内一动点,且P不与ABC接写出PA PB++的最小值.∵90BED HEG Ð=Ð=°,∴BED HED HEG Ð-Ð=Ð-即BEH DEG Ð=Ð,∵EMG BED EBG =Ð+Ð=∠∴EBG GDE Ð=Ð,∵90BAC Ð=°,∴1122ABC S AB AC BC AG =´=´△,∴6824105AB AC AG BC ´´===,针旋转90°交DC 的延长线于点F ,求证:AE CF =;(2)边长4AB =把边AB 沿BE 翻折.①如图2,若点P 落在对角线BD 上,则AE = ;②如图3,点G 在边CD 上,1DG =,连接AG 、BG ,当点P 落在ABG V 内部时(不含边上),线段AE 长度的取值范围为 ;(3)如图4,点M 是正方形ABCD 内一点,连接MA 、MC ,若5AB =,求MA MC +最小值;(4)如图5,点M 是矩形ABCD 内一点,连接,,MA MB MC ,若AB =4BC =,则MA MB MC ++最小值为 .当点P 落到BG 上,连接由折叠的性质可得,∴=EPG EDG ÐÐ∵1DG =,(3)①当A 、M AM MC AC +>,②当点A 、M 、C ∵AB BC =,ABC Ð(4)如图,将V ∴A M AM ¢¢=,BM 又∵60M BM ¢Ð=°∴M BM ¢V 是等边三角形,【点睛】本题考查正方形的性质、折叠的性质、旋转的性质、全等三角形的判定与性质、等腰直角三角形的性质与判定、勾股定理、等边三角形的判定与性质、切线的性质,熟练掌握相关性质是解题的关键.。
初二费马点的典型例题

初二费马点的典型例题(原创版)目录一、初二费马点的概念二、初二费马点的典型例题及解法1.直线与圆的交点问题2.圆与圆的交点问题3.费马点与几何图形的综合应用正文一、初二费马点的概念费马点是几何学中的一个重要概念,特别是在初二数学中,它是解决许多几何问题的关键。
费马点是指在平面上给定一个点,通过这个点可以作出已知线段的垂直平分线,也可以作出已知圆的直径。
费马点具有许多重要的性质,如费马点是任意三角形的垂心,费马点是任意四边形的外心等。
在初二阶段,学生需要掌握费马点的基本概念和性质,以及如何利用费马点解决几何问题。
二、初二费马点的典型例题及解法1.直线与圆的交点问题题目:已知直线 l:x - 2y + 3 = 0 和圆 O:x^2 + y^2 = 4,求直线与圆的交点。
解法:首先,根据直线方程,我们可以得到直线的斜率为 2。
然后,通过圆心 (0, 0) 作直线的垂线,可以得到垂足为费马点。
接着,利用费马点的性质,可以求出直线与圆的交点。
2.圆与圆的交点问题题目:已知圆 O1:x^2 + y^2 = 4 和圆 O2:(x - 2)^2 + (y - 1)^2 = 9,求两圆的交点。
解法:同样地,通过圆心作直线的垂线,可以得到两个圆的费马点。
然后,利用费马点的性质,可以求出两圆的交点。
3.费马点与几何图形的综合应用题目:已知矩形 ABCD,AB = 4,BC = 6,求对角线 AC 和 BD 的交点 E(费马点)。
解法:首先,根据矩形的性质,可以得到对角线 AC 和 BD 的交点 E 即为矩形的费马点。
然后,利用费马点的性质,可以求出 E 点的坐标。
总结:初二费马点是几何学中的一个重要概念,掌握费马点的性质和解法对于解决许多初二几何问题具有关键作用。
中考数学几何模型专题12费马点问题(学生版) 知识点+例题

【压轴必刷】2023年中考数学压轴大题之经典模型培优案专题12费马点问题-年8月17日﹣1665年1月12日),生于法国南部图卢兹(Toulouse )附近的波蒙•德•罗曼,被誉为业余数学家之王.1643年,费马曾提出了一个著名的几何问题:给定不在一条直线上的三个点A ,B ,C ,求平面上到这三个点的距离之和最小的点的位置.另一位数学家托里拆利成功地解决了这个问题:如图1,△ABC (三个内角均小于120°)的三条边的张角都等于120°,即满足∠APB =∠BPC =∠APC =120°的点P ,就是到点A ,B ,C 的距离之和最小的点,后来人们把这个点P 称为“费马点”. 下面是“费马点”的证明过程:如图2,将△APB 绕着点B 逆时针旋转60°得到△A ′P ′B ,使得A ′P ′落在△ABC 外,则△A ′AB 为等边三角形,∴P ′B =PB =PP ′,于是P A +PB +PC =P ′A ′+PP ′+PC ≥A ′C ,∴当A ',P ',P ,C 四点在同一直线上时P A +PB +PC 有最小值为A 'C 的长度,∵P ′B =PB ,∠P 'BP =60°,∴△P 'BP 为等边三角形,则当A ',P ',P ,C 四点在同一直线上时,∠BPC =180°﹣∠P 'PB =180°﹣60°=120°,∠APB =∠A 'PB =180°﹣∠BP 'P =180°﹣60°=120°,∠APC =360°﹣∠BPC ﹣∠APC =360°﹣120°﹣120°=120°,∴满足∠APB =∠BPC =∠APC =120°的点P ,就是到点A ,B ,C 的距离之和最小的点;ABC 所在平面上一点,且∠APB =∠BPC =∠CP A =120°,则点P 叫做△ABC 的费马点.(1)如点P为锐角△ABC的费马点.且∠ABC=60°,P A=3,PC=4,求PB的长.(2)如图(2),在锐角△ABC外侧作等边△ACB′连接BB′.求证:BB′过△ABC的费马点P,且BB′=P A+PB+PC.(3)已知锐角△ABC,∠ACB=60°,分别以三边为边向形外作等边三角形ABD,BCE,ACF,请找出△ABC的费马点,并探究S△ABC与S△ABD的和,S△BCE与S△ACF的和是否相等.【例2】探究问题:(1)阅读理解:①如图(A),在已知△ABC所在平面上存在一点P,使它到三角形顶点的距离之和最小,则称点P为△ABC的费马点,此时P A+PB+PC的值为△ABC的费马距离;②如图(B),若四边形ABCD的四个顶点在同一圆上,则有AB•CD+BC•DA=AC•BD.此为托勒密定理;(2)知识迁移:①请你利用托勒密定理,解决如下问题:如图(C),已知点P为等边△ABC外接圆的上任意一点.求证:PB+PC=P A;②根据(2)①的结论,我们有如下探寻△ABC(其中∠A、∠B、∠C均小于120°)的费马点和费马距离的方法:第一步:如图(D),在△ABC的外部以BC为边长作等边△BCD及其外接圆;第二步:在上任取一点P′,连接P′A、P′B、P′C、P′D.易知P′A+P′B+P′C=P′A+(P′B+P′C)=P′A+;第三步:请你根据(1)①中定义,在图(D)中找出△ABC的费马点P,并请指出线段的长度即为△ABC的费马距离.(3)知识应用:2010年4月,我国西南地区出现了罕见的持续干旱现象,许多村庄出现了人、畜饮水困难,为解决老百姓的饮水问题,解放军某部来到云南某地打井取水.已知三村庄A、B、C构成了如图(E)所示的△ABC(其中∠A、∠B、∠C均小于120°),现选取一点P打水井,使从水井P到三村庄A、B、C所铺设的输水管总长度最小,求输水管总长度的最小值.【例3】如图,在平面直角坐标系xOy中,点B的坐标为(0,2),点D在x轴的正半轴上,∠ODB=30°,OE为△BOD的中线,过B、E两点的抛物线与x轴相交于A、F两点(A在F的左侧).(1)求抛物线的解析式;(2)等边△OMN的顶点M、N在线段AE上,求AE及AM的长;(3)点P为△ABO内的一个动点,设m=P A+PB+PO,请直接写出m的最小值,以及m 取得最小值时,线段AP的长.1.已知:到三角形3个顶点距离之和最小的点称为该三角形的费马点.如果△ABC是锐角(或直角)三角形,则其费马点P是三角形内一点,且满足∠APB=∠BPC=∠CP A=120°.(例如:等边三角形的费马点是其三条高的交点).若AB=AC=,BC=2,P为△ABC的费马点,则P A+PB+PC=;若AB=2,BC=2,AC=4,P为△ABC的费马点,则P A+PB+PC=.2.在△ABC中,若其内部的点P满足∠APB=∠BPC=∠CP A=120°,则称P为△ABC的费马点.如图所示,在△ABC中,已知∠BAC=45°,设P为△ABC的费马点,且满足∠PBA=45°,P A=4,则△P AC的面积为.3.如图,在边长为6的正方形ABCD中,点M,N分别为AB、BC上的动点,且始终保持BM=CN.连接MN,以MN为斜边在矩形内作等腰Rt△MNQ,若在正方形内还存在一点P,则点P到点A、点D、点Q的距离之和的最小值为.4.如果点P是△ABC内一点,且它到三角形的三个顶点距离之和最小,则P点叫△ABC的费马点.已经证明:在三个内角均小于120°的△ABC中,当∠APB=∠APC=∠BPC=120°时,P就是△ABC的费马点.若点P是腰长为的等腰直角三角形DEF的费马点,则PD+PE+PF=.5.法国数学家费马提出:在△ABC内存在一点P,使它到三角形顶点的距离之和最小.人们称这个点为费马点,此时P A+PB+PC的值为费马距离.经研究发现:在锐角△ABC中,费马点P满足∠APB=∠BPC=∠CP A=120°,如图,点P为锐角△ABC的费马点,且。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
费马点及其在中考中的应用
一、费马点的由来
费马(Pierre de Fermat,1601—1665)是法国数学家、物理学家.费马一生从未受过专门的数学教育,数学研究也不过是业余爱好.然而,在17世纪的法国还找不到哪位数学家可以与之匹敌.他是解析几何的发明者之一;概率论的主要创始人;以及独承17世纪数论天地的人.一代数学大师费马堪称是17世纪法国最伟大的数学家.尤其他提出的费马大定理更是困惑了世间智者358年.费马曾提出关于三角形的一个有趣问题:在△ABC内求一点P,使 PA+PB+PC之值为最小,人们称这个点为“费马点”.
二、探索费马点
1.当三角形有一个内角大于或等于120°的时候,则费马点就是这个内角的顶点.
下面来验证这个结论:如图1,对三角形内任意一点P,延长BA至点C′,使得AC′=AC,
作∠C′AP′=∠CAP,并且使得AP′=AP.即把△APC以A为中心做旋转变换.则△APC≌△AP′C′,
∵∠BAC≥120°,∴∠PAP′≤60°.
∴在等腰三角形PAP′中,AP≥PP′,
∴PA+PB+PC≥PP′+PB+ P′C′>BC′=AB+AC.
所以A是费马点.
图
1
图2
2.如果三个内角都在120°以内,那么,费马点就是三角形内与三角形三顶点的连线两两夹角为
120°的点.
如图2,以B点为中心,将△APB旋转60°到△A′BP′.因为旋转60°,且PB=P′B,所以△P′PB为正三角形.
因此,PA+PB+PC=P′A′+P′P+PC.
由此可知当A′,P′,P,C四点共线时,PA+PB+PC=P′A′+P′P+PC为最小.
当A′,P′,P共线时,∵∠BP′P=60°,∴∠A′P′B=∠APB=120°.同理,若P′,P,C共线时,则∵∠BPP′=60°,∴∠BPC=120°.
所以点P为满足∠APB=∠BPC=∠CPA=120°的点.
三、费马点的简单应用
近几年,在全国各地的中考中,时常可以看见费马点的影子.
例1(2009浙江湖州--25)
若P为△ABC所在平面上一点,且∠APB=∠BPC=∠CPA=120°,则点P叫做△ABC的费马点.
(1)若点P为锐角△ABC的费马点,且∠ABC=60°,PA=3,PC=4,
则PB的值为________;
(2)如图3,在锐角△ABC外侧作等边△ACB,连结BB′.
求证:BB′过△ABC的费马点P,且BB′=PA+PB+PC.
解:(1)∵∠PBA+∠PBC=∠PBC+∠PCB=60°,∴∠PBA=∠PCB.
又∠APB=∠BPC=120°,
∴△PBA∽△PCB,则PB2=PA×PC=12,即PB=2
.
(2)证明:在BB′上取点P,使∠BPC=120°,连结AP,再在PB′上
截取PE=PC,连结CE.
∵PC=CE,AC=CB′,∠PCA=∠ECB′,
∴△ACP≌△B′CE.
∴∠APC=∠B′EC=120°,PA=EB′.
∴∠APB=∠APC=∠BPC=120°,
∴P为△ABC的费马点,且BB′=EB′+PB+PE=PA+PB+PC.
例2 (2009北京) 如图,在平面直角坐标系xOy中,△ABC三个点的坐标分别为A(-6,0),B(6,0),
C(0,4),延长AC到点D,使CD=AC,过点D作DE∥AB,交BC的延长线于点E.
(1)求D点的坐标;
(2)作C点关于直线DE的对称点F,分别连结DF,EF,若过B点的直线y=kx+b
将四边形CDFE分成周长相等的两个四边形,试确定此直线的解析式;
(3)设G为y轴上一点,点P从直线y=kx+b与y轴的交点出发,先沿
y轴到达G点,再沿GA到达A点,若P点在y轴上运动的速度是它在直线GA上运动速度的2倍,试确定G点的位置,使P点按照上述要求到达A
点所用的时间最短.(要求:简述确定G点位置的方法,但不要求证明)
【析】本题第三问要求:简述确定G点位置的方法,但不要求证明.如果不知原理,比较难找,用常规数学的方法,会涉及到一元二次方程的判别式的问题,并不容易想到.而用费马点的知识就能轻松找出这个G点.由于直线y=kx+b与y轴的交点坐标在第二问当中可求出M(0,6),所以,本题第三问便可以转化为:AO⊥OM于点O,AO=6,MO=6,G点从M出发,向O 点运动到达G点后,再沿GA到达A点.若G点在MO上运动的速度是它在GA上运动速度的2倍,试确定G点的位置.
(如图5,G点按照上述要求到达A点所用的时间为t)
解法一:方程解法
设GO=x,则MG=6-x,AG=,
则t=,
移项平方得:3x2+(12-4t)x +36+24t-4t2=0,
∵方程有解,
Δ=(12-4t)2-12(36+24t-4t2)≥0 解得t≥6,
将t=6代回方程,求出x=2时,t最小.
解法二:费马点解法
如图6,要使MG+AG最小,即使MG+2AG最小.
作A关于MO的对称点A',
则MG+2AG=MG+AG+A'G,
即MG+AG+A'G最小.故G为△AA'M的费尔马点.作∠GAO=30°,交MO于G点,则∠AGM=∠A'GM=∠AG A'=120°,故G点为所求. OG=2.
由此利用费马点的解法可以看出:
当动点G在OM上的运动速度是在AG上的2倍的时候,动点的位置与MO的长度无关,与AO的长度有关,GO长是AO长的倍.
2009北京中考25题最后一问不需证明其实证明也很简单!(仅供参考)
Q N
O M
G K
B
A
其中K 为DE 与y 轴的交点,由前两个问题容易得知ABK ∆为等边三角形, G 为y 轴上的任意一点,作GN BK ⊥,30BKO ∠=︒,∴12GN KG =
,故速度为2v 走完KG 所用的时间等于速度为v 走完GN 所用的时间,即2KG GN v v
=,故以2v 速度走完KG 和以v 走完GA 的时间和,其实就是以v 速度走完路程AG GN +,由速度一定,路程最短,时间最少!再由垂线段最短,最短路程就是AM ,此时G 点就是Q 点。
求该点坐标就不难了!。
