2009级电磁场理论期末试题-1(A)-题目和答案--房丽丽
电磁场与电磁波期末考试复习试题4套(部分含答案)

电磁场与电磁波期末考试复习资料11.圆柱坐标系中单位矢量 , 。
2.对于矢量A ,若 ,则=+•y x a y x a x )(2 ,=⨯x z a y a x 2 。
3.给定两个矢量z y x a a a A 32-+=,z y a a B +-=4,则矢量A 的单位矢量为 ,矢量B A ⋅= 。
4.已知直角坐标系中点P 1(5,-2,1),P 2(3,1,2),则P1的位置矢量为 ,P1到P2的距离矢量为 。
5.已知球坐标系中单位矢量 。
6.在两半无限大导电平面组成的直角劈形中间放置一点电荷,此时点电荷的镜像电荷个数为 。
7.点电荷q 在自由空间任一点r 处电场强度为 。
8.静电场中导体内的电场为 ,电场强度与电位函数的关系为 。
9.高斯散度定理的积分式为 ,它广泛的用于将一个封闭面积分变成等价的体积分,或者将一个体积分变成等价的封闭面积分。
10.已知任意一个矢量场A ,则其旋度的散度为 。
11.真空中静电场的基本方程的微分形式为 、 、 。
12.分析恒定磁场时,在无界真空中,两个基本场变量为 ,它们之间的关系为 。
13.斯托克斯定理为 ,它表明矢量场A 的旋度沿曲面S 的方向分量的面积分等于该矢量沿围绕此面积曲线边界的线积分。
14.任意一个标量场u ,则其梯度的旋度为 。
15.对于某一矢量 ,它的散度定义式为 ,用哈密顿算子表示为 。
16.介质中静电场的基本方程的积分式为 , , 。
17.介质中恒定磁场的基本方程的微分形式为 、 、 。
18.介质中恒定磁场的基本方程的积分式为 , , 。
19.静电场中两种介质分界面的边界条件是 , 。
20.在无限大的导体平面上方d 处放一点电荷q ,则其镜像电荷电量为 ,位置位于 ;如果一个点电荷置于两平行导体中间,则此点电荷有 镜像电荷。
21.矢量场223z a yz a y x a A z y x ++=在点P(1,1,0)的散度为 。
22.一个半径为a 的接地导体球,一点电荷q 位于距球心d 处,则其镜像电荷带电量为 ,位置位于 ;当点电荷q 向无限远处运动时,其镜像电荷向 运动。
海大 电磁场--A 试题 2008-2009 答案

是
q
F 4 0
Q
D
Rq
D
2
DRq D2 R2
2
(2)
当 q 与 Q 同号,且 Q q
RD3 D2 R2
2
R D
成立时,
F
表现为吸引力。
证明:使用镜像法分析
由于导体球不接地,本身又带电 Q
所以, 必须在导体球内加上两个镜像电荷来等效导体球对球外的影响。
5.当电磁波以大于零的角度 入射于介质表面时,如果没有反射波,则 B 。
A. 为临界角 B. 为布诺斯特角 C.入射波为垂直极化波
1
三、(20 分)
一同轴线的内导体半径为 a,外导体半径为 b,外加电压 U0,中间填充 r
a
的电介质。试求:介质中的电场强度 E 及电位移矢量 D。
解:设内导体单位长度带电荷为 l
2. 在时变电磁场中,根据方程 B 0 ,可定义矢位使 B A ,再根据方程
E
A t
0
,可定义标位,使 E A 。 t
3. 相对于电磁波传播方向,若电磁波的电场和磁场均只有横向分量,则称为 横电磁波(TEM) 波;若只有磁场有纵向分量,则称为 横电波(TE) 波;若只有电场有纵向
相位常数 1 6 rad m
2 r0 1 2.5 9.49 rad m 1v1 6 310 8 1.8 1019 rad s
折射系数 T 22 2 10 0.774 Et
2 1 10 5
Ein
反射波的相量形式和瞬时形式分别为:
电磁场与电磁波期末试题2009A答案

北京工业大学电控学院2008――2009学年第 2 学期《电磁场与电磁波》 课程试题答案一、(12分)研究矢量场的散度和旋度的意义何在? 已知位置矢量为:x y z r e x e y e z =++,求:(1) r ∇•;(2)r ∇⨯;(3)(),k r k ∇•是常矢量。
解:根据亥姆霍兹定理,一个矢量场所具有的性质可以由它的散度和旋度来确定。
所以只要知道了一个矢量场的散度和旋度,就可以完全确定了这个矢量。
()11130(,,)()x y z x y z xy z x y z x y z r e e e e x e y e z xy z e e e r x y z xyzk ae be ce a b c k r e e e kx y z ⎛⎫∂∂∂∇•=++•++=++= ⎪∂∂∂⎝⎭∂∂∂∇⨯==∂∂∂=++⎛⎫∂∂∂∇•=∇•++• ⎪∂∂∂⎝⎭(1)(2)(3)令为常数(ax+by+cz )=(ax+by+cz )=二.(15分)(1)写出麦克斯韦方程组的微分形式;(2)导出稳态场(场量不随时间变化)的电场和磁场的场方程。
(3) 在无源的理想介质空间中,J=0,ρ=0,导出电场和磁场的波动方程。
(提示:E E E2)(∇-•∇∇=⨯∇⨯∇)解:(1)0D H J tBE tB D ρ∂∇⨯=+∂∂∇⨯=-∂∇•=∇•=(2)00 00(3) (a) (b)0 (c)D H J E E D H JB B EH t HE tH ρρεμ⎧∇•=∇⨯=⎨∇⨯=∇⨯=⎩⇒∇•=⎧∇⨯=⎨∇•=∇•=⎩∂∇⨯=∂∂∇⨯=-∂∇•=∇•由于是稳态场,其磁场和电场不随时间变化所以麦氏方程变为无源场的麦氏方程为()()2222222220 (d)b ()()0E E H tE E EE E HtEE H tE E t t EE t HH t μμεμεμεμε=∂∇⨯∇⨯=-∇⨯∂∇⨯∇⨯=∇∇•-∇∂∴∇∇•-∇=-∇⨯∂∂∇•=∇⨯=∂⎛⎫∂∂∴-∇=- ⎪∂∂⎝⎭∂∇-=∂∂∇-=∂∴对()两边取旋度有又,又,电场的波动方程为同理可导出磁场的波动方程电场222222221010=EE v t H H v t ∂∇-=∂∂∇-=∂和磁场的波动方程为其中v三、(15分)(1).写出至少三种求解静电场问题的方法,简要说明其各自特点。
2009EM期末试卷A答案

2009EM 期末试卷A 答案一、写出一般物质中B-D 形式的场定律,并由此导出简单媒质中无源区域的电场波动方程。
(10分)(提示:A A A2)(∇-⋅∇∇=⨯∇⨯∇)解: B-D 形式的场定律为:tB E ∂∂-=⨯∇ tD J H f ∂∂+=⨯∇f D ρ=⋅∇0=⋅∇B4分在简单无源媒质中有:0 =f J , 0=f ρ, E D ε=, H Bμ=. 用场定律变为:t H E ∂∂-=⨯∇μ(1) tE H ∂∂=⨯∇ε(2)0=⋅∇E(3) 0=⋅∇H(4) 2分由公式A A A 2)(∇-⋅∇∇=⨯∇⨯∇,得E E E 2)(∇-⋅∇∇=⨯∇⨯∇对(1)式两边做⨯∇运算,左边=E E E E 22)(-∇=∇-⋅∇∇=⨯∇⨯∇右边=22t E t H ∂∂-=∂⨯∂∇- μεμ从而得到波动方程222=∂∂-∇t E E με 4分二、设圆柱电容器的内导体半径为a ,外导体半径b ,其内一半填充介电常数为1ε的介质,另一半填充介电常数为2ε的介质,如图所示。
当外加电压为0V 时,试求:(1)电容器中的电场强度;(2)单位长度内的储能。
(15分)解:解法一(分离变量法):(1)不妨设内导体电位为0V ,外导体电位为0,按电介质不同将求解区域分为I, II 两块。
对于I 区域,由于不存在自由电荷,所以0)())(()()(12111111=∇-=∇⋅-∇=⋅∇=⋅∇r r r E r Dφεφεε 即0)(12=∇rφ同理,0)(22=∇rφ在求解区域均满足拉普拉斯定理,可用分离变量法求解。
边界条件:根据边界条件可设解的形式为ccr B A r r B A r ln )(ln )(221111+=+=φφ )()(,)()(,,)()(,)()(,,00)(,2,0)(,0,)(,2,)(,0,212211212211110101r r n r n r b r a r r n r n r b r a r b rc r b rc V r a rc V r a rc c cφφφεφεπϕφφφεφεϕφπϕπφπϕφπϕπφπϕ=∂∂=∂∂≤≤==∂∂=∂∂≤≤==≤≤==≤≤==≤≤==≤≤=带入边界条件,解得a b V B B V ab bA A ln ln ln ln ln 021021--==-== 从而,有)(ln ln ln ln )()(021r V ab r b r r cφφφ=--==(2)单位长度存储的电场能为a r E a r E a w W II I S e d )(21d )(21d 222211⎰⎰⎰⎰⎰⎰+== εεab Vr r r a b V r r r a b V c c cb ac c c baln ln 2d d ])ln (ln [21d d ])ln (ln [2122120222010-⋅+=-+-=⎰⎰⎰⎰πεεϕεϕεπππ解法二(电场高斯):(1)设内导体的外表面上单位长度的电荷量为q ,外导体的内表面上单位长度的电荷量为-q 。
电磁场与电磁波期末试卷A卷答案

淮海工学院10 - 11 学年第 2 学期电磁场与电磁波期末试卷(A闭卷)答案及评分标准1.任一矢量A的旋度的散度一定等于零。
(√)2.任一无旋场一定可以表示为一个标量场的梯度。
(√)3.在两种介质形成的边界上,磁通密度的法向分量是不连续的。
(×)4.恒定电流场是一个无散场。
(√)5.电磁波的波长描述相位随空间的变化特性。
(√)6.在两介质边界上,若不存在自由电荷,电通密度的法向分量总是连续的。
(√)7.对任意频率的电磁波,海水均可视为良导体。
(×)8.全天候雷达使用的是线极化电磁波。
(×)9.均匀平面波在导电媒质中传播时,电磁场的振幅将随着传播距离的增加而按指数规律衰减。
(√)10.不仅电流可以产生磁场,变化的电场也可以产生磁场。
(√)二、单项选择题(本大题共10小题,每题3分,共30分)1.设点电荷位于金属直角劈上方,如图所示,则镜像电荷和其所在的位置为[ A ]。
A、-q(-1,2,0);q(-1,-2,0) ;-q(1,-2,0)B、q(-1,2,0);q(-1,-2,0); q(1,-2,0)C、q(-1,2,0);-q(-1,-2,0); q(1,-2,0);D、-q(-1,2,0);q(-1,-2,0); q(1,-2,0)。
2.用镜像法求解静电场边值问题时,判断镜像电荷设置是否正确的依据是[ C ]。
A、镜像电荷的位置是否与原电荷对称;B、镜像电荷是否与原电荷等值异号;C、待求区域内的电位函数所满足的方程与边界条件是否保持不变;D、镜像电荷的数量是否等于原电荷的数量。
3.已知真空中均匀平面波的电场强度复矢量为2π()120 (V/m)j zE z e eπ-=x则其磁场强度的复矢量为[ A ]A、2π=(/)j zyH e e A m-;B、2π=(/)j zyH e e A m;C、2π=(/)j zxH e e A m-;D、2π=-(/)j zyH e e A m-4.空气(介电常数为10εε=)与电介质(介电常数为204εε=)的分界面是0z=的平面。
电磁场2009A参考解答
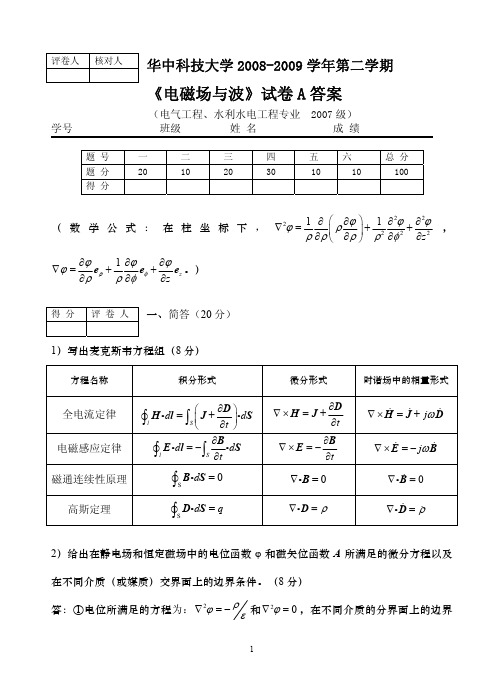
1 2πγ 土a
。
6)坡印廷定理的数学表达式为 能量的守恒和转化的规律 增加率 输的功率
S
∂W = − ∫ ( E × H )idS − ∫ E i J d V ,它描述了 电磁场 S V ∂t ∂W ,式中 表示的物理意义是 体积 V 内电磁能量的 ∂t
, − ∫ ( E × H )idS 表示的物理意义是
H =H 0e-j β z ,式中的E0和H0皆为常矢量,则一定有( C )。
(A)ez×E0=0 和ez×H0=0; (B)E0×H0=0; (C)E0·H0=0。 5)以下是关于场线边界上的边界条件的论述,其中错误的是( B )。 (A)沿着 E 线,
∂ϕ = 0; ∂n
(B)沿着H线,φm = 常数; (C)沿着 B 线,磁矢位 A = 常数。
⎛d ⎞ b = ⎜ ⎟ − a 2 ,(1 分) ⎝2⎠
2
⎛d ⎞ ⎛d ⎞ b + ⎜ − a⎟ b +⎜ − a⎟ τ τ 2 2 ⎝ ⎝ ⎠ , ϕ = −ϕ , U = ϕ − ϕ = ⎠ (2 分) ϕA = ln ln B A AB A B ⎛d ⎞ ⎛d ⎞ 2πε 0 πε 0 b −⎜ − a⎟ b −⎜ − a⎟ ⎝2 ⎠ ⎝2 ⎠ 故两线传输线的单位长度电容为
强度E为
1 q2 q ; 在空间建立的电场能量 W = ; 对应电容参数C = e e r 8πε 0 a 4πε 0 r 2
3
4πε 0a 。
3)在时变电磁场中,由动态位函数 φ 和 A 计算电场强度 E 和磁感应强度 B 的关系式 分别为 B = ∇× A 和 E + ∂ 2ϕ ∇ ϕ − με 2 = − ρ ε ∂t
沿环形圆线 l 积分,得到
2009-2010华师电磁场与电磁波试题及答案

物理与电信工程学院2009 /2010学年(2)学期期末考试试卷《电磁场与电磁波》 试卷(A 卷)专业 年级 班级 姓名 学号题号 一 二 三 总分 得分一、 单项选择题 (每小题2分,共20分)1 两个矢量的矢量积(叉乘)满足以下运算规律( ) A 交换律; B 分配率;C 结合率;D 以上均不满足。
2 以下关于边界条件的描述,正确的是( )A 电场强度切向分量连续;B 电位移矢量切向分量连续;C 电场强度法向分量连续;D 电位移矢量法向分量连续。
3 对于像电荷,下列说法正确的是( )A 像电荷是虚拟电荷,必须置于所求区域之内;B 像电荷是虚拟电荷,必须置于所求区域之外;C 像电荷是真实电荷,必须置于所求区域之内;D 像电荷是真实电荷,必须置于所求区域之外。
4 磁场的散度恒等于零,即0B ∇⋅=,这说明( )A 磁场线有头有尾;B 磁荷是存在的;C 存在磁单极;D 通过任一闭合曲面的磁通量恒等于零。
5时变电磁场的特点是( )A 时变电磁场各自独立;B 时变电磁场是一个不可分离的整体;C 时变电磁场不随时间变化;D 时变电磁场是保守场。
6 下列关于媒质的说法正确的是( )A 均匀、线性、各向异性的无耗媒质一定是色散媒质;B 均匀、线性、各向异性的无耗媒质不一定是色散媒质;C 有损耗导电媒质一定是非色散媒质;D 有损耗导电媒质一定是色散媒质。
7 一平面电磁波从一理想介质斜入射到一理想导体的表面,则在理想介质中传播的是( )A 纯驻波;B 在法线方向上合成波的场量是驻波;C 在法线方向上合成波的场量是行波;D 是均匀平面波。
8 对于处于静电平衡状态的导体,下列说法不正确的是( ) A 导体为等位体; B 导体内部电场为0;C 导体表面切向电场为0;D 导体内部可能存在感应电荷。
9 自由空间中所传输的均匀平面波,是( )A TE 波;B TM 波;C TEM 波;D 以上都不是。
10 电偶极子所辐射的电磁波,在远区场其等相位面为( ) A 球面; B 平面;C 柱面;D 不规则曲面。
(完整word版)电磁场理论复习题(含答案)(word文档良心出品)

第1~2章 矢量分析 宏观电磁现象的基本规律1. 设:直角坐标系中,标量场zx yz xy u ++=的梯度为A,则M (1,1,1)处 A = ,=⨯∇A 0 。
2. 已知矢量场xz e xy e z y e A z y x ˆ4ˆ)(ˆ2+++= ,则在M (1,1,1)处=⋅∇A 9 。
3. 亥姆霍兹定理指出,若唯一地确定一个矢量场(场量为A),则必须同时给定该场矢量的 旋度 及 散度 。
4. 写出线性和各项同性介质中场量D 、E 、B 、H、J 所满足的方程(结构方程): 。
5. 电流连续性方程的微分和积分形式分别为 和 。
6. 设理想导体的表面A 的电场强度为E 、磁场强度为B,则(a )E 、B皆与A 垂直。
(b )E 与A 垂直,B与A 平行。
(c )E 与A 平行,B与A 垂直。
(d )E 、B 皆与A 平行。
答案:B7. 两种不同的理想介质的交界面上,(A )1212 , E E H H == (B )1212 , n n n n E E H H == (C) 1212 , t t t t E E H H == (D) 1212 , t t n n E E H H ==答案:C8. 设自由真空区域电场强度(V/m) )sin(ˆ0βz ωt E eE y -=,其中0E 、ω、β为常数。
则ˆˆˆ222x y z e e e ++A⋅∇A ⨯∇EJ H B E D σ=μ=ε= , ,t q S d J S∂∂-=⋅⎰ tJ ∂ρ∂-=⋅∇空间位移电流密度d J(A/m 2)为:(a ) )cos(ˆ0βz ωt E ey - (b ) )cos(ˆ0βz ωt ωE e y -(c ) )cos(ˆ00βz ωt E ωey -ε (d ) )cos(ˆ0βz ωt βE e y -- 答案:C 9. 已知无限大空间的相对介电常数为4=εr ,电场强度(V/m) 2cos ˆ0dxeE x πρ= ,其中0ρ、d 为常数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课程编号:INF05005 北京理工大学2011-2012学年第一学期
2009级电子类电磁场理论基础期末试题A 卷
班级________ 学号________ 姓名________ 成绩________
一、简答题(共12分)(2题)
1.请写出无源、线性各向同性、均匀的一般导电(0<σ<∞)媒质中,复麦克斯韦方程组的限定微分形式。
2.请写出谐振腔以TE mnp 模振荡时的谐振条件。
并说明m ,n ,p 的物理意义。
二、选择题(每空2分,共20分)(4题)(最好是1题中各选项为同样类型)
1. 在通电流导体(0<σ<∞)内部,静电场( A ),静磁场(B ),恒定电流场(B ),时变电磁场( C )。
A. 恒为零;
B. 恒不为零;
C.可以为零,也可以不为零;
2. 以下关于全反射和全折射论述不正确的是:( B )
A.理想介质分界面上,平面波由光密介质入射到光疏介质,当入射角大于某一临界角时会发生全反射现象;
B.非磁性理想介质分界面上,垂直极化波以某一角度入射时会发生全折射现象;
C.在理想介质与理想导体分界面,平面波以任意角度入射均可发生全反射现象;
D.理想介质分界面上发生全反射时,在两种介质中电磁场均不为零。
3. 置于空气中半径为a 的导体球附近M 处有一点电荷q ,它与导体球心O 的距离为d(d>a),当导体球接地时,导体球上的感应电荷可用球内区域设置的(D )的镜像电荷代替;当导体球不接地且不带电荷时,导体球上的感应电荷可用(B )的镜像电荷代替;
A. 电量为/q qd a '=-,距球心2/d a d '=;以及一个位于球心处,电量为q aq d ''=;
B. 电量为/q qa d '=-,距球心2/d a d '=;以及一个位于球心处,电量为q aq d ''=;
C. 电量为/q qd a '=-,距球心2/d a d '=;
D. 电量为/q qa d '=-,距球心2/d a d '=;
4.时变电磁场满足如下边界条件:两种理想介质分界面上,( C );两种一般导电介质(0<σ<∞)分界面上,(A );理想介质与理想导体分界面上,( D )。
A. 存在s ρ,不存在s J ;
B. 不存在s ρ,存在s J ;
C. 不存在s ρ和s J ;
D. 存在s ρ和s J ;
三、(12分)如图所示,一个平行板电容
器,极板沿x 方向长度为L ,沿y 方向宽
度为W ,板间距离为z 0。
板间部分填充
一段长度为d 的介电常数为ε1的电介质,如两极板间电位差为U ,求:(1)两极板
间的电场强度;(2)电容器储能;(3)电
介质所受到的静电力。
解:(1)在两种介质中,电场都是均匀分布的,由导体表面边界条件
()120
ˆU E E z z ==- (2)电容器储能等于两部分储能之和,或直接由下式计算:
()022*******e L d W dW W CU U z z εε-⎛⎫==+ ⎪⎝⎭
(3)电介质所受到的静电力
()10
2co 012e
U nst
W W F U d z εε=-⎛⎫∂== ⎪∂⎝⎭
四、(12分)如图所示,无限长细导线垂直穿过磁介质与空气的分界面,导线中载有电流I ,附近有一与导线共面的矩形导线框。
试求:(1)电流I 在空间产生的磁场强度H 和磁感应强度B ,(2)系统产生的互感。
图2
解:由安培环路定律
22I rH I H r
ϕϕππ=→= 在上半区域,010ˆ2I B H r
μμϕπ== 在下半区域,2ˆ2I B H r
μμϕπ== 根据互感的定义,21211
M I ψ= ()()()002112ln 2222224r d a r d a r d r d dI I d d d I d d a B r dr B r dr dr dr r r d μμμμπππ=+=+==++ψ=+=+=⎰
⎰⎰⎰故()0ln 4d d a M d
μμπ++=
五、(18分)真空中的平面电磁波,其磁场复矢量表达式为()2ˆˆj y H jx
z e π-=- (1)求波的传播方向、工作频率及对应的电场瞬时值表达式;(2)求波的极化形式;(3)若此平面波垂直入射到4r ε=,1r μ=的介质内,求反射波和折射波的平均坡印亭矢量;
解:波的波矢量ˆ2k y π= ,故82=1,310/c m f m s k πλλ===⨯ ()[][]22200
ˆˆˆˆˆˆˆ120120j y j y j y k H E y jx z e jz x e x jz e πππηππωε---⨯⎡⎤=-=-⨯-=---=+⎣⎦ 故瞬时值为
()[][]8ˆˆˆˆ,120cos(2)120cos(6102)E r t x
jz t y x jz t y πωππππ=+-=+⨯- (2)由于传播方向沿y 方向。
电场具有x 和z 两个分量。
因为ˆˆˆz
x y ⨯=,可见,x 分量滞后于z 分量90度,故为右旋圆极化波。
(3)垂直入射4r ε=,1r μ=的介质内,
12=120=60ηπηπ,,
6012012602,601203601203
R T -⨯==-==++
,120m E =
221120240140ˆˆˆ224093
m r E S y R y y πππηπ⨯=-=-=-
2221202404320ˆˆˆ212093
m t E S y T y y πππηπ⨯===
六、(14分)在尺寸为45mm ×21.1mm 的矩形波导中,未填充介质,传输TE 10模,工作频率5GHz ,(1)求截止波长c λ、波导波长g λ和波阻抗10TE Z 。
(2)若波导内
填充9,1r r εμ==的介质,还能传输什么模式?
(1)()10
c TE
290a mm λ==, 8393101060510mm λ⨯⨯==⨯,(可见2a a λ<<,故可以单模传输)
(
)10g TE λ===
10TE 0=120Z ηπ==
(2)若填充2,1r r εμ==的介质, 则
v =,从而mn f 变小, (
)10831091 1.5101010Hz 9TE f a ⎫=⨯=⨯⎪⎭
(
)208391.51021010Hz 2TE f a ⨯⎛⎫=⨯= ⎪⎝⎭ (
)01
8391.51011010Hz>5GHz 2b TE f ⨯⎛⎫=⨯= ⎪⎝⎭ 故还可以传输TE 20模.
七、(12分)自由空间中赫芝偶极子天线的最大辐射方向1km 处,电场强度振幅为03/E V m =,求:
(1)与最大辐射方向夹角60˚,相同距离处的电场幅度和磁场幅度;
(2)该天线的方向性系数。
解:最大辐射方向出现在=90sin 1θθ︒=,即处,
与最大辐射方向夹角60˚,相同距离处,1=30sin 2
θθ︒=,, 该点处的电场为最大电场强度振幅的1/2,111 1.51.5/,120120E E V m H ππ==
= (2)该天线方向性系数1.5.。
