几何画板怎么过圆外一点做圆的切线
人教版九下数学第二十四章 第2节 第2课时 切线的判定与性质

人教版九下数学第二十四章第2节第2课时切线的判定与性质课标要求:了解直线和圆的位置关系,掌握切线的概念、性质和判定,探索切线与过切点的半径的关系教材分析:切线的性质和判定它是学了直线和圆三种位置关系之后提出的,切线的性质和判定定理是研究三角形的内切圆,切线长定理的基础。
学好它今后数学和物理学科的学习会有很大的帮助。
学情分析:学生在七、八年级基础上有了一定的分析、归纳和简单的逻辑推理能力,以及通过添加辅助线解决几何问题的能力,本节课通过学生动脑动手进一步提升学生的识图能力和总结经验方法的能力。
学之难,教之困,思维误区与障碍:学生普遍的问题是看到题没思路,不会用已学知识,方法解决问题,没有捕捉典型图的能力,识图能力弱,分析能力弱,缺少给什么想什么,缺什么找什么的意识,导致没思路,而且思路不清,逻辑关系混乱,推理过程繁琐。
教学目标:1.通过练习回顾知识,形成相应的知识结构,从而整体复习圆的切线的判定定理与性质定理。
2.通过题组练习,让学生熟练运用圆的切线的判定定理和性质定理解决与圆有关的数学问题,并进一步培养学生运用已有知识解决数学问题的能力。
3.通过运用圆的切线的判定定理和性质定理解决数学问题的过程中,拓宽了解题思路,提高了解题技巧,从而使学生能够灵活应用所学知识解决问题。
教学重点:让学生熟练运用圆的切线的判定定理和性质定理解决与圆有关的数学问题,并归纳总结运用切线的性质和判定解决问题的方法。
教学难点:掌握切线性质和判定解决问题的方法,并能灵活运用。
教学环节一、知识回顾在上面三个图中,直线l和圆的三种位置关系分别是__相交__、__相切__、__相离__.设计意图通过具体图形形象直观的感受切线的特征。
通过几个图形的识别复习了切线的三种判定方法。
以及判定和性质的符号语言。
二、新课导入问题1:我们这一章主要研究了什么图形?请大家看图,你有什么样的方法判断直线与圆相切呢?生活动:教师引导,在图形中,直线l满足了什么条件?“,我们可以把直线与圆相切的定义,从图形的角度来理解.如何重新描述这个定义?引导学生得出:d=r板书:今天我们重点研究切线,如何判断一条直线是否是某个圆的切线呢?定义法:和圆有且只有一个公共点的直线是圆的切线.数量关系法(d=r):到圆心的距离等于半径的直线是圆的切线.例1 如图,在 Rt△ABC 中,∠ABC = 90°,∠BAC 的平分线交 BC 于 D,以 D为圆心,DB 长为半径作⊙D .求证:AC 是⊙O 的切线.证明:如图,过 D 作 DE ⊥AC 于 E.∵∠ABC = 90°∴ DB ⊥AB.∵ AD 平分∠BAC ,DE ⊥AC ,∴ DE = DB = r实例引入法切线的性质与判定的内容看似与生活关系不大,实际上,生活中有不少的圆的切线的例子.本节课的教学中可以从生活中的实例引入,提出问题,激发学生的求知欲.如图所示,下雨天,快速转动雨伞时雨滴飞出的方向和用砂轮打磨工件火星飞出的方向都是沿圆的切线方向飞出的.那么,怎么判定是不是圆的切线呢?图1通过实例引出问题,让学生带着问题去听课,加强学习的针对性,增强学生的听课效果,并让学生明确本节课的知识目标.二:提出问题,问题1:我们这一章主要研究了什么图形?请大家看图1,你能过圆上的点A 画出⊙O 的什么线? 师生活动:学生思考,并动手画一画,然后教师借助几何画板演示,过点A 的无数条直线中,有圆的割线、切线,割线可以画出无数条,而圆的切线只有一条. O A l设计意图:通过问题,引导学生回顾上节课学过的直线与圆的位置关系,为本节课学习切线的判定定理和性质定理作好铺垫.由旧知得出新知,探索切线的判定定理问题2:在生活中,有许多直线和圆相切的实例,你能举出几个吗?设计意图:通过展示实际生活中的图片,让学生感受切线与现实有着密切的联系. 问题3:在图1中,除了上面提到的当直线与圆有唯一公共点时,直线是圆的切线.我们还可以根据什么判断一条直线是圆的切线?你能过点A画出⊙O的切线吗?师生活动:让学生回顾上节课所学内容,什么是圆的切线?学生思考得出,要想准确画出圆的切线,就得出现d=r,因此得需要做出半径r和d.连接OA,过点A 作直线l⊥OA,则此时直线l是⊙O的切线(如图2).问题4:你能从图形的角度概括上面得出的结论吗?师生活动:教师引导,在图形中,直线l满足了什么条件?“垂直于半径”、“经过半径的外端”.为了便于应用,我们可以把直线与圆相切的定义,从图形的角度来理解.如何重新描述这个定义?引导学生得出:经过半径的外端并且垂直于半径的直线是圆的切线,同时引导学生得出切线判定定理的符号语言.设计意图:通过问题,引导学生借助旧知得到新知,也就是利用直线和圆相切的定义得出切线的判定定理;学生通过自己思考,动手画图可以更深刻的感受切线的判定定理.切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线.∵OA⊥l于A∴ l 是⊙O 的切线.4.运用定理,解决问题.例2. 如图,△ABC 中,AB = AC ,以 AB 为直径的 ⊙O 交边 BC 于 P ,PE ⊥AC 于 E. 求证:PE 是 ⊙O 的切线.证明:连接 OP ,如图.∵ AB = AC ,∴∠B =∠C.∵ OB = OP ,∴∠B =∠OPB.∴∠OPB =∠C.∴ OP ∥AC.∵ PE ⊥AC ,∴ PE ⊥OP.∴ PE 为 ⊙O 的切线.三.探索切线的性质定理.问题1:把得到的切线的判定定理中题设结论反过来,结论还成立吗?如图3,l 为⊙O 的切线,切点为A ,那么半径OA 与直线l 是不是一定垂直? 师生活动:学生通过观察思考,发现半径OA 垂直于直线l.师生讨论后发现直接证明垂直并不容易.此时引导学生可以考虑反证法:假设OA 与直线l 不垂直,过点O 作OM ⊥l ,根据垂线段最短的性质,有OM <OA ,这说明圆心O 到直线l 的距离小于半径OA ,于是直线l 就与圆相交,而这与直线l 是⊙O 的切线矛盾.因此OA 与直线l 垂直.从而得到切线的性质定理,同时引导学生得出切线性质定理的符号语言. 切线的性质 O A B E P O A 图3 l圆的切线垂直于经过切点的半径.∵直线 l 是⊙O 的切线,A 是切点,∴直线 l⊥OA例1:直线AB经过⊙O上的点C,并且OA=OB,CA=CB,求证:直线AB是⊙O的切线师生活动:教师引导学生分析证明思路:1中由于直线AB经过⊙O上的点C,所以连接OC,只需证OC⊥AB即可。
《切线长定理》与内切圆

4.已知:△ABC中,∠A=70º,点O是内心,求 ∠BOC的度数。
A
O
B
C
5、已知△ABC的内切圆分别和BC、AC、AB切于
点D、E、F,BC=9cm,AC=13cm,AB=14cm,求AF、
BD和CE的长。
A
F
E
B
D
C
6.如图△ABC中,∠C=90,AC=6,BC=8,三角 形三边与⊙O均相切,切点分别是D、E、F,求⊙O 的半径。
A
P O
B
如何用尺规通过圆外一点画出圆的切线?
A
OO ·
P
B
1.认识切线长:
过圆外一点作圆的切线,这点和切点之间的线段长叫
做这点到圆的切线长.
A
O
·
P
B
切线与切线长是一回事吗?它们有什么区别与联系呢?
2.研究切线长的性质:A
切线长定理:
过圆外一点
引圆的两条
O
P
切线,它们 的切线长相
B
等。
你还会得到哪些结论?再连接AB呢?
切线长定理与内切圆
圆的性质定理:
圆的切线垂直于过切点的半径.
圆的判定定理:
过半径外端且垂直于这条半径的直线是圆的切线.
是基本思路)
新课导入:
过一点A作⊙O的切线,
1.当点A在圆内时,能画⊙O的切线吗? 2.当点A在圆上时,能画⊙O的切线吗? 3.当点A在圆外时,能画⊙O的切线吗?
1.如何过⊙O外一点P画出⊙O的切线? 如下左图,借助三角板,我们可以画出PA是⊙O的切线. 2.这样的切线能画出几条?
A
F
D
O
CE
B
7.已知四边形ABCD的边AB、BC、CD、DA分别与⊙O
几何画板

sketchpad使用方法:外公切线一、制作效果如图,无论是改变两圆的大小,还是圆心距,直线和圆的关系保持不变,即直线始终是两圆的外公切线。
二、思路分析我们在寻求外公切线的作法以前,先看看下图,是否能想起过圆外一个作圆的切线的的尺规作法以PO为直径作圆(先作线段OP的中点,找到圆心)&rar r;作两圆的交点C、D(这一步可省)→作直线PC、PD。
是不是很简单?是不是想起外公切线的尺规作图(其实质就是把两圆的外公切线转化为内公切线),想不起试着分析一下。
如果还不行的话,就看下面的操作步骤吧。
三、操作步骤1. 任画两圆(A,D)(B,C)2. 度量两圆的半径,并计算它们的差3. 以AB为直径画圆4. 画圆(A,(半径⊙AD)-(半径⊙BC=0.94厘米)),与以AB为直径画的圆交于E(其中一个交点)。
5. 作直线BE;作直线(A,E)交圆(A,D)于F6. 作平行线(F,直线BE)7. 作直线FG关于线段BA的对称直线四、拓展研究1.这样尺规作图外公切线的作法,有缺点,当⊙AD的半径小于半径⊙BC时,外公切线不见了(您知道为什么吗?),如何完善?只要在大圆内重复上述步骤,就搞定了,具体如下(1)、计算两圆半径的差(注意是大圆半径减小圆半径)(2)、画圆(B,(半径⊙BC)-(半径⊙AD=0.94厘米)),与以AB为直径画的圆交于I(其中一个交点)。
(3)、作直线(A,I);作直线(B,I)交圆(B,C)于H(4)、作平行线(H,直线ai)(5)、作已作切线关于线段BA的对称直线,即另一条切线。
如下图就算这样作,仍不完善,当两圆半径相等时,切线会不见了。
您能继续完善吗?2.尺规作图得分三种情况(半径之间大于、小于、等于),有没有更简单的作法,有,下面讲一种非尺规作图的方法如上图,分析一下作法。
两圆半径固定,位置固定→确定∠BAF→确定F→确定G→确定一条切线→另一条切线。
具体步骤如下(1)、度量AB即圆心距(2)、计算(3)、B点饶A为中心以计算结果为旋转角旋转得到(4)、作射线(A,)交圆AD于H(5)、作平行线(B,射线AH),交圆BC于I(6)、作直线(H,I)即两圆的一条外公切线(7)、作直线hi关于AB对称的直线,得到另一条切线。
几何画板教程

前 言《几何画板》是教育部基础教育司向全国中小学推荐的辅助教学软件,该软件功能强大,能方便地用动态方式表现对象之间的关系,教师利用该工具平台既可根据自己的教学需要编制与开发课件,又可便于学生进行主动探索,它给人们提供了一个观察几何图形的内在关系,探索几何图形奥妙的环境。
被誉为“21世纪的动态几何”。
特 点1. 动态的图形功能几何画板,顾名思义是“画板”。
像许多Windows 环境下的绘图软件一样,也提供了画点、画线和画圆的工具。
这实际上提供了计算机上的直尺和圆规。
几何画板的【构造】菜单可以帮助用户快速地绘制常用的尺规图形,比如平行线、垂线、以圆心和给出的半径画圆等,因此能画任意一种欧几里得几何图形,而且注重数学表达的准确性。
平行四边形ABCDCAB2.简便的动画功能几何画板可以针对教学的要求制作动画和移动对象。
还可以让几何体转动起来产生三维效果的直观图,培养空间想象能力。
A几何画板提供了平移、旋转、缩放、反射等图形变换功能,可以按指定的值或动态的值对图形进行这些变换,也可以使用由用户定义的向量、角度、距离、比值来控制这些变换。
4.方便的计算功能几何画板提供了度量和计算功能,能够对所作出的对象进行度量,如度量线段的长度,度量弧长、角度、面积等。
还能够对度量出的值进行计算,包括四则运算、函数运算,并把结果动态地显示在屏幕上。
当被测量的对象变动时,显示它们大小的这些数量也随之改变,可以动态地观察它们的变化或者关系。
这样一来,像研究多边形的内角和之类的问题就非常容易了。
许多定量研究也可以借助几何画板来进行。
S △ABC = 8.28 厘米2B5.独特的自定义工具自定义工具就是把绘图过程(步骤)自动记录下来,形成一个工 具,并随文件保存下来,以后可以使用这个工具进行绘图。
几何画板支持直角坐标系和极坐标系,只要给出函数的表达式,几何画板能画出任何一个初等函数的图像。
7.开放的其他功能几何画板可以为图形设置丰富的颜色,可以把颜色与数字关联起来。
过圆外一点作圆的切线的两种方法

过圆外一点作圆的切线是一个有趣且具有一定难度的几何问题。
在数学几何中,有两种方法可以用来找到过圆外一点作圆的切线,分别是几何构造法和解析几何法。
在本文中,我将探讨这两种方法,并对其进行全面评估,以帮助你深入理解这一概念。
1. 几何构造法几何构造法是通过几何图形的构造和推导来寻找问题的解。
在求解过圆外一点作圆的切线时,我们可以利用几何构造法来找到两种方法,即内切和外切。
我们来看内切的情况。
设圆的圆心为O,外点为P。
我们可以通过以下步骤来构造过外点P作圆的内切线:a. 以外点P为圆心,画一条与圆相切的直线L,相切点为T。
b. 连接PT,可得到过外点P作圆的内切线。
接下来,我们来看外切的情况。
同样假设圆的圆心为O,外点为P。
通过以下步骤可以构造过外点P作圆的外切线:a. 以外点P为圆心,画一条与圆相切的直线L,相切点为T。
b. 连接PT,可得到过外点P作圆的外切线。
通过几何构造法,我们可以清晰地看到过圆外一点作圆的内切线和外切线的构造过程,从而更好地理解这一概念。
2. 解析几何法解析几何法是通过坐标系和方程来寻找问题的解。
在求解过圆外一点作圆的切线时,我们同样可以利用解析几何法来找到两种方法。
设圆的方程为(x-a)²+(y-b)²=r²,外点P的坐标为(x₀, y₀)。
我们可以通过以下步骤来求解过外点P作圆的切线方程:a. 联立圆的方程和外点P到圆的距离公式,可得到切线方程。
b. 根据切线方程,可以求解出与圆相切的直线方程。
通过解析几何法,我们可以用数学的方式来推导出过圆外一点作圆的切线方程,从而更加深入地理解这一概念。
总结回顾通过本文的讨论,我们深入探讨了过圆外一点作圆的切线的两种方法,即几何构造法和解析几何法。
在几何构造法中,我们通过构造图形和推导过程来寻找切线;而在解析几何法中,我们通过坐标系和方程来求解切线方程。
这两种方法各有特点,可以帮助我们更全面、深刻地理解这一几何问题。
(完整版)切线长定理教学设计

课题:切线长定理教学过程:一。
提出问题问题1:经过⊙O内一点P能作圆的切线吗?过圆上一点呢?能作几条?(学生操作,教师展示学生作图,学生回答作图过程和理由)二。
探索新知问题2:请同学们在刚才画好的切线上取异于A的一点P,连结PO. 沿着直线PO将纸对折,设与点A重合的点为B,观察并思考:①OB是⊙O的半径吗?②PB是⊙O的切线吗?归纳:1。
经过圆外一点,可以作圆的 2 条切线.2。
切线长定义: 经过圆外一点作圆的切线,这点和切点之间的线段的长。
问题3:切线与切线长的区别?表示切线长线段的两个端点分别是哪两个?(学生回答,教师总结)问题4:如图,过P点作⊙O的两条切线PA,PB,A, B分别是切点. 判断图中的PA与PB,∠OPA与∠OPB有何关系?猜想:在任意的圆中,或不同位置的圆外一点P,过P作圆的两条切线PA,PB,A,B分别为切点。
均有PA=PB,∠OPA=∠OPB吗 ?进一步验证:教师几何画板演示切线长定理,学生观察作答。
(改变圆的大小和P点的位置),验证结论正确,教师口头提问:只用猜想或测量的方法不能说明结论是否正确,同学们能不能运用逻辑推理的方法证明结论?(引导学生写出已知,求证并证明)归纳:切线长定理从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.(板书,画出基本图形,引导学生归纳符号语言)符号语言:∵PA、PB分别切⊙O于A、B∴PA = PB,∠OPA=∠OPB三. 初步运用1.(赤峰中考)如下图,PA、PB是⊙O的两条切线,AC是⊙O的直径,∠P=40°,则∠BAC的度数是 20°。
2。
如上右图,PA、PB是⊙O的两条切线,若∠APB=60°,PA=6cm,那么⊙O的半径是23cm .四。
探究加深继续探究:PA、PB是⊙O的两条切线,连接OA、OB、AB、OP,AB交OP于点M,OP与⊙O交于点N,这个图形是切线长定理的基本图形,那么除了PA=PB,∠OPA=∠OPB,还能得到哪些结论?先独立思考,能写几条就写几条,然后小组讨论交流.要求、鼓励学生:积极思考团结协作亮出自我。
尺规作图——过圆外一点作圆的切线方法归纳

尺规作图 过圆外一点作圆的切线方法归纳胡小华(江苏省南京市金陵中学河西分校㊀210036)摘㊀要:尺规作图是初中平面几何中的重要知识ꎬ是中考的热门题型.本文阐述了用多种方法过圆外一点作圆的切线ꎬ对学生的数学知识㊁方法㊁经验和思维能力都有一定的要求.通过尺规作图既复习了基本作图知识ꎬ又对圆的性质㊁切线的性质㊁以及切线的判定等知识进行了复习.关键词:尺规作图ꎻ切线ꎻ切线的判定中图分类号:G632㊀㊀㊀㊀㊀㊀文献标识码:A㊀㊀㊀㊀㊀㊀文章编号:1008-0333(2019)35-0031-02收稿日期:2019-09-15作者简介:胡小华ꎬ女ꎬ江苏省泰兴人ꎬ本科ꎬ中学一级教师ꎬ从事初中数学教学研究.㊀㊀尺规作图是初中平面几何中的重要知识ꎬ是中考的热门题型ꎬ学生需综合运用所学的知识ꎬ多角度思考问题.在初三第一轮复习时ꎬ我设计了这样一个问题 过圆外一点A作☉O的切线ꎬ尺规作图ꎬ保留作图痕迹ꎬ并说明作图的依据ꎬ比一比谁的画法多 .学生作品展示图1方法一:利用直径所对的圆周角是直角.连接AOꎬ以AO为直径作☉Bꎬ☉B与☉O相交于D㊁E两点ꎬ则ADꎬAE即为所求作的切线.理由:☉B中ȵAO是直径ꎬʑøADO=90ʎ即ODʅAD.ȵAD经过半径OD的外端ꎬʑAD与☉O相切.该方法是由切线想到垂直ꎬ构造直角的常用方法之一是利用直径所对的圆周角是直角这一定理.再由切线图2的判定方法:过半径外端ꎬ并且垂直于半径的直线是圆的切线.切线的作法即转化为主要考虑作半径的垂线的方法ꎬ联系初三刚学过的知识ꎬ我们首先想到的是直径所对的圆周角是直角这一定理ꎬ这一方法也就顺其自然而产生.方法二:利用 等腰三角形三线合一 的性质作垂直.以O为圆心ꎬBC长为半径作弧ꎬ以A为圆心ꎬAO长为半径作弧ꎬ两弧交于点DꎬOD与☉O相交于点Eꎬ连接AEꎬ则AE即为☉O的切线.另一条切线也可以用同样的方法作出.理由:ȵAO=ADꎬOD=BC=2OEꎬʑE为OD的中点.ʑAEʅODꎬʑAE与☉O相切.要作切线想到垂直ꎬ而利用等腰三角形三线合一的性质也是我们常见的构造垂直的方法之一.方法三:利用勾股定理的逆定理构造垂直.分析:先假设切线画出来了ꎬ则斜边长为AO长ꎬ一条直角边长为半径rꎬ根据勾股定理可以求出另一条直角边的长.图3作øDCH=90ʎꎬ在CH上截取半径rꎬ交CH于点Gꎬ以G为圆心ꎬAO长为半径作弧ꎬ交CD于点Fꎬ则CF长即为所求作的切线长.以A为圆心ꎬCF长为半径作弧交圆O于点Eꎬ连接AEꎬ则AE即为所求作的一条切线.理由:ȵøC=90ʎꎬ13ʑFC2+CG2=FG2.又ȵAO=FGꎬCG=OEꎬFC=AEꎬʑAE2+OE2=AO2.ʑAEʅOEꎬʑAE是☉O的切线.图4该作图方法是利用勾股定理的逆定理构造直角ꎬ想法比较独特ꎬ通过先构造直角找到三边关系ꎬ再利用三边关系构造直角ꎬ从而创造切线.学生的思维让人眼前一亮.方法四:利用相似作垂直证半径.延长AO到Dꎬ使得OD=OA.以D为圆心ꎬ以☉O直径长为半径作弧ꎬ以O为圆心ꎬOA长为半径作圆ꎬ交弧于点Fꎬ连接AF.过O点作OEʅAFꎬ交AF于点Eꎬ则AE即为所求作的切线.证明:ȵAD为直径ꎬʑøAFD=90ʎ.ȵOEʅAFꎬʑOEʊDFꎬ㊀㊀ʑәAOEʐәADFꎬʑOEDF=AOAD=12ꎬʑOE=12DF=r.又ȵOEʅAFꎬʑAE是☉O的切线.前三种方法均是连半径ꎬ作垂直ꎬ第四种方法是作垂直证半径ꎬ刚好复习了初中阶段的证明切线的两种方法ꎬ也是学生综合运用知识解决问题能力的一种体现.在复习期间这样一个开放性的问题激发了学生学习的热情和潜能ꎬ围绕数学问题展开的思维碰撞ꎬ无不是学生学习主动性㊁能动性和创造性的综合体现.在解决问题的过程中复习了初中阶段常见的构造垂直的几种重要方法ꎬ我不禁感叹 只要给学生一个舞台ꎬ他们必将还我一片精彩 !㊀㊀参考文献:[1]沈文选.中学数学思想方法[M].长沙:湖南师范大学出版社ꎬ1999.[2]罗增儒.数学思想方法的教学[J].中学教研(数学)ꎬ2004(7):29-30.[责任编辑:李克柏]以情促教㊀践行自主课堂浅议培养初中生数学情感的策略芮亚琴㊀任㊀庆(江苏省宜兴市桃溪中学㊀214200)摘㊀要:数学情感就是学生在数学活动中对数学产生的求知欲及好奇心ꎬ它更多地倾向于数学兴趣ꎬ能对学生的学习产生积极的影响.注重学生数学情感的培养可以促进教学ꎬ是提高学生学习数学的自主性和主动性的必要条件.本文根据笔者多年的教学经验ꎬ结合教学实例ꎬ就如何培养学生的数学情感提出几点建议.关键词:数学情感ꎻ数学兴趣ꎻ主动学习中图分类号:G632㊀㊀㊀㊀㊀㊀文献标识码:A㊀㊀㊀㊀㊀㊀文章编号:1008-0333(2019)35-0032-02收稿日期:2019-09-15作者简介:芮亚琴(1982.2-)ꎬ女ꎬ江苏省宜兴人ꎬ本科ꎬ中学一级教师ꎬ从事初中数学教学研究.任庆(1979.9-)ꎬ男ꎬ江苏省宜兴人ꎬ本科ꎬ中学一级教师ꎬ从事初中数学教学研究.㊀㊀情感是人与生俱来的一种心理活动ꎬ是人们对客观事物是否符合个体需要而产生的态度体验.情感对教学质量有一定的影响ꎬ积极的情感能让学生主动㊁快乐地学习ꎬ养成良好的习惯ꎬ获得一定的成就ꎬ消极的情感则会影响学生的学习效果.当新课标对学生的情感态度目标提出培养要求时ꎬ 数学情感 便作为数学学科上的专有名词被提了出来.初中学生正处在身心快速发展的时期ꎬ在教学中强化情感对学生的学习主动性及自觉性都有着积极的作用.在初中数学教学中ꎬ如何培养学生的数学情感ꎬ对此ꎬ笔者有以下几点粗浅的看法ꎬ供同仁们参考.㊀㊀一㊁渗透情感意义ꎬ体会情感价值什么是数学情感?为何要渗透数学情感的教育?数学情感对数学学习而言有着怎样的意义?让学生明白这些问题的本质是培养学生数学情感的第一步.教师在进行教学时可以将上述问题渗透至教学中ꎬ让学生体会数学情感的价值.如笔者在初二开学的起始阶段ꎬ专门开设了一堂主23。
几何画板绘制圆的切线技巧解析
几何画板绘制圆的切线技巧解析
作圆的切线是几何绘图时常见的问题,圆的切线具有很多特性。
接下来我们一同看看如何用几何画板绘制圆的切线。
1.构造圆和线段。
利用圆工具制作一个圆O。
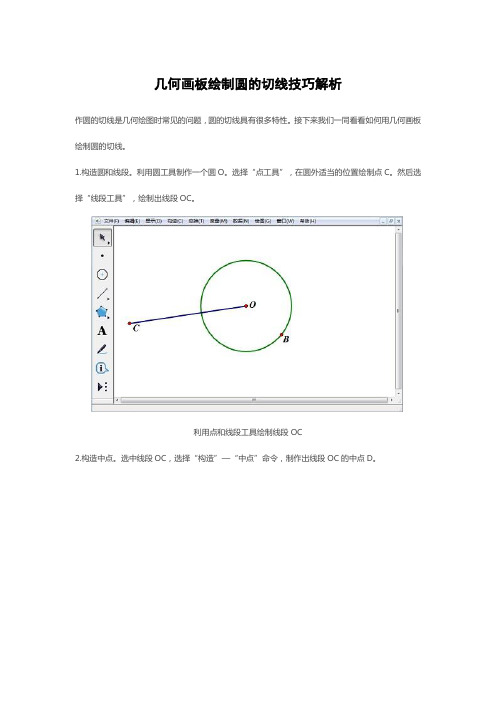
选择“点工具”,在圆外适当的位置绘制点C。
然后选择“线段工具”,绘制出线段OC。
利用点和线段工具绘制线段OC
2.构造中点。
选中线段OC,选择“构造”—“中点”命令,制作出线段OC的中点D。
选中线段OC构造OC的中点
3.作圆。
选中点D和点O,菜单“构造”中选择“以圆心和圆周上的点绘圆”。
选中点D和点O构造圆D
4.构造三角形。
两圆交点为E、F,使用“线段工具”连接线段CF、线段CE、线段OF、线段OE。
用线段工具构造线段CF、CE、OF、OE
5.隐藏圆及多余的点。
选中圆D、点D、点B,选择“显示”—“隐藏对象”命令。
使用隐藏命令隐藏圆D、点D、点B
6.更改线型。
选中线段CO、EO、FO,“显示”菜单中选择“线型”——“细”——“点线”。
圆的切线就绘制完成了。
线段CO、EO、FO的线型更改为点线
以上详细为大家介绍了圆的切线是怎样用几何画板绘制出来的,方便新用户快速入门,大家多多练习就可以掌握。
