基于系统动力学的人口预测
“二孩”背景下人口合理规模预测--以大连市甘井子区为例
“二孩”背景下人口合理规模预测--以大连市甘井子区为例王耕;李优【摘要】人口是社会发展的动力，是国家或一个地区的硬实力，人口问题是可持续发展的核心问题。
今年“二孩”政策的提出，对未来人口规模的预测意义更加重大。
在此背景下，本文以大连市甘井子区为例，运用马尔萨斯人口模型、GM(1，1)灰色模型和系统动力学模型对甘井子区2015-2025年的人口规模做出预测，并进行对比分析。
结果表明：GM(1，1)灰色模型的预测精确度较低，马尔萨斯模型预测精准度次之，系统动力学的预测精准度最好。
预测的最终结果：2020年甘井子区总人口达到151万人，2025年将达到179万人。
%Social development of the population dynamics, is the country's or a region's hard power, population issues are central to sustainable development issues. This year's“second child” policy proposal of more significant projection of future population size. In this context, this paper, ganjingzi district, Dalian, for example, the use of Malthusian population models, GM (1,1) grey modeling and system dynamics modeling to predict population size of 2015-2025, ganjingzi district, and compare. Results showed that GM (1,1) gray model of prediction accuracy is low, maersisi model prediction accuracy, and system dynamics prediction accuracy the best. Predicted final results: in 2020, ganjingzi district population reached 1.51 million in 2025 and reached 1.79 million.【期刊名称】《国土与自然资源研究》【年(卷),期】2016(000)004【总页数】4页(P39-42)【关键词】人口预测;马尔萨斯模型;灰色模型;系统动力学【作者】王耕;李优【作者单位】辽宁师范大学城市与环境学院，辽宁大连116029; 辽宁师范大学海洋经济与可持续发展中心，辽宁大连116029;辽宁师范大学城市与环境学院，辽宁大连116029【正文语种】中文【中图分类】O171人口作为经济社会可持续发展的基础和载体，直接影响区域经济发展的速度和资源环境的规划保护［1］。
人口预测的数学模型与预测方法分析
人口预测的数学模型与预测方法分析人口预测是对未来一定时期内人口数量和结构的变动进行估计和预测的过程。
人口预测在社会经济发展规划、城市规划、教育医疗资源配置等方面具有重要的参考价值。
为了准确预测人口的变动趋势，需要建立合理的数学模型和选择适当的预测方法。
人口预测的数学模型主要包括线性回归模型、指数模型、Logistic模型等。
线性回归模型是一种用来描述两个变量之间线性关系的统计模型，可以用来预测人口随时间的变化。
指数模型假设人口数量按照指数规律增长或减少，适用于人口增长较快的情况。
Logistic模型则适用于人口增长速度放缓后的情况，它是一种描述增长速度逐渐趋近于饱和的模型。
在选择数学模型时，需要综合考虑以下几个因素：人口历史变动趋势、人口自然增长率、人口迁移和流动情况、政策调控等因素。
同时，还需根据实际情况对模型的参数进行合理的设定和修正，以提高预测的准确性。
在预测方法上，常用的有趋势线法、复合增长率法、比较推理法、时间序列分析法和系统动力学方法等。
趋势线法是基于历史数据的发展趋势来进行预测，适用于人口变动趋势比较稳定的情况。
复合增长率法是将历史数据中的增长率按一定规则进行加权平均，再用来推算未来人口的增长率。
比较推理法通过对不同因素的比较和推理，来估计未来人口的变化。
时间序列分析法是根据时间序列数据的历史模式来预测未来的变化趋势。
系统动力学方法则是通过对不同因素的动态关系建立模型，用来探索人口变动的内在机制和规律。
在具体应用时，可以结合不同的数学模型和预测方法，进行多角度的分析和预测。
同时，还需要不断对模型进行修正和优化，以适应不断变化的人口变动趋势和社会经济背景。
此外，还应该注意对预测结果的不确定性进行评估和把握，提供多种可能性的预测结果，为决策者提供科学的参考依据。
根据系统动力学的人口预测
3.2基于系统动力学的人口预测21世纪是人类面临三大问题：第一是人口膨胀，第二是就业困难，第三是环境污染，这三大问题的焦点在于人口。
因此，如何对未来的人口进行预测和控制，一直是人们关心的重要领域。
本课题是在宋健人口模型的基础上，考虑到上海作为一个开放城市，改良建立了双线性开放/动态人口模型。
采用上述基于人口结构模型，预测上海2010—2050年的人口年龄、性别结构。
为了更准确地研究人口系统，我们将人口按0-4岁、5-9岁、10-14岁、…、95-99岁、100岁及以上分群，分为21个群，并假设女性的生育时间以不同的概率分布在15-49岁之间。
然后以政策系数和生育时间的分布概率为政策参数进行仿真分析和政策试验。
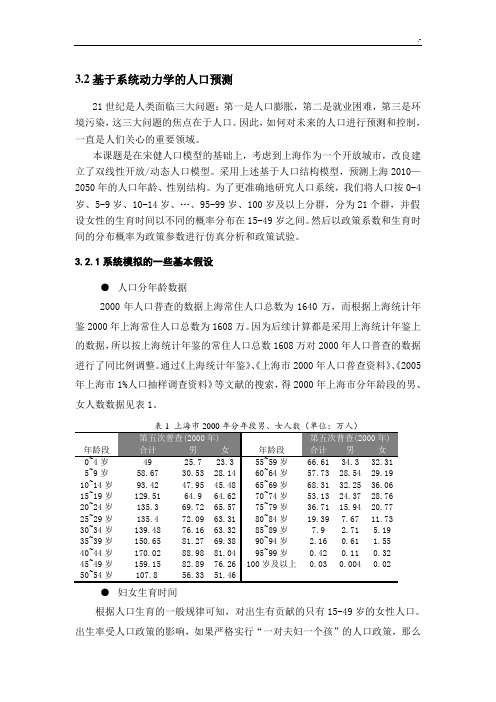
3.2.1系统模拟的一些基本假设●人口分年龄数据2000年人口普查的数据上海常住人口总数为1640万，而根据上海统计年鉴2000年上海常住人口总数为1608万。
因为后续计算都是采用上海统计年鉴上的数据，所以按上海统计年鉴的常住人口总数1608万对2000年人口普查的数据进行了同比例调整。
通过《上海统计年鉴》、《上海市2000年人口普查资料》、《2005年上海市1%人口抽样调查资料》等文献的搜索，得2000年上海市分年龄段的男、女人数数据见表1。
表1 上海市2000年分年段男、女人数（单位：万人）第五次普查(2000年) 第五次普查(2000年)年龄段合计男女年龄段合计男女0~4岁49 25.7 23.3 55~59岁66.61 34.3 32.315~9岁58.67 30.53 28.14 60~64岁57.73 28.54 29.1910~14岁93.42 47.95 45.48 65~69岁68.31 32.25 36.0615~19岁129.51 64.9 64.62 70~74岁53.13 24.37 28.7620~24岁135.3 69.72 65.57 75~79岁36.71 15.94 20.7725~29岁135.4 72.09 63.31 80~84岁19.39 7.67 11.7330~34岁139.48 76.16 63.32 85~89岁7.9 2.71 5.1935~39岁150.65 81.27 69.38 90~94岁 2.16 0.61 1.5540~44岁170.02 88.98 81.04 95~99岁0.42 0.11 0.3245~49岁159.15 82.89 76.26 100岁及以上0.03 0.004 0.0250~54岁107.8 56.33 51.46●妇女生育时间根据人口生育的一般规律可知，对出生有贡献的只有15-49岁的女性人口。
基于动力学模型的人口发展趋势预测
基于动力学模型的人口发展趋势预测近年来，全球人口数量不断增长，人口增长的速度和规模对于经济、资源、环境和社会等多个方面都会产生深远的影响。
因此，对于人口发展趋势的预测和探究是非常必要的。
本文将以动力学模型为基础，分析未来人口发展趋势。
一、动力学模型动力学模型是指对某一系统在时间轴上的演变进行描述的一种数学模型。
它能够通过对系统的因素建立准确的关系式，以使其能够预测在未来一定时间段内该系统的发展状态。
常用的动力学模型有很多，例如生态系统中的Lotka-Volterra模型、物理学中的薛定谔方程、社会学中的传染病动力学模型等。
这些模型大多是基于系统的演化机理进行构建的，它们用数学语言深入描绘了系统内部和其环境之间的动态相互作用，因此它们在预测系统行为和趋势方面具有非常高的准确性和可靠性。
二、基于动力学模型的人口预测在人口学中，常用的动力学模型有人口增长模型和人口结构模型。
人口增长模型是指通过研究各种人口因素，如出生率、死亡率、迁移率等，将它们与时间紧密关联的人口总数进行关系建模，然后用这些关系式来预测未来人口增长的发展趋势。
人口结构模型则是基于人口的年龄、性别、婚姻等分布情况进行研究。
这类模型的关键在于研究人口结构的变化趋势，以及对人口结构的合理调控方法的研究，以达到实现人口数量、性别、年龄等方面的合理分布，从而保证社会平稳发展。
三、实际操作例基于动力学模型的人口预测需要较多的相关数据，如人口普查数据等。
以我国2010年至2019年的人口普查数据为例，本文模拟分别使用人口增长模型和人口结构模型进行预测。
在人口增长模型中，我们假设人口的增长率分别为1.6%、1.5%、1.3%、1.0%、0.7%、0.4%、0.1%、0、-0.1%。
其中，2020年之后的人口增长率为负值，原因是我国的人口老化问题越来越严重，出生率逐渐下降，直接导致人口增长率也逐渐变缓，进而变为负值。
在人口结构模型中，我们将人口分为不同的年龄组，如0-14岁、15-59岁、60岁以上等。
基于系统动力学的江苏省人口预测仿真研究
基于系统动力学的江苏省人口预测仿真研究人口是一个国家的基本资源，对于一个省份来说，人口的增长和变化对经济社会发展有着重要的影响。
江苏省作为中国经济最为发达的省份之一，其人口增长和发展变化更是备受关注。
本文将基于系统动力学的方法，对江苏省人口进行预测仿真研究。
系统动力学是一种用于研究复杂系统的工具，能够模拟和分析系统的动态过程。
在人口预测中，我们需要考虑人口的出生、死亡、迁移等因素，以及这些因素之间的相互作用。
通过构建一个系统动力学模型，可以对人口的变化趋势进行模拟和预测。
我们需要收集江苏省过去几年的人口数据，包括出生率、死亡率、迁移率等指标。
然后，根据这些数据，构建一个基本的人口模型。
模型中的关键变量包括出生人口、死亡人口、迁移人口以及总人口。
出生人口的增加取决于出生率和总人口数，死亡人口的减少取决于死亡率和总人口数，迁移人口的增加或减少取决于迁移率和总人口数。
接下来，我们需要确定模型中的参数和初始条件。
参数包括出生率、死亡率和迁移率，这些参数可以根据历史数据进行估计。
初始条件则是指模型开始运行时的人口数量和特征，可以根据江苏省最新的人口数据确定。
在模型运行过程中，可以通过不断调整参数和初始条件，观察对人口变化的影响。
我们可以进行不同的实验，比如改变出生率、死亡率或迁移率，观察人口数量的变化趋势。
通过模型的仿真运行，可以得到一系列关于人口变化的预测结果。
我们可以对预测结果进行分析和解释。
通过观察人口数量的变化趋势，可以预测未来江苏省人口的发展情况。
我们还可以观察模型中其他变量（比如年龄结构、性别比）的变化趋势，进一步了解人口发展的特点。
基于系统动力学的江苏省人口预测仿真研究
基于系统动力学的江苏省人口预测仿真研究近年来，人口问题一直是社会发展中日益突出的一个问题。
人口数量和结构的变化对于经济、环境、社会等方面都有深远的影响。
对于人口的预测和研究就显得至关重要。
江苏省作为全国人口较多的省份之一，其人口数量和结构的变化直接关系着其经济社会发展的方向。
本文以江苏省为研究对象，基于系统动力学的方法，对江苏省未来的人口变化进行预测和仿真研究。
为了进行仿真研究，我们需要建立一个江苏省人口变化的数学模型。
这个模型可以包括人口数量、人口出生率、人口死亡率、人口迁移率等因素。
人口数量是模型的核心变量，其他因素则是影响人口数量变化的驱动因素。
在建立模型之前，我们需要对江苏省的历史人口数据进行分析。
通过对数据的统计和分析，我们可以发现人口数量的变化趋势，以及其他相关的因素如出生率、死亡率等与人口数量的关系。
然后，我们可以根据历史数据来建立数学模型。
通过分析历史数据的变化趋势，我们可以确定人口数量和其他因素之间的关系，并建立相应的数学方程。
这些方程可以描述人口数量和其他因素之间的动态变化过程。
接下来，我们可以使用系统动力学的仿真工具来进行模拟研究。
通过对模型的参数和初始条件进行设置，我们可以模拟出不同时期的人口变化情况，并预测未来的人口数量和结构变化。
我们可以根据模拟结果进行政策分析和决策支持。
通过对仿真结果的分析，我们可以评估不同政策对于人口变化的影响，并提出相应的政策建议。
基于系统动力学的江苏省人口预测仿真研究可以通过建立数学模型，模拟和预测江苏省未来的人口变化情况，为政府制定人口政策提供科学的依据。
这对于促进江苏省经济社会的可持续发展具有重要意义。
基于系统动力学的江苏省人口预测仿真研究
基于系统动力学的江苏省人口预测仿真研究【摘要】本研究基于系统动力学，利用江苏省的人口数据，建立了一套人口预测仿真模型。
首先进行了数据采集和处理，然后建立了系统动力学模型，并通过验证和结果分析确定了其准确性。
接着进行了参数敏感性分析，对未来发展趋势进行预测。
研究总结表明，该模型在预测江苏省人口变化方面具有较高的精度。
在展望与建议中，我们指出了模型的改进方向，并分析了研究对社会的影响。
这一研究对于江苏省乃至其他地区的人口规划和政策制定具有重要意义，能够为未来的人口管理提供科学参考。
【关键词】系统动力学、江苏省、人口预测、仿真研究、模型建立、数据采集、模型验证、结果分析、参数敏感性、发展趋势、总结、展望、建议、社会影响1. 引言1.1 研究背景江苏省作为中国经济最发达的地区之一，人口规模庞大且动态变化明显。
随着经济发展和城镇化进程的加快，人口结构和分布也在不断调整。
对江苏省人口未来发展趋势进行预测和仿真研究具有重要意义。
基于系统动力学的人口预测模型可以较好地捕捉人口变化的多因素影响，为政府决策和社会发展提供科学依据。
在这一背景下，本研究旨在建立基于系统动力学的江苏省人口预测仿真模型，利用历史数据和趋势分析方法，探讨江苏省未来人口发展的可能走势。
通过对人口数量、结构和分布等方面进行全面分析，为政府制定人口政策和规划提供参考，促进江苏省经济社会可持续发展。
本研究对于深入了解江苏省人口发展规律、推动城市化进程、优化资源配置和促进区域协调发展具有重要意义。
1.2 研究目的江苏省是我国经济发展较快的省份之一，人口规模庞大且经济水平较高。
随着人口老龄化趋势日益加剧，人口结构的变化对江苏省的社会经济发展将产生深远影响。
本研究旨在利用系统动力学模型对江苏省人口进行预测仿真研究，以期能够更准确地预测未来人口变化趋势，为相关部门提供科学依据，为江苏省未来人口政策的制定提供参考。
具体目的包括：探讨江苏省人口增长的规律性和影响因素，分析人口老龄化对经济发展、社会保障和医疗卫生等方面的影响，预测未来人口结构的变化趋势，为制定针对性的人口政策提供科学依据。
基于系统动力学的江苏省人口预测仿真研究
基于系统动力学的江苏省人口预测仿真研究人口预测是社会经济发展中的重要内容，对于规划和决策具有重要的参考价值。
系统动力学是一种研究系统动态变化规律的方法，可以用于人口预测的仿真研究。
本文将基于系统动力学的方法，对江苏省的人口发展进行预测和仿真研究。
我们需要构建一个系统动力学模型来描述江苏省的人口发展。
模型中包括人口的迁入、迁出、出生和死亡四个要素。
迁入和迁出受到经济、政策、教育等因素的影响，可以用一组方程来描述。
出生和死亡受到人口年龄结构、医疗水平、生活水平等因素的影响，也可以用一组方程来描述。
通过对这些方程进行数学建模，可以得到一个动态的人口发展模型。
我们需要收集江苏省的历史人口数据，并进行参数估计。
通过对历史数据的分析，可以获得模型中的各个参数的取值范围。
然后利用系统动力学的方法，对模型进行仿真运行。
仿真过程中，可以通过调整各个参数的取值，来模拟不同的情境和策略。
比如可以通过调整迁入和迁出的参数，来模拟不同地区的人口流动。
通过调整出生和死亡的参数，来模拟不同的医疗水平和生活水平对人口发展的影响。
我们可以根据仿真结果，对江苏省的人口发展进行预测和分析。
通过对不同情境和策略的仿真结果进行对比，可以评估不同因素对人口发展的影响程度。
比如可以评估经济发展对人口迁入的促进作用，或者评估医疗水平对人口死亡率的影响。
通过这些分析，可以为江苏省的规划和决策提供参考，帮助实现人口发展的合理和可持续。
基于系统动力学的方法可以用于江苏省人口预测的仿真研究。
通过构建系统动力学模型、参数估计和仿真运行，可以得到江苏省的人口发展趋势和影响因素。
这种方法有助于提高人口预测的科学性和准确性，为江苏省的人口规划和决策提供参考和支持。
基于GM(1,1)和系统动力学模型的河南省人口模拟比较
基于GM（1，1）和系统动力学模型的河南省人口模拟比较作者：梁志林，李静来源：《中国管理信息化》2013年第15期[摘要] 我国的可持续发展一直受到人口问题的影响，本文以河南省人口作为研究对象，根据河南省2002-2006年人口数据，运用灰色GM（1，1）模型和系统动力学模型对2007-2011年河南省人口进行模拟。
结果表明GM（1，1）模型和系统动力学模型模拟结果有一些差异，系统动力学模型模拟效果较好，对河南省未来人口的预测以及制定合理的人口政策提供了有效的依据。
[关键词] GM（1，1）模型；系统动力学；河南人口；模拟doi ： 10 . 3969 / j . issn . 1673 - 0194 . 2013 . 15. 029[中图分类号] F224；C924.2 [文献标识码] A [文章编号] 1673 - 0194（2013）15- 0042- 021 引言人口问题是困扰我国发展的一个重要问题，我国很多有关政治、社会、经济的政策都要以人口为依据，因此，人口预测是人口发展不可缺少的一个环节，也是人口研究中的重要课题之一。
河南省作为我国人口大省，在现代化建设中，为了实现可持续发展战略，必须正确处理人口与经济、环境、资源等因素的关系。
近年来，随着河南省快速发展，人口急剧增加，加快了资源消耗，环境污染和生态破坏问题也日渐严重，因此，人口问题已成为河南省发展的重要制约因素之一。
本文运用灰色GM（1，1）模型和系统动力学模型对河南省人口进行模拟并比较，为河南省未来人口预测和经济发展提供科学依据，对于中原经济区建设背景下河南省的发展战略制定具有重要意义。
2 灰色GM（1，1）模型2.1 GM（1，1）模型GM（1，1）模型是灰色系统中常用的一种预测模型，它的特点是：可以利用较少的数据进行预测和分析；建模简单，公式简洁，易于求解；具有可检验性。
灰色GM（1，1）模型最大特点是需要数据少，预测精度高，不需要预测对象相关的因素的参与，只需运用预测对象自身的时间序列进行预测。
基于系统动力学的江苏省人口预测仿真研究
基于系统动力学的江苏省人口预测仿真研究
随着社会和经济的发展，人口变化对社会、经济和环境产生的影响越来越大。
因此，预测和规划人口变化是重要的社会和经济问题。
本文基于系统动力学的方法对江苏省的人口变化进行预测和仿真研究。
首先，构建了一个江苏省人口预测模型。
该模型基于系统动力学的思想，将江苏省的人口分为出生、死亡、迁入和迁出四个部分，并考虑了影响人口变化的因素，如经济发展状况、医疗保健水平、教育水平、人口政策等。
模型采用了差分方程的形式，通过对四个部分的积分和微分，计算江苏省的总人口数，并预测未来的人口变化趋势。
接着，使用Vensim软件对该模型进行仿真。
通过调整模型中各因素的参数和初始值，对不同情况下的人口变化进行仿真。
仿真结果显示，随着经济发展的加快和医疗保健水平的提高，江苏省的总人口数将会逐渐增加。
同时，人口老龄化问题也将逐渐加重。
为应对这一问题，需要在教育和就业等方面加强政策引导，促进人口结构的优化。
最后，对模型的结果进行了评估。
评估结果显示，该模型对江苏省人口变化的预测较为准确，可以为相关政策的制定提供科学依据。
但是，该模型仍存在不足之处，例如对不同年龄和性别群体的人口变化预测较为简单，可能需要进一步完善和扩展。
综上所述，本文基于系统动力学的方法对江苏省的人口变化进行了预测和仿真研究。
研究结果表明，经济发展状况、医疗保健水平、教育水平等是影响人口变化的重要因素，需要在相关政策的制定中加以考虑。
该研究有望为未来的人口规划和管理提供有益参考。
基于系统动力学的江苏省人口预测仿真研究
基于系统动力学的江苏省人口预测仿真研究随着经济的不断发展和社会的持续进步，人口变化成为社会发展中不可忽视的重要因素之一。
对于一个地区或国家来说，正确预测和合理规划人口变化趋势，对于资源配置、社会政策和经济发展都具有重要意义。
作为中国东部沿海地区的一个重要经济发达省份，江苏省的人口变化一直备受关注，开展基于系统动力学的江苏省人口预测仿真研究，对于深入了解江苏省人口变化规律，提出相应的政策建议具有积极意义。
一、研究背景二、研究目的本研究旨在通过建立系统动力学模型，分析江苏省人口变化的规律，预测未来的发展趋势，为相关部门提供决策建议。
具体目的如下：1. 分析江苏省人口变化的规律及其影响因素，探究人口变化对经济发展和社会政策的影响。
2. 建立基于系统动力学的江苏省人口预测模型，预测未来的人口数量和结构变化趋势。
3. 提出相应的政策建议，为江苏省未来的经济发展和社会政策制定提供决策依据。
三、研究方法1. 收集江苏省相关的人口数据和社会经济数据，如人口数量、人口结构、生育率、死亡率、人口迁移率、经济增长率等。
四、研究成果通过对江苏省人口的系统动力学仿真研究，得出了以下结论：1. 江苏省人口增长率逐渐趋缓，人口数量将在未来几十年内趋于稳定。
2. 人口结构将发生明显的变化，老龄化程度不断加剧，劳动力人口逐渐减少。
3. 人口迁移将继续加剧城乡和地区之间的不平衡，城市将面临更多的人口压力。
4. 经济发展水平将对人口变化产生重要影响，经济发展水平较高的地区人口增长率较快。
在此基础上，本研究提出了以下政策建议：1. 加强人口政策的调控，促进生育率的提高，推动人口结构的优化。
2. 加大对老龄化问题的关注，完善相关社会保障措施，促进老龄人口的健康和幸福。
3. 加强城乡和地区之间的人口调控，促进资源的合理配置和城乡一体化发展。
4. 加强对经济发展水平较低地区的支持，促进区域经济的均衡发展，减少人口迁移的不平衡。
五、结论与展望本研究通过基于系统动力学的江苏省人口预测仿真研究，揭示了江苏省人口变化的规律和趋势，并提出了相应的政策建议。
基于动力学模型的人口预测研究
基于动力学模型的人口预测研究【摘要】本文基于动力学模型对人口增长进行预测研究。
引言部分介绍了研究背景、目的和意义。
正文分析了动力学模型的理论基础，详细讨论了人口数据的收集与处理方法，以及基于动力学模型的人口增长预测技术。
模型评估与优化部分探讨了如何提高模型的准确性和可靠性。
通过人口增长趋势预测分析，揭示了未来人口变化的可能趋势。
结论部分总结了基于动力学模型的人口预测研究成果，展望了未来研究方向，并提出了结论和建议。
本研究将为人口规划和政策制定提供重要参考，有助于应对人口变化带来的挑战。
【关键词】动力学模型、人口预测、人口增长、数据处理、模型评估、预测分析、研究成果、未来展望、结论和建议。
1. 引言1.1 研究背景近年来，全球人口不断增长，人口结构也发生了巨大的变化。
人口增长与发展关系密切，人口预测成为了一个重要的研究领域。
基于动力学模型的人口预测研究因其具有较高的准确性和可靠性备受关注。
动力学模型是一种描述系统变化随时间推移的数学模型，通过对人口数量变化规律的分析和建模，可以预测未来人口的增长趋势。
人口数据的收集与处理是基于动力学模型的人口预测研究的基础。
通过对历史人口数据的收集和整理，可以建立起一个全面的人口数据库。
在处理数据时，需要考虑到数据的准确性和完整性，并对数据进行清洗和筛选，以确保模型的准确性。
基于动力学模型的人口增长预测是通过建立数学模型，模拟人口数量随时间的变化，并通过模型的参数估计和优化，得出人口增长的未来趋势。
模型评估与优化是保证预测结果准确性的关键步骤，需要通过对模型的拟合程度和预测精度进行评估，进而调整模型参数以提高预测准确性。
人口增长趋势预测分析是基于动力学模型的人口预测研究的重点内容，通过对未来人口增长趋势的分析，可以为政府决策和社会发展提供重要依据。
基于动力学模型的人口预测研究具有重要的理论和现实意义。
1.2 研究目的研究目的主要是通过基于动力学模型的人口预测研究，探索人口增长的规律和趋势，为政府决策和社会发展提供科学依据。
基于系统动力学的江苏省人口预测仿真研究
基于系统动力学的江苏省人口预测仿真研究江苏省位于中国东部，是中国人口最多的省份之一。
随着经济的快速发展和城市化进程的加快，江苏省的人口数量不断增加。
人口数量的变化对于地区经济、社会发展、资源利用和环境保护等方面都具有重要意义。
对江苏省人口的预测和研究具有重要的现实意义。
本文基于系统动力学的方法，对江苏省人口的变化进行了预测和仿真研究。
系统动力学是一种将系统中各个部分之间的相互作用和反馈关系考虑在内的系统分析方法，它可以揭示各种复杂系统中的内在规律和演化趋势。
我们建立了一个人口增长模型，考虑到人口的出生率、死亡率和迁入率等因素。
通过对江苏省历史人口数据进行分析和拟合，我们得出了江苏省人口增长的动力学方程。
然后，我们根据该方程对江苏省未来人口的变化进行了预测。
根据我们的模型和数据分析，我们得出了以下几个结论：江苏省的人口数量在未来几十年内将继续增长，但增长速度将逐渐减缓。
这是由于江苏省经济的快速发展和城市化进程的加快，人口的自然增长和迁入增长将逐渐受到限制。
随着人口的增长，江苏省的人口结构也将发生变化。
老年人口将比例增加，而年轻人口比例将逐渐减少。
这对于江苏省的社会保障、医疗、教育等方面提出了新的挑战。
江苏省的人口增长对资源利用、环境保护等方面也提出了新的要求。
随着工业化和城市化的加速，资源的供给和环境的负担将面临更大的压力。
需要加强资源的节约利用和环境的保护，以实现可持续发展。
本文基于系统动力学的方法对江苏省人口的预测和仿真进行了研究。
得出了江苏省人口将继续增长但增长速度逐渐减缓的结论，并对未来人口结构和资源利用等方面提出了一些建议。
这对于江苏省的经济社会发展具有重要的指导意义。
我国人口系统动力学仿真预测研究
我国人口系统动力学仿真预测研究刘涛【期刊名称】《河北企业》【年(卷),期】2015(000)012【总页数】1页(P93)【作者】刘涛【作者单位】河北科技大学经济管理学院【正文语种】中文本文通过运用Vensim PLE等软件建立系统动力学模型并结合我国人口历年统计数据，对我国人口数量未来50年（2015—2065）变化趋势进行仿真预测。
模型仿真预测结果表明：在我国现行人口政策不变的条件下，未来50年后我国人口年出生率将降至4‰左右，年出生人口降至500万左右；而年死亡率将升至10‰左右，年死亡人口增至1300万左右；我国总人口将在2036年达到峰值14.33亿之后开始下降。
本文的人口模型仿真预测结果可以作为我国调整和完善现行人口政策的依据，有一定的参考价值。
一、问题的提出和研究意义人口特征对于一个国家的社会和经济发展有着重要的影响。
本文拟构建出人口系统动力学模型对反映我国人口特征的总人口、年出生人口、年死亡人口、年出生率和年死亡率指标进行50年仿真预测分析，从而为我国为达到社会经济目标而调整和完善现行人口政策提供参考依据。
二、绘制系统动力学流图首先明确指标要素之间的因果关系：年出生人口增加和年死亡人口降低都会增加总人口，而年出生人口大小取决于总人口和年出生率，年死亡人口大小取决于总人口和年死亡率。
其次确定变量类型，总人口是本系统的唯一流位变量，年出生人口和年死亡人口是本系统的流率变量，年出生率和年死亡率是非状态变量，同时在模型中加入shadow variable，<Time>。
运用Vensim PLE软件绘制总人口模型系统流图。
图1 总人口模型系统流图三、编写系统动力学方程首先给出流位变量总人口的初值和相关变量的函数关系。
流位变量总人口的初值为我国2013年末总人口136072万；根据统计年鉴的人口历史数据，运用SPSS统计软件进行回归分析，得到年出生率与Time的回归方程以及年死亡率与Time的回归方程（1998年—2014年人口相关数据）。
基于系统动力学的江苏省人口预测仿真研究
基于系统动力学的江苏省人口预测仿真研究作者：李香霞来源：《管理观察》2019年第09期摘要：人口是社会经济活动的主体，对人口数量的研究有利于把握经济的发展。
本文以江苏省为研究对象，通过Vensim软件建立系统动力学仿真模型，研究在不同城镇化发展水平下江苏省人口在2017-2035年间的变化。
仿真结果表明：在江苏省现行人口政策不变的情况下，高情景下，江苏省总人口将在2022年达到峰值8032.25万人之后缓慢下降。
中情景下，江苏省人口一直缓慢增加，并且在2024年达到峰值8032.46万人之后缓慢下降。
低情景下，江苏省人口缓慢增加并且在2031年达到峰值8032.53万人之后缓慢下降。
关键词：系统动力学;城镇化水平;人口规模;人口预测中图分类号：C92-03 文献标识码：A1江苏省人口预测江苏省位于中国东部沿海地区，是我国重要经济圈的组成部分，2016年底常住人口7998.6万人，占全国5.78%的人口量，其当年地区生产总值是85900.94亿元，约占国内生产总值的10.38%，这就相当于江苏省一个人口能够创造出两个人的贡献。
人口规模是反映一个地区基本情况的重要指标，它受该地区基础设施、功能布局、环境、经济等因素的影响，因此，讨论江苏省人口发展趋势能对区域经济发展规划有较大的作用。
人口预测是根据人口现状历史发展趋势以及对影响人口发展的各种因素的假说，对未来人口规模、水平和趋势所做的测算。
在人口预测的过程中需要注意要对目标对象的现有人口水平，影响人口规模的因素以及各要素之间的联系这几个方面进行综合了解，以提高预测的精确度。
相关学者在人口预测方面尝试采用多种方法，主要有线性回归法、logistic曲线模型法、灰色模型法、系统动力学方法等。
人口是一个复杂的系统，它需要考虑多方面因素，介于此，本文选用系统动力学方法对江苏省人口进行仿真预测。
该方法可以从系统的角度，综合考虑影响到人口数量的诸多可能性因素，用计算机进行系统模拟，得出由多项指标组合而成的预测值后，然后根据需要与可能选择最优预测值，而模型方程形式灵活，能够有效进行系统的动力研究，有助于进行多方案比较分析，它可以对未来人口发展趋势进行更为科学合理的预判。
基于系统动力学的江苏省人口预测仿真研究
基于系统动力学的江苏省人口预测仿真研究系统动力学是一种用于研究动态系统的方法，它可以帮助分析系统中的各种因素和变量之间的相互作用，从而预测系统未来的发展趋势。
在人口学领域，系统动力学可以应用于人口预测仿真研究，帮助政府和社会组织制定人口政策和规划。
本文将基于系统动力学的方法，对江苏省的人口发展进行预测仿真研究，为未来的人口政策制定提供参考。
一、研究背景江苏省是中国人口大省之一，拥有庞大的人口资源。
随着经济的发展和社会变革，江苏省的人口结构面临着诸多挑战和变化。
为了更好地应对人口发展带来的各种挑战，有必要对江苏省的人口未来发展趋势进行预测，并制定相应的政策和措施。
系统动力学是一种有效的方法，可以帮助研究人员分析人口系统中的各种因素和变量之间的相互影响，从而预测人口的未来发展趋势。
本研究选择系统动力学方法，对江苏省的人口发展进行预测仿真研究。
二、研究目的本研究旨在通过系统动力学的方法，对江苏省的人口发展进行预测仿真研究，重点关注人口数量、人口结构、人口流动等相关因素，并探讨其未来的发展趋势。
通过研究，可以为江苏省未来的人口政策制定提供科学的参考，促进人口资源的合理利用和人口结构的优化调整，进而推动经济社会的可持续发展。
三、研究内容1.建立系统动力学模型本研究将通过收集江苏省历年的人口数据，包括人口数量、性别比例、年龄结构、人口迁移等相关因素，建立系统动力学模型。
通过对历史数据的分析，确定各个因素之间的关系和影响因素，构建相应的系统动力学模型。
2.模型参数设定在建立系统动力学模型的基础上，本研究将设定各个因素的参数，包括人口增长率、生育率、死亡率、迁移率等相关参数。
通过对各个参数的设定，可以模拟出不同的发展情景，从而分析其对人口未来发展的影响。
3.模拟预测人口发展趋势在模型参数设定后，本研究将进行人口发展趋势的模拟预测。
通过对不同情景的模拟，可以得出江苏省未来人口数量、结构的变化趋势，预测未来的人口发展情况。
基于GM(1,1)和系统动力学模型的河南省人口模拟比较
ｋ ＝ ｌ ， ２， …， ｎ （ ４）
２ ． ２ 模 型模 拟
以２ ０ ０ ２ — ２ ０ ０ ６年 河 南 省 人 口作 为 样 本 值 ，即原 始 时 间 序 列
为：
Ｇ Ｍ（ １ ， １ ） 模 型是 灰 色 系 统 中 常用 的一 种 预 测模 型 ， 它 的特 点 是： 可 以利 用 较 少 的数 据 进 行 预 测 和 分 析 ； 建模简单 ， 公式简 洁 ， 易 于求 解 ； 具 有 可检 验 性 。 灰色 Ｇ Ｍ（ １ ， １ ） 模 型 最 大 特 点 是需 要 数 据少 ， 预测精度 高 ， 不 需 要 预 测 对 象 相 关 的 因素 的参 与 ． 只 需 运 用 预 测 对 象 自身 的 时 间 序 列进 行 预 测 。 人 口预 测 受 到 很 多 因素 的影响如出生 、 死亡 、 疾病 、 自然 灾 害 等 ， 因 此 人 口的 预 测 无 法 做 到精确的程度 ， 具有灰色系统的特点 ， 这 为 采 用 灰 色 模 型 进 行 人 口预测 提 供 了依 据 。 灰色Ｇ Ｍ（ １ ， １ ） 模 型 的建 立 步 骤 如下 ： 设 为非负序列 ．
基于系统动力学模型的北京人口规模预测_王蓓
人口规模是反映一个区域或城市基本情况的重要指标。
人口规模预测是城市总体规划编制过程中一项重要且具挑战性的基础性工作。
对于城市本身而言，其用地规模、功能布局、基础设施及公共服务设施配给等都与人口规模有着密切的关系。
因此，人口规模预测合理与否，将对未来城市建设和发展产生至关重要的影响。
北京作为国家首都，特殊的发展背景促使它具有一般城市难以比拟的超强集聚力，催生了人口规模的膨胀，其增长态势远超出人们的预期，对此最直接的体现是在近几次城市总体规划中，规划人口目标往往在规划年后4～5年时间就被突破，约占整个规划年限的三分之一。
在此背景下，选用相对科学合理的预测方法从而尽可能反映北京的城市特点和人口发展规律，将是提高未来人口规模预测结果可信度的关键。
通常来讲，人口预测是以人口发展的历史趋势及现状特征为基础，对未来人口的发展变化提出较为合理的假定条件，从而获得对未来人口的规模判断。
相关的人口预测方法包括平均增长率法、带眷系数法、剩余劳动力转化法等传统方法，以及线性回归法、Logistic曲线模型法、GM（1，1）灰色模型法、系统动力学方法等现代方法。
其中，传统方法中的平均增长率法、带眷系数法、剩余劳动力转化法等均适用于城市发展的初期阶段，不适合经济发展程度较高、人口规模较大、城镇化水平相对较高的城市。
而在现代方法中，线性回归法尤其是多元线性回归，通过考虑人口发展与社会经济的关系间接预判人口发展趋势，较为贴合社会实际；Logistic曲线模型法考虑到人口总数增长的有限性，即随着人口总数的增长，其人口增长率会逐渐下降，这点较之人口指数模型更为符合实际情况；GM （1，1）灰色模型法在缺乏大量历史数据或分布规律非线性的情况下，通过合理的技术处理，对系统动态过程进行描述；系统动力学方法通过采用专用语言，借助计算机进行系统模拟，并通过运行得出由多项指标组合而成的预测值后，根据需要与可能选择最优预测值，确定相应实施方案。
用于人口与发展研究的系统动力学模型
专题三：中国人口理论与方法建设用于人口与发展研究的系统动力学模型蔡林陈海杰(中国人民大学人口与发展研究中心)摘要：实施可持续发展战略，落实科学发展观，构建和谐社会，人口是关键。
人口研究是复杂的系统工程问题，而系统动力学正是解决这类复杂动态反馈性系统问题最有效的手段之一。
本文总结了改革开放30年来我国人口调控的成果和存在的问题：介绍了系统动力学(SD)研究方法的特点，系统动力学人口研究的基本模型：对系统动力学在人口研究中的应用情况进行了述评：提出了拓展系统动力学人口研究领域，并向安全与预警方向发展。
建立系统动力学国家人口调控模型，加强人口与社会发展关系研究的建议。
关键词：人口；系统动力学：SD：可持续发展：科学发展观一、概述我国从20世纪70年代中期就开始实施越来越严格的计划生育政策，并实现了人口再生产类型的历史性转变，进入了稳定低生育水平的新时期，使我国人口过快增长的势头得到了有效控制，30年多来少生了4亿多人。
但是，我国仍然存在着严重的人口问题。
一是人口规模过大并继续增长；二是低生育水平还不稳定：三是老龄化程度不断提高；四是出生婴儿性别比失衡将导致婚姻挤压现象；五是人口素质亟待提高：六是大量的人口需要生态移民；七是流动人口急剧增加；八是“人口红利”即将消失，人力资源短缺与就业压力同时存在。
人口问题是个复杂的系统问题，人口的诸多问题与社会经济的发展和生态环境的状况有着复杂的互动关系，而系统动力学就是解决这类复杂系统问题最有效的方法之一．二、系统动力学的特点系统动力学简称S D(s y st e m dynamics)，是一种分析研究复杂动态反馈性系统，认识和解决系统问题的系统方法．它是系统科学的一个重要分支：也是-fl新兴的交叉学科；被誉为“战略与策略实验室”。
总体而言，系统动力学基于系统论，吸收了控制论和信息论的精髓，通过结构分析和信息反馈来认识系统问题和解决系统问题．212从系统方法论来说，系统动力学是结构的方法、功能的方法和历史的方法的统一。
基于系统动力学的江苏省人口预测仿真研究
基于系统动力学的江苏省人口预测仿真研究
随着城镇化的进程不断加速，人口规模和结构的变化已成为一个复杂而广泛的问题。
本文通过系统动力学方法，结合江苏省人口统计数据，构建了一个基于系统动力学的江苏
省人口预测模型，以探讨江苏省未来的人口趋势。
首先，本文通过数据分析，得出江苏省自2000年以来的人口趋势和结构变化。
我们发现，江苏省的总人口和城镇人口在此期间呈现出上升趋势，而乡村人口则持续下降。
同时，随着人口年龄结构的变化，江苏省老龄化程度逐步加重。
在此基础上，本文构建了一个基于系统动力学的江苏省人口预测模型。
该模型由人口
增长、死亡率、出生率、迁入率、迁出率等几个主要变量组成，并通过这些变量的交互作用，预测了未来20年江苏省总人口、城镇人口和乡村人口的变化趋势。
在模型的仿真过程中，我们发现江苏省人口的城镇化趋势将持续加速，城镇人口占比
将从现在的69%上升到74%左右，乡村人口占比将从31%下降到26%左右。
同时，在20年内，江苏省总人口将达到1.4亿人左右，老龄化程度也将继续加重。
基于此，我们提出了一些政策建议。
首先，需要加快城镇化进程，改善城市基础设施
建设，提高城市生活质量，以吸引更多的乡村人口城镇化。
其次，需要加强老龄人口的社
会保障和医疗保健，以保障他们的生活质量和健康。
最后，政府应该加强人口普查和数据
监测，及时掌握人口变化趋势，为政策制定提供科学依据。
总之，基于系统动力学的江苏省人口预测模型，为我们探讨江苏省未来的人口趋势和
结构变化提供了新的思路和方法，并为政策制定提供了科学依据。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
3.2基于系统动力学的人口预测21世纪是人类面临三大问题：第一是人口膨胀，第二是就业困难，第三是环境污染，这三大问题的焦点在于人口。
因此，如何对未来的人口进行预测和控制，一直是人们关心的重要领域。
本课题是在宋健人口模型的基础上，考虑到上海作为一个开放城市，改良建立了双线性开放/动态人口模型。
采用上述基于人口结构模型，预测上海2010—2050年的人口年龄、性别结构。
为了更准确地研究人口系统，我们将人口按0-4岁、5-9岁、10-14岁、…、95-99岁、100岁及以上分群，分为21个群，并假设女性的生育时间以不同的概率分布在15-49岁之间。
然后以政策系数和生育时间的分布概率为政策参数进行仿真分析和政策试验。
3.2.1系统模拟的一些基本假设●人口分年龄数据2000年人口普查的数据上海常住人口总数为1640万，而根据上海统计年鉴2000年上海常住人口总数为1608万。
因为后续计算都是采用上海统计年鉴上的数据，所以按上海统计年鉴的常住人口总数1608万对2000年人口普查的数据进行了同比例调整。
通过《上海统计年鉴》、《上海市2000年人口普查资料》、《2005年上海市1%人口抽样调查资料》等文献的搜索，得2000年上海市分年龄段的男、女人数数据见表1。
表1 上海市2000年分年段男、女人数（单位：万人）第五次普查(2000年) 第五次普查(2000年)年龄段合计男女年龄段合计男女0~4岁49 25.7 23.3 55~59岁66.61 34.3 32.315~9岁58.67 30.53 28.14 60~64岁57.73 28.54 29.1910~14岁93.42 47.95 45.48 65~69岁68.31 32.25 36.0615~19岁129.51 64.9 64.62 70~74岁53.13 24.37 28.7620~24岁135.3 69.72 65.57 75~79岁36.71 15.94 20.7725~29岁135.4 72.09 63.31 80~84岁19.39 7.67 11.7330~34岁139.48 76.16 63.32 85~89岁7.9 2.71 5.1935~39岁150.65 81.27 69.38 90~94岁 2.16 0.61 1.5540~44岁170.02 88.98 81.04 95~99岁0.42 0.11 0.3245~49岁159.15 82.89 76.26 100岁及以上0.03 0.004 0.0250~54岁107.8 56.33 51.46●妇女生育时间根据人口生育的一般规律可知，对出生有贡献的只有15-49岁的女性人口。
出生率受人口政策的影响，如果严格实行“一对夫妇一个孩”的人口政策，那么任何一个女性在一生中只能生育一次。
我们假设生育时间是在15-49岁之间均匀分布，于是有出生率=1/35≈2.9%。
通过对统计资料和参考文献的整理和分析，可得妇女生育时间到俄分布规律如表所示。
表2 妇女生育时间的分布规律●性别比性别比是一个统计数据，是指新生婴儿中男性人口与女性人口的比例。
新出生的人口可能是男性，也可能是女性。
在自然出生的情况下，男性和女性的概率都是50%。
但是根据前面的分析，新生婴儿中，男性与女性的平均性别比为105：100。
●政策系数政策系数是一个政策参数，表明计划生育政策执行的严格程度。
如果严格执行“一对夫妇一个孩”的人口政策，政策系数=1，随着执行程度的放松，其值增加。
例如，如果实施“一对夫妇两个孩”的人口政策，政策系数=2。
●男、女性出生速率根据政策系数，有男性出生速率=“女性15-49”*出生率*（性别比）/（100+性别比）*政策系数；女性出生速率=“女性15-49”*出生率*100/（100+性别比）*政策系数。
●死亡率但不同年龄组死亡率存在差异。
0-10岁组是少年儿童阶段，死亡率呈下降趋势，10-14岁组死亡率水平为最低，以后随着年龄的增长，死亡率逐步上升。
由于上海市2008年男性预期寿命为79.06岁，女性预期寿命为83.50岁，人均寿命已经达到较高的水平，接近许多世界发达国家的水平，上升的空间已经不是很大，故在未来若干年中死亡率减低的速度必然逐步减弱。
以2000年男性、女性死亡率为基期我们假设截止2050年上海人均死亡率每十年分别较上一个十年下降10%。
表3 上海市分年龄死亡率对比分析1990年（‰）1995年（‰）2000年（‰）2005年（‰）0-4岁 2.88 0.939 1.1 0.985-9岁0.32 0.298 0.24 0.0710-14岁0.33 0.375 0.21 0.2315-19岁0.45 0.608 0.25 0.0520-24岁0.54 0.59 0.36 0.0825-29岁0.61 0.927 0.38 0.2130-34岁0.8 0.938 0.51 0.4235-39岁 1.18 0.88 0.87 0.6140-44岁 1.52 2.303 1.43 1.0545-49岁 2.36 2.293 1.99 1.6650-54岁 4.25 3.641 3.01 2.0555-59岁7.04 6.254 4.73 3.4360-64岁11.71 10.874 8.21 6.0365-69岁19.89 17.217 14.66 11.7670-74岁34.96 29.4 27.13 17.9675-79岁62.95 54.411 48.68 37.1280-84岁106.48 94.775 89.11 63.6185-89岁166.33 150.899 155.35 124.8390-94岁276.33 215.847 262.48 187.7295-99岁282.609 354.52 358.33100岁以上142.857 384.62●净迁入人口按照前面的分析，以相同的速率进行。
3.2.2人口系统模型根据以上的分析，建立人口系统模型如下：<女性5-9岁><女性10-14岁><女性20-24岁><女性30-34岁><女性35-39岁><女性40-44岁>图1 各年龄段人口系统模型公式说明：(001) 女性出生速率=("女性15-19岁"*"P15-19"+"女性20-24岁"*"P20-24"+"女性25-29岁"*"P25-29"+"女性30-34岁"*"P30-34"+"女性35-39岁"*"P35-39"+"女性40-44岁"*"P40-44"+"女性45-49岁"*"P45-49" )/5*100/(100+性别比)*政策(002) "女性0-4岁"= INTEG (女性出生速率-F1-FD1,23.3)(003) "女性5-9岁"= INTEG (F1-F2-FD2,30.53)(004) "女性10-14岁"= INTEG (F2-F3-FD3,47.95)(005) "女性15-19岁"= INTEG (F3-F4-FD4,64.9)(006) "女性20-24岁"= INTEG (F4-F5-FD5+"女性20-24岁净迁入",69.72) (007) "女性25-29岁"= INTEG (F5-F6-FD6+"女性25-29岁净迁入",72.09) (008) "女性30-34岁"= INTEG (F6-F7-FD7+"女性30-34岁净迁入",76.16) (009) "女性35-39岁"= INTEG (F7-F8-FD8+"女性35-39岁净迁入",81.27) (010) "女性40-44岁"= INTEG (F8-F9-FD9+"女性40-44岁净迁入",88.98) (011) "女性45-49岁"= INTEG (+F9-F10-FD10+"女性45-49岁净迁入",82.89) (012) "女性50-54岁"= INTEG (F10-F11-FD11+"女性50-54岁净迁入",56.33) (013) "女性55-59岁"= INTEG (F11-F12-FD12,34.3)(014) "女性60-64岁"= INTEG (F12-F13-FD13,28.54)(015) "女性65-69岁"= INTEG (F13-F14-FD14,32.25)(016) "女性70-74岁"= INTEG (F14-F15-FD15,24.37)(017) "女性75-79岁"= INTEG (F15-F16-FD16,15.94)(018) "女性80-84岁"= INTEG (F16-F17-FD17,7.67)(019) "女性85-89岁"= INTEG (F17-F18-FD18,2.71)(020) "女性90-94岁"= INTEG (F18-F19-FD19,0.61)(021) "女性95-99岁"= INTEG (F19-F20-FD20,0.11)(022) 女性100岁及以上= INTEG (F20-FD21,0.004)(023) 男性出生速率=("女性15-19岁"*"P15-19"+"女性20-24岁"*"P20-24"+"女性25-29岁"*"P25-29"+"女性30-34岁"*"P30-34"+"女性35-39岁"*"P35-39"+"女性40-44岁"*"P40-44"+"女性45-49岁"*"P45-49" )/5*性别比/(100+性别比)*政策(024) "男性0-4岁"= INTEG (男性出生速率-M1-MD1,25.7)(025) "男性5-9岁"= INTEG (M1-M2-MD2,28.14)(026) "男性10-14岁"= INTEG (M2-M3-MD3,45.48)(027) "男性15-19岁"= INTEG (M3-M4-MD4,64.62)(028) "男性20-24岁"= INTEG (M4-M5-MD5+"男性20-24岁净迁入", 65.57) (029) "男性25-29岁"= INTEG (M5-M6-MD6+"男性25-29岁净迁入", 63.31) (030) "男性30-34岁"= INTEG (M6-M7-MD7+"男性30-34岁净迁入", 63.32) (031) "男性35-39岁"= INTEG (M7-M8-MD8+"男性35-39岁净迁入", 69.38) (032) "男性40-44岁"= INTEG (M8-M9-MD9+"男性40-44岁净迁入", 81.04) (033) "男性45-49岁"= INTEG ( +M9-M10-MD10+"男性45-49岁净迁入", 76.26) (034) "男性50-54岁"= INTEG (M10-M11-MD11+"男性50-54岁净迁入",51.46) (035) "男性55-59岁"= INTEG (M11-M12-MD12,32.31)(036) "男性60-64岁"= INTEG (M12-M13-MD13,29.19)(037) "男性65-69岁"= INTEG (M13-M14-MD14,36.06)(038) "男性70-74岁"= INTEG (M14-M15-MD15,28.76)(039) "男性75-79岁"= INTEG (M15-M16-MD16, 20.77)(040) "男性80-84岁"= INTEG (M16-M17-MD17, 11.73)(041) "男性85-89岁"= INTEG (M17-M18-MD18,5.19)(042) "男性90-94岁"= INTEG (M18-M19-MD19,1.55)(043) "男性95-99岁"= INTEG (M19-M20-MD20, 0.32)(044) 男性100岁及以上= INTEG (M20-MD21,0.02)(045) F1="女性0-4岁"/5*(1-FDR1/1000)(046) F2="女性5-9岁"/5*(1-FDR2/1000)(047) F3="女性10-14岁"/5*(1-FDR3/1000)(048) F4="女性15-19岁"/5*(1-FDR4/1000)(049) F5="女性20-24岁"/5*(1-FDR5/1000)(050) F6="女性25-29岁"/5*(1-FDR6/1000)(051) F7="女性30-34岁"/5*(1-FDR7/1000)(052) F8="女性35-39岁"/5*(1-FDR8/1000)(053) F9="女性40-44岁"/5*(1-FDR9/1000/1000)(054) F10="女性45-49岁"/5*(1-FDR10/1000)(055) F11="女性50-54岁"/5*(1-FDR11/1000)(057) F13="女性60-64岁"/5*(1-FDR13/1000) (058) F14="女性65-69岁"/5*(1-FDR14/1000) (059) F15="女性70-74岁"/5*(1-FDR15/1000) (060) F16="女性75-79岁"/5*(1-FDR16/1000) (061) F17="女性80-84岁"/5*(1-FDR17/1000) (062) F18="女性85-89岁"/5*(1-FDR18/1000) (063) F19="女性90-94岁"/5*(1-FDR19/1000) (064) F20="女性95-99岁"/5*(1-FDR20/1000) (065) FD1="女性0-4岁"*FDR1/1000 (066) FD2="女性5-9岁"*FDR2/1000 (067) FD3="女性10-14岁"*FDR3/1000 (068) FD4="女性15-19岁"*FDR4/1000 (069) FD5="女性20-24岁"*FDR5/1000 (070) FD6="女性25-29岁"*FDR6/1000 (071) FD7="女性30-34岁"*FDR7/1000 (072) FD8="女性35-39岁"*FDR8/1000 (073) FD9="女性40-44岁"*FDR9/1000 (074) FD10="女性45-49岁"*FDR10/1000 (075) FD11="女性50-54岁"*FDR11/1000 (076) FD12="女性55-59岁"*FDR12/1000 (077) FD13="女性60-64岁"*FDR13/1000 (078) FD14="女性65-69岁"*FDR14/1000 (079) FD15="女性70-74岁"*FDR15/1000 (080) FD16="女性75-79岁"*FDR16/1000 (081) FD17="女性80-84岁"*FDR17/1000 (082) FD18="女性85-89岁"*FDR18/1000 (083) FD19="女性90-94岁"*FDR19/1000 (084) FD20="女性95-99岁"*FDR20/1000 (085) FD21=女性100岁及以上*FDR21/1000(087) M2="男性5-9岁"/5*(1-MDR2/1000) (088) M3="男性10-14岁"/5*(1-MDR3/1000) (089) M4="男性15-19岁"/5*(1-MDR4/1000) (090) M5="男性20-24岁"/5*(1-MDR5/1000) (091) M6="男性25-29岁"/5*(1-MDR6/1000) (092) M7="男性30-34岁"/5*(1-MDR7/1000) (093) M8="男性35-39岁"/5*(1-MDR8/1000) (094) M9="男性40-44岁"/5*(1-MDR9/1000) (095) M10="男性45-49岁"/5*(1-MDR10/1000) (096) M11="男性50-54岁"/5*(1-MDR11/1000) (097) M12="男性55-59岁"/5*(1-MDR12/1000) (098) M13="男性60-64岁"/5*(1-MDR13/1000) (099) M14="男性65-69岁"/5*(1-MDR14/1000) (100) M15="男性70-74岁"/5*(1-MDR15/1000) (101) M16="男性75-79岁"/5*(1-MDR16/1000) (102) M17="男性80-84岁"/5*(1-MDR17/1000) (103) M18="男性85-89岁"/5*(1-MDR18/1000) (104) M19="男性90-94岁"/5*(1-MDR19/1000) (105) M20="男性95-99岁"/5*(1-MDR20/1000) (106) MD1="男性0-4岁"*MDR1/1000 (107) MD2="男性5-9岁"*MDR2/1000 (108) MD3="男性10-14岁"*MDR3/1000 (109) MD4="男性15-19岁"*MDR4/1000 (110) MD5="男性20-24岁"*MDR5/1000 (111) MD6="男性25-29岁"*MDR6/1000 (112) MD7="男性30-34岁"*MDR7/1000 (113) MD8="男性35-39岁"*MDR8/1000 (114) MD9="男性40-44岁"*MDR9/1000 (115) MD10="男性45-49岁"*MDR10/1000(117) MD12="男性55-59岁"*MDR12/1000 (118) MD13="男性60-64岁"*MDR13/1000 (119) MD14="男性65-69岁"*MDR14/1000 (120) MD15="男性70-74岁"*MDR15/1000 (121) MD16="男性75-79岁"*MDR16/1000 (122) MD17="男性80-84岁"*MDR17/1000 (123) MD18="男性85-89岁"*MDR18/1000 (124) MD19="男性90-94岁"*MDR19/1000 (125) MD20="男性95-99岁"*MDR20/1000 (126) MD21=男性100岁及以上*MDR21/10000-4<女性<女性10-14岁><女性<女性20-24岁><女性25-29岁><女性<女性35-39岁><女性40-44岁>>图2 三阶段人口模型(127)"0-4岁"="女性0-4岁"+"男性0-4岁" (128)"5-9岁"="女性5-9岁"+"男性5-9岁" (129)"10-14岁"="女性10-14岁"+"男性10-14岁" (130)"0-14岁"="0-4岁"+"10-14岁"+"5-9岁" (131)"0-14岁比重"="0-14岁"/总人口*100 (132)"15-19岁"="女性15-19岁"+"男性15-19岁" (133)"20-24岁"="女性20-24岁"+"男性20-24岁" (134)"25-29岁"="女性25-29岁"+"男性25-29岁" (135)"30-34岁"="女性30-34岁"+"男性30-34岁" (136)"35-39岁"="女性35-39岁"+"男性35-39岁" (137)"40-44岁"="女性40-44岁"+"男性40-44岁" (138)"45-49岁"="女性45-49岁"+"男性45-49岁" (139)"50-54岁"="女性50-54岁"+"男性50-54岁" (140)"55-59岁"="女性55-59岁"+"男性55-59岁" (141)"60-64岁"="女性60-64岁"+"男性60-64岁" (142) "15-64岁"="15-19岁"+"20-24岁"+"25-29岁"+"30-34岁"+"35-39岁"+"40-44岁"+"45-49岁"+"50-54岁"+"55-59岁"+"60-64岁"(143)"15-64岁比重"= "15-64岁"/总人口*100 (144)"65岁及以上"=总人口-"15-64岁"-"0-14岁" (145) "65岁及以上比重"="65岁及以上"/总人口*100<0-4<5-9<10-14<15-19岁<20-24岁><25-29岁>岁>岁>岁><70-74岁>岁>岁>>图3 总人口系统模型(146) "65-69岁"="女性65-69岁"+"男性65-69岁"(147) "70-74岁"="女性70-74岁"+"男性70-74岁"(148) "75-79岁"="女性75-79岁"+"男性75-79岁"(149) "80-84岁"="女性80-84岁"+"男性80-84岁"(150) "85-89岁"="女性85-89岁"+"男性85-89岁"(151) "90-94岁"="女性90-94岁"+"男性90-94岁"(152) "95-99岁"="女性95-99岁"+"男性95-99岁"(153) "100岁及以上"=女性100岁及以上+男性100岁及以上(154) 总人口="0-4岁"+"5-9岁"+"10-14岁"+"15-19岁"+"20-24岁"+"25-29岁"+"30-34岁"+"35-39岁"+"40-44岁"+"45-49岁"+"50-54岁"+"55-59岁"+"60-64岁"+"65-69岁"+"70-74岁"+"75-79岁"+"80-84岁"+"85-89岁"+"90-94岁"+"95-99岁"+"100岁及以上"3.2.3人口系统仿真与政策试验在前面的假设成立，以及数据输入以后，利用21个群构成的人口系统模型进行仿真模拟分析。