第五章多相平衡3资料
合集下载
第五章之5.3多相离子平衡
因为溶解的BaSO4完全电离，[Ba2+]=[SO42-]=1.04×10-5mol.l-1
所以298K时，BaSO4的溶度积常数为1.08×10-10
比较AgCl和Ag2CrO4溶解度
• 溶解度
在100g溶剂中，达到饱和时所加入的溶 质的量（g或mol）。
298K时，Ksp(AgCl)=1.8×10-10， Ksp(Ag2CrO4)=1.1×10-12 ，求它们的溶解度。
开始浓度 / mol.dm-3 溶解 / mol.dm-3 平衡浓度 / mol.dm-3 从而解得：
AgCl(s)
形成更多的 AgCl, 溶解度减小
Ag+ Cl-
• Ksp < Q
Ksp
Q
X*X=X2 AgCl在纯水中的溶解度为 1.32×10-5 mol.dm-3
反应发生的方向
例5-17 试求室温下，AgCl在 0.10 mol.dm-3 NaCl溶液中的溶 解度。已知Ksp(AgCl)=1.77×10-10。
如果 C Ag CCl Q K sp ( AgCl ) 10 可形成AgCl, CCl- 多大时AgI可以转化为AgCl？临界时：
10
永久硬度的消除
CCa 2 C SO
4 2
5.3.5. 5.3.5. 沉淀的转化
Q K sp
+
Q’<Ksp,溶解
CCa 2 CCO 2 Q K sp
解：
所以可利用生成难溶氢氧化物将它们很好地分开。 如果不考虑因加入试剂而造成体积的改变，根据 溶度积原理使Fe3+沉淀完全(10-6M)而不使Mg2+沉淀 的条件是：
Mg2+ 开始沉淀时：
物理化学课件第五章 多相平衡
d ln p sub H m 2 dT RT
当温度变化不大时，subHm可看作常数
p2 sub H m 定积分: ln p1 R
1 1 T T 2 1
C-C方程
山东理工大学
25
三、固－液平衡 dp
dT
fus H m T fusVm
-----Clapeyron方程
克拉贝龙方程 克劳修斯-克拉贝龙方程
Trouton规则
山东理工大学
19
克拉贝龙方程 设某物质在一定T，p时达两相平衡： T, p平衡 相()
G=0
相()
dG()
T+dT, p+dp 平衡 所以dG()=dG()
相()
G=0
dG()
相()
当n=1mol时，即dGm()=dGm()
上式两边分别代入基本公式 dGm= – SmdT + Vmdp
山东理工大学
20
得 –Sm()dT + Vm()dp = –Sm()dT + Vm()dp
移项: [Vm()－Vm()]dp =[Sm()–Sm()]dT 整理为: dp /dT=Sm/ Vm 对于可逆相变Sm=Hm(可逆相变焓)/T
第五章 多相平衡
克 相 克 律 方 程
水 的 相 图
二 组 分 系 统
完 全 互 溶 双 液 系 统
部 分 互 溶 双 液 系 统
完 全 不 互 溶 双 液 系 统
低 共 熔 混 合 物
有 化 合 物 的 固 液 系 统
三 角 坐 标 图 表 示 法
习 题 课
引 言
相平衡是热力学在化学领域中的重要应用之一 研究多相系统的平衡在化学、化工的科研和生产 中有重要的意义，例如：溶解、蒸馏、重结晶、萃取、
第五章多相离子平衡.
(2) 浓度必须用体积物质的量浓度,严格说应是活度
（3）多相离子平衡系统中，必须有未溶解的固相存 o K 在,否则离子积不等于 sp 。
二、溶度积与溶解度的关系
（The Relationship of Solubility Product and Solubility）
1.溶解度 定义：在一定的温度下达到溶解平衡时，一定量 的溶剂中含有溶质的质量，定量地表明了物质的溶解性. 一般用每100克溶剂中溶解溶质的质量来表示 也可用每升溶剂中溶质的摩尔数来表示。 由于难溶电解质的溶解度很小，所以虽然是饱和溶液， 但此饱和溶液很稀，则 溶液 水 1 可以把摩尔溶解度 换算成g / 100g H2O. 2．溶解度so (mol·dm3)与 K sp 的换算
一般式：
AgCl(s):
o Ksp
An Bm (s)
nA (aq) mB (aq)
o Ksp
m
n
o mn Ksp (nS0 )n (mS0 )m nn mm S0
2 s0
Mg(OH)2(s):
s0 (2s0 ) 4
2
3 s0
例 1：已知25℃时，AgCl的溶解度为1.92103 g·dm3， 试求该温度下AgCl的溶度积。 3
BaSO 4 (s) Ba 2+ + SO 24
组成，pH改变、配合物生成等有关。 *难溶电解质的简单水合离子的浓度与其摩尔溶解度往 往不是等同的。 例如Ag3PO4的溶解度为s0: [PO3 ] s0 4
s0 [PO ] [HPO ] [H 2 PO ] [H3PO4 ] [PO ]{1
3 4 2 4 4 3 4
目的要求: 通过分析和计算掌握溶度积原理及 其应用，以及多重平衡问题。
物理化学第五章 多相平衡
f ( K 1) 2 K ( 1) K 2
F = K – Φ + 2 吉布斯相律
f=自由度，K=独立组分数，Φ=相数
一定条件下，f=K-Φ+1（凝固相系统或指定一个变量）
如果考虑电场、磁场，则f=K-Φ+n
例1 (1) 仅由 NH4Cl(s) 部分分解，建立如下反应平衡： NH4Cl (s) =NH3(g)+HCl(g) (2) 由任意量的 NH4Cl (s) 、NH3(g)、HCl(g) 建立如下反应 平衡： NH4Cl (s) =NH3(g)+HCl(g) 试求(1) 、(2)两种情况下，系统的 组分数 K=？自由度数f =? 解： (1) K = S - R - R´= 3 - 1 - 1=1 f = K - Φ + 2= 1 - 2 + 2 = 1 (2) K = S - R - R´= 3 - 1 - 0 =2 f =K-Φ+2= 2-2+2=2
xB 0.0 0.2 t =79.7 ℃ 0. 8 p / 102 kPa 0. 6 0. 4 p* 0. 2 yG,B=0.60 0. 0.2 0 0.0 C6H5CH3(A) 0.4 y
B
0.4 xL,B= 0.35 0.43 x' = xB= 050
0.6
0.8
1.0
* pB
l(A+B) L M ' M G
K=S-R=3-1=2
要注意独立二字：
C ( s) H 2O( g ) CO( g ) H 2 ( g ) C (s) C O2 (g) 2 C O(g) C O (g) H2O (g) C O2 ( g) H2 (g) (1) (2) (3)
物理化学第五章-相平衡PPT课件
第6页/共82页
5.2 相律
相律（phase rule）
F=C–P+2
相律是相平衡体系中揭示相数P ，独立组分数C和
自由度 F之间关系的规律，可用上式表示。式中2
通常指T，p两个变量。相律最早由Gibbs提出，所 以又称为Gibbs相律。如果除T，p外，还受其它力
场影响，则2改用n表示，即：
F=C–P+n
2021/7/14
第10页/共82页
水的相图
2021/7/14
第11页/共82页
水的相图
OA 是气-液两相平衡线，即水的蒸气压曲线。它 不能任意延长，终止于临界点。临界点T 647 K , p 2.2107 Pa ，这时气-液界面消失。高于临界温 度，不能用加压的方法使气体液化。
OB 是气-固两相平衡线，即 冰的升华曲线，理论上可延长 至0 K附近。
斜率为正。
OC线 dp H fus m
dT T V fus
fusH 0, fusV 0
斜率为负。
第20页/共82页
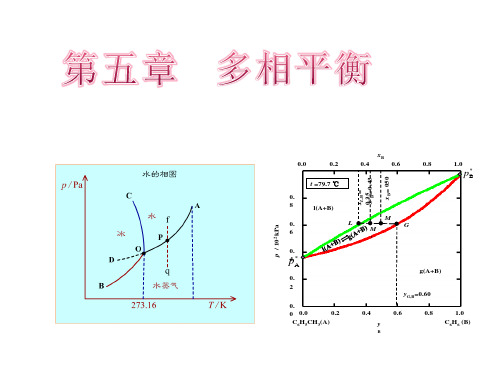
5.4 二组分理想液态混合物的气－液平衡相图
p-对x图于二和组分T体-x系图，C=2,F=4-P 。P至少为1，则 F
最多为3。这三个变量通常是T，p 和组成 x。所以要
表示二组分体系状态图，需用三个坐标的立体图表示。
在液相线和气相线之间的梭 形区内，是气-液两相平衡。
2021/7/14
第25页/共82页
T-x图
(2) T-x图 亦称为沸点-组成图。外压为大气压力，当溶
液的蒸气压等于外压时，溶液沸腾，这时的温度 称为沸点。某组成的蒸气压越高，其沸点越低， 反之亦然。
T-x图在讨论蒸馏时十分有用，因为蒸馏通常 在等压下进行。T-x图可以从实验数据直接绘制。 也可以从已知的p-x图求得。
物化课件第五章-相平衡)
(4)C=3, Φ =2， f = 3– 2 + 1 = 2 (T以及I2在任一相
中的浓度)
§5.4 单组分系统的相平衡
1、Clapeyron方程 2、Clausius-Clapeyron方程
液-气平衡 固-气平衡 固-液平衡 3、单组分系统相律——水的相图
第五章 多相平衡
返回目录 退出
单组分系统的相律
若将CaCO3(s)单独放在一密闭容器中，达平衡后C=？
容器内有CaCO3(s)+CaO(s)+CO2(g)。 S=3，R=1，R’=0，C=3– 1– 0=2。 因CaO(s)和CO2(g)在两相中，没有浓度关系。
注意：系统确定后，其组分数是确定的，物种数有一定随 意性，可以随人们考虑问题的出发点不同而不同。
=RT/p (设气体为理想气体)
整理为:
vapH m RT 2
dp pdT
d ln p dT
Clausius---
Clapeyron方程
积分:
d ln p
vapH m RT 2
dT
适用于液气或固气 两相平衡
第五章 多相平衡
返回目录 退出
若温度变化不大时，vapHm为常数 d ln p
பைடு நூலகம்
第五章 多相平衡
第五章 多相平衡
返回目录 退出
例 NaCl-H2O系统
NaCl，H2O: S=2, R=0, R’=0, C=2 NaCl不饱和水溶液 S=3： Na+, Cl－, H2O, R=0, R’=1: [Na+]=[Cl－], 所以 C= 3– 1=2 NaCl饱和水溶液，有NaCl(s)存在
S=4：NaCl(s), Na+, Cl－, H2O, R=1: NaCl(s) = Na++ Cl－,
物化第五章多相平衡PPT.
3、 游泳要由家长、老师或可靠的人带领，或结伴，不能单独游泳。
再考虑H O的电离平衡,Ｓ=６, NaCl,H O, Na ,Cl , H , 第一课时 家庭用电的“三不能”和“三不要”
+-+
（3）不能将断丝的灯泡搭起来再用。2断丝后搭起来的灯泡比原来的更亮，但这时的功率增大了，2 超过了灯泡设计的承受能力，会使灯
组分数和物种数是完全不同的概念,无化学反应发生,
Ｋ=Ｓ
一、基本概念
2. 物种数和组分数
如系统中有化学平衡存在,Ｋ不一定等于Ｓ
如PCl5,PCl3,Cl2三种物质组成系统,存在化学平衡: PCl5(g)=PCl3(g)+Cl2(g)
这时:Ｓ=３,Ｋ=２３.
因为只要确定两种物质,则第三种物质就必然存在,并且其 组成可由Ｋ 所确定
所以:Ｋ=Ｓ-Ｒ
Ｒ——独立的化学平衡数
一、基本概念
2. 物种数和组分数
注意：化学平衡一定要是独立的,例如 C(s),CO(g),CO2(g),H2O(g),H2(g) ５种物质组成的系统, 可以写出三个化学平衡:
(1) C(s)+ H2O(g)=CO(g)+ H2(g) (2) C(s)+ C2O(g)=2CO(g) (3) CO(s)+ H2O(g)=CO2(g)+ H2(g) 但上述三个平衡中只有两个是独立的,可由其中任意两个
通过相加减得到第三个.因此Ｒ=２３.
一、基本概念
2. 物种数和组分数
如有特殊限制条件,情况又将不同
如PCl5,PCl3,Cl2三种物质组成系统中,若指定 mol(PCl3)/mol(Cl2)=1,或开始时只有PCl5,则平衡时
mol(PCl3)/mol(Cl2)=1,这时就存在一浓度限制条件,因此Ｋ=
第五章 多相平衡PhaseEquilibrium 物理化学课件
C=S－R－R
§5.1 相律 Phase Rule
例如： PCl5(g) = PCl3(g) + Cl2(g) S=3，R=1，C=S –R =2
又如 PCl5(g) 分解，产物完全是分解得到。则 PCl3 :Cl2=1:1，
则R′=1， C=S –R –R’=3 –1 –1=1 例如反应：
(1) C(s) + H2O(g) = CO(g) +H2(g) (2) C(s) + CO2(g) = 2CO(g) (3) CO(g) + H2O(g) = CO2(g) +H2(g) (1)–(2)=(3)，独立的反应为2，R=2， S=5
指定了压力和温度，f* = f – 2
(2) 相律的推导
相律就是在平衡系统中，联系系统内相数、组分数、自 由度数及影响物质性质的外界因素(如温度、压力、重 力场、磁场等)之间关系的规律。 IUPAC: The number of degrees of freedom, F, that a system containing C components can have when P phases are in equilibrium, is given as: F=C-P+2
T T T P
(2)压力平衡条件：达到平衡时各相的压力相等
p p p P
(2) 相律的推导
（3） 相 (编号为 ，Ⅱ，······P) 中的化学势相等，相变 达到平衡，即
1( ) 1( ) 1(P )
2( ) 2( )
(2) 相律的推导
设有 S 种物质在 P 个相中， 描述一个相的状态要 T，p，(x1, x2, …xs)
(S–1)种独立变量 所以总变量数= P(S –1) + 2
§5.1 相律 Phase Rule
例如： PCl5(g) = PCl3(g) + Cl2(g) S=3，R=1，C=S –R =2
又如 PCl5(g) 分解，产物完全是分解得到。则 PCl3 :Cl2=1:1，
则R′=1， C=S –R –R’=3 –1 –1=1 例如反应：
(1) C(s) + H2O(g) = CO(g) +H2(g) (2) C(s) + CO2(g) = 2CO(g) (3) CO(g) + H2O(g) = CO2(g) +H2(g) (1)–(2)=(3)，独立的反应为2，R=2， S=5
指定了压力和温度，f* = f – 2
(2) 相律的推导
相律就是在平衡系统中，联系系统内相数、组分数、自 由度数及影响物质性质的外界因素(如温度、压力、重 力场、磁场等)之间关系的规律。 IUPAC: The number of degrees of freedom, F, that a system containing C components can have when P phases are in equilibrium, is given as: F=C-P+2
T T T P
(2)压力平衡条件：达到平衡时各相的压力相等
p p p P
(2) 相律的推导
（3） 相 (编号为 ，Ⅱ，······P) 中的化学势相等，相变 达到平衡，即
1( ) 1( ) 1(P )
2( ) 2( )
(2) 相律的推导
设有 S 种物质在 P 个相中， 描述一个相的状态要 T，p，(x1, x2, …xs)
(S–1)种独立变量 所以总变量数= P(S –1) + 2
多相平衡
• 每个相中有K个组分时，则只要任意指定 (K-1)个组分的浓度，就可以表明该相的浓 度，系统中有Φ个相，需要指定Φ(K-1)个浓 度，方能确定系统中各个相的浓度；平衡 时各相的温度和压力均相同，故应再加上 两个变量。
• 因此，表明系统状态所需的变量数应为
f=Φ(K-1)+2
• 但是，这些变量之间不是相互独立的，因为 在多相平衡时，还必须有“每一组分在每一 相中的化学势相等”这一热力学条件，即
f=Φ(K-1)+2-K(Φ-1)=K-Φ+2
在某一相中少了一个组分，则在该相中的 浓度变量亦减少一个；在考虑相平衡时， 亦将减少一个化学势相等的关系式。
即在Φ(K-1)中减少1时，K(Φ-1)中也必然 减少1。所以 f=K-Φ+2仍成立。
• 若指定了温度或指定了压力，则
f=K-Φ+1
• 若温度与压力均指定，则
即
K=S-R
R即为系统中的“独立化学平衡数”。
• 如系统中有C（s）、CO（g）、H2O（g）、CO2（g）和 H2(g)五种物质，在它们之间可以有三个化学 平衡式：
•
⑴C H O CO H （s）+ 2 （g）====
（g）+ 23;
2（g）====
（g）
•
⑶CO H O CO H （g）+ 2 （g）====
• 在不考虑重力场、磁场等因素，只考虑温度和压 力的影响时，平衡系统中相数、组分数和自由度 数之间的关系可以有下列形式：
•
f=K-Φ+2
• f表示系统的自由度，K表示组分数，Φ表示相数， 2即为温度和压力两变量。
相律的推导如下：
• 假设一平衡系统中有K个组分，Φ个相。如 果K个组分在每个相中均存在。
• 因此，表明系统状态所需的变量数应为
f=Φ(K-1)+2
• 但是，这些变量之间不是相互独立的，因为 在多相平衡时，还必须有“每一组分在每一 相中的化学势相等”这一热力学条件，即
f=Φ(K-1)+2-K(Φ-1)=K-Φ+2
在某一相中少了一个组分，则在该相中的 浓度变量亦减少一个；在考虑相平衡时， 亦将减少一个化学势相等的关系式。
即在Φ(K-1)中减少1时，K(Φ-1)中也必然 减少1。所以 f=K-Φ+2仍成立。
• 若指定了温度或指定了压力，则
f=K-Φ+1
• 若温度与压力均指定，则
即
K=S-R
R即为系统中的“独立化学平衡数”。
• 如系统中有C（s）、CO（g）、H2O（g）、CO2（g）和 H2(g)五种物质，在它们之间可以有三个化学 平衡式：
•
⑴C H O CO H （s）+ 2 （g）====
（g）+ 23;
2（g）====
（g）
•
⑶CO H O CO H （g）+ 2 （g）====
• 在不考虑重力场、磁场等因素，只考虑温度和压 力的影响时，平衡系统中相数、组分数和自由度 数之间的关系可以有下列形式：
•
f=K-Φ+2
• f表示系统的自由度，K表示组分数，Φ表示相数， 2即为温度和压力两变量。
相律的推导如下：
• 假设一平衡系统中有K个组分，Φ个相。如 果K个组分在每个相中均存在。
第五章多相体系—相平衡Heter...
第五章多相体系—相平衡Heterogeneous SystemPhase EquilibriumIntroduction: 多相体系的分离& 提纯第一节相律1.1 基本概念相：体系中物理性质与化学性质完全均匀的部分相数：一个体系所含相的数目，用符号P表示气体：一般只有一相；（P＝1）液体：完全互溶，只有一相；部分互溶，有几层就有几相；(P＝1，2，3……）固体：有几种固体就有几相。
固态溶液：“固溶体”（P＝1）相变化过程（相变）；相平衡状态；相界面独立组分数：形成一个热力学平衡体系所需要的最少物种数，简称组分数，用符号C 表示。
组分数＝物种数－独立的化学平衡数－独立的限制条件数C ＝S －R －R ´S ：物种数，即体系所含物质的数目R ：独立的化学平衡反应数R ´：独立的限制条件数，比如浓度，比例等例如，由NH 4Cl(s)、HCl(g)和NH 3(g)构成的体系，①体系的S=3②三种物质之间又存在化学反应NH 4Cl(s)＝HCl(g)+NH 3(g) R=1③若该混合物是由NH 4Cl(s)分解而得，则体系中HCl(g)与NH 3(g)的浓度比保持1:l ，即存在关系式y HCl = y NH 3，则R'=1因此：由NH 4Cl(s)分解而得到的混合物，C=3-1-1=1，该体系为单组分体系独立组分数：形成一个热力学平衡体系所需要的最少物种数，简称组分数，用符号C表示。
组分数＝物种数－独立的化学平衡数－独立的限制条件数C＝S －R－R´S：物种数，即体系所含物质的数目R：独立的化学平衡反应数R´：独立的限制条件数，比如浓度，比例等例如：N2+3H2= 2NH3高温、催化剂存在时S = 3, R = 1, R´= 0, 则：C=3-1-0 = 2 （双组分系统）高温、催化剂存在且N2：H2＝1 : 3 时S = 3, R = 1, R´= 1, 则：C=3-1-1 = 1 （单组分系统）自由度数：确定和保持平衡状态所需的独立改变的变量的数目，称为自由度数，用F 表示。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2、物种数和组分数
（2）在CaCO3的分解反应中，S =? K =? 解： CaCO3(s) = CaO(s) + CO2(g)， S = 3，K = 3 – 1 = 2。 即双组分系统。
（3）NH4Cl(s) = NH3(g) + HCl(g)，若此反应是NH4Cl的分解 反应，S =? K =?
2、物种数和组分数
（4）如果系统中还有固体NaCl， 则 S = 6，即NaCl、H+、OH-、 H2O、Na+和Cl-， 但 R = 2（水的电离平衡，NaCl的溶解平衡）， R’ = 2（浓度条件）， 所以 K = 6 – 2 – 2 = 2。 因此物种数虽然随考虑问题的方法不同而异， 但组分数则是确定不变的！
（2）系因统为由只C(要s)有, C任O意(g)两, H种2O物(g质),，CO则2第(g)三, H种2(物g)质组就成，S =? K =? 解：S 必= 5然，存在在它，们而之且间其存组在成三可个由化平学衡平常衡数式确定，
1）并C(不s)在+ 于H2起O(始g)时=是CO否(放g) 入+ H此2种(g)物质。 2）C(s) + CO2(g) = 2CO(g) 3）CO(g) + H2O(g) = CO2(g) + H2(g)
2、物种数和组分数
（1）在PCl5的分解反应中， 若指定PCl3(g)和Cl2(g)的物质的量之比为1:1， 则系统中PCl3(g)和Cl2(g)的物质的量之比一定为1:1。 此时 S = 3，K = 3 – 1 – 1 = 1。 即单组分系统。 若一开始只有PCl5存在， ∵ PCl5(g) ⇌ PCl3(g) + Cl2(g) 此时 S = 3，K = 3 – 1 – 1 = 1。 即单组分系统。
第五章 多相平衡
主要内容包括： 1、相律：多相平衡体系所共同遵守的规律； 2、相图：表达多相系统的状态如何随着温度、
压力、浓度等强度性质而变的几何图形。
5.1 相律
❖ 基本概念 1、相和相数
系统中物理及化学性质完全均匀的部分，称为相。 多相系统中，相与相间有着明显的界面； 越过界面时，物理或化学性质发生突变。
第五章 多相平衡
• 相平衡、热平衡和化学平衡是热力学在化学领域中的重要应用，
也是化学热力学的主要研究对象。多相体系相平衡的研究有着重
要的实际意义。 例:（1）研究金属冶炼过程中的相的变化，根据相变进而研究金属
的成分、结构与性能之间的关系。 （2）各种天然的或人工合成的熔盐体系（主要是硅酸盐，如水
泥、陶瓷、炉渣、耐火粘土、石英岩等），天然的盐类（如岩 盐、盐湖等）以及一些工业合成产品，都是重要的多相体系。 （3）开发并利用属于多相体系的天然资源，用适当的方法如溶 解、蒸馏、结晶、萃取、凝结等从各种天然资源中分离出所需 的成分，这些过程都需要有关的相平衡的知识。
相数：系统中所包含的相的总数。以符号表示。
1、相和相数
例： （1）气体
无限混和
一个气相
思考：一=整1 块CaCO3的结一晶相是（乙几醇相+？水）
（2）液体
按其互溶程度 两相（CCl4+水）
如果把它=1粉，粹2，为3 10块小颗三粒相，共存它是几相？
（3）固体 固溶体
一相
=1
一般是有多少种固体，便有多少相； =1，2，3…
解：S = 3, K = 3 – 1 – 1 = 1。即单是可以随着人们考虑问题的出 发点不同而不同的，但在平衡系统中的组分数却是确定的。
如由NaCl和H2O构成的系统 （1）如果只考虑相平衡，则 S = K = 2； （2）如果只是NaCl的水溶液，
2、物种数和组分数
例：P144/习题1 确定H2(g)+I2(g)=2HI(g)平衡系统中的组分数。 （1） 反应前只有HI；
S = 3，R = 1，R’ = 1，K = S – R – R’ = 3 – 1 – 1 = 1 （2）反应前有等物质的量的H2和I2；
2、物种数和组分数
❖ 物种数与组分数之间的关系 （A）如果系统中没有化学反应发生，则在平衡系统中就 没有化学平衡存在，
则：组分数 = 物种数 即 K=S （B）如果系统中有化学平衡存在， 则：组分数 = 物种数 – 独立化学平衡数 即 K=S–R
R 表示系统中的独立化学平衡数
2、物种数和组分数
（1）由PCl5 (g) 、PCl3(g)和Cl2(g)组成的系统中，S =? K = ? 解： ∵ PCl5(g) ⇌ PCl3(g) + Cl2(g) ∴ S = 3；K = S – R = 3 – 1 = 2；
不同晶型不同相；不同种类不同相；与其是否连续无关
2、物种数和组分数
物种数：系统中所含的化学物质数。以符号S 表示。 注意，不同聚集态的同一种化学物质不能算两个物种！ 例： 水和水气，其物种数S = 1，而不是2。 组分数：足以表示系统中各相组成所需要的最少独立物种数。
以符号K 表示。 注意，组分数和物种数是两个不同的概念! 在多相平衡中，重要的是组分数这一概念。
第五章 多相平衡
• 在一个封闭的多相体系中，相与相之间可以有热的交换、功的
传递和物质的交流。对具有个相(,,…)体系的热力学平衡，
实际上包含了如下四个平衡条件：
热平衡条件：T()=T()=…=T()
热力学平衡
压力平衡条件： p()=p()=…=p() 相平衡条件： B()= B()=…= B()
化学平衡条件： BB=0
R = 2，而不是3， 故K = S – R = 5 – 2 = 3。
2、物种数和组分数
（C）如果系统中除化学平衡外，还存在一些特殊的限制条件， 如浓度关系，
则 组分数 = 物种数 – 独立化学平衡数 – 独立限制条件数
即 K = S – R – R’
R’表示独立的限制条件数
注意物质之间的浓度关系数只有在同一相中方能应用，不同相 之间不存在此种限制条件。
则有H2O、Na+和Cl-，即 S = 3， 由于溶液必须保持电中性，其中Na+和Cl-的浓度相等， 因此 K = 3 – 1 = 2； （3）如果还考虑H2O的电离， 则有H+、OH-、H2O、Na+和Cl-，即 S = 5， 但 R = 1（水的电离平衡），R’ = 2（浓度条件）， 因此 K = 5 – 1 – 2 = 2；