线性分组码-习题
线性分组码

系统码的校验矩阵和生成矩阵可以转换。
13
线性分组码的性质
线性分组码中任意两个码字的模2加仍为一个码字,这个性 质称为码的封闭性。 零矢量必须是任一线性分组码中的一个码字,称为零码字。 生成矩阵中各行都是一个码字,且生成矩阵的各行是线性 无关的(任意两行相加不为零)。任意码字C是生成矩阵中 各行的某一线性组合。 校验矩阵的各行应该是线性无关的,否则将得不到r个线性 无关的监督关系式,从而得不到r个独立的监督位。
23
汉明码
汉明码实际上是(2m-1, 2m-m-1)线性分组码,其校验行有m行,共有 n=2m-1列,任一列都不为零且两两互不相等,因此能纠正任何单 个错误。 汉明码的校验矩阵一般有两种构造方式: 一是校验矩阵的标准形式,即H=[PI] 式中P为m×(n-m)维矩阵,I为m×m维单位阵。按这种校验矩阵编 出的码是系统码。 二是校验矩阵的列是按二进制数的自然顺序从左到右排列的非零 列,例如,当n=7,k=4时,H中的第一列为[0 0 1],第二列为[0 1 0],…,第七列为[1 1 1],按这种校验矩阵编出的码是非系统码。 发生单个错误时,伴随式是H中与错误位置对应的列,所以汉明码 伴随式二进制数的值就是错误位置的序号。
14
例题-由生成矩阵生成码字
由生成矩阵 所有码字为
m 000
1 0 0 1 1 1 0 G 0 1 0 0 1 1 1 0 0 1 1 1 0 1
生成的(7,3)码的
C 0000000
0 0 0 1 1 1 1
0 1 1 0 0 1 1
1 0 1 0 1 0 1
在校验方程的矩阵形式中,令
1 1 则校验方程可以写成 H 1 0
HCT=0 或CHT=0
信息论与编码复习题

一、填空题1. 设信源X 包含4个不同离散消息,当且仅当X 中各个消息出现的概率为___1/4___时,信源熵达到最大值,为__2__,此时各个消息的自信息量为__2 __。
2.如某线性分组码的最小汉明距dmin=4,则该码最多能检测出___3____个随机错,最多能纠正__1____个随机错。
3.克劳夫特不等式是唯一可译码___存在___的充要条件。
4.平均互信息量I(X;Y)与信源熵和条件熵之间的关系是___(X;Y)=H(X)-H(X/Y )___。
5._信源___提高通信的有效性,_信道____目的是提高通信的可靠性,_加密__编码的目的是保证通信的安全性。
6.信源编码的目的是提高通信的 有效性 ,信道编码的目的是提高通信的 可靠性 ,加密编码的目的是保证通信的 安全性 。
7.设信源X 包含8个不同离散消息,当且仅当X 中各个消息出现的概率为__1/8__时,信源熵达到最大值,为___3____。
8.自信息量表征信源中各个符号的不确定度,信源符号的概率越大,其自信息量越_小___。
9.信源的冗余度来自两个方面,一是信源符号之间的__相关性__,二是信源符号分布的__不均匀性__。
10.最大后验概率译码指的是 译码器要在已知r 的条件下找出可能性最大的发码 作为译码估值 ,即令 =maxP( |r)_ __。
11.常用的检纠错方法有__前向纠错___、反馈重发和混合纠错三种。
二、单项选择题1.下面表达式中正确的是(A )。
A.∑=j i j x y p 1)/( B.∑=i i j x y p 1)/( C.∑=j j j iy y x p )(),(ω D.∑=ii j i x q y x p )(),( 2.彩色电视显像管的屏幕上有5×105 个像元,设每个像元有64种彩色度,每种彩度又有16种不同的亮度层次,如果所有的彩色品种和亮度层次的组合均以等概率出现,并且各个组合之间相互独立。
线性分组码-习题

1. 已知一个(5, 3)线性码C 的生成矩阵为:11001G 011010111⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦(1)求系统生成矩阵;(2)列出C 的信息位与系统码字的映射关系;(3)求其最小Hamming 距离,并说明其检错、纠错能力; (4)求校验矩阵H ;(5)列出译码表,求收到r =11101时的译码步骤与译码结果。
解:(1)线性码C 的生成矩阵经如下行变换:23132110011001101101011010011100111100111001101101010100011100111⎡⎤⎡⎤⎢⎥⎢⎥−−−−−−→⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎡⎤⎡⎤⎢⎥⎢⎥−−−−−−→⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦将第、加到第行将第加到第行得到线性码C 的系统生成矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=111000*********S G (2)码字),,,(110-=n c c c c 的编码函数为[][][]111000*********)(210m m m m f c ++==生成了的8个码字如下(3) 最小汉明距离d =2,所以可检1个错,但不能纠错。
(4) 由],[],,[)()(k n Tk n k k n k k n I A H A I G --⨯-⨯-==,得校验矩阵⎥⎦⎤⎢⎣⎡=1010101111H(5) 消息序列m =000,001,010,011,100,101,110,111,由c =mGs 得码字序列c 0=00000, c 1=00111,c 2=01010, c 3=01101, c 4=10011, c 5=10100,c 6=11001, c 7=11110则译码表如下:当接收到r =(11101)时,查找码表发现它所在的列的子集头为(01101),所以将它译为c =01101。
2.设(7, 3)线性码的生成矩阵如下010101000101111001101G ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦(1)求系统生成矩阵;(2)求校验矩阵; (3)求最小汉明距离; (4)列出伴随式表。
第八章线性分组码

第八章线性分组码8.1 什么是检错码?什么是纠错码?两者有什么不同?答:能发现错误但不能纠正错误的码称为检错码;不仅能发现错误而且还能纠正错误的码称为纠错码。
8.2 试述分组码的概念,并说明分组码的码率r的意义。
答:分组码是把信息序列以每k个码元分组,即每k个码元组成一个信息组。
n表示码长,k 表示信息位的数目,码率r=k/n,它说明在一个码字中信息为所占的比重。
8.3 什么是码的生成矩阵和校验矩阵?一个(n,k)线性分组码的生产矩阵和校验矩阵各是几行几列的矩阵?答:线性分组码的2个码字将组成n维向量空间的一个k维子空间,而线性空间可由其基底张成,因此线性分组码的个码字完全可由k个独立的向量组成的基底张成。
设k个向量为(7.3-2)将它们写成矩阵形式:(7.3-3)(n,k)码中的任何码字,均可由这组基底的线性组合生成。
即C=MG=(mk-1,mk-2,m0)G式中M=(mk-1,mk-2,m0)是k个信息元组成的信息组。
这就是说,每给定一个信息组,通过式(7.3-3)便可求得其相应的码字。
故称这个由k 个线性无关矢量组成的基底所构成的k×n阶矩阵G为码的生成矩阵(Generator Matrix)。
校验矩阵H 的每一行代表求某一个校验位的线性方程的系数(n-k)线性分组码有r=n-k 个校验元,故须有r 个独立的线性方程,因此H 矩阵必由线性无关的r 行组成,是一个(n-k)×n 阶矩阵,一般形式为一个(n,k )线性分组码生成矩阵有k 行n 列校验矩阵有(n-k)行n 列。
8.4 什么样的码成为系统码?系统码的生成矩阵和校验矩阵在形式上有何特点?答:若信息组为不变的形式,称在码字的任意k 位中出现的码为系统码;一个系统码的生成矩阵G ,其左边k 行k 列是一个k 阶单位方阵,系统码的校验矩阵H ,其右边r 行r 列组成一个r 阶单位方阵。
8.5 什么是对偶码?试举例说明之。
6.2 线性分组码

13
线性分组码的性质
• 线性分组码中任意两个码字的模 2 加仍为一个码字,这个 性质称为码的封闭性。 封闭性 • 零矢量必须是任一线性分组码中的一个码字,称为零码字。 零码字 • 生成矩阵中各行都是一个码字,且生成矩阵的各行是线性无 关的(任意两行相加不为零)。任意码字 C 是生成矩阵中 各行的某一线性组合。 • 校验矩阵的各行应该是线性无关的,否则将得不到 r 个线性 无关的监督关系式,从而得不到 r 个独立的监督位 。
由于gip是系统码的生成矩阵则有?则得一致校验矩阵为??????????1001110g01001110011101101111011101111101101011??????????????????????tpqp和1011000111010011000100110001????????????hqi例题16由生成矩阵生成码字由生成矩阵生成的73码的所有码字为100111001001110011101??????????gmc00000000000010011101010010010101101110101001001110101101001111011010011111110100线性分组码17?1校验矩阵与生成矩阵?2线性分组码的纠检错能力?3校验矩阵与最小距离的关系?4线性分组码的伴随式?5线性分组码的译码?6汉明码线性分组码的检纠错能力18?信道编码后的码字在信道传输过程中由于干扰的存在使得一些码元发生错误产生错误码字
16
线性分组码
• • • • • • 1 2 3 4 5 6 校验矩阵与生成矩阵 线性分组码的纠、检错能力 校验矩阵与最小距离的关系 线性分组码的伴随式 线性分组码的译码 汉明码
线性分组码
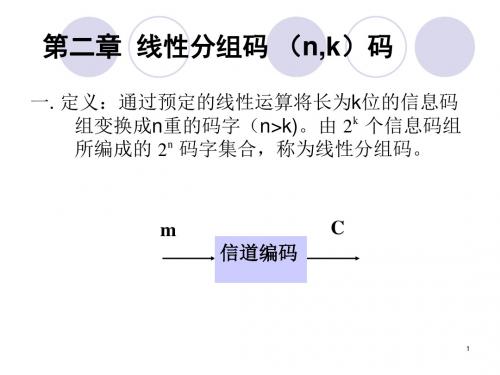
C mG
G是一个k*n阶矩阵,称为(n,k)码的生成矩阵。
7
1 0 G 0
0 0 1 0 0 1
p11 p 21 p k1
p12 p 22 pk 2
p1( n k ) p 2( nk ) I P k pk ( nk )
n 1
u和v之间的距离表示2个码字对应位不同的数目。
如(7,3)码的两个码字:u=0011101
v=0100111
它们之间的距离d=4
4
码的最小距离的dmin :在(n,k)线性码字集合中, 任意两个码字间的距离最小值,是衡量抗干扰能力的 重要参数,dmin越大,抗干扰能力越强。 码字的重量W:码字中非零码元符号的个数;在二元 线性码中,码字的重量是码字中含“1”的个数。 码的最小重量Wmin:线性分组码中,非零码字重量的 最小值,称为码的最小重量,表示为:
限, 性能界限,即码的译码错误概率的上、下 限。 对码距限而言,最重要的限是汉明限,普 洛特金限和吉尔伯特-瓦尔沙莫夫限,汉 明码和普洛特金限告诉我们,在给定码长n 和码的传输速率R=k/n下,最小距离可以达 到的最大值,故它们都是上限,而吉尔伯 特一瓦尔沙莫夫限给出了码的最小距离的 下限。
HC 0
T
T
r=n-k
H
阵是n列,(n-k)行的矩阵;
为了得到确定的码,r个监督方程必须是线性
无关的,即要求H阵的秩为r。
6
2. 生成矩阵G
把方程组写成矩阵的形式为
h11 h 21 h r1
h12 h1k h 22 h 2k h r2 h rk
m 信道编码
C
线性分组码的例子

ab 集合Grm(r,m)={v0,v1,…,vm,v1v2,v1v3,…,vm-1vm ,…,
vm-r+1…vm}共有k(r,m)个元素,是(2m,k)RM码的生成向 量,即可张成整个码空间的基。将每个元素看成矩阵 的一行,就得到生成矩阵。 集合Grm(r-1,m)是Grm(r,m)的真子集,是r-1阶RM码的 生成矩阵。
这 个码的交织构成了一个(
)交织码,记为
观察上述11个生成向量,注意到除了v1v2,其他生成向量每连续4个分量一组求和都是0,可推出:
当且仅当上述矩阵的每一行的错误模式都是可 维数(信息序列的长度):
观察上述11个生成向量,注意到除了v1v2,其他生成向量每连续4个分量一组求和都是0,可推出:
纠正错误模式时,错误可纠正 若w(sP)=2 or 3,则令e=(0,sP)并转步骤8
量首构成了标准阵的所有陪集首
(23,12)格雷码通过增加一个总的奇偶校验位,构成(24,12)码,最小距离为8,但非完备码
m-r-1阶RM码(m-r-1,m)的对偶码是r阶RM码(r,m)
可将所有重量为t=1的n=2 -1个向量作为陪集 交织码简单说就是按列的方式传输码字
aij被正确译码后,考虑
m
格雷码的译码
设错误模式为e=(x,y),校正子s=eHT=(x,y) HT =(x,y)[I P]T=x+yPT=x+yP,可得到y=(x+s)P
对任何可纠正错误模式e,满足w(e)<4,有四种可能: (1)w(y)=0,w(x)<=3, (2)w(y)=1,w(x)<=2,
(3)w(y)=2,w(x)<=1, (4)w(y)=3,w(x)<=0,令ej分别表示 这四种可能的错误模式,ej=(x,y),其中w(y)=j,
信息论基础——线性分组码
17
线性分组码的基本概念
信息位 00 01 10 11 x2 x0 x1 00000 x3 x0 x x x 01101 0 1 4 码字 10111 11010
信息位k=2 码字数M=4
可见,码字的三个校验元都由其前两位线 性组合得到,即可由的线性方程组求得;
18
线性分组码的基本概念
f1 : GF (2) 2 GF (2)5
信息位 00 01 10 11 码字 00000 01101 10111 11010
1 ( 0 1 ) 1 ( 1 0 ) 1 1
f( 1 1 ) 1 1 0 1 0
1 ( 0 1 1 0 1 )1 ( 1 0 1 1 1 ) 1 1 0 1 0
30
线性分组码的基本概念
汉明距离: 指(n,k)分组码中两个码字xn 、 yn对应位取 值不同的个数;记为d(xn , yn).
5 5 ( 1 0 1 0 1 ) , y ( 0 1 1 1 1 ) 例: x
d(x ,y ) 3
5 5
31
线性分组码的基本概念
线性分组码的最小距离: 称(n,k)分组码中任两个码字汉明距离的最小 值,为该分组码的最小距离d.
f ( 1 ( 0 1 ) 1 ( 1 0 ) ) 1 ( 0 1 1 0 1 ) 1 ( 1 0 1 1 1 ) 线性编码
19
线性分组码的基本概念
例题1: 下面是某个(n,k)线性二元码的全部码字
x16=000000 x26=100011 x36=010101 x46=001111 x56=110110 x66=101100 x76=011010 x86=111001 求n、k的值;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 已知一个(5, 3)线性码C 的生成矩阵为:
11001G 0
11010
1
11⎡⎤
⎢⎥=⎢⎥⎢⎥⎣⎦
(1)求系统生成矩阵;
(2)列出C 的信息位与系统码字的映射关系;
(3)求其最小Hamming 距离,并说明其检错、纠错能力; (4)求校验矩阵H ;
(5)列出译码表,求收到r =11101时的译码步骤与译码结果。
解:
(1)线性码C 的生成矩阵经如下行变换:
23132110011
00110110101101001110
0111100111
001101101010100011100111⎡⎤⎡⎤
⎢⎥⎢⎥−−−−−−→⎢⎥⎢
⎥⎢⎥⎢⎥⎣⎦⎣⎦
⎡⎤⎡⎤⎢⎥⎢⎥−−−−−−→⎢⎥⎢
⎥⎢⎥⎢⎥⎣⎦⎣⎦
将第、加到第行
将第加到第行
得到线性码C 的系统生成矩阵为
⎥⎥
⎥⎦
⎤⎢⎢⎢⎣⎡=111000*********S G (2)码字),,,(110-=n c c c c 的编码函数为
[][][]111000*********)(210m m m m f c ++==
生成了的8个码字如下
(3) 最小汉明距离d =2,所以可检1个错,但不能纠错。
(4) 由],[],,[)()(k n T
k n k k n k k n I A H A I G --⨯-⨯-==,得校验矩阵
⎥⎦
⎤⎢⎣⎡=1010101111H
(5) 消息序列m =000,001,010,011,100,101,110,111,由c =mGs 得码字序列
c 0=00000, c 1=00111,c 2=01010, c 3=01101, c 4=10011, c 5=10100,c 6=11001, c 7=11110
则译码表如下:
当接收到r =(11101)时,查找码表发现它所在的列的子集头为(01101),所以将它译为c =01101。
2.设(7, 3)线性码的生成矩阵如下
010101000101111001101G ⎡⎤
⎢⎥=⎢⎥
⎢⎥⎣⎦
(1)求系统生成矩阵;
(2)求校验矩阵; (3)求最小汉明距离; (4)列出伴随式表。
解:
(1)生成矩阵G 经如下行变换
13
23
01010101
0011010010111001011110011010
10101010011011
0011010010111010101001010100010111⎡⎤⎡⎤
⎢⎥⎢⎥−−−−→⎢⎥⎢
⎥⎢⎥⎢⎥⎣⎦⎣⎦
⎡⎤⎡⎤⎢⎥⎢⎥−−−−−→⎢⎥⎢
⎥⎢⎥⎢⎥⎣⎦⎣⎦
交换第、行交换第、行
得到系统生成矩阵:
100110101010100010111S G ⎡⎤
⎢⎥=⎢⎥
⎢⎥⎣⎦
(2)由],[],,[)()(k n T
k n k k n k k n I A H A I G --⨯-⨯-==,得校验矩阵为
1101000101010001100101010001H ⎡⎤⎢⎥⎢
⎥=⎢⎥
⎢⎥
⎣⎦
(3)由于校验矩阵H 的任意两列线性无关,3列则线性相关,所以最小汉明距离d =3。
(4)(7, 3)线性码的消息序列m =000,001,010,011,100,101,110,111,由c =mGs 得码字序列:c 0=0000000,c 1=0010111,c 2=0101010,c 3=0111101,c 4=1001101,c 5=1011010,c 6=1100111,c 7=1110000。
又因伴随式有
24=16
种组合,差错图样为1的有771=⎛⎫
⎪⎝⎭
种,
差错图样为2的有7212=⎛⎫ ⎪⎝⎭
种,而由T
T
Hr He =,则计算陪集首的伴随式,构造伴
随表如下:
3.已知一个(6, 3)线性码C 的生成矩阵为:
.0 1 1 1 0 01 1 0 0 1 01 0 1
0 0 1G ⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡=
(1) 写出它所对应的监督矩阵H ;
(2) 求消息M =(101)的码字;
(3) 若收到码字为101010,计算伴随式,并求最有可能的发送码字。
解:
(1)线性码C 的生成矩阵G 就是其系统生成矩阵G S ,所以其监督矩阵H 直接得出:
101100011010110001H =⎡⎤
⎢⎥⎢⎥⎢⎥⎣⎦
(2)消息M =(m 0,m 1,m 2)=(101),则码字c 为:
[][][]()100101001110101011c f m ==+=
(3)收到码字r =(101010),则伴随式
()()101011110101010001100010001T
rH ⎡⎤⎢⎥⎢⎥⎢⎥
==⎢
⎥⎢⎥⎢⎥
⎢⎥⎣⎦
又(6, 3)线性码的消息序列m =000,001,010,011,100,101,110,111,由c =mGs 得码字序列:c 0=000000,c 1=001110,c 2=010011,c 3=011101,c 4=100101,c 5=101011,c 6=110110,c 7=111000。
伴随式有23=8种情况,则计算伴随式得到伴随表如下:
伴随式(001)对应陪集首为(000001),而c=r+e ,则由收到的码字r =(101010),最有可能发送的码字c 为:c =(101011)。
4.设(6, 3)线性码的信息元序列为x 1x 2x 3,它满足如下监督方程组
⎪⎩⎪
⎨⎧=++=++=++0
00
631
532421x x x x x x x x x (1)求校验矩阵,并校验10110是否为一个码字; (2)求生成矩阵,并由信息码元序列101生成一个码字。
解:
(1)由监督方程直接得监督矩阵即校验矩阵为:
110100011010101001H =⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦
因为收到的序列10110为5位,而由(6, 3)线性码生成的码字为6位,所以10110不是码字。
(2)由],[],,[)()(k n T
k n k k n k k n I A H A I G --⨯-⨯-==,则生成矩阵为:
100101010110001011S G G =⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦
信息码元序列M=(101),由c =mGs 得码字为c :
()()()()012100101010110001011101110c m m m =++=。
